BUDOWA ATOMU

Rozwój teorii atomistycznej

John Dalton -

początek XIX wieku

Założenia:

1. Wszystkie

substancje

składają

się

z

niezmiernie

małych,

niepodzielnych

cząstek zwanych atomami, zachowujących swoją

indywidualność we wszystkich przemianach chemicznych.

2. Atomy danego pierwiastka

są identyczne pod każdym względem

(np.

mają jednakową masę). Atomy różnych pierwiastków różnią się

swoimi

właściwościami.

3.

Związki chemiczne powstają wskutek łączenia się atomów różnych
pierwiastków w określonych i stałych stosunkach liczbowych. Masy
atomów nie ulegają zmianie w czasie reakcji chemicznej.

Czy wszystkie

założenia są słuszne???

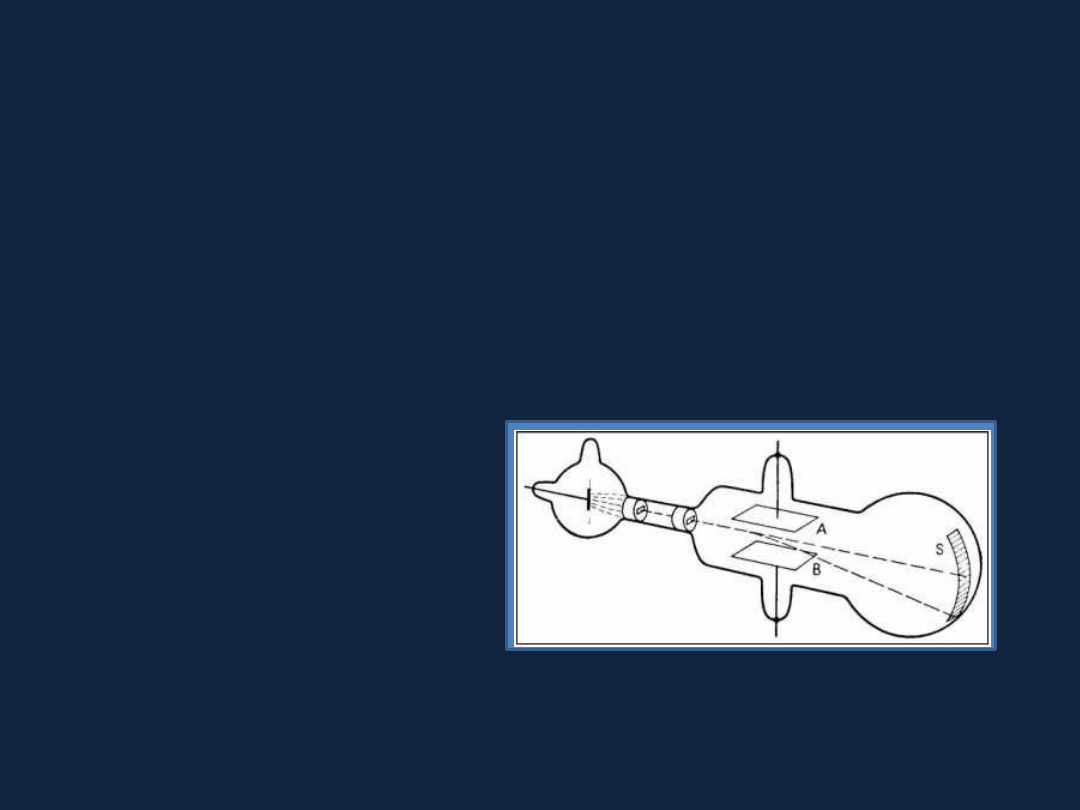
Doświadczenie J.J. Thomsona – 1897 rok

Pierwszy dowód istnienia wewnętrznej struktury atomu – odkrycie elektronu.

Badania nad promieniami katodowymi emitowanymi w warunkach próżniowych.

Stwierdzenie istnienia ujemnie
naładowanych cząstek, które
s

ą identyczne niezależnie od

materiału, z którego wykonano
katodę.

Wyznaczenie stosunku
ładunku elektronu do jego
masy e/m = 1,7588 x 10

8

C/g

Eksperymenty Roberta Millikana (1913 rok)

Wyznaczenie

ładunku elektronu

-

1.6220 x 10

-19

C

(najmniejszy

ładunek jaki udało się wykryć, wszystkie inne ładunki

stanowią wielokrotność tego ładunku – dlatego został nazwany ładunkiem
elementarnym)

Na podstawie tych i poprzednich

badań wyznaczono

masę elektronu

,

która

wynosi -

9.109 x 10

-28

g

Hipoteza dotycząca rozmieszczenia elektronów w jądrze atomowym

Atom

obojętny

elektrycznie

–

powinien

zawierać

ładunek dodatni równoważący

ujemne

ładunki elektronów .

Gdzie te

ładunki mogą być zlokalizowane ???

- model

„ciasta z rodzynkami”

Badania Ernesta Rutherforda (1908 rok)

Bombardowania cząstkami alfa (α) cienkiej folii platynowej

Rys. 1.9 str 7 Atkins1

Wyjaśnienie obserwowanych efektów – atom zawiera gęste, niemal
punktowe dodatnio

naładowane jądro, otoczone przez wielki niemal pusty

obszar, w

którym rozmieszczone są elektrony.

Jądrowy model atomu

1.

Atomy są zbudowane z cząstek subatomowych (elektrony, protony,
neutrony).

2.

Protony i neutrony tworzą zwarte, centralne ciało zwane jądrem
atomowym.

3.

Elektrony tworzą w przestrzeni chmurę otaczającą jądro.

Cząstka

Symbol

Ładunek

Masa [g]

Elektron

e

-

-1

9,109 x 10

-28

Proton

p

+1

1,673 x 10

-24

Neutron

n

0

1,675 x 10

-24

Elektron, proton i neutron

– podstawowe właściwości

Rozmiary atomu i jądra atomowego

Cząstka

Szacowany rozmiar

Atom

10

-10

m

Jądro atomowe

10

-14

– 10

-15

m

Elektron

10

-15

m

Czy to wszystko co wiemy o budowie atomu???

Jakie znamy cząstki elementarne???

Cząstkami elementarnymi nazywamy wszystkie cząstki, które są
niezbędne do wyjaśnienia własności wszystkich form materii.

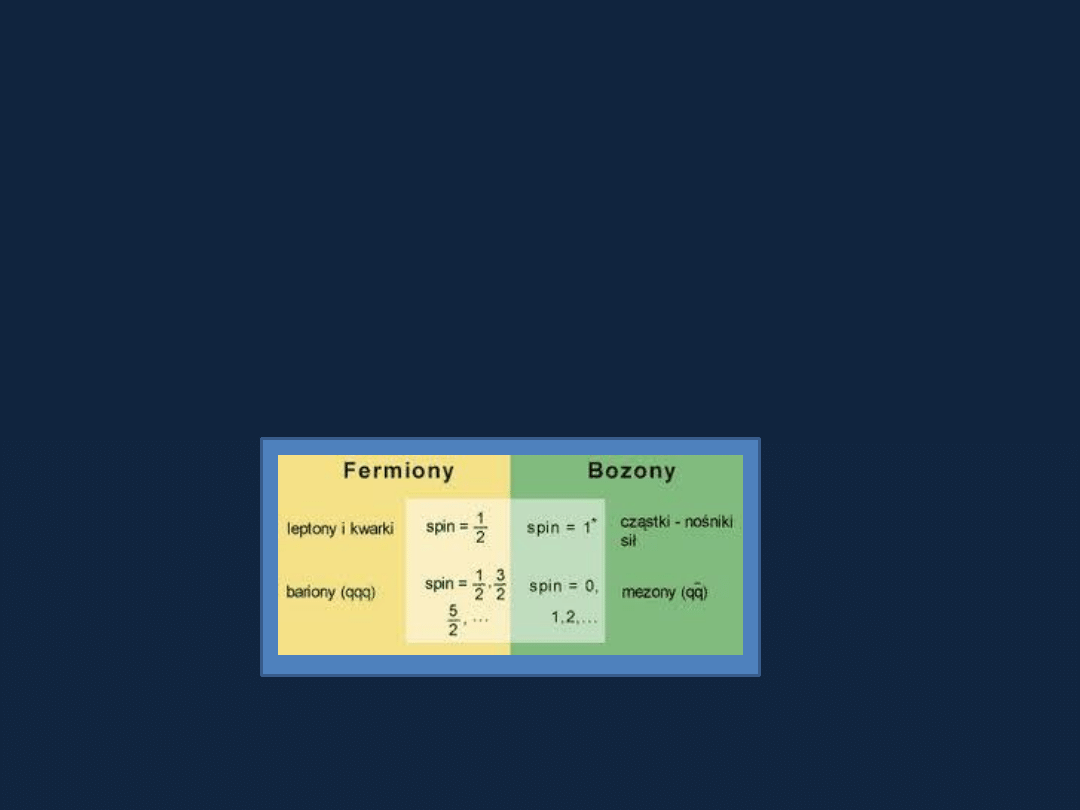
Model Standardowy zakłada istnienie:

-

12 cząstek, z których złożona jest materia – fermiony,

-

12 cząstek, które są odpowiedzialne za przenoszenie oddziaływań

między innymi cząstkami – bozony.

Od czego

zależą właściwości atomu???

Właściwości jądra

zależą od ilości

protonów i neutronów

.

Liczba

protonów

określa

ładunek elektryczny jądra

oraz decyduje o tym

jakiego rodzaju pierwiastka jest dany atom

.

Układ i ilość elektronów

wokół jądra decyduje

o przebiegu reakcji

chemicznych

z

udziałem danego atomu.

Ilość neutronów może wpływać na trwałość jądra atomowego i mieć
znaczenie np. w reakcjach

jądrowych.

LICZBA ATOMOWA I LICZBA MASOWA

Atom w normalnym stanie jest elektrycznie obojętny

l

iczba ładunków elementarnych w jądrze = liczbie elektronów

(liczba protonów = liczbie elektronów)

Liczba atomowa (Z)

– liczba dodatnich ładunków elementarnych

w atomie

Liczba masowa (A)

- liczba

nukleonów w jądrze atomowym (czyli suma

protonów i neutronów)

X

A

Z

Np.

He

4

2

O

16

8

Nukleony

– cząstki

jądra atomowego

(protony, neutrony)

IZOTOPY

Izotopy

– atomy o jednakowej liczbie atomowej (należące do tego

samego pierwiastka), lecz o

różnej liczbie masowej – ta sama liczba

protonów, różna liczba neutronów

Właściwości izotopów tego samego pierwiastka są niemal identyczne.
Większość pierwiastków posiada izotopy.
Mieszanina

izotopów danego pierwiastka występującego w przyrodzie

zachowuje zazwyczaj

stały skład.

Nuklidy

– atomy poszczególnych izotopów

H

1

1

O

16

8

Cl

35

17

D

2

1

T

3

1

O

17

8

O

18

8

Cl

37

17

Udział: 99,985% - 0,015% - 10

-16

%

Udział: 99,759% - 0,037% - 0,204%

Udział: 75,53% - 24,47%

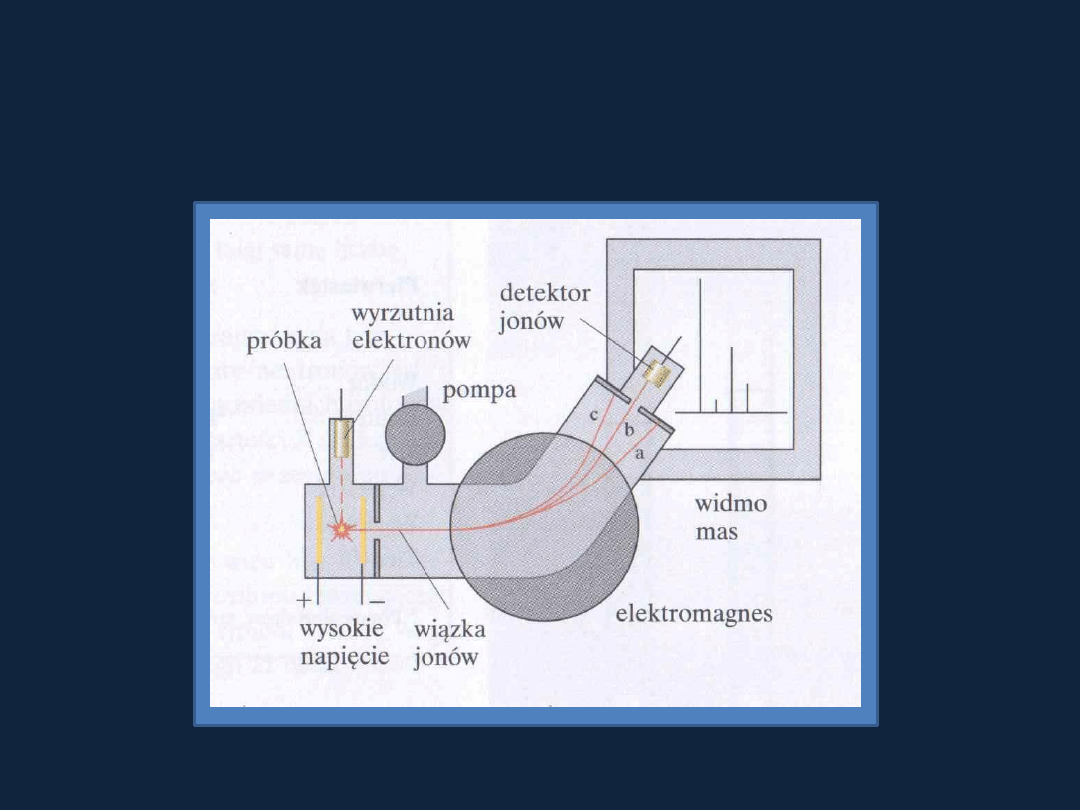
Istnienie izotopów wykazano doświadczalnie na początku XX wieku
za pomocą spektrometru mas

Rys str 11 Atkins1

MASA ATOMOWA

W celu ułatwienia porównywania mas nuklidów pochodzących od różnych
pierwiastków przyjęto jednostkę tzw. względnej masy atomowej (jednostka
masy atomowej

– j.m.a. - [u] – unit), która wynosi 1/12 część masy nuklidu

lżejszego izotopu węgla.

Względna masa atomowa

– to liczba określająca ile razy masa atomu

danego izotopu jest większa od 1/12 masy atomu węgla

12

C.

Średnia względna masa atomowa (masa atomowa)

– średnia ważona

względnych mas atomowych poszczególnych izotopów tego samego
pierwiastka.

Do obliczenia masy atomowej potrzebne są dane dotyczące:
a)

względnych mas atomowych poszczególnych izotopów,

b)

zawartości tych izotopów.

Przykład:

Węgiel

udziały poszczególnych izotopów –

12

C

– 0,989;

13

C

– 0,011

Względna masa atomowa -

12

C

– 12,000000;

13

C

– 13,003355

Średnia względna masa atomowa – A

r

Masa cząsteczkowa

– liczba określająca ile razy masa danej cząsteczki jest

większa od 1/12 masy atomu węgla

12

C.

Masa molowa

– masa jednego mola materii (jednostka np. - g/mol).

Masa atomowa i masa cząsteczkowa dotyczą pojedynczego indywiduum,
natomiast masa molowa określonej ich ilości.

A

r

= 0,989 ∙ 12,000000 + 0,011 ∙ 13,003355 = 12,011

Modele budowy

jądra atomowego

Model kroplowy

Ten model

zakłada, że nukleony w jądrze zachowują się w podobny sposób

jak

cząsteczki w kropli cieczy – dlatego właściwości jądra powinne być

podobne do

właściwości kropli cieczy.

Podobieństwa – jądro atomowe kształt kulisty, oddziaływanie jądrowe i siły
elektrostatyczne

mogą odpowiadać siłą występującym w kropli cieczy (np.

lepkość, czy napięcie powierzchniowe.
Model ten nie

wyjaśnia wszystkich zachodzących zjawisk.

Model

powłokowy

Ten model jest podobny do modelu

powłokowego układu elektronów

w atomie.
Zakłada, że nukleony poruszają się w polu jądra utworzonym przez inne
cząstki. Pole wytworzone przez nukleony zostało nazwane potencjałem
jądrowym (uśrednienie oddziaływań pomiędzy nukleonami).
J

ądra atomowe o „wypełnionych powłokach” są stabilniejsze niż jądra

sąsiednie.

Liczby

protonów, neutronów dla których wypełnione są powłoki nazwano

liczbami magicznymi.

Liczby magiczne dla protonów i neutronów to: 2, 8, 20, 28, 50, 82, 126.

Trwałość jąder atomowych

Znane jest około 270 trwałych nuklidów.

Liczba protonów

Liczba neutronów

Liczba trwałych

nuklidów

parzysta

parzysta

ponad 160

parzysta

nieparzysta

ponad 50

nieparzysta

parzysta

około 50

nieparzysta

nieparzysta

kilka

Jakie

siły działają na nukleony w jądrze?

Siły odpychania elektrostatycznego między protonami, które znajdują się
w

małych odległościach od siebie.

Jednak znamy jądra bardzo trwałe. Co równoważy ten efekt?

Siły przyciągania, które równoważą, a nawet przewyższają siły
odpychania -

są to tzw

.

siły jądrowe

– silne oddziaływania pomiędzy

nukleonami,

którym podlegają niezależnie od ich ładunku elektrycznego.

Cecha

charakterystyczną sił jądrowych – szybko zanikają w miarę

wzrostu

odległości (nie przekraczają rozmiarów jądra).

Energia wiązania nukleonów w jądrze – defekt masy

Przykład:

Beryl

– liczba atomowa – 4; liczba masowa – 9;

czyli jądro Be składa się z 4 protonów, 5 neutronów oraz 4 elektronów

Masa teoretyczna:

rodzaj i ilość

cząstek

masa [u]

masa 4 elektronów

4 ∙ 0,0005486 = 0,0021944

masa 5

neutronów

5 ∙ 1,0072764 = 4,0291056

masa 4 protonów

4 ∙ 1,0086650 = 5,0433250

masa

całkowita

= 9,0746250

Masa oznaczona eksperymentalnie (rzeczywista) wynosi

– 9,01218 [u]

Różnica: m

teoret.

– m

rzecz.

= 0,0624 [u] ???

Teoria

względności Einsteina

mówi, że w przyrodzie mogą zachodzić

procesy, w

których masa układu może ulec zmianie nie tylko na skutek

wymiany substancji z otoczeniem, ale wskutek wymiany energii.

E = mc

2

W analizowanym przypadku

różnica masy wynosi 0,0624 [u].

1 mol berylu (ok. 9 g)

– energia ok. 5,6 x 10

12

J

– co jest równoważne

energii

powstałej ze spalenia ponad 168 ton węgla.

Defekt (deficyt) masy

– różnica pomiędzy teoretyczną i rzeczywistą

masą atomu równoważna energii sił spajających jądro atomowe (energii
wiązania jądra).

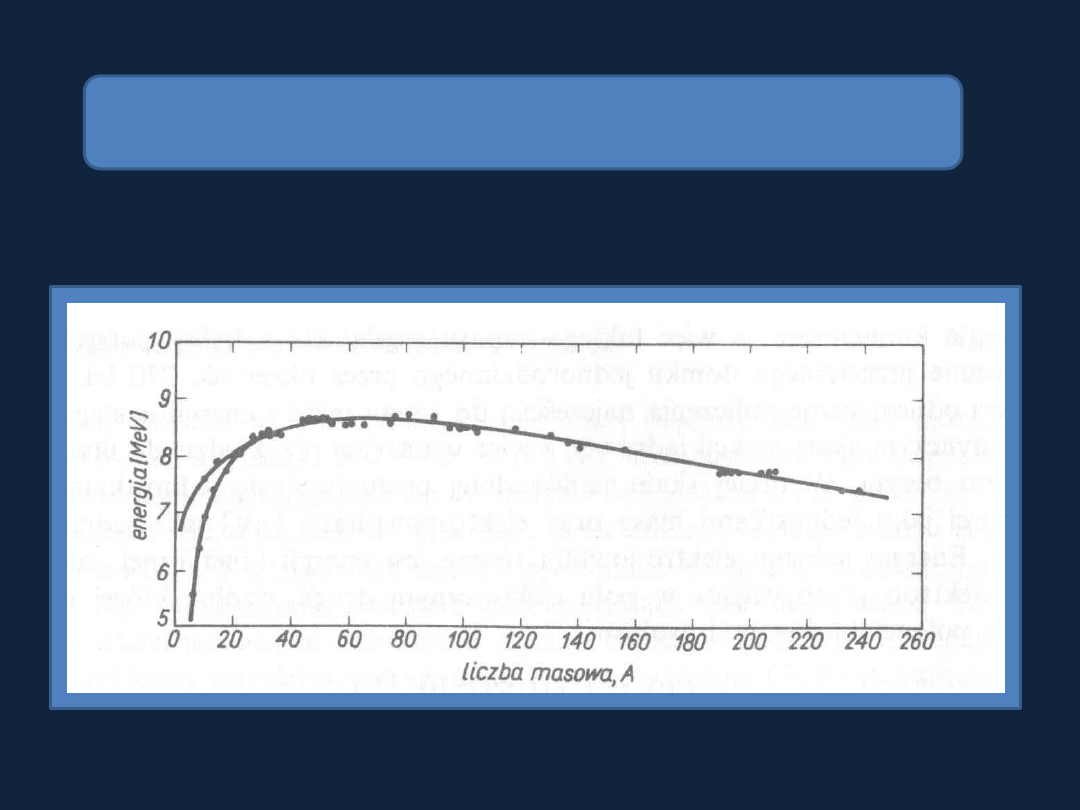
Zależność energii wiązania nukleonów w jądrze

od liczby masowej pierwiastka

Rys. 2.1 str 32
Bielanski1

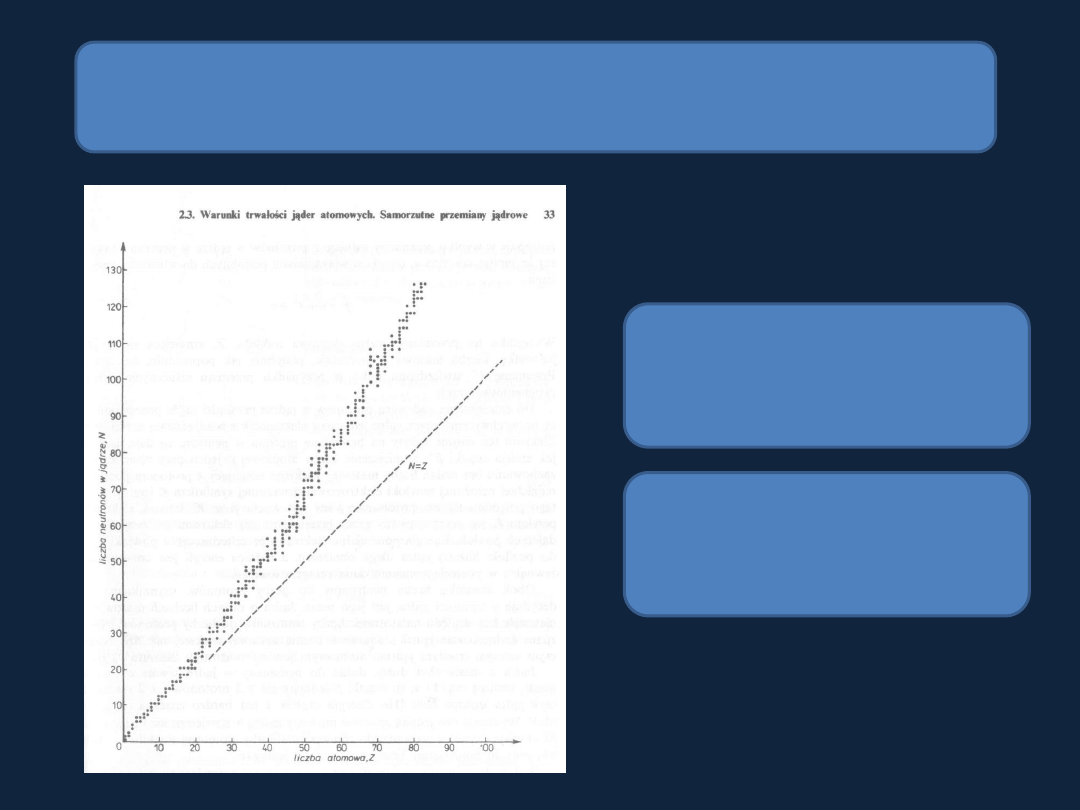
Zawartość neutronów w trwałych jądrach atomowych w zależności

od liczby atomowej pierwiastków

Małe liczby atomowej -

stosunek neutronów do

protonów (n/p) jest bliski 1

W przypadku wyższych

liczb atomowych stosunek

n/p nie przekracza 1,6

Rys. 2.2 str
33 Bielański

Przemiany jąder atomowych

Część jąder atomowych jest nietrwałych i może ulegać różnego rodzaju
przemianom

jądrowym.

Przemiany

jądrowe mogą być spowodowane oddziaływaniami wewnątrz

jąder atomowych lub oddziaływaniami z cząstkami elementarnymi (np.
neutronem).

Przemiany

jądrowe można podzielić na:

1) reakcje syntezy - w tym przypadku z

jąder lżejszych powstają jądra,

które posiadają większą liczbę atomową lub liczbę masową

2) reakcje rozpadu

– liczby atomowe lub liczby masowe produktów są

mniejsze

niż liczby atomowe lub liczby masowe produktów (dochodzi

do rozpadu

jąder na mniejsze)

Jakie

są cechy charakterystyczne reakcji jądrowej?

Jądra atomowe pierwiastków przekształcają się w jądra atomowe
innych

pierwiastków, innych izotopów tego samego pierwiastka lub

przechodzą na inny stan energetyczny.

W

reakcję

jądrową

są

zazwyczaj

zaangażowane

cząstki

elementarne (np. protony, neutrony), a przebieg reakcji jest
związany z emisją bądź uwolnieniem bardzo dużej ilości energii.

W

przeciwieństwie do reszty reakcji chemicznych nie obserwuje się

wpływu temperatury lub ciśnienia na szybkość reakcji jądrowej.

Promieniotwórczość i rodzaje promieniowania

Zjawisko

promieniotwórczości

jest

związane ze zdolnością jąder

atomowych do rozpadu

promieniotwórczego, w wyniku którego

obserwuje

się

emisję promieniowania

:

1)

cząstek alfa (α)

2)

cząstek beta (β) – elektronów lub pozytonów

3) promieniowania gamma

(γ) o wysokiej energii

Rozpad typu alfa (

α)

Reakcja

jądrowa, której wynikiem jest powstanie lżejszego jądra

atomowego oraz emisja

cząstki alfa – czyli jądra atomu helu

4

2

He

2+

X

A

Z

Y

A-4

Z-2

He

2+

4

2

+

U

238

92

Th

234

90

He

2+

4

2

+

Rozpad typu

(β)

Reakcja

jądrowa, której wynikiem jest otrzymanie jądra atomowego o

liczbie atomowej o jeden

większej lub mniejszej w stosunku do jądra

pierwotnego

Rozpad

β

-

W wyniku tej przemiany neutron zostaje

zastąpiony protonem, dodatkowo

obserwuje

się powstanie elektronu i antyneutrino elektronowego

Rozpad

β

+

Wynikiem tego rozpadu jest w

przeciwieństwie do poprzedniego

przypadku przemiana protonu w neutron, obserwuje

się również

powstanie pozytonu i neutrino

X

A

Z

Y

A

Z+1

+

elektron

+

antyneutrino

X

A

Z

Y

A

Z-1

+

pozyton

+

neutrino

Emisja promieniowania

(γ)

Proces, w

którym emitowane jest wyłącznie promieniowanie gamma

(promieniowanie elektromagnetyczne). Nie obserwuje

się emisji innych

cząstek. Liczba atomowa i liczba masowa pierwiastka pozostaje bez
zmian. Zmienia

się jedynie stan energetyczny jądra atomowego.

Może następować po rozpadzie alfa lub beta, po których jądro
znajduje

się w stanie wzbudzonym i jest związane z powrotem jądra

atomowego do stanu podstawowego o

niższej energii.

X

A

Z

Y*

A

Z+1

+

elektron

+

antyneutrino

Y*

A

Z+1

Y

A

Z+1

+

γ

Szybkość rozpadu promieniotwórczego

Szybkość rozpadu nietrwałych jąder atomowych danego pierwiastka jest
proporcjonalna do

ilości jeszcze nie rozłożonych atomów.

Szybkość rozpadu promieniotwórczego można przedstawić za pomocą
następującego równania:

λN = - (ΔN / Δt)

gdzie: N

– liczba nierozłożonych atomów pierwiastka, ΔN – liczba

przedstawiająca ubytek atomów (ze względu na ich rozpad) w przedziale
czasu

Δt, λ – stała rozpadu promieniotwórczego.

Przekształcając powyższe równanie, możemy obliczyć liczbę atomów
N

pozostającą po określonym czasie t:

N = N

0

∙ e

-

λt

gdzie: N

0

– początkowa liczba atomów pierwiastka radioaktywnego

Korzystając z przedstawionych wcześniej zależności można obliczyć
tzw

. okres

półtrwania izotopu promieniotwórczego – T

1/2

Jest to czas, w

którym ulega rozpadowi połowa ilości danego izotopu

Zakładając, że t = T

1/2

oraz N = N

0

/2, otrzymujemy:

T

1/2

= ln

2 / λ

Okres

półtrwania nie zależy od ilości początkowej izotopu.

Jest to

wielkość używana do charakteryzowania szybkości rozkładu

promieniotwórczego.

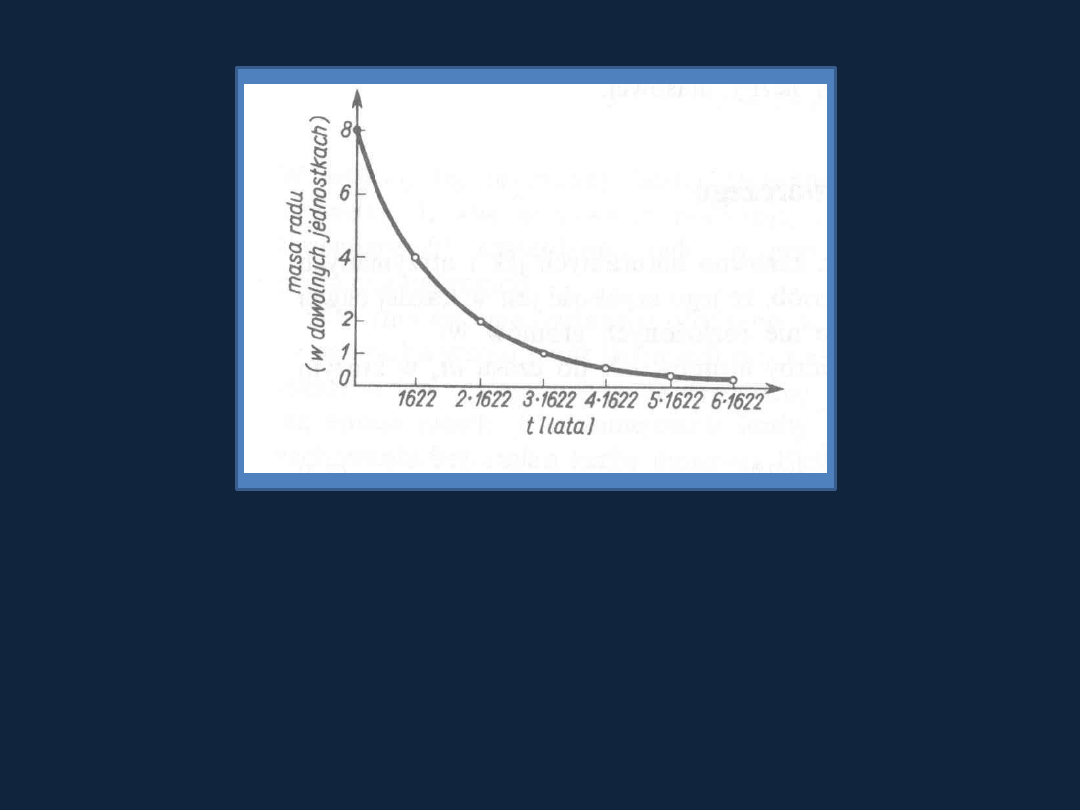
Rys. 2.3 str 36
Bielan1

Wartości jakie może przyjmować okres półtrwania różnych nuklidów
wahają się w szerokich granicach, np.:

U

238

92

Po

214

84

- 4,51 x 10

9

lat

- 1,62 x 10

-4

s

Reakcje

łańcuchowe

Następuje rozszczepienie jąder atomowych w wyniku których
następuje emisja cząstek elementarnych biorących udział w rozpadzie
kolejnych

jąder.

gdzie: n-neutron, X, Y

– jądra atomów powstałych podczas rozpadu

Liczby masowe

produktów rozpadu przyjmują wartości od 72 do 161

(w produktach rozszczepienia uranu wykryto

około 300 izotopów 37

różnych pierwiastków).

U + n

X + Y + (2-3)n

235

92

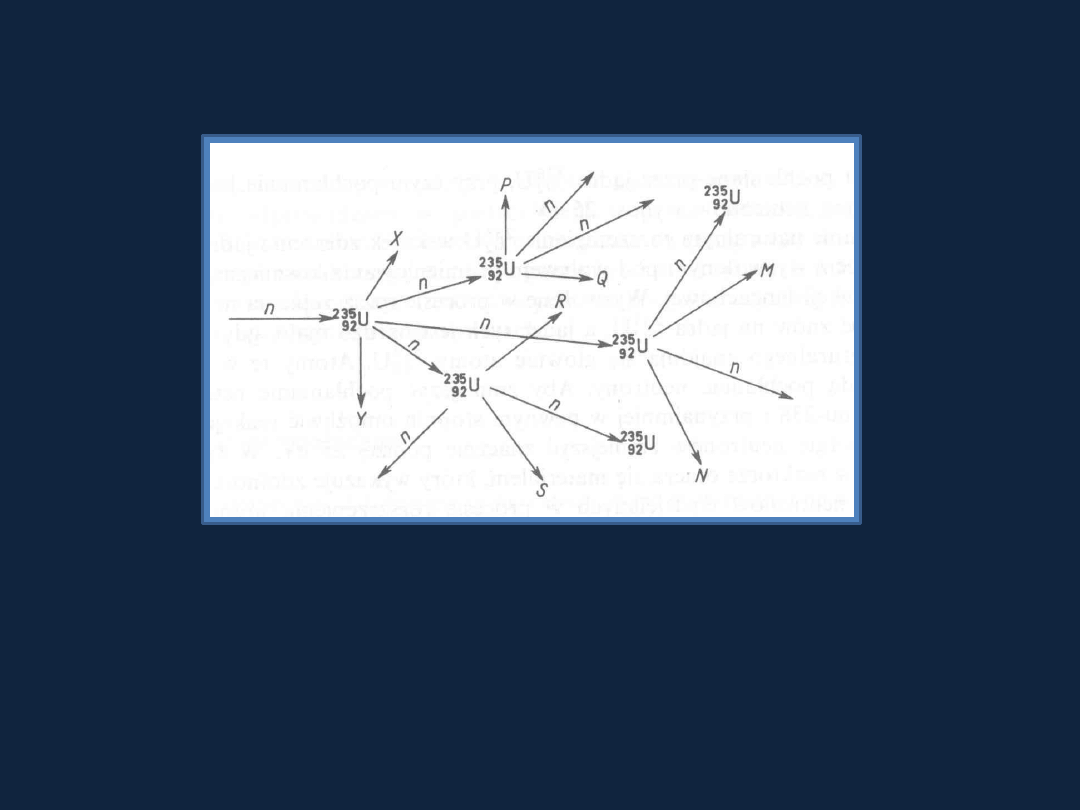
Rys 2.9 str 47 Bielan1

Łańcuchowa reakcja rozpadu jąder uranu

235

U.

Ruda uranowa zawiera 99,3% izotopu

238

U

– niezbędne wzbogacanie

Masa krytyczna

235

U

– ok. 20 kg

Rozszczepienie 1g izotopu

235

U

– energia powstała ze spalenia ok. 2500 kg

węgla

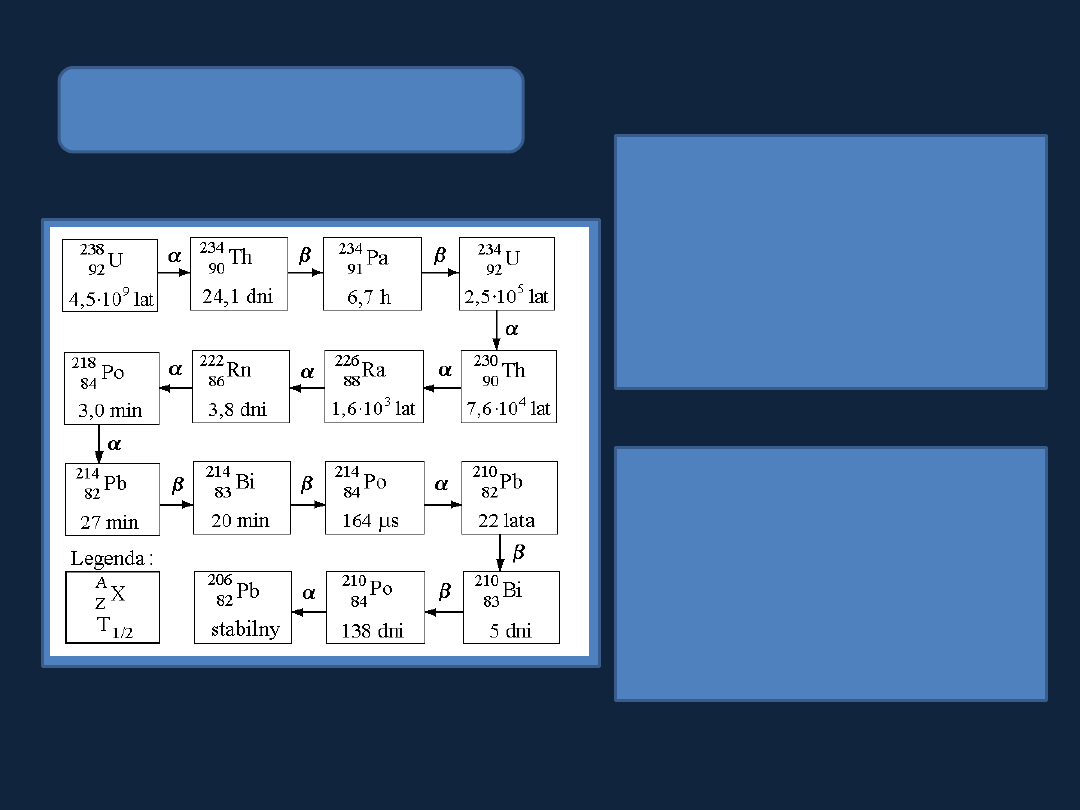
Szeregi

promieniotwórcze

Szereg uranowo-radowy

Wśród pierwiastków występujących
w przyrodzie

wyróżnia się 3 szeregi

promieniotwórcze: uranowo-radowy
(wywodzący się od izotopu

238

U),

uranowo-aktynowy

(wywodzący się

od

izotopu

235

U)

i

torowy

(wywodzący się od izotopu

232

Th).

Każdy

szereg

rozpoczyna

się

nuklidem

stosunkowo

trwałym,

zanikającym wolniej niż inne nuklidy
stanowiące ogniwa szeregu i kończy
się nuklidem niepromieniotwórczym,
który

nie

ulega

już

dalszym

przemianom.

ELEKTRONOWA

STRUKTURA ATOMU

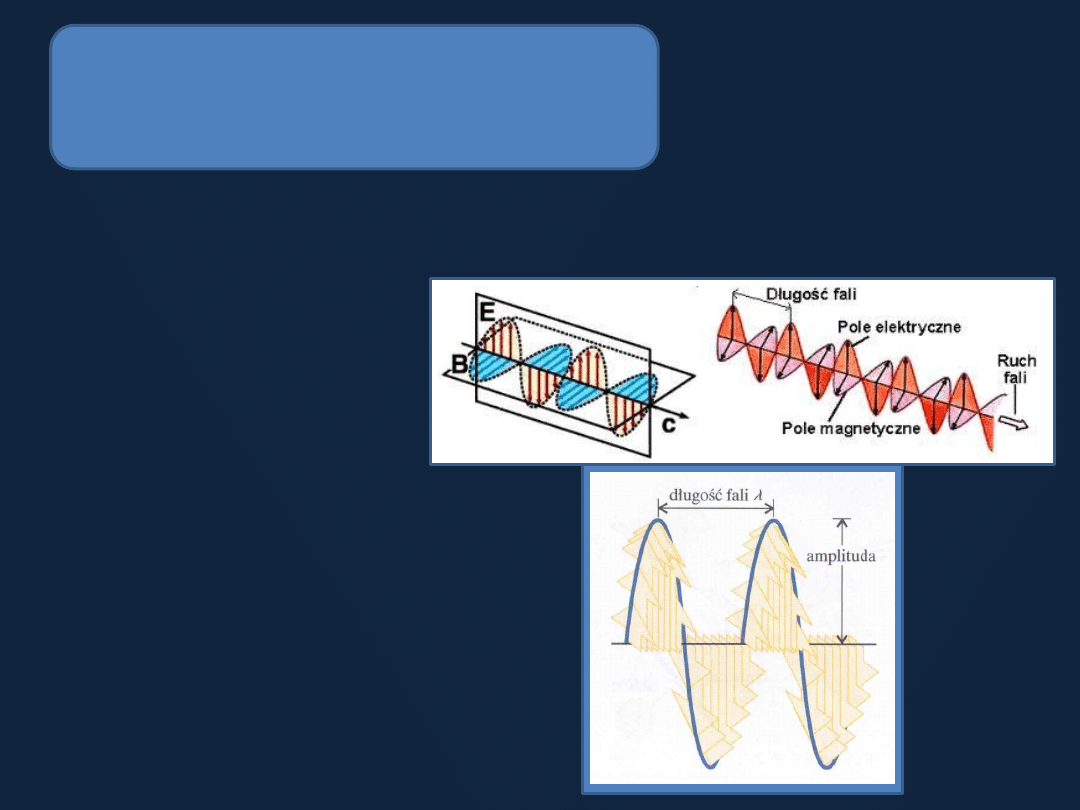
Dwoista natura światła i elektronów
(dualizm korpuskularno-falowy)

Światło - promieniowanie elektromagnetyczne jest falą charakteryzowaną
przez częstość i amplitudę.

Rys. 7.4 str
282 Atkins
lub
podobny

Częstość – liczba cykli
całkowitych zmian kierunku
fali

Jednostka

– herc (Hz)

1 Hz = 1/s

Częstość promieniowania
widzialnego

– rząd 10

14

Hz

Światło:
zielone 5,7x10

14

Hz,

żółte 5,2x10

14

Hz,

czerwone 4,3x10

14

Hz

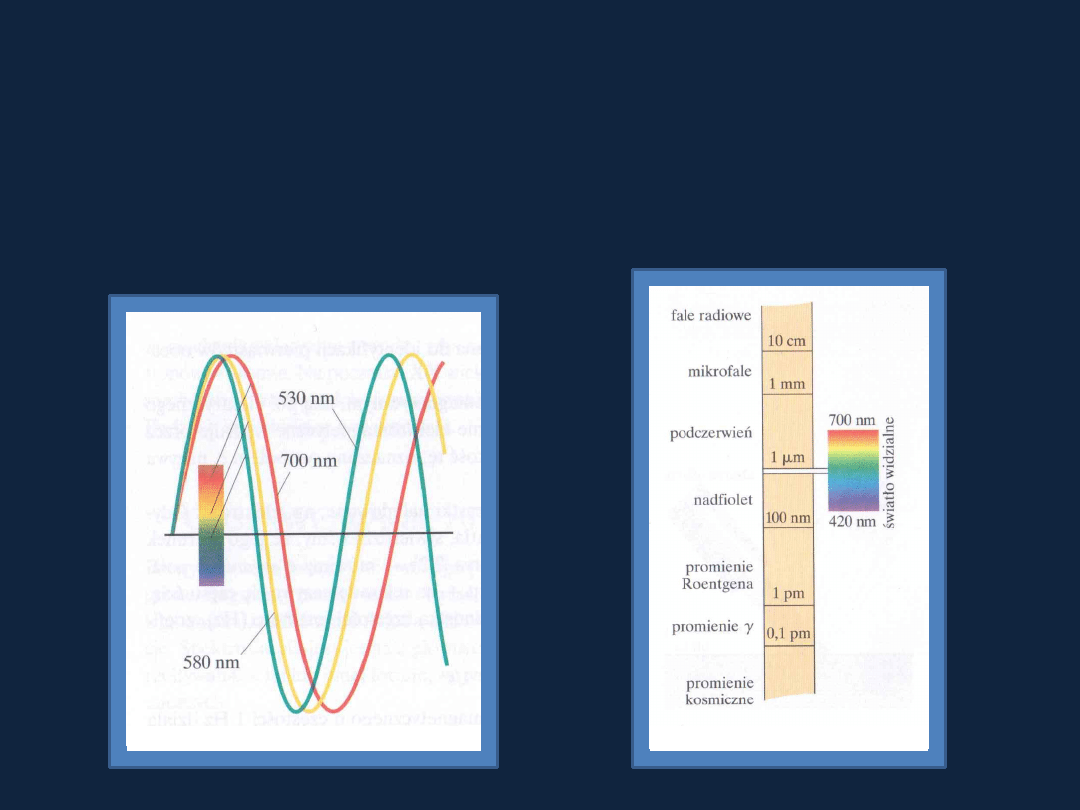
Rys. 7.3 a
str 282
Atkins

Rys. 7.6
str 283
Atkins

Zależność pomiędzy długością fali i częstością:

λ ∙ ν = c

gdzie:

λ – długość fali, ν – częstość, c - prędkość

Teoria kwantowa Plancka

Mechanika klasyczna

mówi o tym, że promieniowanie i materia mogą

mieć

dowolną

energię

–

nie

tłumaczy

to

jednak

wyników

eksperymentów dla małych obiektów takich jak elektrony.

Mechanika kwantowa

– może wyjaśniać zachowanie takich obiektów.

Promieniowanie elektromagnetyczne przenosi

energię w przestrzeni.

Światło jest emitowane nie w sposób ciągły, ale małymi porcjami, które
nazwano fotonami.

Energia fotonu jest proporcjonalna do częstości promieniowania:

E = h

∙ ν

gdzie: E

– energia fotonu, ν – częstość, h – stała Plancka

wartość h wynosi: 6,63 ∙ 10

-34

J

∙ s

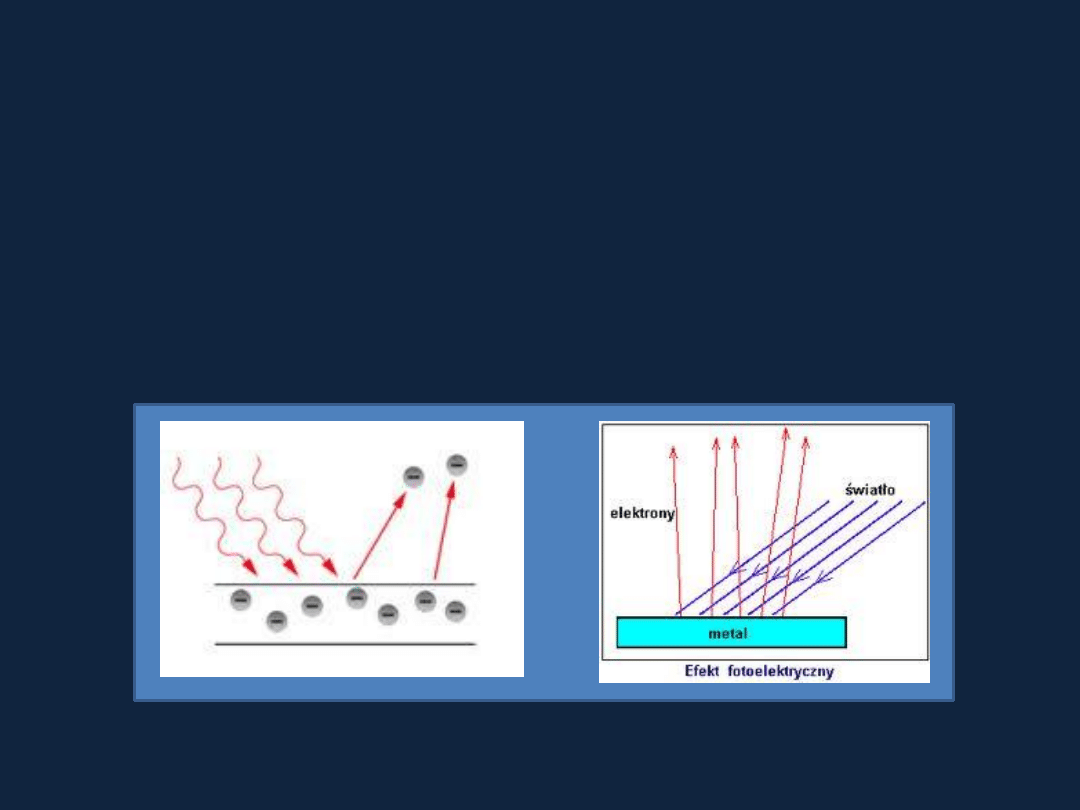
Rys. efekt
fotoelektryczny
z internetu

Z

równania wynika, że im większa jest częstość i tym samym mniejsza

długość fali tym większą energię niosą fotony promieniowania.

Dlatego np. promieniowanie w zakresie nadfioletu jest bardziej
szkodliwe dla

człowieka i może powodować poparzenia słoneczne.

Jeszcze

większą energię mają fotony promieniowania rentgenowskiego.

Efekt fotoelektryczny

Emisja elektronów z metalu, na którego powierzchnię działa promieniowanie
elektromagnetyczne.

Emisja

elektronów następuje przy określonej długości promieniowania

(dostatecznie

duża energia fotonu, żeby nastąpiła emisja elektronu).

Gdy energia

fotonów rośnie powyżej wartości progowej wzrasta

energia kinetyczna emitowanych

elektronów.

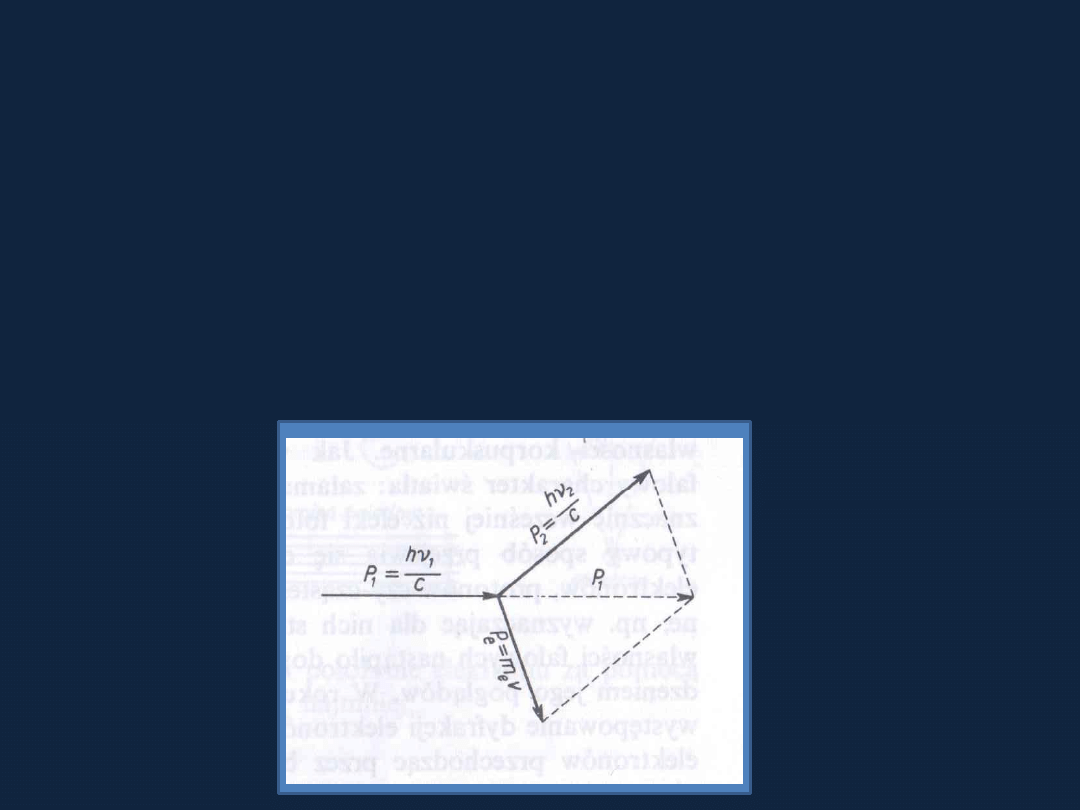
Efekt Comptona

Charakter korpuskularny
Zderzenie fotonu ze swobodnym elektronem

Rys. 3.3. str 59
Bielan

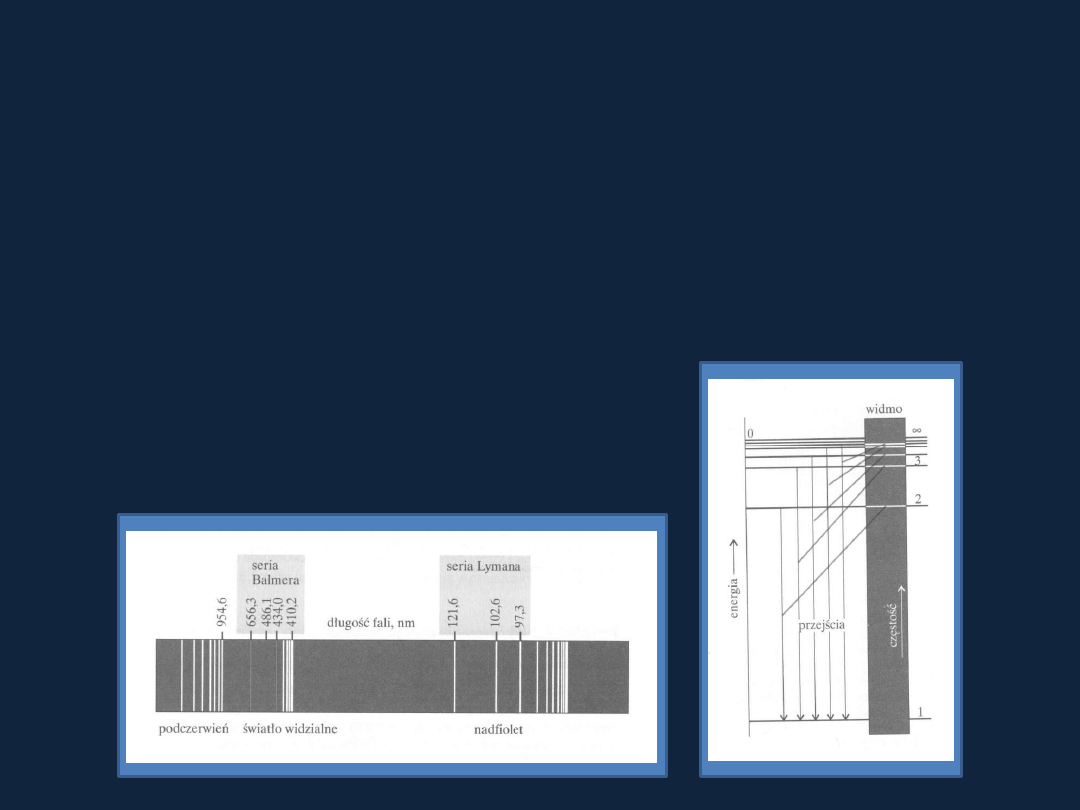
Widmo emisyjne wodoru

Atom emituje promieniowanie tylko przy

niektórych częstościach.

W atomie elektron

może występować tylko w określonych stanach

energetycznych

– poziomy energetyczne.

Przejściu elektronu z jednego poziomu na niższy towarzyszy emisja
energii

odpowiadającej różnicy tych poziomów w postaci fotonu

promieniowania.

Energia takiego fotonu -

E = h

ν

Rys. 7.9 str 286
Atkins

Hipoteza

Louis’a de Broglie’a

Wszelka materia wykazuje właściwości falowe

λ = h/mv = h/p

gdzie:

λ – długość fali, h – stała Plancka, m – masa, v – prędkość, p - pęd

Zgodnie ze wzorem

pęd fotonów (duża prędkość, mała masa) jest z reguły

mniejszy

niż pęd elektronów (mniejsza prędkość, ale większa masa) –

dlatego

fotonom

odpowiadają większe długości fali niż elektronom

– w przypadku fotonów dostrzega się bardziej ich właściwości falowe,
a

elektronów właściwości korpuskularne.

Davisson i Germer

– eksperyment potwierdzający hipotezę de Broglie’a

Elektrony

ugięte na krysztale dają obraz dyfrakcyjny na płycie

fotograficznej. Obraz ten odpowiada wynikowi

obliczeń wykonanych na

podstawie

równania de Broglie’a.

Rys. na str
289 góra
Atkins

Zasada

nieoznaczoności Heisenberga

Nie

można określić jednocześnie położenia (x) i pędu cząstki (p).

Δx ∙ Δp ≥ h

Im

dokładniejszy pomiar pędu, tym mniej dokładny pomiar położenia

cząstki i odwrotnie.

W rezultacie zamiast

określać dokładne położenie cząstki zakłada się

istnienie

określonego

prawdopodobieństwa

napotkania

cząstki

w danym miejscu przestrzeni.

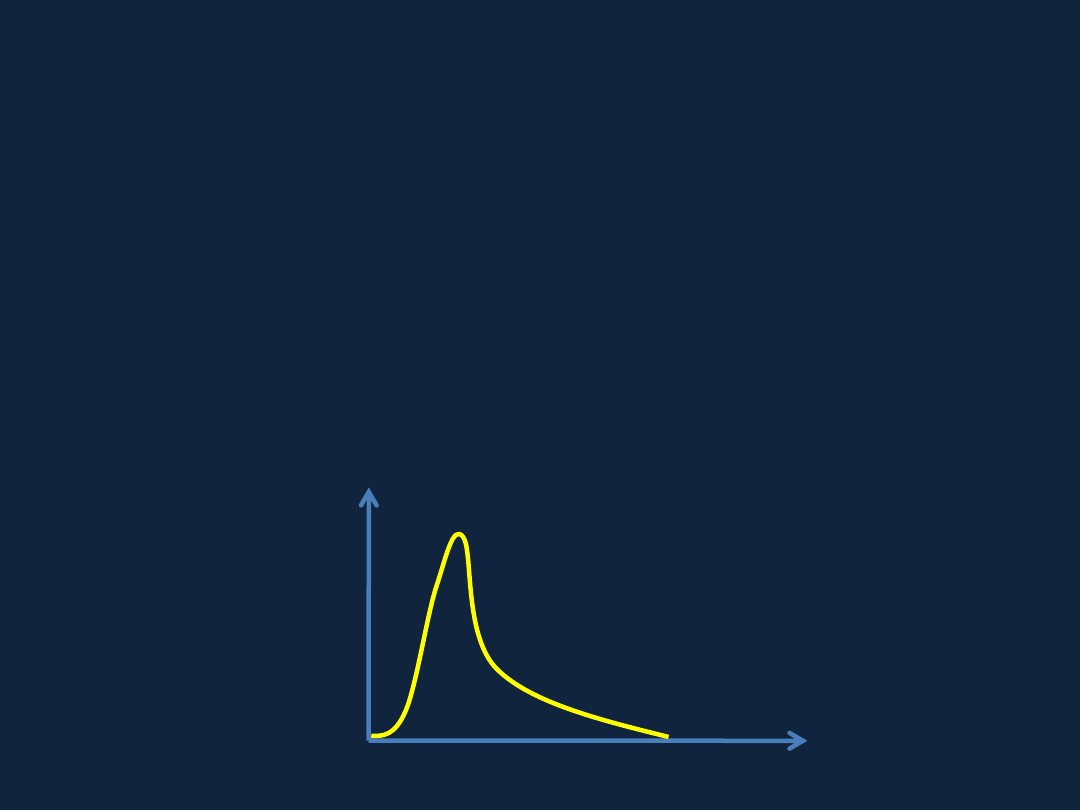
Gęstość prawdopodobieństwa napotkania elektronu (ϱ)

ϱ = W/dv

gdzie: W

– prawdopodobieństwo, v – objętość

W =

ϱ ∙ dv

ϱ = ϱ (x, y, z)

– gęstość jest zależna od miejsca

∫

ϱ ∙ dv = 1

całka prawdopodobieństwa napotkania cząstki
w całej przestrzeni wynosi 1

v

Odległość

Gęstość
prawdopodobieństwa

1s

Funkcje falowe i równanie Schrödingera

Równanie str. 64
Bielan

Ψ (psi) – amplituda fali
x, y, z

– współrzędne położenia elektronu w przestrzeni

E

– całkowita energia elektronu

V

– energia potencjalna elektronu

Rozwiązaniem równania Schrödingera są funkcje, które umożliwiają
obliczenie kształtu fali związanej z dowolną cząstką.

Fale mogą występować tylko dla pewnych wartości energii – poziomy
energetyczne elektronów.

Kwadrat

amplitudy

fali

elektronowej

jest

proporcjonalny

do

gęstości

prawdopodobieństwa znalezienia elektronu w danej objętości.

W =

ϱ (x, y, z) ∙ dv = [Ψ(x, y, z)]

2

Orbital

– funkcja falowa będąca rozwiązaniem równania Schrödingera dla

elektronu

znajdującego się na jednej z powłok elektronowych.

O orbitalu

mówimy, kiedy mamy na myśli obszar tzw. „chmury elektronowej”,

w

którym prawdopodobieństwo napotkania elektronu jest bardzo duże (0,9).

Energia i

kształt orbitalu zależą od energii oddziaływania elektromagnetycznego

z

jądrem atomowym i pozostałymi elektronami oraz energii danego elektronu.

Dostarczenie dodatkowej energii z

zewnątrz będzie skutkowało wzbudzeniem

elektronów (przeniesieniem ich na wyższy stan energetyczny) lub jonizacją
atomu (emisja elektronu).

Energia elektronu

– liczby kwantowe

Główna liczba kwantowa – n

Określa energię elektronu – średnią odległość od jądra atomowego – tym
samym informuje o rozmiarze orbitalu.

Im

wyższa wartość n, tym większa energia orbitalu i tym słabiej związany

elektron w atomie.

n = 1, 2, 3, 4

… (oznaczenie – K, L, N, M…)

Orbitalna (poboczna) liczba kwantowa

– l

Określa kształt orbitalu.

l - przyjmuje

wartości od 0 do 1-n (oznaczenie – s, p, d, f…)

Magnetyczna liczba kwantowa

– m

Informuje o orientacji przestrzennej orbitalu (określa kierunek).

Przyjmuje wartości od –l do l

Spinowa liczba kwantowa

Określa stan spinowy elektronowy (związana z ruchem wirowym)

Przyjmuje wartości -1/2 lub +1/2

Przykład:

Atom pierwiastka znajdującego się w 2 okresie układu okresowego
Głowna liczba kwantowa n = 1 i 2
Poboczna liczba kwantowa l = 0 (dla n = 1) i l = 0 i 1 (dla n = 2)
Magnetyczna liczba kwantowa m = 0 (dla n = 1) oraz m = 0 (dla n = 2 i l = 0)
oraz m = -1, 0, 1 (dla n = 2 i l =1)
Każdej wartości m odpowiada możliwość obsadzenia powłoki przez
2 elektrony o różnym spinie -1/2 lub +1/2.

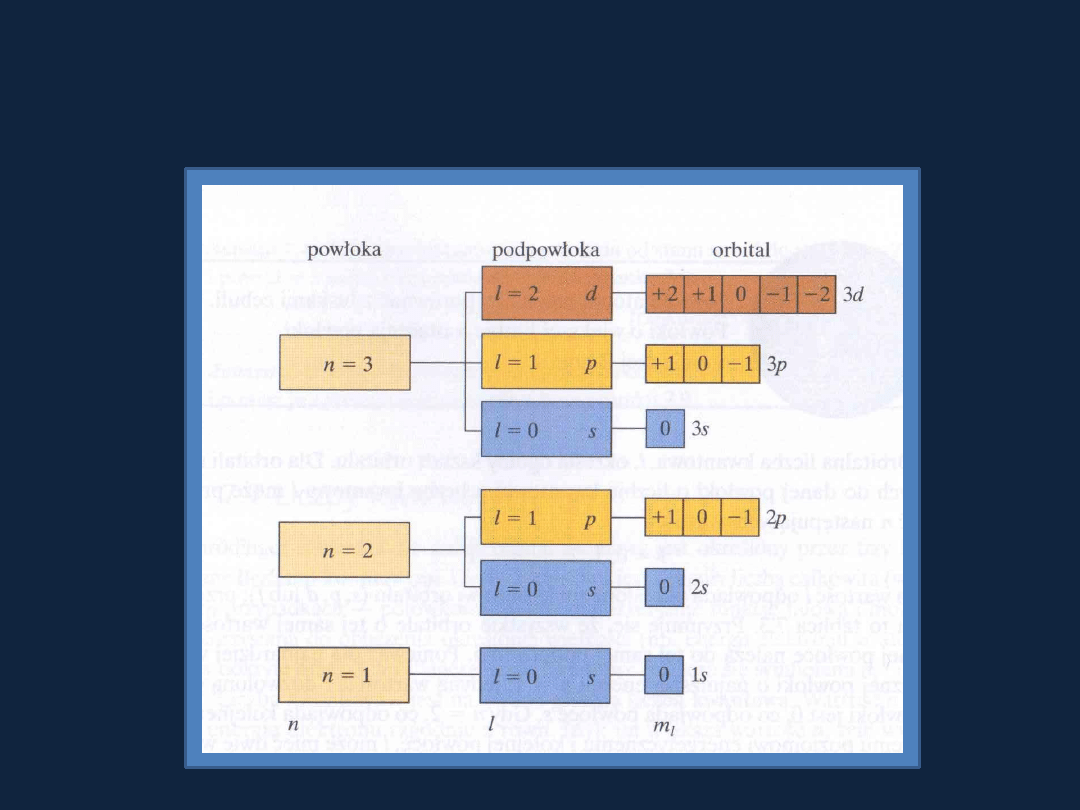
Układ powłok, podpowłok i orbitali w atomie oraz ich powiązanie

z wartościami liczb kwantowych

Rys. 7.23 str 296 Atkins

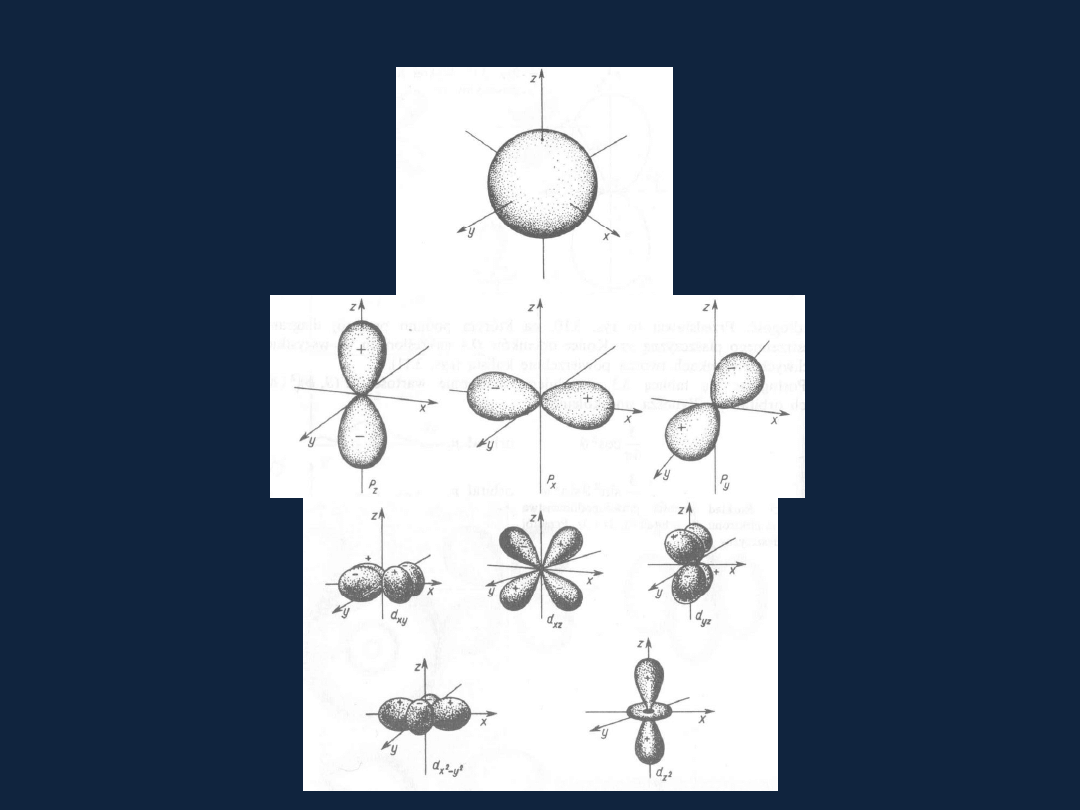
Kształt orbitali

Rys z Bielańskiego od str 75

Rys 3.11
3.13
3.14

Orbital s

Orbitale p

Orbitale d

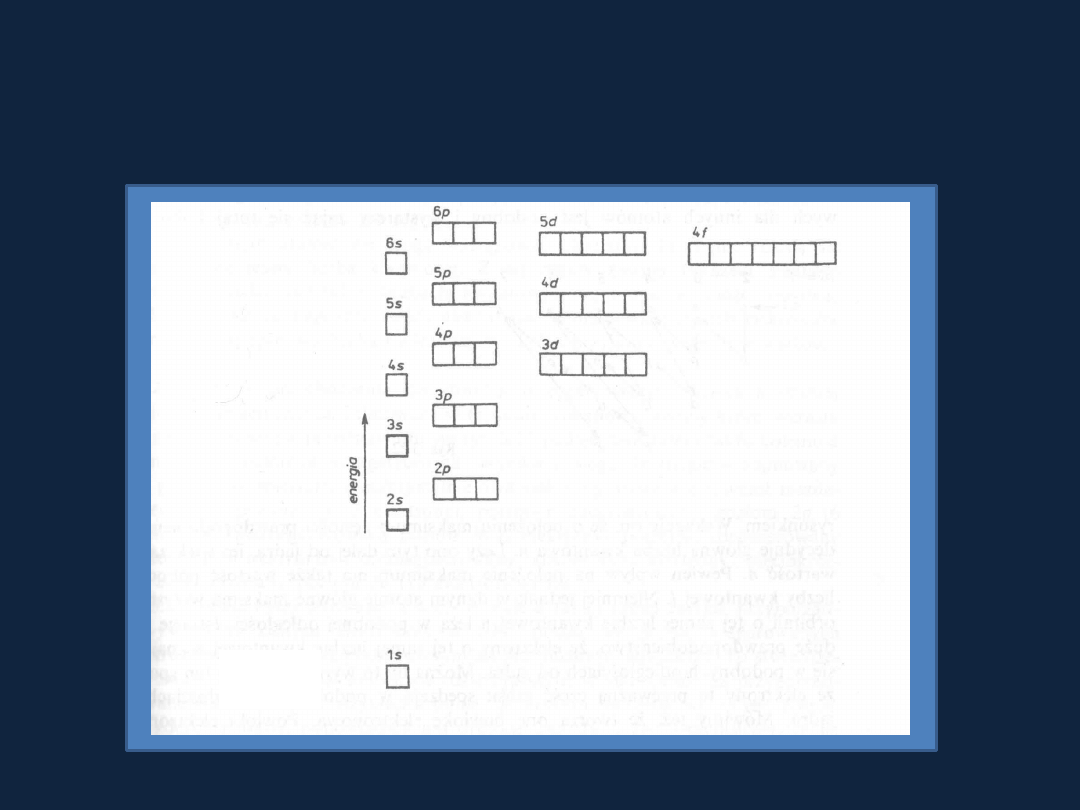
Schemat poziomów energetycznych w atomach wieloelektronowych

Rys. 3.21 str 87
Bielanski

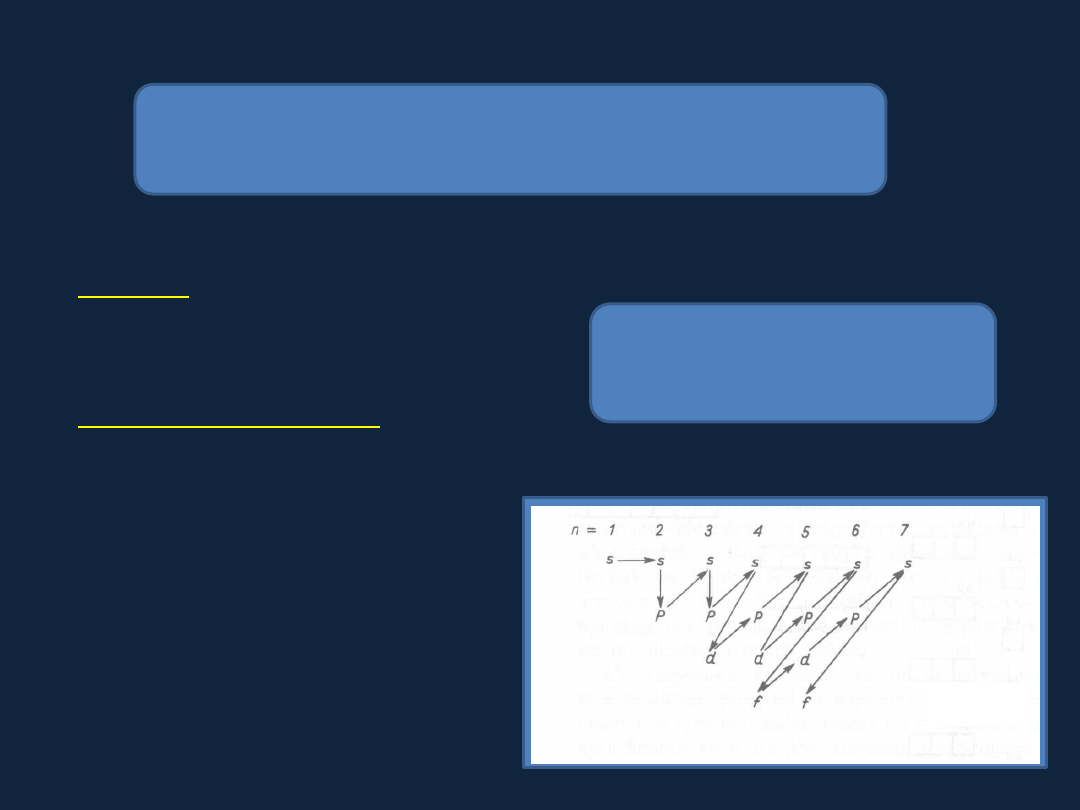
Zasady rozbudowy powłok elektronowych

Przykład:
Brom

–

35

Br

- liczba atomowa 35,

4 okres, 17 grupa układu okresowego

Konfiguracja elektronowa

1s

2

2s

2

2p

6

3s

2

3p

6

4s

2

3d

10

4p

5

(informacja dotyczy

– typu orbitalu,

poziomu energetycznego

podpowłoki

oraz liczby elektronów na podpowłoce)

Rys. 3.22 str.
88 Bielan

Schemat kolejności rozbudowy
powłok elektronowych

Na początku zapełniane są

orbitale o najniższej energii

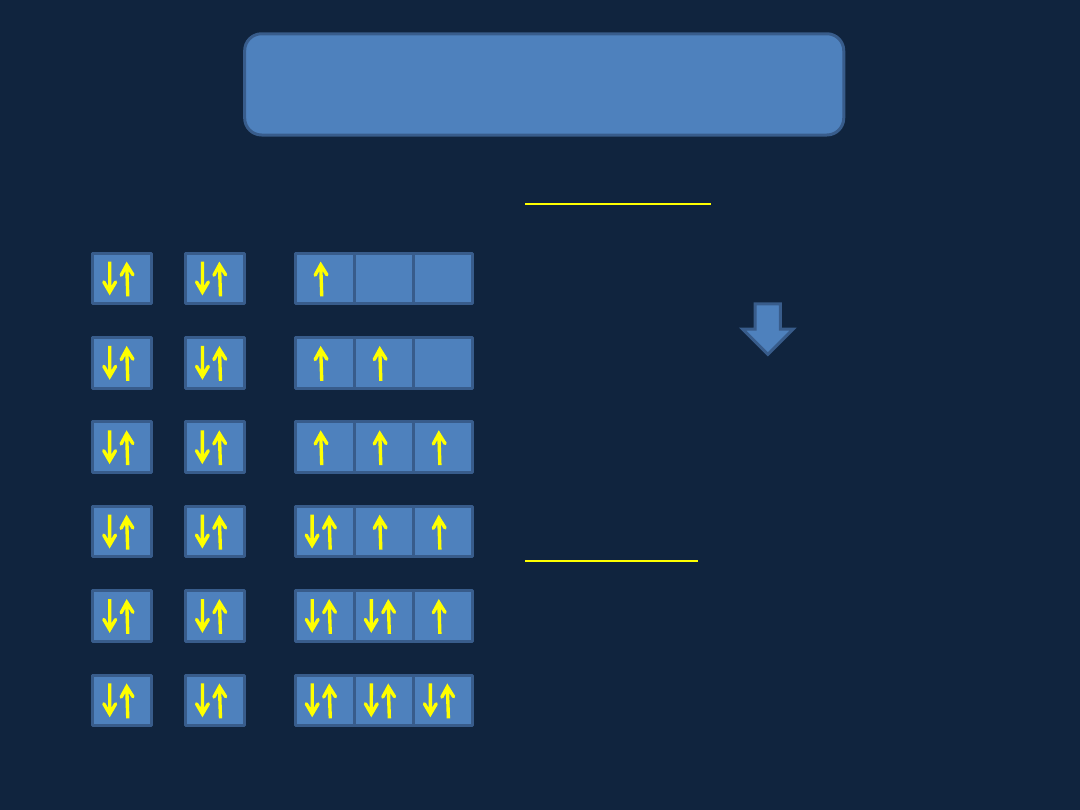
Zakaz Pauliego

i Reguła Hunda

B

C

N

O

F

Ne

1s 2s

2p

Zakaz Pauliego

W atomie nie mogą występować atomy,
które nie różnią się przynajmniej jedną
liczbą kwantową.

Dowolny orbital może być obsadzony
przez najwyżej 2 elektrony.
Gdy elektrony zajmują ten sam orbital,
ich spiny muszą być sparowane.

Reguła Hunda

Orbitale o tej samej energii
przyporządkowywane są kolejnym
elektronom, tak aby liczba
niesparowanych elektronów była jak
największa.

Obsadzanie

powłok elektronowych – metale bloku d

Stwierdzono,

że w przypadku metali przejściowych atom ma mniejszą

energię jeżeli podpowłoka 3d jest zapełniona w połowie (d

5

) lub

całkowicie

(d

10

).

Dążenie

do

takiej

konfiguracji

objawia

się

przeniesieniem jednego z

elektronów z podpowłoki 4s, np.:

24

Cr

– 1s

2

, 2s

2

, 2p

6

, 3s

2

, 3p

6

, 4s

1

, 3d

5

29

Cu

– 1s

2

, 2s

2

, 2p

6

, 3s

2

, 3p

6

, 4s

1

, 3d

10

Podobną sytuację obserwujemy również dla innych pierwiastków, np.:

46

Pd - 1s

2

, 2s

2

, 2p

6

, 3s

2

, 3p

6

, 4s

2

, 3d

10

, 4p

6

, 4d

10

47

Ag - 1s

2

, 2s

2

, 2p

6

, 3s

2

, 3p

6

, 4s

2

, 3d

10

, 4p

6

, 5s

1

, 4d

10