
Część 1
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
1
POLITECHNIKA POZNAŃSKA
INSTYTUT KONSTRUKCJI BUDOWLANYCH
ZAKŁAD MECHANIKI BUDOWLI
ĆWICZENIE NR 2
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
OD OBCIĄŻENIA RZECZYWISTEGO.
SPRAWDZENIE RÓWNANIA RÓŻNICZKOWEGO
Agnieszka Sysak
Gr 3
Agnieszka Sysak Gr 3
2004-04-19
Część 1
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
2
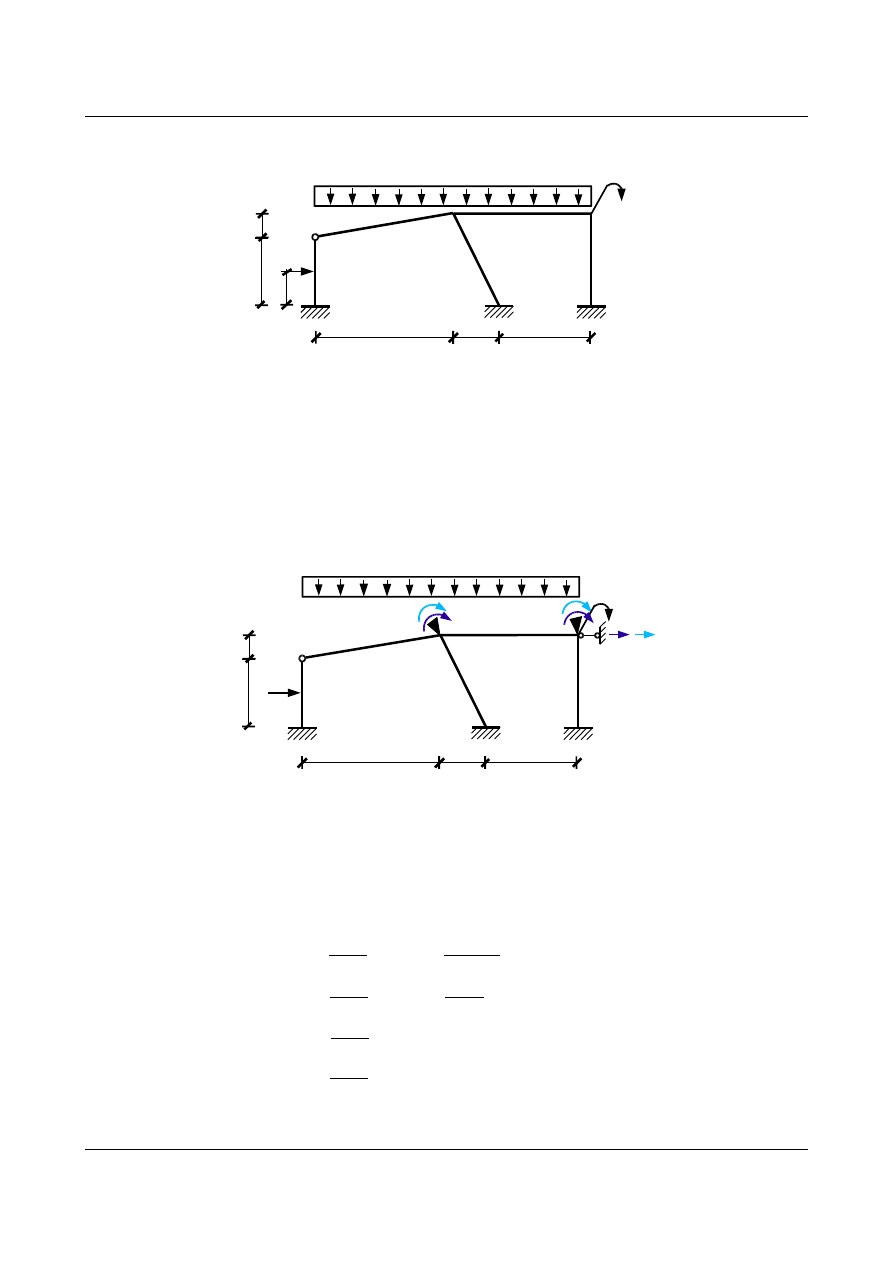
Dla układu
1
3
6
2
4
[m]
20 kN
2 kN/m
2 kNm
J
1
J
1
J
1
J
2
J
2
1,5
przyjęto przekroje z dwuteowników walcowanych:
J
1
⇒
I 220 J
1
=3060 cm
4
J
2
⇒
I 240 J
2
=4250 cm
4
J
1
=J
czyli:
J
2
=1,389 J
Układ jest trzykrotnie geometrycznie niewyznaczalny (SGN = 3). Przyjęto dla niego układ podstawowy:
1
3
6
2
4
[m]
20 kN
2 kN/m
2 kNm
0
1
2
3
4
5
u
3
R
3
R
2
φ
3
φ
2
R
1
Ponieważ dodaliśmy do układu podpory, zakładamy, że reakcje w tych podporach są równe zero:
R
1
=0
R
2
=0
R
3
=0
Korzystając z wzorów transformacyjnych zapisano wzory na poszczególne przęsłowe momenty
przywęzłowe:
M
01
=
3 EJ
1
l
01
0
−
01
−
3 ⋅20 ⋅l
01
16
M
21
=
3 EJ
2
l
12
2
−
12
2 ⋅l
12
x 2
8
M
25
=
2 EJ
1
l
25
2
2
5
−3
25
M
52
=
2 EJ
1
l
25
2
2
5
−3
25
Agnieszka Sysak Gr 3
2004-04-19
Część 1
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
3
M
23
=
2 EJ
2
l
23
2
2
3
−3
23
−
2 ⋅l
23
2
12
M
32
=
2 EJ
2
l
23
2
2
3
−3
23
2 ⋅l
23
2
12
M
34
=
2 EJ
1
l
34
2
3
4
−3
34
M
43
=
2 EJ
1
l
34
3
2
4
−3
34
gdzie:
l
ij
– długości prętów:
l
01
=3[m]
l
23
=6 [m]
l
34
=4 [m]
l
12
=
37 [m]
l
12
x
=6 [m]
l
12
y
=1 [m]
l
25
=
20 [m]
l
25
x
=2 [m]
l
25
y
=4 [m]
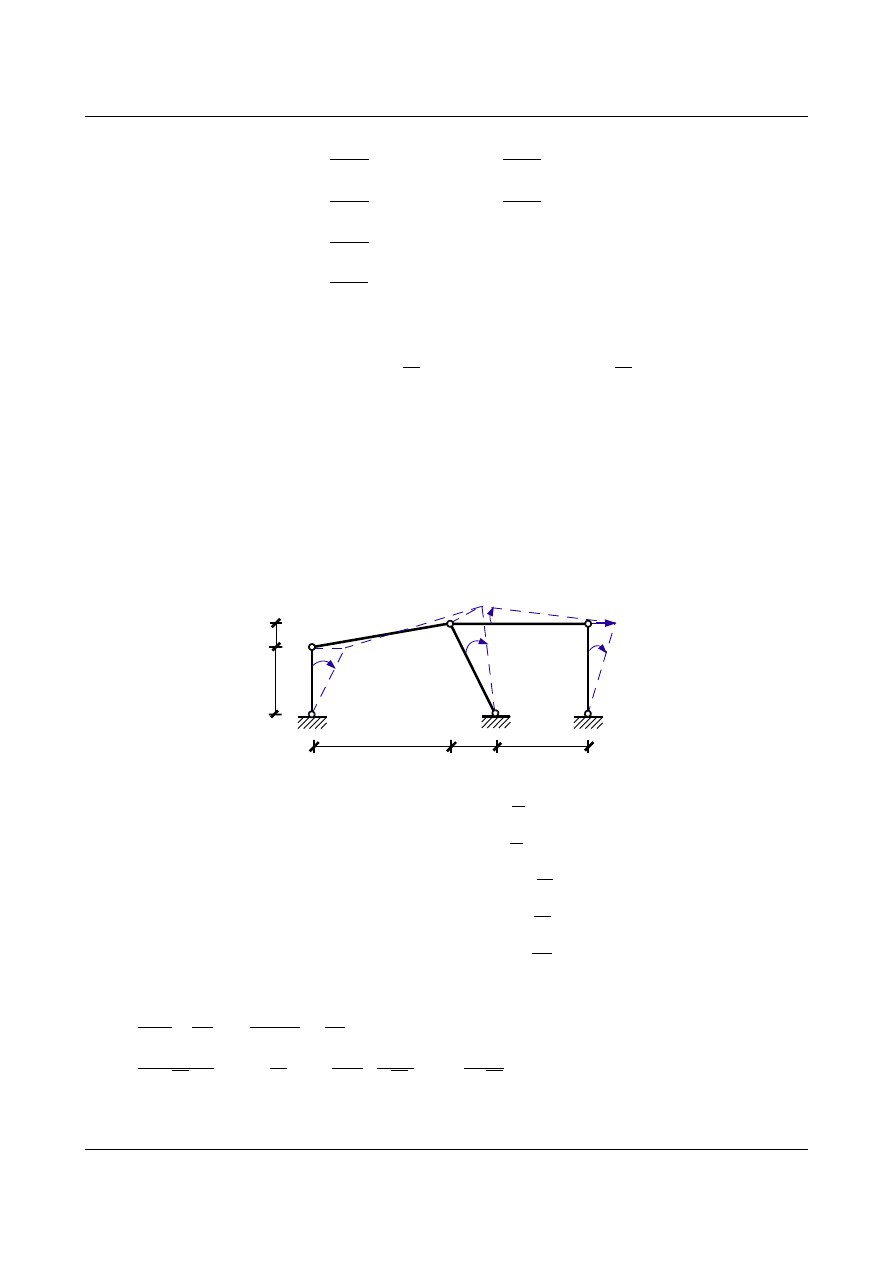
Niewiadome kąty obrotu węzłów i przesuwy nazwano:
2
=Z
1
3
=Z
2
u
3
=Z
3
Nieznane kąty obrotu cięciwy prętów uzależniamy od niewiadomej Z
3
zapisując równania łańcucha
kinematycznego układu.
1
3
6
2
4
[m]
Z
3
ψ
01
0
1
2
3
4
ψ
34
ψ
25
ψ
23
5
ψ
12
43
4 ⋅
34
=Z
3
⇒
34
= 1
4
Z
3
523
4 ⋅
25
=Z
3
⇒
25
= 1
4
Z
3
5234
−2 ⋅
25
6 ⋅
23
=0
⇒
23
= 1
12
Z
3
01234
6 ⋅
12
6 ⋅
23
=0
⇒
12
=− 1
12
Z
3
0123
3 ⋅
01
1 ⋅
12
=Z
3
⇒
01
= 13
36
Z
3
Obliczone wartości podstawiamy do zapisanych wcześniej wzorów na momenty przywęzłowe:
M
01
= 3 EJ
3
−13
36
Z
3
− 3
⋅20 ⋅3
16
=−13
36
EJ Z
3
−11,25
M
21
= 3
⋅1,389 EJ
37
[
Z
1
−
− 1
12
Z
3
]
2
⋅6
2
8
= 4,167
37
EJ Z
1
1,389
4
37
EJ Z
3
9
Agnieszka Sysak Gr 3
2004-04-19
Część 1
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
4
M
25
= 2 EJ
20
[
2 Z
1
−3 ⋅
1
4
Z
3
]
= 4
20
EJ Z
1
− 1,5
20
EJ Z
3
M
52
= 2 EJ
20
[
Z
1
−3 ⋅
1
4
Z
3
]
= 2
20
EJ Z
1
− 1,5
20
EJ Z
3
M
23
= 2
⋅1,389 EJ
6
[
2 Z
1
Z
2
−3 ⋅
1
12
Z
3
]
− 2
⋅6
2
12
= 2,778
3
EJ Z
1
1,389
3
EJ Z
2
− 1,389
12
EJ Z
3
−6
M
32
= 2
⋅1,389 EJ
6
[
Z
1
2 Z
2
−3 ⋅
1
12
Z
3
]
2
⋅6
2
12
= 1,389
3
EJZ
1
2,778
3
EJ Z
2
− 1,389
12
EJ Z
3
6
M
34
= 2 EJ
4
[
2 Z
2
−3 ⋅
1
4
Z
3
]
=EJ Z
2
− 3
8
EJ Z
3
M
43
= 2 EJ
4
[
Z
2
−3 ⋅
1
4
Z
3
]
= 1
2
EJ Z
2
− 3
8
EJ Z
3
Rozpisując układ równań kanonicznych otrzymamy:
R
1
=r
11
⋅Z
1
r
12
⋅Z
2
r
13
⋅Z
3
r
1 P
=0
R
2
=r
21
⋅Z
1
r
22
⋅Z
2
r
23
⋅Z
3
r
2 P
=0
R
2
=r
31
⋅Z
1
r
32
⋅Z
2
r
33
⋅Z
3
r
3 P
=0
Wartości r
ij
i r
iP
otrzymamy z równań równowagi poszczególnych węzłów oraz z równania pracy wirtualnej
dla stanów Z
1
= 1, Z
2
= 1, Z
3
= 1 oraz P.
•
Stan Z
1
= 1
1
3
6
2
4
[m]
0
1
2
3
4
5
20
2
20
4
1,389
3
2,778
3
37
4,167
[·EJ]
1
3
6
2
4
[m]
ψ
01
0
1
2
3
4
ψ
34
ψ
25
ψ
23
5
ψ
12
r
31
r
21
r
11
z
3
=1
r
11
− 2,778
3
EJ −
4
20
EJ −
4,167
37
EJ =0
⇒
r
11
=2,5055 EJ
r
21
− 1,389
3
EJ =0
⇒
r
21
=0,4630 EJ
r
31
⋅
1
4,167
37
EJ
12
2,778
3
1,389
3
EJ
23
4
20
2
20
EJ
25
=0
⇒
r
31
=−0,3941 EJ
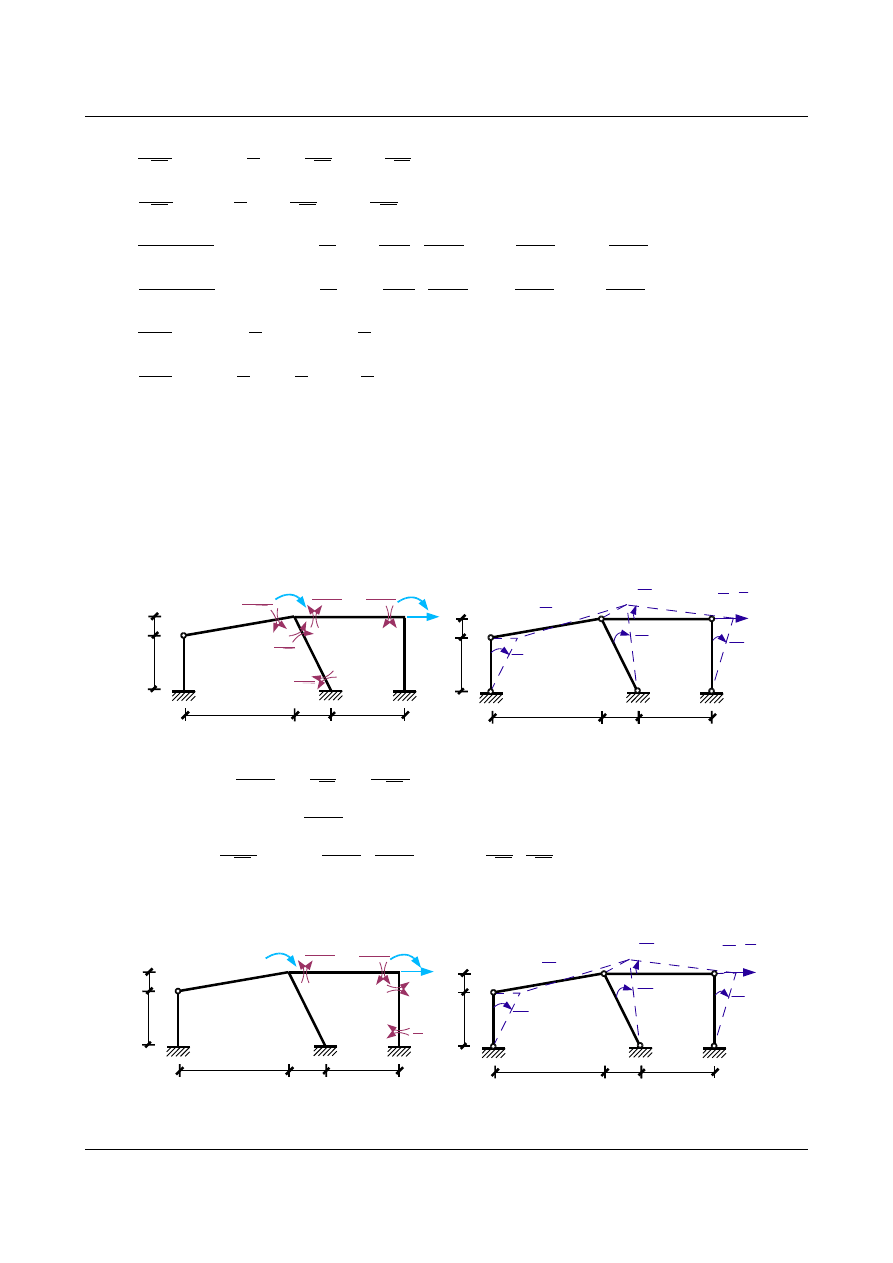
•
Stan Z
2
= 1
1
3
6
2
4
[m]
0
1
2
3
4
5
1,389
3
2,778
3
1
1
2
[·EJ]
1
3
6
2
4
[m]
ψ
01
0
1
2
3
4
ψ
34
ψ
25
ψ
23
5
ψ
12
z
3
=1
r
22
r
12
r
32
Agnieszka Sysak Gr 3
2004-04-19
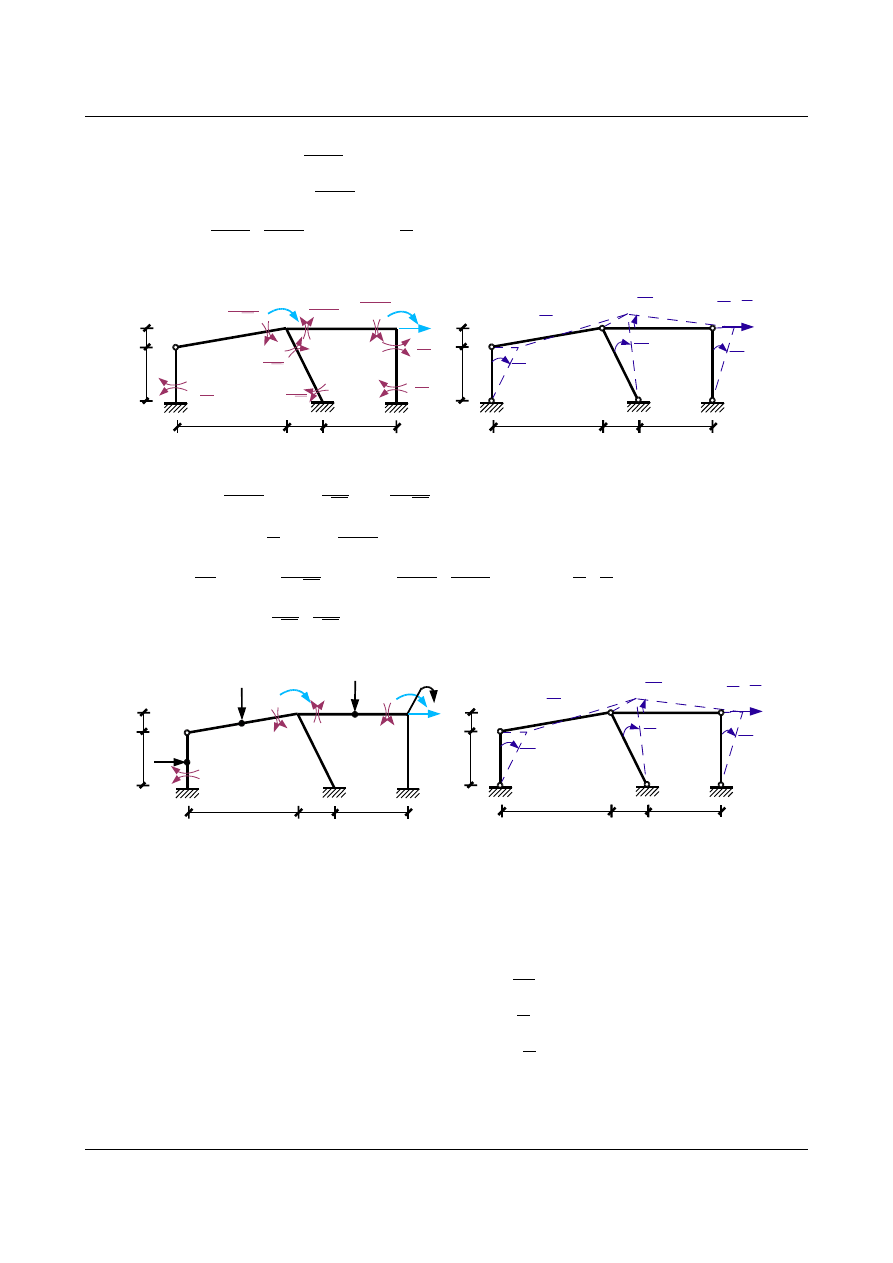
Część 1
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
5
r
12
− 1,389
3
EJ =0
⇒
r
12
=0,4630 EJ
r
22
−1 −
2,778
3
EJ =0
⇒
r
22
=1,9260 EJ
r
32
⋅
1
1,389
3
2,778
3
EJ
23
1
1
2
EJ
34
=0
⇒
r
32
=−0,4908 EJ
•
Stan Z
3
= 1
1
3
6
2
4
[m]
0
1
2
3
4
5
1
3
6
2
4
[m]
ψ
01
0
1
2
3
4
ψ
34
ψ
25
ψ
23
5
ψ
12
z
3
=1
r
23
r
13
[·EJ]
-13
36
- 3
8
- 3
8
1,389
12
-
1,389
12
-
20
1,5
-
20
1,5
-
37
1,389
4
r
33
r
13
−
−1,389
12
EJ
−
− 1,5
20
EJ
− 1,389
4
37
EJ =0
⇒
r
13
=−0,3941 EJ
r
23
−
− 3
8
EJ
−
−1,389
12
EJ
=0
⇒
r
23
=−0,4908 EJ
r
33
⋅
1
−13
36
EJ
01
1,389
4
37
EJ
12
−1,389
12
− 1,389
12
EJ
23
− 3
8
− 3
8
EJ
34
− 1,5
20
− 1,5
20
EJ
25
=0
⇒
r
33
=0,5097 EJ
•
Stan P
1
3
6
2
4
[m]
0
1
2
3
4
5
1
3
6
2
4
[m]
ψ
01
0
1
2
3
4
ψ
34
ψ
25
ψ
23
5
ψ
12
z
3
=1
r
2P
r
1P
-11,25
6
-6
9
[kNm]
20 kN
12 kN
12 kN
A
B
C
2 kNm
r
3P
r
1 P
−−6 −9=0
⇒
r
1 P
=3,0 [kNm]
r
2 P
2−6 =0
⇒
r
2 P
=4,0 [kNm]
W równaniu pracy wirtualnej, z którego obliczymy r
3P
wystąpią przemieszczenia, na których pracują siły
działające na ten układ (u
A
, v
B
, v
C
). Obliczymy je z równań łańcucha kinematycznego:
0 A
1,5
01
=u
A
⇒
u
A
= 13
24
01 B
3
12
=v
B
⇒
v
B
=−1
4
43C
−3
23
=v
C
⇒
v
C
=−1
4
r
3 P
⋅
1 −11,25
01
9
12
6−6
23
20 u
A
12 v
B
12 v
C
=0
⇒
r
3 P
=−0,0208 [kN ]
Agnieszka Sysak Gr 3
2004-04-19
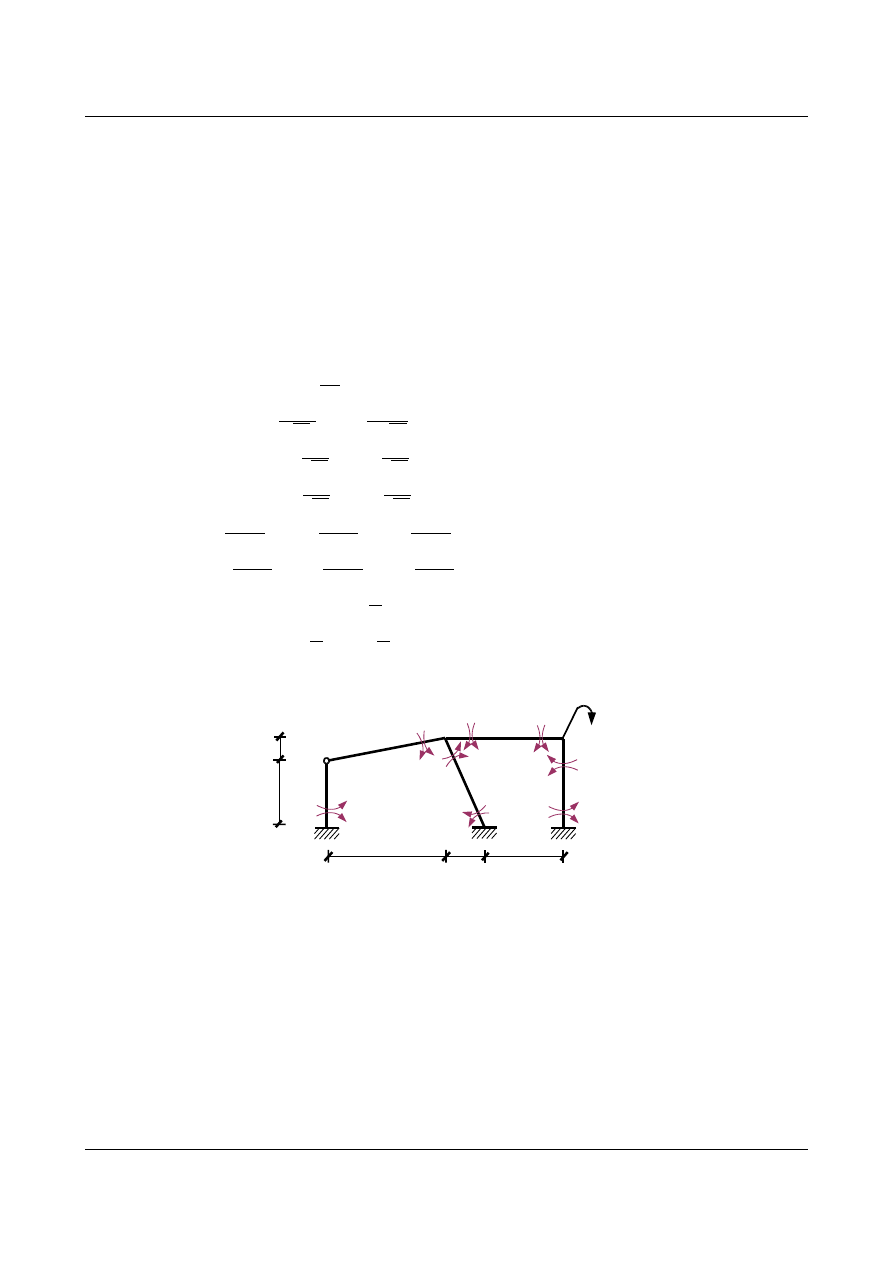
Część 1
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
6
Obliczone wartości r
ij
i r
iP
podstawiamy do układu równań kanonicznych i obliczamy wartości
niewiadomych kątów obrotu węzłów i przesuwu:
{
2,5055 EJ Z
1
0,4630 EJ Z
2
−0,3941 EJ Z
3
3,0 =0
0,4630 EJ Z
1
1,9260 EJ Z
2
−0,4908 EJ Z
3
4,0 =0
−0,3941 EJ Z
1
−0,4908 EJ Z
2
0,5097 EJ Z
3
−0,0208 =0
{
EJ Z
1
=−1,2547
EJ Z
2
=−2,6663
EJ Z
3
=−3,4967
Obliczmy zatem wartości momentów przywęzłowych:
M
01
=−13
36
EJ Z
3
−11,25 =−9,9873 [kNm]
M
21
= 4,167
37
EJ Z
1
1,389
4
37
EJ Z
3
9 =7,9409 [kNm]
M
25
= 4
20
EJ Z
1
− 1,5
20
EJ Z
3
=0,0506 [kNm]
M
52
= 2
20
EJ Z
1
− 1,5
20
EJ Z
3
=0,6117 [kNm]
M
23
= 2,778
3
EJ Z
1
1,389
3
EJ Z
2
− 1,389
12
EJ Z
3
−6 =−7,9916 [kNm]
M
32
= 1,389
3
EJ Z
1
2,778
3
EJ Z
2
− 1,389
12
EJ Z
3
6 =3,3548 [kNm]
M
34
=EJ Z
2
− 3
8
EJ Z
3
=−1,3550 [kNm]
M
43
= 1
2
EJ Z
2
− 3
8
EJ Z
3
=−0,0219 [kNm]
Sprawdzenie równowagi momentów w węzłach:
1
3
6
2
4
[m]
0
1
2
3
4
5
9,9873
3,3548
7,9916
7,9409
[kNm]
2 kNm
0,6117
0,0506
0,0219
1,3550
węzeł 2 :
7,9409 0,0506 −7,9916 =−0,0001 [kNm]≈0
węzeł 3:
3,3548 −1,3550 −2 =−0,0002 [kNm]≈0
Tnące i normalne obliczamy wycinając myślowo kolejne pręty i równoważąc węzły.
Agnieszka Sysak Gr 3
2004-04-19
Część 1
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
7
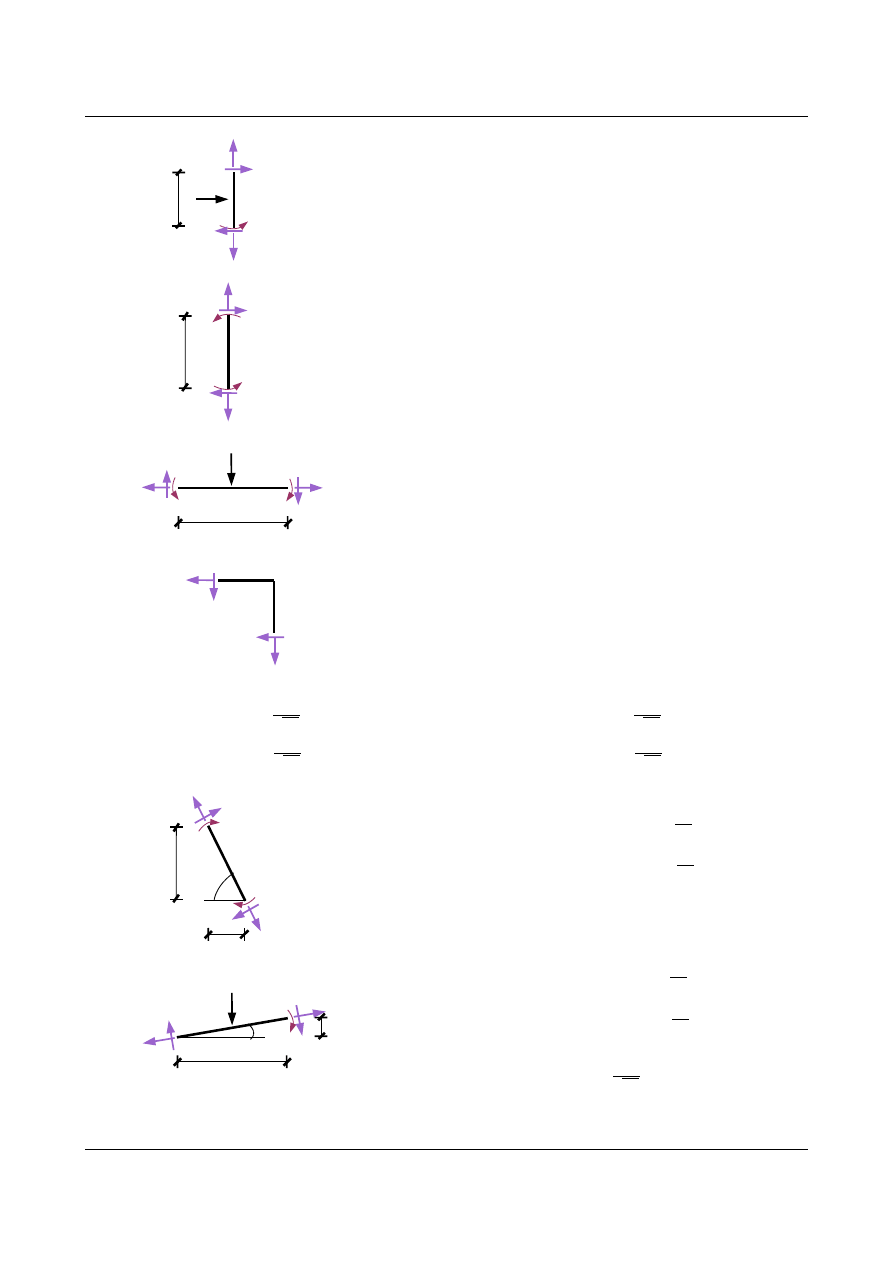
3
9,9873
T
10
N
10
T
01
N
01
0
1
20 kN
∑
M
0
: −9,987320 ⋅1,5 T
10
⋅3 =0
⇒ T
10
=−6,6709 [kN ]
∑
M
1
: 20 ⋅1,5 −T
01
⋅3 9,9873 =0
⇒ T
01
=13,3291 [kN ]
∑
Y : N
01
=N
10
0,0219
1,3550
3
4
4
N
43
N
34
T
34
T
43
∑
M
3
: 1,3550 0,0219 −T
43
⋅4 =0
⇒ T
43
=0,3442 [kN ]
∑
M
4
: 1,3550 0,0219 −T
34
⋅4 =0
⇒ T
34
=0,3442 [kN ]
∑
Y : N
34
=N
43
2
3
3,3548
7,9916
N
23
N
32
T
23
T
32
12 kN
6
∑
M
2
: −7,9916 3,3548 T
32
⋅6 12 ⋅3 =0
⇒ T
32
=−5,2272 [kN ]
∑
M
3
: −7,9916 3,3548 T
23
⋅6 −12 ⋅3 =0
⇒ T
23
=6,7728 [kN ]
∑
X : N
23
=N
32
N
34
0,3442
5,2272
N
32
∑
X : N
32
0,3442 =0
⇒
N
32
=N
23
=−0,3442 [kN ]
∑
Y : N
34
5,2272 =0
⇒
N
34
=N
43
=−5,2272 [kN ]
sin =
1
37
cos =
6
37
sin =
4
20
cos =
2
20
2
5
0,6117
0,0506
T
52
T
25
N
25
N
52
4
2
β
∑
M
2
: 0,0506 0,6117 T
52
⋅
20=0
⇒ T
52
=−0,1481 [kN ]
∑
M
5
: 0,0506 0,6117 T
25
⋅
20=0
⇒ T
25
=−0,1481 [kN ]
∑
: N
25
=N
52
1
2
7,9409
N
21
N
12
12 kN
T
21
T
12
6
1
α
∑
M
1
: 12 ⋅3 7,9409 T
21
⋅
37=0
⇒ T
21
=−7,2238 [kN ]
∑
M
2
: 7,9409 −12 ⋅3 T
12
⋅
37=0
⇒ T
12
=4,6127 [kN ]
∑
∨: N
12
12 ⋅
1
37
=N
21
Agnieszka Sysak Gr 3
2004-04-19
Część 1
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
8
N
10
6,6709
α
N
12
4,6127
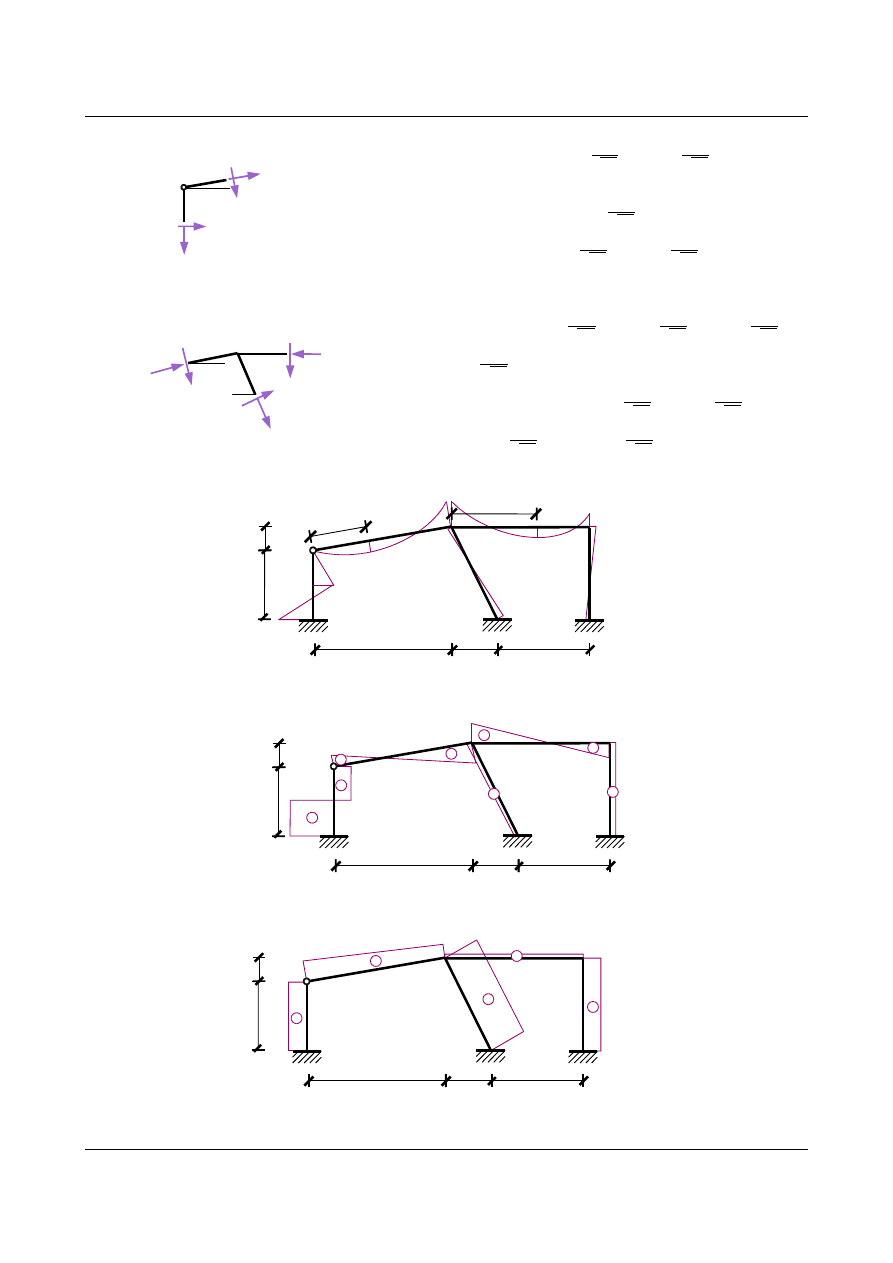
∑
X : 6,6709 N
12
⋅ 6
37
4,6127 ⋅
1
37
=0
⇒
N
12
=−7,5317 [kN ]
⇒
N
21
=N
12
12 ⋅
1
37
=−5,5589 [kN ]
∑
Y : N
10
−N
12
⋅ 1
37
4,6127 ⋅
6
37
=0
⇒
N
10
=N
01
=−5,7881 [kN ]
0,1481
N
25
0,3442
6,7728
7,2238
5,5589
α
β
∑
X : −0,3442 7,2238 ⋅
1
37
5,5589 ⋅
6
37
0,1481 ⋅
4
20
N
25
⋅ 2
20
=0
⇒
N
25
=N
52
=−14,4430 [kN ]
spr
∑
Y : −6,7728 −7,2238 ⋅
6
37
5,5589 ⋅
1
37
0,1481 ⋅
2
20
−−14,4430⋅
4
20
=0,000009≈0
1
3
6
2
4
[m]
0
1
2
3
4
5
9,9873
4,3814
7,9409
1,3550
0,0506
0,6117
0,0219
3,3548
7,9916
M
(n)
[kNm]
3,7146
2,37
3,4761
3,39
1
3
6
2
4
[m]
0
1
2
3
4
5
13,3291
-6,6709
4,6127
-5,2272
-7,2238
-0,1481
0,3442
6,7728
T
(n)
[kN]
+
-
-
+
-
+
+
-
1
3
6
2
4
[m]
0
1
2
3
4
5
-5,7881
-7,5317
-14,4430
-5,2272
-0,3442
-5,5589
N
(n)
[kN]
-
-
-
-
-
Agnieszka Sysak Gr 3
2004-04-19
Część 1
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
9
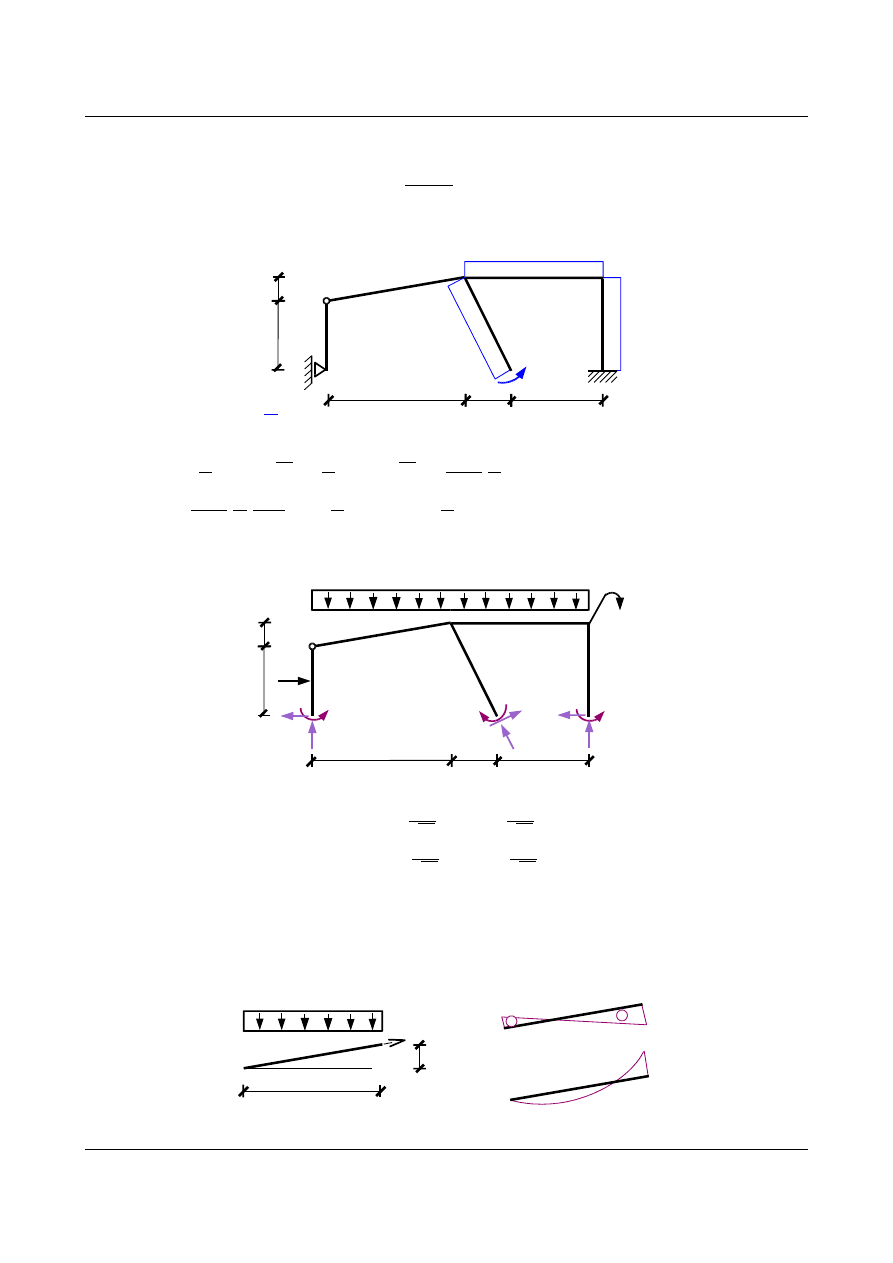
•
Kontrola kinematyczna
1⋅=
∑∫
M
n
⋅
M
0
EJ
dx
Obliczmy zatem zerowy kąt obrotu φ
5
węzła 5 dla nowego układu podstawowego:
1
3
6
2
4
[m]
0
1
2
3
4
5
M
0
[ - ]
1
1
1
1
EJ
5
= 1
2
⋅0,0506 ⋅
20⋅1 −
1
2
⋅0,6117 ⋅
20⋅1
1
1,389
⋅1
2
⋅7,9916 3,3548⋅6 ⋅1 −
− 1
1,389
⋅2
3
⋅2
⋅6
2
8
⋅6 ⋅1
1
2
⋅1,3550 ⋅4 ⋅1 −
1
2
⋅0,0219 ⋅4 ⋅1 =−0,0001 ≈0
•
Sprawdzenie statyczne:
1
3
6
2
4
[m]
0
1
2
3
4
5
9,9873
0,6117
0,0219
2 kN/m
20 kN
2 kNm
13,3291
5,7811
5,2272
0,3442
0,1481
14,4430
∑
X : 20 −13,3291 −0,3442 0,1481 ⋅
4
20
−14,4430 ⋅
2
20
=0,00006 [kN ]≈0
∑
Y : 2 ⋅12 −5,7811 −5,2272 −0,1481 ⋅
2
20
−14,4430 ⋅
4
20
=0,00726 [kN ]≈0
∑
M
5
: 0,6117 5,7811 ⋅62−9,987320 ⋅1,5 −0,0219 −5,2272 ⋅4
2 2 ⋅4 ⋅2−2 ⋅8 ⋅4 =−0,0575 [kNm]≈0
Korzystając z równania różniczkowego linii ugięcia znaleźć równanie momentów zginających i sił
poprzecznych dla pręta 12 i porównać otrzymany wynik z rozwiązaniem otrzymanym metodą
przemieszczeń.
6
1
α
x
2 kN/m
4,6127
-7,2238
-
+
7,9409
M [kNm]
T [kN]
1
2
Agnieszka Sysak Gr 3
2004-04-19
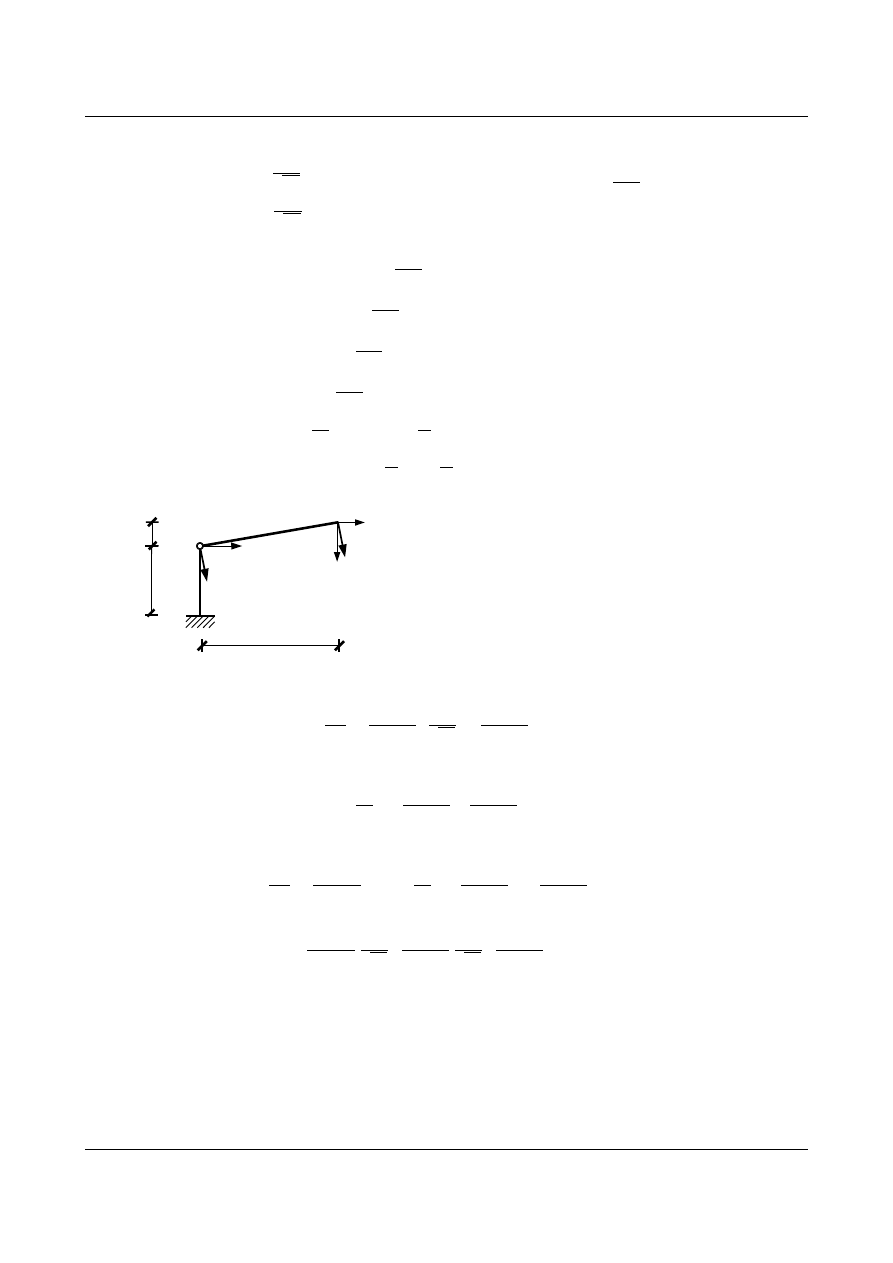
Część 1
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
10
sin =
1
37
cos =
6
37
EJ
d
4
y
dx
4
=q
q=2 ⋅cos
2
=1,946
1,389 EJ
d
4
y
d x
4
=1,946
EJ
d
4
y
dx
4
=1,4010
EJ
d
3
y
dx
3
=1,4010 xA
EJ
d
2
y
dx
2
=0,7005 x
2
A xB
EJ
dy
dx
=0,2335 x
3
1
2
A x
2
B xC
EJ y=0,0584 x
4
1
6
A x
3
1
2
B x
2
C xD
1
3
6
[m]
0
1
2
w
1
w
II
w
I
w
y
II
w
x
II
w
I
=w
1
⋅sin
w
II
=w
II
x
⋅sin w
II
y
⋅cos
01
3
01
=w
1
w
I
=3 ⋅
13
36
⋅
− 3,4967
EJ
⋅ 1
37
=−0,6228
EJ
012
0
01
6
12
=w
II
y
w
II
y
=6 ⋅
− 1
12
⋅
− 3,4967
EJ
= 1,7484
EJ
012
3
01
1
12
=w
II
x
w
II
x
=3 ⋅
13
36
⋅
− 3,4967
EJ
1 ⋅
− 1
12
⋅
− 3,4967
EJ
=− 3,4967
EJ
w
II
=− 3,4967
EJ
⋅ 1
37
1,7484
EJ
⋅ 6
37
= 1,1498
EJ
Warunki brzegowe:
Agnieszka Sysak Gr 3
2004-04-19
Część 1
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ
11
x=0
y=w
I
=−0,6228
EJ
⇒ D=−0,6228
x=0
M x=0
⇒ B=0
x=
37
y=w
II
= 1,1498
EJ
x=
37
y==z
1
=−1,2547
EJ
⇒
{
A=−3,3203
C=7,9189
Sprawdzenie wartości tnących i momentów:
T x=−1,389 EJ
d
3
y
dx
3
M x=−1,389 EJ
d
2
y
dx
2
T x=1,389 ⋅−1,4010 x3,3203
M x=1,389 ⋅−0,7005 x
2
3,3203 x
x=0
M x=0
T x=4,6119 [kN ]
x=
37
M x=−7,9477 [kNm]
T x=−7,2251 [kN ]
Sprawdzić naprężenia normalne wywołane momentami zginającymi w obu grupach prętów.
y
z
z
max
z
=
M
max
J
y
⋅z
max
z
z dop
=21,5
kN
cm
2
dla J
1
= 3060 cm
4
(I 220 → z
max
= 11 cm) M
max
=9,9873 kNm:
z
= 998,73
3060
⋅11 =3,59
[
kNcm
cm
4
⋅cm=
kN
cm
2
]
3,59
kN
cm
2
21,5
kN
cm
2
dla J
2
= 4250 cm
4
(I 240 → z
max
= 12 cm) M
max
=7,9916 kNm:
z
= 799,16
4250
⋅12 =2,26
[
kNcm
cm
4
⋅cm=
kN
cm
2
]
2,26
kN
cm
2
21,5
kN
cm
2
Naprężenia normalne w obu przekrojach są dużo mniejsze od naprężeń dopuszczalnych, zatem należałoby
przyjąć mniejsze przekroje.
Agnieszka Sysak Gr 3
2004-04-19
Wyszukiwarka
Podobne podstrony:
Metoda przemieszczen- obciazenie1
Metoda przemieszczen- obciazenie3
Metoda przemieszczen obciazenie5
Metoda przemieszczen obciazeni Nieznany
Metoda przemieszczen obciazenie3
Metoda przemieszczen obciazenie8
Metoda przemieszczen obciazenie3
Metoda przemieszczen obciazenie5
Metoda przemieszczen obciazenie6
Metoda przemieszczen obciazenie2
belka obroty i przesuwy metoda przemieszczeń
Linie wpływu Metoda przemieszczeń mmp belka lw
Metoda przemieszczeń
Uproszczona metoda obliczania obciążenia cieplnego pomieszczenia
cwicz mechanika budowli metoda przemieszczen rama ugiecie
Metoda przemieszczen projekt4
więcej podobnych podstron