6 [kN/m]

2

4

6

6

I

1

I

1

I

1

I

1

I

2

I

2

Rys.1.1. Zadany schemat ramy statycznie niewyznaczalnej

SGN =

∑



∑



∑



∑



∑

=

∑

=

1/18

SGN

=3

(1.2)

W pierwszej kolejności przyjmuję odpowiedni układ podstawowy:

6 [kN/m]

2

4

I

1

I

1

I

1

I

1

I

2

I

2

0

1

2

3

4

6

5

6

R

2

R

1

R

3

φ

3

=z

3

u

2

=z

1

φ

2

=z

2

Rys.1.2.Układ podstawowy

Układ równań kanonicznych metody przemieszczeń przyjmuje postać:

{

R

1

=0

R

2

=0

R

3

=0

}

{

r

11

z

1

r

12

z

2

r

13

z

3

R

1 P

=0

r

21

z

1

r

22

z

2

r

23

z

3

R

2 P

=0

r

31

z

1

r

32

z

2

r

33

z

3

R

3 P

=0

}

(1.3)

Wykorzystując wzory transformacyjne metody przemieszczeń określę wartości przęsłowych przywęzłowych
momentów M

ik

jako funkcji z

1

, z

2

, z

3

, “P”, co w późniejszym etapie umożliwi obliczenie współczynników

Tomasz Terlecki gr 3 KBI

2/18

r

ik

równań kanonicznych.

Otrzymujemy zatem:

M

01

=

3 EI

1

l

01

⋅

0

−

01

=

−3 EI

4

⋅

01

M

10

=0

[kNm]

Rys.1.3. Pręt 01

M

12

=0

M

21

=

3 EI

2

l

12

⋅

2

−

12



q⋅l

12

x



2

8

=

3⋅1,389 ⋅EI

2



10

⋅ z

2

−

12



6⋅6

2

8

[kNm]

Rys.1.4. Pręt 12

M

23

=

2 EI

1

l

23

⋅2 

2



3

−3 

23

=EI⋅2 z

2

z

3

−3 

23



M

32

=

2 EI

1

l

23

⋅

2

2 

3

−3 

23

=EI⋅ z

2

2 z

3

−3 

23



[kNm]

Rys.1.5. Pręt 23

Tomasz Terlecki gr 3 KBI

3/18

4

I

1

0

1

6 [kN/m]

2

6

I

2

1

2

2

I

1

2

3

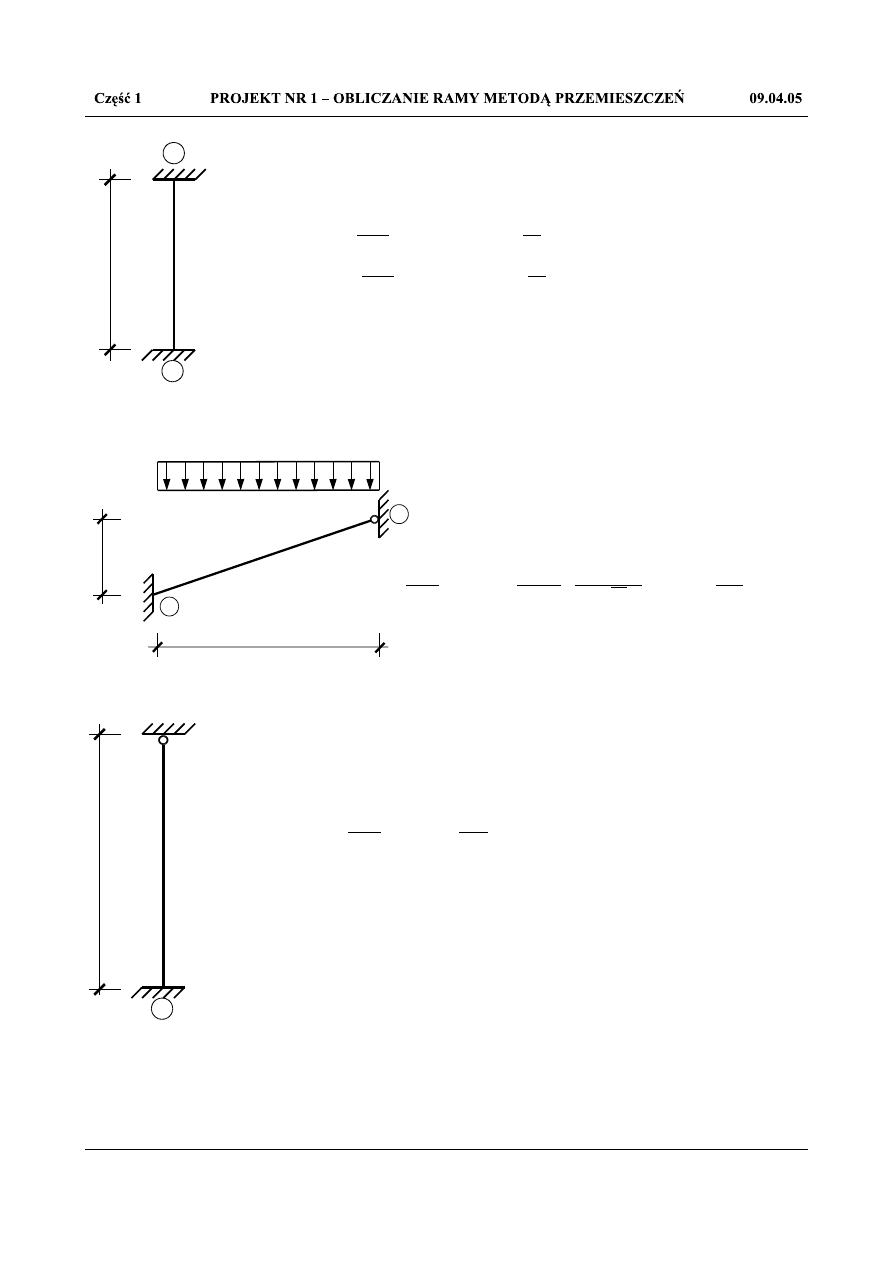
M

34

=

2 EI

1

l

34

⋅2 

3



4

−3 

34

=

EI

2

⋅2 z

3

−3 

34



M

43

=

2 EI

1

l

34

⋅

3

2 

4

−3 

34

=

EI

2

⋅ z

3

−3 

34



[kNm]

Rys.1.6. Pręt 34

M

53

=0

M

35

=

3 EI

2

l

35

⋅

3

−

35

−

q⋅l

35

x



2

8

=

3⋅1,389 EI

2



10

⋅ z

3

−

35

−

6⋅6

2

8

[kNm]

Rys.1.7 Pręt 35

M

56

=0

M

65

=

3 EI

1

l

56

⋅

6

−

56

=

−EI

2

⋅

56



[kNm]

Rys.1.8. Pręt 56

Tomasz Terlecki gr 3 KBI

4/18

4

I

1

3

4

6 [kN/m]

2

6

I

2

3

5

6

I

1

6

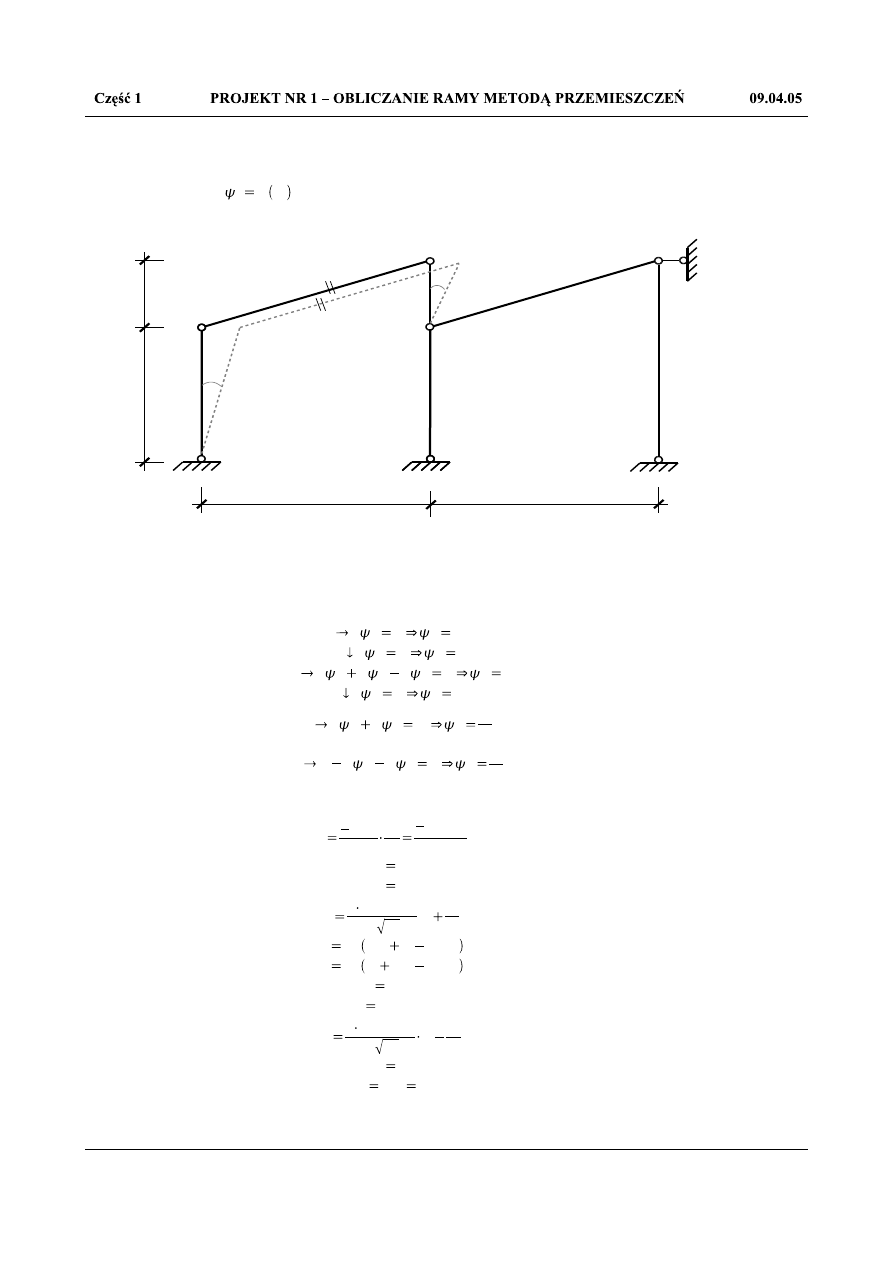
Pojawiające się wartości kątów obrotów cięciw (prętów) należy określić z równania łańcucha
kinematycznego jako funkcje niezależnych przesuwów (tutaj z

1

):

Określenie funkcji

ik

f z

1

:

2

4

6

6

ψ

01

ψ

23

Rys.1.9 Łańcuch kinematyczny w stanie z

1

Rozpisuję równanie łańcucha kinematycznego dla podanych niżej dróg:

56

6

56

0

56

0

4356 6

35

0

35

0

4356

4

34

2

35

6

56

0

34

0

012 6

12

0

12

0

012

4

01

2

12

z

1

01

z

1

4

234

z

1

2

23

4

34

0

23

z

1

2

[rad]

(1.4)

Stąd wartości momentów przęsłowych wynoszą;

M

01

3 EI

4

z

1

4

3 EI z

1

16

M

10

0

M

12

0

M

21

3 1,389 EI

2 10

z

2

6

3

8

M

23

EI 2 z

2

z

3

1,5 z

1

M

32

EI z

2

2 z

3

1,5 z

1

M

34

EI z

3

M

43

0,5 EI z

3

M

35

3 1,389 EI

2 10

z

3

6

3

8

M

53

0

M

65

M

56

0

[kNm]

(1.5)

Na podstawie wzorów 1.5. określam wartości momentów od poszczególnych stanów obciążeń:

Tomasz Terlecki gr 3 KBI

5/18

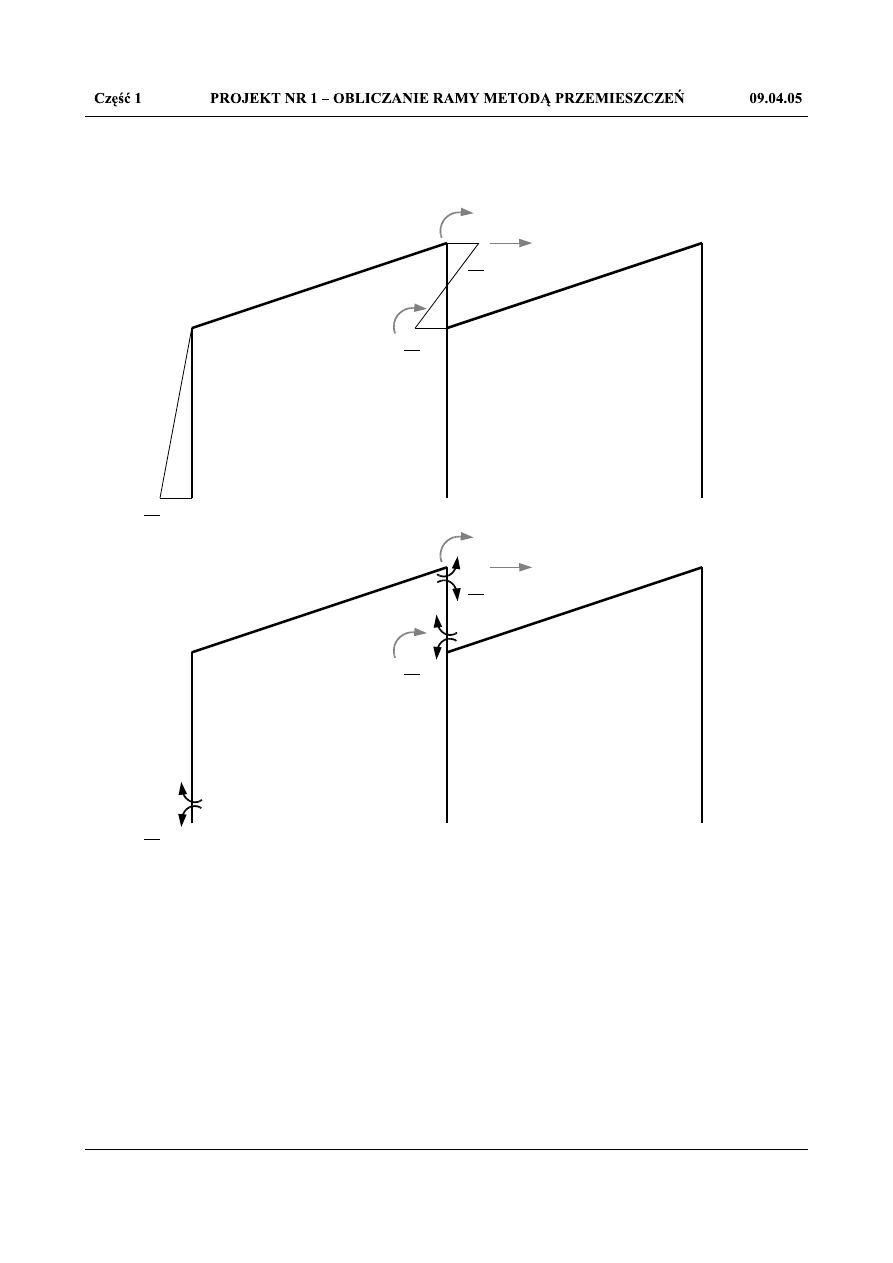
Stan z

1

=1

3

16

E I

1

3
2 E I

1

3
2 E I

1

r

11

r

31

r

21

3

16

E I

1

3
2 E I

1

3
2 E I

1

r

11

r

31

r

21

-

-

-

Rys.1.10. Stan z

1

=1 – M

1

(0)

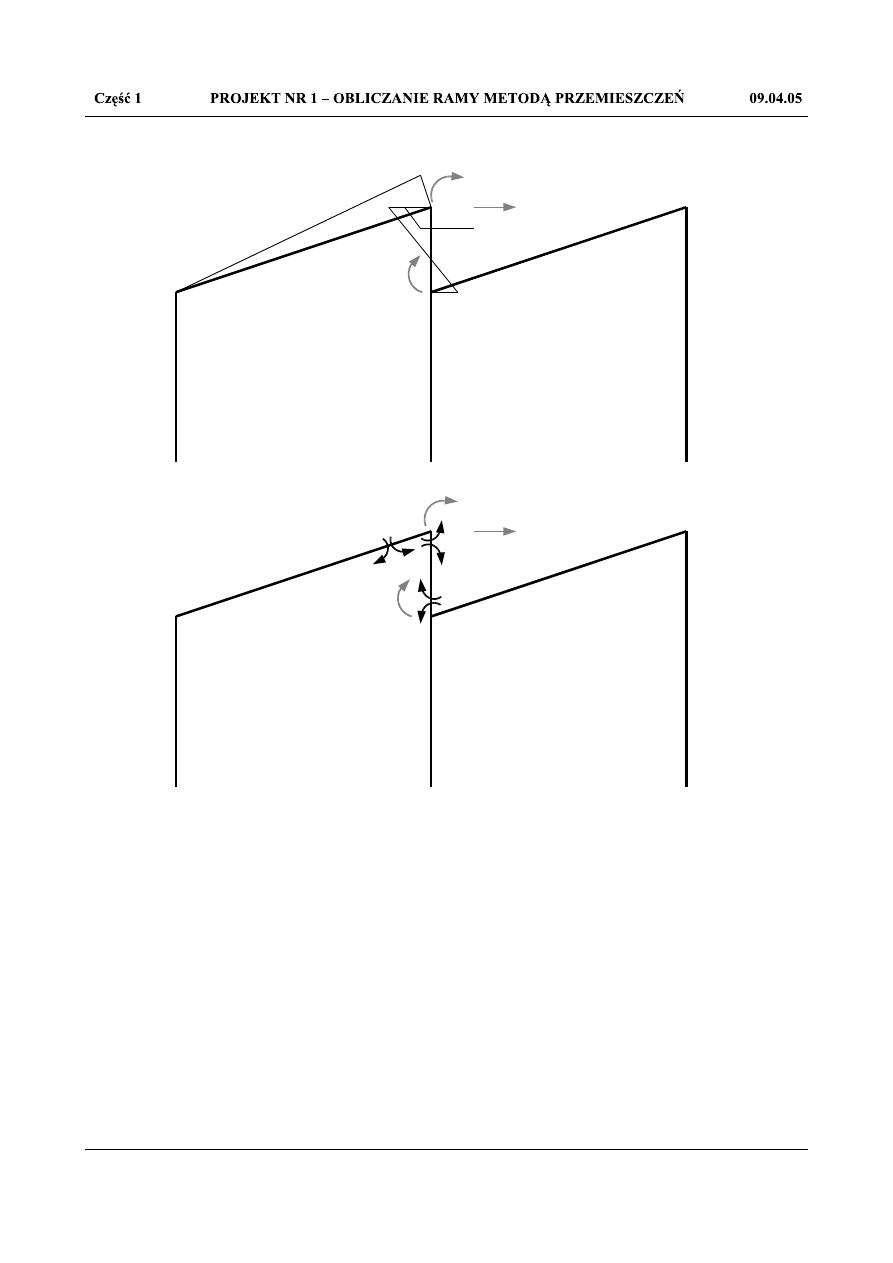
Stan z

2

=1

Tomasz Terlecki gr 3 KBI

6/18

2 E I

1

E I

1

r

12

r

32

r

22

2 E I

1

E I

1

r

12

r

22

0,659 E I

1

r

32

0,659 E I

1

Rys.1.11. Stan z

2

=1- M

2

(0)

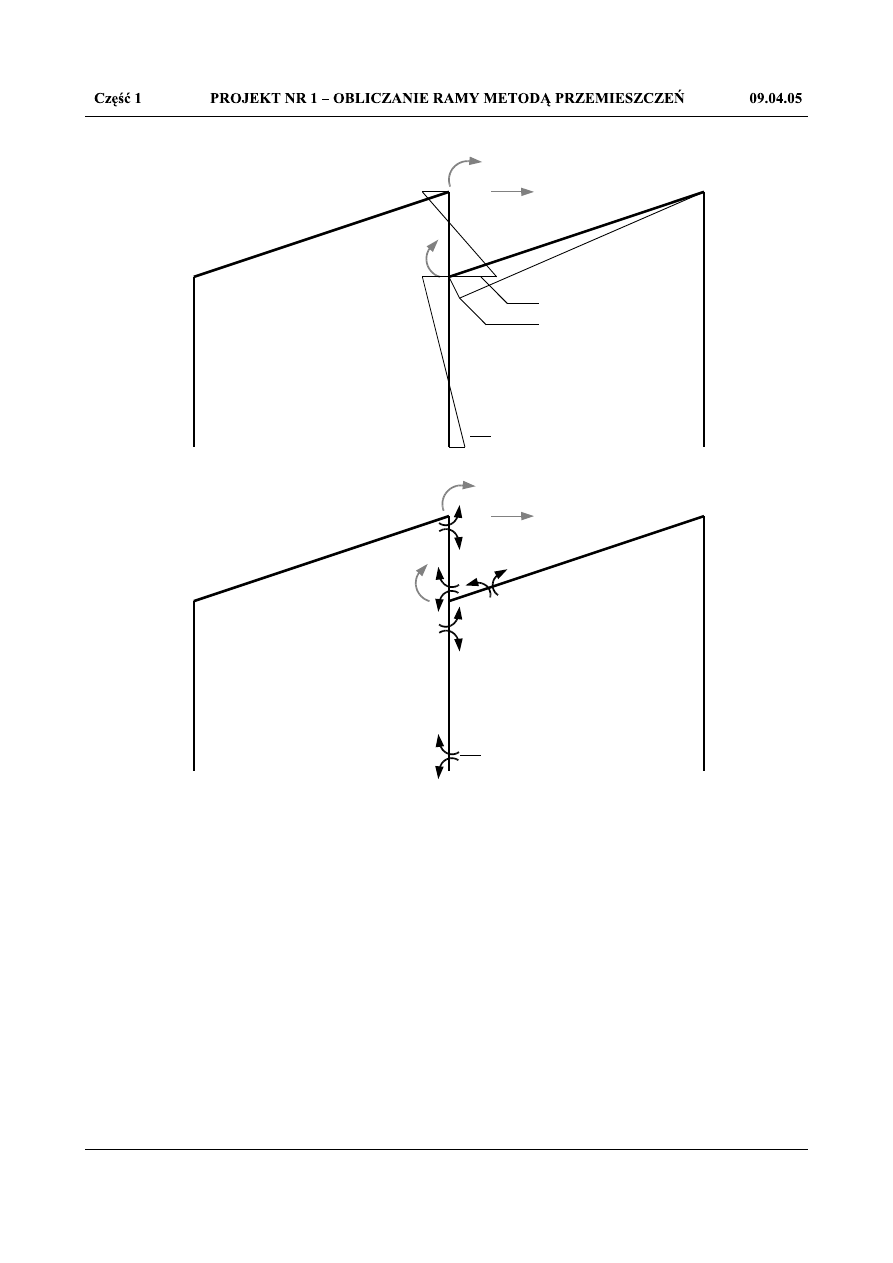
Stan z

3

=1

Tomasz Terlecki gr 3 KBI

7/18

E I

1

2 E I

1

r

13

r

33

r

23

E I

1

r

13

r

23

r

33

0,659 E I

1

E I

1

E I

1

2

E I

1

2

2 E I

1

E I

1

0,659 E I

1

Rys.1.12 Stan z

3

=1- M

3

(0)

Stan P

Tomasz Terlecki gr 3 KBI

8/18

R

1P

R

3P

R

2P

27

-27

27

27

R

1P

R

3P

R

2P

Rys.1.13 Stan P – obciążenie zewnętrzne -M

P

[kNm]

Tomasz Terlecki gr 3 KBI

9/18

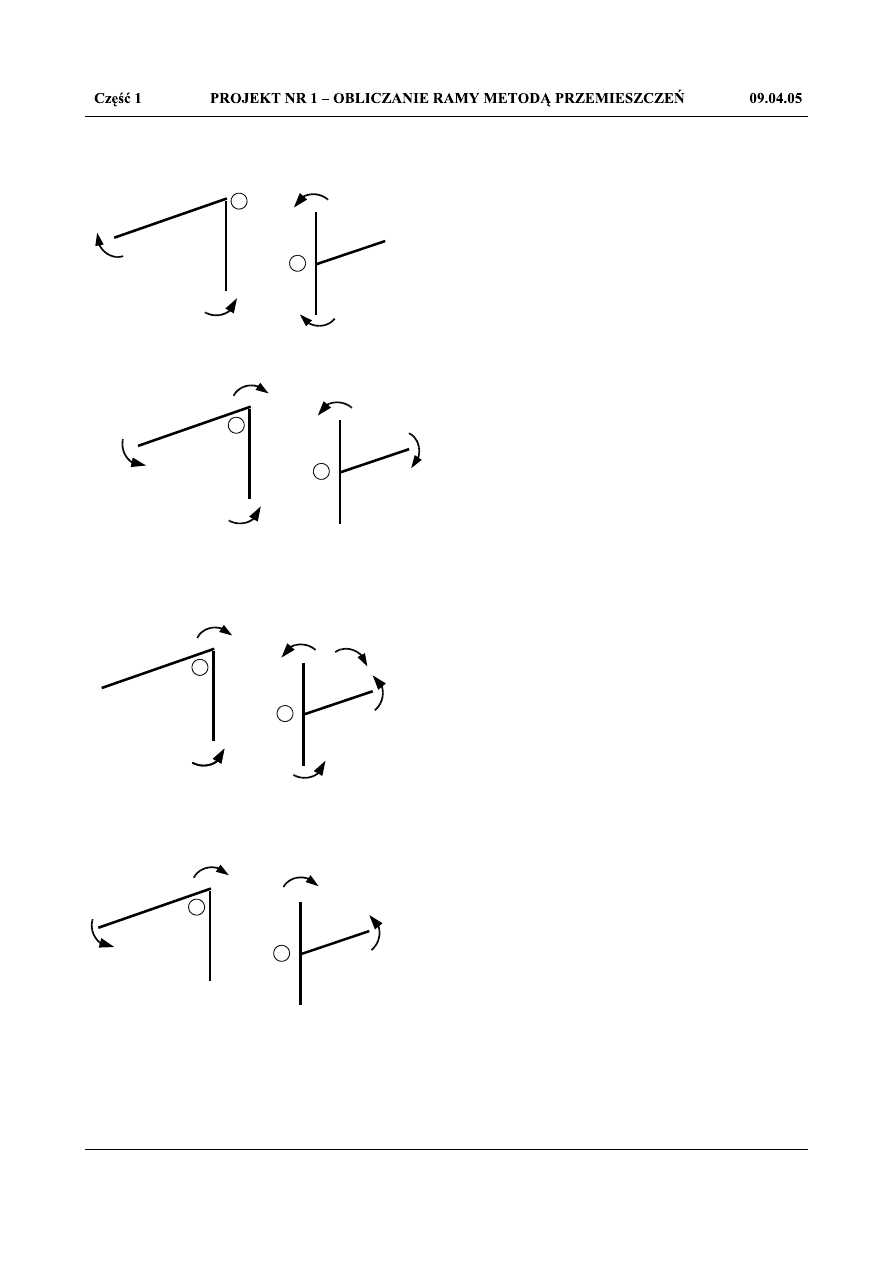
Określenie współczynników r

ik

dla drugiego i trzeciego równania kanonicznego a więc r

21

, r

22

, r

23

, R

2P ,

r

31

, r

32

,

r

33

, R

3P

z wykorzystaniem równowagi węzła 2 i 3:

r

21

=−1,5 EI

r

31

=−1,5 EI

Rys.1.14 Równowaga węzła 2 i 3 w stanie z

1

=1

r

22

=0,6592 EI =2,659 EI

r

32

=EI

Rys.1.15 Równowaga węzła 2 i 3 w stanie z

2

=1

r

23

=EI

r

33

=3,659 EI

Rys.1.16 Równowaga węzła 2 i 3 w stanie z

3

=1

R

2 P

=27

R

3 P

=−27 [kNm]

Rys.1.17 Równowaga węzła 2 i 3 w stanie P

Tomasz Terlecki gr 3 KBI

10/18

r

21

-1,5EI

2

-1,5EI

3

r

31

r

22

2EI

2

EI

3

r

32

0,659EI

r

23

EI

2

2EI

3

r

23

EI

EI

0,659EI

R

2P

2

3

R

3P

27

-27

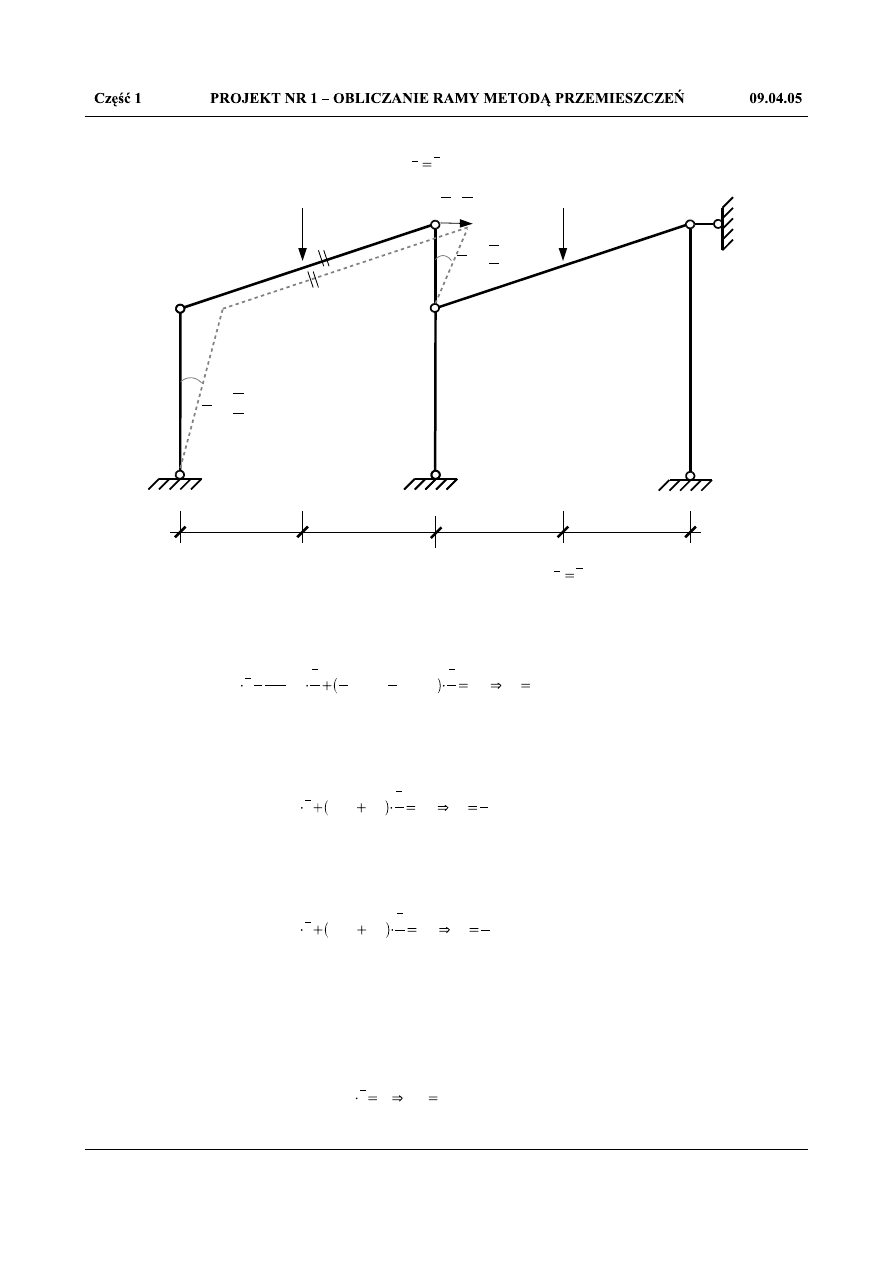
Aby obliczyć pozostałe współczynniki układu równań kanonicznych r

ik

należy skorzystać z zasady pracy

wirtualnej w wirtualnym stanie przemieszczeń

z

1

1

3

ψ

01

=

4

1

ψ

23

=

4

1

36 [kN]

36 [kN]

3

3

3

z

1

=1

Rys.1.18. Stan wirtualny przemieszczeń

z

1

1

Obliczając pracę sił w stanie rzeczywistym z

1

=1 na przemieszczeniach wirtualnych jak na rysunku 1.18

otrzymujemy:

r

11

1

3

16

EI

1
4

1,5 EI

1,5 EI

1
2

0

r

11

1,547 EI

(1.6)

Obliczając pracę sił w stanie rzeczywistym z

2

=1 na przemieszczeniach wirtualnych jak na rysunku 1.18

otrzymujemy:

r

12

1

2 EI

EI

1
2

0

r

12

1,5 EI

(1.7)

Obliczając pracę sił w stanie rzeczywistym z

3

=1 na przemieszczeniach wirtualnych jak na rysunku 1.18

otrzymujemy:

r

13

1

2 EI

EI

1
2

0

r

13

1,5 EI

(1.8)

Aby obliczyć pracę sił w stanie rzeczywistym P oprócz wirtualnych kątów obrotu prętów przedstawionych
na rysunku 1.18. musimy znać również wirtualne przemieszczenia pionowe punktów przyłożenia
wypadkowych sił rzeczywistych od obciążenia ciągłego na prętach 12 i 35. Pręt 35 nie ulega
przemieszczeniu, natomiast pręt 12 ulega wyłącznie przesunięciu równoległemu w poziomie. Obliczając
pracę sił w stanie rzeczywistym P na przemieszczeniach wirtualnych jak na rysunku 1.18 otrzymujemy:

R

1 P

1 0

R

1 P

0 [kN]

(1.9)

Tomasz Terlecki gr 3 KBI

11/18

Uwzględniając powyższe wartości współczynników r

ik

układ równań kanonicznych 1.3. przyjmie postać:

{

1,547 EI z

1

−1,5 EI z

2

−1,5 EI z

3

=0

−1,5 EI z

1

2,659 EI z

2

EI z

3

27=0

−1,5 EI z

1

EI z

2

3,659 EI z

3

−27=0

}

(1.10)

Rozwiązanie powyższego układu jest następujące:

EI z

1

=−10,6897

EI z

2

=−19,2947

EI z

3

=8,2701

(1.11)

Podstawiając wartości niewiadomych (1.11) do wzorów 1.5. otrzymam następujące wartości przęsłowych
momentów przywęzłowych:

M

01

=2,004

M

10

=0

M

12

=0

M

21

=14,287

M

23

=−14,285

M

32

=13,280

M

34

=8,270

M

43

=4,135

M

35

=−21,551

M

53

=0

M

56

=0

M

65

=0

[kNm]

(1.12)

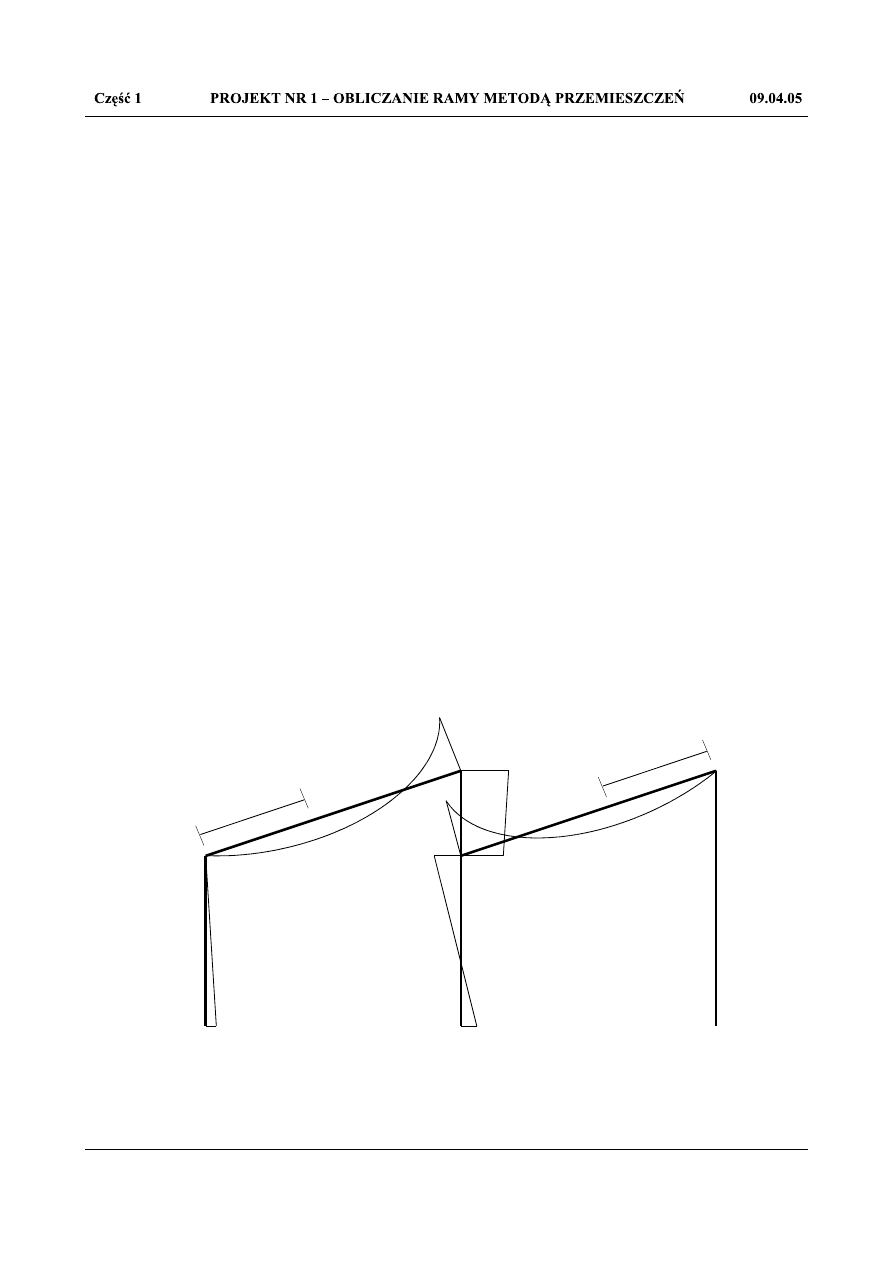
14,287

21,551

2,004

14,285

8,270

4,135

13,280

20,33

2,74

17,3

2,53

Rys.1.19. Momenty zginające w układzie statycznie niewyznaczalnym M

(n)

[kNm]

Tomasz Terlecki gr 3 KBI

12/18

Wstępną kontrolę wykonuję poprzez sprawdzenie równowagi węzła 2 i 3.

Z równowagi węzła 2 otrzymam:

∑

M =14,285−14,287=−0,002 ≈0 [ kNm]

(1.13)

Z równowagi węzła 3 otrzymam:

∑

M =21,551−13,280−8,270=0,001 ≈0 [ kNm]

(1.14)

Mając określone wartości momentów zginających na każdym pręcie układu mogę obliczyć wartości sił
tnących w tych prętach

∑

M

1

=0 ⇒T

01

=T

10

=−0,501 [kN ]

Rys.1.20. Pręt 01

∑

M

1

=0 ⇒14,287T

21

⋅



406⋅6⋅3=0 ⇒ T

21

=−19,335 [kN ]

∑

M

2

=0 ⇒T

12



40−6⋅6⋅314,287=0 ⇒ T

12

=14,817 [kN ]

Rys.1.21. Pręt 12

Tomasz Terlecki gr 3 KBI

13/18

I

1

0

1

N

10

N

01

T

01

T

10

2,004

6 [kN/m]

2

6

I

2

1

2

N

21

N

12

T

12

T

21

14,287

∑

M

2

=0 ⇒13,28−14,285T

32

⋅2=0 ⇒T

32

=T

23

=0,503 [kN ]

Rys.1.22. Pręt 23

∑

M

3

=0 ⇒8,274,1354 T

43

=0 ⇒T

34

=T

43

=−3,101 [kN ]

Rys.1.23. Pręt 34

∑

M

5

=0 ⇒−21,551−36⋅3T

35

⋅



40=0

T

35

=20,484 [kN ]

∑

M

3

=0 ⇒−21,55136⋅3T

53

⋅



40=0

T

53

=−13,669 [kN ]

Rys.1.24. Pręt 35

Tomasz Terlecki gr 3 KBI

14/18

N

23

N

32

T

32

T

23

13,280

2

I

1

2

3

14,285

4

I

1

3

4

N

34

N

43

T

43

T

34

4,135

8,2701

6 [kN/m]

2

6

I

2

3

5

N

53

N

35

T

35

T

53

21,551

Zestawiając otrzymane wyniki otrzymuję:

14,817

- 0,501

19,335

0,503

- 3,101

13,669

+

-

+

+20,484

-

Rys.1.25. Siły tnące w układzie statycznie niewyznaczalnym T

(n)

[kN]

Wyznaczając wartości sił normalnych występujących w zadanej ramie korzystam z równowagi węzłów.

N

12

14,817

1

α

0,501

N

10

α

Rys.1.26. Równowaga węzła 1

Mając dane:

sin

1

10

cos

3

10

(1.15)

Z równowagi węzła 1:

X

0 : 0,501 14,817 sin

N

12

cos

0

N

12

5,467 kN

Y

0 : N

01

14,817 cos

N

12

sin

0

N

01

15,785 kN

(1.16)

Tomasz Terlecki gr 3 KBI

15/18

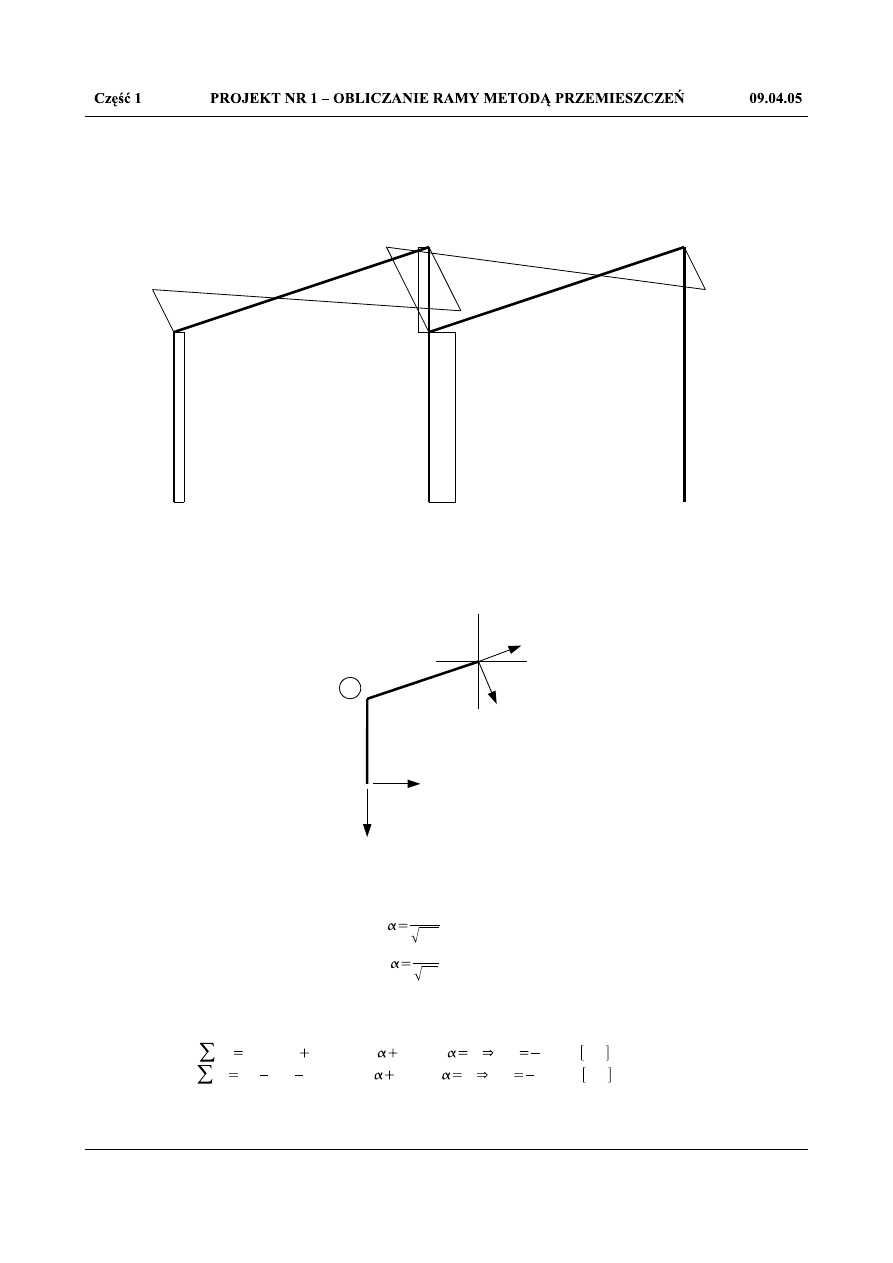
N

21

19,335

2

α

0,503

N

23

α

Rys.1.27.Równowaga węzła 2

Z równowagi węzła 2:

∑

X =0 :− N

21

cos 19,335 sin −0,503=0 ⇒ N

21

=5,915 [kN ]

∑

Y =0 :−N

21

sin −19,335 cos = N

23

⇒ N

23

=−20,213 [kN ]

(1.17)

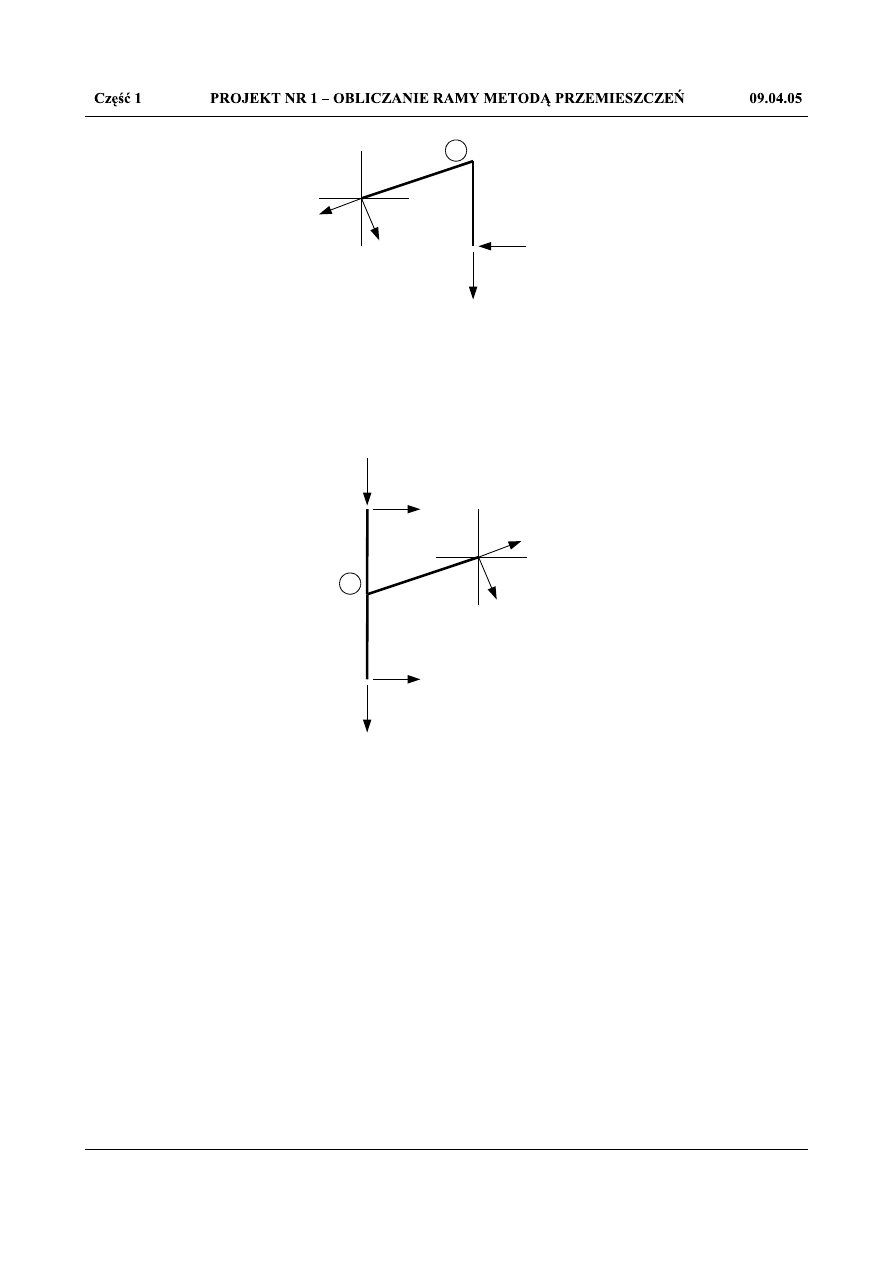
N

35

20,484

3

α

3,101

N

34

α

0,503

20,213

Rys.1.28.Równowaga węzła 3

Z równowagi węzła 3:

∑

X =0 : 0,503 N

35

cos 20,484 sin 3,101=0 ⇒ N

35

=−10,627 [kN ]

∑

Y =0 :−20,213 −N

34

−20,484 cos N

35

sin =0 ⇒ N

34

=−43,006 [kN ]

(1.18)

Aby wykonać równowagę węzła 5 konieczne jest określenie wartości poziomej reakcji H

5

w podporze

występującej w tym węźle. Wykorzystam w tym celu obliczone wcześniej wartości sił z tnących, bowiem
dla całego układu:

∑

X =0 : 0,5013,101−H

5

=0 ⇒ H

5

=3,602 [kN ]

(1.19)

Tomasz Terlecki gr 3 KBI

16/18

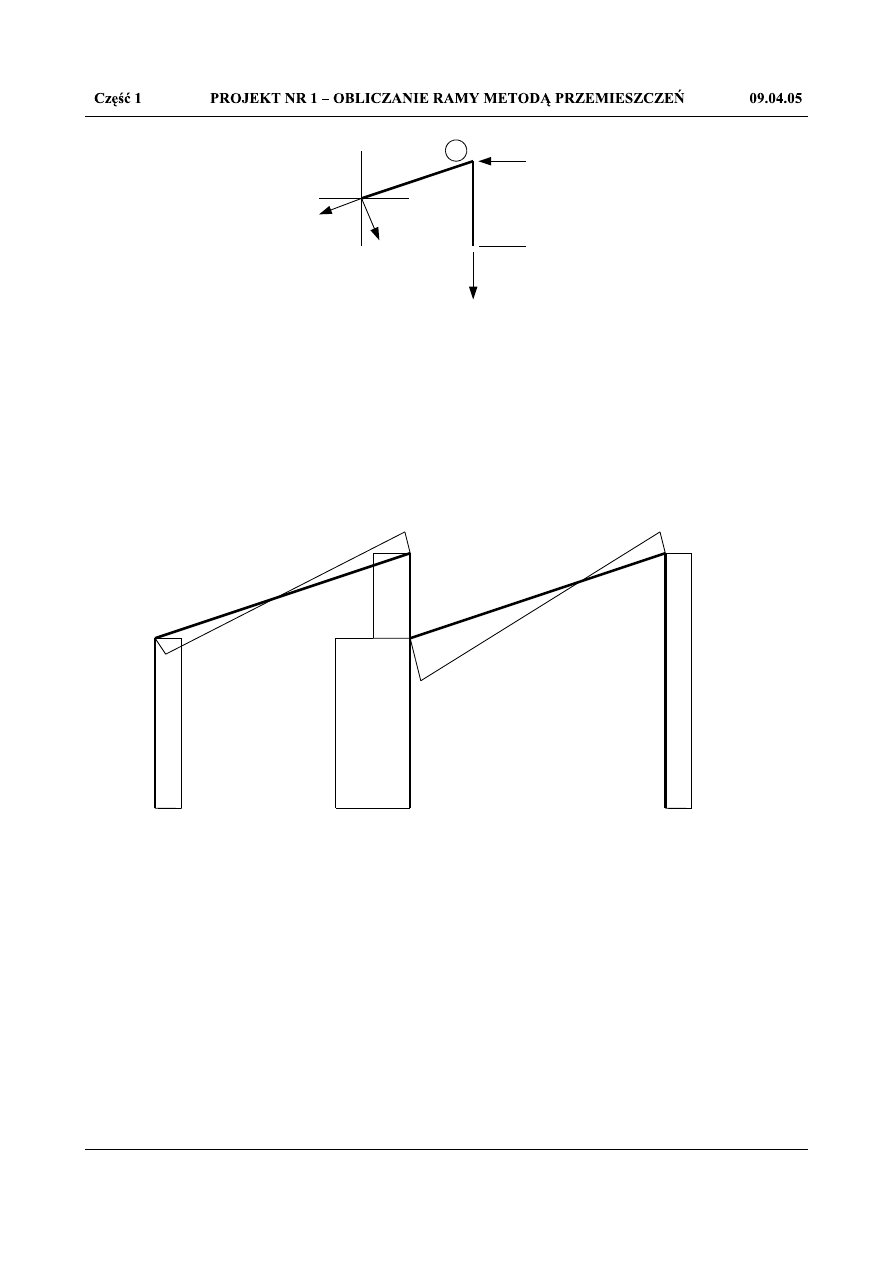
Rys.1.29.Równowaga węzła 5

Z równowagi węzła 5:

∑

X =0 : N

53

cos =13,669 sin −3,602 ⇒ N

53

=0,759 [ kN ]

∑

Y =0 :− N

53

sin −13,669 cos = N

56

⇒ N

56

=−13,208 [kN ]

(1.20)

Zestawiając otrzymane wyniki otrzymuję:

5,467

- 15,785

10,627

-

-

-

5,915

+

43,006

20,213

-

+

0,759

- 13,208

Rys.1.30. Siły normalne w układzie statycznie niewyznaczalnym N

(n)

[kN]

Tomasz Terlecki gr 3 KBI

17/18

N

53

13,669

5

α

0,0

N

56

α

3,602

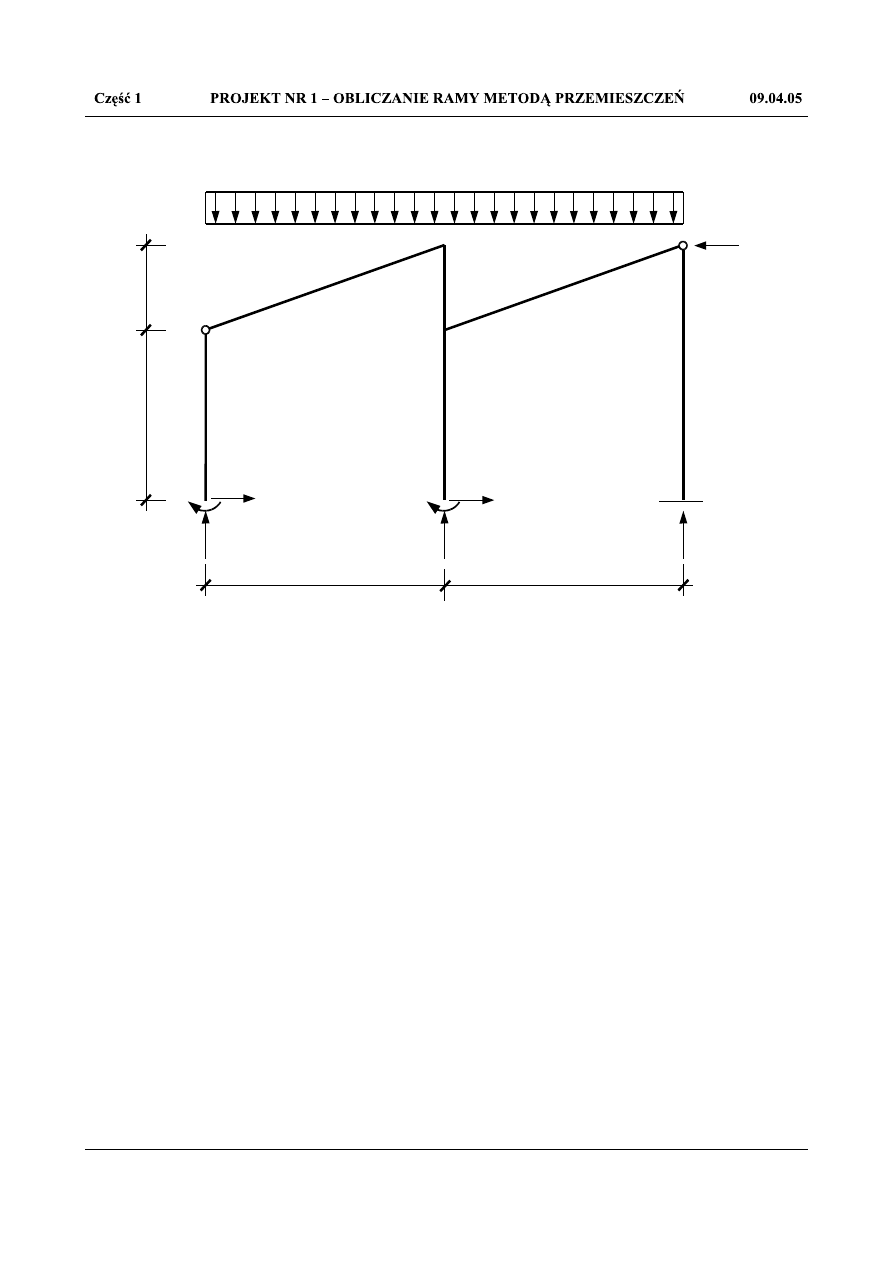
Aby sprawdzić poprawność uzyskanych wyników dokonuję kontroli statycznej:

6 [kN/m]

2

4

6

6

13,208

0,0

3,602

43,006

15,785

3,101

0,501

2,004

4,135

A

Rys.1.31. Kontrola statyczna-siły działające na zadany układ

∑

X =0 : 0,5013,101−3,602=0 [ kN ]

∑

Y =0 :−7215,78543,00613,208=−1⋅10

−3

≈0 [kN ]

∑

M

A

=0 : 2,0044,13515,785⋅6−13,208 ⋅6−3,602 ⋅6=−0,011 ≈0 [kNm]

(1.21)

Tomasz Terlecki gr 3 KBI

18/18