Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

1

1.

POLITECHNIKA POZNA

ŃSKA

Instytut Konstrukcji Budowlanych
Zakład Mechaniki Budowli

PROJEKT NR 1-OBLICZENIE RAMY METOD

Ą PRZEMIESZCZEŃ

1.1. Wpływ obci

ążenia zewnętrznego

Zadanie:

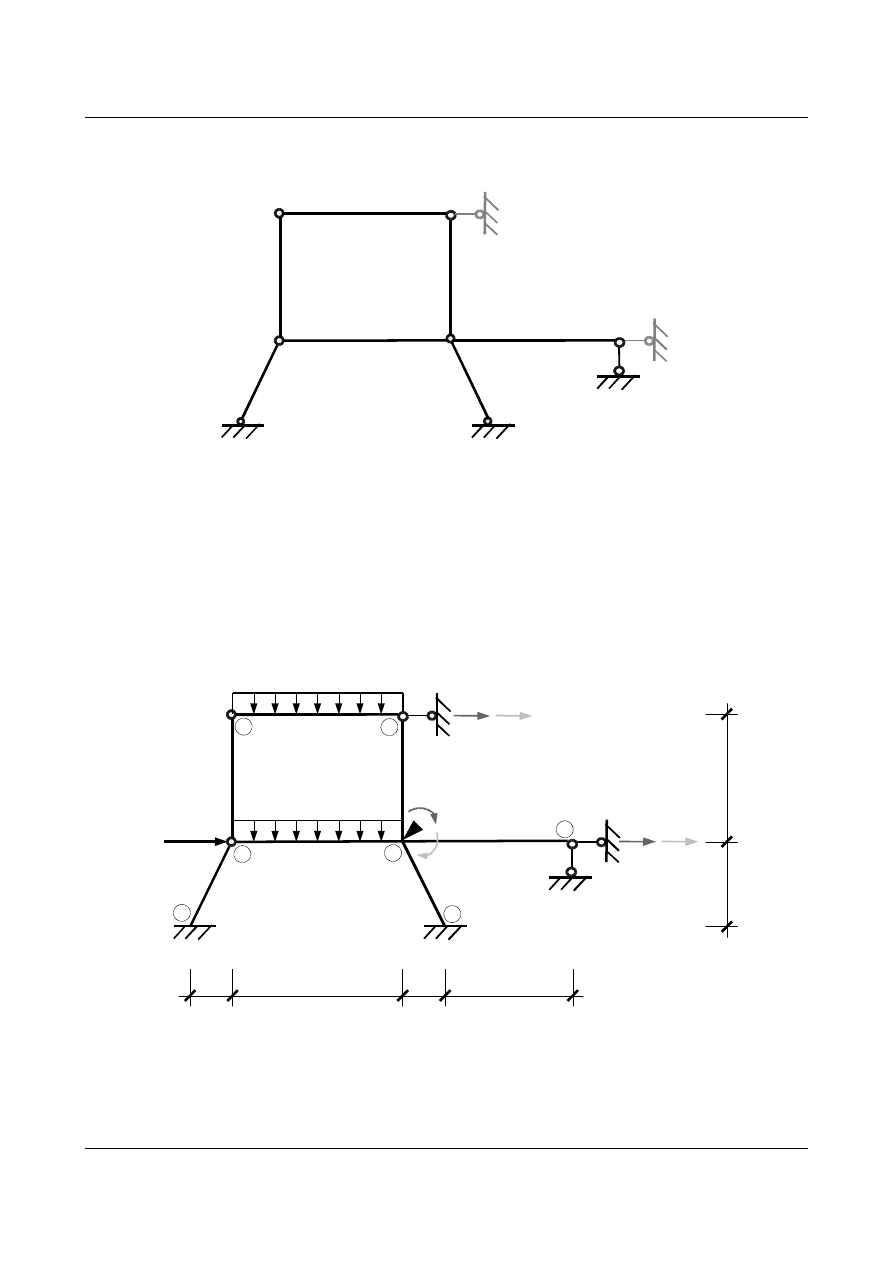
Dla układu przedstawionego na rysunku 1.1 obliczy

ć i wykonać wykresy sił przekrojowych powstałych od

obci

ążenia zewnętrznego. Dokonać odpowiednich sprawdzeń wyników.

10 kN

2 kN/m

6 kN/m

I

1

I

1

I

1

I

1

I

2

I

2

I

2

1

4

1

3

3

2

Rys.1.1. Rama statycznie niewyznaczalna

W zadaniu przyj

ęto przekroje:

I 220 ; I

1

=3060 [cm

4

]=I

I 240 ; I

2

=4250 [cm

4

]=1,389I

Okre

ślenie stopnia geometrycznej niezmienności wg zależności

SGN

=

∑



∑



(1.1)

gdzie:

∑



- liczba w

ęzłów sztywnych układu (z wyłączeniem węzłów podporowych)

∑



- liczba niezale

żnych przesuwów możliwych w układzie

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

2

Liczb

ę w.w. przesuwów określam wykorzystując łańcuch kinematyczny jak na rysunku 1.2:

Rys.1.2.Ła

ńcuch kinematyczny

Jak łatwo zauwa

żyć

∑

=2

, natomiast

∑

=1

st

ąd otrzymujemy:

SGN

=3

(1.2)

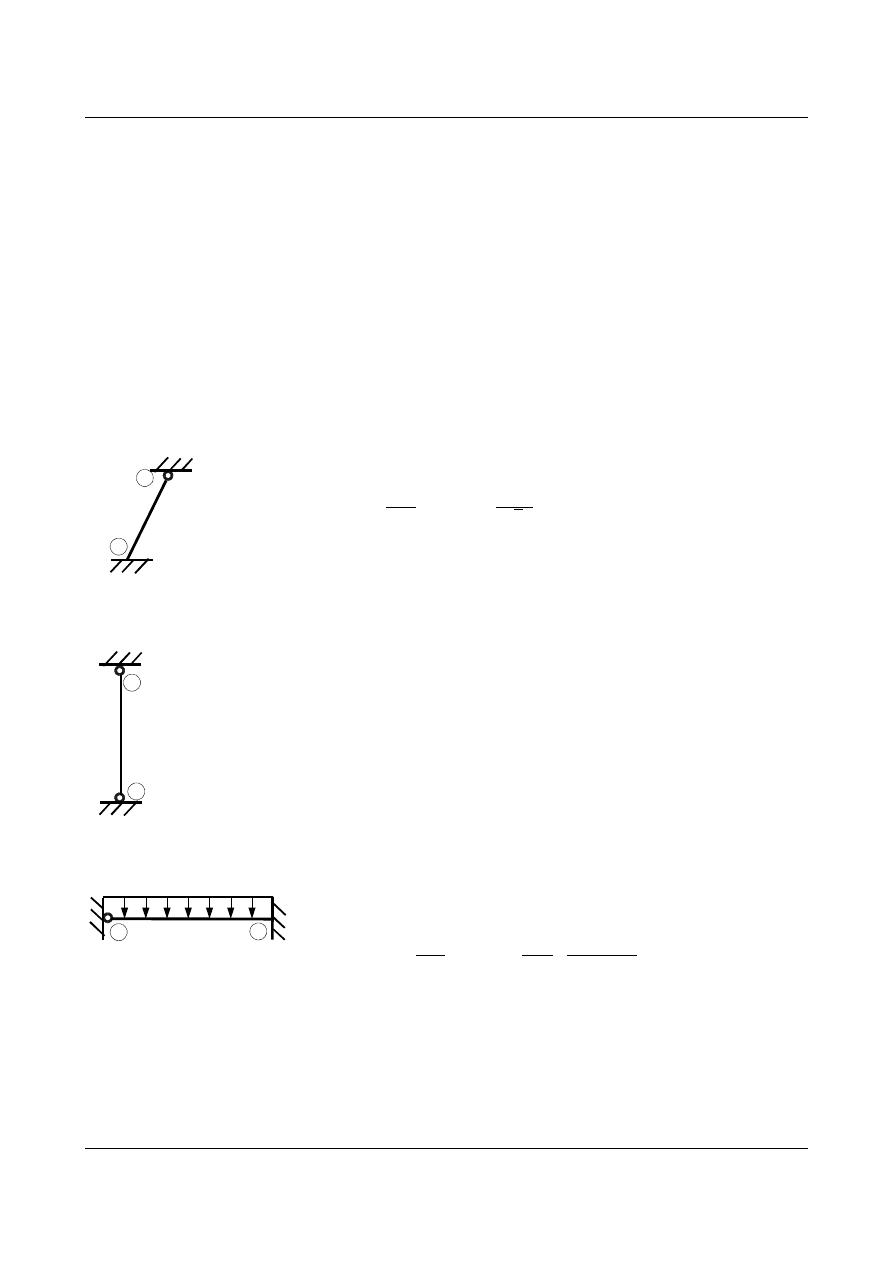
Aby rozpocz

ąć rozwiązywanie zadania metodą przemieszczeń w pierwszej kolejności przyjmuję odpowiedni

układ podstawowy:

10 kN

2 kN/m

6 kN/m

I

1

I

1

I

1

I

1

I

2

I

2

I

2

u

3

=z

1

R

1

u

6

=z

2

R

2

φ

4

=z

3

R

3

1

0

2

3

4

5

6

1

4

1

3

3

2

Rys.1.3.Układ podstawowy

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

3

Identyczno

ść statyczną układu podstawowego z wyjściowym zapewnia układ równań kanonicznych:

{

R

1

=0

R

2

=0

R

3

=0

}

{

r

11

z

1

r

12

z

2

r

13

z

3

R

1P

=0

r

21

z

1

r

22

z

2

r

23

z

3

R

2P

=0

r

31

z

1

r

32

z

2

r

33

z

3

R

3P

=0

}

(1.3)

Aby okre

ślić wartości współczynników r

ik

nale

ży określić wartości momentów zginających wywołanych

stanami z

1

=1, z

2

=1, z

3

=1 oraz stanem obci

ążenia rzeczywistego (siłami zewnętrznymi). W tym celu po

pierwsze nale

ży skorzystać ze wzorów transformacyjnych metody przemieszczeń umożliwiających znalezienie

momentów M

ik

jako funkcji z

1

, z

2

, z

3

, “P”.

Otrzymujemy zatem:

M

01

=

3EI

1

l

01

⋅

0



01

=

3EI



5

⋅

01

M

10

=0

[kNm]

Rys.1.4. Pr

ęt 01

M

12

=0

M

21

=0

[kNm]

Rys.1.5. Pr

ęt 12

M

14

=0

M

41

=

3EI

2

l

14

⋅

4



14



6

⋅4

2

8

=

3

⋅1,389EI

4

⋅ z

3



14

12

[kNm]

Rys.1.6. Pr

ęt 14

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

I

1

1

0

I

1

1

2

I

2

1

4

6 kN/m

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

4

M

23

=0

M

32

=0

[kNm]

Rys.1.7. Pr

ęt 23

M

34

=0

M

43

=

3EI

1

l

34

⋅

4



34

=EI⋅ z

3



34



[kNm]

Rys.1.8 Pr

ęt 34

M

45

=

2EI

1

l

45

⋅2 

4



5

3 

45

=

2EI



5

⋅2z

3

3 

45



M

54

=

2EI

1

l

45

⋅

4

2 

5

3 

45

=

2EI



5

⋅ z

3

3 

45



[kNm]

Rys.1.9. Pr

ęt 45

M

64

=0

M

46

=

3EI

2

l

46

⋅

4



46

=

3

⋅1,389 EI

4

⋅z

3



46



[kNm]

Rys.1.10. Pr

ęt 46

Pojawiaj

ące się wartości kątów obrotów cięciw (prętów) należy określić z równania łańcucha kinematycznego

jako funkcje niezale

żnych przesuwów (tutaj z

1

oraz z

2

):



ik

= f  z

1,

z

2

= f  z

1

 f  z

2



(1.4)

I etap to okre

ślenie funkcji



ik

= f  z

1



:

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

I

2

2

3

2 kN/m

I

1

4

5

I

2

4

6

4

3

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

5

z

1

Ψ

34

1

0

2

3

4

5

6

Ψ

12

Rys.1.11 Ła

ńcuch kinematyczny w stanie z

1

Jak łatwo stwierdzi

ć w tym przypadku:



12

=

34



01

=

14

=

45

=

46

=

23

=0

[rad]

(1.5)

Rozpisuj

ąc natomiast równanie łańcucha kinematycznego na drodze 0123 na kierunek poziomy otrzymujemy:

0123

 02 

01

3

12

=z

1

⇒

12

=

34

=

z

1

3

[rad]

(1.6)

II etap to okre

ślenie funkcji



ik

= f  z

2



:

Ψ

12

z

2

Ψ

34

Ψ

01

Ψ

45

Ψ

14

Ψ

23

Ψ

46

Rys.1.12 Ła

ńcuch kinematyczny w stanie z

2

Rozpisuj

ę równanie łańcucha kinematycznego dla podanych niżej dróg:

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

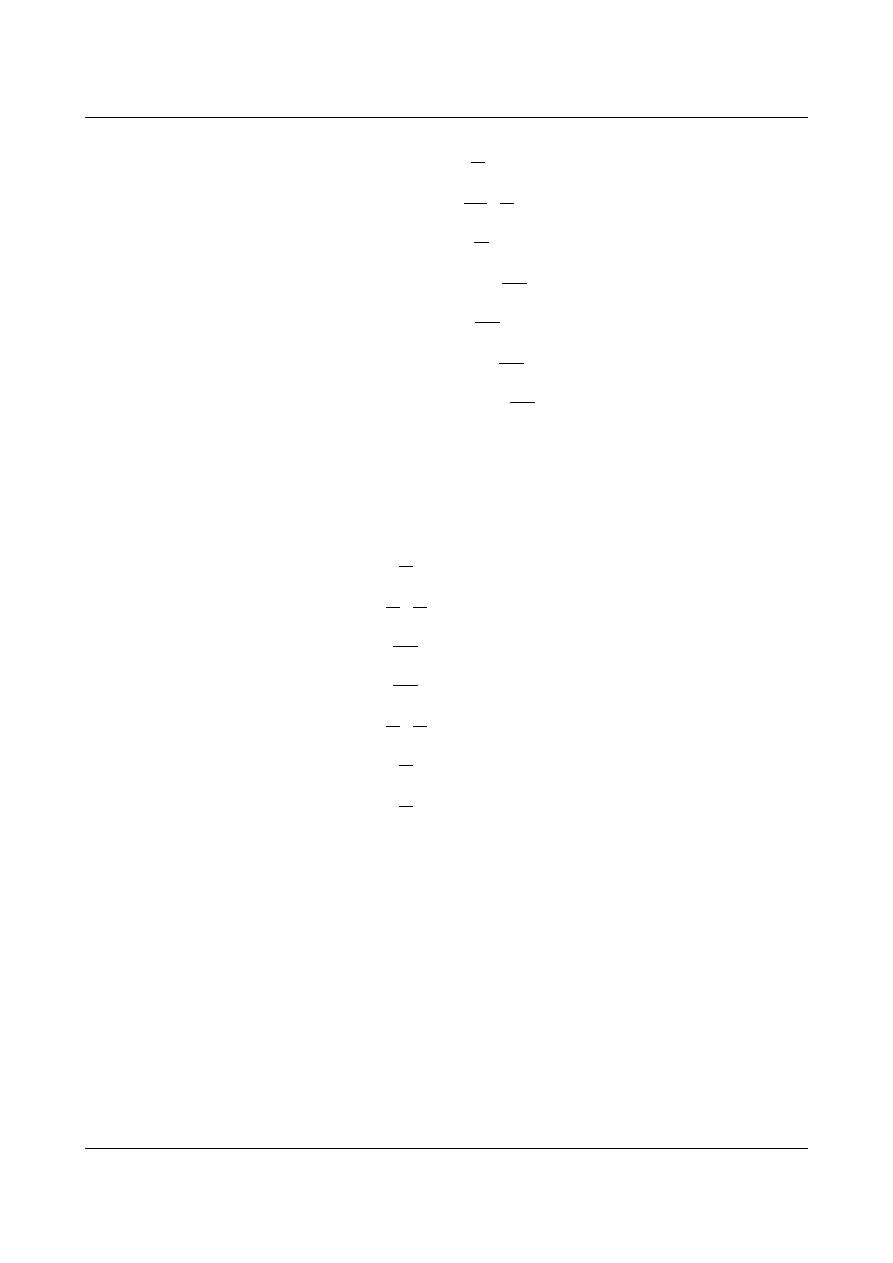
Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

6

546

 02

45

=z

2

⇒

45

=

z

2

2

546

 0

45

4

46

=0 ⇒

46

=



45

4

=

z

2

8

0146

 02 

01

=z

2

⇒

01

=

z

2

2

0146

 0

01

4

14

4

46

=0 ⇒

14

=

z

2

4

346

 03

34

0=z

2

⇒

34

=

z

2

3

0123

 02

01

3

12

0=0 ⇒

12

=

z

2

3

012346

 0

01

4

23

4

46

=0 ⇒

23

=

z

2

4

[rad]

(1.7)

Zestawienie



ik

= f  z

1,

z

2

= f  z

1

 f  z

2



(z zasady superpozycji):



01

=

z

2

2



12

=

z

1

3



z

2

3



23

=

z

2

4



14

=

z

2

4



34

=

z

1

3



z

2

3



45

=

z

2

2



46

=

z

2

8

[rad]

(1.8)

St

ąd wartości momentów przęsłowych wynoszą;

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

7

M

01

=

3EI



5

⋅

z

2

2

M

10

=0

M

12

=0

M

21

=0

M

14

=0

M

41

=

4,167 EI

4

⋅ z

3



z

2

4

12

M

23

=0

M

32

=0

M

34

=0

M

43

=EI⋅ z

3



z

1

3



z

2

3



M

45

=

2EI



5

⋅2z

3



3
2

⋅z

2



M

54

=

2EI



5

⋅z

3



3
2

⋅z

2



M

64

=0

M

46

=

4,167 EI

4

⋅ z

3



z

2

8



[kNm]

(1.9)

Na podstawie wzorów 1.9 okre

ślam wartości momentów od poszczególnych stanów obciążeń:

Stan z

1

=1

1

0

2

3

4

5

6

EI
3

-EI
3

r

11

r

21

r

31

Rys.1.13. Stan z

1

=1 – M

1

(0)

Stan z

2

=1

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

8

0,671 EI

r

12

r

22

r

32

1,342 EI

0,26 EI

1,342 EI

0,13 EI

EI
3

-1,342 EI

0,26 EI

-1,342 EI

-0,13 EI

EI
3

-0,671 EI

Rys.1.14. Stan z

2

=1- M

2

(0)

Stan z

3

=1

r

13

r

23

r

33

0,894 EI

1 EI

1,042 EI

0,894 EI

1,042 EI

1,789 EI

1,042 EI

1 EI

1,789 EI

1,042 EI

Rys.1.15. Stan z

3

=1- M

3

(0)

Stan P

4

R

1P

R

3P

12

R

2P

12

24

8

10

Rys.1.16 Stan P – obci

ążenie zewnętrzne -M

P

[kNm]

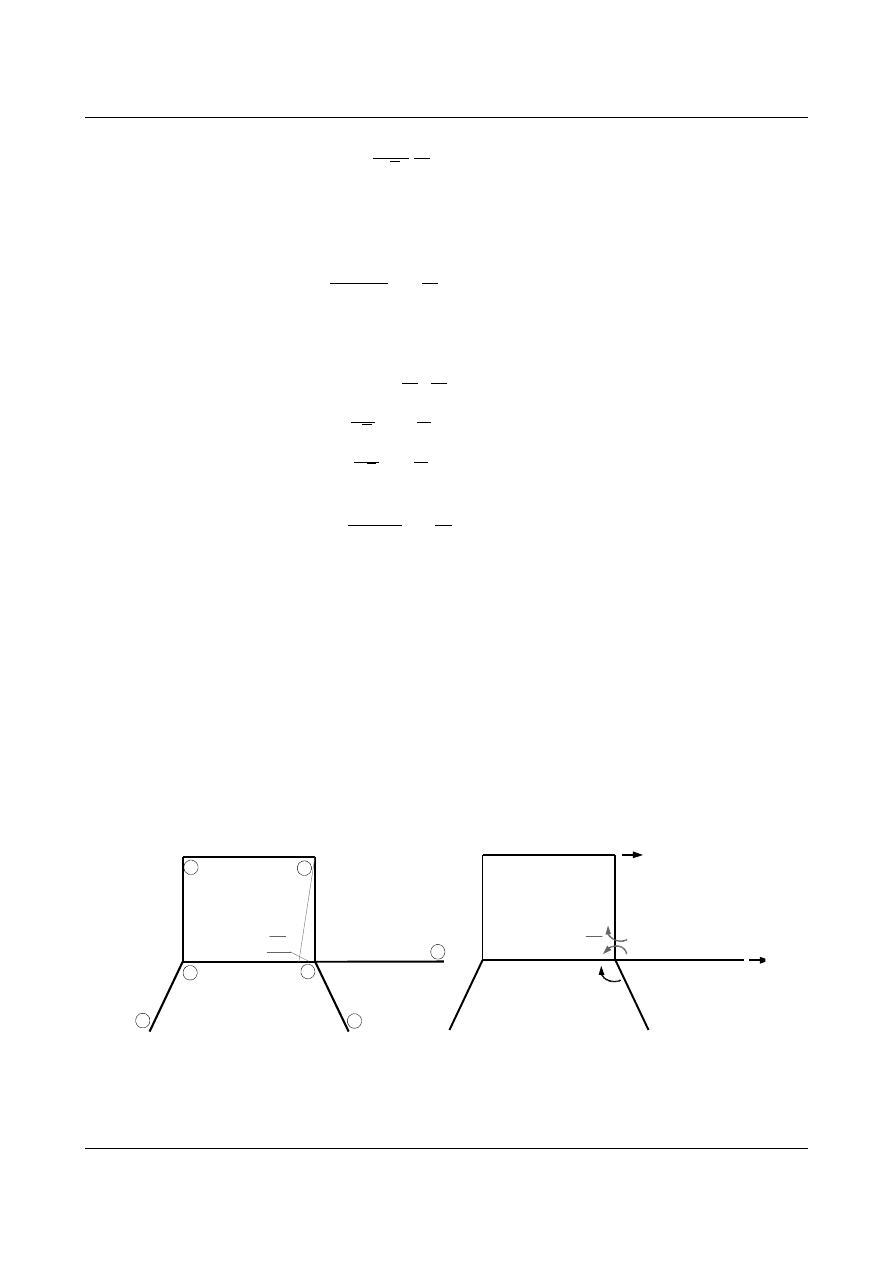
Okre

ślenie współczynników r

ik

dla trzeciego równania kanonicznego a wi

ęc r

31

, r

32

, r

33

, R

3P

z wykorzystaniem

równowagi w

ęzła 4:

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

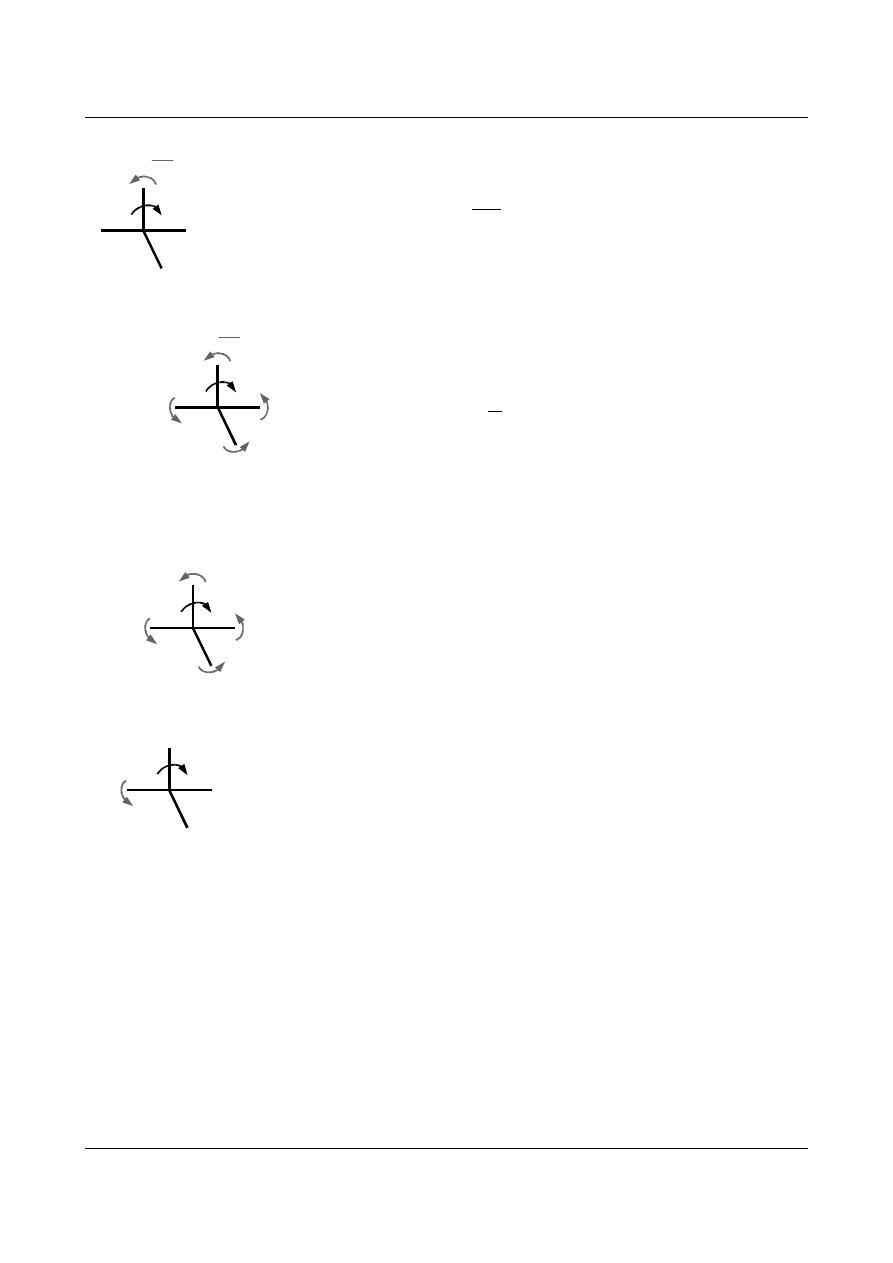
Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

9

r

31

=

EI

3

Rys.1.17 Równowaga w

ęzła 4 w stanie z

1

=1

r

32

=EI 

1
3

0,261,3420,13

r

32

=0,8787 EI

Rys.1.18 Równowaga w

ęzła 4 w stanie z

2

=1

r

33

=EI 1 2 ⋅1,0421,789

r

33

=4,873 EI

Rys.1.19 Równowaga w

ęzła 4 w stanie z

3

=1

R

3P

=12 [kNm]

Rys.1.20 Równowaga w

ęzła 4 w stanie P

Aby obliczy

ć pozostałe współczynniki układu równań kanonicznych r

ik

nale

ży skorzystać z zasady pracy

wirtualnej w wirtualnym stanie przemieszcze

ń.

Stan wirtualny I -



z

1

=1

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

r

31

- EI
3

r

32

0,26 EI

-1,342 EI

-0,13 EI

EI
3

r

33

1,042 EI

1,789 EI

1,042 EI

1 EI

R

3P

12

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

10

z

1

=1

Ψ

34

=

1

0

2

3

4

5

6

Ψ

12

=

1
3

1
3

Rys.1.21. Stan wirtualny przemieszcze

ń z

1

=1

Obliczaj

ąc pracę sił w stanie rzeczywistym z

1

=1 na przemieszczeniach wirtualnych jak na rysunku 1.21

otrzymujemy:

r

11

⋅1

1

3

⋅

EI

3

=0 ⇒r

11

=

EI

9

(1.10)

Obliczaj

ąc pracę sił w stanie rzeczywistym z

2

=1 na przemieszczeniach wirtualnych jak na rysunku 1.21

otrzymujemy:

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

11

r

12

⋅1

1

3

⋅

EI

3

=0 ⇒ r

12

=

EI

9

(1.11)

Obliczaj

ąc pracę sił w stanie rzeczywistym z

3

=1 na przemieszczeniach wirtualnych jak na rysunku 1.21

otrzymujemy:

r

13

⋅1

1

3

⋅EI=0 ⇒ r

13

=

EI

3

(1.12)

Obliczaj

ąc pracę sił w stanie rzeczywistym P na przemieszczeniach wirtualnych jak na rysunku 1.21

otrzymujemy:

R

1P

⋅1=0 ⇒R

1P

=0 [kN ]

(1.13)

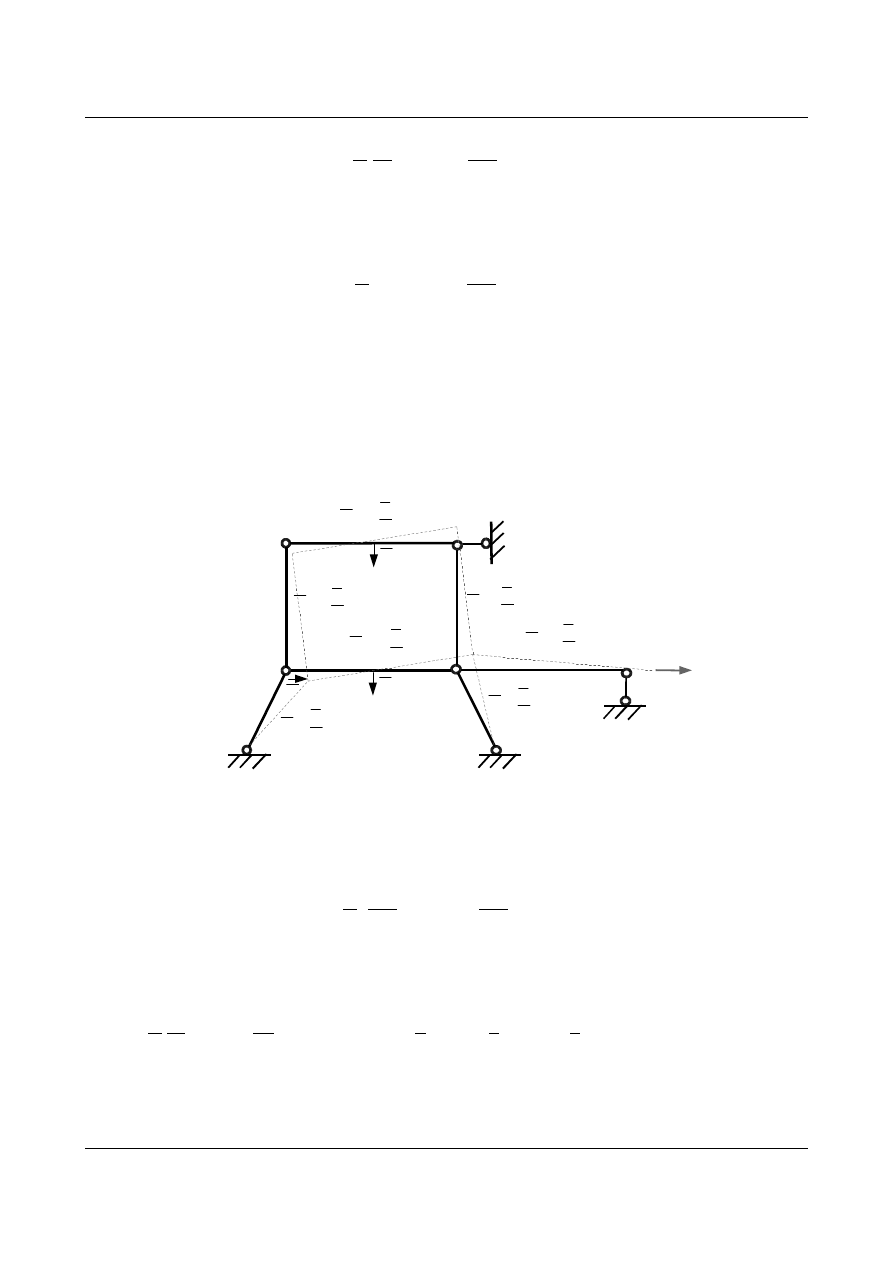
Stan wirtualny II -

z

2

=1

Rys.1.22. Stan wirtualny przemieszcze

ń



z

2

=1

Obliczaj

ąc pracę sił w stanie rzeczywistym z

1

=1 na przemieszczeniach wirtualnych jak na rysunku 1.22

otrzymujemy:

r

21

⋅1

1

3

⋅

EI

3

=0 ⇒r

11

=

EI

9

(1.14)

Obliczaj

ąc pracę sił w stanie rzeczywistym z

2

=1 na przemieszczeniach wirtualnych jak na rysunku 1.22

otrzymujemy:

r

22

⋅1

1

3

⋅

EI

3

0,26 EI⋅

1

4

1,3421,342 EI⋅

1

2

0,13EI⋅

1

8

0,671 EI⋅

1

2

=0 ⇒r

22

=1,87 EI

(1.15)

Obliczaj

ąc pracę sił w stanie rzeczywistym z

3

=1 na przemieszczeniach wirtualnych jak na rysunku 1.22

otrzymujemy:

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

Ψ

12

= -

1
3

z

2

=1

Ψ

34

= -

1
3

1
3

Ψ

01

=

1

1
2

Ψ

45

=

1

1

2

Ψ

14

= -

1

1

4

Ψ

23

= -

1

1
4

Ψ

46

=

1

1

8

v

A

v

B

u

1

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

12

r

23

⋅1EI⋅

1

3

1,042EI⋅

1

4

1,7890,894EI⋅

1
2

1,042 EI⋅

1
8

=0 ⇒r

23

=0,8782 EI

(1.16)

Aby obliczy

ć pracę sił w stanie rzeczywistym P oprócz wirtualnych kątów obrotu prętów przedstawionych na

rysunku 1.22. musimy zna

ć również wirtualne przemieszczenia pionowe punktów A, B (punkty przyłożenia sił

wypadkowych od obci

ążenia ciągłego na prętach 14 i 23) oraz poziome przemieszczenie wirtualne węzła 1

(jako droga, na której prac

ę wykonuje pozioma siła 10 [kN]).

Warto

ści szukanych przemieszczeń wyznaczam z równania łańcucha kinematycznego:

01

 02 ⋅ 



01

= u

1

⇒ 

u

1

=2 ⋅

1

2

= 

1

012A

 0 



01

2 



23

= 

v

A

⇒ v

A

=

1

2

2 ⋅

1

4

=0

01B

 0 



01

2 



14

= 

v

B

⇒ 

v

B

=

1

2

2 ⋅

1
4

=0

(1.17)

St

ąd z zasady pracy wirtualnej:

R

2P

⋅112 ⋅

1

4

 

1

⋅10=0 ⇒ R

2P

=7 [kN ]

(1.18)

Uwzgl

ędniając powyższe wartości współczynników r

ik

układ równa

ń kanonicznych 1.3. przyjmie postać:

{

EI

9

z

1



EI

9

z

2



EI

3

z

3

=0



EI

9

z

1

1,87EI z

2

0,879 EI z

3

7=0



EI

3

z

1

0,879EI z

2

4,873 EI z

3

12=0

}

(1.19)

Rozwi

ązanie powyższego układu jest następujące:

EI z

1

=4,735

EI z

2

=2,352

EI z

3

=2,362

(1.20)

Podstawiaj

ąc wartości niewiadomych (1.20) do wzorów 1.9. otrzymam następujące wartości przęsłowych

momentów przyw

ęzłowych:

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

13

M

01

=1,578

M

10

=0

M

12

=0

M

21

=0

M

14

=0

M

41

=10,152

M

23

=0

M

32

=0

M

34

=0

M

43

=0

M

45

=7,381

M

54

=5,268

M

64

=0

M

46

=2,767

[kNm]

(1.21)

Rys.1.23. Momenty zginaj

ące w układzie statycznie niewyznaczalnym M

(n)

[kNm]

Maksymalne warto

ści momentów wynoszą:

∣M

max1

∣=7,381 [kNm ]

dla pr

ętów o sztywności EI

1

∣M

max2

∣=10,152 [kNm]

dla pr

ętów o sztywności EI

2

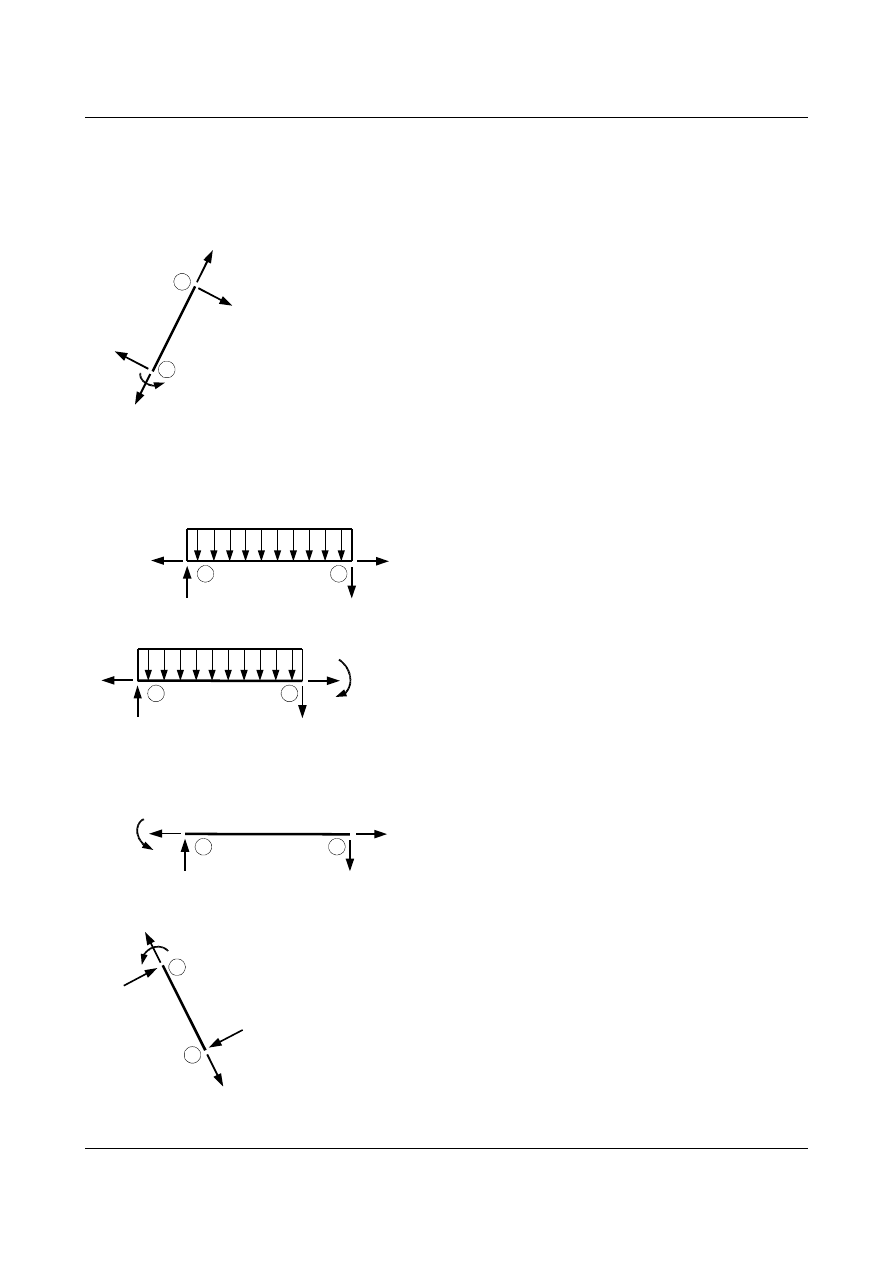
Wst

ępną poprawność wyników wykazuję poprzez sprawdzenie równowagi węzła 4:

10,152

2,767

7,381

Rys.1.24 Równowaga w

ęzła 4

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

10,152

4

1,578

5,268

7,381

2,767

7,46

1,58

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

14

∑

M

=7,3812,76710,152=0,004 ≈0 [kNm]

(1.22)

Maj

ąc określone wartości momentów zginających na każdym pręcie układu mogę obliczyć wartości sił

tn

ących w tych prętach

∑

M

0

=0 ⇒T

01

=T

10

=0,706 [kN ]

Rys.1.25. Pr

ęt 01

T

12

=T

21

=0 [kN]

T

34

=T

43

=0 [kN]

∑

M

2

=0 ⇒T

32

=4 [kN]

∑

M

3

=0 ⇒T

23

=4 [kN]

Rys.1.26. Pr

ęt 23

∑

M

1

=0 ⇒T

41

=14,538 [kN ]

∑

M

4

=0 ⇒T

14

=9,462 [kN ]

Rys.1.27. Pr

ęt 14

∑

M

4

=0 ⇒T

64

=0,692 [kN ]

∑

M

6

=0 ⇒T

46

=0,692 [kN ]

Rys.1.28. Pr

ęt 46

∑

M

4

=0 ⇒T

54

=5,657 [kN]

T

45

=T

54

=5,657 [kN ]

Rys.1.29 Pr

ęt 45

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

1

0

N

01

N

10

T

10

T

01

1,578

2

3

N

23

N

32

T

32

T

23

2 [kN/m]

1

4

N

14

N

41

T

41

T

14

6 [kN/m]

10,152

4

6

N

46

N

64

T

64

T

46

2,767

N

54

N

45

T

54

T

45

7,381

4

5

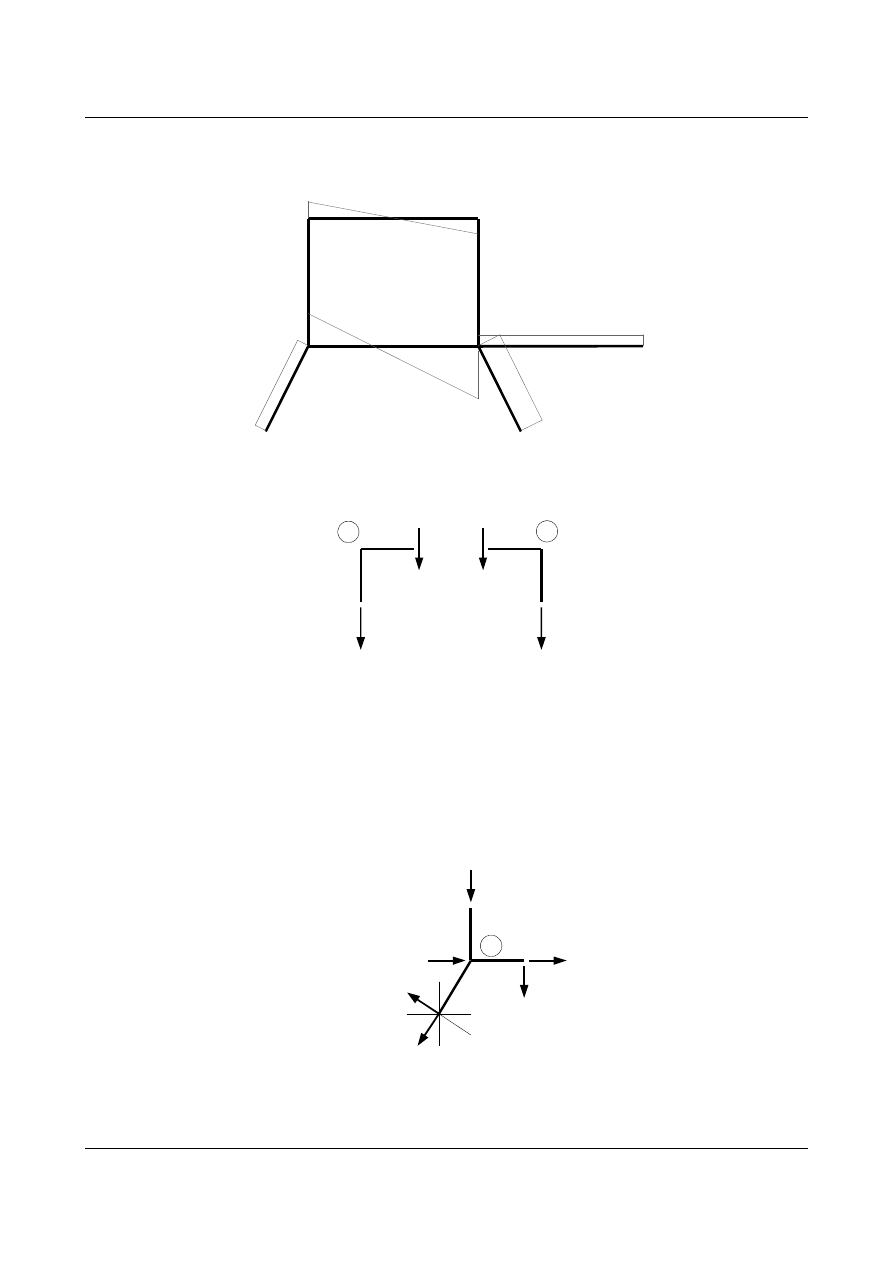
Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

15

Zestawiaj

ąc otrzymane wyniki otrzymuję:

4

4

-

+

+

-

9,462

14,538

+ 5,657

+

0,692

+

0,706

Rys.1.30. Siły tn

ące w układzie statycznie niewyznaczalnym T

(n)

[kN]

Wyznaczaj

ąc wartości sił normalnych występujących w zadanej ramie korzystam z równowagi węzłów.

4 [kN]

N

12

=N

21

N

34

=N

43

2

3

Rys.1.31. Równowaga w

ęzłów 2 i 3

Z równowagi w

ęzła 2:

N

12

=N

21

=4 [kN ]

(1.23)

Z równowagi w

ęzła 3:

N

34

=N

43

=4 [kN ]

(1.24)

10

4

N

14

=N

41

9,462

0,706

N

01

=N

10

α

α

1

Rys.1.32.Równowaga w

ęzła 1

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

16

Dane:

sin

=



5

5

; cos

=

2



5

5

Z równowagi w

ęzła 1:

∑

Y

=0 :49,462N

01

cos

0,706 sin=0 ⇒N

01

=N

10

=14,698 [kN ]

∑

X

=0 :10N

14

0,706 cos 14,698 sin=0 ⇒N

14

=N

41

=15,942 [kN ]

(1.25)

Dla pr

ęta 46 otrzymujemy:

N

46

=N

64

=0 [kN ]

(1.26)

4

15,942

14,538

0,692

N

45

=N

54

α

α

5,657

4

Rys.1.33.Równowaga w

ęzła 4

Dane:

sin

=



5

5

; cos

=

2



5

5

Z równowagi w

ęzła 4:

∑

X

=0 :15,9425,657cos N

45sin

=0 ⇒ N

45

=N

54

=24,333 [kN]

(1.27)

Zestawiaj

ąc otrzymane wyniki otrzymuję:

Rys.1.34. Siły normalne w układzie statycznie niewyznaczalnym N

(n)

[kN]

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

4

4 -

-

-

-

14,698

-

15,942

24,333

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

17

Aby sprawdzi

ć poprawność uzyskanych wyników dokonuję kontroli statycznej:

10 kN

2 kN/m

6 kN/m

0,706

14,698

α

α

0,692

24,333

α

α

5,657

1,578

5,268

Rys.1.35. Kontrola statyczna-siły działaj

ące na zadany układ

∑

X

=0 :0,706 cos14,698 sin105,657 cos 24,333 sin =0,00014 ≈0 [kN ]

∑

Y

=0 :14,69824,333 cos 0,7065,657sin 0,6922 ⋅46 ⋅4=0,00423 ≈0 [kN ]

∑

M

1

=0:1,5780,706⋅



5

5,2686 ⋅4 ⋅22 ⋅4 ⋅20,692 ⋅824,333cos ⋅5sin ⋅2

5,657 cos ⋅2sin ⋅5=0,0187 ≈0 [kNm]

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater

Cz

ęść 1

PROJEKT NR 1 – OBLICZANIE RAMY METOD

Ą PRZEMIESZCZEŃ

18

Sprawdzenie napr

ężeń normalnych wywołanych momentami zginającymi.

Napr

ężenia określam wg zależności:

 =

∣M

max

∣

I

y

⋅z

max

 ≤

dop

Przyjmuj

ę:



dop

=19 [kN /cm

2

]

Na pr

ętach o sztywności EI

1

maksymalny moment zginaj

ący:

∣M

max1

∣=7,381 [kNm]=738,1 [kNcm]

dla

I

1

=3060 [cm

4

], I 220  z

max

=11 cm

st

ąd:

 =

738,1

3060

⋅11 =2,65 [

kN

cm

2

]

2,65

[

kN

cm

2

]≤19 [

kN

cm

2

]

Na pr

ętach o sztywności EI

2

maksymalny moment zginaj

ący:

∣M

max 2

∣=10,152 [kNm ]=1015,2 [kNcm]

dla

I

2

=4250 [cm

4

], I 240  z

max

=12 cm

st

ąd:

 =

1015,2

4250

⋅12=2,87 [

kN

cm

2

]

2,87

[

kN

cm

2

]≤19 [

kN

cm

2

]

Napr

ężenia w obu przypadkach są znacznie mniejsze od dopuszczalnych . Wniosek: kształtowniki, z których

wykonano konstrukcj

ę mogłyby mieć mniejsze przekroje.

Anna Zielona gr 3KBI Metoda przemieszcze

ń

AlmaMater