
Krzysztof Wójtowicz
Strona 1
Politechnika Poznańska Projekt wykonał: Krzysztof Wójtowicz
Instytut Konstrukcji Budowlanych Konsultacje: dr inż. Przemysław Litewka
Zakład Mechaniki Budowli
Obliczenie Ramy Metodą Przemieszczeń
Zakładamy przekroje dwuteowe:
I1- I220 -I1=3060 cm
4
I2- I240 -I2=4250 cm
4
1,389I1
I2
1,389
3060
4250
I1
I2
=
⇒
=
=
Krzysztof Wójtowicz
Strona 2
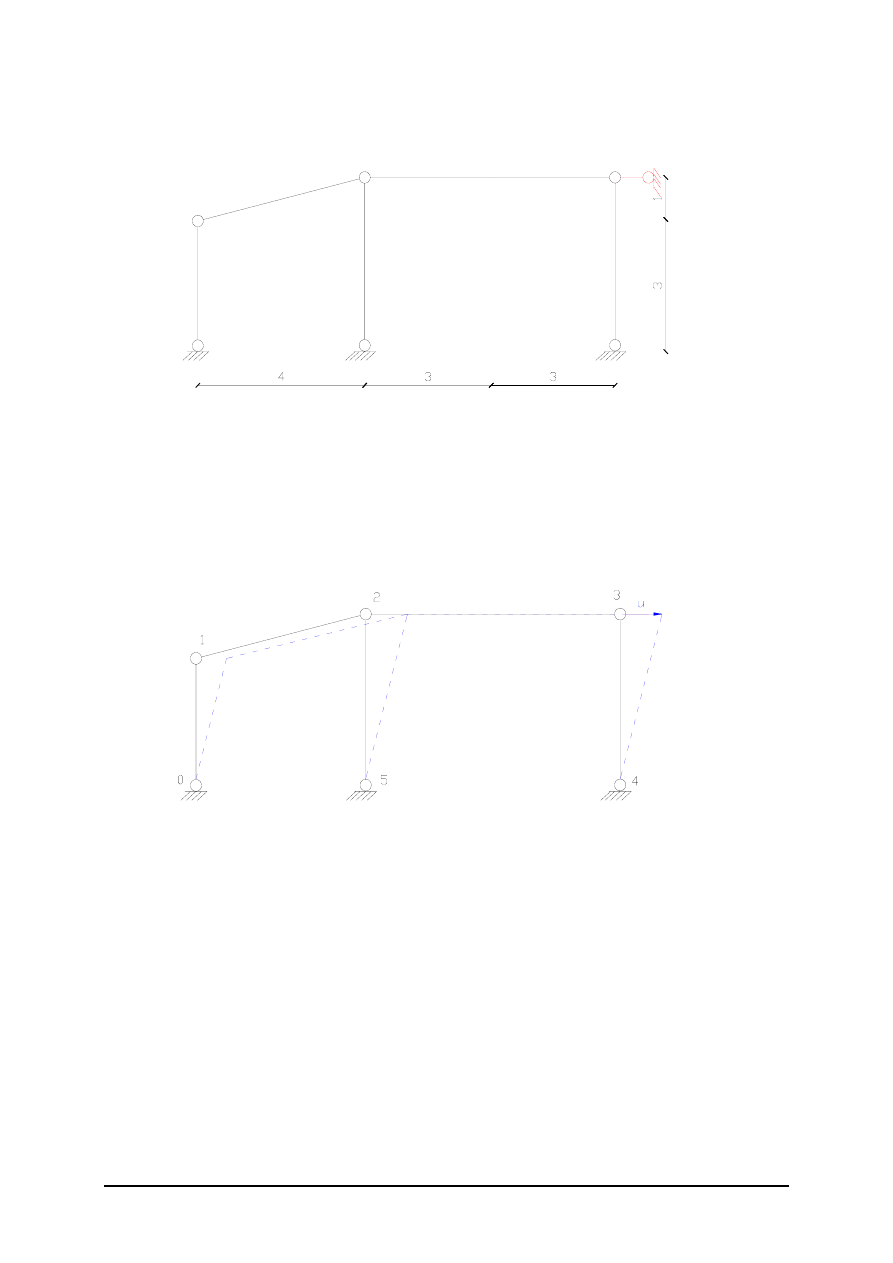
Tworzymy łańcuch kinematyczny w celu określenia niezależnych przemieszczeń.
Aby układ był kinematycznie niezmienny i statycznie wyznaczalny wystarczy dodać 1
podporę, w naszym przypadku jest to podpora oznaczona kolorem czerwonym. Zatem
układ posiada jedno niezależne przemieszczenie „u”, któremu towarzyszą
przemieszczenia kątowe „
Ψ
” poszczególnych prętów.
Ponieważ pręty nie ulegają skróceniu (pręt 52 oraz 43 nie dozna przemieszczenia
pionowego) zatem pręty 12 i 23 doznają tylko przemieszczeń poziomych równych „u” a
kąt
Ψ
52
=
Ψ
43

Krzysztof Wójtowicz
Strona 3
Równania łańcucha kinematycznego
Ψ
23
=0 – z uwagi na brak przesuwu pionowego pręta 43 oraz 52
43
→
0+
Ψ
43
*4= u
⇒
Ψ
43
=
Ψ
52
= 0,25u =0,25
⋅
z3
0125
↓
0+
Ψ
01
*0+
Ψ
12
*4+0= 0
⇒
Ψ
12
=0
012
→
0+
Ψ
01
*3+
Ψ
12
*1= u
⇒
Ψ
01
=
z3
0,3333
0,3333u
u
3
1
⋅
=
=
Układ podstawowy
SGN=3
z1, z2, z3- przemieszczenia po kierunku reakcji R1, R2 ,R3
=
+
+
+
=
+
+
+
=
+
+
+
⇒
=
=
=
0
r
z3
r
z2
r
z1
r
0
r
z3
r
z2
r
z1
r
0
r
z3
r
z2
r
z1
r
0
R3
0
R2
0
R1
3P
33
32
31
2P
23
22
21
1P
13
12
11

Krzysztof Wójtowicz
Strona 4
Zapisujemy momenty węzłowe dla poszczególnych prętów korzystając z wzorów
transformacyjnych
1,5
z3
0,6666EI
z1
1,333EI
12
3
2
z3)
0,3333
3
0
z1
(2
3
2EI
M
1,5
z3
0,6666EI
z1
0,6667EI
12
3
2
z3)
0,3333
3
z1
0
(2
3
2EI
M
1
1
2
1
10
1
1
2
1
01
+
⋅
−
⋅
=
⋅
+
⋅
⋅
−
+
⋅
=
−
⋅
−
⋅
=
⋅
−
⋅
⋅
−
+
⋅
=
z3
0,3750EI
z2
1EI
z3)
0,25
3
0
z2
(2
4
2EI
M
z3
0,3750EI
z2
0,5EI
z3)
0,25
3
z2
0
(2
4
2EI
M
z3
0,1875EI
z3)
0,25
(0
4
3EI
M
22,5
z2
0,6945EI
16
6
20
3
0)
(z2
6
)
3E(1,389I
M
0,1667
z1
0,6738EI
z2
1,348EI
12
1
2
0)
3
z1
z2
(2
4,123
)
2E(1,389I
M
0,1667
z2
0,6738EI
z1
1,348EI
12
1
2
0)
3
z2
z1
(2
4,123
)
2E(1,389I
M
1
1
1
25
1
1
1
52
1
1
43
1
1
23
1
1
2
1
21
1
1
2
1
12
⋅
−
⋅
=
⋅
⋅
−
+
⋅
=
⋅
−
⋅
=
⋅
⋅
−
+
⋅
=
⋅
−
=
⋅
⋅
−
=
−
⋅
=
⋅
⋅
−
−
=
+
⋅
+
⋅
=
⋅
+
⋅
−
+
⋅
=
−
⋅
+
⋅
=
⋅
−
⋅
−
+
⋅
=

Krzysztof Wójtowicz
Strona 5
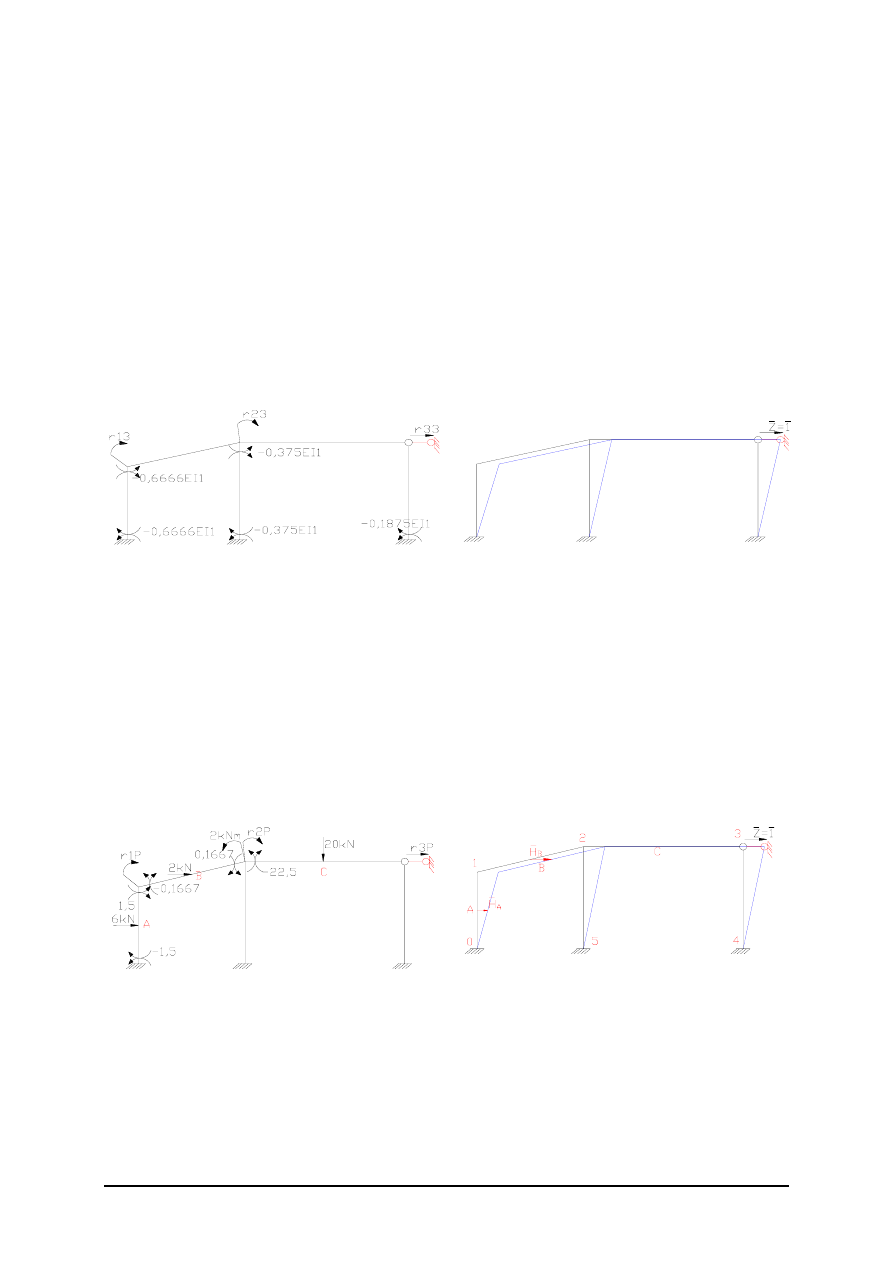
Krzysztof Wójtowicz
Strona 6
Z równowagi węzłów otrzymujemy
r
11
-1,348EI
1
-1,333EI
1
=0
⇒ r
11
=2,681EI
1
r
12
-0,6738EI=1=0
⇒ r
12
= r
21
= 0,6738EI
1
r
13
- (-0,6666EI
1
)=0
⇒ r
13
= r
31
= -0,6666EI
1
r
22
-0,6945EI-EI
1
-1,348EI
1
=0
⇒ r
22
= 3,0425EI
1
r
23
- (-0,375EI
1
)=0
⇒ r
23
= r
32
= -0,375EI
1
r
1P
- (-0,1667)-1,5=0
⇒ r
1P
= 1,3333kNm
r
2P
-2- (-22,5)-0,1667=0
⇒ r
2P
= -20,333kNm
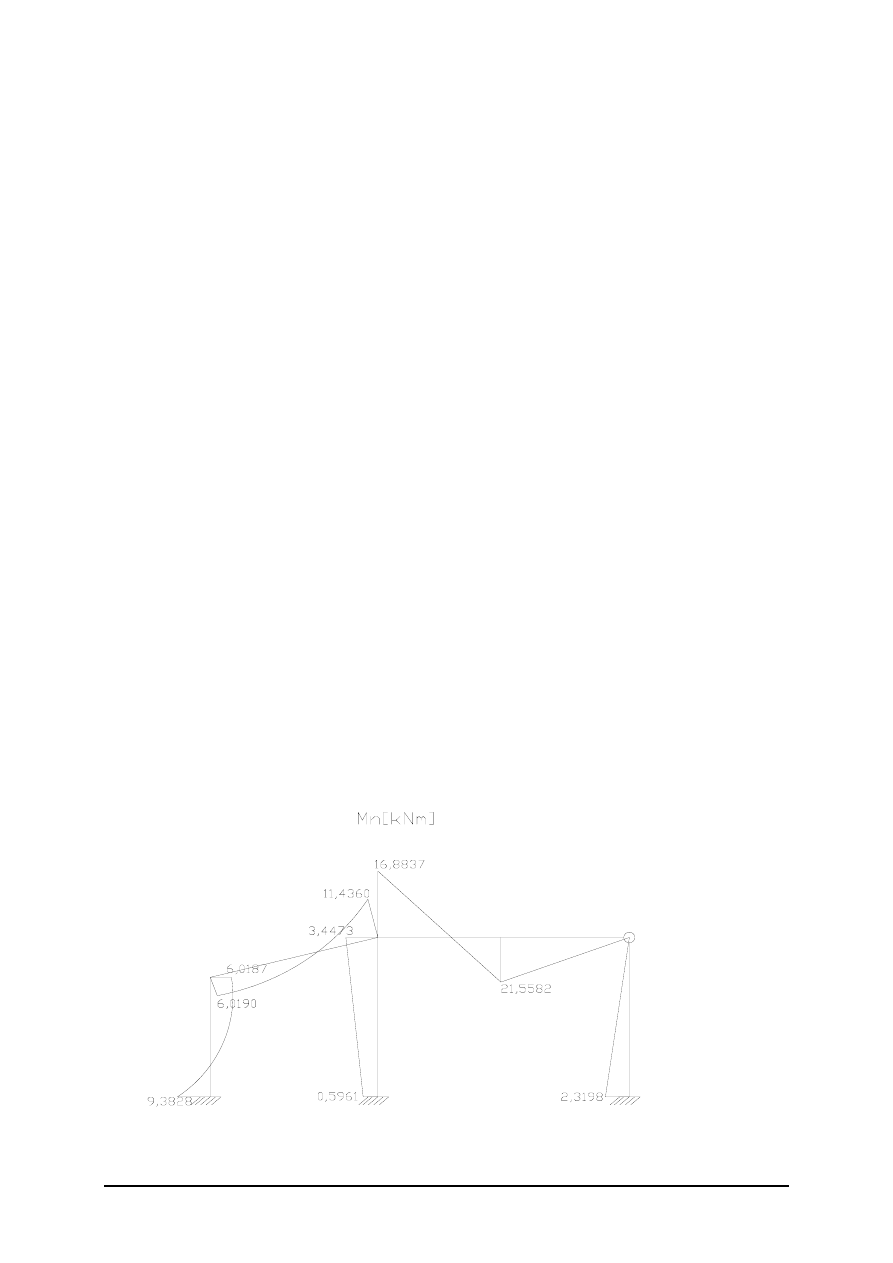
Korzystając z zasady pracy wirtualnej obliczamy pozostałe reakcje.
Ψ=0,3333
Ψ =0,25
Ψ=0,25
_
_
_
_
− −
0
0,25
)
0,1875EI
(
0,25
)
0,375EI
(
2
0,3333
)
0,6666EI
(
2
1
r
_____
1
_____
1
________
1
_
33
=
⋅
−
+
⋅
−
⋅
+
⋅
−
⋅
+
⋅
r
33
= 0,6787EI
1
−
−
_
_
_
_
Ψ=0,25
Ψ=0,25
Ψ=0,3333
0A
→
0+
01
_
ψ
*1,5=H
A
⇒ H
A
=
___
5
,
0
Krzysztof Wójtowicz
Strona 7
H
B
=
_
1 ponieważ pręty 01, 52, 43 nie doznają przesuwu pionowego zatem pręt 12 ulegnie
tylko przesuwowi poziomemu o wartości 1
Ponieważ pręt 23 doznaje przesuwu poziomego siła pionowa P=20kN nie wykona pracy.
0
1
2
0,5
6
0,3333
1,5)
1,5
(
1
r
_
___
________
_
3P
=
⋅
+
⋅
+
⋅
+
−
+
⋅
r
3P
= -5kN
Podstawiając do układu równań kanonicznych otrzymujemy:
=
−
⋅
+
⋅
−
⋅
−
=
−
⋅
−
⋅
+
⋅
=
+
⋅
−
⋅
+
⋅
0
5
6787
,
0
375
,
0
6666
,
0
0
333
,
20
375
,
0
0425
,
3
6738
,
0
0
333
,
1
6666
,
0
6738
,
0
681
,
2
3
1
2
1
1
1
3
1
2
1
1
1
3
1
2
1
1
1
z
EI
z
EI
z
EI
z
EI
z
EI
z
EI
z
EI
z
EI
z
EI
=
=
=
37202
,
12
086853
,
8
546538
,
0
1
3
1
2
1
1
EI
z
EI
z
EI
z
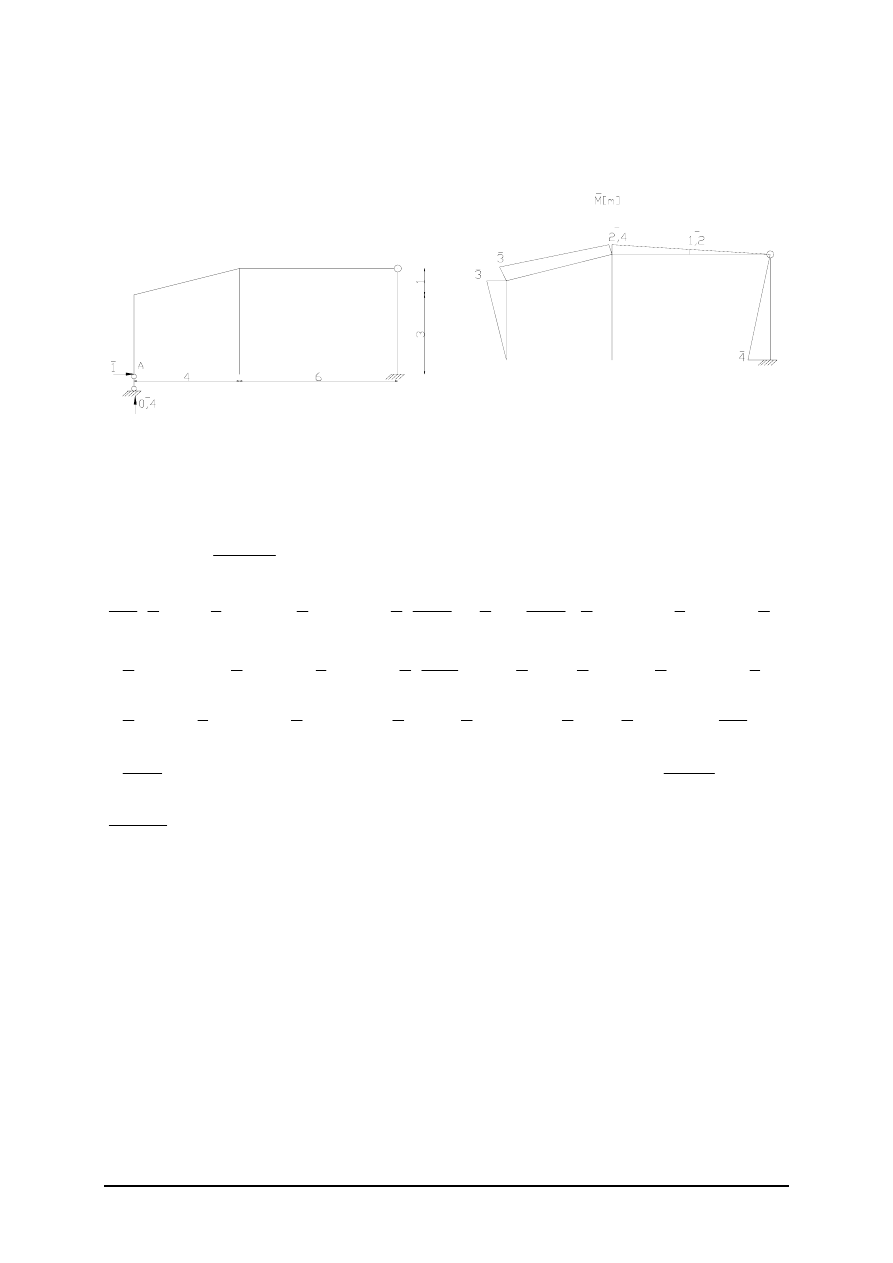
Podstawiając do wzorów transformacyjnych otrzymujemy wartości momentów
kNm
kNm
-6,0187
1,5
12,372024
0,6666
0,546538
1,333
M
3828
,
9
1,5
2,37202
1
0,6666
0,546538
0,6667
M
10
01
=
+
⋅
−
⋅
=
−
=
−
⋅
−
⋅
=
3,4473kNm
12,37202
0,3750
8,086853
1
M
5961
,
0
12,37202
0,3750
8,086853
0,5
M
3198
,
2
12,37202
0,1875
M
8837
,
16
22,5
8,086853
0,6945
M
4360
,
11
0,1667
0,546538
0,6738
8,086853
1,348
M
0190
,
6
0,1667
8,086853
0,6738
0,546538
1,348
M
25
52
43
23
21
12
=
⋅
−
⋅
=
−
=
⋅
−
⋅
=
−
=
⋅
−
=
−
=
−
⋅
=
=
+
⋅
+
⋅
=
=
−
⋅
+
⋅
=
kNm
kNm
kNm
kNm
kNm
Krzysztof Wójtowicz
Strona 8
Kontrola kinematyczna
H
A
= 0
⇒
0
1
_
=
⋅
∑∫
dx
EI
M
M
N
[
]
%
1
,
0
%
100
3723
,
12
0128
,
0
0128
,
0
3723
,
12
)
8698
,
25
7396
,
15
651
,
14
85541
,
1
794
,
27
241
,
1
(
389
,
1
1
75
,
6
9818
,
3
1
3198
,
2
3
2
4
4
2
1
]
5582
,
21
3
2
3
2
,
1
2
1
)
5582
,
21
3
2
8837
,
16
3
1
(
3
2
,
1
2
1
)
5582
,
21
3
1
8837
,
16
3
2
(
3
4
,
2
2
1
4
,
5
2
1
123
,
4
8
1
2
3
2
)
019
,
6
3
1
436
,
11
3
2
(
123
,
4
4
,
2
2
1
)
019
,
6
3
2
436
,
11
3
1
(
123
,
4
3
2
1
[
389
,
1
1
3
2
1
3
8
3
2
3
2
)
0187
,
6
3
2
3828
,
9
3
1
(
3
3
2
1
1
1
1
2
2
1
=
⋅
=
+
−
−
+
−
+
−
+
+
−
−
=
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
−
⋅
−
⋅
⋅
⋅
⋅
+
+
⋅
−
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
−
⋅
−
⋅
⋅
⋅
⋅
+
+
⋅
−
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
−
⋅
−
⋅
⋅
⋅
⋅
EI
EI
EI

Krzysztof Wójtowicz
Strona 9
Obliczenie sił tnących
(
siły tnące obliczamy z sumy momentów, dlatego siły normalne pomijamy na rysunkach gdyż nie
wchodzą one do równań momentowych)
8,1338kN
T
0
1,5
3
2
9,3828
-
6,0187
-
3
T
:
M
2,1338kN
T
0
1,5
3
2
9,3828
-
6,0187
-
3
T
:
M
01
01
1
10
10
0
=
=
⋅
⋅
−
⋅
=
=
⋅
⋅
+
⋅
∑
∑
kN
9910
,
3
T
0
0,5
1
2
-
0
6
11,43
6,0190
4,123
T
:
M
4,4761kN
T
0
0,5
1
2
11,4360
6,0190
4,123
T
:
M
12
12
2
21
21
1
−
=
=
⋅
⋅
+
+
⋅
−
=
=
⋅
⋅
+
+
+
⋅
∑
∑
kN
8140
,
12
T
0
3
20
16,8837
6
T
:
M
kN
1861
,
7
T
0
3
0
2
16,8837
6
T
:
M
23
23
3
32
32
2
=
=
⋅
−
−
⋅
−
=
=
⋅
+
−
⋅
∑
∑
kN
5800
,
0
T
0
3198
,
2
4
T
:
M
kN
5800
,
0
T
0
3198
,
2
4
T
:
M
34
34
4
43
43
3
=
=
−
⋅
=
=
−
⋅
∑
∑
kN
7128
,
0
T
0
4473
,
3
5961
,
0
4
T
:
M
kN
7128
,
0
T
0
4473
,
3
5961
,
0
4
T
:
M
52
52
2
25
25
5
−
=
=
+
−
⋅
−
=
=
+
−
⋅
∑
∑

Krzysztof Wójtowicz
Strona 10
Obliczenie sił normalnych
(siły normalne obliczamy z sumy na poszczególne osie dlatego momenty pomijamy na rysunkach
gdyż nie wchodzą one w skład równań)
sin
α
=0,24254
cos
α
=0,97014
kN
N
X
19725
,
3
0
1338
,
2
24254
,
0
9910
,
3
97014
,
0
N
0
1338
,
2
sin
9910
,
3
cos
N
:
12
12
12
=
=
−
⋅
−
⋅
=
−
⋅
−
⋅
∑
α
α
4,64729kN
N
0
0,24254
3,19725
0,97014
3,9910
N
-
0
sinα
3,19725
cosα
3,9910
N
-
:
Y
10
10
10
=
=
⋅
+
⋅
+
=
⋅
+
⋅
+
∑
kN
N
Y
kN
N
X
1861
,
7
0
1861
,
7
N
-
:
5800
,
0
0
5800
,
0
N
-
:
34
34
32
32
−
=
=
−
−
=
=
−
∑
∑
kN
N
N
N
5800
,
0
0
N
:
X
32
23
23
32
−
=
=
=
−
∑
kN
2559
,
1
N
0
0,97014
N
-
0,24254
4,4761
0,7128
0,5800
-
0
cosα
N
-
sinα
4,4757
0,7128
0,5800
-
:
X
21
21
21
=
=
⋅
⋅
+
+
=
⋅
⋅
+
+
∑
17,4610kN
N
0
0,24254
2559
,
1
0,97014
4,4761
N
-
12,814
-
0
sinα
2559
,
1
cosα
4,4761
N
-
12,814
-
:
Y
25
25
25
−
=
=
⋅
−
⋅
−
=
⋅
−
⋅
−
∑
α
−3,9910
2,1338
−7,1861
0,5800
Ν
32
Ν
α
25
Ν
−0,7128
−4,4761
21
Ν
12,814
−0,5800

Krzysztof Wójtowicz
Strona 11
Ν 10
Ν 01
Ν 25
Ν 52
Ν 34
Ν 43
2,1332
8,1332
−0,7132
−0,7132
0,5798
0,5798
N
01
=N
10
N
52
=N
25
N
43
=N
34
N
01
=4,64729kN N
52
=-17,4610kN
N
43
=-7,1861kN
+
−
+
−
+
−
8,1338
2,1338
−3,991
−4,4761
12,814
12,814
−71861
−7,1861
0,5800
0,5800
−0,7128
−0,7128

Krzysztof Wójtowicz
Strona 12
Sprawdzenie statyczne
%
01
,
0
%
100
8,1338
0,001
0
0,001
4
2
0,58
-
0,7128
8,1338
-
:
X
=
⋅
≈
=
⋅
+
+
∑
kN
%
00095
,
0
%
100
20
00019
,
0
00019
,
0
20
1861
,
7
4610
,
17
64729
,
4
:
Y
=
⋅
−
=
−
+
+
−
∑
kN
0,0005%
100%
140
0,0007
0007
,
0
71,861
-
69,844
-
1,74
2,1384
-
24,4014
2,3198
-
0,5961
-
9,3828
-
140
9
-
1
-2
10
7,1861
-
4
17,461
-
3
0,58
3
0,7128
-
-
3
8,1338
2,3198
-
0,5961
-
9,3828
-
7
20
1,5
3
2
-
0,5
1
2
2
-
:
M
A
=
⋅
=
+
+
+
+
+
=
⋅
⋅
⋅
+
⋅
⋅
+
⋅
+
⋅
⋅
⋅
⋅
+
∑
kNm
Sprawdzenie naprężeń normalnych od momentu zginającego dla poszczególnych
grup prętów.
Dla pręta 23 największy moment wynosi 21,5582kNm – I=4250cm
4
I240
Dla pręta 01 największy moment wynosi 9,3828kNm – I=3060cm
4
I220
Naprężenia graniczne dla stali f
d
=215MPa
MPa
cm
kN
cm
cm
kNcm
MPa
cm
kN
cm
cm
kNcm
7
,
33
37
,
3
11
3060
28
,
938
8
,
60
08
,
6
12
4250
82
,
2155
2
4
2
4
=
=
⋅
=
=
⋅
Naprężenia są o wiele mniejsze od naprężeń dopuszczalnych . Należy zmienić
przekroje na mniejsze. Ponieważ wartości momentów nie zależą od wartości sztywności
przekrojów tylko ich stosunku ponowne obliczenie momentów dla nowych przekrojów
nie jest konieczne gdy zachowamy ten stosunek.
Wyszukiwarka
Podobne podstrony:
Metoda przemieszczen- obciazenie1
Metoda przemieszczen- obciazenie3
Metoda przemieszczen obciazenie5
Metoda przemieszczen obciazeni Nieznany
Metoda przemieszczen obciazenie4
Metoda przemieszczen obciazenie3
Metoda przemieszczen obciazenie8
Metoda przemieszczen obciazenie3
Metoda przemieszczen obciazenie5
Metoda przemieszczen obciazenie6
belka obroty i przesuwy metoda przemieszczeń
Linie wpływu Metoda przemieszczeń mmp belka lw
Metoda przemieszczeń
Uproszczona metoda obliczania obciążenia cieplnego pomieszczenia
cwicz mechanika budowli metoda przemieszczen rama ugiecie
Metoda przemieszczen projekt4
więcej podobnych podstron