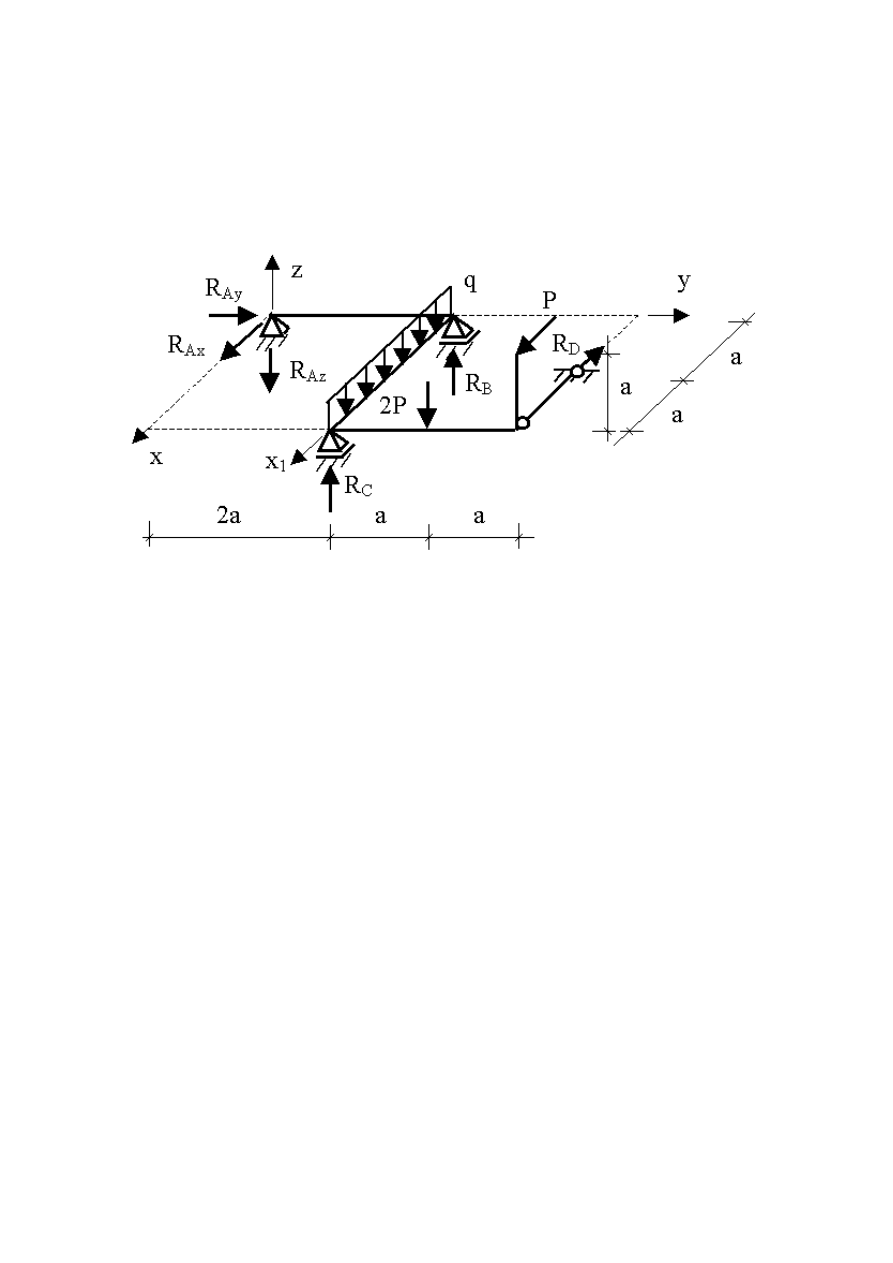
Przykład 5.8. Układ przestrzenny V

Obliczyć reakcje.

Przyjęto: P = qa.

Przedstawiony układ przestrzenny oparty jest na podporze przegubowej nieprzesuwnej w

punkcie A, na podporach przegubowych przesuwnych w punktach B i C oraz na podporze

przegubowej nieprzesuwnej w punkcie D za pośrednictwem pręta dwuprzegubowego. Nie

znamy sześciu reakcji: R

Ax

, R

Ay

, R

Az

,, R

B

, R

C

i R

D

. Zatem układ jest statycznie wyznaczalny.

Dla przedstawionego na schemacie układu przestrzennego można zapisać sześć warunków

równowagi. Zatem układ jest statycznie wyznaczalny. Zapisując kolejne równania równowagi

należy dążyć do tego, aby były to równania z jedną niewiadomą.

0

1

=

∑

ix

M

0

2

2

=

−

⋅

Pa

a

R

Az

→

qa

P

R

Az

=

=

0

=

∑

iy

M

0

2

2

2

2

=

+

⋅

+

⋅

⋅

+

⋅

−

Pa

a

P

a

a

q

a

R

C

→

qa

P

R

C

5

.

3

5

.

3

=

=

0

=

∑

iz

P

0

2

2

=

−

⋅

−

+

+

−

P

a

q

R

R

R

B

C

Az

→

qa

P

R

B

5

.

1

5

.

1

=

=

0

=

∑

iy

P

0

=

Ay

R

0

=

∑

iz

M

0

4

4

=

⋅

+

⋅

−

a

R

a

P

D

→

qa

P

R

D

=

=

0

=

∑

ix

P

0

=

+

−

P

R

R

D

Ax

→

0

=

Ax

R

2

W celu sprawdzenia poprawności obliczeń korzystamy z warunku równowagi, z którego nie

korzystaliśmy poprzednio

0

=

∑

ix

M

0

3

2

2

2

2

2

=

⋅

−

⋅

+

⋅

+

⋅

⋅

−

a

P

a

R

a

R

a

a

q

C

B

→

0

6

7

3

4

2

2

2

2

=

−

+

+

−

qa

qa

qa

qa