Podstawy Konstrukcji Maszyn

Podstawy Konstrukcji Maszyn

Wały i osie – część II

Wały i osie – część II

Wały i osie – nr 2

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

l

1

l

2

l

P

1

P

2

A

B

P

2

P

1

α

1

α

2

r

1

r

2

x

y

Dane:

P

1

=10000N

r

1

=0,08m

l=0,4m

r

2

=0,05m

l

1

=0,1m

α

1

=60

0

l

2

=025m

α

2

=120

0

stal 45 ulepszana cieplnie
Z

go

=250MPa

Z

sj

=300MPa

Obliczamy wartości siły P

2

z warunku równowagi momentów:

kN

m

m

kN

r

r

P

P

r

P

r

P

16

05

,

0

08

,

0

10

2

1

1

2

2

2

1

1

=

⋅

=

⋅

=

⇒

⋅

=

⋅

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

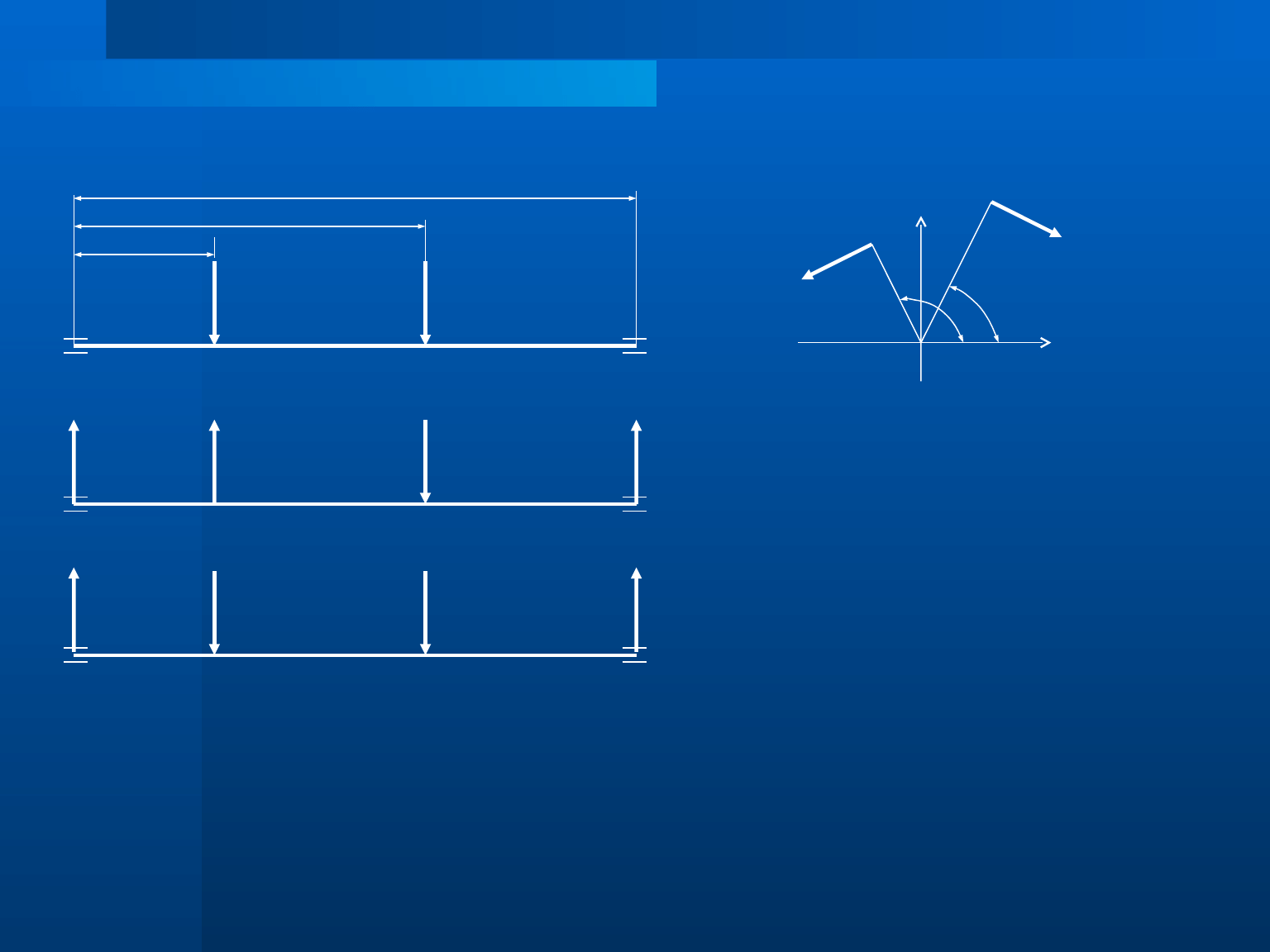
Wały i osie – nr 3

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

l

1

l

2

l

P

1

P

2

P

1x

P

2x

P

1y

P

2y

A

B

R

Bx

R

By

R

Ax

R

Ay

płaszczyzna xz

płaszczyzna yz

Dane:

P

1

=10000N

r

1

=0,08m

l=0,4m

r

2

=0,05m

l

1

=0,1m

α

1

=60

0

l

2

=025m

α

2

=120

0

stal 45 ulepszana cieplnie
Z

go

=250MPa

Z

sj

=300MPa

Obliczamy wartości składowych sił w płaszczyznach xz i yz:

kN

kN

P

P

kN

kN

P

P

kN

kN

P

P

kN

kN

P

P

y

y

x

x

8

5

,

0

16

60

cos

5

5

,

0

10

60

cos

856

,

13

8660

,

0

16

60

sin

66

,

8

8660

,

0

10

60

sin

0

2

2

0

1

1

0

2

2

0

1

1

=

⋅

=

⋅

=

=

⋅

=

⋅

=

=

⋅

=

⋅

=

=

⋅

=

⋅

=

P

2

P

1

α

1

α

2

r

1

r

2

x

y

Wały i osie – nr 4

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

∑

=

+

−

+

=

0

0

2

1

Bx

x

x

Ax

ix

R

P

P

R

P

∑

=

⋅

+

⋅

−

⋅

=

0

0

2

2

1

1

l

R

l

P

l

P

M

Bx

x

x

ixA

Bx

x

x

Ax

R

P

P

R

−

+

−

=

⇒

2

1

Obliczamy wartości reakcji z warunków równowagi sił w kierunku x i y, oraz z warunków równowagi
momentów względem łożysk:

P

1x

P

2x

R

Bx

R

Ax

płaszczyzna xz

l

l

P

l

P

R

x

x

Bx

2

2

1

1

⋅

+

⋅

−

=

⇒

kN

m

m

kN

m

kN

R

Bx

495

,

6

4

,

0

25

,

0

856

,

13

1

,

0

66

,

8

=

⋅

+

⋅

−

=

kN

kN

kN

kN

R

Ax

299

,

1

495

,

6

856

,

13

66

,

8

−

=

−

+

−

=

Ujemna wartość reakcji R

Ax

oznacza błędnie założony zwrot. Należy więc go skorygować.

l

1

l

2

l

Wały i osie – nr 5

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

P

1y

P

2y

R

By

R

Ay

płaszczyzna yz

∑

=

+

−

−

=

0

0

2

1

By

y

y

Ay

iy

R

P

P

R

P

∑

=

⋅

+

⋅

−

⋅

−

=

0

0

2

2

1

1

l

R

l

P

l

P

M

By

y

y

iyA

By

y

y

Ay

R

P

P

R

−

+

=

⇒

2

1

l

l

P

l

P

R

x

x

Bx

2

2

1

1

⋅

+

⋅

−

=

⇒

kN

m

m

kN

m

kN

R

By

25

,

6

4

,

0

25

,

0

8

1

,

0

5

=

⋅

+

⋅

=

kN

kN

kN

kN

R

Ay

75

,

6

25

,

6

8

5

=

−

+

=

l

2

l

l

1

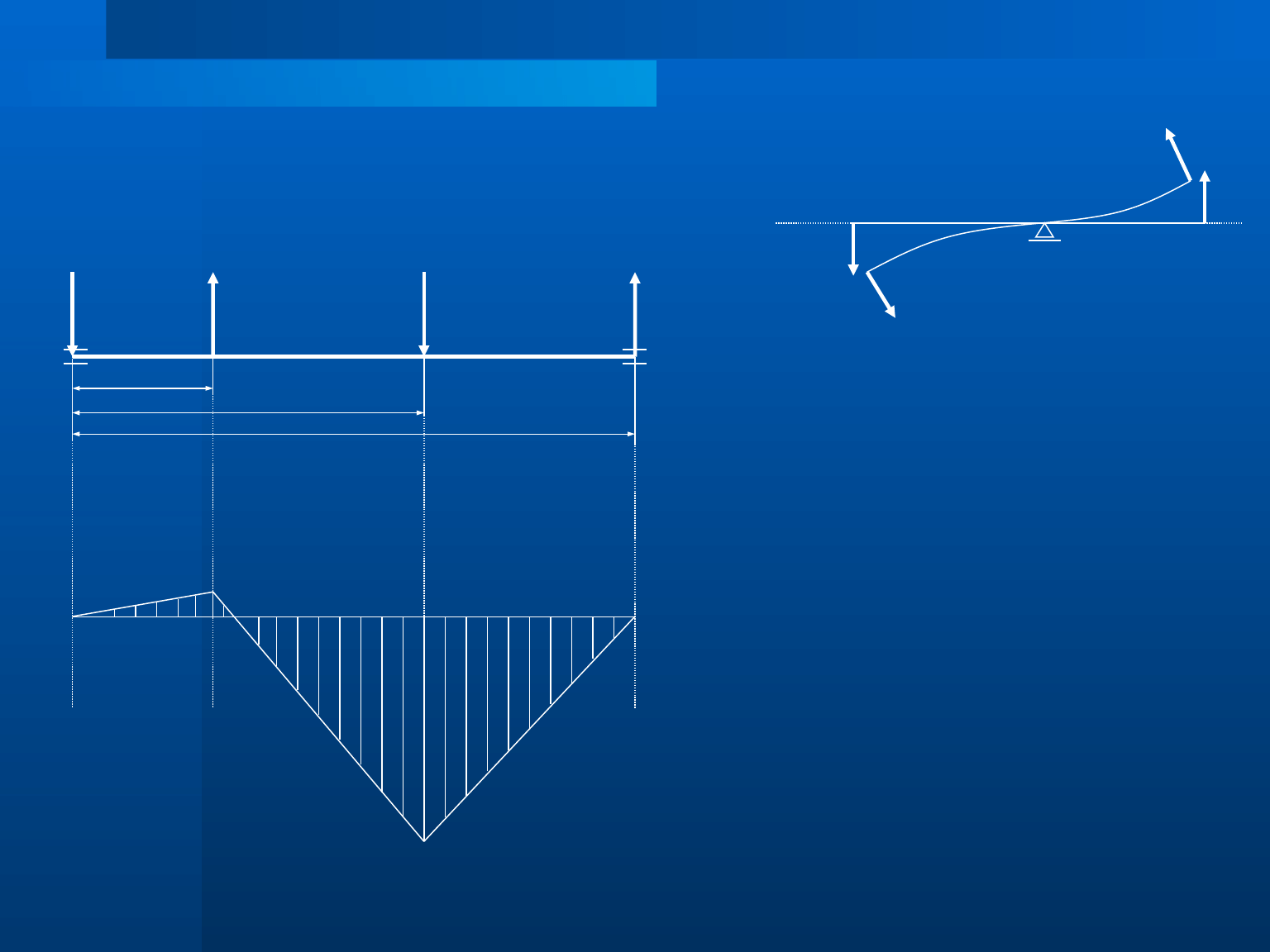
Wały i osie – nr 6

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

0

=

gxA

M

Nm

m

kN

l

R

M

Ax

gx

9

,

129

1

,

0

299

.

1

1

1

=

⋅

=

⋅

=

(

)

Nm

m

m

kN

m

kN

l

l

P

l

R

M

x

Ax

gx

25

,

974

)

1

,

0

25

,

0

(

66

,

8

25

,

0

299

,

1

1

2

1

2

2

−

=

=

−

⋅

−

⋅

=

=

−

⋅

−

⋅

=

Obliczamy wartości momentów gnących w płaszczyznach xz i yz.

P

1x

P

2x

R

Bx

R

Ax

płaszczyzna xz

(

)

Nm

m

m

kN

l

l

R

M

Bx

gx

25

,

974

)

25

,

0

4

,

0

(

495

,

6

2

2

−

=

−

⋅

=

=

−

⋅

−

=

lub

0

=

gxB

M

M

gxA

M

gx1

M

gx2

M

gxB

l

2

l

l

1

P

P

M

M

g

g

(+)

(+)

M

M

g

g

(-)

(-)

Za dodatni moment gnący
przyjmujemy ten, który
powoduje ugięcie wału ku
dołowi.

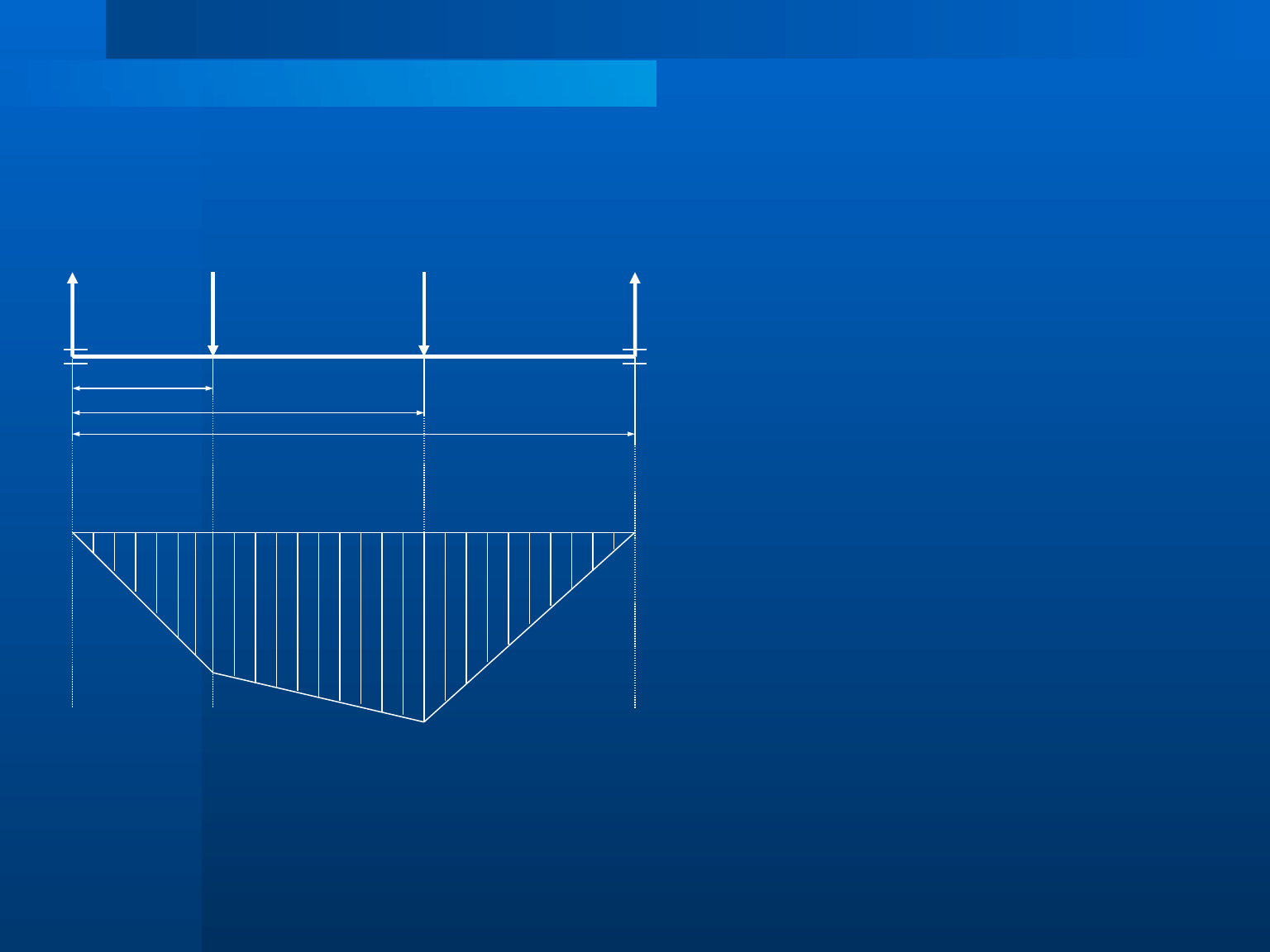
Wały i osie – nr 7

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

P

1y

P

2y

R

By

R

Ay

płaszczyzna yz

0

=

gyA

M

Nm

m

kN

l

R

M

Ay

gy

675

1

,

0

75

,

6

1

1

−

=

⋅

−

=

⋅

−

=

(

)

Nm

m

m

kN

m

kN

l

l

P

l

R

M

y

Ay

gy

5

,

937

)

1

,

0

25

,

0

(

5

25

,

0

75

,

6

1

2

1

2

2

−

=

=

−

⋅

+

⋅

−

=

=

−

⋅

+

⋅

−

=

(

)

Nm

m

m

kN

l

l

R

M

By

gy

5

,

937

)

25

,

0

4

,

0

(

25

,

6

2

2

−

=

−

⋅

−

=

=

−

⋅

−

=

lub

0

=

gyB

M

M

gyA

M

gy1

M

gy2

M

gyB

l

2

l

l

1

Wały i osie – nr 8

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

0

=

gA

M

(

) (

)

Nm

Nm

Nm

M

M

M

gy

gx

g

385

,

687

675

9

,

129

2

2

2

1

2

1

1

=

−

+

=

=

+

=

(

) (

)

Nm

Nm

Nm

M

M

M

gy

gx

g

061

,

1352

5

,

937

25

,

974

2

2

2

2

2

2

2

=

=

−

+

−

=

=

+

=

Obliczamy wartości momentów gnących wypadkowych

0

=

gB

M

1

2

A

M

gA

M

g1

M

g2

M

gB

B

Wały i osie – nr 9

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

5

=

l

χ

cm

KN

P

5

=

χ

cm

m

l

l

cm

m

l

l

cm

m

l

l

l

l

l

8

5

4

,

0

'

5

5

25

,

0

'

2

5

1

,

0

'

2

2

1

1

=

=

=

=

=

=

=

=

=

χ

χ

χ

1

2

A

B

R

Ax

P

1x

P

2x

R

Bx

Metoda wykreślna wyznaczania momentów gnących

Mnożnik długości

Mnożnik sił

O

H=5cm

cm

R

cm

P

cm

P

cm

cm

kN

kN

R

R

Bx

x

x

P

Ax

Ax

299

,

1

'

7712

,

2

'

723

,

1

2598

,

0

5

299

,

1

'

2

'

1

=

=

=

=

=

=

χ

A

1

2

B

R

Ax

R

Bx

P

1x

P

2x

M

g1x

’

M

g2x

’

Mnożnik momentów:

kN

cm

cm

KN

H

P

l

M

125

5

5

5

=

⋅

⋅

=

⋅

⋅

=

χ

χ

χ

Obliczamy momenty:

Nm

kNcm

kN

cm

M

M

M

x

g

x

g

125

5

,

12

125

10

,

0

'

1

1

=

=

⋅

=

⋅

=

χ

Nm

kNcm

kN

cm

M

M

M

x

g

x

g

975

5

,

97

125

78

,

0

'

2

2

−

=

−

=

⋅

−

=

⋅

=

χ

płaszczyzna xz

Wały i osie – nr 10

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

2

1

2

1

1

gy

gx

g

M

M

M

+

=

Metoda wykreślna wyznaczania momentów gnących

M

g1x

’

M

g1y

’

M

g1

’=0,55 cm

M

g1x

’=0,1 cm

M

g1y

’=0,54 cm

Obliczamy moment wypadkowy

Nm

kNcm

kN

cm

M

M

M

g

g

5

,

687

75

,

68

125

55

,

0

'

1

1

=

=

⋅

=

⋅

=

χ

Wartości momentów odczytane z wykresów

Wały i osie – nr 11

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

Nm

m

kN

r

P

r

P

M

s

800

08

,

0

10

2

2

1

1

=

⋅

=

⋅

=

⋅

=

2

2

2

2

2

1

2













+

=









+









=

s

g

x

x

s

x

g

red

M

M

W

W

M

W

M

α

α

σ

Obliczamy moment skręcający, który działa pomiędzy przekrojem 1 i 2

Wyznaczamy moment zastępczy zakładając obustronne zginanie wału i jednostronne zmienne
skręcanie.

( )

2

2

s

g

red

ατ

σ

σ

+

=

x

g

g

W

M

=

σ

o

s

s

W

M

=

τ

32

3

d

W

x

π

=

16

3

d

W

o

π

=

o

x

W

W

2

=

⇒

gdzie

gdzie

zatem

i

2

2

2













+

=

s

g

z

M

M

M

α

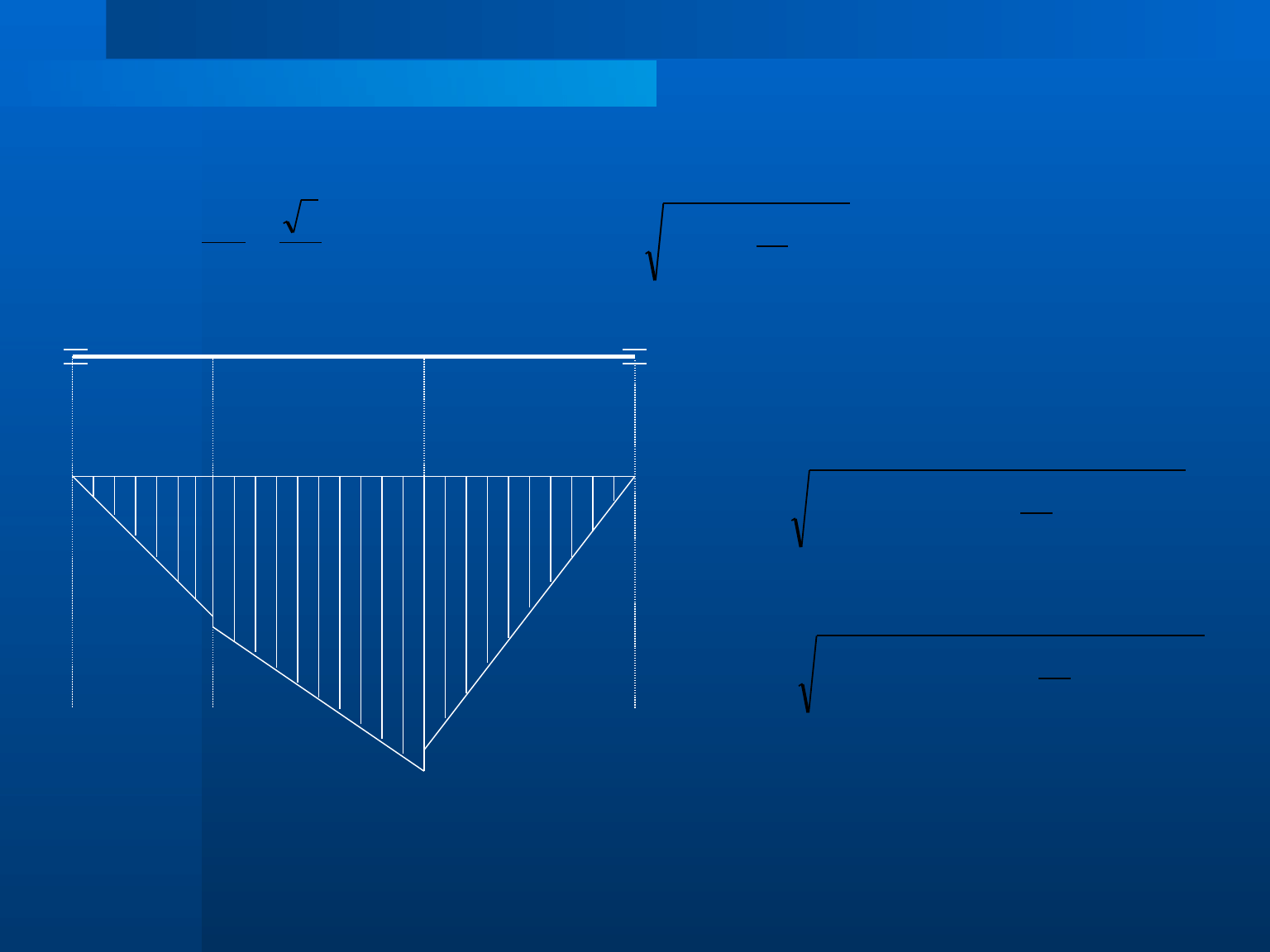
Wały i osie – nr 12

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

0

=

zA

M

Nm

Nm

Nm

M

z

75

,

769

)

800

(

16

3

)

385

,

687

(

2

2

1

=

=

+

=

Nm

Nm

Nm

M

z

73

,

1395

)

800

(

16

3

)

061

,

1352

(

2

2

2

=

=

+

=

2

3

=

=

sj

go

k

k

α

Dla tego typu zmienności obciążenia wartość współczynnika redukcyjnego α wynosi:

zatem:

2

2

16

3

s

gi

zi

M

M

M

+

=

1

2

A

M

zA

M

z1

M

z2

B

0

=

zB

M

M

zB

Wały i osie – nr 13

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

go

x

z

red

k

W

M

≤

=

σ

MPa

MPa

x

Z

k

go

go

5

,

62

4

250

=

=

=

W przypadku, gdy dominuje zginanie mamy warunek:

Dopuszczalne naprężenia przy obustronnie zmiennym zginaniu przyjmujemy przy założonym
współczynniku bezpieczeństwa x=4 wynoszą:

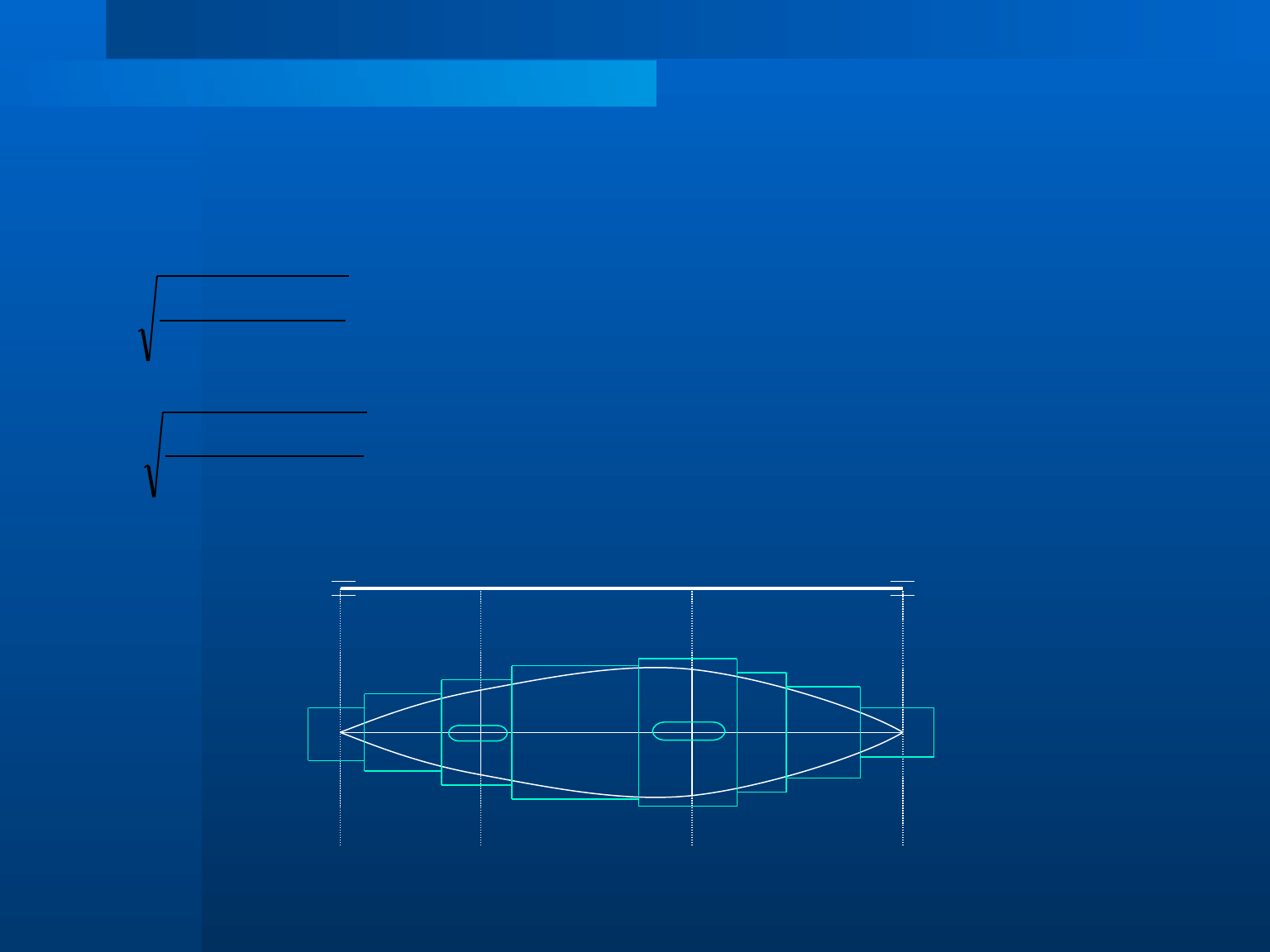
Dla przekroju okrągłego wału mamy:

32

3

d

W

x

π

=

Stąd po przekształceniach otrzymujemy wzór na średnicę wału:

3

32

go

z

k

M

d

π

≥

Wały i osie – nr 14

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

mm

m

MPa

Nm

d

6

,

50

05060

,

0

5

,

62

75

,

769

32

3

1

=

=

⋅

⋅

≥

π

mm

m

MPa

Nm

d

96

,

84

08496

,

0

5

,

62

73

,

1395

32

3

2

=

=

⋅

⋅

≥

π

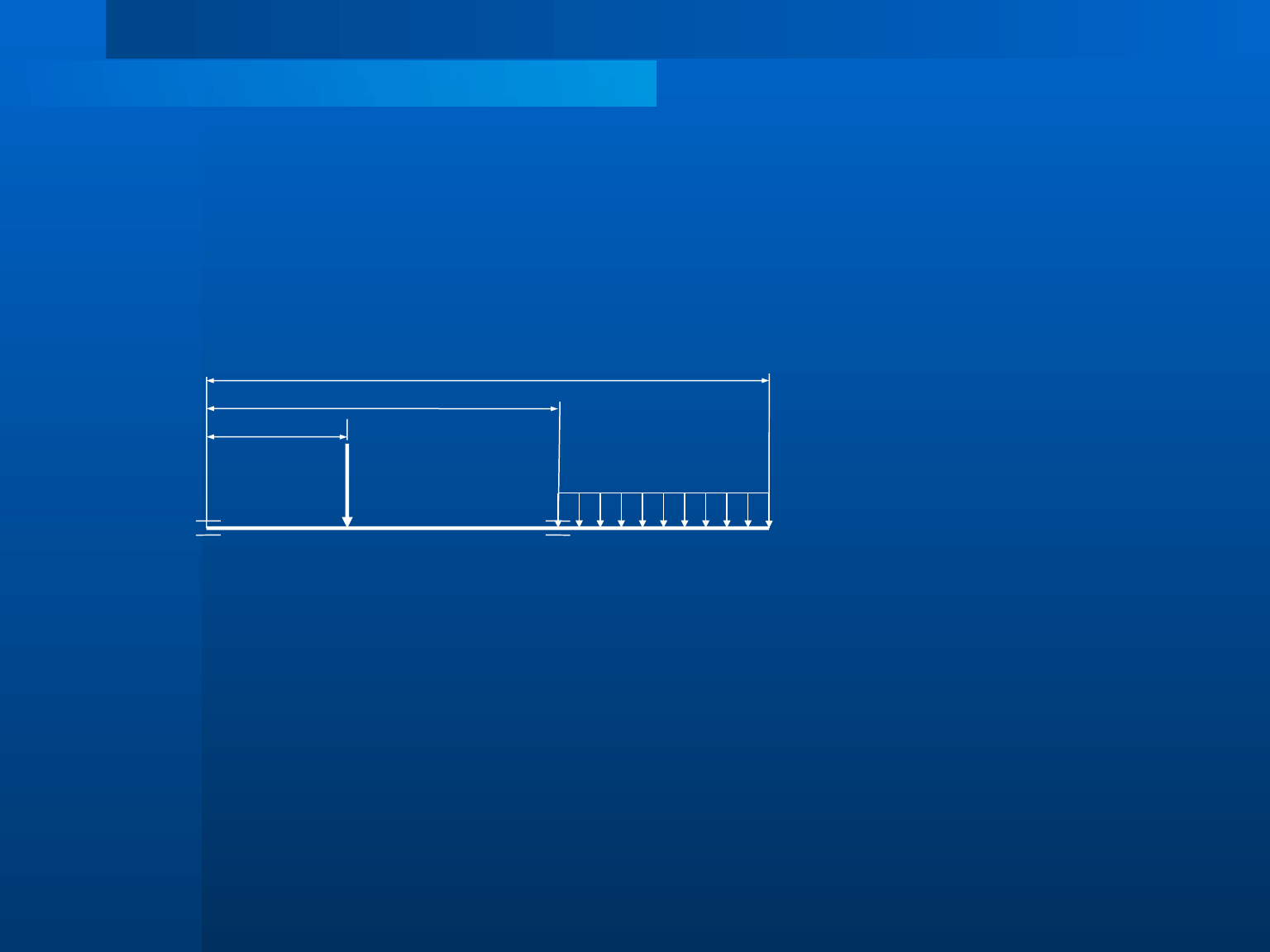
0

≥

A

d

Obliczenia średnic teoretycznych wału

0

≥

B

d

1

2

A

B

Wały i osie – nr 15

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

l

1

l

2

l

P

1

q

A

B

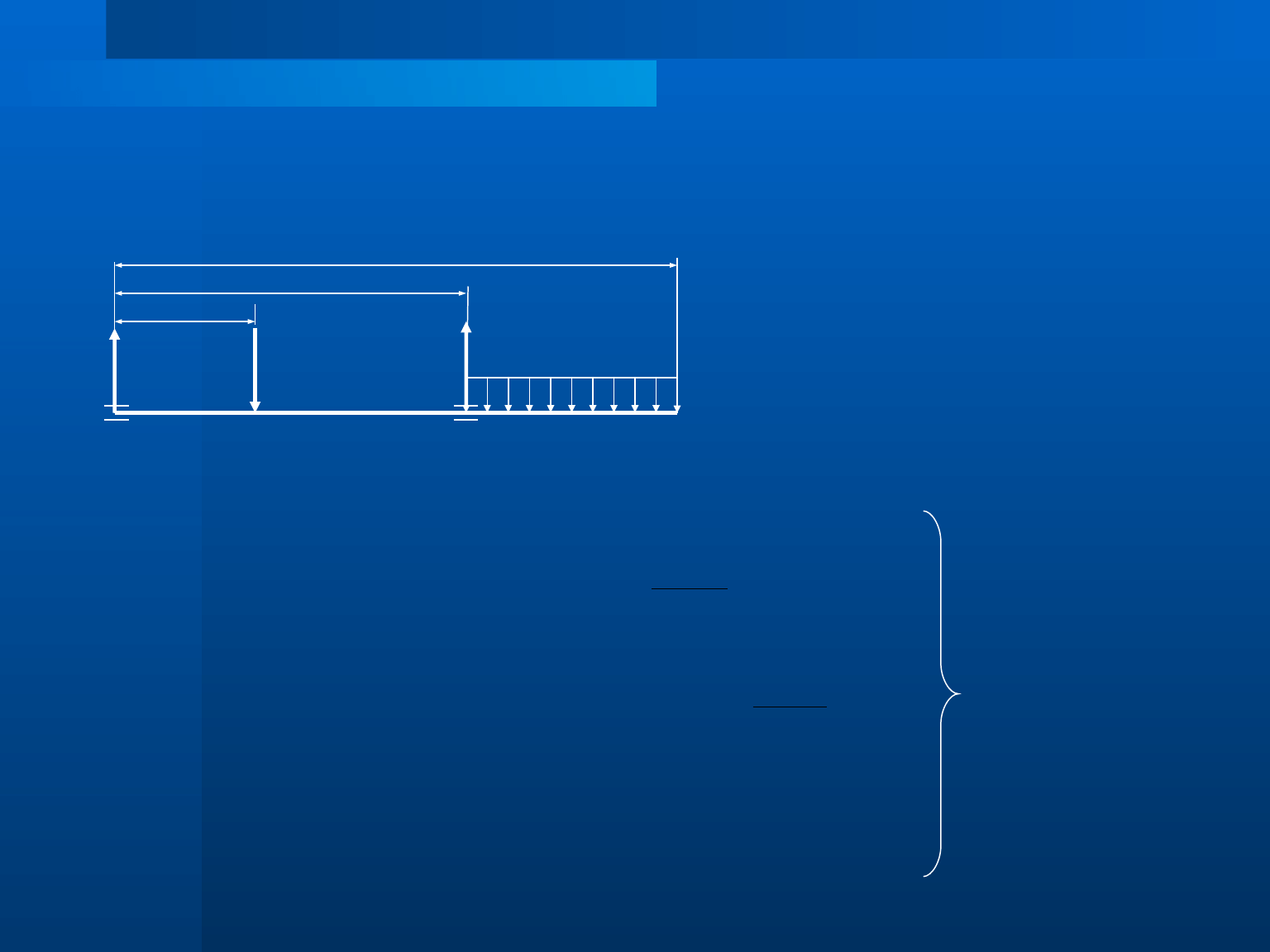
Dane:

P

1

= 10 kN

q = 2

kN

/

m

l = 6 m
l

1

= 2 m

l

2

= 4 m

l

3

= 6 m

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

Wały i osie – nr 16

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

(

)

∑

=

+

−

+

⋅

−

⋅

=

0

2

0

2

2

2

1

l

l

l

l

q

l

R

l

P

M

B

iA

(

)

∑

=

−

−

−

−

⋅

+

⋅

−

=

0

2

)

(

0

2

2

1

2

2

l

l

l

l

q

l

l

P

l

R

M

A

iB

∑

=

−

−

+

−

=

0

)

(

0

2

l

l

q

R

P

R

P

B

A

i

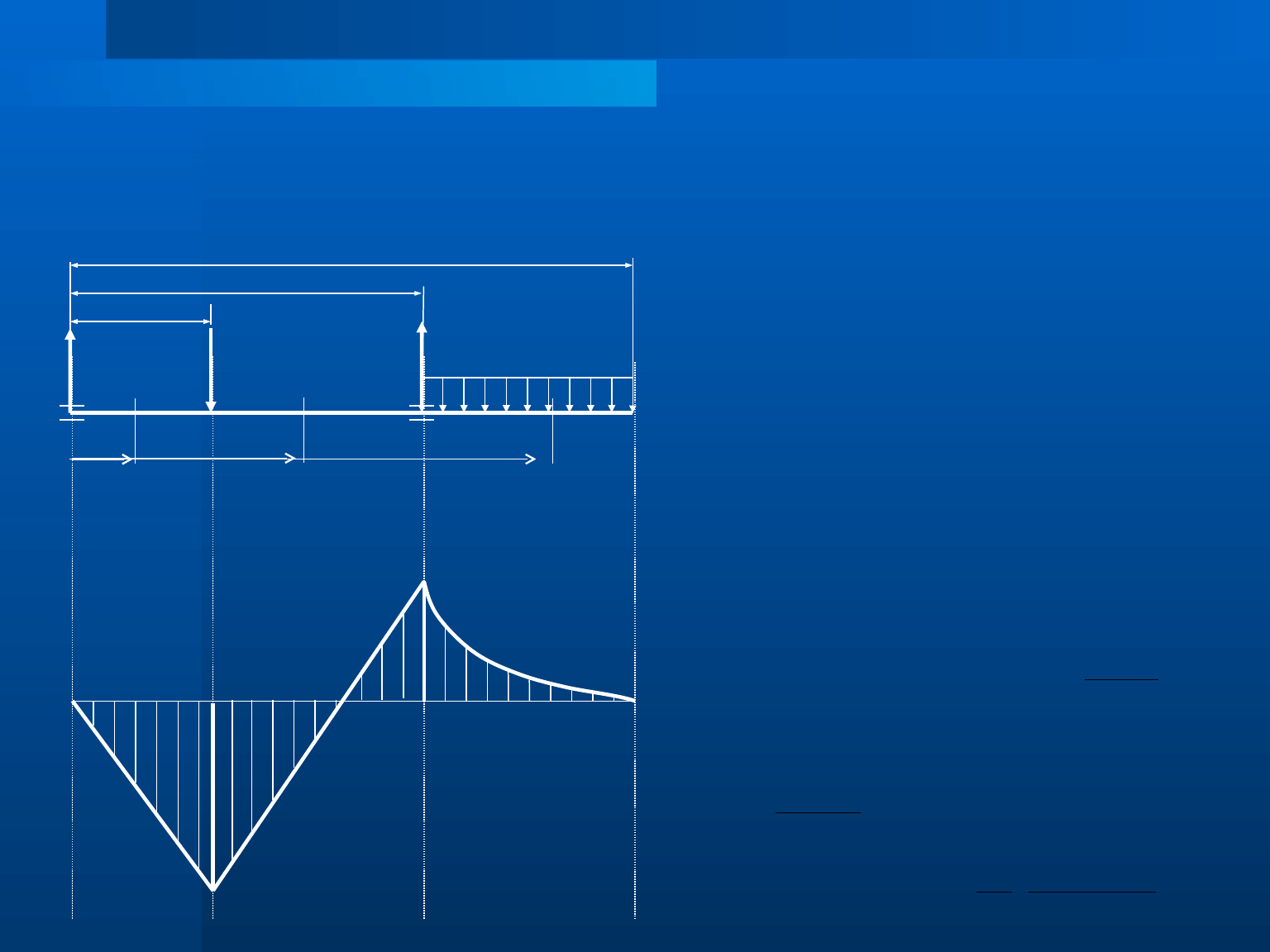
Obliczamy wartości reakcji z warunków równowagi sił oraz z warunków równowagi momentów względem
łożysk:

l

1

l

2

l

P

1

q

A

B

R

A

R

B

kN

R

kN

R

B

A

10

4

=

=

Dane:

P

1

= 10 kN

q = 2

kN

/

m

l = 6 m
l

1

= 2 m

l

2

= 4 m

l

3

= 6 m

Wały i osie – nr 17

Wały i osie

Wały i osie

dr inż. Piotr Chwastyk

Obliczenia wstępne - przykład

Obliczenia wstępne - przykład

0

=

gA

M

kNm

m

kN

l

R

M

A

g

8

2

4

1

1

−

=

⋅

−

=

⋅

−

=

(

)

kNm

m

m

kN

m

kN

l

l

P

l

R

M

A

B

4

)

2

4

(

10

4

4

1

2

2

=

−

⋅

+

⋅

−

=

=

−

⋅

+

⋅

−

=

Obliczamy wartości momentów gnących

M

gA

M

g1

M

g2

M

gB

l

1

l

2

l

P

1

q

A

B

R

A

R

B

Przedział 0 – l

1

x

R

M

A

g

⋅

−

=

−

)

1

0

(

1

2

Przedział l

1

–

l

2

(

)

1

)

1

(

l

x

P

x

R

M

A

B

g

−

⋅

+

⋅

−

=

−

Przedział

l

2

- l

2

)

(

)

(

)

(

2

2

2

1

)

(

2

l

x

l

x

q

l

x

R

l

x

P

x

R

M

B

A

B

l

g

−

⋅

−

⋅

+

−

⋅

−

−

−

⋅

+

⋅

−

=

−

0

2

)

4

6

(

2

)

4

6

(

10

)

2

6

(

10

6

4

2

)

(

)

(

)

(

2

2

2

2

1

=

−

⋅

+

−

⋅

−

−

−

⋅

+

⋅

−

=

−

⋅

+

+

−

⋅

−

−

⋅

+

⋅

−

=

m

m

m

kN

m

m

kN

m

m

kN

m

kN

l

l

q

l

l

R

l

l

P

l

R

M

B

A

gB

x

x

x