Równoległe i szeregowe łączenie

kondensatorów i cewek indukcyjnych

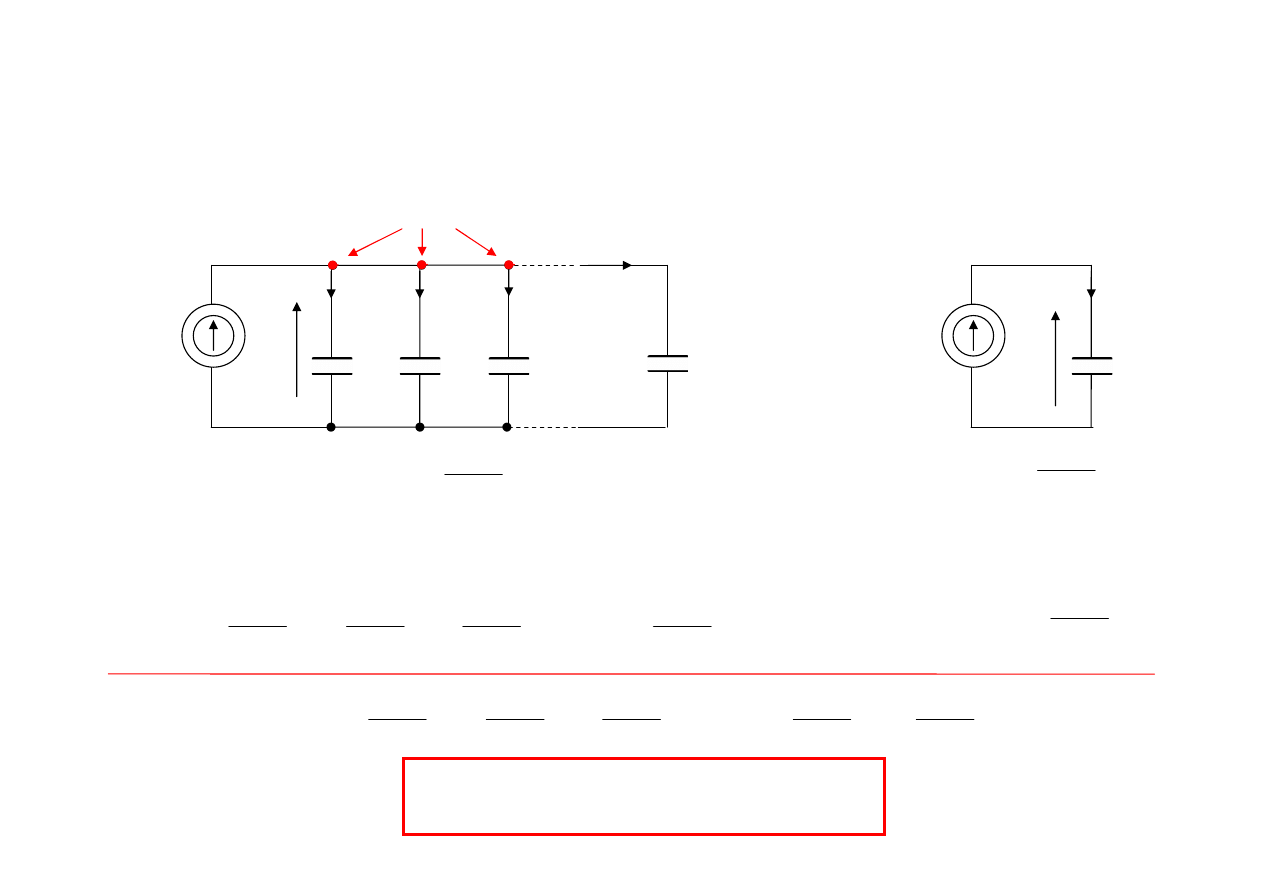
Równoległe łączenie kondensatorów

Prąd w j-tej gałęzi:

Węzeł ‘w’:

i

1

(t)+ i

2

(t) + i

3

(t)+ ……. + i

n

(t) = J(t)

J(t)

C

1

i

1

(t)

i

2

(t)

i

n

(t)

i

3

(t)

w

C

2

C

3

C

n

u(t)

J(t)

C

Z

u(t)

≡

( )

( )

dt

t

du

C

t

J

Z

=

( )

( )

( )

( ) ( )

t

J

dt

t

du

C

dt

t

du

C

dt

t

du

C

dt

t

du

C

n

=

+

+

+

+

.......

3

4

5

( )

( )

( )

( )

( )

dt

t

du

C

dt

t

du

C

dt

t

du

C

dt

t

du

C

dt

t

du

C

Z

n

=

+

+

+

+

.......

3

4

5

( )

( )

dt

t

du

C

t

i

j

j

=

≡

Pojemność zastępcza n kondensatorów połączonych równolegle jest równa sumie

algebraicznej ich pojemności

n

Z

C

C

C

C

C

+

+

+

=

.......

3

2

1

i(t)

( )

( )

dt

t

du

C

t

i

Z

=

( ) ( )

t

J

t

i

=

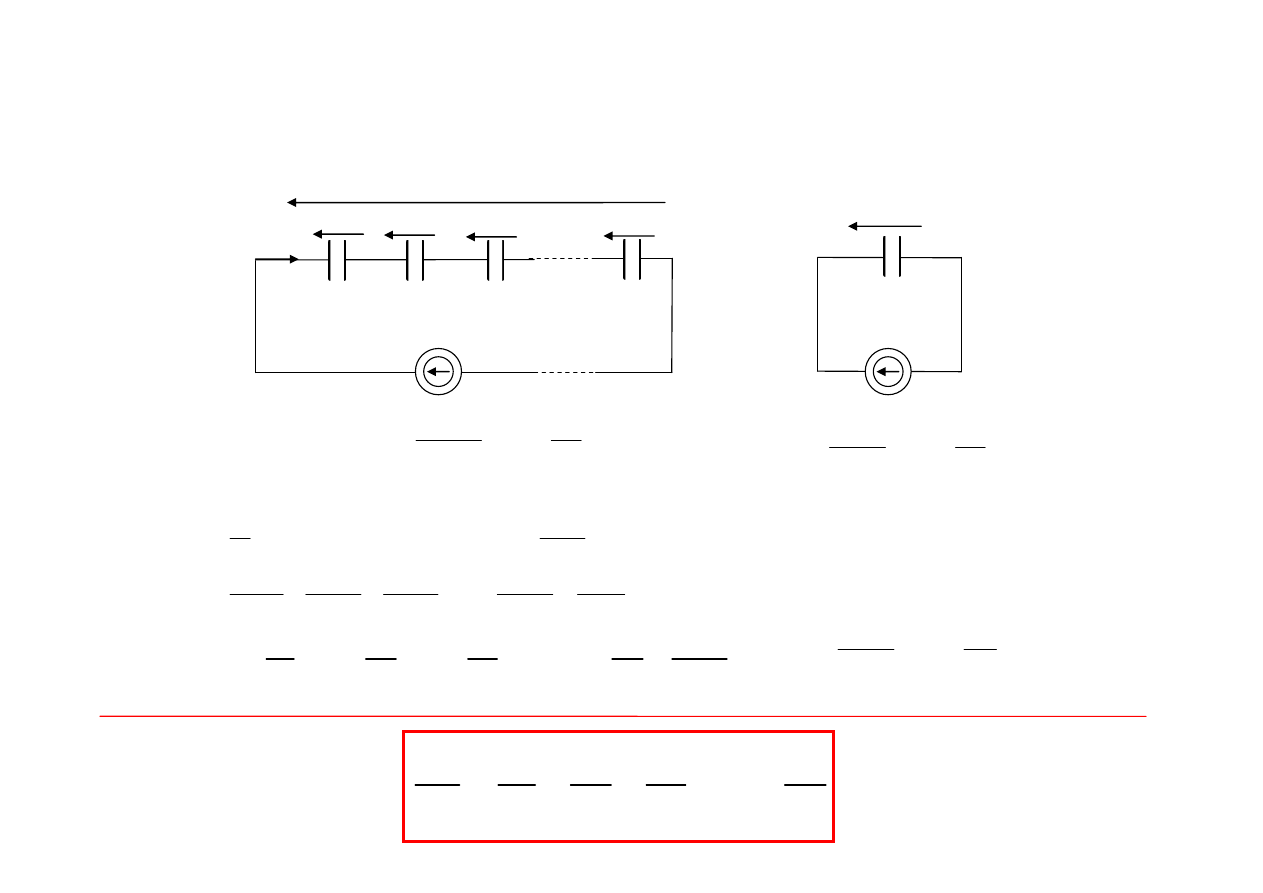
Dla j-tego kondensatora:

oczko :

u

1

(t)+ u

2

(t) + u

3

(t)+ ……. + u

n

(t) = u(t)

( )

( ) ( )

( )

(

)

( )

dt

t

du

t

u

t

u

t

u

t

u

dt

d

n

=

+

+

+

+

...

3

2

1

( )

( )

( )

( )

( )

dt

t

du

dt

t

du

dt

t

du

dt

t

du

dt

t

du

n

=

+

+

+

+

...

3

2

1

( )

j

j

C

t

J

dt

t

du

1

)

(

=

( )

Z

C

t

J

dt

t

du

1

)

(

=

≡

( )

( )

( )

( )

( )

dt

t

du

C

t

J

C

t

J

C

t

J

C

t

J

n

=

+

+

+

+

1

...

1

1

1

3

2

1

( )

j

C

t

J

dt

t

du

1

)

(

=

n

Z

C

C

C

C

C

1

.......

1

1

1

1

3

2

1

+

+

+

=

Odwrotność pojemności zastępczej n kondensatorów połączonych szeregowo jest

równa sumie algebraicznej odwrotności ich pojemności

Szeregowe łączenie kondensatorów

u(t)

J(t)

i (t)

u

1

(t)

C

3

C

2

C

1

C

n

u

2

(t)

u

3

(t)

u

n

(t)

≡

J(t)

u(t)

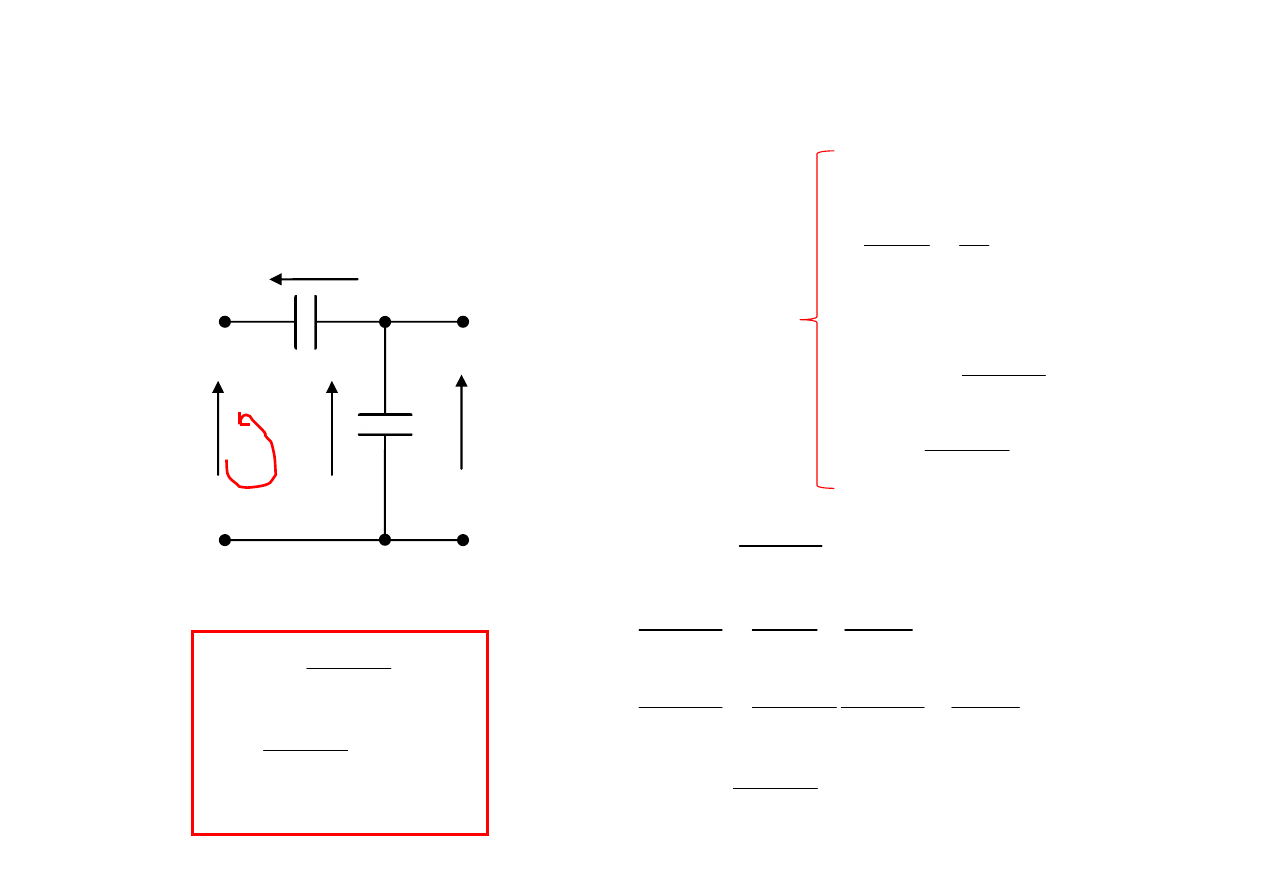
Dzielnik pojemnościowy

Szeregowe łączenie kondensatorów

Pojemnościowy dzielnik napięciowy

( )

( )

( )

( )

( )

( )

( )

( )

( )

2

1

2

1

2

1

1

2

1

1

C

C

C

C

C

dt

t

du

C

t

i

t

u

t

u

t

i

C

dt

t

du

t

u

t

u

t

u

Z

wej

Z

wyj

wej

+

=

=

=

=

+

=

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

t

u

t

u

C

C

C

t

u

dt

t

du

dt

t

du

C

C

C

dt

t

du

dt

t

du

dt

t

du

dt

t

du

t

u

R

R

t

u

t

U

wyj

wej

wej

wej

wyj

wyj

wyj

wej

wej

+

+

=

+

+

=

+

=

+

+

=

2

1

2

2

2

1

1

2

1

2

1

Współczynnik podziału napięcia - K

II prawo Kirhchoffa:

pojemność zastępcza:

( )

( )

1

0

2

1

1

2

1

1

≤

≤

+

=

+

=

K

C

C

C

K

t

u

C

C

C

t

u

wej

wyj

u

2

(t)

C

1

C

2

u

wej

(t)

u

wyj

(t)

u

1

(t)

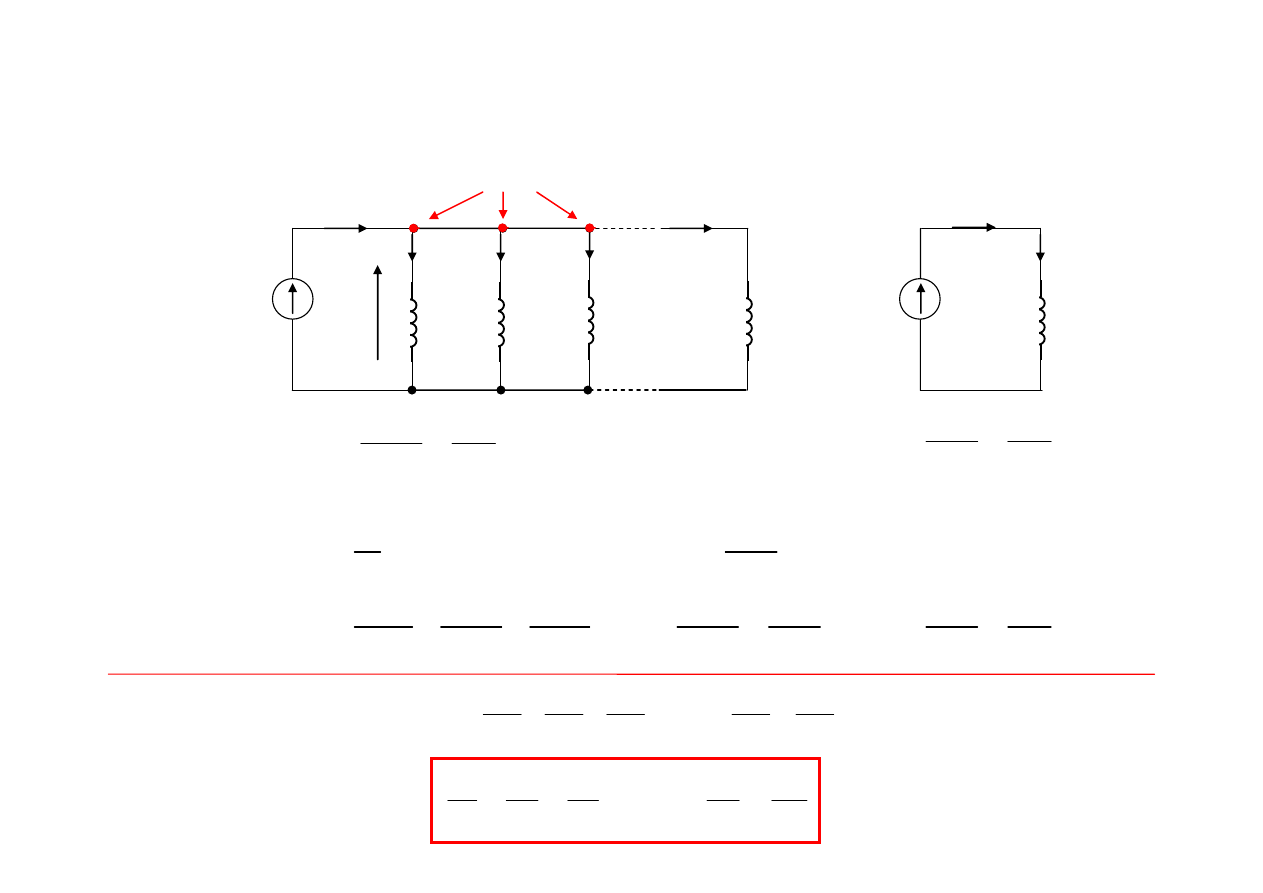
Dla j-tej cewki:

Węzeł ‘w’:

i

1

(t)+ i

2

(t) + i

3

(t)+ ……. + i

n

(t) = i(t)

( ) ( ) ( )

( ) ( )

Z

n

L

t

u

L

t

u

L

t

u

L

t

u

L

t

u

=

+

+

+

+

.......

3

2

1

( ) ( )

j

j

L

t

u

dt

t

di

=

≡

( ) ( ) ( )

( )

(

)

( )

( )

( )

( )

( )

( )

dt

t

di

dt

t

di

dt

t

di

dt

t

di

dt

t

di

dt

t

di

t

i

t

i

t

i

t

i

dt

d

n

n

=

+

+

+

+

=

+

+

+

+

.....

...

3

2

1

3

2

1

( ) ( )

Z

L

t

u

dt

t

di

=

Równoległe łączenie cewek indukcyjnych

( ) ( )

Z

L

t

u

dt

t

di

=

Odwrotność indukcyjności zastępczej n cewek indukcyjnych połączonych szeregowo
jest równa sumie algebraicznej odwrotności ich indukcyjności

Z

n

L

L

L

L

L

1

1

.......

1

1

1

3

2

1

=

+

+

+

+

u(t)

≡

i(t)

i

1

(t)

i

2

(t)

i

n

(t)

i

3

(t)

w

u(t)

u(t)

i(t)

L

Z

L

3

L

2

L

1

L

n

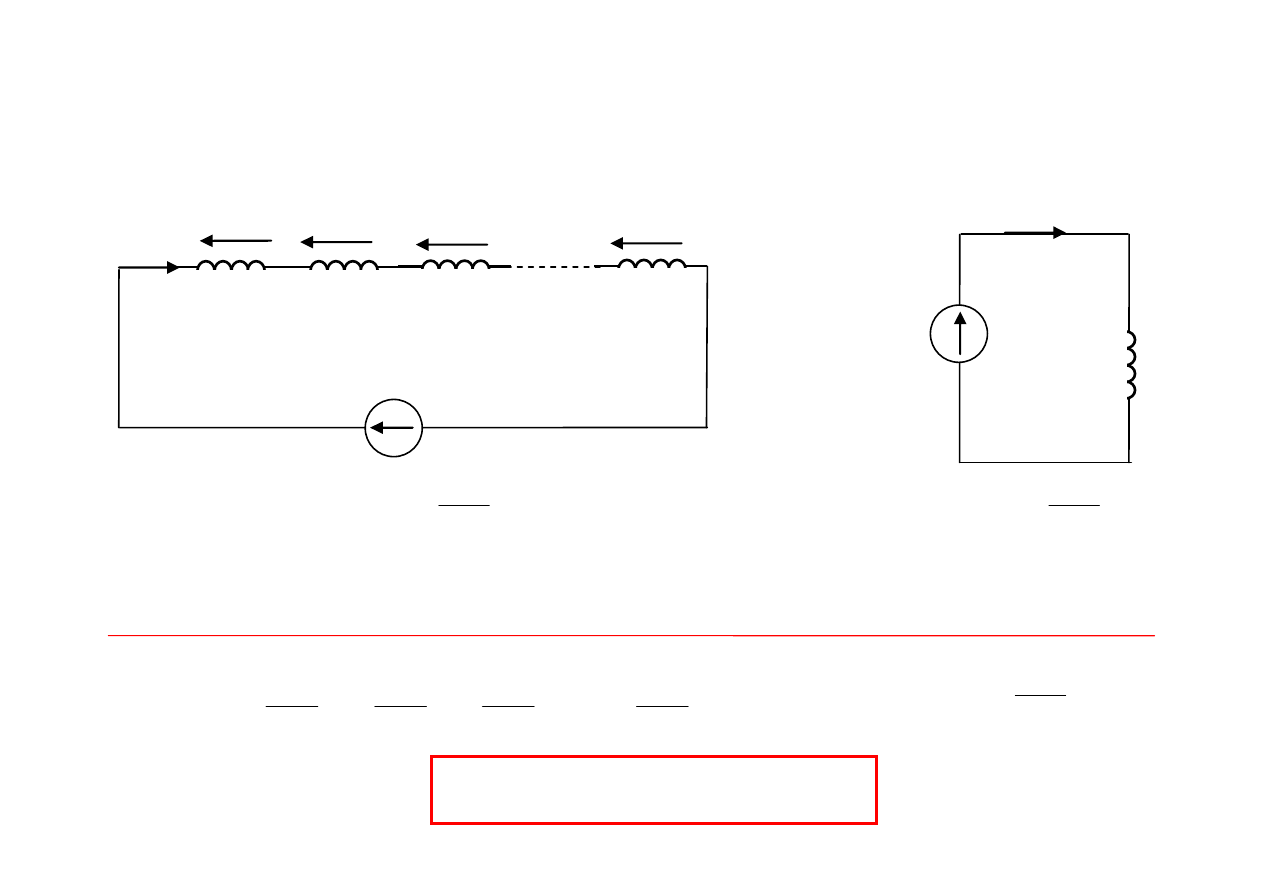
Dla j-tej cewki:

oczko :

U

1

(t)+ U

2

(t) + U

3

(t)+ ……. + U

n

(t) = U(t)

( )

( )

( )

( )

( )

t

U

dt

t

di

L

dt

t

di

L

dt

t

di

L

dt

t

di

L

n

=

+

+

+

+

...

3

2

1

dt

t

di

L

t

U

j

j

)

(

)

(

=

≡

dt

t

di

L

t

U

Z

)

(

)

(

=

Szeregowe łączenie cewek indukcyjnych

Indukcyjność zastępcza n cewek indukcyjnych połączonych równolegle jest równa
sumie algebraicznej ich indukcyjności

n

Z

L

L

L

L

L

+

+

+

+

=

...

3

2

1

dt

t

di

L

t

U

Z

)

(

)

(

=

u(t)

i (t)

u

1

(t)

L

3

L

2

L

1

L

n

u

2

(t)

u

3

(t)

u

n

(t)

≡

u(t)

i(t)

L

Z