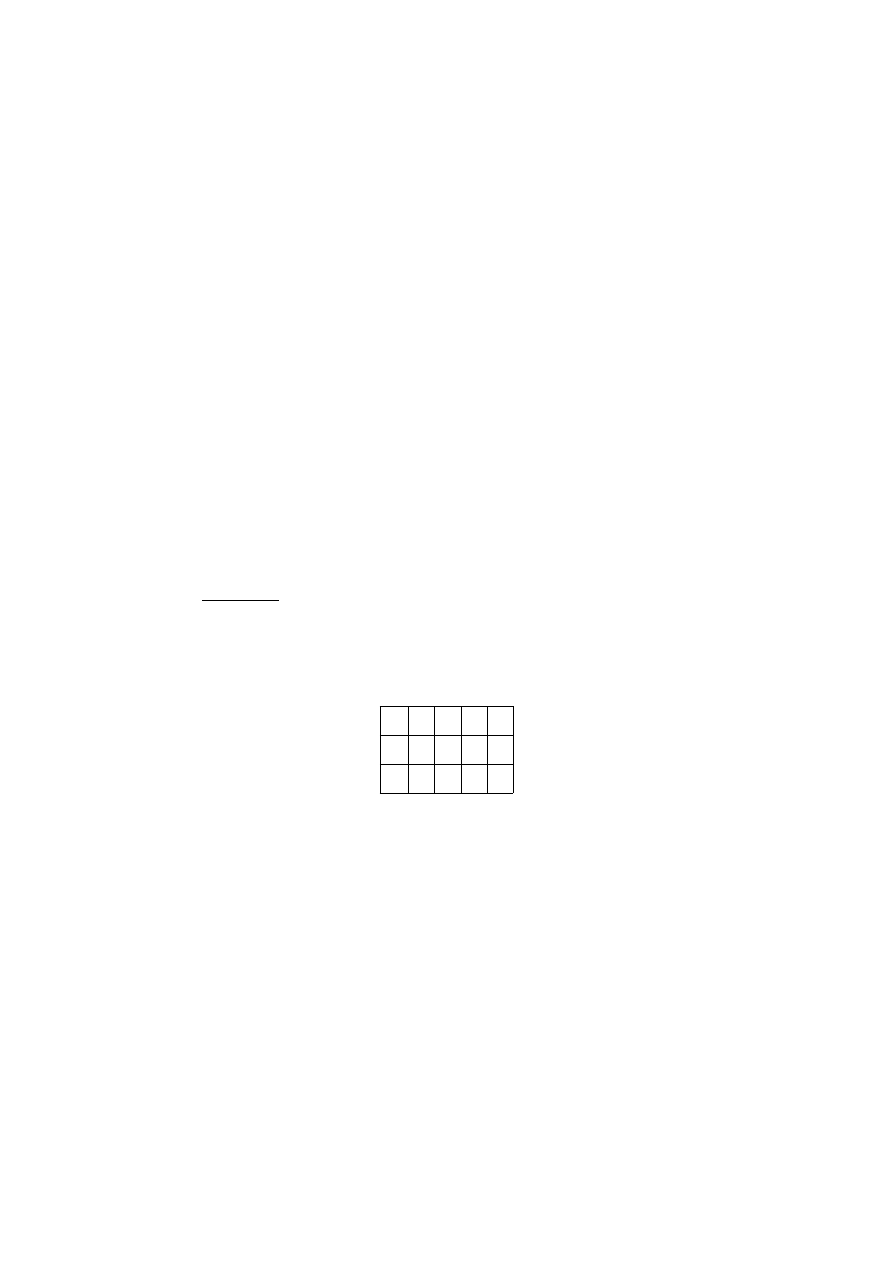
Egzamin z Matematyki Dyskretnej dla 1 roku Informatyki (z dnia 23 czerwca 2008)
u dr W. Kraśkiewicza

1. Zdefiniuj NWD pary liczb całkowitych.

Przedstaw algorytm Euklidesa. Co możesz powiedzieć o efektywności algorytmu?

2. Zdefiniuj liczby pierwsze i uzasadnij, że jest ich nieskończenie wiele. Sformułuj zasadnicze

twierdzenie arytmetyki.

3. Sformułuj i udowodnij chińskie twierdzenie o resztach.

Znajdź wszystkie x, dla których:

x ≡5mod 17

x≡10 mod 25

4. Sformułuj zasadę włączeń i wyłączeń. Ile jest naturalnych rozwiązań równania

X

1



X

2



X

3



X

4



X

5

=

40

spełniających nierówność 0X

i



9 ?

5. Niech a

n

oznacza liczbę ciągów ternarnych (tj. o wartościach 0,1 i 2) długości n,

w których każde dwa symbole niezerowe są podzielone przynajmniej jednym zerem.
Znajdź wzór rekurencyjny oraz wzór zwarty dla ciągu a

n



n=0

∞

Czemu jest równe

a

10

6. Szereg generujący dla ciągu a

n



n=0

∞

dany jest wzorem

At =

23t5t

2

1−3tt

3

Podaj wzór rekurencyjny dla tego ciągu oraz jego 5 pierwszych wyrazów.

7. Zdefiniuj pojęcie wielomianu wieżowego (szachowego) i oblicz ten wielomian dla

szachownicy

X X

X

X

X X

X

X X