Wykład 5

18.III.2002

wersja na dzień 19 marca 2002 roku

5.1 Funkcje Green’a poprzez metodę obra-

zów

Rozpatrzmy sferę S o promieniu R ze środkiem w początku układu. Dla ~r 6= 0

określamy przekształcenie inwersji

~r 7→ ~r

∗

=

R

2

r

2

~r

(5.1)

Punkty ~r i ~r

∗

nazywają się symetrycznymi względem sfery S.

Definicja. Niech funkcja f(~r) będzie funkcją harmoniczną na zewnątrz sfery
S

. Przekształceniem Kelvin’a funkcji f nazywamy funkcję

f

∗

(~r

∗

) =

R

r

∗

f

R

2

r

∗2

~r

∗

!

Bezpośrednim rachunkiem (vide Ćwiczenia treningowe) pokazuje się, że

jeśli funkcja f jest harmoniczna na zewnątrz sfery S, to funkcja f

∗

(~r

∗

) jest

harmoniczna wewnątrz sfery S. Zauważmy, że gdy r = R to przekształcenia
inwersji i przekształcenie Kelvin’a stają się tożsamościami:

~r

∗

= ~r

(5.2)

f

∗

(~r

∗

) = f(~r)

(5.3)

Rozpatrzmy nieruchomy ładunek punktowy q umieszczony w punkcie ~a. W
próżni ładunek ten generuje potencjał elektrostatyczny

Φ(~r) =

q

|~r − ~a|

(5.4)

24

WYKŁAD 5.

18.III.2002

25

spełniający równanie

4Φ(~r) = −4qπδ(~r − ~a)

Oznacza to, że wszędzie z wyjątkiem punktu ~r = ~a potencjał spełnia równa-
nie jednorodne

4Φ(~r) = 0

W szczególności, gdy z początku układu wyprowadzimy sferę o promieniu R,
to wszędzie na zewnątrz sfery potencjał będzie spełniał równanie Laplace’a.

Wykonajmy na funkcji Φ przekształcenia Kelvin’a względem naszej sfery.

Otrzymamy w wyniku funkcję

Φ

∗

(~r

∗

) =

R

r

∗

q

|R

2

~r

∗

/r

∗2

− ~a|

=

R

r

∗

q

R

4

/r

∗2

+ a

2

− 2R

2

a

cos θ/r

∗

(5.5)

Po przekształceniach otrzymujemy

Φ

∗

(~r

∗

) =

q R

a

√

r

∗2

+ a

∗2

− 2r

∗

a

∗

cos θ

(5.6)

gdzie

a

∗

=

R

2

a

jest długością wektora ~a

∗

otrzymanego z ~a przekształceniem inwersji wzglę-

dem naszej sfery.

Z ogólnych własności przekształcenia Kelvin’a wynika, że

• funkcja Φ

∗

(~r) spełnia równanie Laplace’a dla {~r: r < R} czyli wewnątrz

sfery

• funkcja Φ

∗

(~r) jest równa funkcji Φ(~r) gdy r = R

• punkt ~

a

∗

leży na zewnątrz sfery (o ile tylko a < R)

Jednocześnie funkcja (5.6) ma postać potencjału elektrostatycznego związa-
nego z ładunkiem punktowym qR/a umieszczonym w punkcie ~a

∗

.

5.1.1 Powierzchnia graniczna – wnętrze sfery

Rozpatrzmy teraz funkcję, która jest różnicą:

Ω(~r) = Φ(~r) − Φ

∗

(~r)

i zbadajmy jej własności dla r ¬ R. Widać natychmiast, że

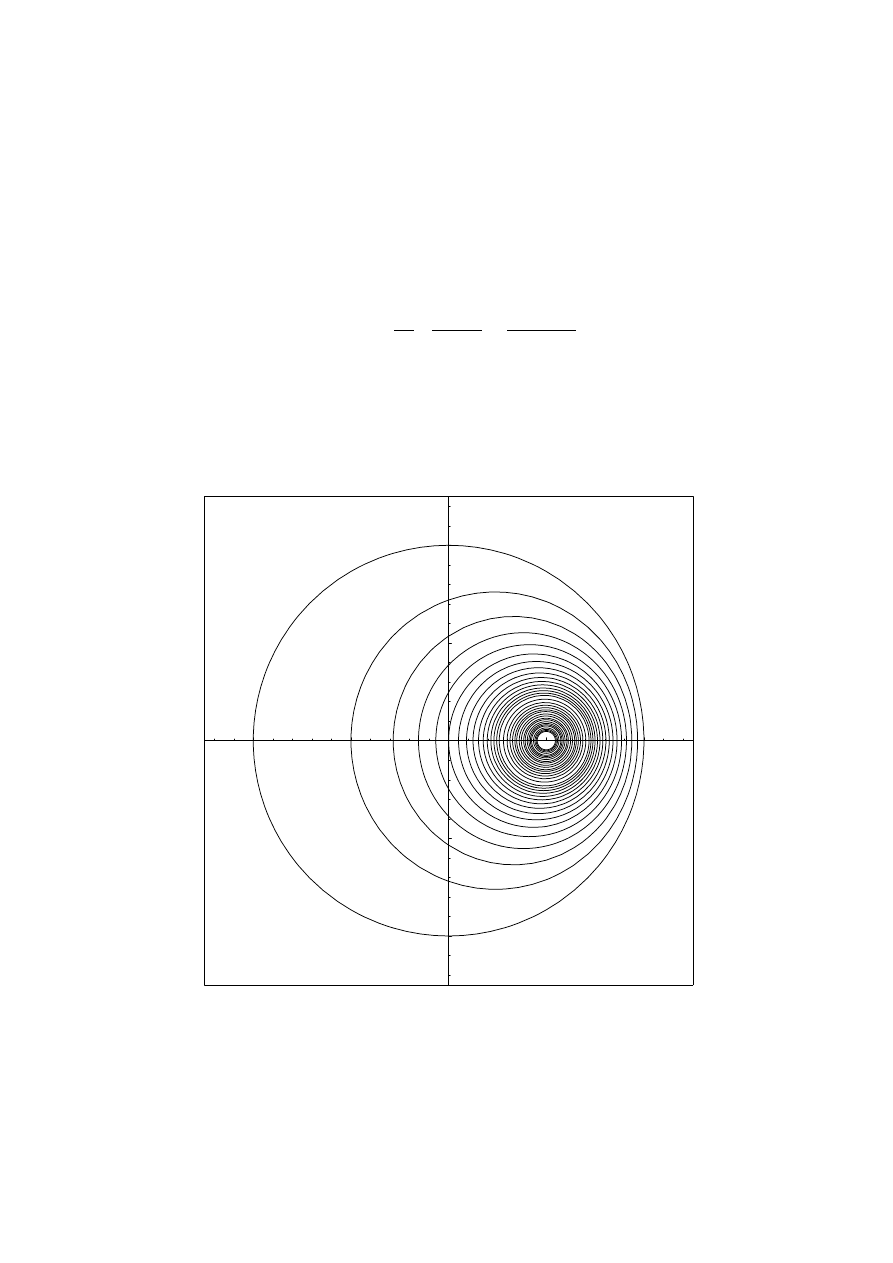
WYKŁAD 5.

18.III.2002

26

•

4Ω = −4qπδ(~r − ~a)

• Ω(~

r

)|

r

=R

= 0

W ten sposób pokazaliśmy, że funkcja

G

(~r,~a) = −

1

4π

1

|~r − ~a|

−

R

a |~r − ~a

∗

|

!

(5.7)

jest funkcją Green’a rozwiązującą zagadnienie Dirichleta dla sfery o promie-
niu R. Funkcja ta z dokładnością do czynnika −1/4π odpowiada potencjało-

wi elektrostatycznemu wytworzonemu przez ładunek punktowy umieszczony
wewnątrz uziemionej przewodzącej sfery. Potencjał ten przedstawiony jest na
rys. (5.1). Sfera o środku w początku układu ma promień R = 2. Ładunek

-2

-1

1

2

-2

-1

1

2

Rysunek 5.1: Przekrój przez powierzchnie ekwipotencjalne punktowego ła-
dunku wewnątrz uziemionej sfery

WYKŁAD 5.

18.III.2002

27

punktowy umieszczony jest w punkcie o współrzędnych (1, 0, 0). Na rysun-
ku przedstawiony jest przekrój powierzchni ekwipotencjalnych płaszczyzną
z

= 0. Ponieważ sfera jest uziemiona to na zewnątrz sfery potencjał jest

równy zeru.

Widać zatem, że funkcja Green’a G(~r, ~r

0

) (5.7) rozwiązująca zagadnienie

Dirichleta dla wnętrza sfery o promieniu R ma postać, która formalnie odpo-
wiada potencjałowi elektrostatycznemu dwóch ładunków punktowych: jeden
o ładunku jednostkowym umieszczony wewnątrz sfery w punkcie ~r

0

,

(r

0

< R

)

i drugi o ładunku −R/r

0

.

Ten drugi ładunek (ładunek – obraz, ładunek –

duch) umieszczony jest w punkcie ~r

∗

0

powstałym z z ~r

0

przez przekształcenie

inwersji (5.1).

5.1.2 Powierzchnia graniczna – płaszczyzna

Przypadek graniczny promienia sfery R → ∞ odpowiada zagadnieniu, gdy

obszarem V jest półprzestrzeń, której jednym brzegiem jest płaszczyzna, na-
tomiast pozostała część brzegu znajduje się w nieskończoności. Przy takim
przejściu granicznym za stały parametr obieramy odległość ładunku od po-
wierzchni sfery. Odległość tą oznaczamy jako δ :

δ

= R − a .

Przez δ

∗

oznaczmy odległość ładunku–obrazu od powierzchni sfery. Wtedy

obliczona z (5.7) odległość r

∗

od środka sfery jest równa R + δ

∗

i związek

(5.7) daje

R

+ δ

∗

=

R

2

R − δ

Mamy stąd

δ

∗

=

Rδ

R − δ

,

co w granicy R → ∞ daje δ = δ

∗

.

Również wielkość ładunku–obrazu pozostaje taka sama (co do wartości

bezwzględnej):

q

∗

=

qR

a

=

qR

R − δ

→ q dla R → ∞

.

WYKŁAD 5.

18.III.2002

28

5.2 Zadania i ćwiczenia

Zadania z listy nr 4

Zadanie 1.
Pokazać, że dla przekształcenia inwersji mamy

• ~

r

∗∗

= ~r

• rr

∗

= R

2

Zadanie 2.
Na wykładzie została wyprowadzona funkcja Green’a dla wnętrza sfery o
promieniu R przy założeniu, że środek sfery pokrywa się ze środkiem układu
współrzędnych. Wyznaczyć postać funkcji Green’a jeśli środek sfery znajduje
się w punkcie ~

R.

Zadanie 3.
Napisać jawną postać funkcji Green’a dla płaszczyzny.

• Naszkicować powierzchnie ekwipotencjalne oraz linie sił pola elektrycz-

nego generowane przez ładunek punktowy znajdujący się w odległości
a

od uziemionej płaszczyzny przewodzącej.

• Obliczyć gęstość ładunku indukowanego na płaszczyźnie.

• Obliczyć ładunek indukowany na płaszczyźnie zawarty wewnątrz okrę-

gu o promieniu R. Środek okręgu wyznaczony jest przez rzut prosto-
padły ładunku na płaszczyznę.

Ćwiczenia treningowe

Ćwiczenie 1.
Zapisać przekształcenie inwersji we współrzędnych sferycznych.
Ćwiczenie 2.
Pokazać, że zachodzi

4

(~

r

∗

)

f

∗

(~r

∗

) =

r

5

R

5

4f(~r)

Ćwiczenie 3.
Otrzymać wynik

(5.6) posługując się wyłącznie zapisem wektorowym

Φ(~r

∗

) =

R

r

∗

q

|R

2

~r

∗

/r

∗2

− ~a|

,

tzn. bez rozpisywania wyrażenia na pierwiastek itd. . .

WYKŁAD 5.

18.III.2002

29

Wskazówka

: wykorzystać fakt, że każdy wektor ~

b można zapisać jako

~b = b ~n

b

,

gdzie

~n

b

=

~b

b

.

Potem w przedostatnim kroku trzeba jeszcze coś zauważyć, co wiąże się z wła-
snościami iloczynu skalarnego. Potem jest już z górki.