Pas m owa teor ia cia

»

sta

»

ych 1

PASMOWA TEORIA CIAº STAºYCH

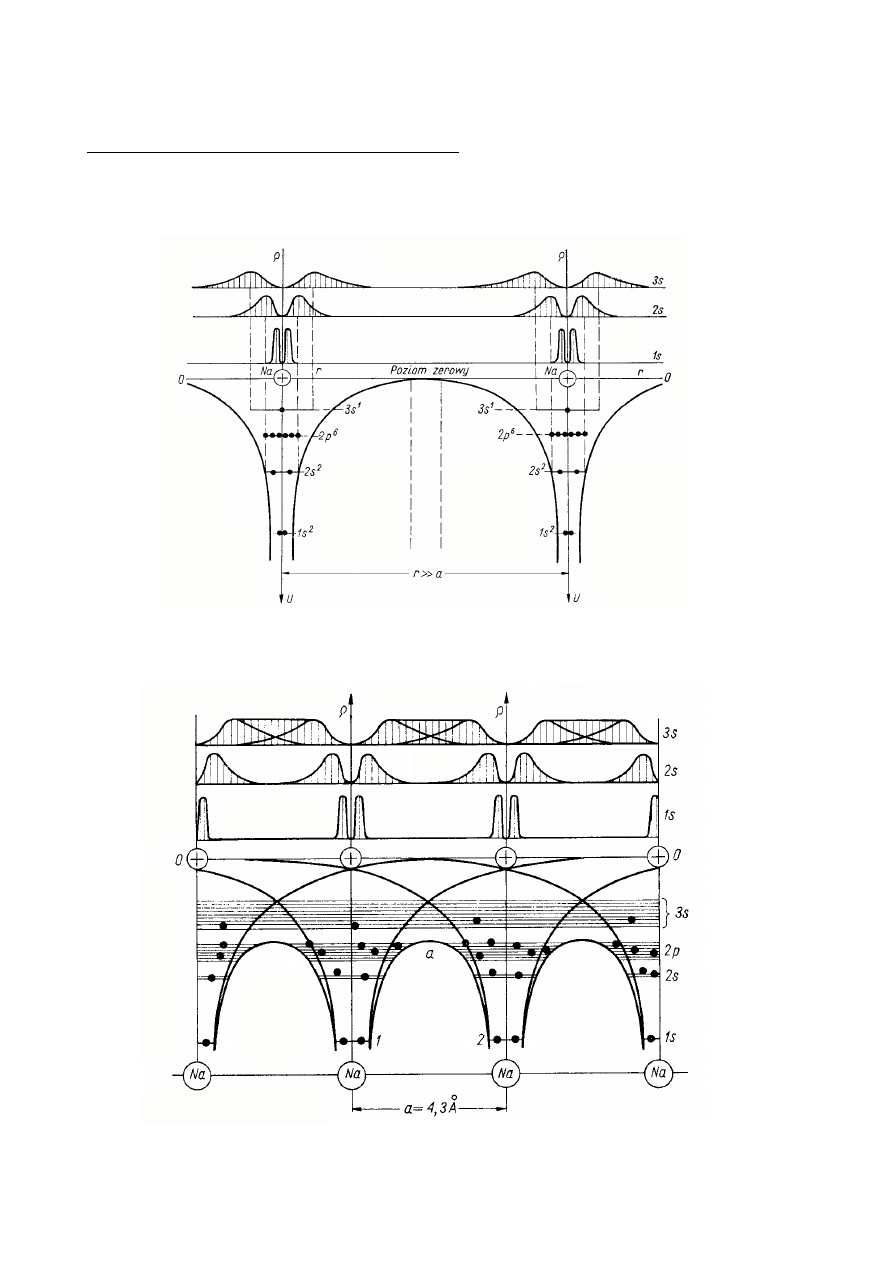
Skolektywizowane elektrony w metalu
Weïmy pod uwag“ pewn iloу atomów jakiegoÑ metalu, np. sodu.
Atom sodu zawiera 11 elektronów o konfiguracji 1s

2

2s

2

2p

6

3s

1

Schemat energetyczny dla atomów sodu znajdujcych si“ w odleg»oÑciach znacznie wi“kszych od sta»ej sieci

Schemat energetyczny dla atomów sodu znajdujcych si“ w odleg»oÑciach rz“du sta»ej sieci

Pas m owa teor ia cia

»

sta

»

ych 2

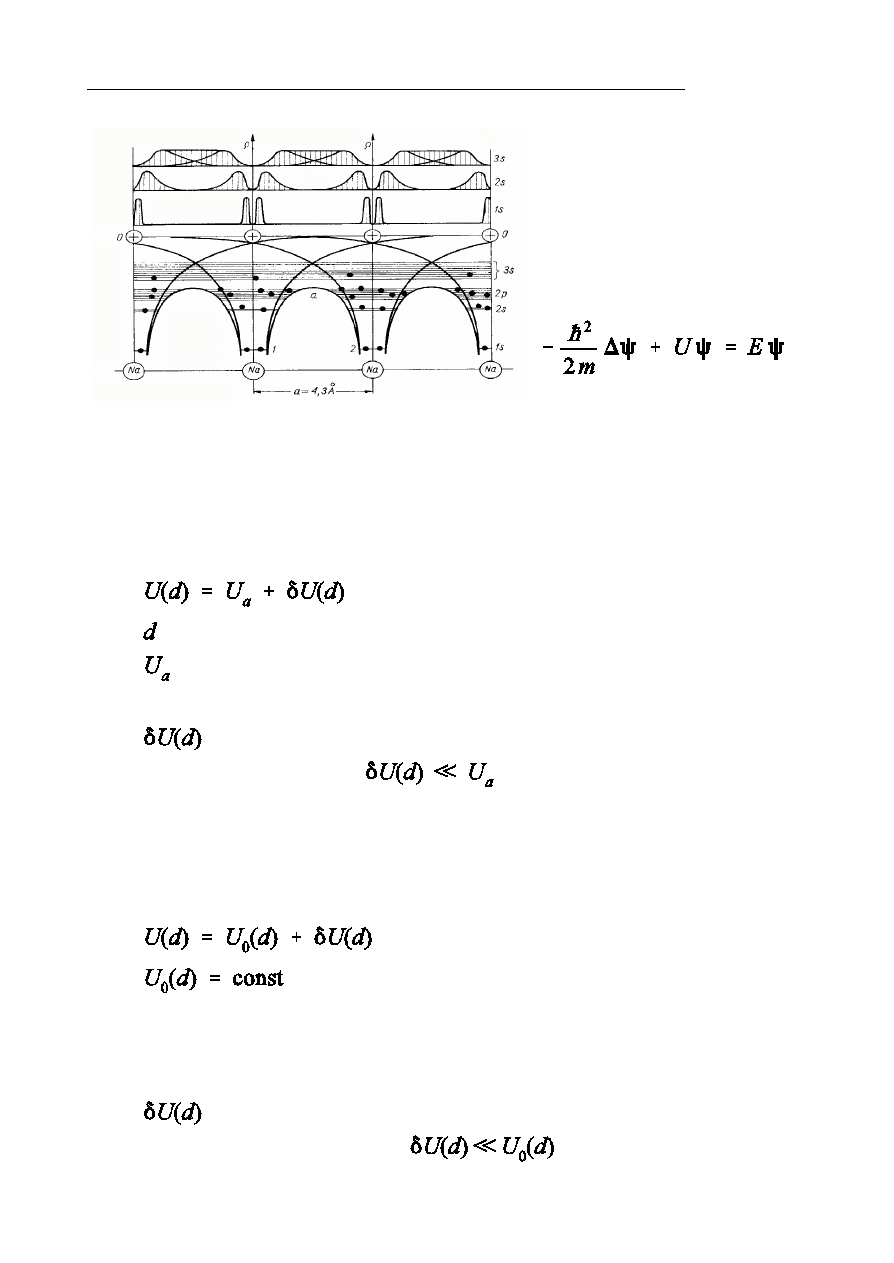
Pasmowy charakter widma energetycznego elektronów w metalu

W teorii cia»a sta»ego, podobnie jak w teorii atomu, zasadniczym zadaniem
jest okreÑlenie widma energetycznego i stanów stacjonarnych
skolektywizowanych elektronów w krysztale.
Poniewaó zagadnienie to jest bardzo z»oóone, stosuje si“ szereg przyblióe½:

- przyblióenie adiabatyczne,
- przyblióenie jednoelektronowe,
- przyblióenie silnie zwizanych elektronów,
- przyblióenie elektronów swobodnych,
- przyblióenie s»abo zwizanych elektronów.

Przyblióenie adiabatyczne

Masa jder jest znacznie wi“ksza od masy elektronów. Dlatego jdra
poruszaj si“ znacznie wolniej. Kryszta» moóe byƒ traktowany jako
sk»adajcy si“ z dwóch niezaleónych poduk»adów:
- pr“dkich elektronów,
- praktycznie nieruchomych jder.

W ten sposób zagadnienie uk»adu jder i elektronów moóna sprowadziƒ do
prostszego zagadnienia stanu samych elektronów w nieruchomej sieci jder.

Przyblióenie jednoelektronowe

Pozwala zredukowaƒ problem ruchu wielu elektronów do zagadnienia ruchu
jednego elektronu w wypadkowym polu

jonów sieci i pozosta»ych

elektronów, czyli do rozwizania jednoelektronowego równania
Schrödingera

Pas m owa teor ia cia

»

sta

»

ych 3

Sens fizyczny przyblióe½ silnie i s»abo zwizanych elektronów

W przyblióeniu jedno-
ele kt ro no wym n a l eó y
rozwizaƒ równanie:

W krysztale moóna wyróóniƒ dwa rodzaje obszarów:

1)

Obszary silnie zmieniajcego si“ potencja»u sieci (10-15% obj“toÑci).
Pole jest tu praktycznie takie samo jak w izolowanych atomach.

-

najmniejsza odleg»oу atomów w krysztale,

-

energia potencjalna elektronu w izolowanym atomie

(funkcja okresowa o okresie równym sta»ej sieci),

-

poprawka uwzgl“dniajca wp»yw ssiednich w“z»ów sieci

na energi“ (

).

2)

Obszary o nieznacznie zmieniajcym si“ potencjale - g»ówna cz“у
obj“toÑci kryszta»u.

- energia potencjalna elektronu w polu jonów

dodatnich przy za»oóeniu, óe to pole jest
kompensowane przez pole wszystkich pozosta»ych
elektronów prócz danego

- uwzgl“dnia nieca»kowit kompensacj“ pola przez

elektrony [

]

Pas m owa teor ia cia

»

sta

»

ych 4

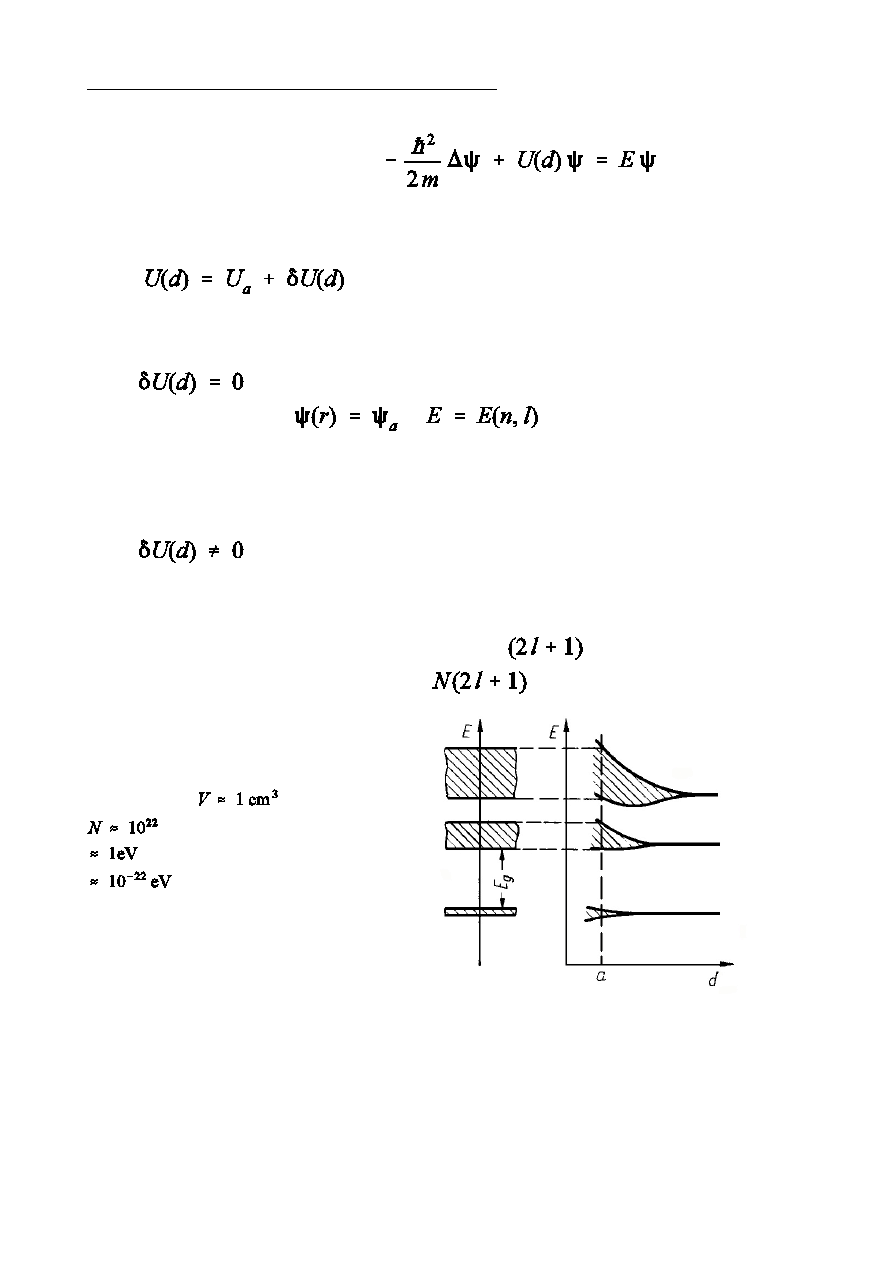
Przyblióenie silnie zwizanych elektronów

Celem rozwizania równania

i korzystamy z

postaci energii potencjalnej charakterystycznej dla obszaru silnego pola

JeÑli

(przyblióenie zerowe, kryszta» bez oddzia»ywa½)

Otrzymujemy

,

- takie jak dla atomu

izolowanego; kaódy poziom energetyczny jest N-krotnie zwyrodnia»y,
gdzie N - liczba atomów w sieci.

JeÑli

(kryszta»)

Oddzia»ywanie to prowadzi do usuni“cia zwyrodnienia i
rozszczepienia danego poziomu niezwyrodnia»ego na N blisko siebie
leócych podpoziomów, a w przypadku

krotnego zwyrodnienia

(bez uwzgl“dnienia spinu) na

podpoziomów.

Powstaje pasmo

Przyjmujc

otrzymujemy

atomów, co przy szerokoÑci pasma

daje odleg»oу mi“dzy poziomami

. Widmo energetyczne w paÑmie

jest praktycznie cig»e.

Najwi“ksze zmiany wyst“puj dla stanów elektronów walencyjnych,
nieznaczne dla elektronów wewn“trznych.
Pasma energii dozwolonych s oddzielone pasmami energii wzbronionych.
Ze wzrostem energii szerokoу pasm energii dozwolonych roÑnie, a energii
wzbronionych maleje.

Pas m owa teor ia cia

»

sta

»

ych 5

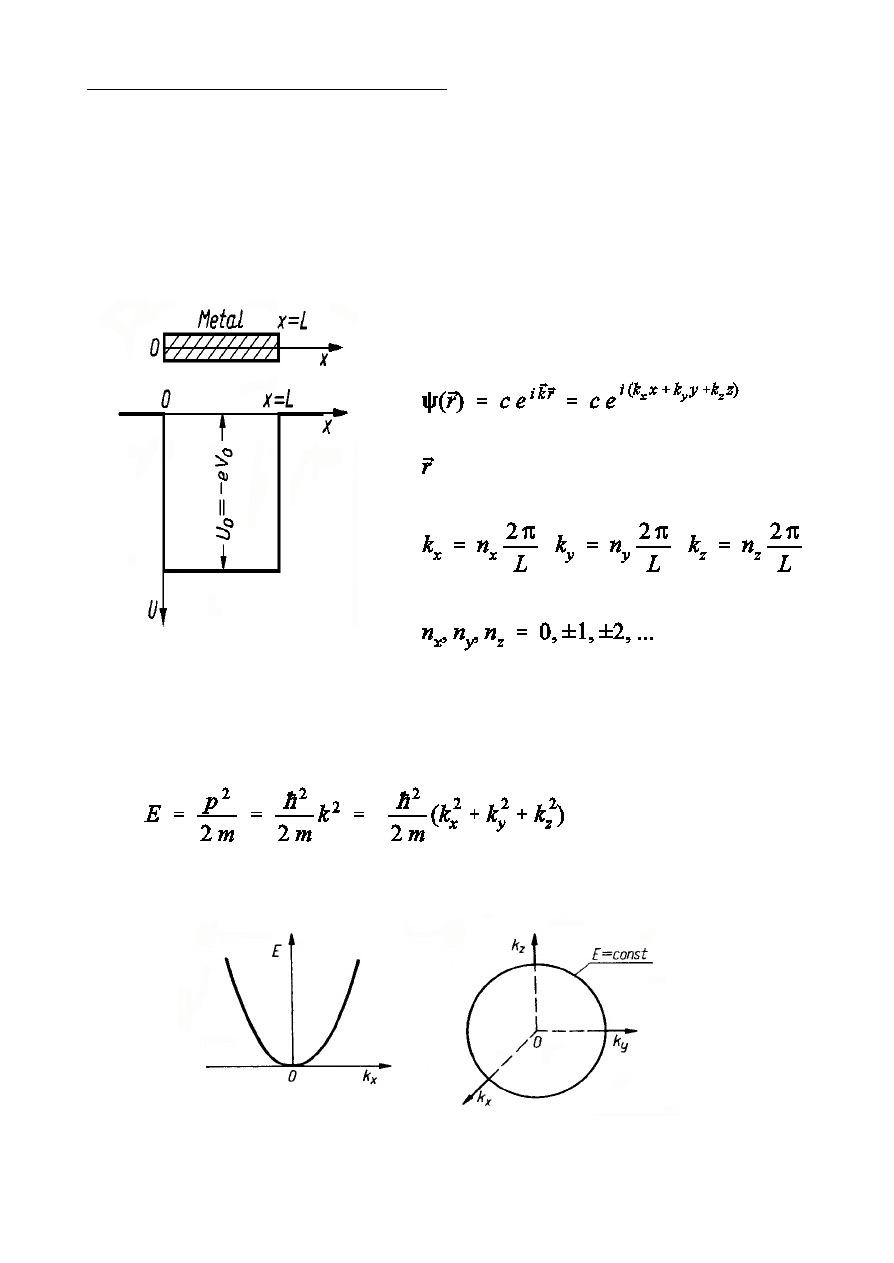
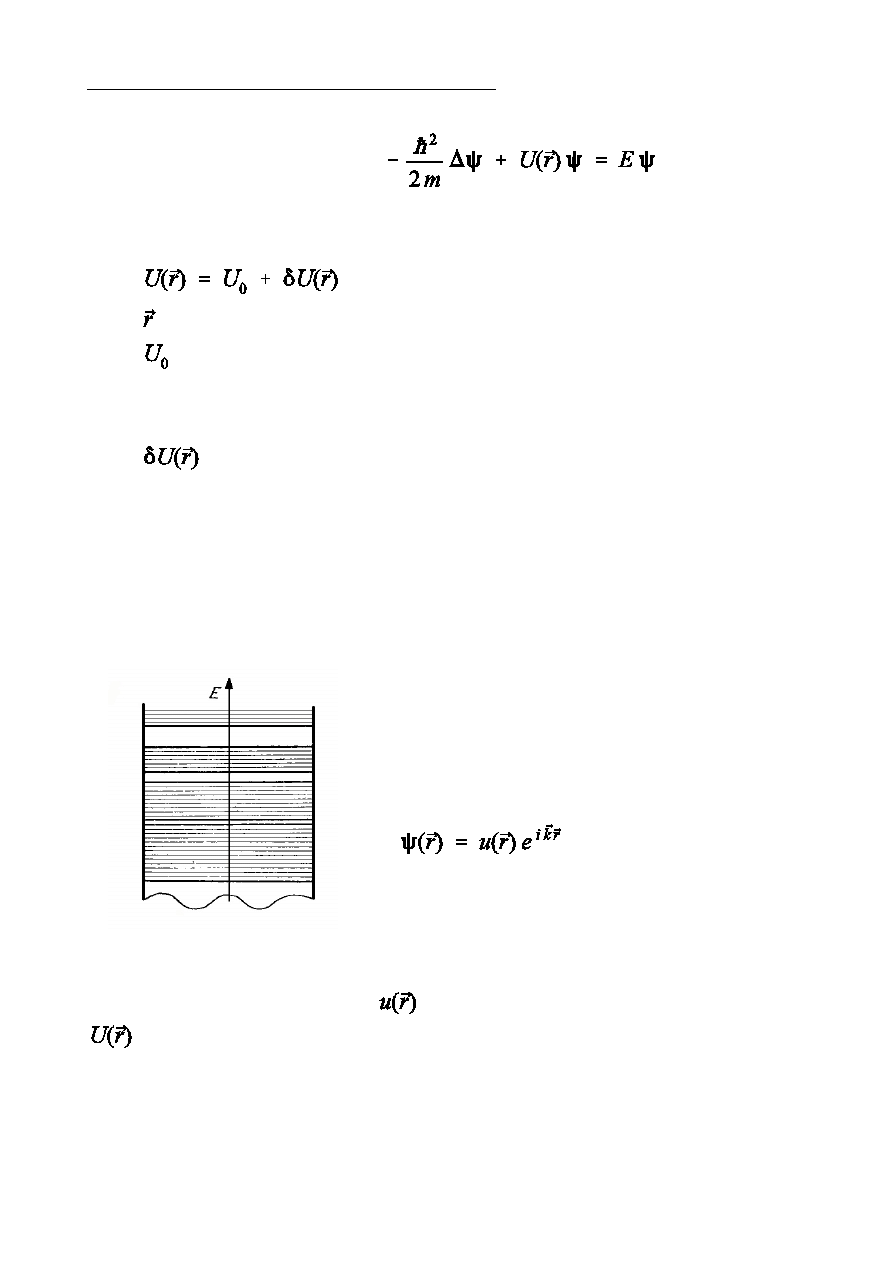
Przyblióenie elektronów swobodnych

W przyblióeniu elektronów swobodnych kryszta» przedstawia si“ jako jam“
potencjaln o p»askim dnie

Ruch elektronu opisany jest fal p»ask

- wektor po»oóenia

,

,

Energia elektronu jest kwadratow funkcj wektora falowego

Pas m owa teor ia cia

»

sta

»

ych 6

Przyblióenie s»abo zwizanych elektronów

Celem rozwizania równania

i korzystamy z

postaci energii potencjalnej charakterystycznej dla obszaru s»abego pola

- wektor po»oóenia,

-

energia potencjalna elektronu w polu jonów dodatnich przy

za»oóeniu, óe to pole jest kompensowane przez pole
wszystkich pozosta»ych elektronów prócz danego.

- uwzgl“dnia

nieca»kowit kompensacj“ pola przez

elektrony. Funkcja okresowa o okresie równym sta»ej sieci.

W przyblióeniu s»abo zwizanych elektronów model kryszta»u moóna
przedstawiƒ jako jam“ potencja»u ze s»abo pofalowanym cnem.

Podobnie jak w modelu elektronów swobodnych,
rozwizania poszukuje si“ w postaci fali p»askiej,
ale o nieco zmodyfikowanej amplitudzie

-

funkcja Blocha

Konkretna postaƒ funkcji

jest okreÑlona przez postaƒ funkcji

wchodzcej do równania Schrödingera.

Ilustracj metody s»abo zwizanego elektronu jest model Kroniga-Penney’a
dla kryszta»u liniowego.

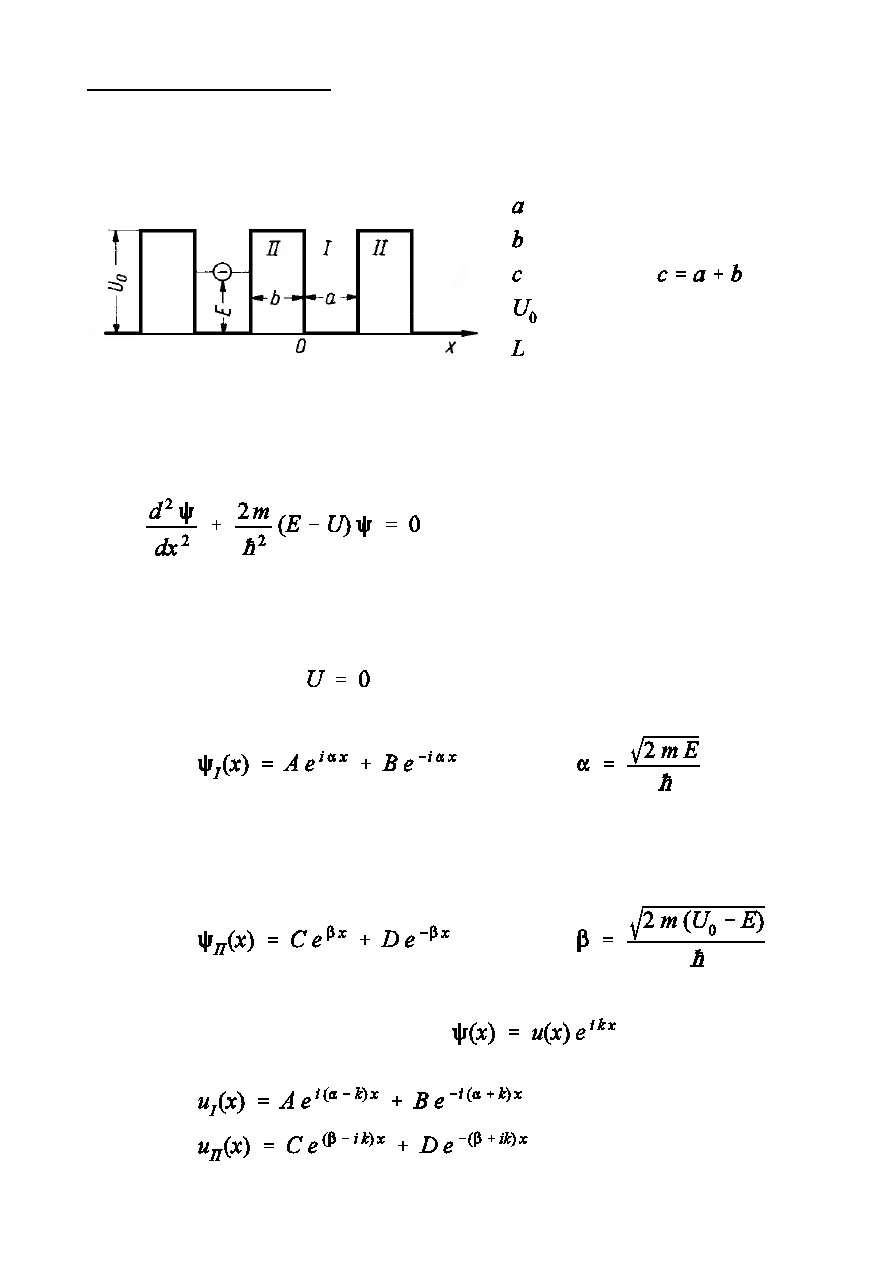
Pas m owa teor ia cia

»

sta

»

ych 7

Model Kroniga-Penney’a

Rozwaómy ruch elektronu w liniowym »a½cuchu prostoktnych jam
potencjalnych.

- szerokoу jamy

- szerokoу bariery

- sta»a sieci (

)

- wysokoу bariery

- d»ugoу »a½cucha

Równanie Schrödingera

Rozwizania

Obszar I

Obszar II

Na podstawie postaci funkcji Blocha

otrzymujemy