Wartością bezwzględną (modułem) liczby rzeczywistej a jest liczba ∣a∣ spełniająca równości:

∣

a∣=a gdy a≥0

∣

a∣=−a gdy a0

Przykłady:



5

2

=

5 gdy ab ,



−

5

2

=−−

5=5 gdy ab





a−b

2

=∣

a−b∣=a−b gdy ab ,





a−b

2

=∣

a−b∣=−a−b=b−a gdy ab

Logarytm o podstawie a liczby dodatniej b to wykładnik c potęgi, do której należy podnieść a, aby
otrzymać liczbę b:

log

a

b=c ⇔ a

c

=

b

Liczbę b nazywa się liczbą logarytmowaną. Zakłada się, że a i b są liczbami dodatnimi oraz

a≠1 . Z określenia logarytmu natychmiast wynika, że potęga o podstawie a i wykładniku

log

a

b

jest równa b:

a

log

a

b

=

b

Zapis bez indeksu log a nie jest jednoznaczny. W różnych dziedzinach może oznaczać logarytm
naturalny, dziesiętny lub binarny. Dlatego, gdy podstawa nie wynika z kontekstu użycia, należy
używać zapisu jednoznacznego:

●

logarytm dziesiętny - log

10

x=log x

●

logarytm naturalny - log

e

x=ln x

●

logarytm binarny -

log

2

x=lg x

●

logarytm o podstawie a - log

a

x

Prawa działań na logarytmach wynikają z praw dotyczących wyrażeń potęgowych:

●

logarytm jedności równa się zero:

log

a

1=0

●

logarytm podstawy logarytmu równa się jedności:

log

a

a=1

●

logarytm iloczynu dwóch lub kilku czynników równa się sumie logarytmów
poszczególnych czynników:

log

a



b⋅c=log

a

blog

a

c

●

logarytm ilorazu dwóch liczb równa się różnicy logarytmów dzielnej i dzielnika:

log

a

b
c

=

log

a

b−log

a

c

●

logarytm liczby w danej potędze równa się iloczynowi wykładnika potęgi i logarytmu tej
liczby:

log

a

b

c

=

c⋅log

a

b

log

a

n



b

c

=

c
n

⋅

log

a

b

●

logarytm o podstawie w formie potęgowej

a

c

równa się iloczynowi odwrotności potęgi c i

logarytmowi o podstawie a:

log

a

c

b=

1
c

⋅

log

a

b

Zależności między logarytmami o różnych podstawach:

●

iloraz logarytmów dwóch liczb b, a przy jednakowej podstawie c równa się logarytmowi
pierwszej liczby b przy podstawie równej drugiej liczbie a:

log

c

b

log

c

a

=

log

a

b

●

jeśli jedna liczba logarytmowana jest równa podstawie logarytmu drugiej liczby
logarytmowanej i odwrotnie, to iloczyn tych liczb równa się jedności:

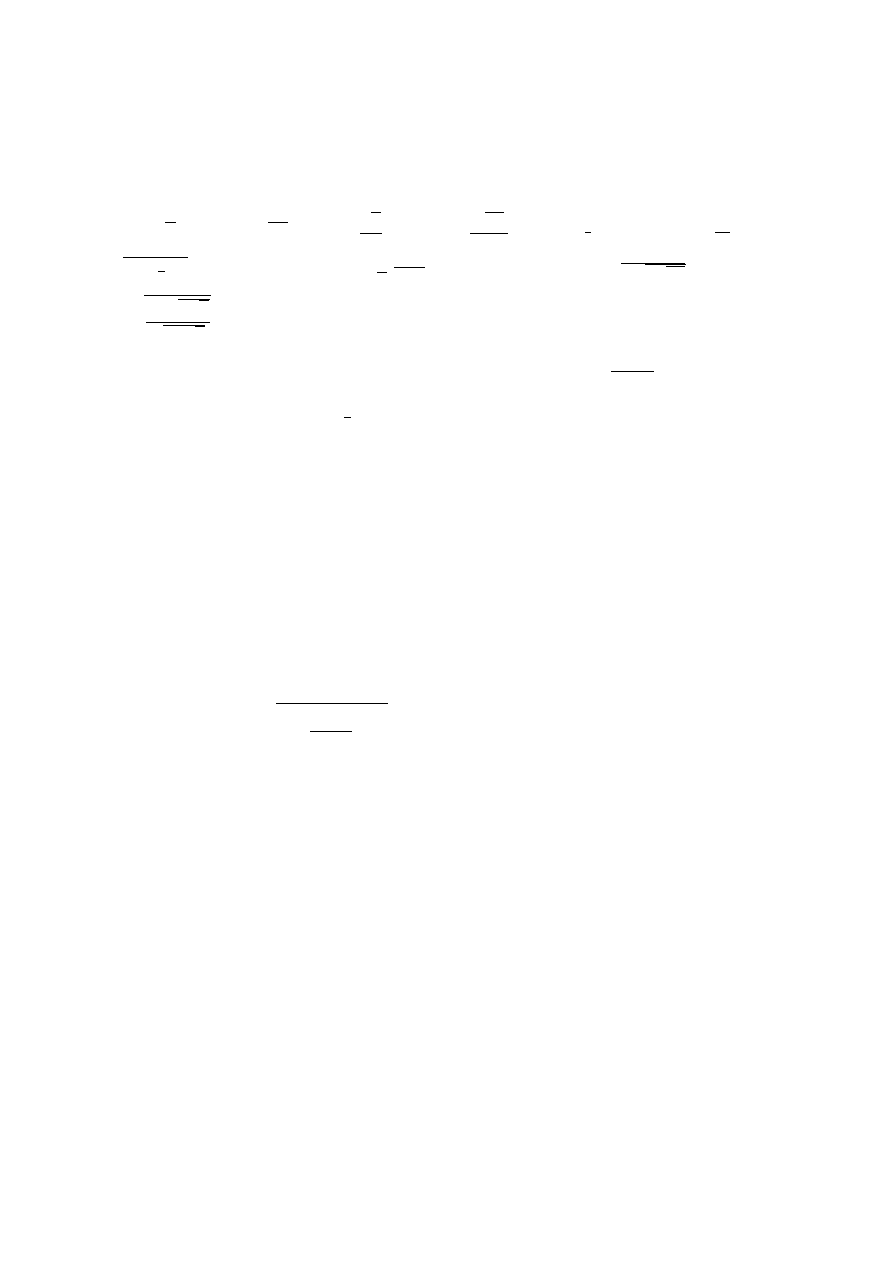
log

a

b⋅log

b

a=1

log e⋅ln 10=1

Ćwiczenia:

1. Oblicz:

a) log

2

2



2 b) log

3

9



27 c) log

5



5

25

d) log 10



10

1000

e) log

3



3

27 f) log

9

tan





6



g)



10

2

1
2

lg 16

h)

log

3

5 log

25

27

i)



3



9



1

5 log

5

3

j) 2

log

3

5

−

5

log

3

2

k) log



2



6



15

l) log



15



3



5



25



3

2. Wykazać prawdziwość wzoru na zmianę podstaw logarytmów:

log

c

b

log

c

a

=

log

a

b

3. Udowodnij, że log

a

xlog

1
a

x=0

4. Liczba osobników Digitalis purpurea przeżywających w czasie t (przeżywalność mierzona

liczbą osobników, każdego miesiąca, poczynając od pojawienia się siewek) określona jest
równaniem y=100 e

−

0,231 t

:

a) jaki jest początkowa liczba roślin,
b) jaki jest czas po którym połowa siewek przeżyje
Digitalis purpurea jest rośliną monokarpiczną, kiełkującą na wiosnę i kwitnącą w lato
następnego roku. Zakładając, że 15 miesięcy jest potrzebne, aby uzyskać dojrzałość
płciową, jak wiele osobników najprawdopodobniej przeżyje do tego czasu.

5. Znając równanie na zmianę frekwencji alleli przy założeniu kodominacji (tzn. homozygoty

mają różne wartości dostosowania, zaś heterozygota posiada dostosowanie o wartości, która
jest średnią dwóch homozygotycznych genotypów) znaleźć czas (liczony w liczbie
generacji) po jakim frekwencja allelu

A

2

zmieni się z

q

0

=

0,2

do

q

t

=

0,6

(przy

s=0,001

:

q

t

=

1

1



1−q

0

q

0



e

−

st

.