Układy nieliniowe

Podstawy automatyki

Układy nieliniowe wykazują cztery właściwości

znacznie

różniące je od układów liniowych:

1) nie

spełniają zasady superpozycji,

2) charakter odpowiedzi w stanie ustalonym w

sposób

istotny

zależy od amplitudy sygnału sterującego lub

amplitudy

zakłócenia,

3)

odpowiedź w stanie ustalonym oprócz częstotliwości
pochodzącej od wymuszenia lub zakłócenia może

dodatkowo

zawierać inne harmoniczne,

4)

stabilność układów w istotny sposób zależy od wartości
warunków początkowych, przykładowo:

•

dla

małych wartości warunków początkowych układ

może być stabilny,

•

dla

dużych wartości warunków początkowych układ

może być niestabilny.

Zasada superpozycji - przypomnienie

Zasada superpozycji stosowana jest w analizie i syntezie

liniowych

układów regulacji. Brzmi ona następująco:

Reakcja układu liniowego na sumę sygnałów

jest równa sumie reakcji na każdy sygnał osobno.

Układy nieliniowe - przykład

Mamy trzy układy regulacji z jednostkowym sprzężeniem
zwrotnym:

1) układ liniowy opisany funkcją przejścia toru głównego

1

s

s

4

G(s)

2







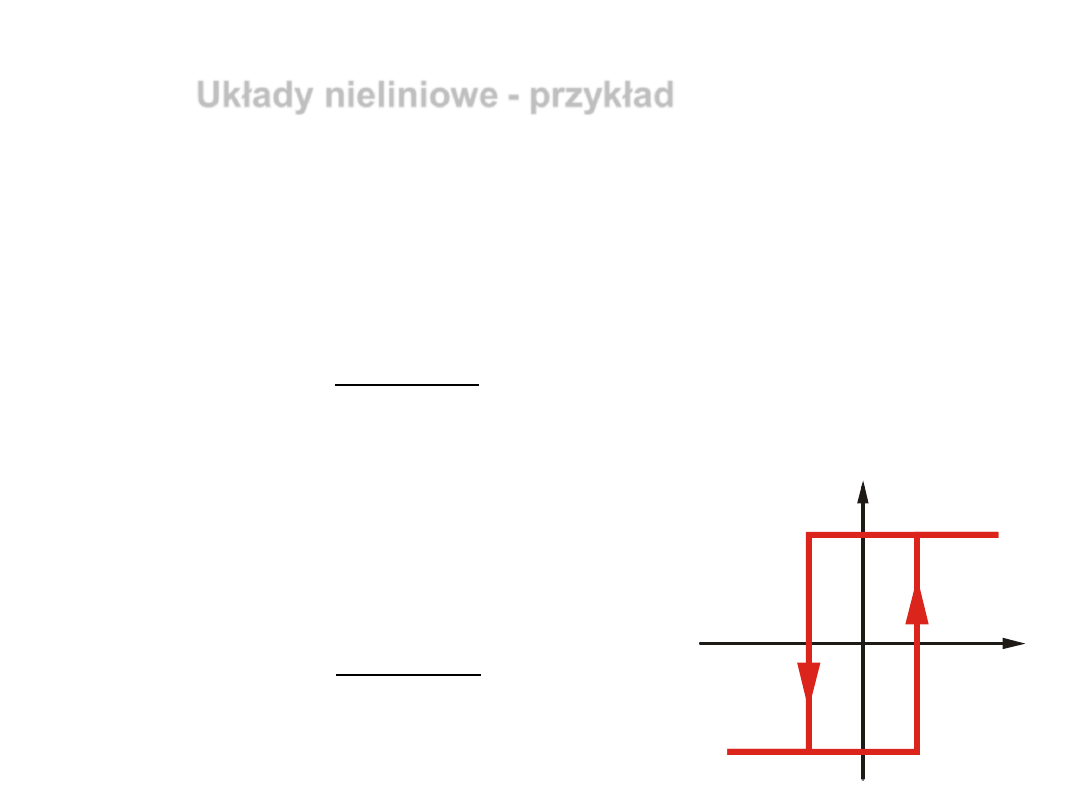
2)

układ nieliniowy zawierający człon

liniowy opisany

poniższą funkcją przejścia

oraz

człon o charakterystyce przekaźnika

dwupołożeniowego

e

u

0 .5

2

-0 .5

-2

1

s

s

2

G(s)

2







Układy nieliniowe - przyklad

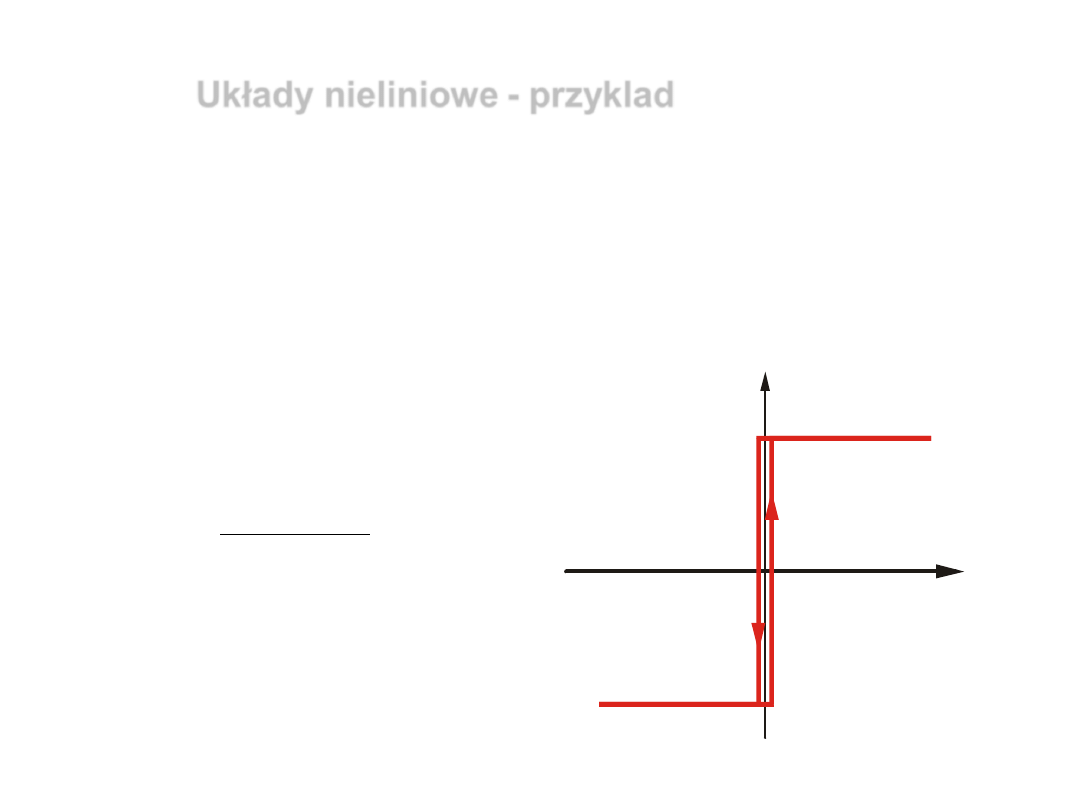
3)

układ nieliniowy zawierający człon liniowy opisany poniższą

funkcją przejścia oraz człon o charakterystyce przekaźnika
dwupołożeniowego

1

s

s

2

G(s)

2







e

u

0 .0 5

2

-0 .0 5

-2

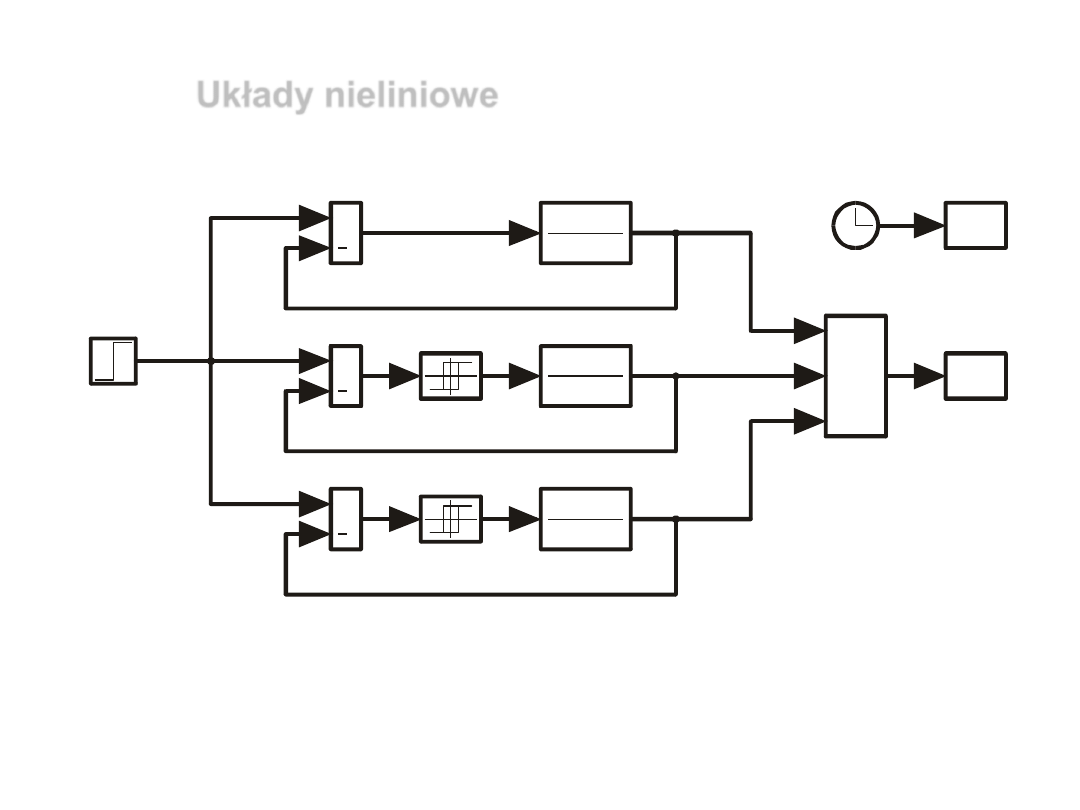
Układy nieliniowe

Schematy blokowe układów regulacji

t

w

+

e

4

s +s +1

2

y 1

U k ła d 1

+

e

P rz e k_ 1

u

2

s +s +1

2

y 2

U k ła d 2

+

e

P rz e k_ 2

u

2

s +s +1

2

y 3

U k ła d 3

M ux

y

Układy nieliniowe - przykład

Wszystkie układy poddano jednocześnie działaniu poniższych

sygnałów skokowych:

-

sygnału w(t) = A

w

·1(t), gdzie A

w

= 1 i otrzymano wyniki jak

na rysunku 1.

-

sygnału w(t) = A

w

·1(t), gdzie A

w

= 4 i otrzymano wyniki jak

na rysunku 2.

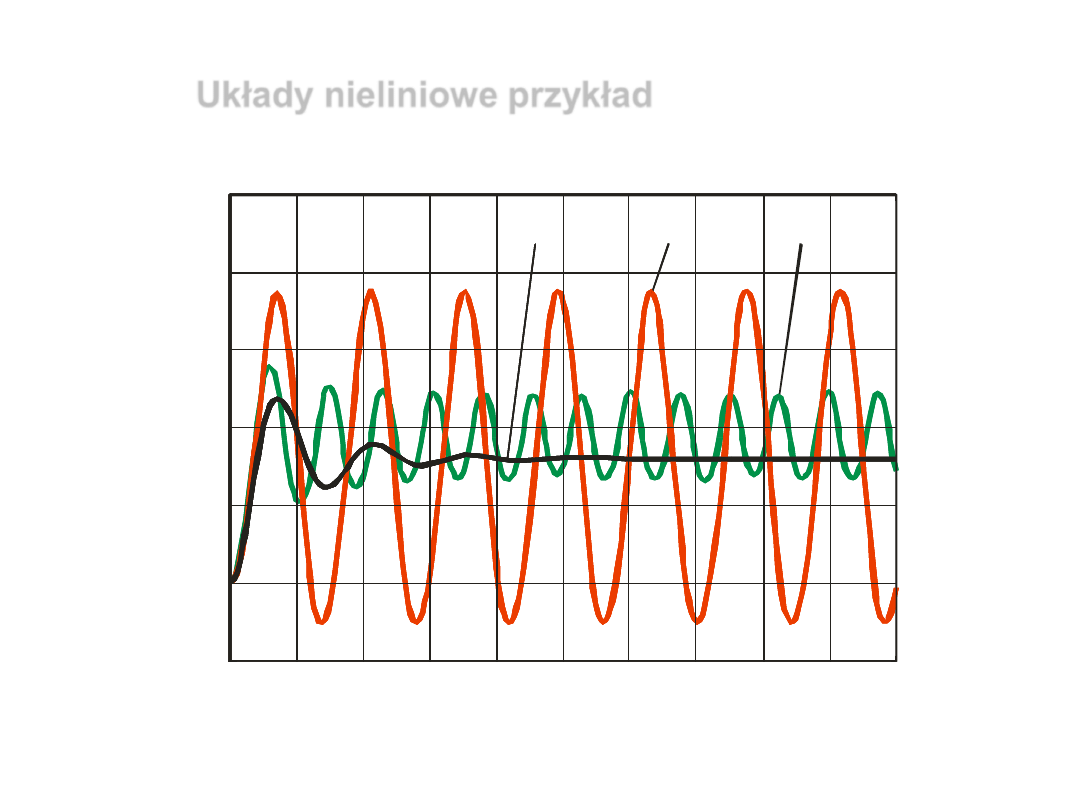
Układy nieliniowe przykład

Rys. 1.

Charakterystyki skokowe układów dla A

w

= 1

0

2

4

6

8

10

12

14

16

18

20

Czas [s]

-0.5

0.0

0.5

1.0

1.5

2.0

2.5

y

Układ 1

Układ 2

Układ 3

w(t)=1*1(t)

0

2

4

6

8

10

12

14

16

18

20

Czas [s]

-0.5

0.0

0.5

1.0

1.5

2.0

2.5

y

Układ 1

Układ 2

w(t)=1*1(t)

0

2

4

6

8

10

12

14

16

18

20

Czas [s]

-0.5

0.0

0.5

1.0

1.5

2.0

2.5

y

Układ 1

w(t)=1*1(t)

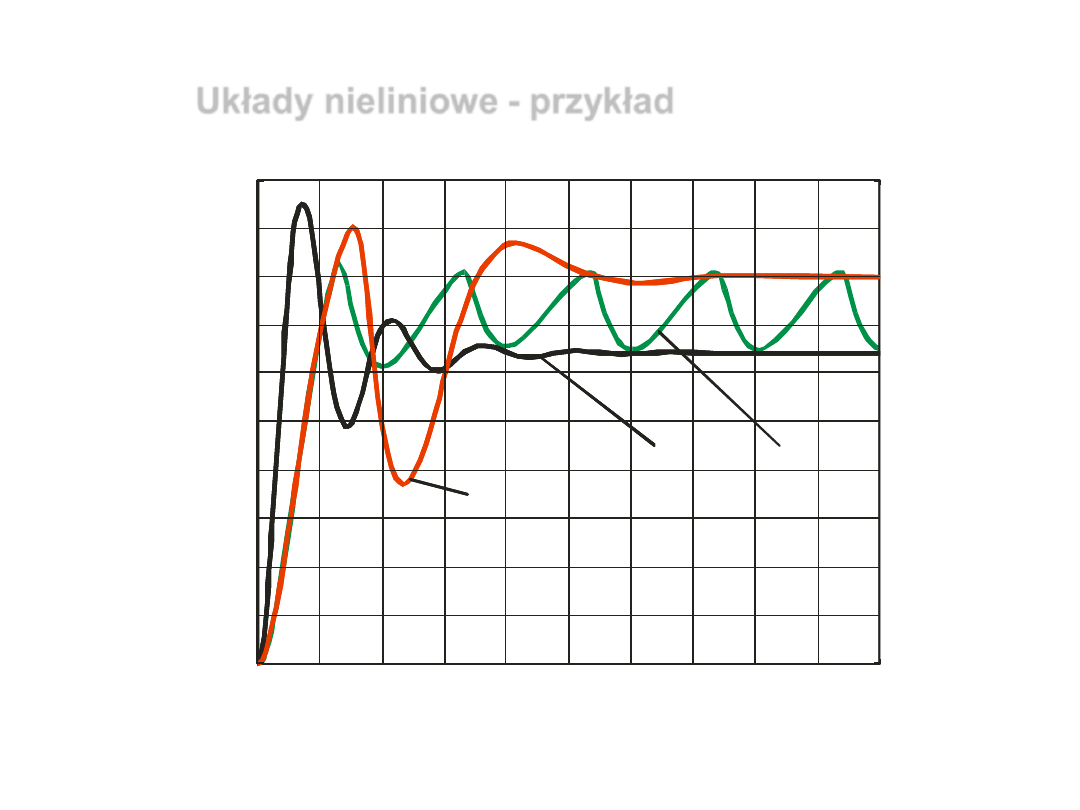
Układy nieliniowe - przykład

Rys. 2.

Charakterystyki skokowe układów dla A

w

= 4

0

2

4

6

8

10

12

14

16

18

20

Cz as [s]

0. 0

0.5

1. 0

1.5

2. 0

2.5

3. 0

3.5

4. 0

4.5

5. 0

y1,

y

2,

y

3

Układ 1

Układ 2

Układ 3

w(t)=4 *1 (t)

0

2

4

6

8

10

12

14

16

18

20

Cz as [s]

0. 0

0.5

1. 0

1.5

2. 0

2.5

3. 0

3.5

4. 0

4.5

5. 0

y1,

y

2,

y

3

w(t)=4 *1 (t)

0

2

4

6

8

10

12

14

16

18

20

Cz as [s]

0. 0

0.5

1. 0

1.5

2. 0

2.5

3. 0

3.5

4. 0

4.5

5. 0

y1,

y

2,

y

3

Układ 1

w(t)=4 *1 (t)

0

2

4

6

8

10

12

14

16

18

20

Cz as [s]

0. 0

0.5

1. 0

1.5

2. 0

2.5

3. 0

3.5

4. 0

4.5

5. 0

y1,

y

2,

y

3

Układ 1

Układ 2

w(t)=4 *1 (t)

Układy nieliniowe - przykład

Wnioski :

-

układ 1 zachowuje się tak, że na podstawie charakte-

rystyki dla A

w

= 1

można wyznaczyć charakterystykę dla

A

w

= 4,

- w przypadku

układu 2 i 3 na podstawie charakterystyk

dla A

w

= 1 nie

można wyznaczyć charakterystyk dla A

w

=

4.

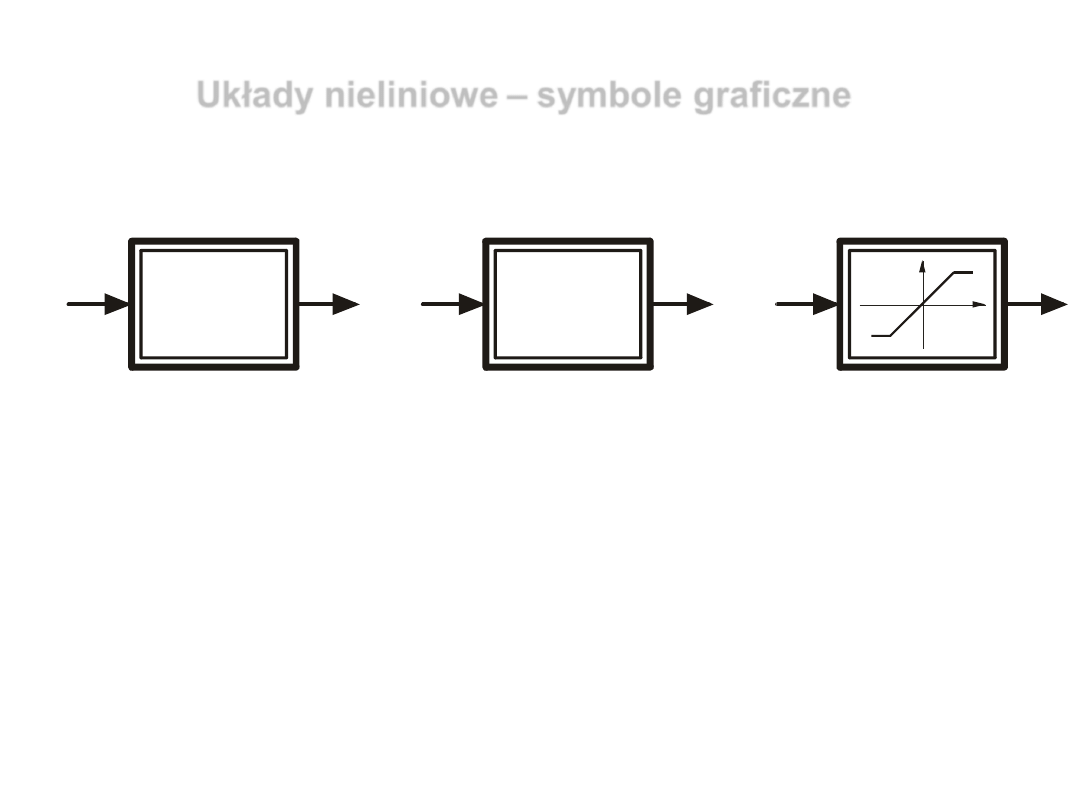
Układy nieliniowe – symbole graficzne

Symbole graficzne

członów nieliniowych:

a) symbol

ogólny;

b) charakterystyka dana wzorem;

c) charakterystyka dana graficznie

a)

u

y

b)

u

y f u

=

( )

y

c)

u

u

y

y

Układy nieliniowe

Ogólnie odpowiedź y(t) członu nieliniowego jest związana z

wymuszeniem u(t) tego

członu nieliniowym równaniem

różniczkowym n-tego rzędu

0

t)

u,

,...,

u

,

u

y,

,...,

y

,

F(y

-1)

(m

(m)

-1)

(n

(n)



y

D

dt

y

d

y

n

n

n

(n)





gdzie:

u

D

dt

u

d

u

n

m

m

(m)





Układy nieliniowe

W przypadku szczególnym powyższe równanie może przyjąć
postać algebraiczną przedstawiającą model nieautonomiczny

F(y,u,t) = 0

Gdy czas nie

występuje w postaci jawnej, to człon opisujemy

równaniem autonomicznym, nazywanym charakterystyką
statyczną

F(y,u) = 0

którą zwykle staramy się przedstawić w postaci

y = f(u)

Układy nieliniowe – wybrane charakterystyki
statyczne

Do bardzo

często spotykanych członów nieliniowych zaliczamy:

a)

człon ze strefą nieczułości,

b)

człon z nasyceniem,

c)

człon ze strefą nieczułości i nasyceniem,

d)

człon ze skokiem początkowym i nasyceniem,

e)

przekaźnik dwupołożeniowy bez histerezy,

f)

przekaźnik dwupołożeniowy z histerezą,

g)

przekaźnik trójpołożeniowy bez histerezy,

h)

przekaźnik trójpołożeniowy z histerezą.

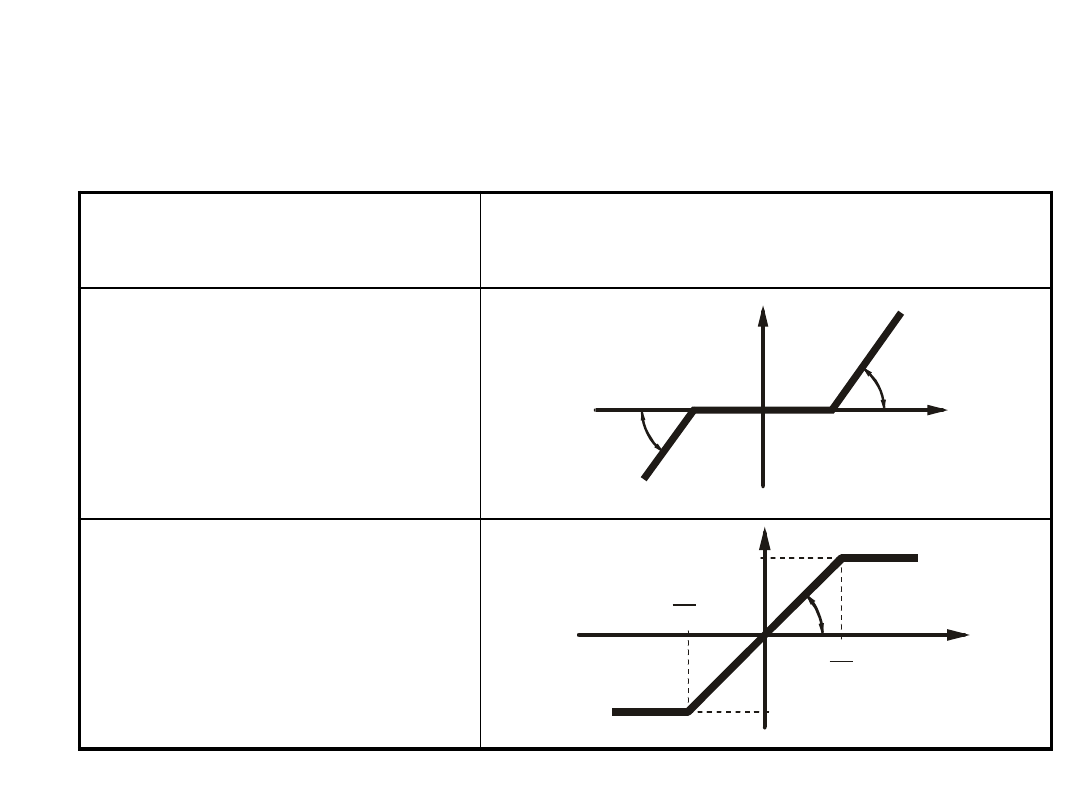
Charakterystyki statyczne wybranych członów
nieliniowych

Nazwa członu

Charakterystyka członu y = f(u)

Człon ze strefą
nieczułości

0

u

y

α

- a

a

α

k

=

tg α

0

u

y

α



B

k

-B

B

k

B

k

=

tg α

Człon z
nasyceniem

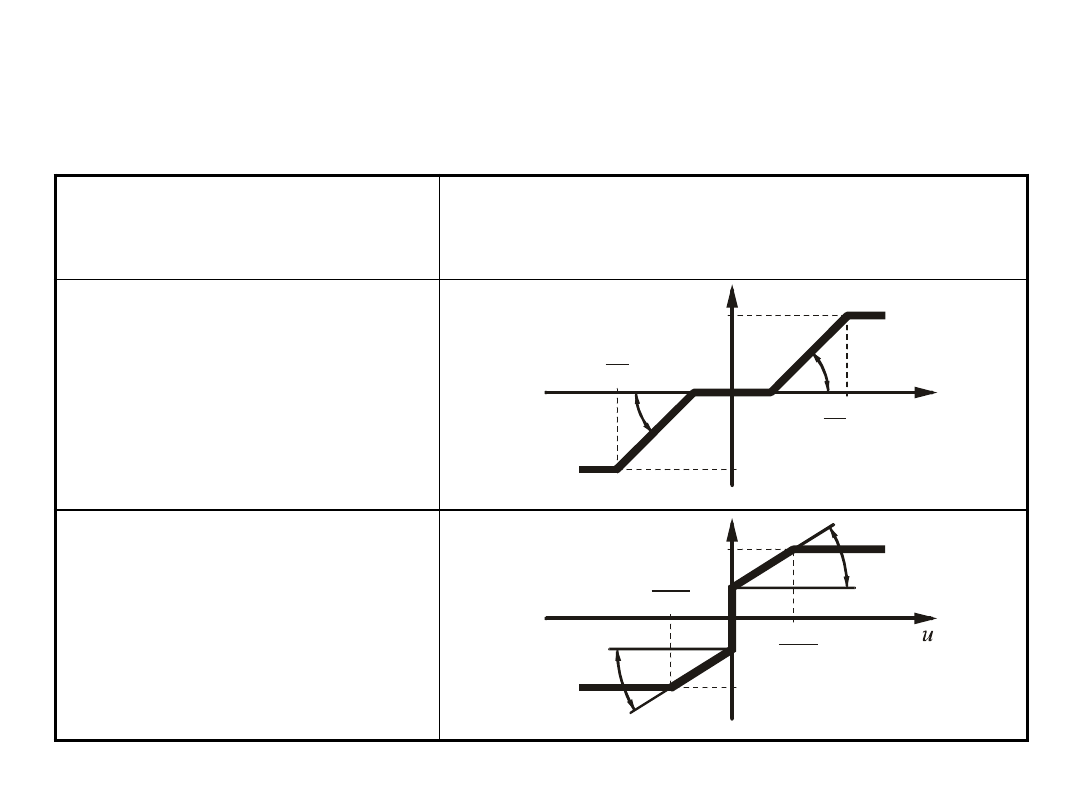
Charakterystyki statyczne wybranych członów
nieliniowych

Nazwa członu

Charakterystyka członu y = f(u)

Człon ze strefą
nieczułości
i nasyceniem

0

u

y





a

B

k

-B

α

-a

a

α

+ a

B

k

B

k

=

tg α

0

y

α



B b

k



-B

-b

b

B b

k



B

α

k

=

tg α

Człon ze
skokiem
początkowym
i nasyceniem

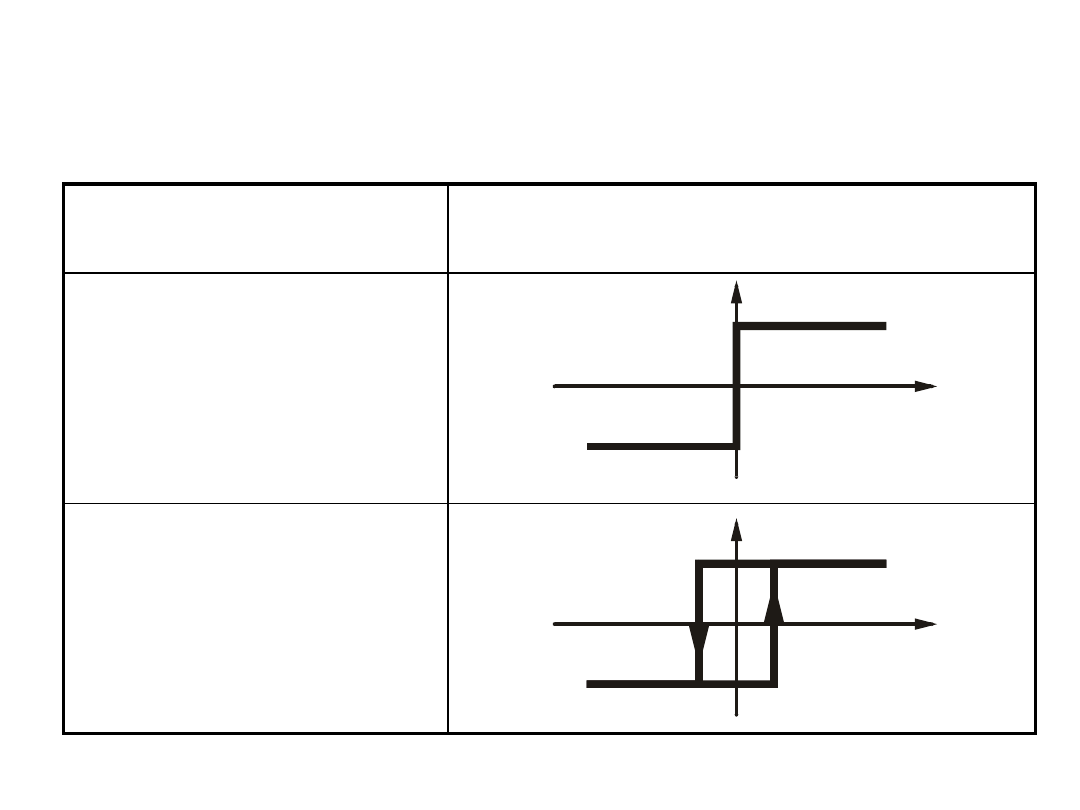
Charakterystyki statyczne wybranych członów
nieliniowych

Nazwa członu

Charakterystyka członu y = f(u)

0

u

y

-B

B

y

0

u

-a

-B

B

a

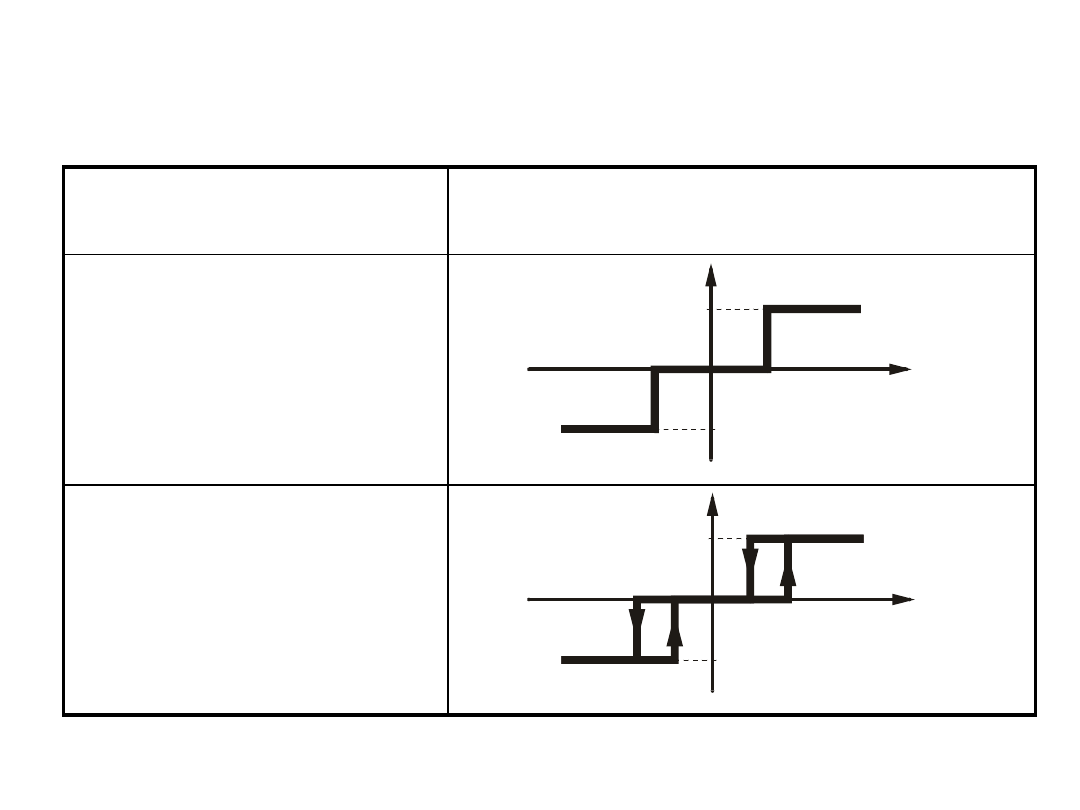
Przekaźnik
dwupołożeniowy
bez histerezy
(idealny)

Przekaźnik
dwupołożeniowy
z histerezą
(rzeczywisty)

Charakterystyki statyczne wybranych członów
nieliniowych

Nazwa członu

Charakterystyka członu y = f(u)

a

0

u

y

- a

-B

B

0

u

y

-a

1

- a

2

-B

B

a

1

a

2

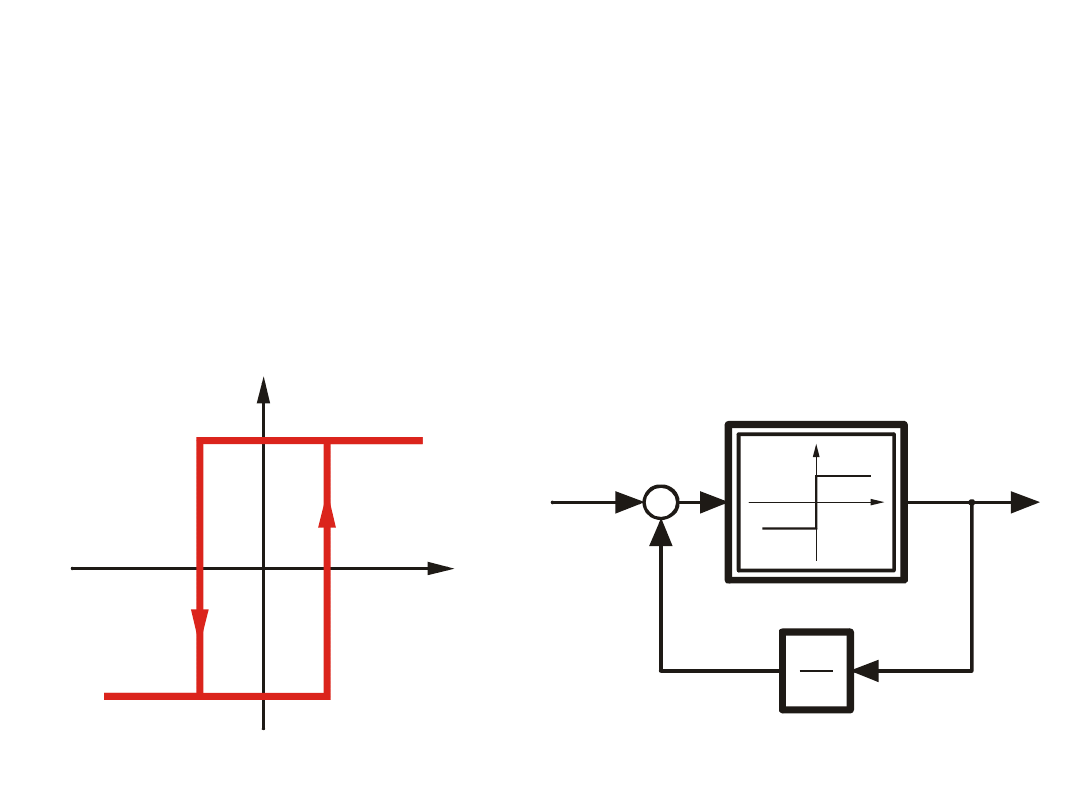
Przekaźnik
trójpołożeniowy
bez histerezy
(idealny)

Przekaźnik
trójpołożeniowy z
histerezą
(rzeczywisty)

Wybrane schematy zastępcze członów
przekaźnikowych

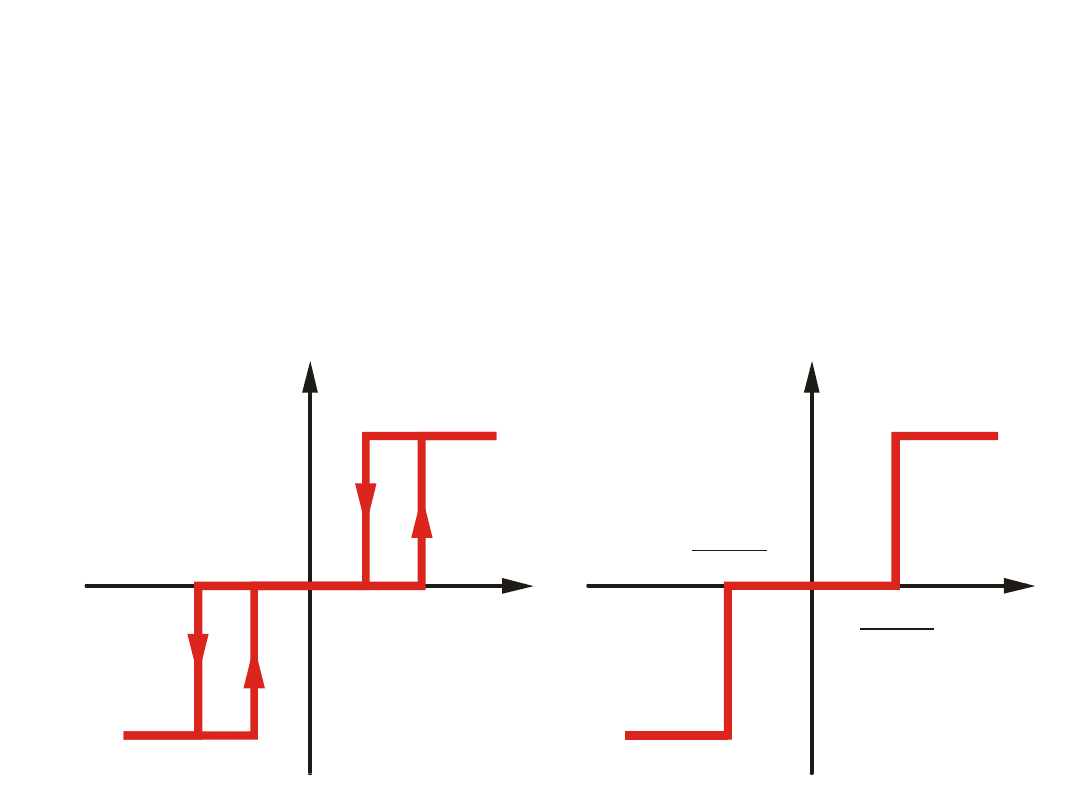
Dla charakterystyki

przekaźnika dwupołożeniowego z histerezą

konstruujemy schemat

zastępczy zawierający charakterystykę

przekaźnika idealnego i obwód sprzężenia zwrotnego jak na
rysunku

poniżej.

u

y

a

B

-a

-B

u

-B

B

y

a
B

–

Wybrane schematy zastępcze członów
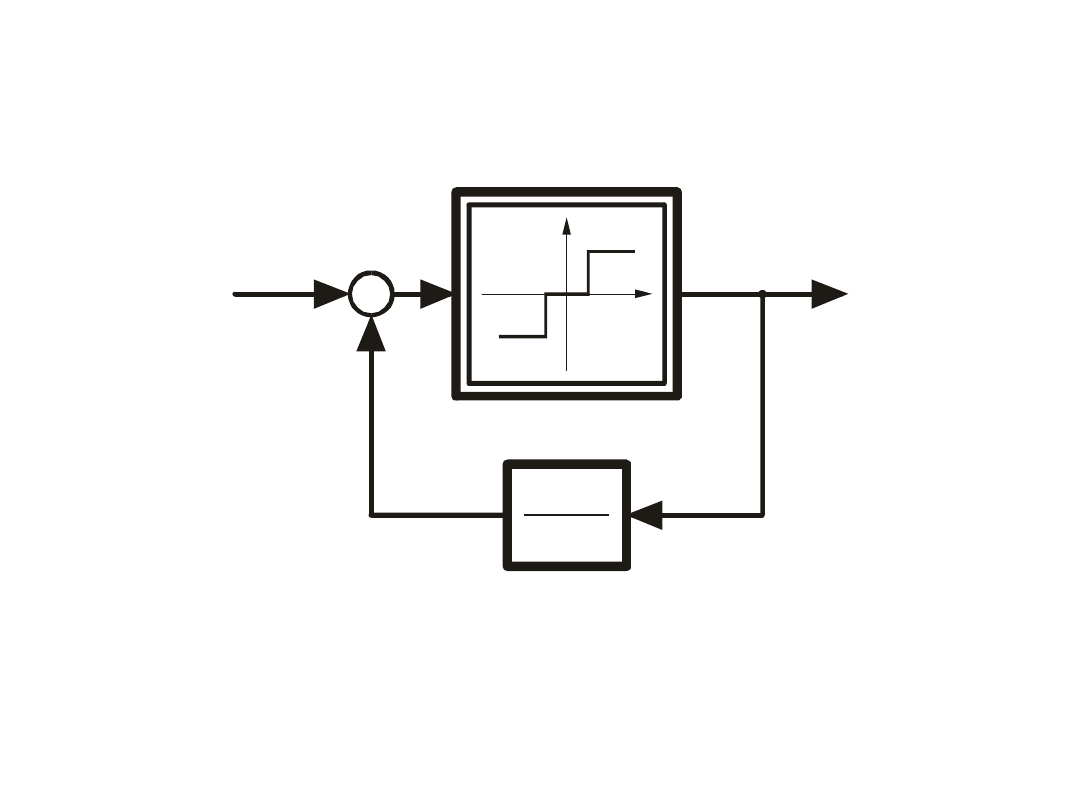
przekaźnikowych

Dana jest charakterystyka

przekaźnika trójpołożeniowego z

histerezą oraz charakterystyka przekaźnika idealnego
przechodząca przez środek pola histerezy.

u

y

a

1

a

2

B

-a

2

-a

1

-B

u

y

B

-B

–

+

2

a

a

1

2

a

a

1

2

+

2

Wybrane schematy zastępcze członów
przekaźnikowych

u

-B

B

y

a a

B

2

1

-

2

–

Schemat zastępczy przekaźnika trójpołożeniowego z
histerezą.

Przekształcanie schematów blokowych

Schematy blokowe

układów z członami nieliniowymi można

przekształcać podobnie jak schematy układów liniowych.
Obowiązuje przy tym warunek konieczny i dostateczny prze-
kształcenia:

Zastąpienie

części

schematu

układem

równoważnym nie może powodować zmian w
pozostałych częściach schematu nie podlegającym
przekształceniu.

Kolejność występowania członów nieliniowych
ma istotne znaczenie dla

właściwości układu i

nie wolno jej

zmieniać.

Stąd wynika podstawowa zasada przekształcania:

Przekształcanie schematów blokowych

Dopuszczalne

przekształcenia schematów blokowych:

1) szeregowe

połączenie członów,

2)

równoległe połączenie członów,

3) przenoszenie

węzła zaczepowego.

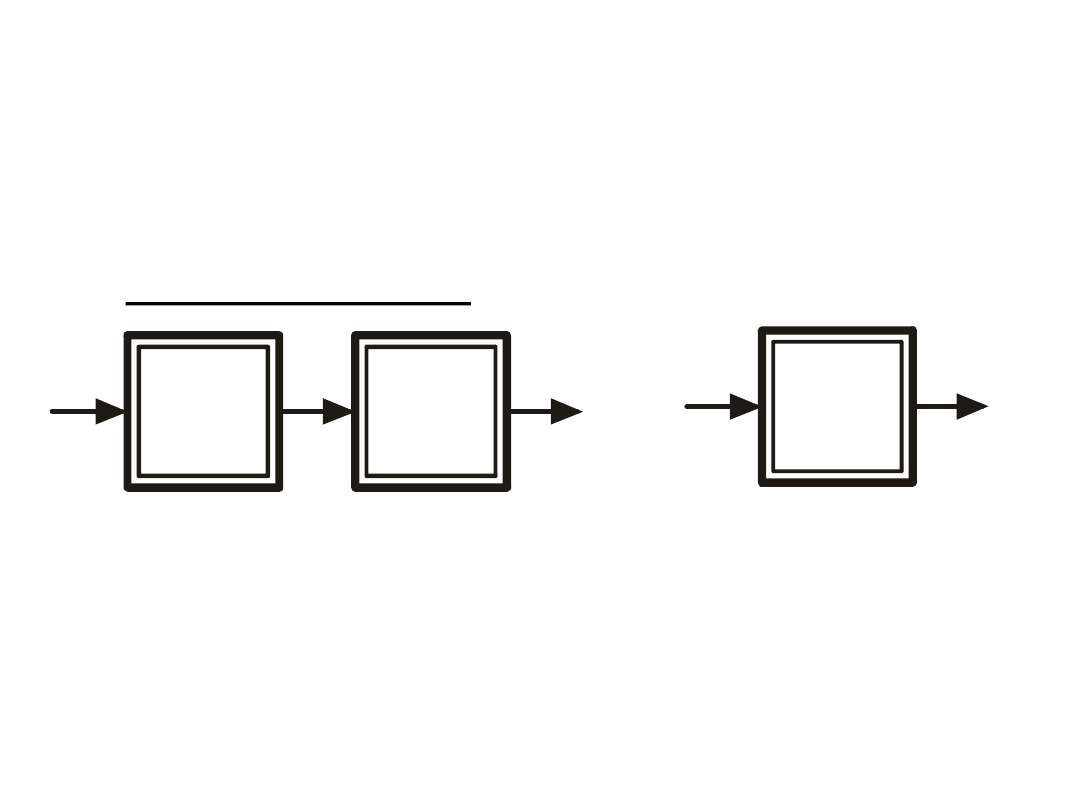
Przekształcanie schematów blokowych

Rozważamy fragment układu złożony z dwóch członów
nieliniowych o znanych charakterystykach statycznych
połączonych szeregowo:

Dwa człony nieliniowe połączone
szeregowo.

u

f u

1

( )

u

1

f u

2

1

( )

y

u

f u

( )

y

Człon zastępczy równoważny
układowi z rysunku obok.

Po podstawieniu charakterystyki pierwszego

członu do

charakterystyki drugiego

członu otrzymujemy

y = f

2

(u

1

) = f

2

[f

1

(u)] = f(u)

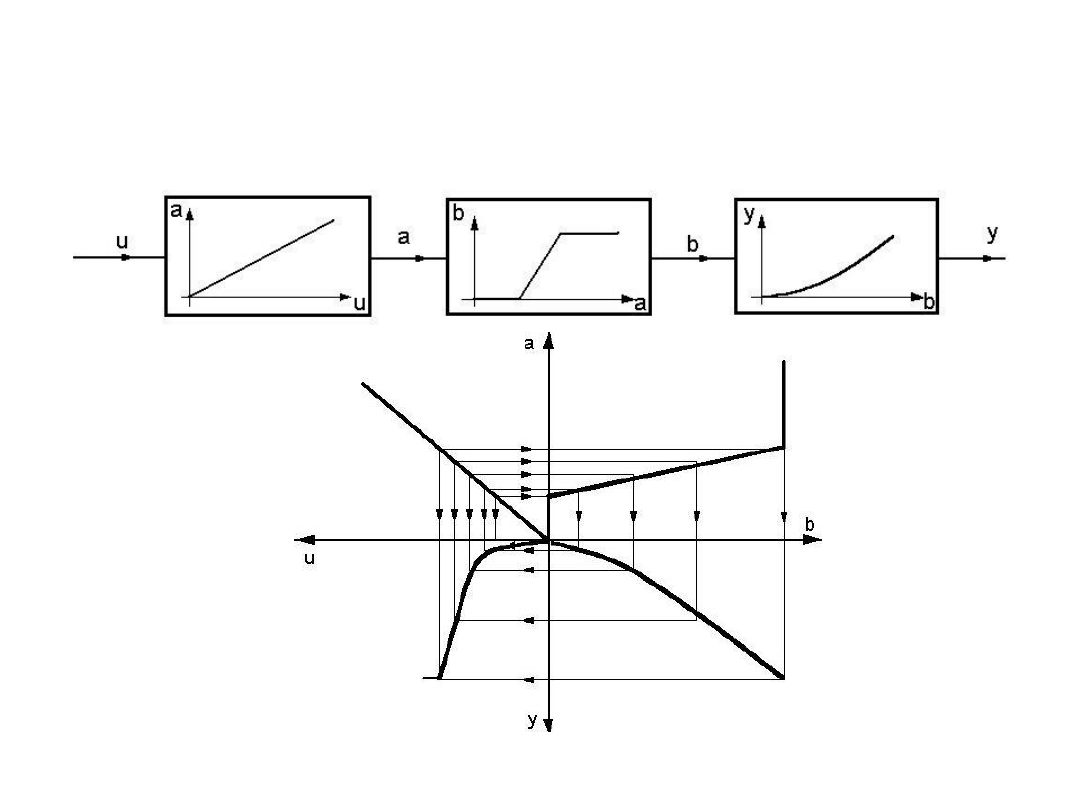
Graficzne wyznaczanie charakterystyki członu zastępczego

dla członów nieliniowych połączonych szeregowo

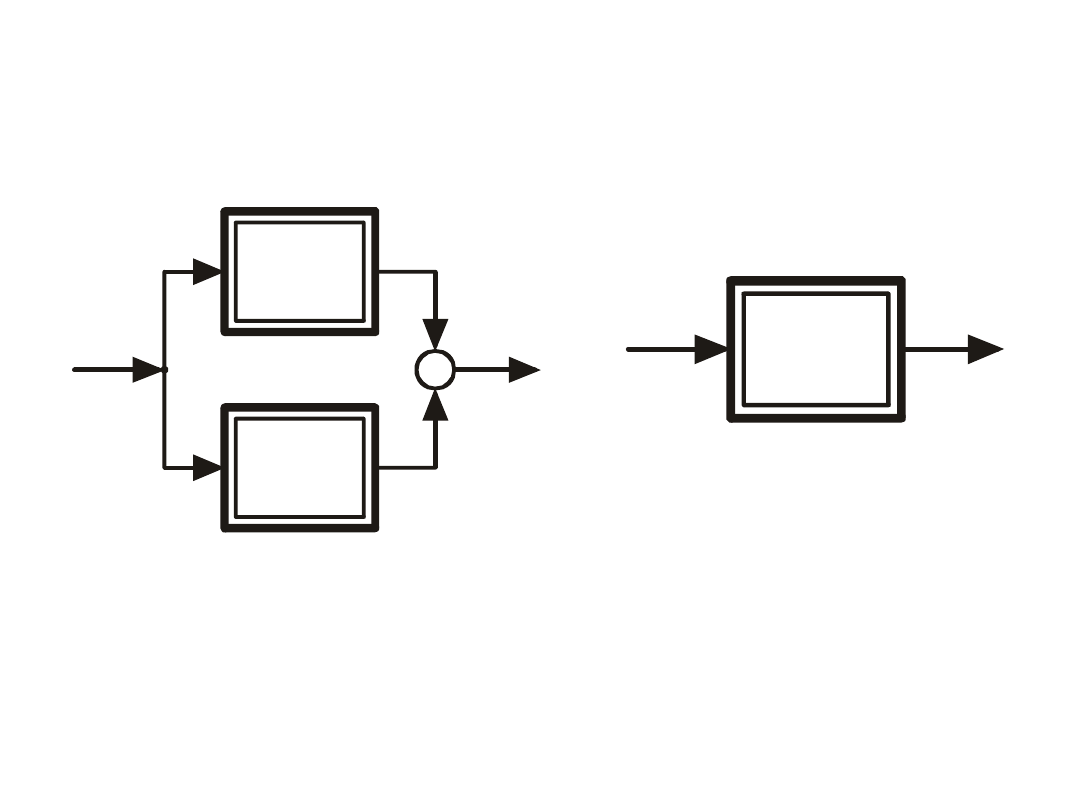
Przekształcanie schematów blokowych

Człon zastępczy równoważny
układowi ze schematu obok

Dwa człony nieliniowe połączone
równolegle

u

f u

1

( )

f u

2

( )

y

+

y

1

+

y

2

u

f u

( )

y

Równoległe połączenie członów

Z istoty

połączenia równoległego wynika, że charakterystyka członu

zastępczego jest równa sumie charakterystyk członów składowych

y = y

1

+ y

2

= f

1

(u) +

f

2

(u) = f(u)

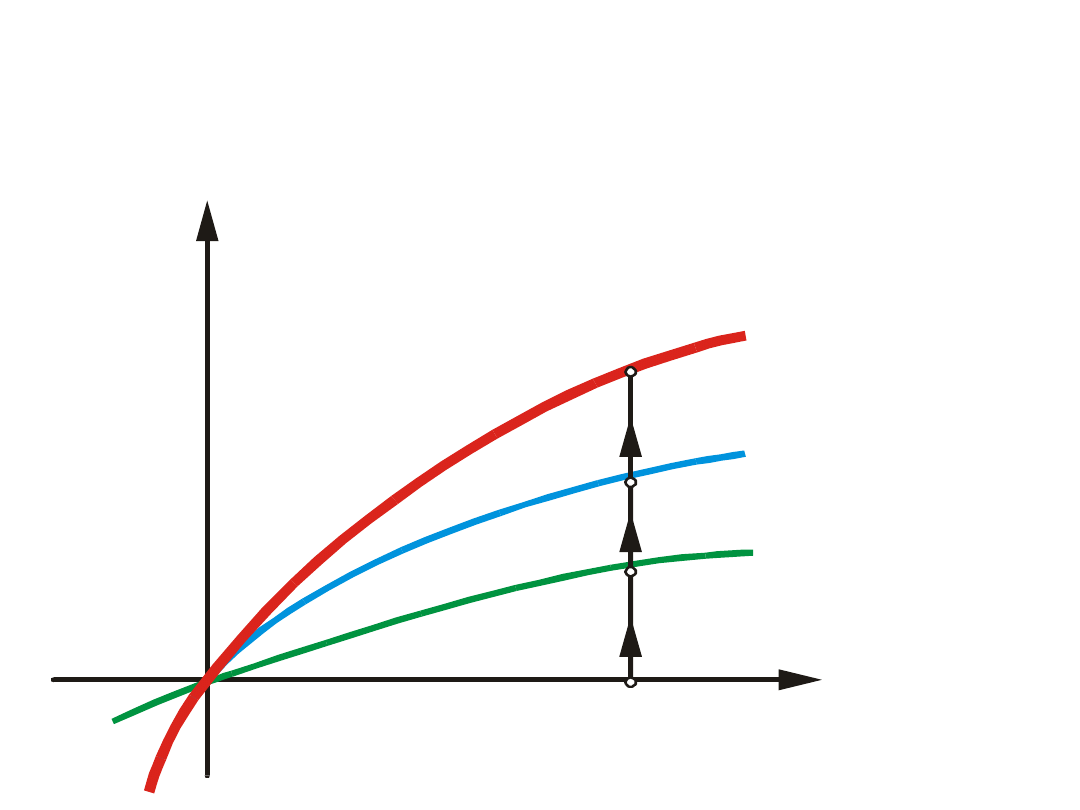
Graficzne wyznaczanie charakterystyki członu zastępczego

dla członów nieliniowych połączonych równolegle

u

y , y , y

1

2

y

f u

1

1

=

( )

y

f u

2

2

=

( )

y f u

=

( )

1

2

3

4

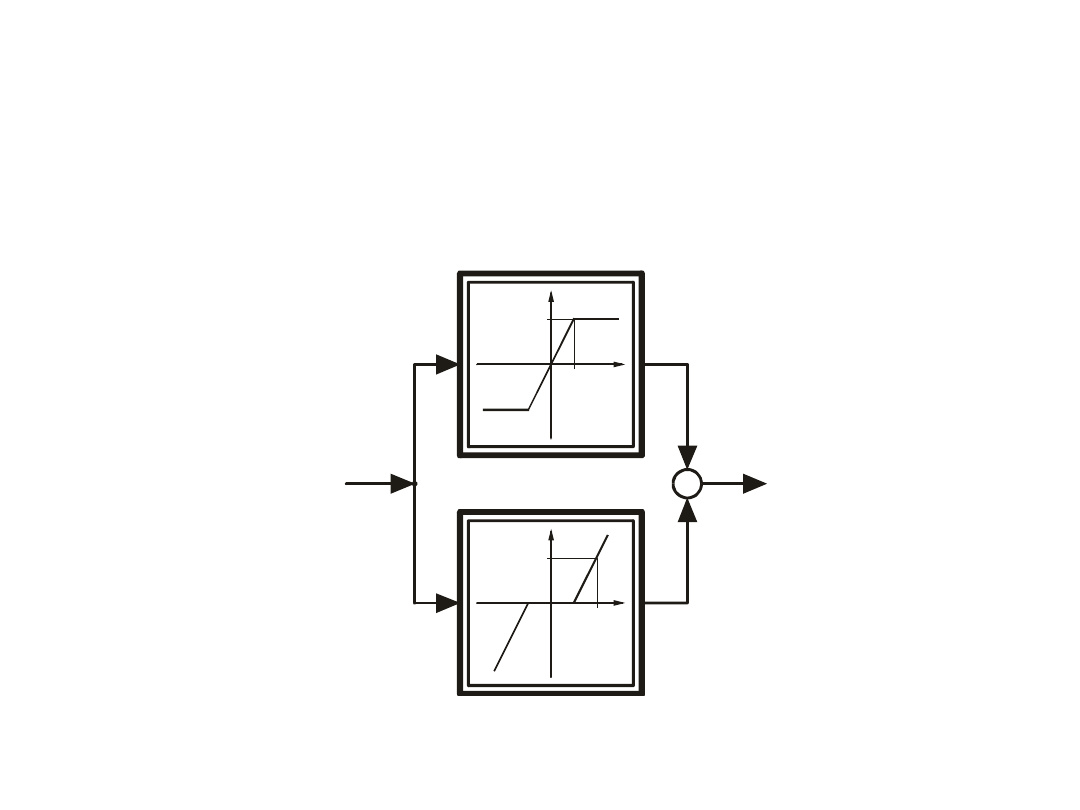
Przekształcanie schematów blokowych – przykład

Wyznaczyć charakterystykę członu zastępczego dla podanego niżej
równoległego połączenia członów o znanych charakterystykach
statycznych.

Dwa człony nieliniowe połączone równolegle

u

2

4

2

4

4

y

+

y

1

+

y

2

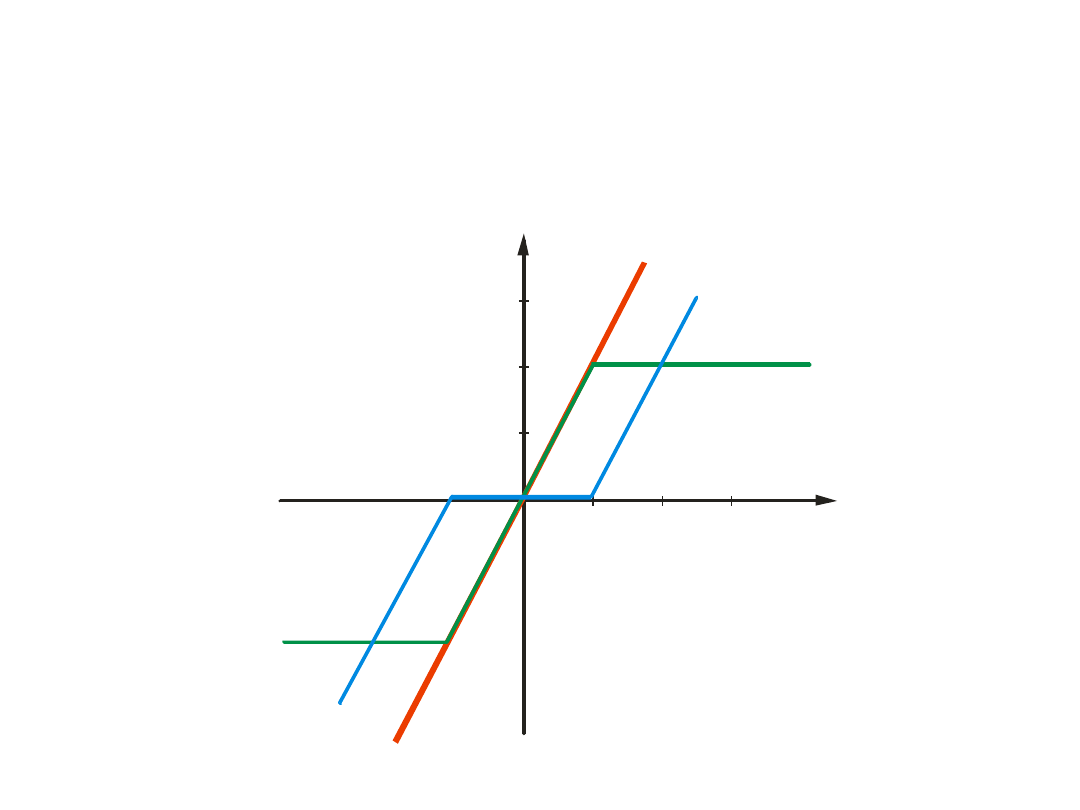
Przekształcanie schematów blokowych – przykład

Rozwiązaniem

jest

charakterystyka
pokazana na rysunku.
Charakterystyka
wypadkowa jest liniowa
lub

zbliżona do liniowej.

Charakterystyki dla podanych układów

u

0

2

4

6

y , y , y

1

2

2

4

6

y f u

=

( )

y f u

1

1

=

( )

y f u

2

2

=

( )

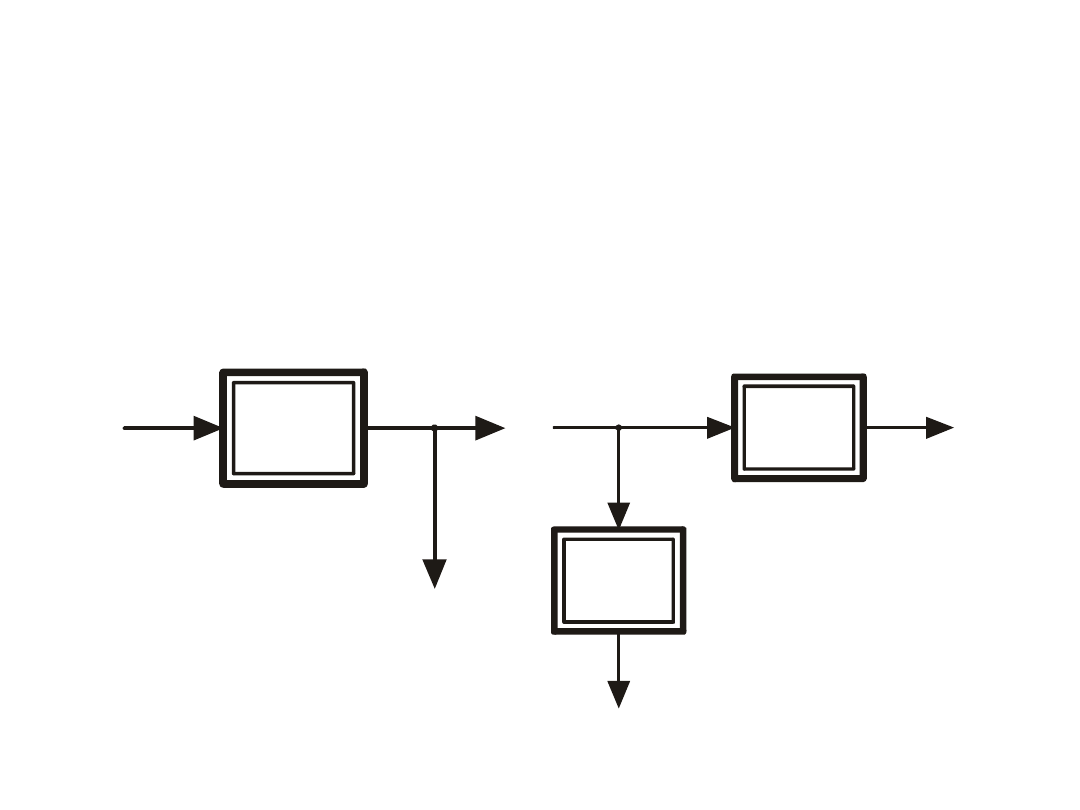
Przenoszenie węzła zaczepowego przed blok

Przeniesienie

węzła zaczepowego przed blok nieliniowy

zgodnie z warunkiem koniecznym i dostatecznym wymaga
wprowadzenia dodatkowego

członu nieliniowego takiego,

jak

człon dany. Otrzymamy wtedy schemat pokazany

poniżej na rysunku.

Przekształcony schemat
z rysunku obok

Schemat blokowy z węzłem
zaczepowym za blokiem

u

f u

( )

y

y

u

f u

( )

y

f u

( )

y

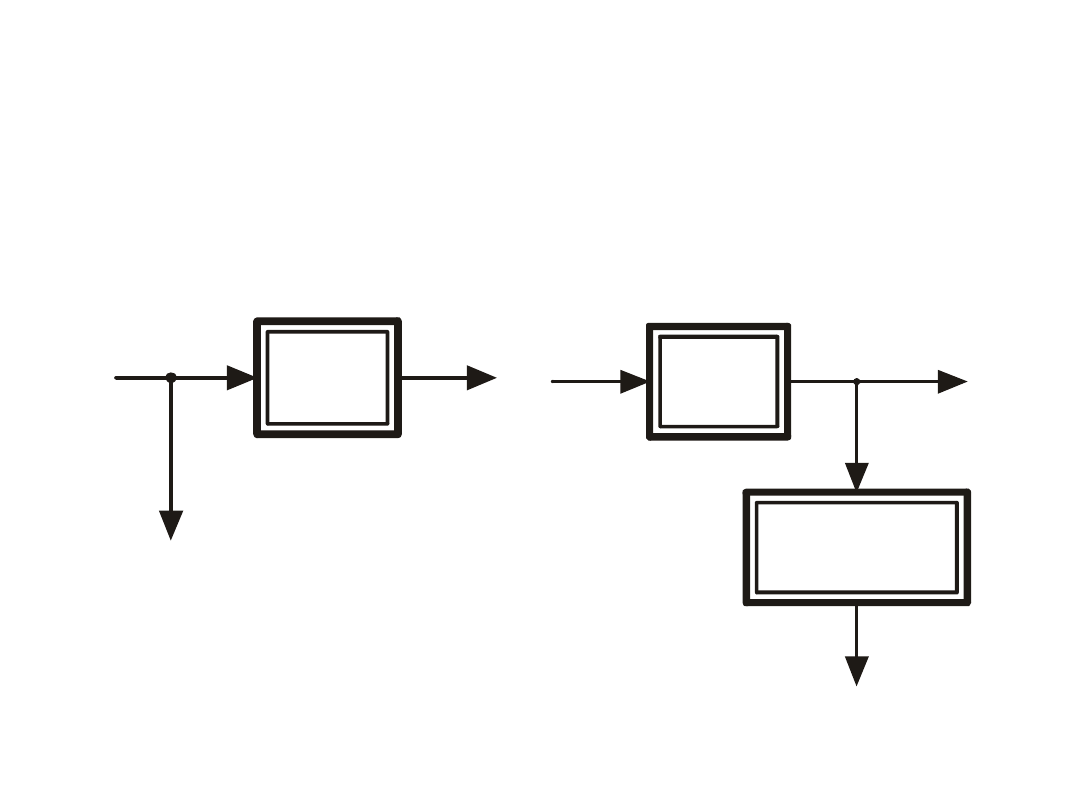
Przenoszenie węzła zaczepowego za blok

Przeniesienie

węzła zaczepowego za blok nieliniowy

zgodnie z warunkiem koniecznym i dostatecznym wymaga
wprowadzenia dodatkowego

członu nieliniowego o cha-

rakterystyce odwrotnej do charakterystyki danej.

Przekształcony schemat z
rysunku obok

Schemat blokowy z węzłem
zaczepowym przed blokiem

u

f u

( )

y

u

u

u

f u

( )

y

y

φ ( )

( )

y

f

u

=

-1

u

Układy regulacji przekaźnikowej

Przekaźnikowe

regulatory

nieciągłe,

dwupołożeniowe

i

trójpołożeniowe, tworzą nieliniowe układy regulacji.

Regulatory

dwupołożeniowe

są stosowane do obiektów o dużych

stałych czasowych, na przykład w układach regulacji ciśnienia,
poziomu i temperatury.

Do grupy

regulatorów nieciągłych należą również

regulatory

trójpołożeniowe

,

generujące trzy stany-wysoki, niski i zerowy,

które mogą odpowiadać obrotom silnika nawrotnego w lewo, w
prawo i zatrzymaniu.

Elementy

trójpołożeniowe objęte pętlą korekcyjnego ujemnego

sprzężenia zwrotnego i sterujące silnikami wykonawczymi,
nazywają się

regulatorami krokowymi

.

Regulacja dwupołożeniowa

W charakterze regulatora dwustawnego RD

występuje element mający charakterystykę

przekaźnikową -przekaźnik, stycznik, tyrystor.

RD

y

z

+

y (t)

-

e(t)

Obiekt

u(t)

u

e

e

1

e

2

L

H

Regulatory dwupołożeniowe stosuje się do stabilizacji:
• temperatury (

termostaty

), na przykład w podgrzewaczach paliwa,

• poziomu cieczy (

mombreje

), na przykład w zbiornikach

rozchodowych,

• ciśnienia (

presostaty

), na przykład w zbiornikach sprężonego

powietrza.

Sygnał wyjściowy regulatora dwupołożeniowego
przyjmuje dwa stany: L (low) i H (high).

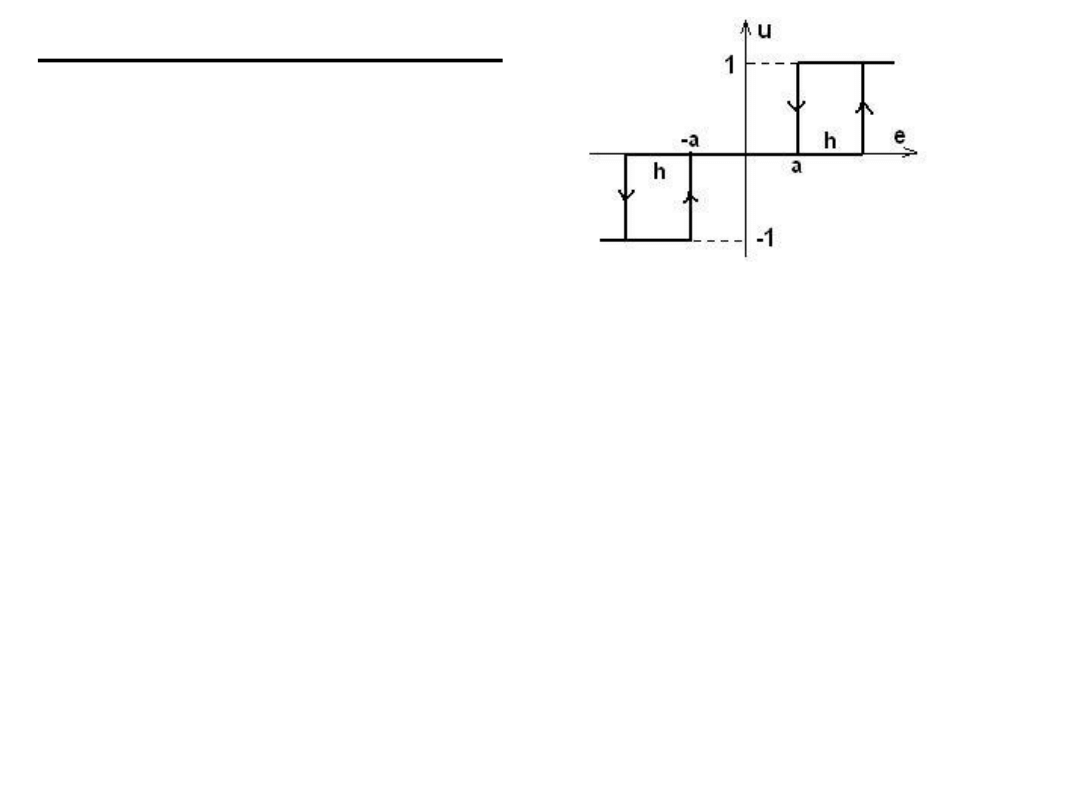
Regulacja trójpołożeniowa

W porównaniu z regulatorami dwupołożeniowymi dodatkowym

parametrem charakterystyki statycznej, oprócz strefy histerezy h,

jest strefa nieczułości a.

Istotne znaczenie regulatorów trójpołożeniowych wynika

z możliwości sterowania silnikami nawrotnymi - trzy stany na

wyjściu odpowiadają kierunkowi obrotów w prawo, w lewo oraz
stop.

Zastosowanie regulatora trójpołożeniowego bez dodatkowych

członów dynamicznych nie daje dobrych rezultatów.

Charakterystyka statyczna
regulatora trójpołożeniowego ma
trzy stany: -1, 0, 1

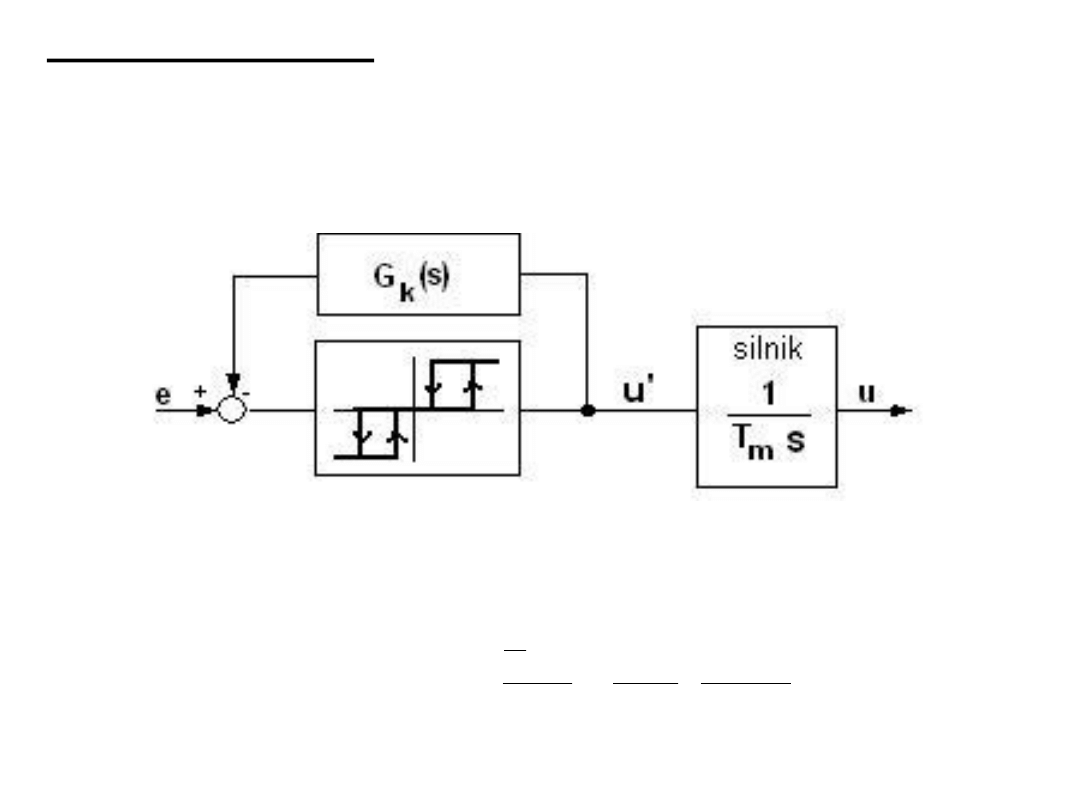
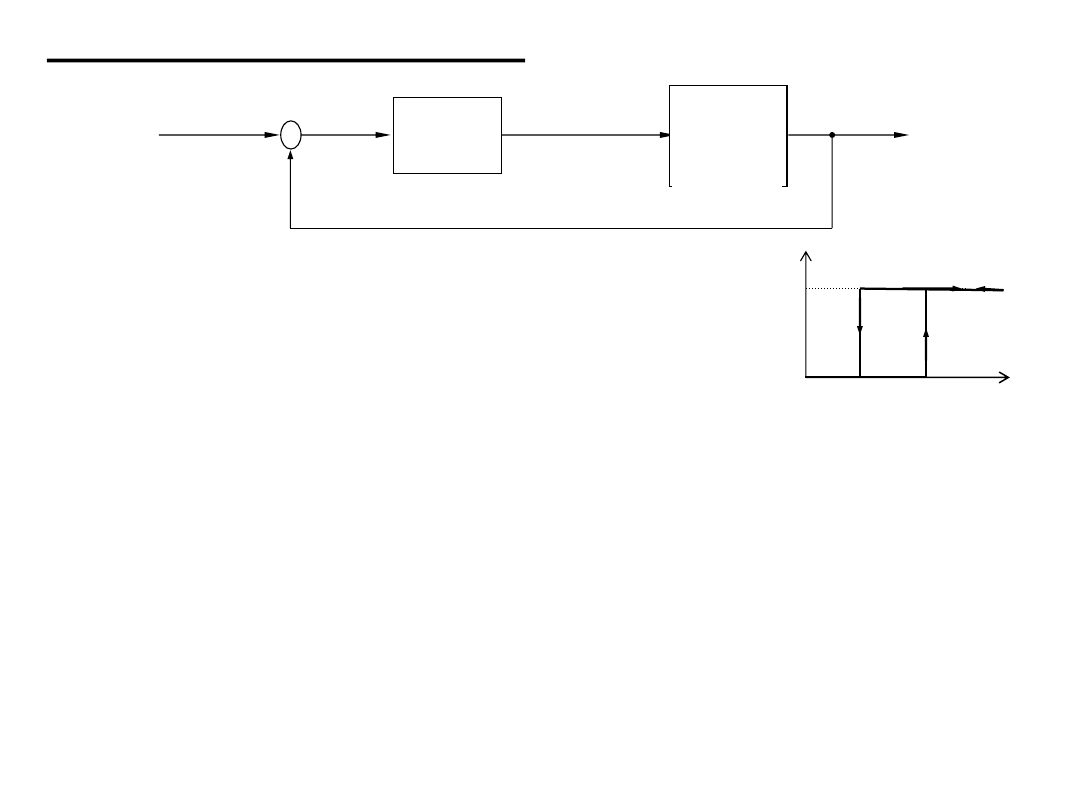
Regulacja krokowa

Przy powolnych zmianach e(t) oraz dla

uśrednionych wartości

można wyznaczyć transmitancję regulatora krokowego:

Regulator trójpołożeniowy zintegrowany z silnikiem wykonawczym
i

zaopatrzony w korekcję własności dynamicznych nazywa się

regulatorem krokowym:

)

s

(

G

1

sT

1

)

s

(

e

)

s

(

u

)

s

(

G

k

m

RK







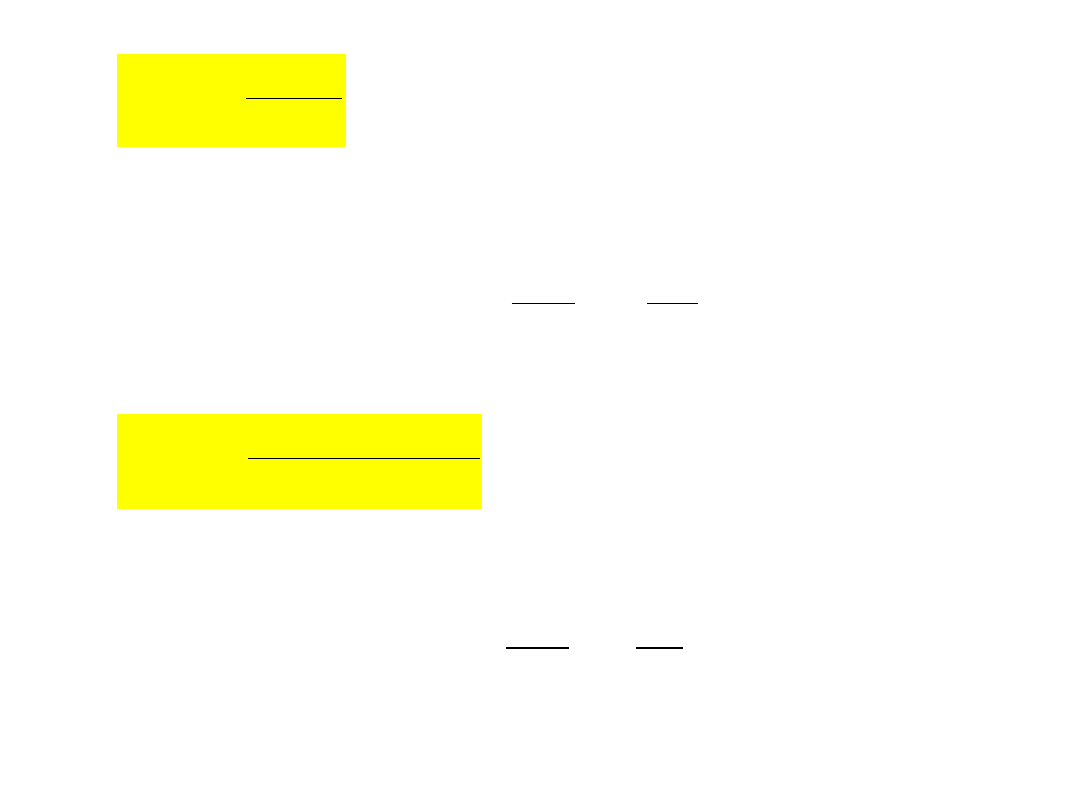
Dla


regulator krokowy

ma własności regulatora PI:

Dla

regulator krokowy ma

własności regulatora PID:

1

s

T

k

(s)

G

i

k





















i

m

i

RK

sT

1

1

kT

T

)

s

(

G

1

s

T

s

T

T

k

)

s

(

G

i

2

d

i

k

























d

i

m

i

RK

sT

sT

1

1

kT

T

)

s

(

G

Nastawy

regulatorów krokowych PI i PID są prawie takie same

jak

regulatorów o wyjściu ciągłym, ponadto dobiera się

szerokość pętli histerezy h i strefy nieczułości a, w
następujący sposób:

-

szerokości strefy nieczułości a jest w przybliżeniu równa
maksymalnej

wartości uchybu ustalonego,

-

zwykle przyjmuje się h/a<0.5 ponieważ wzrost strefy
histerezy pogarsza stabilność układu,

Nastawy regulatorów krokowych

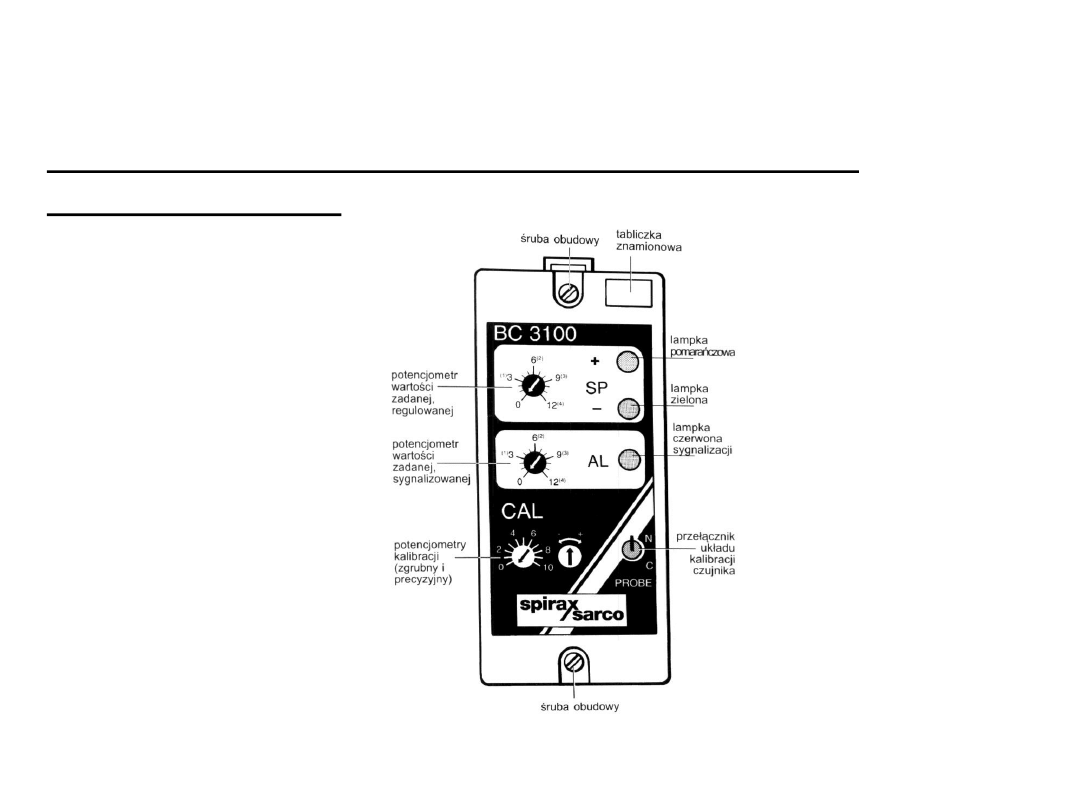
Przykłady regulatorów przekaźnikowych

stosowanych na statkach

Regulator dwupołożeniowy przewodności BC 3100
firmy Spirax Sarco

Regulator przeznaczony jest do pracy w układach regulacji

i sygnalizacji zasolenia wody kotłowej, z wykorzystaniem

pomiaru przewodności.

Regulator wyposażony jest standardowo w nastawialne wyjście

sygnalizacyjne, a także analogowe 0(4)-20 mA, reprezentujące

wartość mierzoną przewodności w jednostkach odpowiadających
wybranemu zakresowi regulatora.

Regulator BC 3100 posiada sześć zakresów, wybieranych

wewnętrznym przełącznikiem, dostępnym po zdjęciu obudowy.

Regulator posiada również wejście przystosowane do podłączenia

oporowego czujnika temperatury PT 100, w celu ewentualnej

kompensacji temperaturowych zmian przewodności wody
w

warunkach zmieniającego się ciśnienia i temperatury.

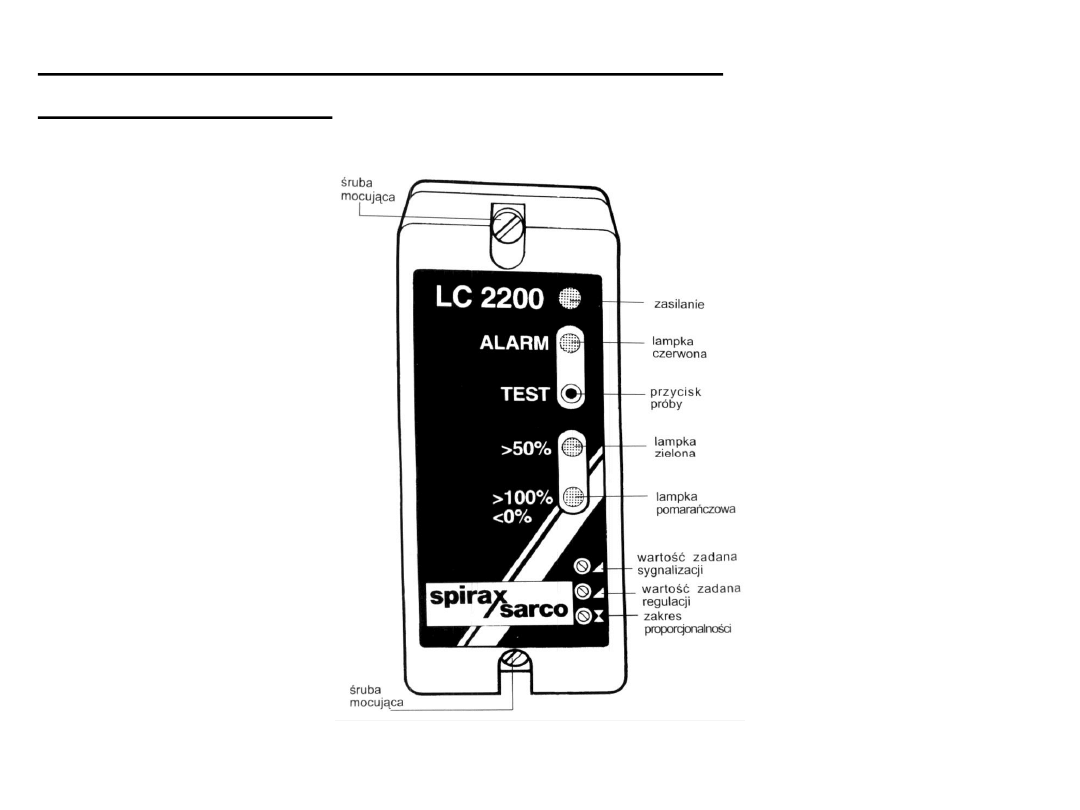
Regulator krokowy poziomu wody LC 2200
firmy Spirax Sarco

Regulator jest zalecany do współpracy z przetwornikiem

pojemnościowym poziomu w układach regulacji krokowej
poziomu wody w kotle, zbiorniku pod odgazowywaczem,
wodniarce, itp.

Można także wykorzystać sygnały pomiarowe z dowolnego

przetwornika ciśnienia, różnicy ciśnień lub temperatury.

Sygnał nastawiający regulatora jest dostosowany do współpracy z

siłownikiem elektrycznym, wyposażonym w nadajnik

potencjometryczny położenia zaworu.

Drugi kanał wyjściowy, także dwustanowy, służy do sygnalizacji

stanu krytycznego wielkości mierzonej. Wyjście sygnalizacyjne

wyposażone jest w filtr, umożliwiający sygnalizację stanów

poziomu na przykład burzliwie zachowującej się wody.

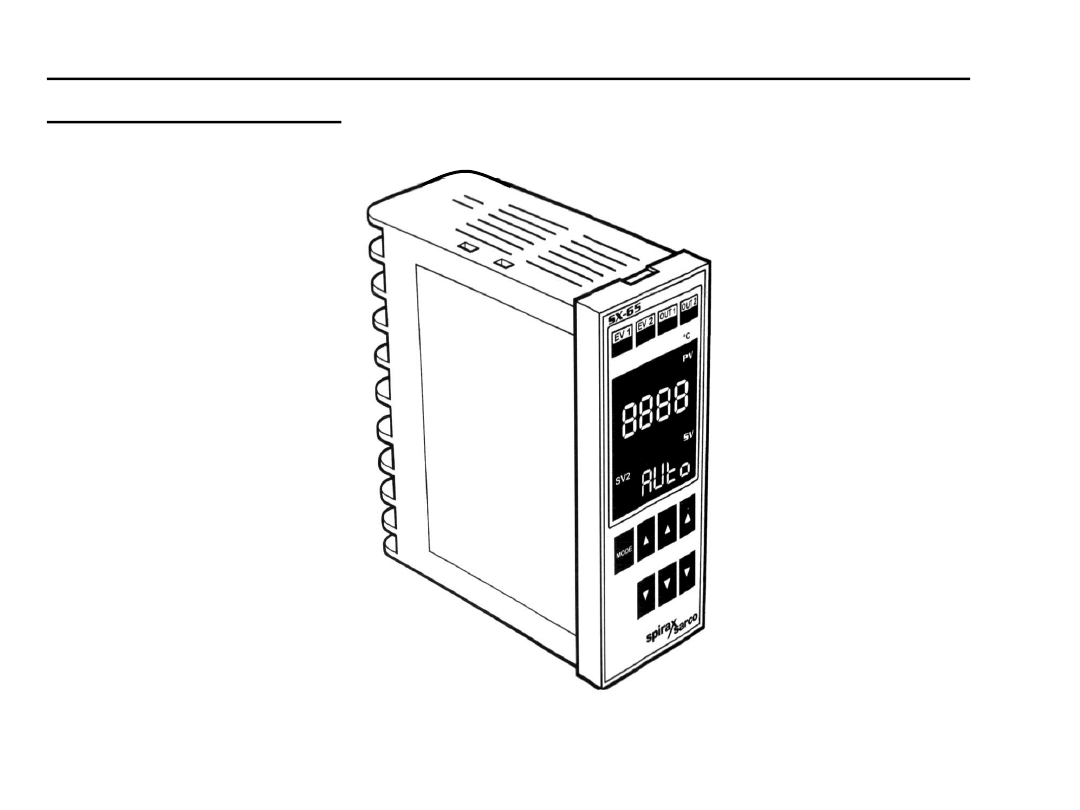
Regulator elektroniczny przekaźnikowy temperatury SX65
firmy Spirax Sarco

Regulator jest przeznaczony do stałowartościowej- ciągłej,

krokowej lub

dwupołożeniowej regulacji temperatury we

współpracy z czujnikiem oporowym Pt 100 i elementami

wykonawczymi, przyjmującymi sygnał analogowy, prądowy
4-

20 mA lub z przekaźnika (siłowniki elektryczne).

Możliwości regulatora:
• dwie przełączane zdalnie wartości zadane,
• regulacja według algorytmu PID z możliwością takiej

jego

modyfikacji, aby otrzymać algorytmy pochodne

-

regulację P lub dwupołożeniową,

• dwie programowalne sygnalizacje,
• blokada klawiatury elewacyjnej,
• ochrona przed przeregulowaniem,
• ogranicznik sygnału wyjściowego.

Dziękuję za uwagę.