1

MIGRACJA WILGOCI W

PRZEGRODZIE

wg PN-EN ISO 13788

POLITECHNIKA GDA

Ń

SKA

Sławomir Kosik

KATEDRA PODSTAW BUDOWNICTWA

KATEDRA PODSTAW BUDOWNICTWA

I IN

ś

YNIERII MATERIAŁOWEJ

I IN

ś

YNIERII MATERIAŁOWEJ

ZAKRES NORMY

a)

obliczenia temperatury powierzchni wewnętrznej komponentu
budowlanego lub elementu budynku, poniżej której
prawdopodobny jest rozwój pleśni, przy zadanej temperaturze i
wilgotności powietrza wewnętrznego; metodę można również
zastosować do szacowania ryzyka kondensacji na innych
powierzchniach

b)

oszacowania ryzyka kondensacji wewnętrznej wskutek dyfuzji
pary wodnej

1.0. ZAKRES NORMY

2

ZAŁOśENIA OBLICZEŃ KONDENSACJI

Przyjmuje się brak wilgoci budowlanej i nie jest ona brana pod uwagę
w szeregu ważnych zjawisk fizycznych obejmujących:

- zależność współczynnika przewodzenia ciepła od wilgoci;

- uwalnianie i absorpcję ciepła utajonego;

- zmienność właściwości materiałów w zależności od wilgotności;

- podciąganie kapilarne i transport wilgoci w fazie ciekłej wewnątrz
materiałów;

- ruch powietrza przez pęknięcia lub wewnątrz przestrzeni
powietrznych;

- zdolność materiałów do zawilgocenia sorpcyjnego

1.0. ZAKRES NORMY

NORMY UZUPEŁNIAJĄCE

1.

PN-EN 12524: 2003 Materiały i wyroby budowlane. Właściwości
cieplno-wilgotnościowe. Tabelaryczne wartości obliczeniowe.

2.

PN-EN 6946: 1999 Komponenty budowlane i elementy budynku.
Opór cieplny i współczynnik przenikania ciepła. Metoda obliczania

3.

PN-B-02025: 2001 Obliczanie sezonowego zapotrzebowania na
ciepło do ogrzewania budynków mieszkalnych i zamieszkania
zbiorowego

4.

PN-EN ISO 9346: 1998 Izolacja cieplna. Wymiana masy.
Wielkości fizyczne i definicje.

5.

PN-82/B-02402 Ogrzewnictwo. Temperatury ogrzewanych
pomieszczeń

2.0. POWOŁANIA NORMATYWNE

3

DEFINICJE, SYMBOLE,

JEDNOSTKI

POJĘCIA I DEFINICJE

1. Czynnik temperaturowy na powierzchni wewnętrznej

e

i

e

si

Rsi

f

θ

θ

θ

θ

−

−

=

2. Obliczeniowy czynnik temperaturowy na powierzchni wewnętrznej

e

i

e

i

s

Rsi

f

θ

θ

θ

θ

−

−

=

min

,

min

,

3. Minimalna dopuszczalna temperatura

Najniższa temperatura powierzchni, poniżej której rozpoczyna się
rozwój pleśni

3.0. DEFINICJE, SYMBOLE, JEDNOSTKI

4

POJĘCIA I DEFINICJE

4. Dyfuzyjnie równoważna grubość warstwy powietrza

d

s

d

×

=

µ

5. Wilgotność względna

sat

p

p

=

ϕ

6. Krytyczna wilgotność powierzchni

Wilgotność względna przy powierzchni, przy której następuje
rozwój pleśni

3.0. DEFINICJE, SYMBOLE, JEDNOSTKI

DANE WEJŚCIOWE DO

OBLICZEŃ

5

WŁAŚCIWOŚCI MATERIAŁÓW I WYROBÓW

4.0. DANE WEJŚCIOWE DO OBLICZEŃ

1. Współczynnik przewodzenia ciepła -

λ

[W/m*K]

2. Opór cieplny – R [m

2

*KW]

3. Współczynnik oporu dyfuzyjnego -

µ

[-]

4. Dyfuzyjnie równoważna grubość warstwy powietrza – s

d

[m]

Do obliczeń stosujemy wartości obliczeniowe podane w specyfikacjach
materiałów i wyrobów lub tabelaryczne wartości podane w normach –
np. PN-EN 12524: 2003

Współczynnik przewodzenia ciepła

λ

i współczynnik oporu dyfuzyjnego

µ

stosowane są w odniesieniu do materiałów jednorodnych, zaś opór

cieplny R i dyfuzyjnie równoważna grubość warstwy powietrza s

d

do

wyrobów złożonych lub wyrobów bez zdefiniowanej grubości.

TEMPERATURY

4.0. DANE WEJŚCIOWE DO OBLICZEŃ

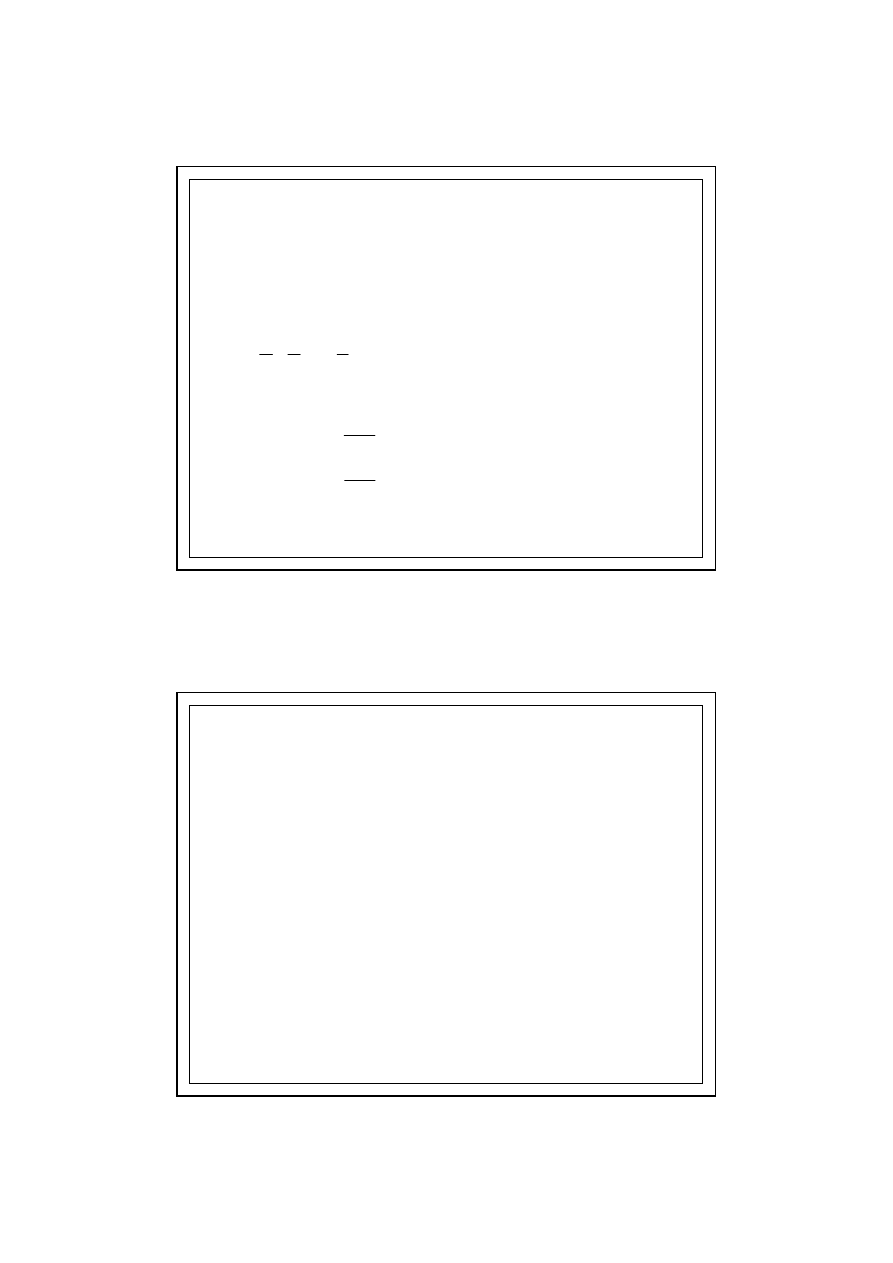
1)

Temperatura powietrza zewnętrznego

– jako średnią dla każdego miesiąca dla danej stacji meteorologicznej

wg PN-B-02025:2001

2)

Temperatura gruntu przylegającego do komponentu budowlanego

– średnia temperatura powietrza zewnętrznego (dla Polski + 8

°

C)

3)

Temperatura powietrza wewnętrznego

– wg PN-82/B-02402

6

WARUNKI WILGOTNOŚCIOWE

4.0. DANE WEJŚCIOWE DO OBLICZEŃ

1)

Wilgotność powietrza zewnętrznego /definiowana w postaci
wilgotności objętościowej v

c

lub ciśnienia pary wodnej p

e/

Średnie miesięczne ciśnienie pary wodnej

)

(

e

sat

e

e

p

p

θ

ϕ

×

=

Ciśnienie cząstkowe pary wodnej nasyconej w funkcji temperatury

θ

θ

+

×

×

=

5

,

237

269

,

17

5

,

610

e

p

sat

dla

θ ≥

0

°

C

θ

θ

+

×

×

=

5

,

265

875

,

21

5

,

610

e

p

sat

dla

θ

< 0

°

C

WARUNKI WILGOTNOŚCIOWE

4.0. DANE WEJŚCIOWE DO OBLICZEŃ

2) Warunki wilgotnościowe w gruncie

Zakłada się stan nasycenia (

ϕ

=1)

3) Wilgotność powietrza wewnętrznego

p

p

p

e

i

∆

+

=

v

v

v

e

i

∆

+

=

Wartości

∆

v i

∆

p należy przyjąć zgodnie z oczekiwanym

sposobem użytkowania budynku mnożąc uzyskane wartości
przez współczynnik 1,10 ,aby zapewnić margines
bezpieczeństwa

7

KLASY WILGOTNOŚCI WEWNĘTRZNEJ

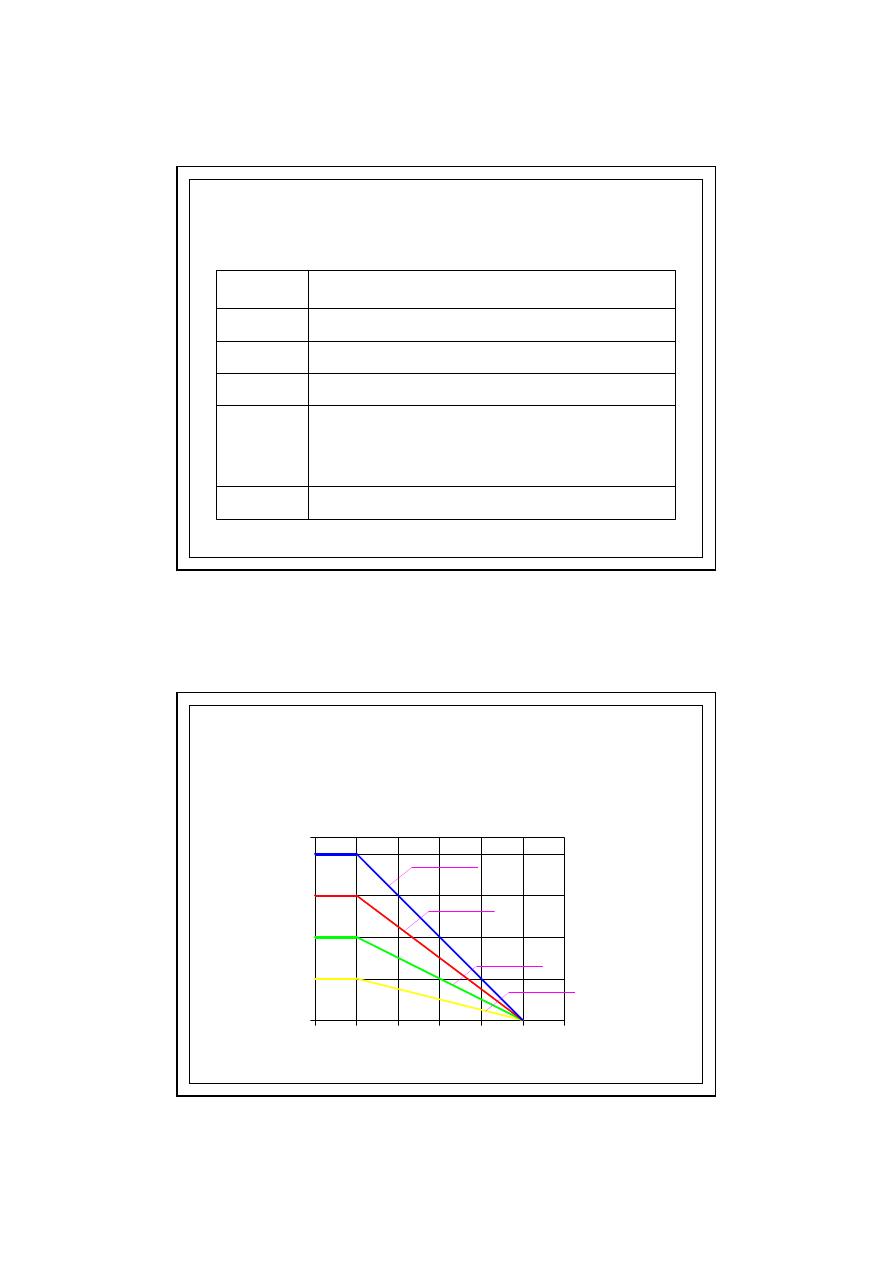
4.0. DANE WEJŚCIOWE DO OBLICZEŃ

Budynki specjalne, np.pralnia, browar, basen k

ą

pielowy

5

Mieszkania zag

ę

szczone, hale sportowe, kuchnie,

stołówki; budynki ogrzewane grzejnikami gazowymi bez
przewodów spalinowych

4

Mieszkania mało zag

ę

szczone

3

Biura, sklepy

2

Powierzchnia magazynowa

1

Budynek

Klasa

wilgotno

ś

ci

∆

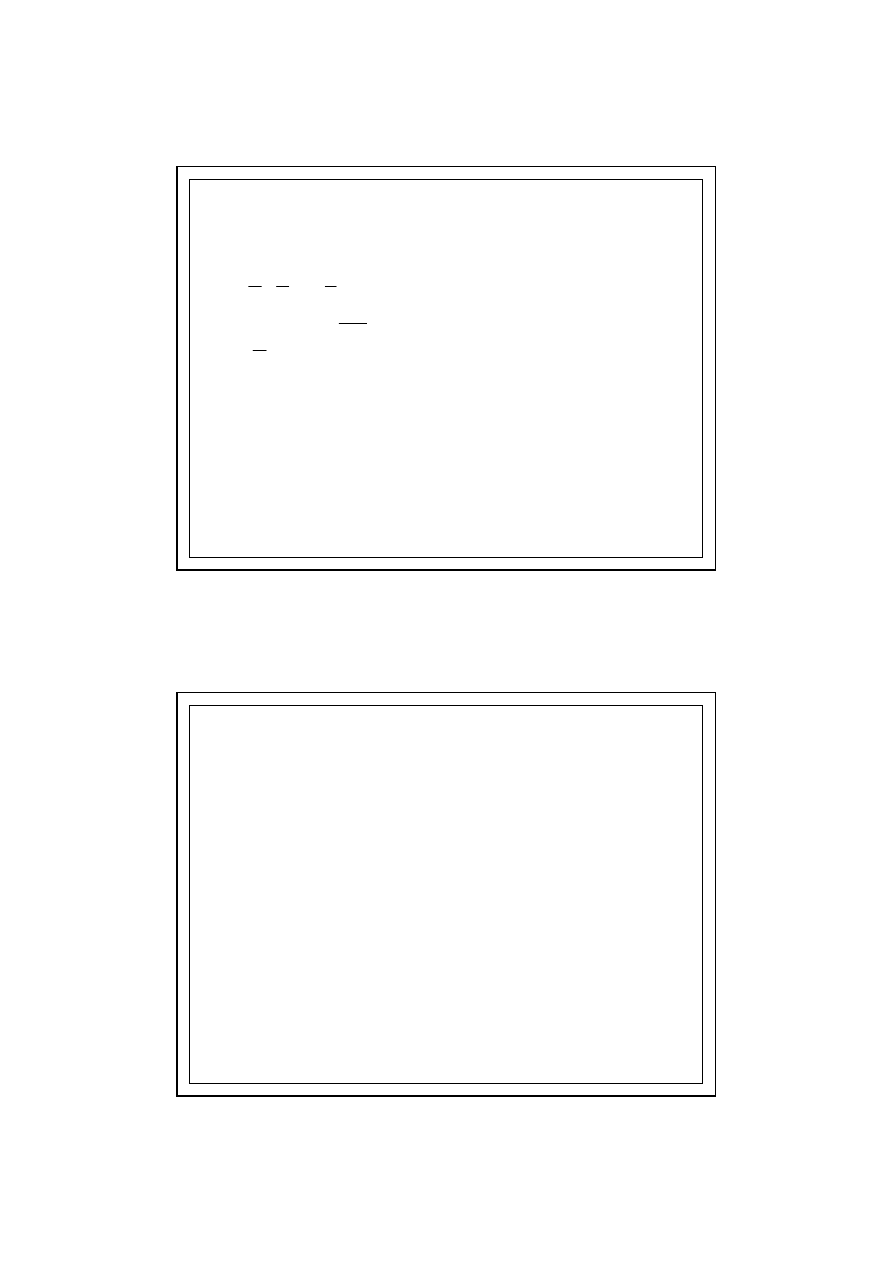
p W ZALEśNOŚCI OD KLASY

WILGOTNOŚCI WEWNĘTRZNEJ

4.0. DANE WEJŚCIOWE DO OBLICZEŃ

-5

0

5

10

15

20

25

270

540

810

1080

∆

p

[ Pa ]

ś

rednia miesi

ę

czna temperatura zewn

ę

trzna

[

o

C]

y= -54x+1080

y= -40,5x+810

y= -27x+540

y= -13,5x+270

1

2

3

4

5

8

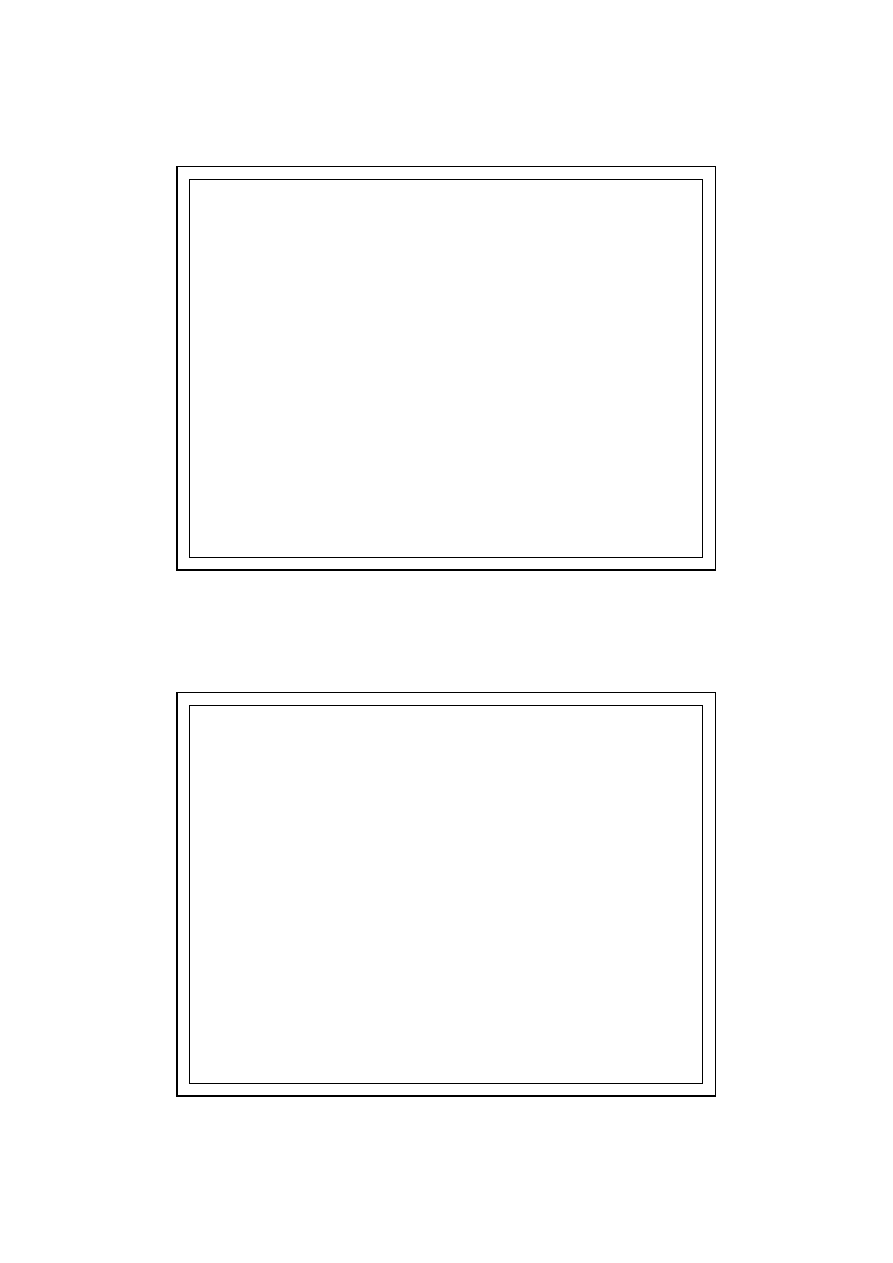
PRZYKŁAD OBLICZENIA p

i

)

(

e

sat

e

e

p

p

θ

ϕ ×

=

θ

θ

θ

+

×

×

=

5

,

265

875

,

21

5

,

610

)

(

e

p

e

sat

Pa

p

sat

824

)

2

.

4

(

=

4.0. DANE WEJŚCIOWE DO OBLICZEŃ

Dane :

θ

e

= 4,2

º

C ;

ϕ

e

= 88 %

Pa

p

e

725

824

88

,

0

=

×

=

p

p

p

e

i

∆

+

=

∆

p określamy wg wcześniejszego jako wartość y dla linii

pomiędzy 3 i 4 klasą wymnożoną przez współczynnik bezp. 1,10

Pa

x

y

9

,

639

810

2

,

4

5

,

40

810

5

,

40

=

+

×

−

=

+

−

=

Pa

y

p

704

1

,

1

9

,

639

1

,

1

=

×

=

×

=

∆

Pa

p

i

1429

704

725

=

+

=

OPORY PRZEJMOWANIA CIEPŁA

4.0. DANE WEJŚCIOWE DO OBLICZEŃ

Opór przejmowania ciepła na powierzchni zewnętrznej

R

se

= 0,04 m

2

x K/W

Opór przejmowania ciepła na powierzchni wewnętrznej

- na oszkleniach i ramach R

si

= 0,13 m

2

x K/W

- pozostałe powierzchnie wewnętrzne R

si

= 0,25 m

2

x K/W

Wartość oporu przejmowania ciepła na wewnętrznej powierzchni
równa 0,25 została przyjęta jako najgorszy przypadek ryzyka
kondensacji w narożu

9

PROJEKTOWANIE POD KĄTEM

UNIKNIĘCIA PLEŚNI

TOK OBLICZEŃ CZYNNIKA TEMPERATUROWEGO

NA POWIERZCHNI WEWNĘTRZNEJ KONIECZNEGO

DO UNIKNIĘCIA KRYTYCZNEJ WILGOTNOŚCI

POWIERZCHNI

5.0. PROJEKTOWANIE POD KĄTEM UNIKNIĘCIA PLEŚNI

Aby uniknąć rozwoju pleśni wilgotność względna powierzchni nie powinna
przekraczać wartości 0,8 przez kilka dni.

1.

Określenie średniej temperatury zewnętrznej dla poszczególnych
miesięcy wg PN-B-02025:2001

θ

e

2.

Określenie wilgotności zewnętrznej powietrza dla poszczególnych
miesięcy wg wskazań normy

φ

e

3.

Obliczenie p

e

dla poszczególnych miesięcy

4.

Obliczenie

∆

p dla poszczególnych miesięcy

5.

Obliczenie p

i

dla poszczególnych miesięcy

10

TOK OBLICZEŃ CZYNNIKA TEMPERATUROWEGO

NA POWIERZCHNI WEWNĘTRZNEJ KONIECZNEGO

DO UNIKNIĘCIA KRYTYCZNEJ WILGOTNOŚCI

POWIERZCHNI

8

,

0

)

(

i

si

sat

p

p

=

θ

5.0. PROJEKTOWANIE POD KĄTEM UNIKNIĘCIA PLEŚNI

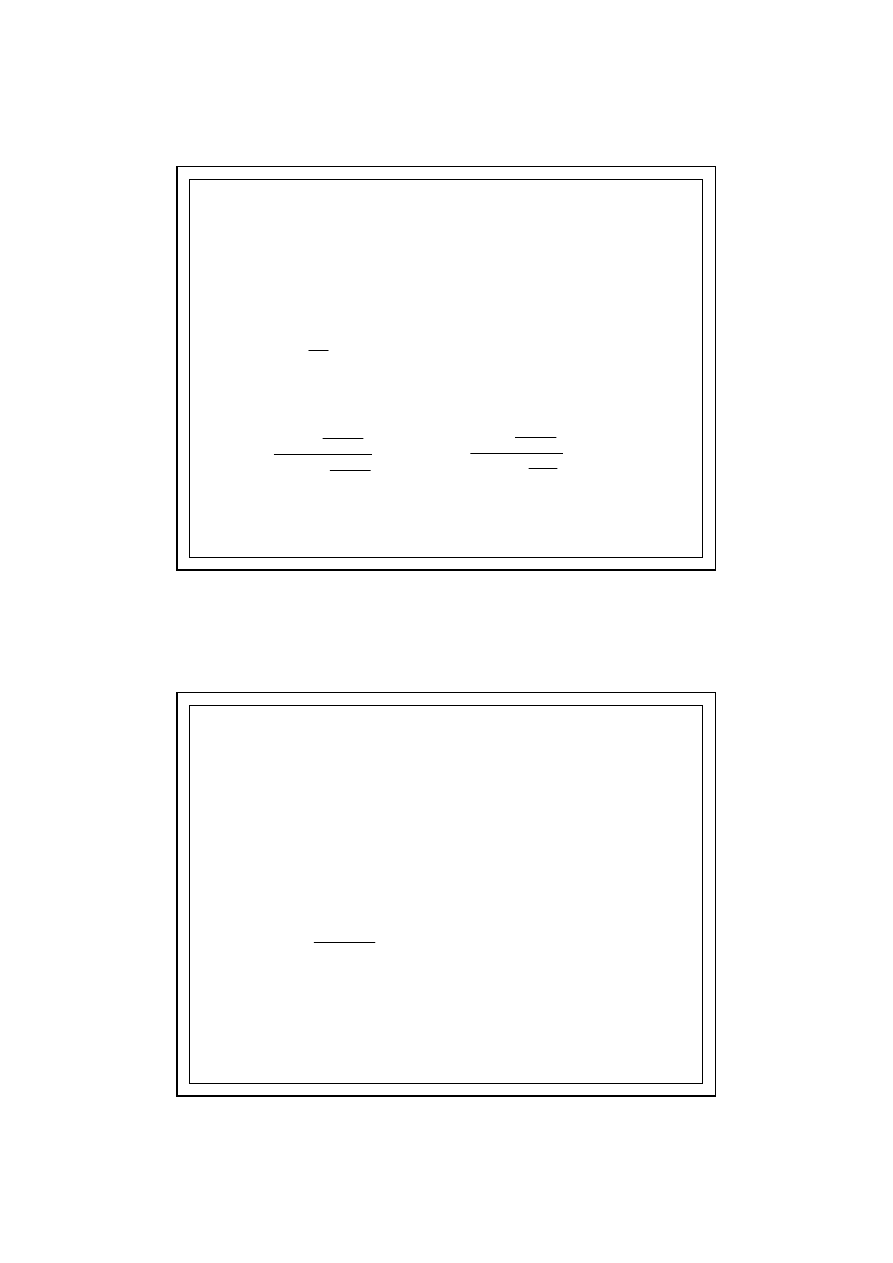
6. Określenie p

sat

(

θ

si

) dla każdego miesiąca wg wzoru

7. Określenie min temperatury poniżej której występuje
niebezpieczeństwo pojawienia się pleśni wg wzorów

5

,

610

)

(

ln

269

,

17

5

,

610

)

(

ln

5

,

237

min

,

si

sat

si

sat

si

p

p

θ

θ

θ

−

=

dla p

sat

≥ 610,5 Pa

)

5

,

610

ln(

875

,

21

)

5

,

610

)

(

ln(

5

,

265

min

,

sat

si

sat

si

p

p

−

=

θ

θ

dla p

sat

< 610,5 Pa

TOK OBLICZEŃ CZYNNIKA TEMPERATUROWEGO

NA POWIERZCHNI WEWNĘTRZNEJ KONIECZNEGO

DO UNIKNIĘCIA KRYTYCZNEJ WILGOTNOŚCI

POWIERZCHNI

e

i

e

i

s

Rsi

f

θ

θ

θ

θ

−

−

=

min

,

min

,

5.0. PROJEKTOWANIE POD KĄTEM UNIKNIĘCIA PLEŚNI

8. Określenie temperatury wewnętrznej wg PN-82/B-02402

9. Określenie min wskaźnika obliczeniowego dla każdego
miesiąca poniżej którego istnieje niebezpieczeństwo pojawienia
się pleśni wg wzoru

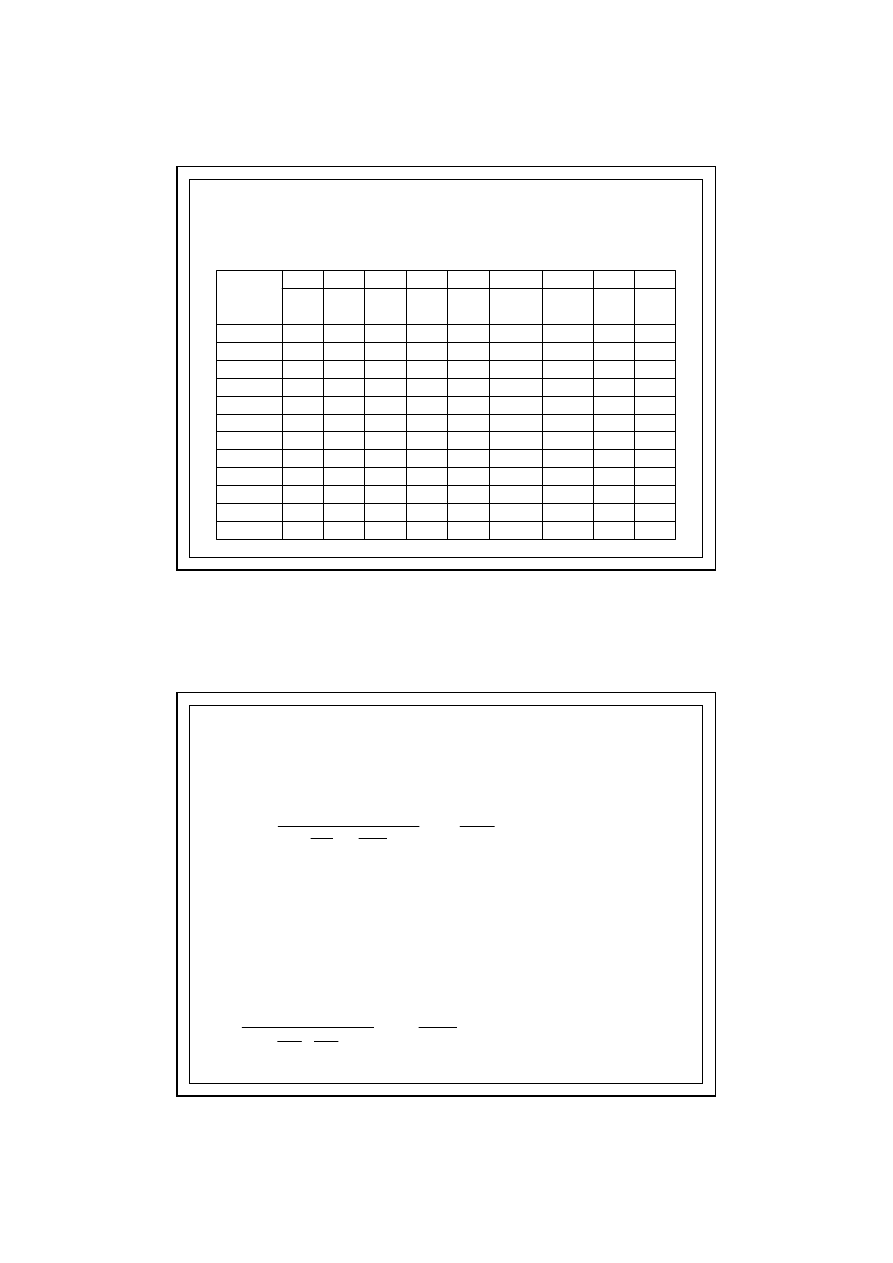
10. Obliczenie temperaturowego czynnika powierzchniowego dla
rozpatrywanej przegrody

U

R

U

f

si

Rsi

×

−

=

−

)

(

1

11. Sprawdzenie warunku f

Rsi

> f

Rsi,min

dla wszystkich miesięcy

11

PRZYKŁAD OBLICZENIOWY

5.0. PROJEKTOWANIE POD KĄTEM UNIKNIĘCIA PLEŚNI

0,784

20

15,8

1797

1437

860

578

0,90

0,7

grudzie

ń

0,741

20

15,9

1806

1445

704

741

0,90

4,2

listopad

0,690

20

16,6

1887

1510

490

1020

0,89

9,0

pa

ź

dziernik

0,668

20

17,9

2047

1637

285

1352

0,87

13,6

wrzesie

ń

0,683

20

19,1

2212

1769

125

1645

0,84

17,2

sierpie

ń

0,562

20

18,9

2177

1742

116

1626

0,82

17,4

lipiec

0,456

20

17,7

2019

1615

192

1424

0,80

15,7

czerwiec

0,518

20

15,7

1779

1423

401

1022

0,78

11,0

maj

0,647

20

15,1

1714

1371

619

752

0,80

6,1

kwiecie

ń

0,752

20

15,4

1752

1402

820

582

0,85

1,6

marzec

0,770

20

15,1

1716

1373

891

482

0,88

-1,3

luty

0,778

20

15,2

1728

1382

891

491

0,92

-1,6

stycze

ń

°C

°C

Pa

Pa

Pa

Pa

°C

fRsi

θ

i

θ

si(min)

psat(

θ

si)

pi

∆

p

pe

φ

e

θ

e

Miesi

ą

c

9

8

7

6

5

4

3

2

1

PRZYKŁAD OBLICZENIOWY

K

m

W

U

×

=

+

+

+

=

2

888

,

0

04

,

0

82

,

0

015

.

0

*

2

3

,

0

24

,

0

25

,

0

1

5.0. PROJEKTOWANIE POD KĄTEM UNIKNIĘCIA PLEŚNI

1. ściana z gazobetonu gr 24 cm + 2x tynk cementowo-wapienny

)

,

(

778

,

0

888

,

0

)

25

,

0

888

,

0

(

1

styczeń

grudzień

f

f

Rsi

Rsi

≤

=

×

−

=

−

Wartość f

Rsi

jest mniejsza od wartości f

Rsi

obliczeniowego w

miesiącach grudniu i styczniu, a więc istnieje wtedy
niebezpieczeństwo pojawienia się pleśni

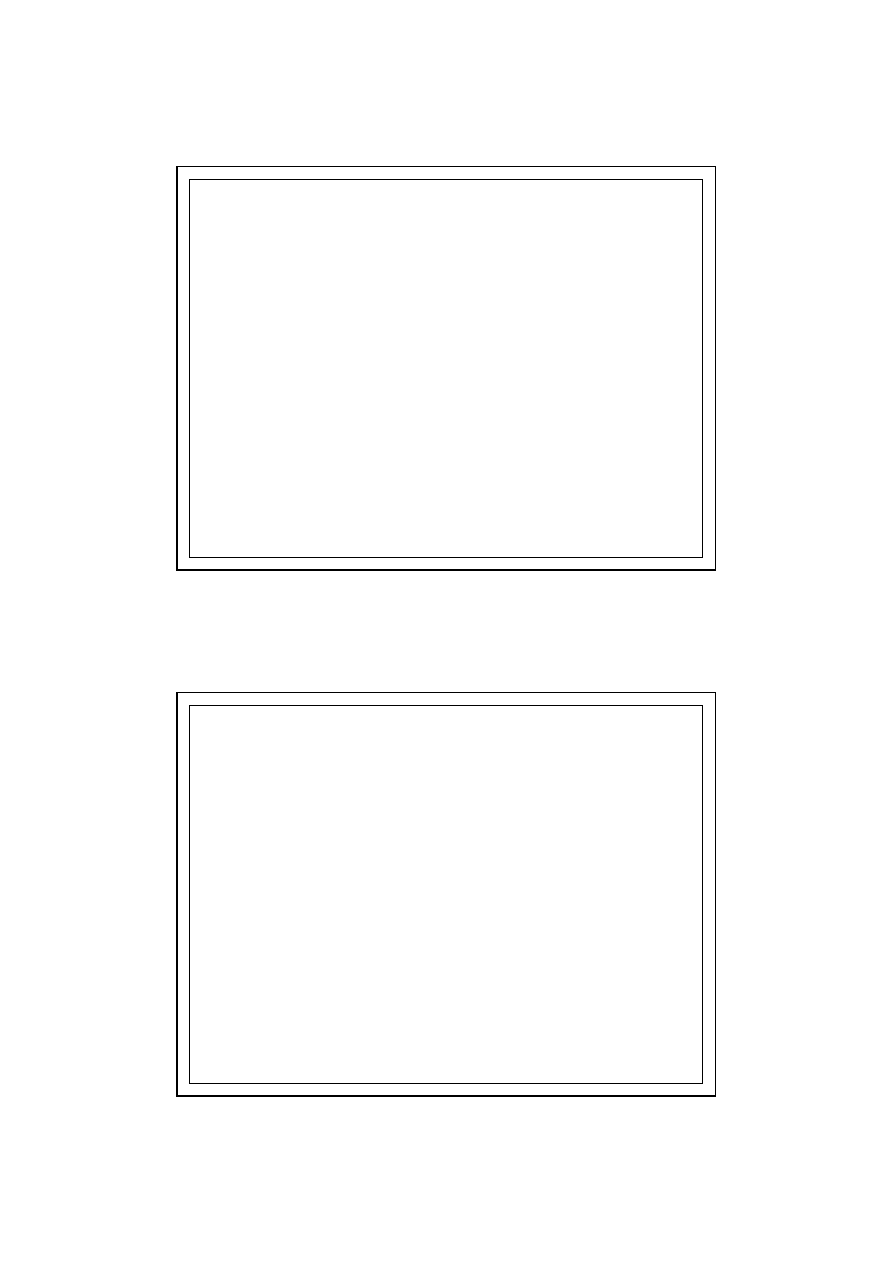
1. ściana z gazobetonu gr 24 cm + 6 cm styropianu

K

m

W

U

×

=

+

+

+

=

2

437

,

0

04

,

0

05

,

0

06

,

0

3

,

0

24

,

0

25

,

0

1

f

Rsi

= 0,891 > f

Rsi

max

obliczeniowe

12

KONDENSACJA

MIĘDZYWARSTWOWA

ZALECENIA

6.0. KONDENSACJA MIĘDZYWARSTWOWA

1.

Prezentowana metoda powinna służyć jako sposób szacowania,
nie zaś narzędzie służące do dokładnego przewidywania.

2.

Jest przydatna przy porównywaniu różnych budynków i oceny
skutków modyfikacji

3.

Nie dostarcza ona dokładnych prognoz warunków
wilgotnościowych wewnątrz budowli w warunkach eksploatacji.

4.

Nie jest właściwym narzędziem do obliczeń związanych z
wysychaniem wilgoci budowlanej.

13

OPIS MATEMATYCZNY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Zakłada się, że przepływ wilgoci przez przegrodę zachodzi wyłącznie wskutek

dyfuzji pary wodnej opisanej równaniem:

d

S

p

x

p

g

∆

×

=

∆

∆

×

=

0

0

δ

µ

δ

]

[

2

s

m

kg

×

gdzie : δ

0

= 2 x 10

-10

]

[

Pa

s

m

kg

×

×

- przenikalność pary wodnej w powietrzu

∆p [Pa] – różnica ciśnień

µ [-] – czynnik krotności wyrażający stosunek grubości warstwy materiału

do grubości warstwy powietrza o takiej samej przepuszczalności pary wodnej;

x [m] – grubość warstwy materiału

x

S

d

∆

×

=

µ

[m] – grubość równoważnej warstwy powietrza

GĘSTOŚĆ STRUMIENIA CIEPŁA

]

[

2

m

W

6.0. KONDENSACJA MIĘDZYWARSTWOWA

R

d

q

θ

θ

λ

∆

=

∆

×

=

gdzie :

λ

[W/m

2

xK] – współczynnik przewodzenia ciepła

θ

[K] – temperatura

R [m

2

xK/W] – opór cieplny przegrody

d [m] – grubość warstwy

14

ZAŁOśENIA METODY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

W obliczeniach przepływu wilgoci przyjęto następujące uproszczenia :

- pominięcie uzależnienia przewodzenia ciepła od zawilgocenia materiału;

- stosowanie stałych właściwości materiałów;

- pominięcie wpływu ruchu powietrza przez pęknięcia lub wewnątrz szczelin
powietrznych;

- pominięcie wpływu podciągania kapilarnego i transportu wilgoci w fazie

ciekłej;

- założenie warunków brzegowych stałych w przeciągu miesiąca;

- pominięcie aspektu higroskopijności większości materiałów (absorpcji pary

wodnej);

- przyjęcie jednokierunkowego transportu wilgoci;

- zaniedbanie wpływu promieniowania słonecznego i długofalowego.

TOK OBLICZEŃ

6.0. KONDENSACJA MIĘDZYWARSTWOWA

1.

Podział elementu budowlanego na szereg równoległych, przylegających
do siebie warstw.

2.

Obliczenie dla każdej warstwy oporu cieplnego i równoważnej grubości
warstwy powietrza (elementy o wysokim oporze cieplnym – np.
materiały izolacyjne – należy podzielić na kilka warstw o oporze
cieplnym nie większym niż 0,25 m

2

xK/W traktując je jako osobne

warstwy)

3.

Obliczenia należy rozpocząć od dowolnego miesiąca - tzw. miesiąca
próbnego - sprawdzając czy wystąpi kondensacja. Jeżeli nie występuje
obliczenia należy powtórzyć dla kolejnych miesięcy, aż do stanu gdy:

- nie stwierdzi się kondensacji w żadnym miesiącu

- stwierdzi się miesiąc z kondensacją i jest to miesiąc początkowy

4. Obliczenia należy wykonać dla wszystkich miesięcy roku sumując

ilości skondensowanego i odparowanego kondensatu.

15

OPÓR CIEPLNY I GRUBOŚĆ RÓWNOWAśNA

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Sumowanie oporów i równoważnej grubości warstw powietrza
przeprowadza się od strony zewnętrznej

∑

=

+

=

n

i

i

se

n

R

R

R

1

'

∑

=

=

n

i

i

d

n

d

S

S

1

,

,

'

Całkowity opór cieplny i całkowita grubość równoważna

∑

+

+

=

=

N

i

si

i

se

T

R

R

R

R

1

'

∑

=

=

N

i

i

d

T

d

S

S

1

,

,

'

TEMPERATURA NA STYKU WARSTW

6.0. KONDENSACJA MIĘDZYWARSTWOWA

)

(

'

'

e

i

T

n

e

n

R

R

θ

θ

θ

θ

−

×

+

=

Obliczenie temperatury przeprowadza si

ę od strony zewnętrznej

gdzie:
θe [˚ C] – temperatura zewnętrzna (wg PN-B-02025:2001)

θi [˚ C] – temperatura wewnętrzna (wg PN-82/B-02403)

R’

n

[m

2

xK/W] – suma oporów do powierzchni styku licz

ąc od strony zew.

R’

T

[m

2

xK/W] – całkowity opór cieplny przegrody

16

CIŚNIENIE CZĄSTKOWE PARY WODNEJ

)

(

e

sat

e

e

p

p

θ

ϕ

×

=

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Dla obliczonych temperatur wyznacza się ciśnienie cząstkowe pary wodnej
nasyconej na styku warstw oraz na powierzchniach przegrody wg wzorów

θ

θ

+

×

×

=

5

,

237

269

,

17

5

,

610

e

p

sat

dla

θ ≥

0

°

C

θ

θ

+

×

×

=

5

,

265

875

,

21

5

,

610

e

p

sat

dla

θ

< 0

°

C

Określa się rzeczywiste ciśnienie pary wodnej po stronie zewnętrznej i
wewnętrznej przegrody

p

p

p

e

i

∆

+

=

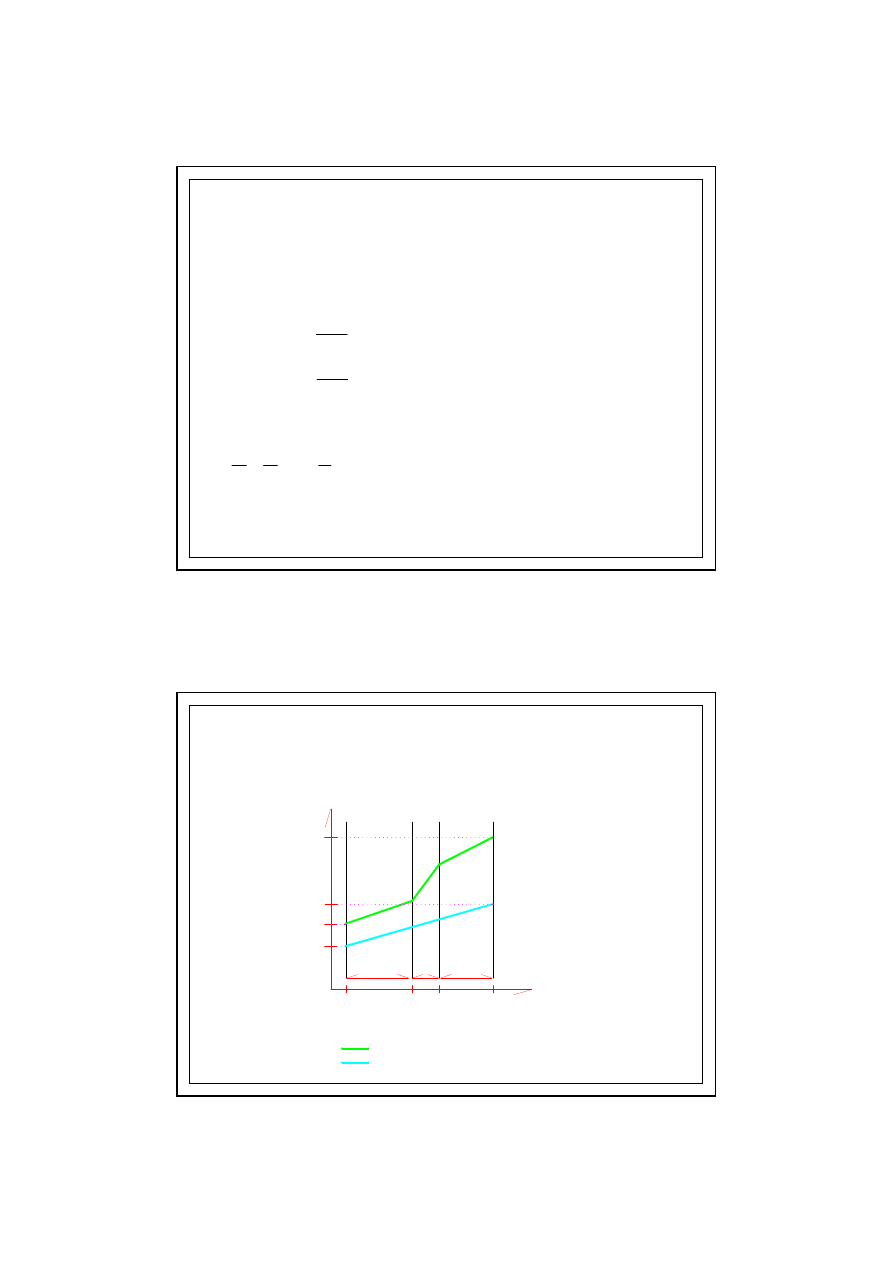
WYKRES p/ s

d

(brak kondensacji)

6.0. KONDENSACJA MIĘDZYWARSTWOWA

S

d

1

S

d

2

S

d

3

0

S'

dT

S

d [m]

p

[Pa]

ci

ś

nienie

grubo

ść

równowa

ż

na

p

e

p

i

p

sat(i)

p

sat(e)

wykres ci

ś

nienia pary wodnej nasyconej

wykres ci

ś

nienia rzeczywistego pary wodnej

17

STRUMIEŃ PARY WODNEJ PRZENIKAJĄCEJ

PRZEZ ELEMENT BUDOWLANY

T

d

e

i

S

p

p

g

,

0

'

−

=

δ

]

[

2

s

m

kg

×

t

g

g

c

c

×

=

'

6.0. KONDENSACJA MIĘDZYWARSTWOWA

gdzie:

p

i

, p

e

[Pa] – ciśnienia rzeczywiste pary wodnej

S’

d,T

[m] – całkowita grubość równoważna warstwy powietrza

]

[

2

m

kg

gdzie:

t [s] – ilość sekund w miesiącu

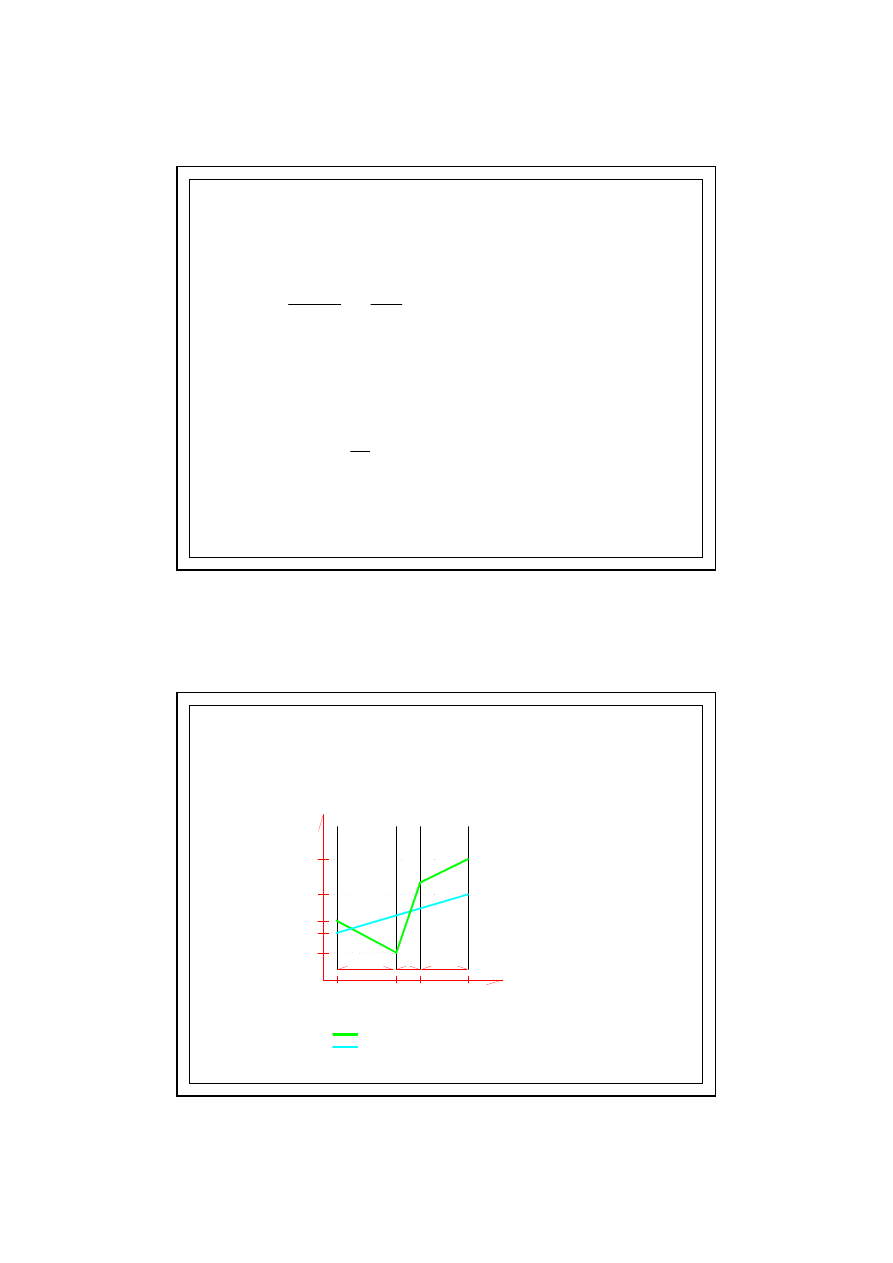
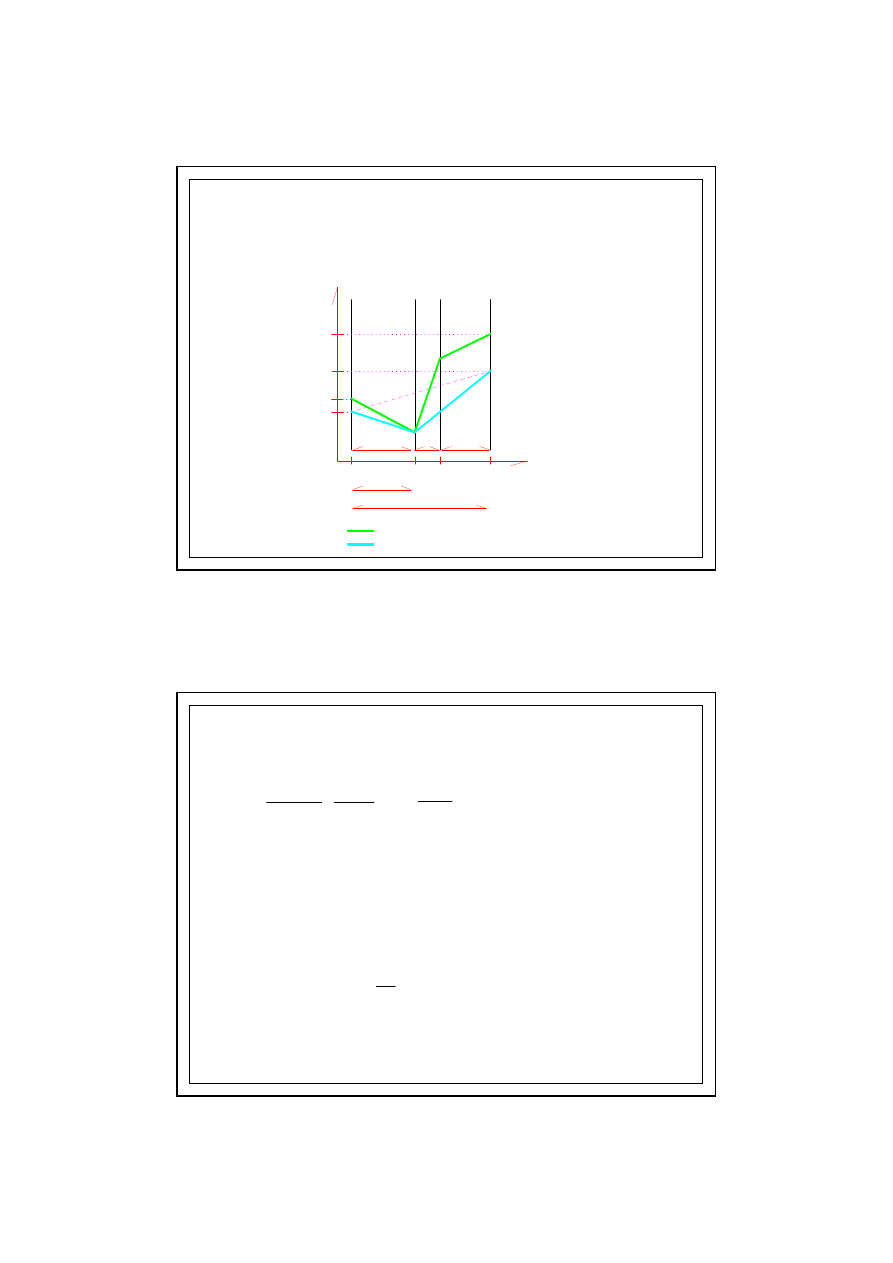
WYKRES p/s

d

(przypadek kondensacji)

6.0. KONDENSACJA MIĘDZYWARSTWOWA

S'

d,T

wykres ci

ś

nienia pary wodnej nasyconej

wykres ci

ś

nienia rzeczywistego pary wodnej

0

[m]

grubo

ść

równowa

ż

na

S

d

p

min

p

sat(i)

p

e

p

i

p

sat(e)

p

ci

ś

nienie

S

d

1

S

d

2

S

d

3

[Pa]

18

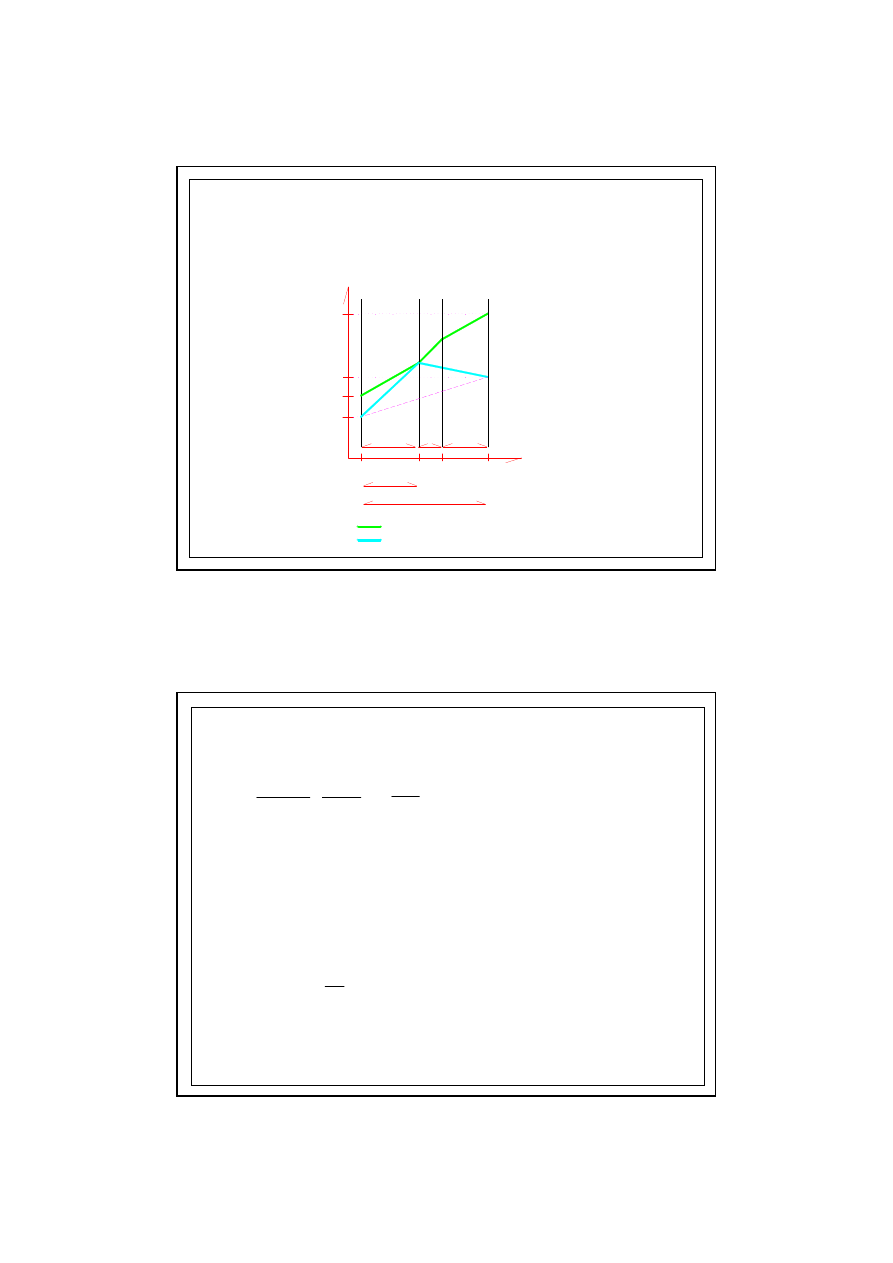
ODGIĘCIE WYKRESU p

rzeczywistego

6.0. KONDENSACJA MIĘDZYWARSTWOWA

S'

d,T

wykres ci

ś

nienia pary wodnej nasyconej

wykres ci

ś

nienia rzeczywistego pary wodnej

0

[m]

grubo

ść

równowa

ż

na

S

d

p

sat(i)

p

e

p

i

p

sat(e)

p

ci

ś

nienie

S

d

1

S

d

2

S

d

3

[Pa]

S'

d,c

S'

d,T

ILOŚĆ WYKROPLONEGO KONDENSATU

t

g

g

c

c

×

=

'

6.0. KONDENSACJA MIĘDZYWARSTWOWA

)

'

'

'

(

,

,

,

0

c

d

e

c

c

d

T

d

c

i

c

S

p

p

S

S

p

p

g

−

−

−

−

=

δ

]

[

2

s

m

kg

×

gdzie:

p

i

, p

e

[Pa] – ciśnienia rzeczywiste pary wodnej

p

c

[Pa] – max ciśnienie pary wodnej nasyconej w przegrodzie

S’

d,T

[m] – całkowita grubość równoważna warstwy powietrza

S’

d,c

[m] – grubość równoważna do miejsca max ciśnienia cząstkowego

]

[

2

m

kg

gdzie:

t [s] – ilo

ść sekund w miesiącu

19

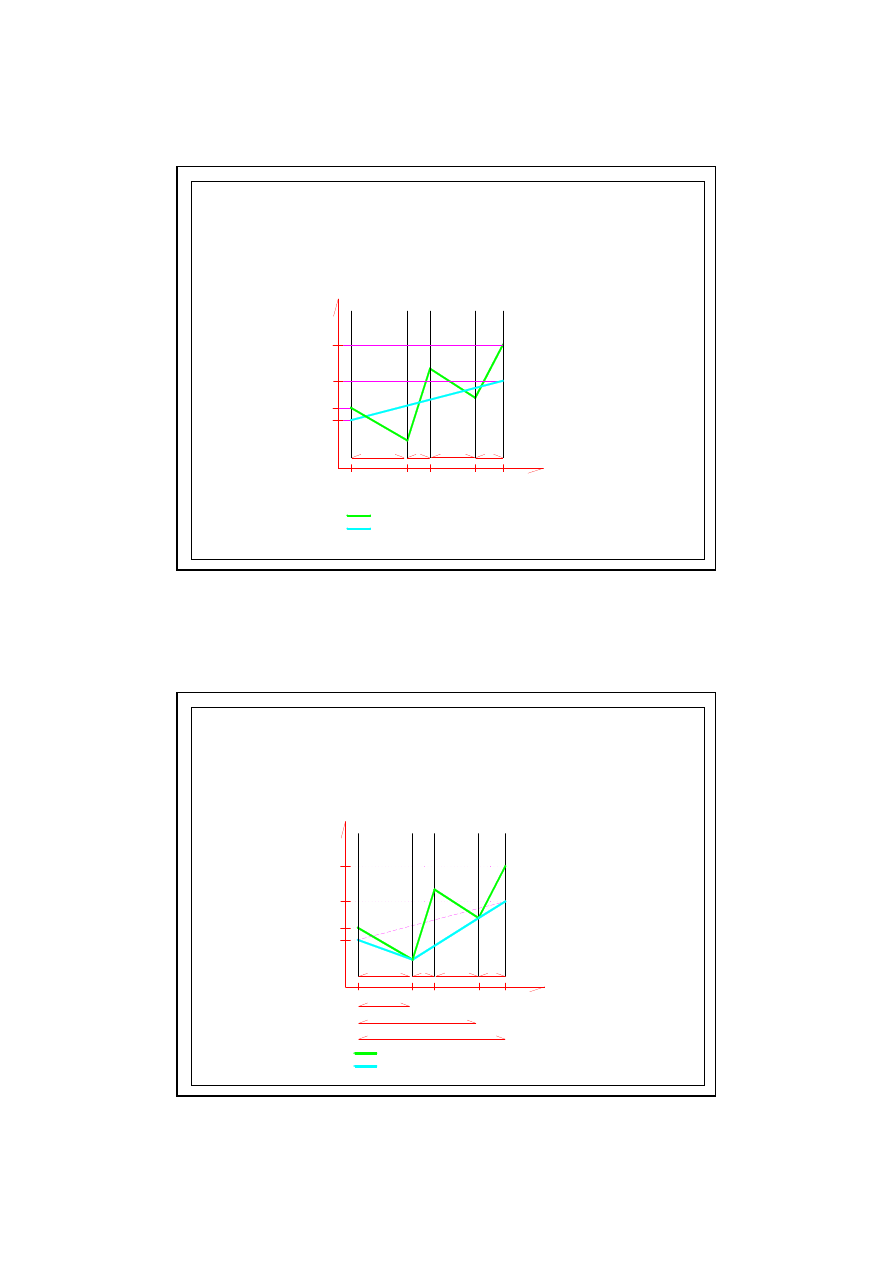
WYKRES p/s

d

(przypadek parowania)

6.0. KONDENSACJA MIĘDZYWARSTWOWA

S

d

3

S

d

2

[Pa]

ci

ś

nienie

S

d

1

p

e

p

sat(e)

p

i

p

sat(i)

[m]

S

d

grubo

ść

równowa

ż

na

S'

d,T

S'

dT

S'

d,c

0

wykres ci

ś

nienia rzeczywistego pary wodnej

wykres ci

ś

nienia pary wodnej nasyconej

STRUMIEŃ PAROWANIA

]

[

2

s

m

kg

×

t

g

g

cv

cv

×

=

'

6.0. KONDENSACJA MIĘDZYWARSTWOWA

)

'

'

'

(

,

,

,

0

c

d

e

c

c

d

T

d

c

i

cv

S

p

p

S

S

p

p

g

−

−

−

−

=

δ

gdzie:

p

i

, p

e

[Pa] – ciśnienia rzeczywiste pary wodnej

p

c

[Pa] – max ciśnienie pary wodnej nasyconej w przegrodzie

S’

d,T

[m] – całkowita grubość równoważna warstwy powietrza

S’

d,c

[m] – grubość równoważna do miejsca max ciśnienia cząstkowego

]

[

2

m

kg

Wielkość strumienia parowania, w odróżnieniu od kondensacji,

wyrażona jest liczbą ujemną.

20

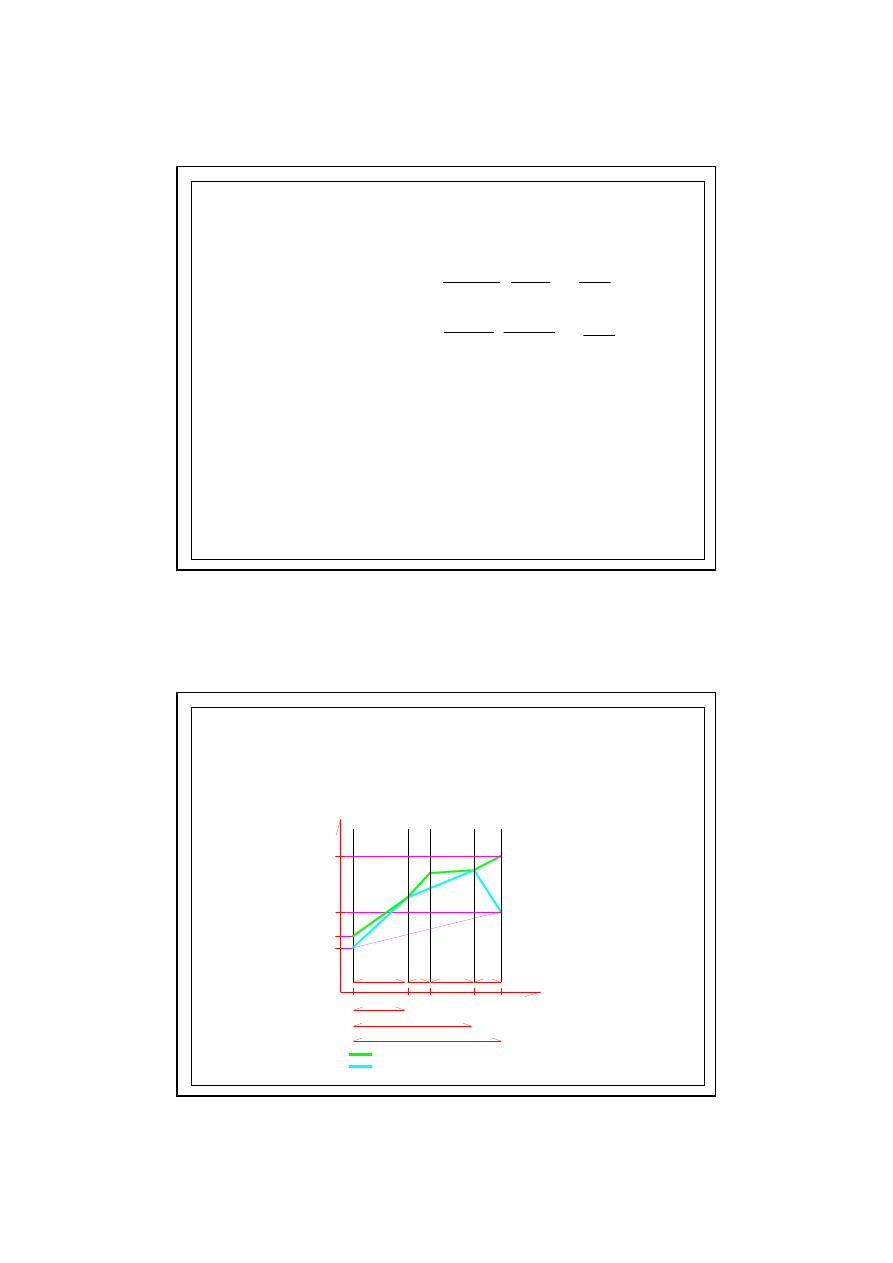
WYKRES p/s

d

(przypadek podwójnej kondensacji)

6.0. KONDENSACJA MIĘDZYWARSTWOWA

S

d

4

S

d

3

S

d

2

S

d

1

[Pa]

p

ci

ś

nienie

p

sat(i)

p

i

p

e

p

sat(e)

[m]

S

d

S'

d,T

grubo

ść

równowa

ż

na

wykres ci

ś

nienia pary wodnej nasyconej

wykres ci

ś

nienia rzeczywistego pary wodnej

0

ODGIĘCIE WYKRESU p

rzeczywistego

6.0. KONDENSACJA MIĘDZYWARSTWOWA

0

wykres ci

ś

nienia rzeczywistego pary wodnej

wykres ci

ś

nienia pary wodnej nasyconej

grubo

ść

równowa

ż

na

S'

d,T

S'

d,c1

S'

d,T

S

d [m]

p

sat(e)

p

e

p

i

p

sat(i)

ci

ś

nienie

p

[Pa]

S

d

1

S

d

2

S

d

3

S

d

4

S'

d,c2

p

c1

p

c2

21

ILOŚĆ WYKROPLONEGO KONDENSATU

)

'

'

'

(

1

,

1

1

,

2

,

1

2

0

1

c

d

e

c

c

d

c

d

c

c

c

S

p

p

S

S

p

p

g

−

−

−

−

=

δ

]

[

2

s

m

kg

×

)

'

'

'

'

(

1

,

2

,

1

2

2

,

,

2

0

2

c

d

c

d

c

c

c

d

T

d

c

i

c

S

S

p

p

S

S

p

p

g

−

−

−

−

−

=

δ

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Powierzchnia stykowa g

c1

Powierzchnia stykowa g

c2

]

[

2

s

m

kg

×

gdzie:

p

i

, p

e

[Pa] – ciśnienia rzeczywiste pary wodnej

p

c

[Pa] – max ciśnienie pary wodnej nasyconej w przegrodzie

S’

d,T

[m] – całkowita grubość równoważna warstwy powietrza

S’

d,c

[m] – grubość równoważna do miejsca max ciśnienia cząstkowego

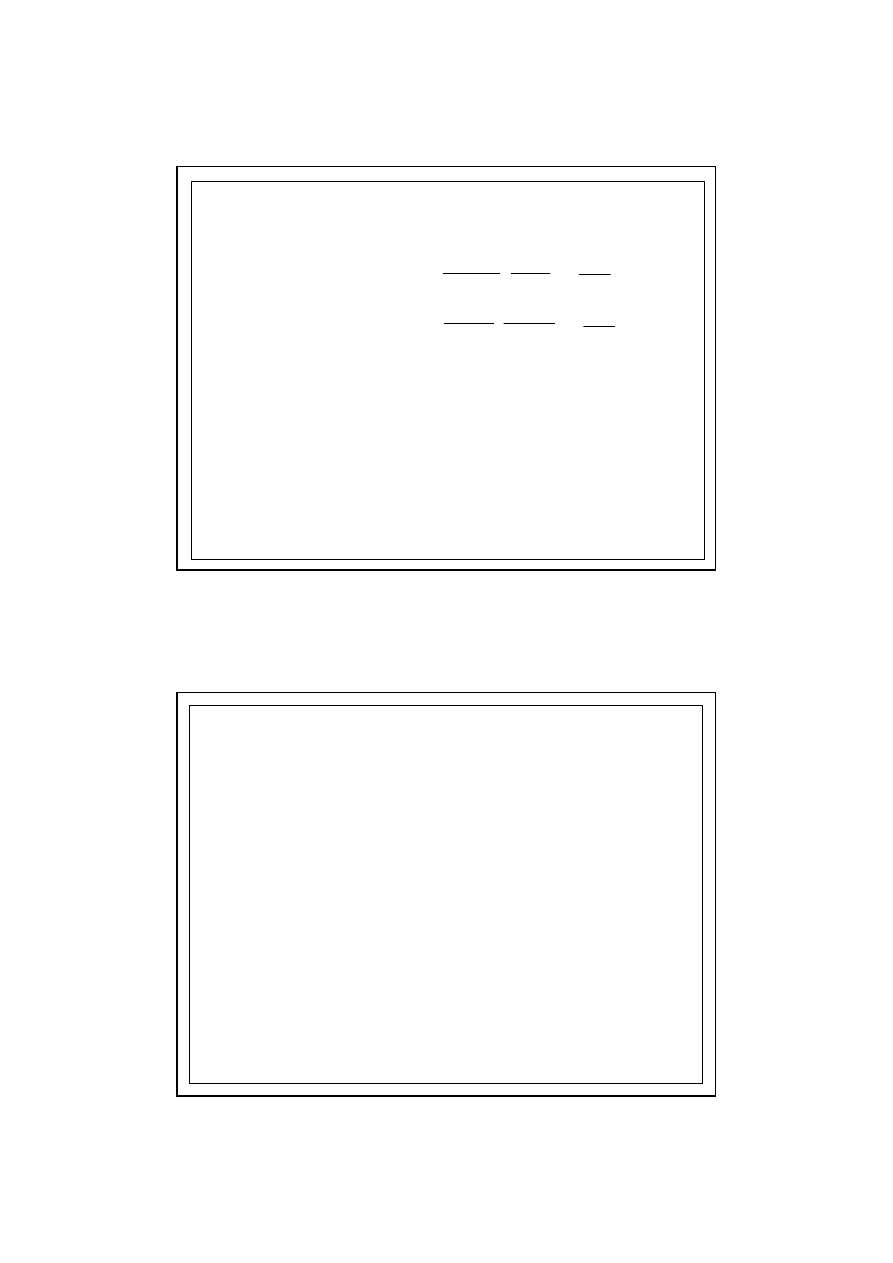
WYKRES p/s

d

(przypadek dwumiejscowego

parowania)

6.0. KONDENSACJA MIĘDZYWARSTWOWA

p

c2

p

c1

S'

d,c2

S

d

4

S

d

3

S

d

2

S

d

1

[Pa]

p

ci

ś

nienie

p

sat(i)

p

i

p

e

p

sat(e)

[m]

S

d

S'

d,T

S'

d,c1

S'

d,T

grubo

ść

równowa

ż

na

wykres ci

ś

nienia pary wodnej nasyconej

wykres ci

ś

nienia rzeczywistego pary wodnej

0

22

STRUMIEŃ DWUMIEJSCOWEGO PAROWANIA

6.0. KONDENSACJA MIĘDZYWARSTWOWA

)

'

'

'

(

1

,

1

1

,

2

,

1

2

0

1

c

d

e

c

c

d

c

d

c

c

c

S

p

p

S

S

p

p

g

−

−

−

−

=

δ

]

[

2

s

m

kg

×

)

'

'

'

'

(

1

,

2

,

1

2

2

,

,

2

0

2

c

d

c

d

c

c

c

d

T

d

c

i

c

S

S

p

p

S

S

p

p

g

−

−

−

−

−

=

δ

Powierzchnia stykowa g

c1

Powierzchnia stykowa g

c2

]

[

2

s

m

kg

×

gdzie:

p

i

, p

e

[Pa] – ciśnienia rzeczywiste pary wodnej

p

c

[Pa] – max ciśnienie pary wodnej nasyconej w przegrodzie

S’

d,T

[m] – całkowita grubość równoważna warstwy powietrza

S’

d,c

[m] – grubość równoważna do miejsca max ciśnienia cząstkowego

Wielkość strumienia parowania, w odróżnieniu od kondensacji,

wyrażona jest liczbą ujemną.

INTERPRETACJA WYNIKÓW

6.0. KONDENSACJA MIĘDZYWARSTWOWA

1.

Brak kondensacji na powierzchniach stykowych warstw we wszystkich
miesiącach roku, Konstrukcję określamy jako wolną od wewnętrznej
kondensacji.

2.

Kondensat występuje na jednej powierzchni stykowej lub kilku, ale z
każdej z nich wyparowuje w przeciągu miesięcy letnich

Należy uwzględnić max ilość kondensatu na powierzchni styku

określając ryzyko degradacji i pogorszenia właściwości cieplnych i
sprawdzając zgodność z wymogami zawartymi w normach i przepisach

3.

Kondensacja występująca na jednej powierzchni stykowej lub kilku nie
odparowuje w przeciągu miesięcy letnich.

W tym przypadku należy stwierdzić wadliwość przegrody oraz określić

ilość kondensatu pozostałą na każdej powierzchni stykowej po 12
miesiącach

23

MIGRACJA KONDENSATU

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Opisana metoda zakłada, że kondensacja występująca w danej
płaszczyźnie pozostaje przy niej. W rzeczywistości kondensat może
migrować w warstwy po każdej stronie powierzchni stykowej. Stopień
migracji można oszacować przy pomocy krytycznej zawartości wilgoci w
materiale w

cr

powyżej której następuje przenoszenie w fazie ciekłej.

80 - 110

Cegła wapienno-piaskowa

125

Beton

180

Zaprawa cementowa

60 - 130

Cegła

120

Beton komórkowy

W

cr

[kg/m

3

]

Materiał

cr

a

w

w

M

d

=

Grubość, na której rozłożona jest wilgoć

M

a

[kg/m

2

] – ilość nagromadzonej wilgoci

[m]

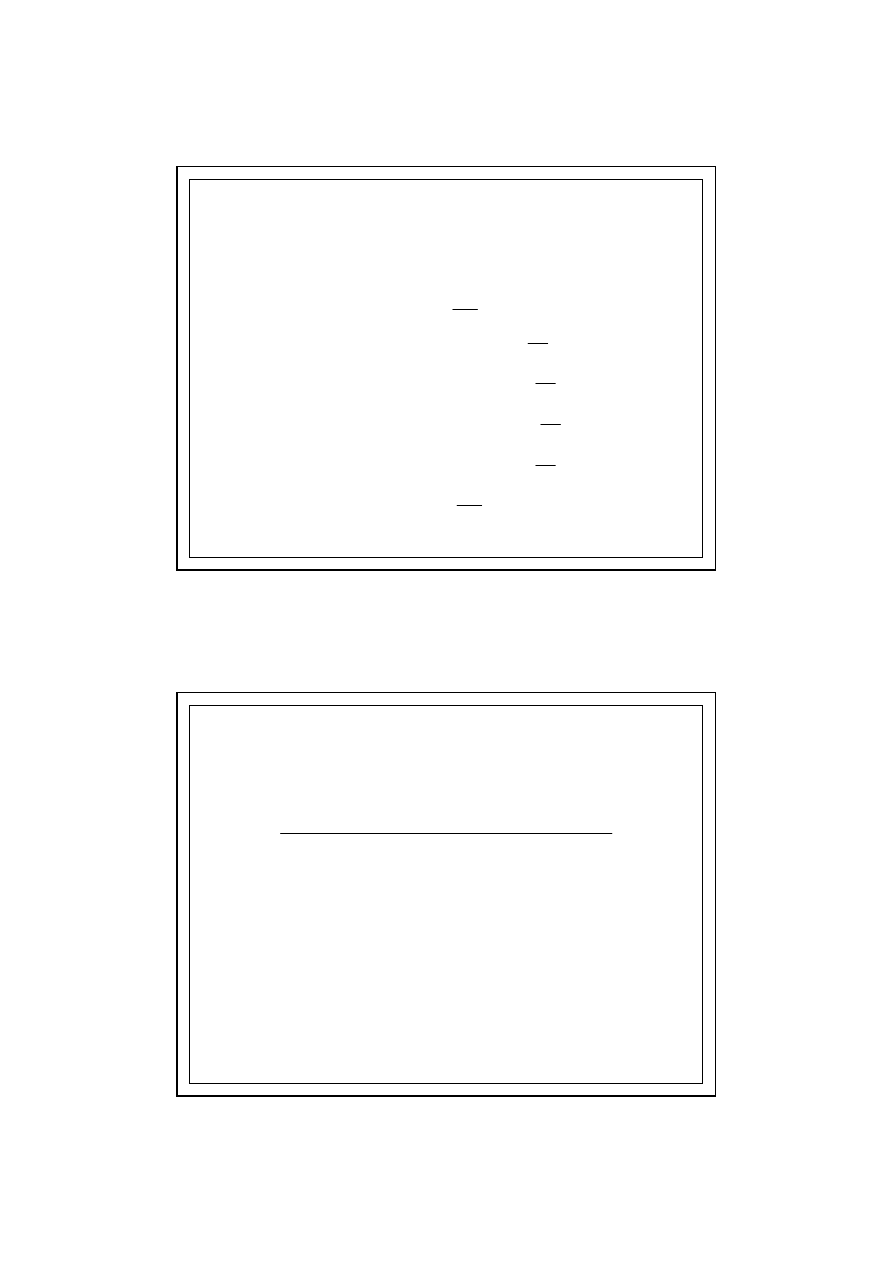
PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Przekrój przegrody

STRONA
ZEWN

Ę

TRZNA

STRONA
WEWN

Ę

TRZNA

mur
ceglany

styropian

tynk
wewn

ę

trzny

tynk
zewn

ę

trzny

24

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Dane :

powietrze zewnetrzne

Rse

0.04

m

2

K

⋅

W

⋅

:=

tynk zewnetrzny

d1

1 cm

⋅

:=

*

λ

1

1

W

m K

⋅

⋅

:=

µ

1

10

:=

mur ceglany

d2

25 cm

⋅

:=

λ

2

1.0

W

m K

⋅

⋅

:=

µ

2

40

:=

styropian

d3

4 cm

⋅

:=

λ

3

0.05

W

m K

⋅

⋅

:=

µ

3

60

:=

tynk mineralny

d4

1 cm

⋅

:=

*

λ

4

0.2

W

m K

⋅

⋅

:=

µ

4

10

:=

powietrze wewnetrzne

Rsi

0.13

m

2

K

⋅

W

⋅

:=

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Dane klimatyczne:

0,88

0,7

20°

grudzie

ń

0,88

4,2

20°

listopad

0,83

9

20°

pa

ź

dziernik

0,79

13,6

20°

wrzesie

ń

0,75

17,2

20°

sierpie

ń

0,73

17,4

20°

lipiec

0,69

15,7

20°

czerwiec

0,68

11

20°

maj

0,72

6,1

20°

kwiecie

ń

0,78

1,6

20°

marzec

0,84

-1,3

20°

luty

0,85

-1,6

20°

stycze

ń

φ

e

θ

e

θ

i

Miesi

ą

c

25

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Opory warstw:

R1

d1

λ

1

:=

R1

0.01

m

2

K

⋅

W

=

R2

d2

λ

2

:=

R2

0.25

m

2

K

⋅

W

=

R3

d3

λ

3

:=

R3

0.8

m

2

K

⋅

W

=

R4

d4

λ

4

:=

R4

0.05

m

2

K

⋅

W

=

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Grubości równoważne

Sd1

µ

1 d1

⋅

:=

Sd1

0.1 m

=

Sd2

µ

2 d2

⋅

:=

Sd2

10 m

=

Sd3

µ

3 d3

⋅

:=

Sd3

2.4 m

=

Sd4

µ

4 d4

⋅

:=

Sd4

0.1 m

=

SdT

Sd1

Sd2

+

Sd3

+

Sd4

+

:=

*

SdT

12.6 m

=

26

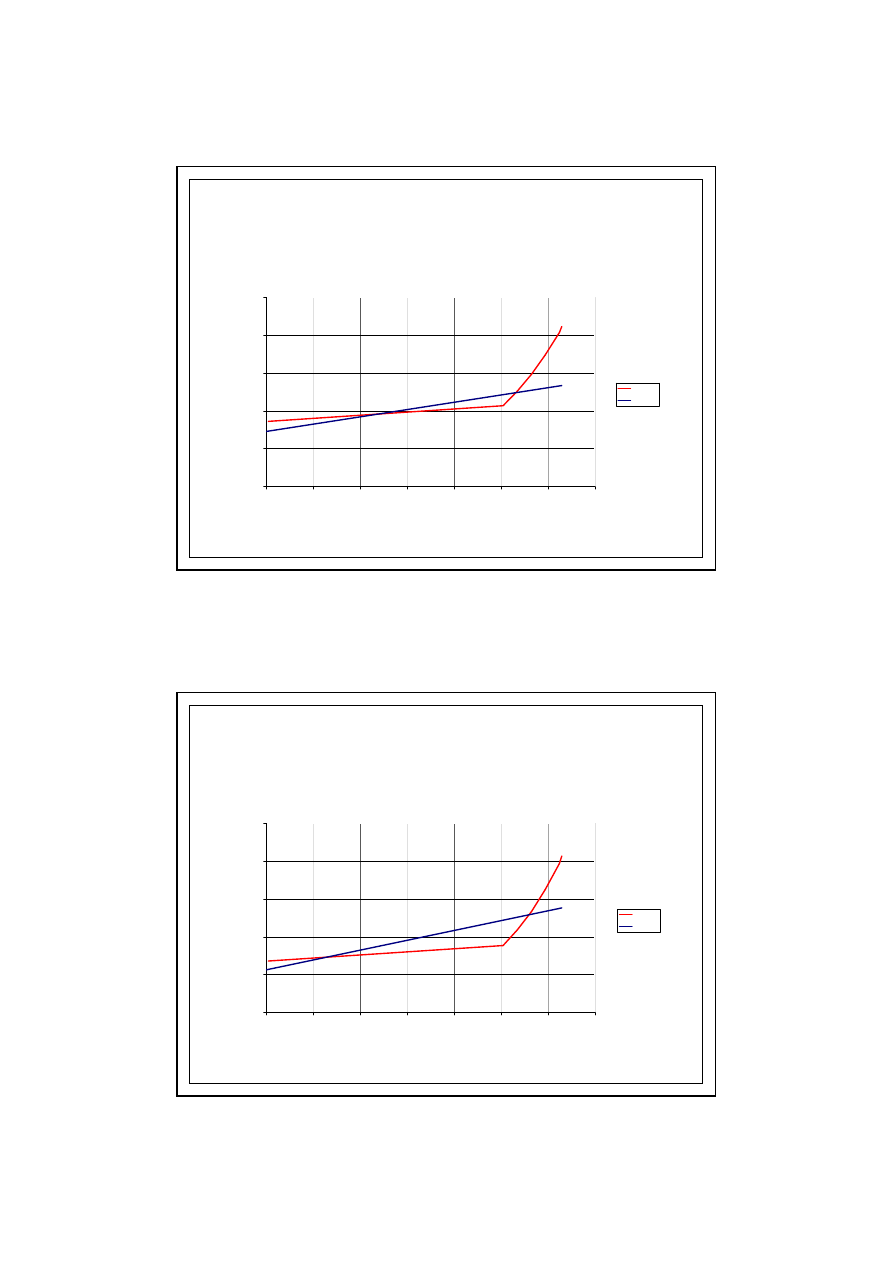
PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Wykres - LISTOPAD

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ść

równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Wykres - GRUDZIEŃ

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ść

równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

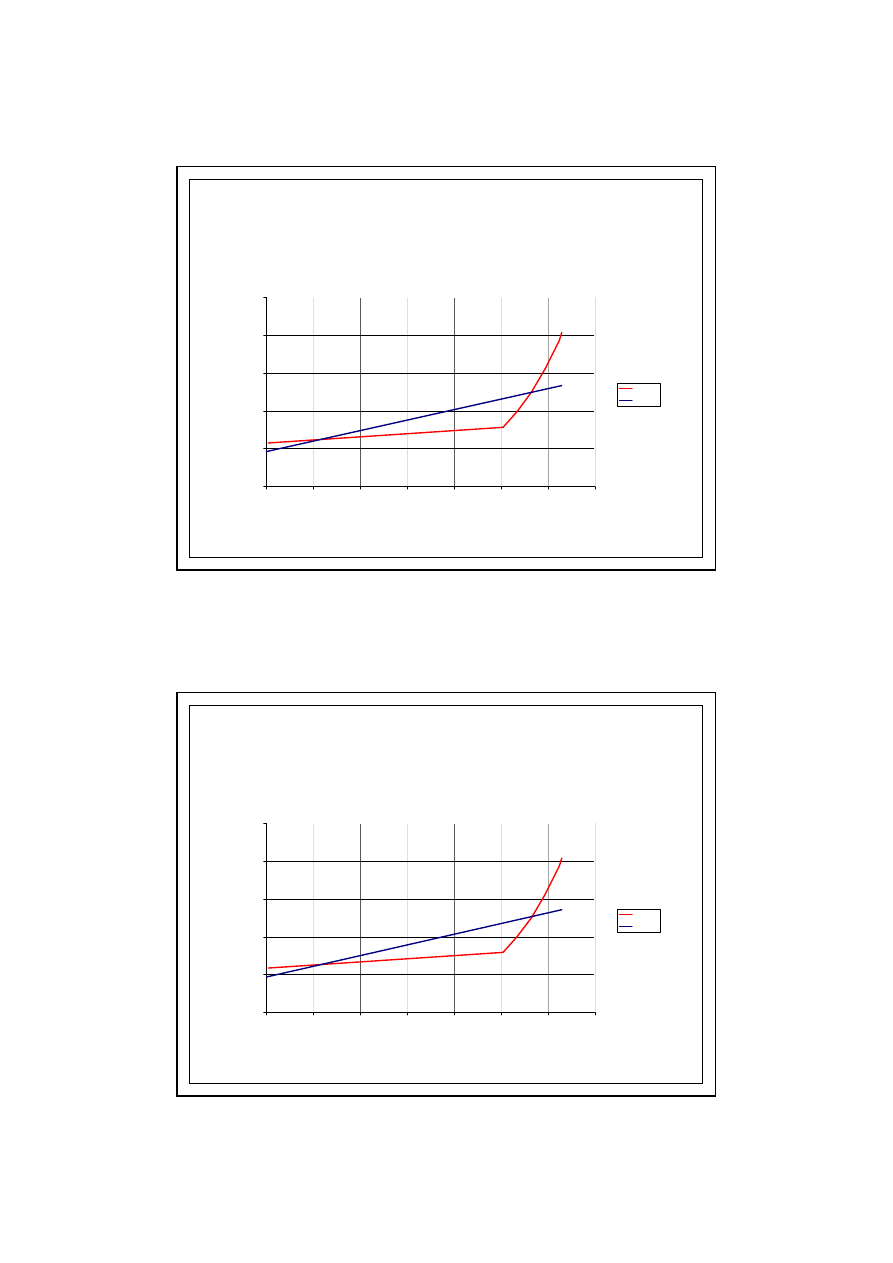
27

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Wykres - STYCZEŃ

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ść

równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Wykres - LUTY

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ść

równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

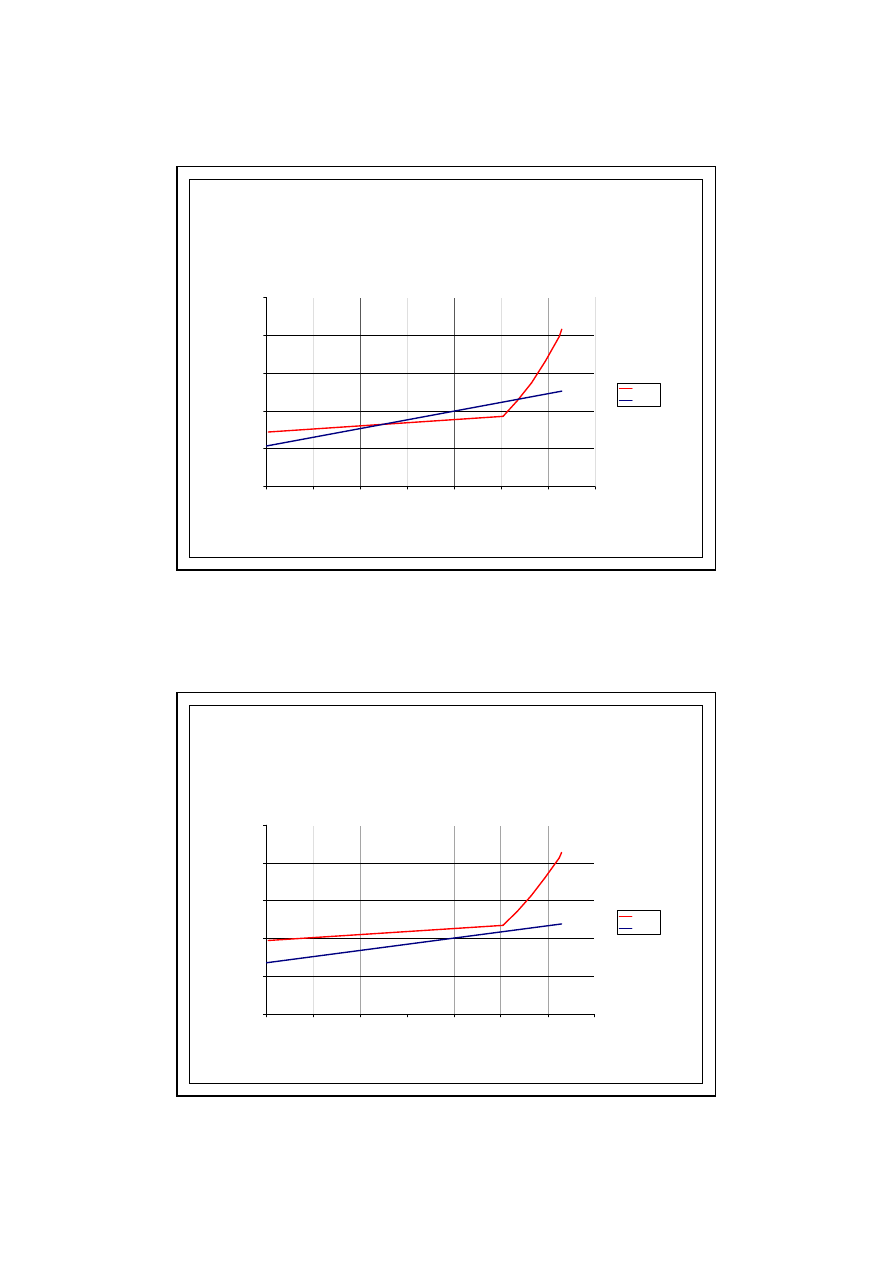
28

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Wykres - MARZEC

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ść

równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Wykres - KWIECIEŃ

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ść

równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

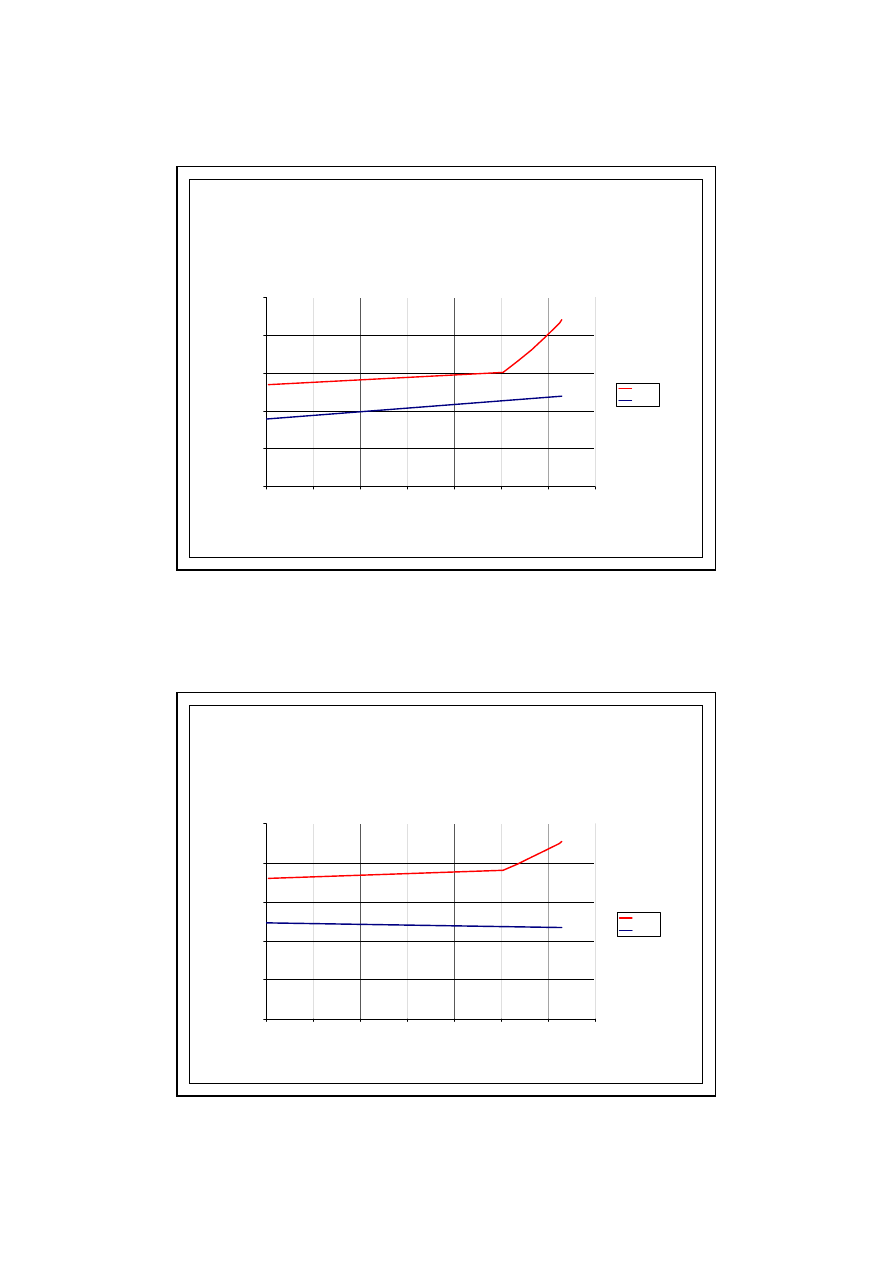
29

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Wykres - MAJ

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ść

równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Wykres - CZERWIEC

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ść

równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

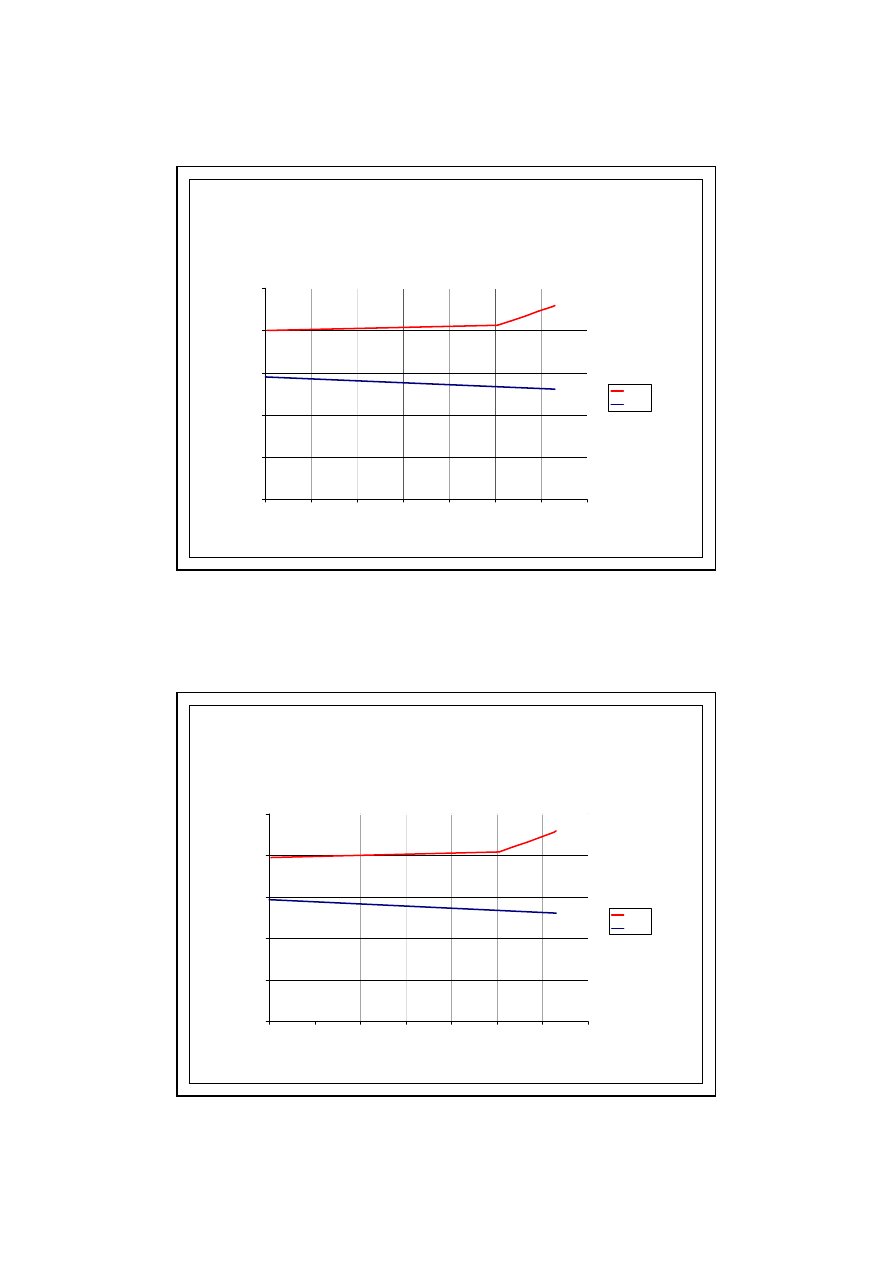
30

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ś

c równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

Wykres - LIPIEC

PRZYKŁAD OBLICZENIOWY

6.0. KONDENSACJA MIĘDZYWARSTWOWA

Wykres - SIERPIEŃ

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ś

c równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

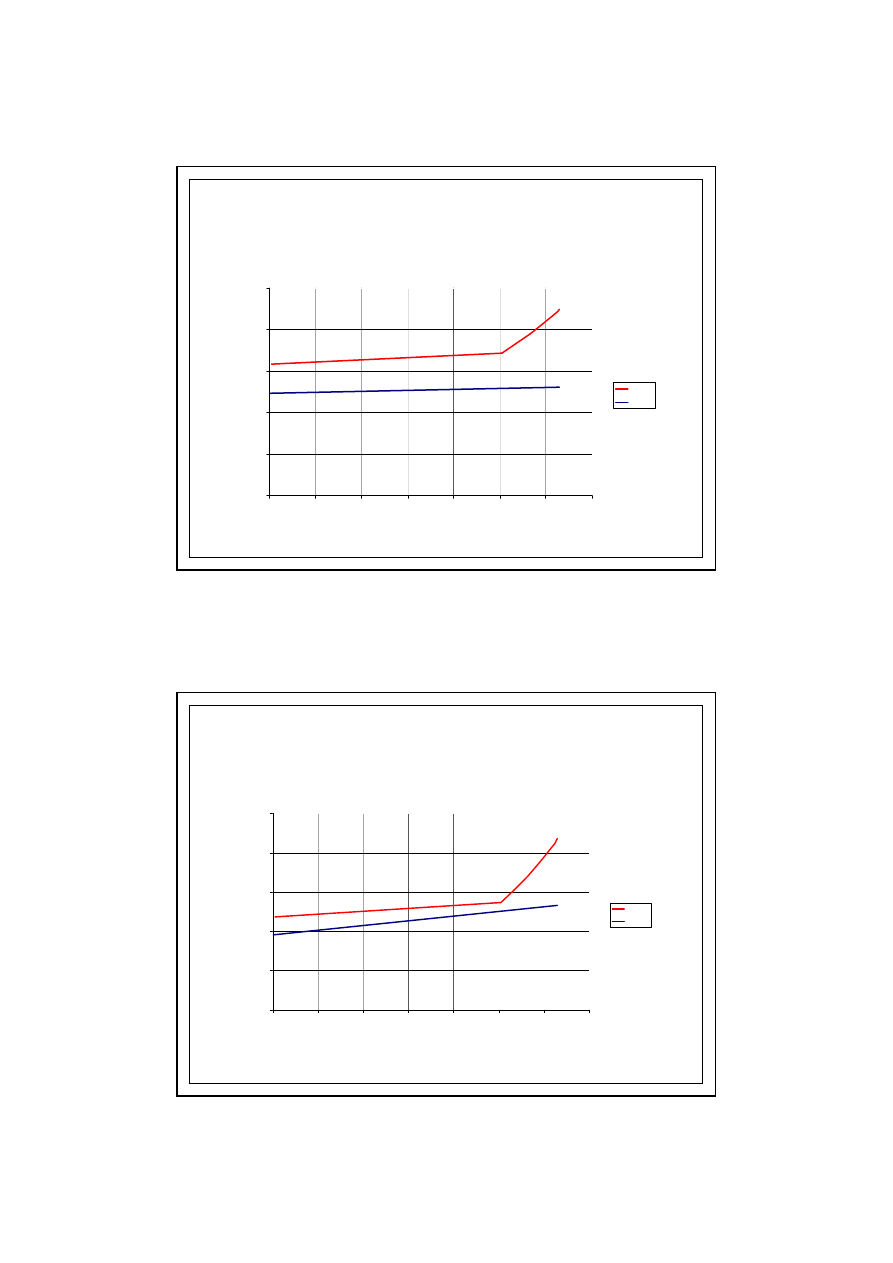
31

PRZYKŁAD OBLICZENIOWY

Wykres - WRZESIEŃ

6.0. KONDENSACJA MIĘDZYWARSTWOWA

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ś

c równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

PRZYKŁAD OBLICZENIOWY

6.0.KONDENSACJA MIĘDZYWARSTWOWA

Wykres - PAŹDZIERNIK

0,0

500,0

1000,0

1500,0

2000,0

2500,0

0

2

4

6

8

10

12

14

grubo

ś

c równowa

ż

na [m]

c

i

ś

n

ie

n

ie

[

P

a

]

psat

przecz

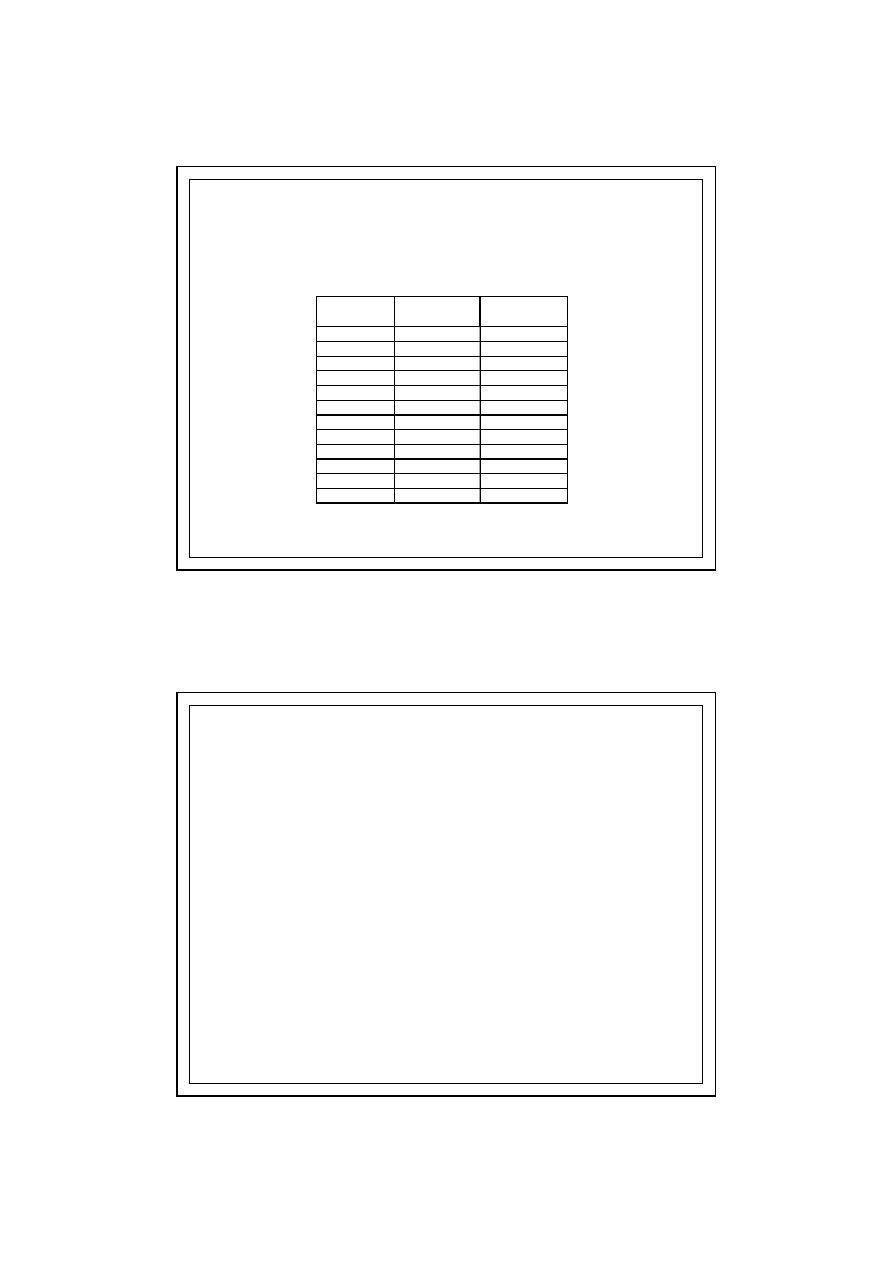
32

PRZYKŁAD OBLICZENIOWY

6.0.KONDENSACJA MIĘDZYWARSTWOWA

ZESTAWIENIE WYNIKÓW

MIESI

Ą

C

gc

Ma

kg/m2

kg/m2

listopad

0,038

0,038

grudzie

ń

0,094

0,132

stycze

ń

0,111

0,243

luty

0,112

0,355

marzec

0,58

0,935

kwiecie

ń

-0,02

0,915

maj

-0,106

0,809

czerwiec

-0,212

0,597

lipiec

-0,225

0,372

sierpie

ń

-0,22

0,152

wrzesie

ń

-0,135

0,017

pa

ź

dziernik

-0,039

0

PRZYKŁAD OBLICZENIOWY - WNIOSKI

6.0.KONDENSACJA MIĘDZYWARSTWOWA

1. W rozważanym przypadku kondensująca się wilgoć
odparowuje w przeciągu roku.

2. Należy wziąć pod uwagę, czy max ilość kondensującej się
wilgoci nie obniży znacząco właściwości termoizolacyjnych
przegrody i nie spowoduje destrukcji materiałów przegrody.

33

DZIĘKUJĘ ZA UWAGĘ !