Po wstępnym dobraniu przekroju
trzonu słupa i sprawdzeniu jego
nośności, następnym elementem
wymagającym obliczeń są przewiązki.

Jest to element postaci płaskownika,
którego podstawowym zadaniem w
konstrukcji jest zapewnienie
współpracy gałęzi słupa. Przewiązki
mają decydujący wpływ na stateczność
gałęzi i słupa jako całości.

W przypadku słupów ściskanych
osiowo – projektuje się przewiązki,
natomiast w przypadku słupów
ściskanych mimośrodowo –
skratowania.

Określenie siły poprzecznej
występującej w pręcie o przekroju
złożonym jest niezbędne do
prawidłowego obliczenia przewiązek i
skratowań.

Teoretyczne wyznaczenie siły
poprzecznej na podstawie całki ogólnej
równania różniczkowego wyboczonej
osi pręta nie jest możliwe, ponieważ
nie znamy przemieszczenia osi tego
pręta.

Dla uproszczenia siłę poprzeczną
określa się z warunku istnienia
losowych mimośrodów. Powstają one
wskutek nieosiowego obciążenia oraz
krzywoliniowości trzonu słupa.

Siła ta występuje dopiero po
wyboczeniu pręta. Oznacza to, że
dopóki słup jest prosty – siła
poprzeczna nie występuje, ale jest ona
jakby w przygotowaniu (konstrukcja
słupa jest zabezpieczona przed
negatywnym działaniem sił
poprzecznych pochodzących od
losowych mimośrodów).

Wstępny mimośród może być
wywołany zakrzywieniem
kształtowników walcowanych (wada
produkcyjna), metodami obróbki oraz
odkształceniami powstającymi przy
łączeniu gałęzi (naprężenia
spawalnicze).

N

N

N

N

N

cr

N

cr

M

Q

x

M

x

M

max

a)

b)

c)

d)

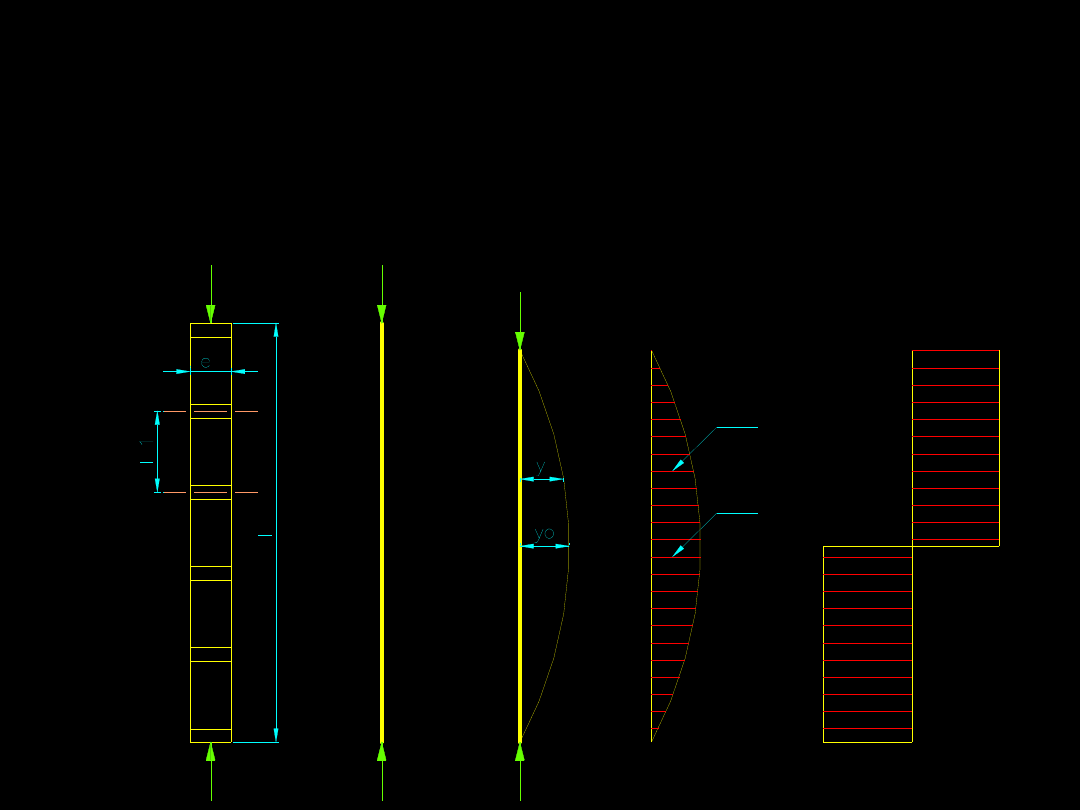
e)

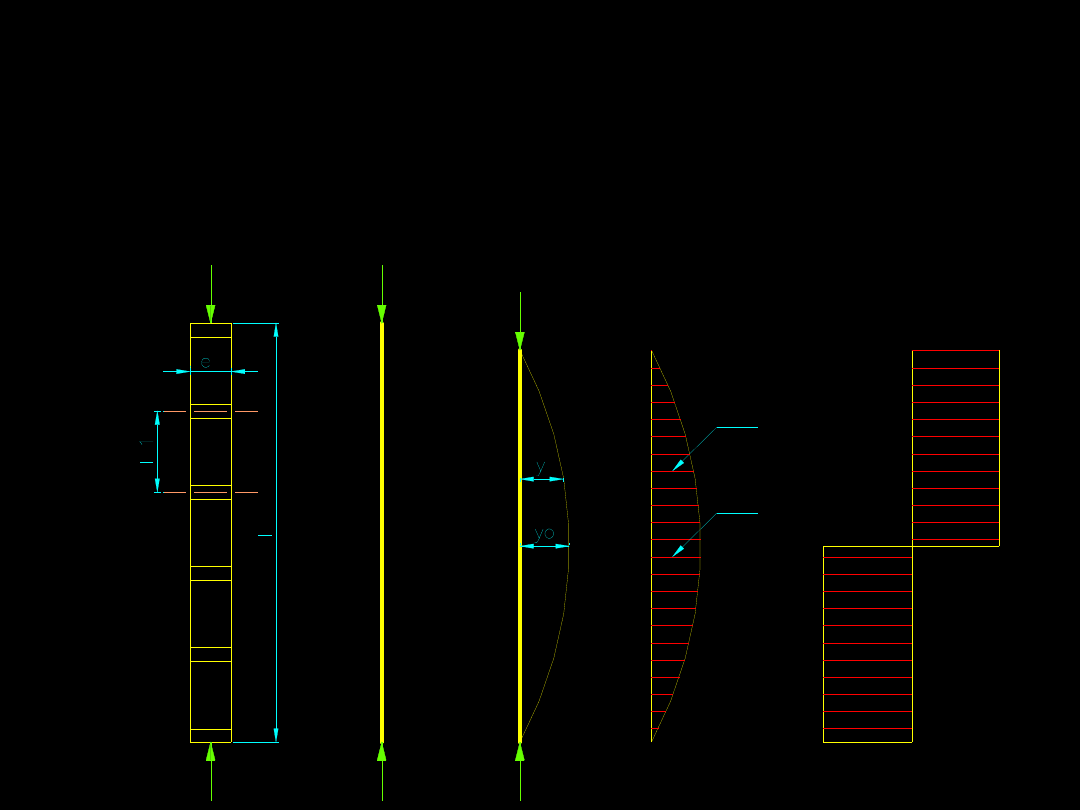
Dopóki siła N działa osiowo (nie ma mimośrodów) – nie
występują siły poprzeczne (rysunek a). Z chwilą
pojawienia się losowych mimośrodów (rysunek b)
następuje przemieszczenie osi pręta (rys c).

N

N

N

N

N

cr

N

cr

M

Q

x

M

x

M

max

a)

b)

c)

d)

e)

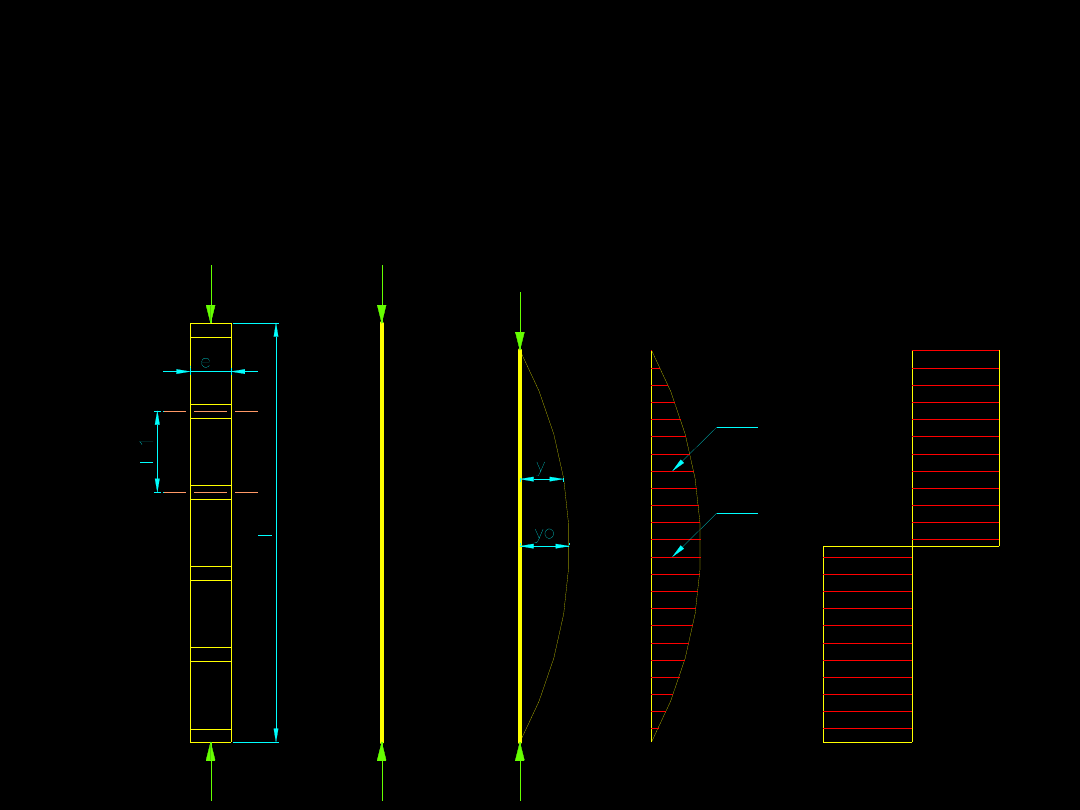
Przemieszczenie osi powoduje z kolei powstanie w
przekroju poprzecznym momentu zginającego (rysunek
d) i siły poprzecznej (rysunek e).

N

N

N

N

N

cr

N

cr

M

Q

x

M

x

M

max

a)

b)

c)

d)

e)

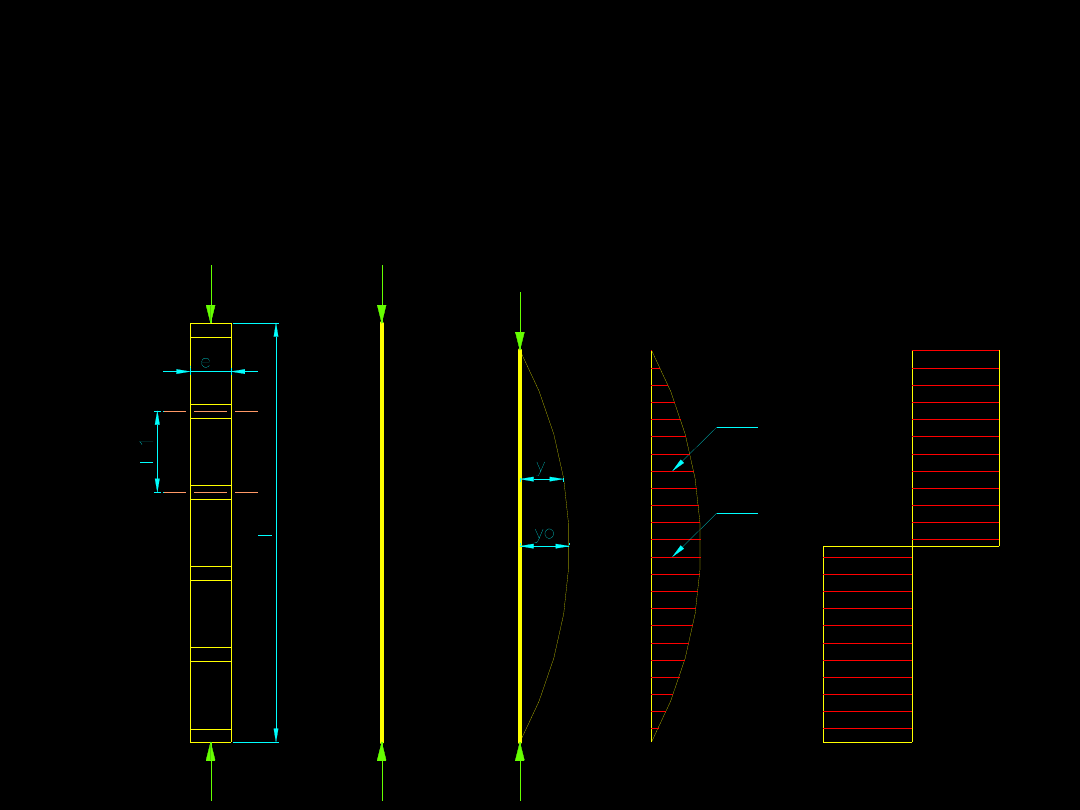
Graniczny mimośród jaki może powstać jest określony
przez graniczny, maksymalny moment, który przejmuje
trzon pręta i który powoduje powstanie w nim naprężeń
równych granicy plastyczności.

Funkcją tego momentu jest tak zwana zastępcza siła
poprzeczna.

N

N

N

N

N

cr

N

cr

M

Q

x

M

x

M

max

a)

b)

c)

d)

e)

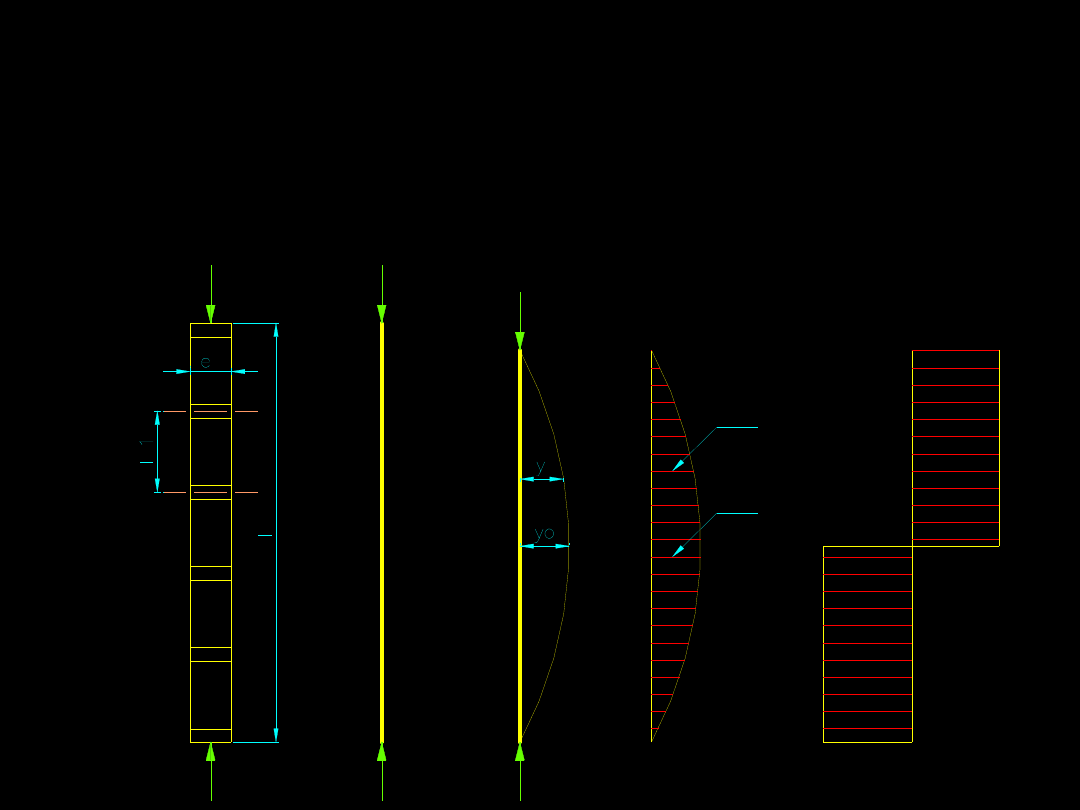
Jej wielkość jest proporcjonalna do strzałki ugięcia pręta
i do siły ściskającej oraz do smukłości i przekroju pręta.

Oblicza się ją przyjmując, że moment zginający M

x

= N ·

y

N

N

N

N

N

cr

N

cr

M

Q

x

M

x

M

max

a)

b)

c)

d)

e)

Jeżeli założymy, że krzywa ugięcia (rysunek c) trzonu
pręta będzie miała kształt cosinusoidy,:

to...



l

y

y

o

x

cos







l

x

y

N

y

N

M

o

x

cos













...po podstawieniu otrzymujemy:

Wiedząc, że siła poprzeczna jest pierwszą
pochodną momentu zginającego
(wytrzymałość materiałów, mechanika
budowli), otrzymujemy:

l

x

l

y

N

dx

dM

Q

o

x

x

















sin

Maksymalna siła poprzeczna wystąpi dla x =
l / 2:

o

y

N

l

Q









max

Z kolei maksymalne naprężenia w przekroju
pręta (w pojedynczej jego gałęzi) mogą
osiągnąć wartość granicy plastyczności:

e

o

cr

cr

R

A

e

y

N

A

N













1

1

max

2



e

o

cr

cr

R

A

e

y

N

A

N













1

1

max

2



naprężenia pochodzące
od krytycznej siły
ściskającej mogąca
wywołać
uplastycznienie stali

(stal może osiągnąć
granicę plastyczności
R

e

);

naprężenia pochodzące
od krytycznej siły
wywołującej moment,
który może
spowodować
uplastycznienie stali

(stal może osiągnąć
granicę plastyczności
R

e

);

Wiedząc, że naprężenia krytyczne to
stosunek siły krytycznej i pola przekroju
trzonu słupa, możemy zapisać:

Podstawiając powyższe równanie do
równania na σ

max

otrzymujemy:

1

2 A

N

A

N

cr

cr

cr









2

1

e

R

y

cr

e

o





















W teorii plastyczności współczynnik
wyboczeniowy określany jest jako stosunek
naprężeń krytycznych do granicy
plastyczności stali:

I ostatecznie wzór na y

o

wygląda następująco:

e

cr

R







2

1

1

e

y

o





















Podstawiając y

o

do wzoru na Q

max

otrzymujemy:

2

1

1

e

y

o





















o

y

N

l

Q









max























1

1

2

max





N

e

l

Q

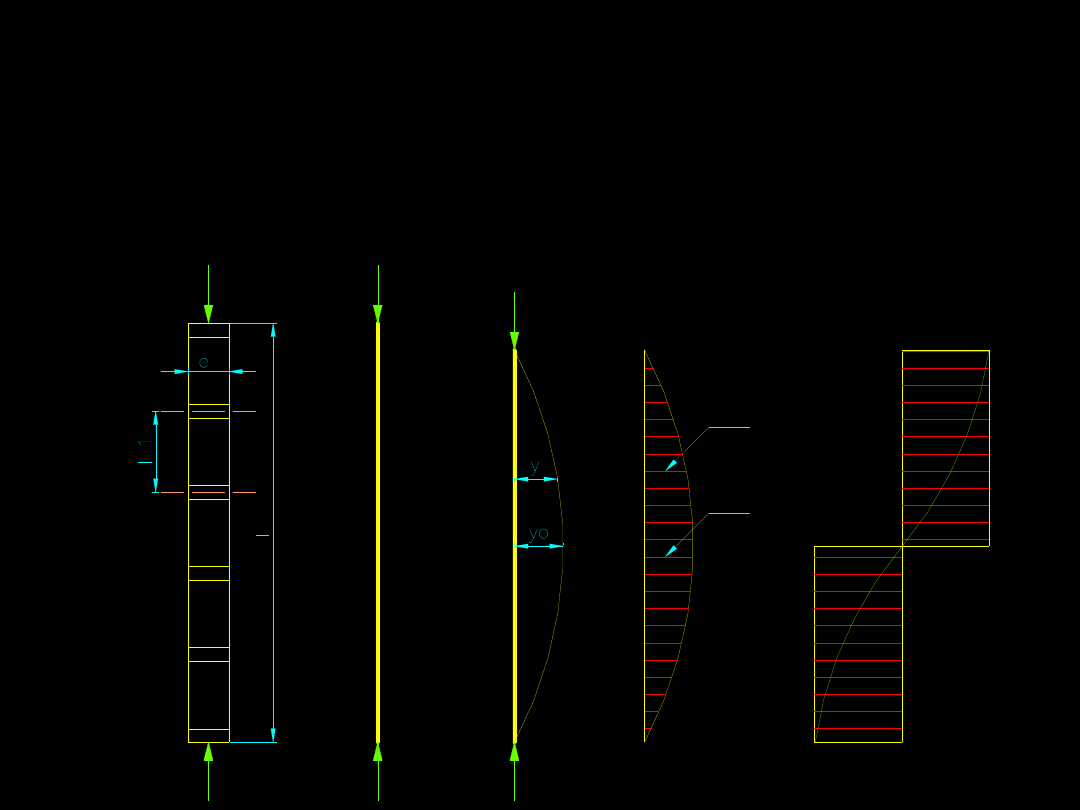
Wynika z tego, że siła poprzeczna wzdłuż osi pręta ma
charakter zmienny (zbliżony do sinusoidy  rysunek

e), ale w celu uproszczenia obliczeń przyjmuje się
stałą wartość tej siły równą Q

max.

N

N

N

N

N

cr

N

cr

M

Q

x

M

x

M

max

a)

b)

c)

d)

e)

W przepisach różnych krajów występują
różnice we wzorze na siłę poprzeczną.

Norma do obliczania i projektowania
konstrukcji metalowych PN90/B-03200
zakłada, że siła poprzeczna na całej długości
słupa jest stała i przyjmuje się ją w zależności
od obciążenia.

Jeżeli konstrukcja jest obciążona tylko osiowo
siłą N, wówczas:

Q ≥ 0,012 ·A ·f

d

A – pole przekroju poprzecznego pręta;

Jeżeli obok siły osiowej N działa również
odciążenie zewnętrzne wywołujące siłę
poprzeczną V (o wartości maksymalnej),
wówczas zastępczą siłę poprzeczną
obliczamy:

Q = 1,2·V ale nie miej niż Q ≥ 0,012 ·A ·f

d

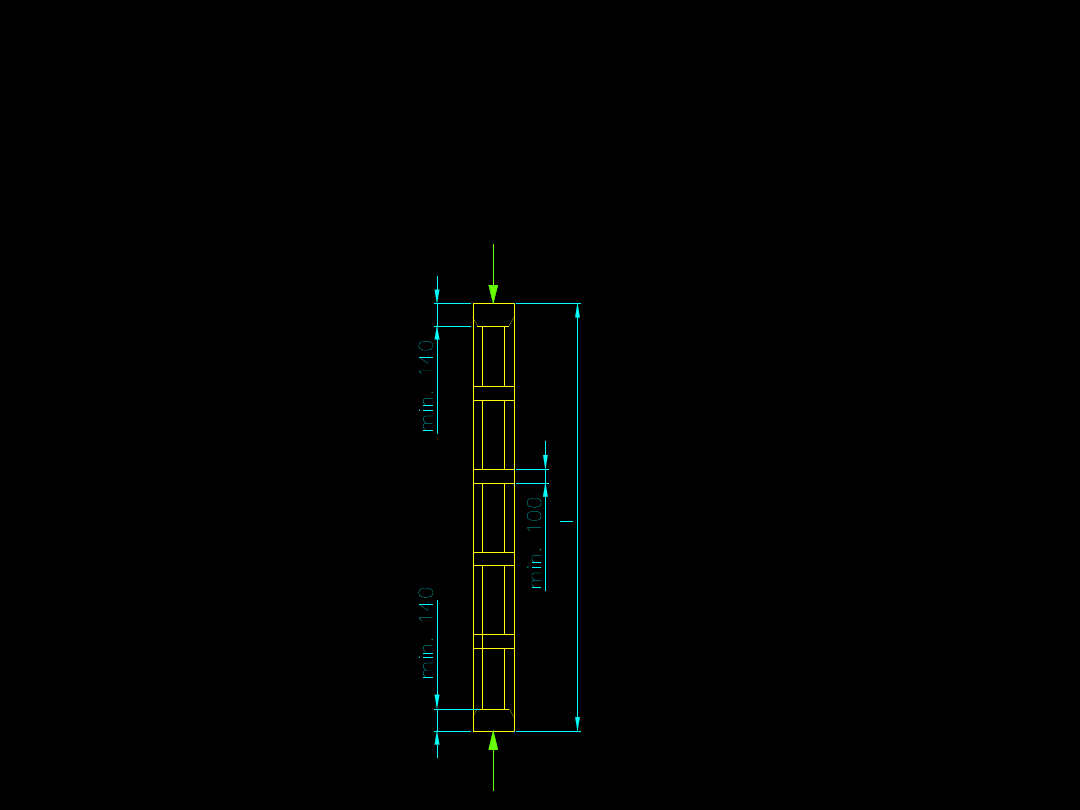
Ogólne wytyczne do projektowania przewiązek.

1. Przewiązki skrajne powinny mieć wysokość nie

mniejszą niż 140 mm (i nie mniej niż 150%
szerokości przewiązek pośrednich);

N

N

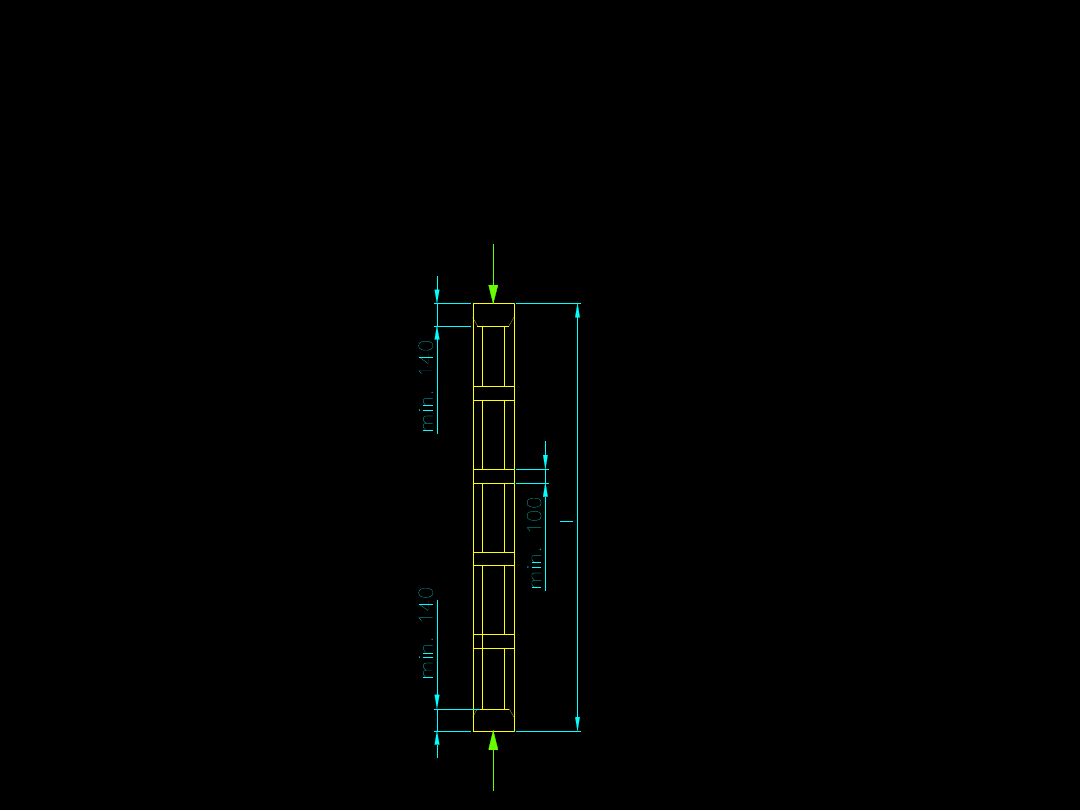
Ogólne wytyczne do projektowania

przewiązek.

2. Przewiązki pośrednie powinny mieć

wysokość nie mniejszą niż 100 mm.

N

N

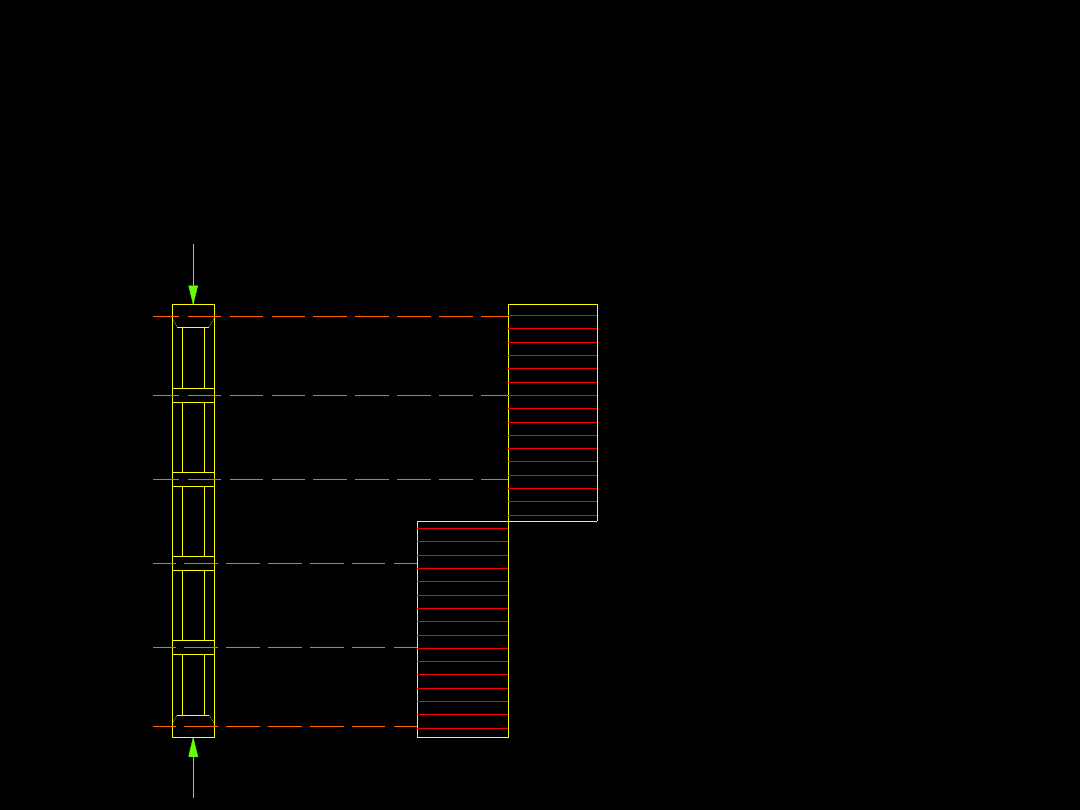
Ogólne wytyczne do projektowania

przewiązek.

3. Ilość przewiązek musi być parzysta.

N

N

Q

x

Przy parzystej

liczbie przwiązek,

każda pracuje na

siłę poprzeczną w

słupie Q

x

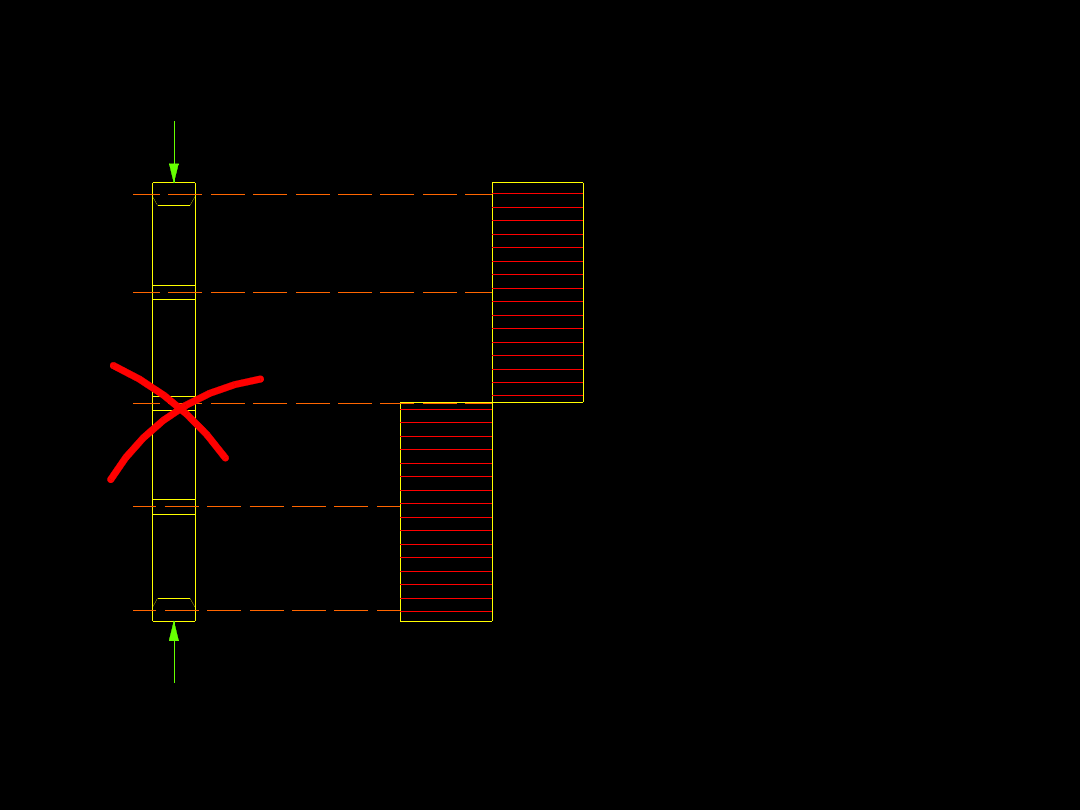
N

N

Q

x

Przy nieparzystej

liczbie przwiązek,

przewiązka środkowa

nie pracuje na żadną

siłę i jest niepotrzebna.

Ogólne wytyczne do projektowania

przewiązek.

3. Osiowy rozstaw przewiązek nie jest

ograniczony, ale ograniczona jest smukłość
pojedynczej gałęzi – powinna być mniejsza
od smukłości całego pręta.

Jak podaje prof. Żółtowski w książce
„Konstrukcje metalowe – cześć I” –
doświadczenia projektowe wykazały, że
smukłość pojedynczej gałęzi λ

1

powinna

spełniać warunek:

y





8

,

0

1



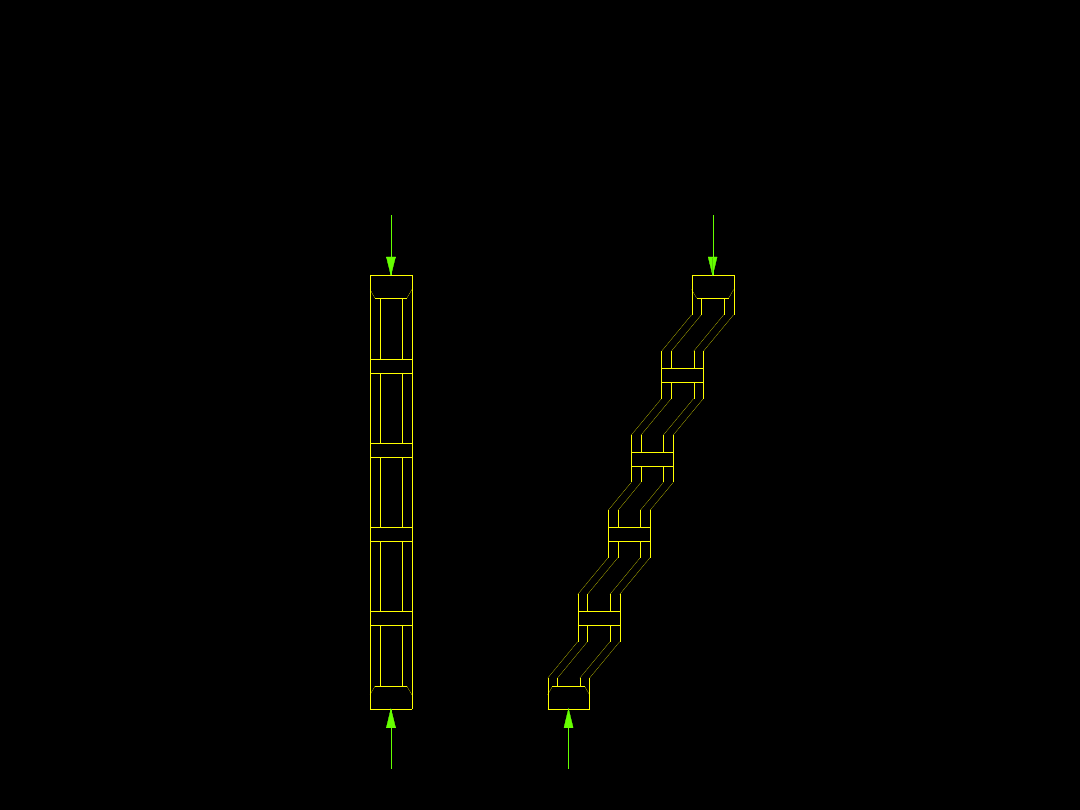
W przypadku niezachowania istnieje ryzyko
wyboczenia słupa w takiej formie:

N

N

N

N

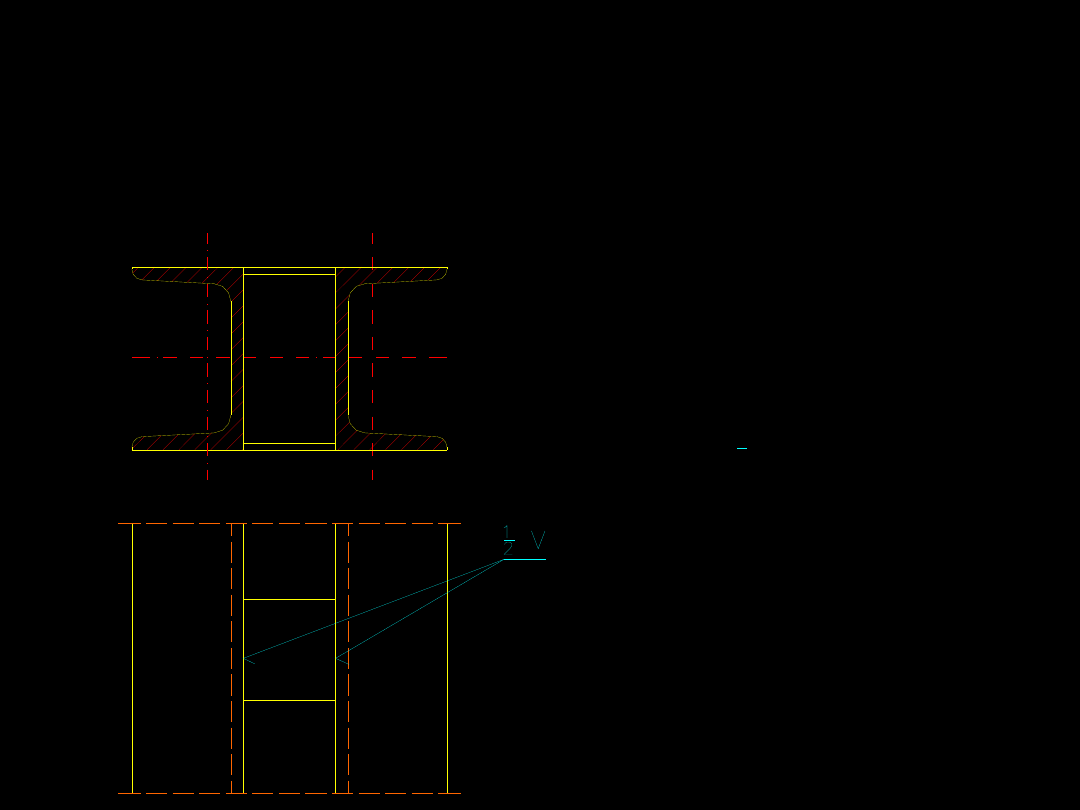
Rozwiązania konstrukcyjne przewiązek w
słupie o przekroju złożonym są następujące:

Przewiązka znajduje się

w płaszczyźnie półek gałęzi

słupa i jest przymocowana
spoiną czołową

1

2

V

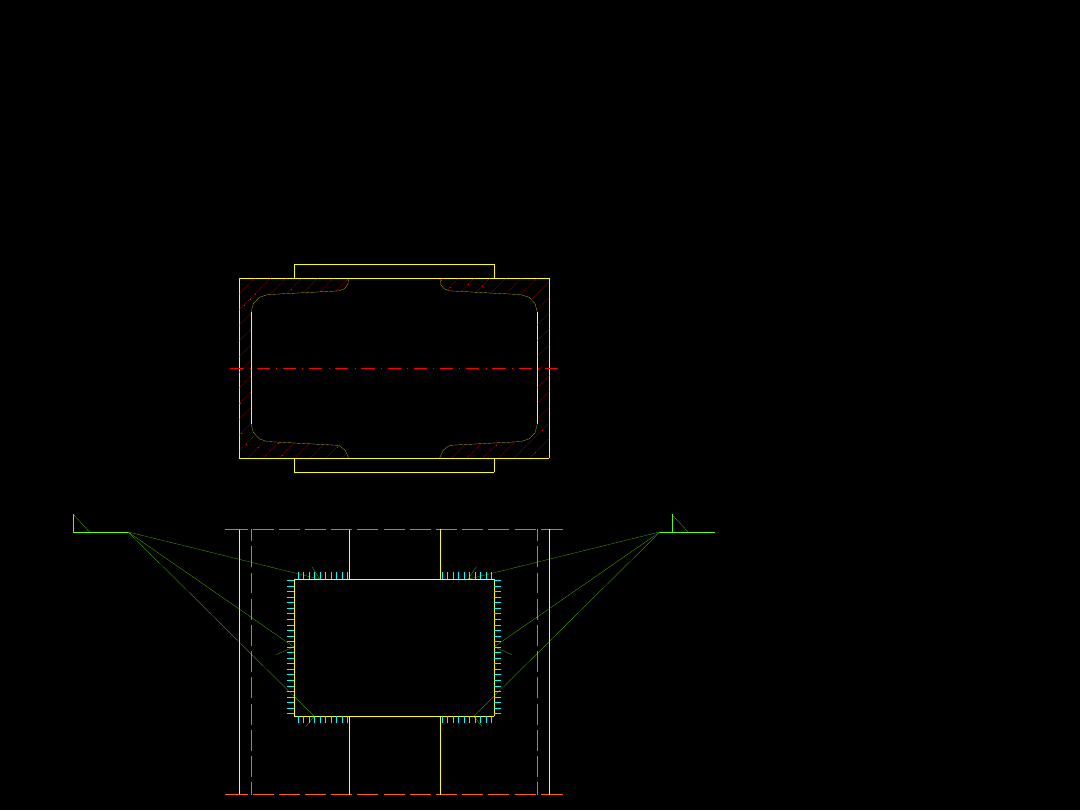
Rozwiązania konstrukcyjne przewiązek w
słupie o przekroju złożonym są następujące:

Przewiązka

wykonana z

płaskownika w

sposób
nakładkowy.
Przywierdzona jest

do gałęzi słupa

spoinami

pachwinowymi.

a

a

Rozwiązania konstrukcyjne przewiązek w
słupie o przekroju złożonym są następujące:

Przewiązki można mocować do gałęzi słupa także za

pomocą łączników punktowych (śruby, nity), ale to

rozwiązanie jest stosowane rzadko z powodu większej

pracochłonności wykonania niż w przypadku spawania.

Wymiarowanie przewiązki należy
rozpocząć od obliczenia sił
przekrojowych w przewiązce.

Obliczenie siły ścinającej T w
przewiązce przeprowadza się przy
następujących założeniach:

-siła poprzeczna Q jest stała w
rozpatrywanym przedziale słupa;

-przewiązka jest nieskończenie
sztywna;

-przemieszczenie gałęzi ma postać
antysymetryczną;

Przy takich założeniach możemy przystąpić
do

obliczania sił przekrojowych w

przewiązce.

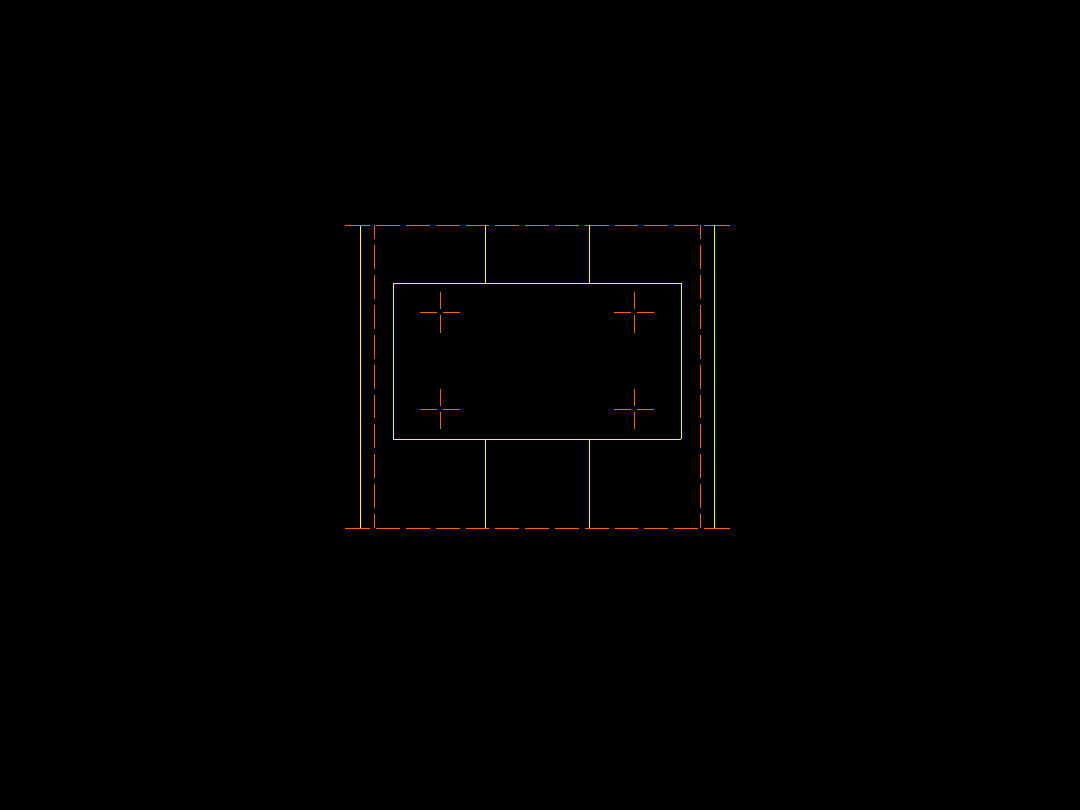
Słup z przewiązkami oblicza się jak belkę
bezprzekątnikową (belkę Vierendeela).

Przyjmuje się w przybliżeniu, że w gałęziach
w środku odstępu między przewiązkami l

1

/

2 oraz w środku przewiązki (w osi słupa)
znajdują się przeguby. W każdym z
przegubów dwóch gałęzi zaczepia się siłę
Q / 2. W przegubach przewiązek z kolei
zaczepia się siłę T.

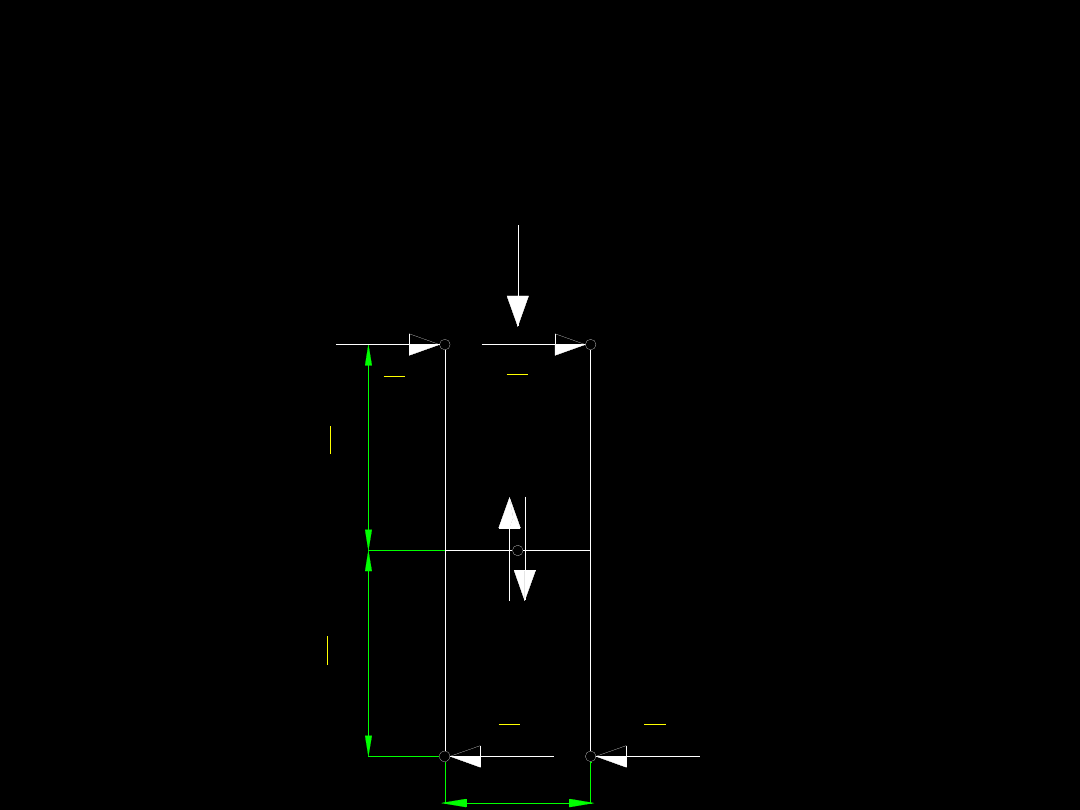
Wygląda to następująco:

e

T

T

N

Q

2

Q

2

Q

2

Q

2

l

1

2

l

1

2

Rama Vierendeela.

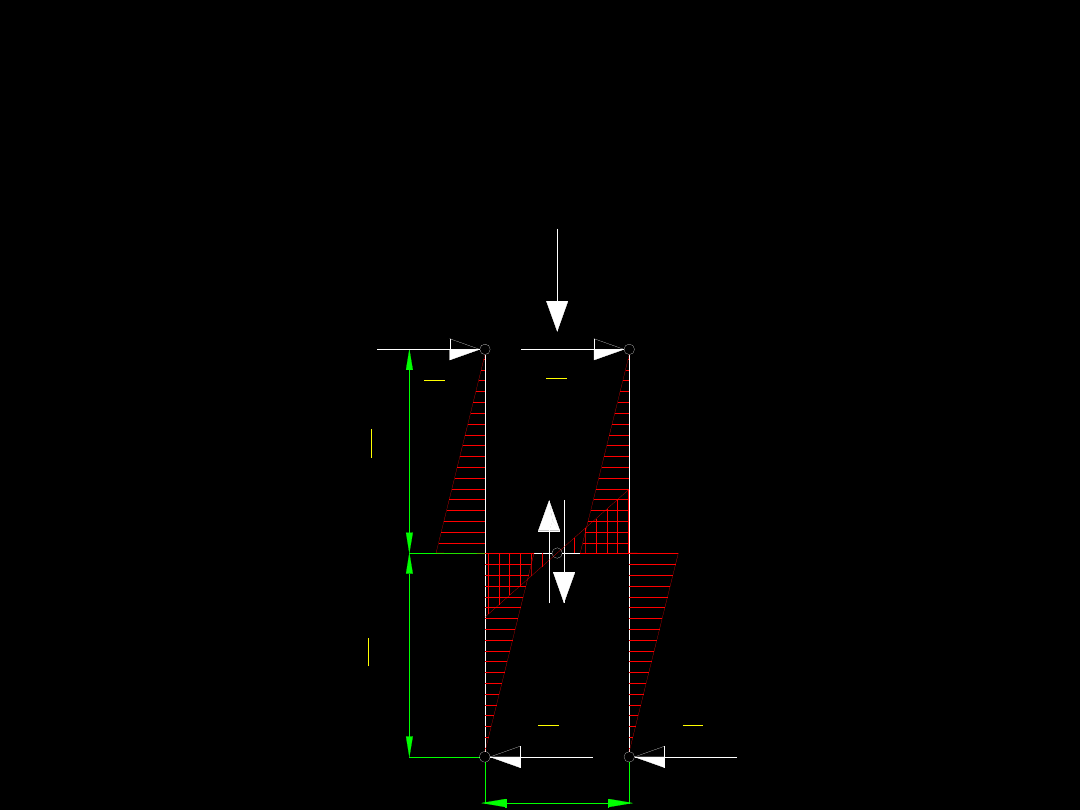
Mając siły możemy naszkicować wykres sił
poprzecznych w rozpatrywanym ustroju...

e

T

T

N

Q

2

Q

2

Q

2

Q

2

l

1

2

l

1

2

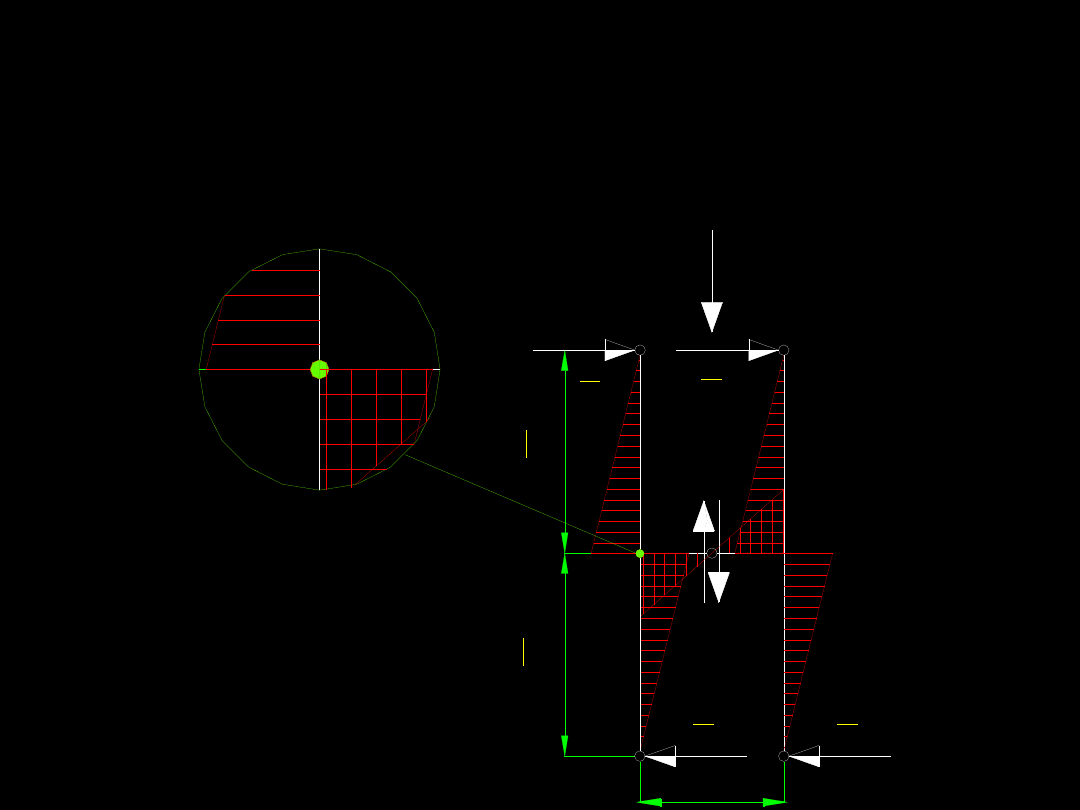
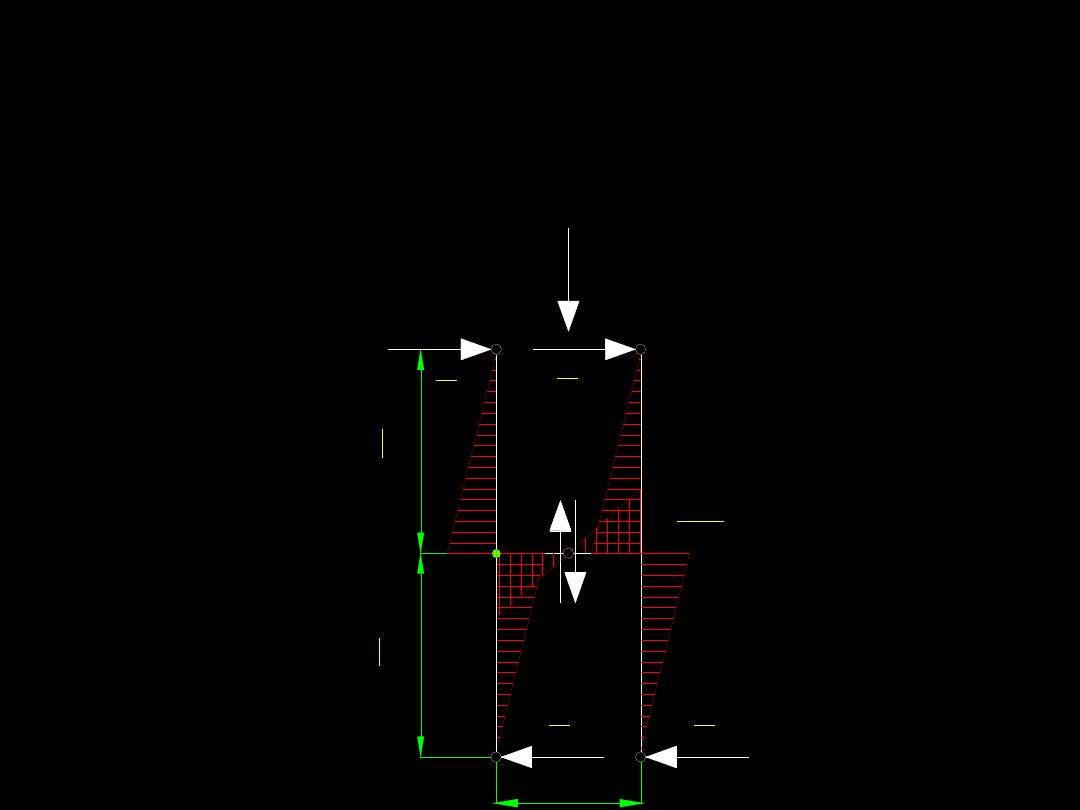
Aby obliczyć siły wewnętrzne w przewiązce
przyjmujemy punkt A i układamy względem
tego punktu równanie równowagi momentów
zaczepionych sił.

e

T

T

N

Q

2

Q

2

Q

2

Q

2

l

1

2

l

1

2

A

A

e

T

T

N

Q

2

Q

2

Q

2

Q

2

l

1

2

l

1

2

A

4

Q l

1

0

2

2

2

2

2

0

1

1





















n

e

T

l

Q

l

Q

M

A

e

l

n

Q

1

T





Po przekształceniu otrzymujemy wzór na siłę
poprzeczną w przewiązce.

Q – siła poprzeczna w trzonie słupa (Q ≥
0,012 ·A ·f

d

);

l

1

– rozstaw przewiązek;

e – osiowy odstęp gałęzi słupa;

n – liczba płaszczyzn przewiązek przeciętych
osią y-y

Skoro występuje w przekroju przewiązki siła
poprzeczna – występuje także moment,
zwany również momentem zamocowania.

z – odległość między środkami ciężkości
spoin lub nitów łączących przewiązki słupa.

2

z

T

M





Norma PN90/B-03200 w punkcie 4.7.3.
podaje następujące wzory na siłę poprzeczną i
moment w przewiązkach:

a

m

n

l

Q

V

Q











)

1

(

1

n

m

l

Q

M

Q







1

gdzie:

Q – siła poprzeczna w trzonie słupa (Q ≥
0,012 ·A ·f

d

);

l

1

– rozstaw przewiązek;

a – osiowy odstęp gałęzi słupa;

n – liczba płaszczyzn przewiązek;

m – ilość gałęzi trzonu słupa;

Obliczanie przewiązek rozpoczyna się
od wstępnego przyjęcia wymiarów.

Zgodnie z tym co mówi norma,
wysokość przewiązek pośrednich
powinna mieć minimum 100 mm,
natomiast skrajne minimum 140 mm
(czasem można w literaturze spotkać
150 mm).

Grubość przewiązek przyjmuje się z
reguły
6 - 12 mm lub też w granicach od 1/10
– 1/25 długości przewiązki.

Długość przewiązki powinno się
dobierać w granicach 0,5 – 0,75
szerokości trzonu słupa.

Odstępy pomiędzy przewiązkami
powinny być równe lub prawie równe.

Ilość przewiązek – parzysta – ilość
odstępów pomiędzy przewiązkami –
nieparzysta!!!

Obliczamy zastępczą siłę poprzeczną
wg wzoru:

Q ≥ 0,012 ·A ·f

d

A – pole przekroju poprzecznego pręta;

f

d

– wytrzymałość stali na ściskanie [MPa];

42

Znając zastępczą siłę poprzeczną
obliczamy siły i momenty działające na
przewiązki według wcześniej podanych
wzorów.

a

m

n

l

Q

V

Q











)

1

(

1

n

m

l

Q

M

Q







1

gdzie:

Q – siła poprzeczna w trzonie słupa (Q ≥ 0,012 ·A
·f

d

);

l

1

– rozstaw przewiązek (przyjęty podczas

sprawdzania nośności trzonu);

a – osiowy odstęp gałęzi słupa;

n – liczba płaszczyzn przewiązek;

m – ilość gałęzi trzonu słupa;

Następny krokiem jest sprawdzenie
klasy przekroju.

Sprawdzenie wykonujemy dla zginania
i ścinania, ponieważ na takie siły
pracuje przewiązka.

Klasa przekroju przewiązki ze względu
na zginanie:









...

....

w

w

t

b

Klasa .......



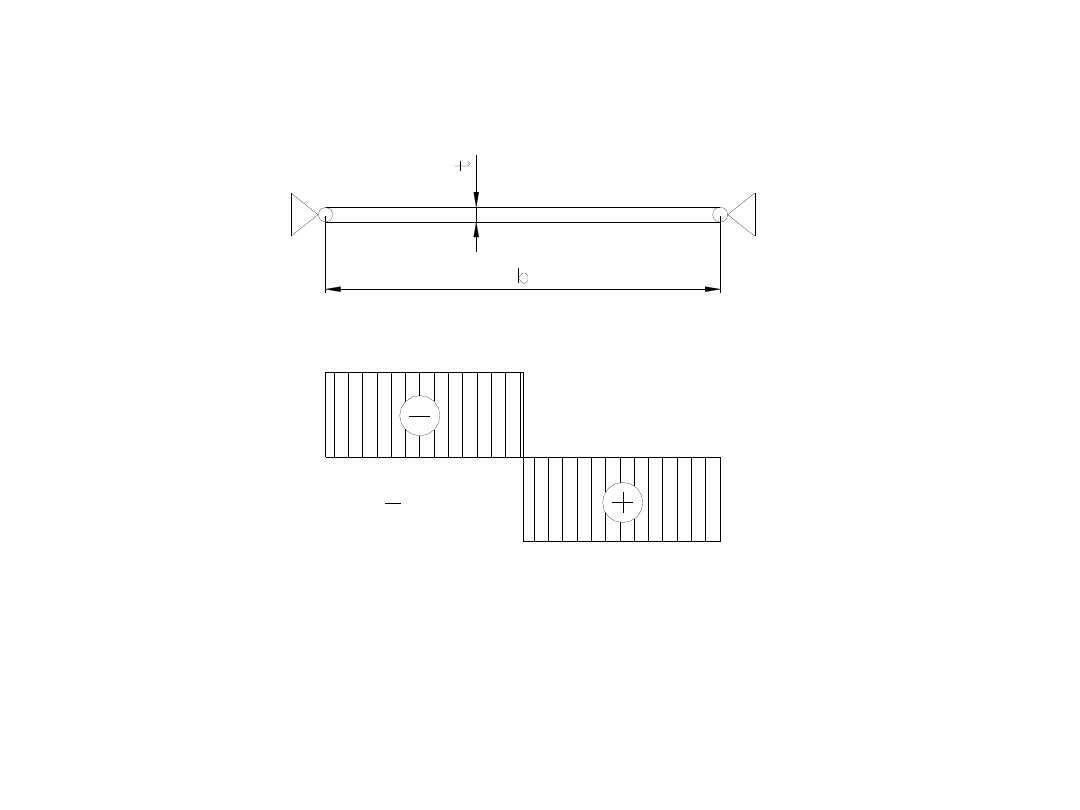
1

2

Przyjmujemy następujący charakter
podparcia i wykres momentów:

Graniczne wartości smukłości podaje
tabela 6 PN90/B-03200

Ponieważ nasza przewiązka jest także
ścinana – należy sprawdzić, czy jest
ona odporna na miejscową utratę
stateczności przy czystym ścinaniu.

Wykonuje się to poprzez sprawdzenie
smukłości przy ścinaniu. Jednocześnie
tabela 7 podaje pole przekroju
czynnego przy ścinaniu.

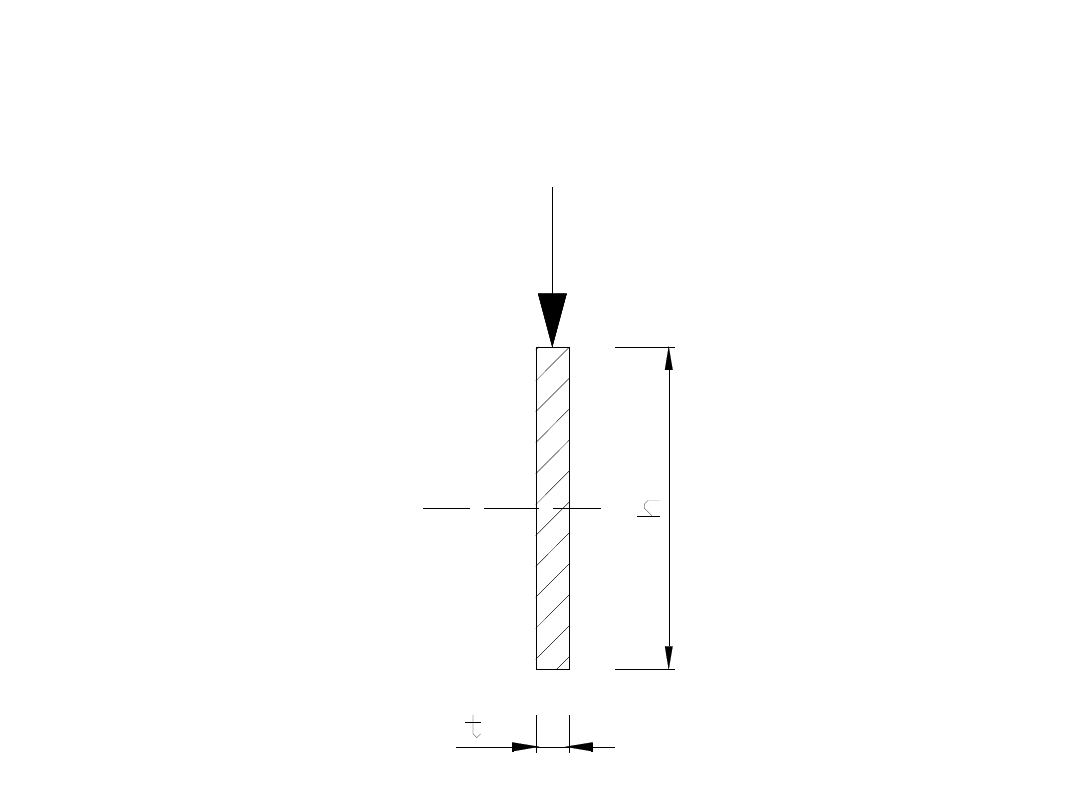
Dla przewiązki, która jest
płaskownikiem pole przekroju
czynnego przy ścinaniu wg tab.7 PN
wynosi A

ν

= 0,9·h·t, gdzie h i t to...



V

i

i

...wymiary jak na rysunku (h –
wysokość przewiązki; t – grubość
przewiązki)









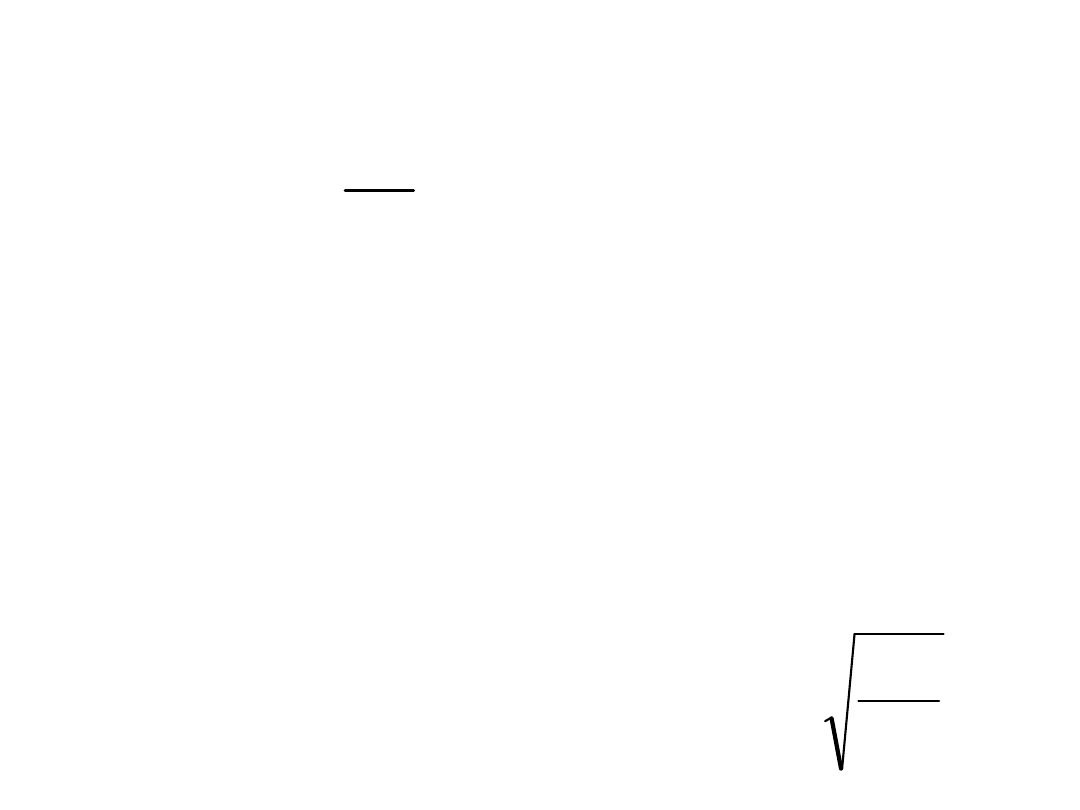
15

....

t

h

Smukłość przewiązki dla ścinania:

Jeżeli powyższy warunek jest
spełniony – wówczas możemy
uznać, że element jest
zabezpieczony przez miejscową
utratą stateczności. Przy czym ε –
wskaźnik smukłości według
wzoru:

d

f

215





W przypadku nie spełnienia
poprzedniej nierówności (obliczona
smukłość jest większa od granicznej
podanej w tabeli 7), wówczas przekrój
przewiązki kwalifikuje się do klasy 4
pod względem ścinania i jest on
podatny na miejscową utratę
stateczności.

Będzie to miało wpływ przy dalszych
obliczeniach dotyczących obliczeniowej
nośności przekroju ze względu na
ścinanie.

Sprawdzenie nośności przewiązki ze
względu na moment oraz na siłę
poprzeczną.

- jeżeli przekrój przewiązki został
zakwalifikowany pod względem
zginania do klasy I lub II, wówczas
nośność obliczeniową obliczmy:

d

p

R

f

W

M









α

p

– obliczeniowy współczynnik rezerwy plastyczności,

wg załącznika 4 – rozdział 2 PN

α

p

>1 - tylko dla przekrojów obciążonych statycznie i

zginanych w płaszczyźnie symetrii przekroju; w
pozostałych przypadkach należy przyjmować α

p

= 1;

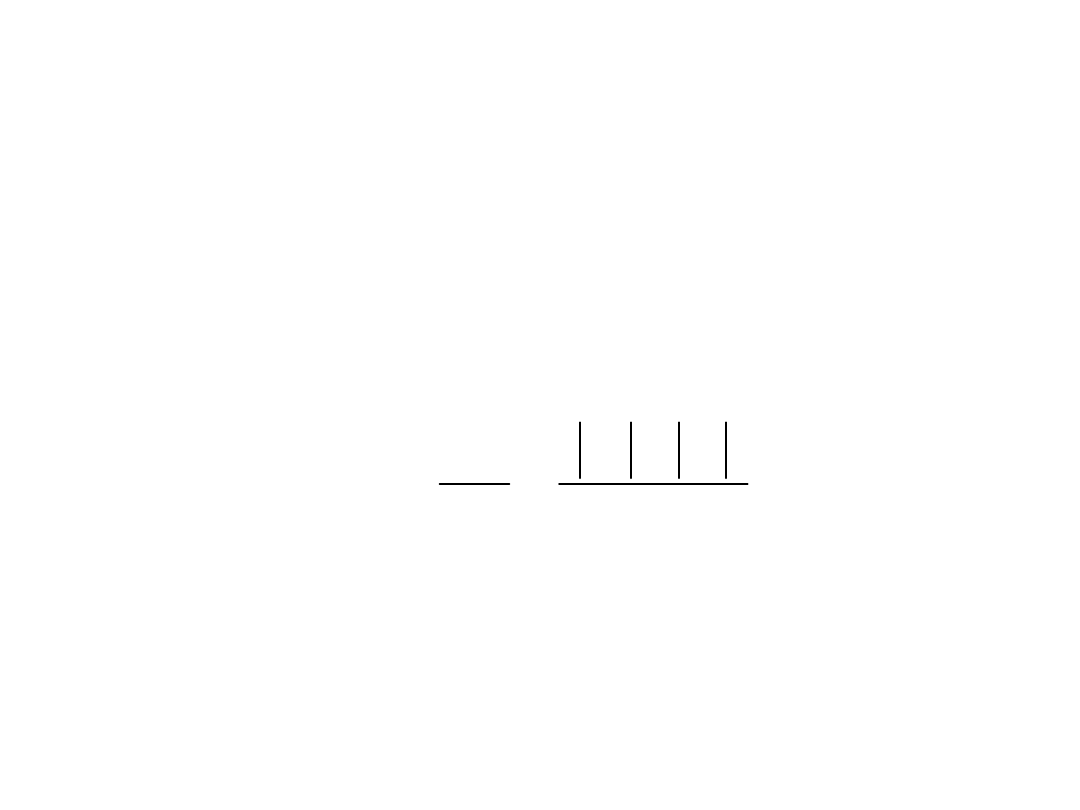
W naszym przypadku norma zezwala
na α

p

>1 (nasz przekrój jest obciążony

statycznie i zginany w płaszczyźnie
symetrii przekroju).

Obliczenie α

p

wg załącznika

polega na

obliczeniu współczynnika rezerwy
plastycznej przekroju przy zginaniu
wg wzoru:

W

S

S

W

W

t

c

pl

pl

)

(









α

pl

– współczynnik rezerwy plastycznej przekroju przy

zginaniu;

W

pl

– wskaźnik oporu plastycznego przy zginaniu,

równy sumie bezwzględnej wartości mom. statycznych
ściskanej (A

c

) i rozciąganej (A

t

) strefy przekroju

względem osi obojętnej

Zakłada się, że :

A

c

= A

t

=0,5A

W naszym przypadku przyjmujemy
także, że zasięg strefy ściskanej jest
równy zasięgowi strefy rozciąganej.

S

c

=S

t

=S

W

S

W

W

pl

pl

)

2

( 







Dla przypomnienia:

MOMENT STATYCZNY, WYRAŻANY W
[cm

3

] lub w [m

3

] TO ILOCZYN

ROZPATRYWANEGO POLA PRZEKROJU I
ODLEGŁOŚCI JEGO ŚRODKA CIĘŻKOŚCI
OD OSI OBOJĘTNEJ CAŁEGO
PRZEKROJU.

S = A·a

[cm

3

]

A – pole przekroju;
a – odległość środka ciężkości rozpatrywanej
strefy od osi

Mając obliczony współczynnik rezerwy
plastycznej α

pl

przekroju możemy

przystąpić do wyznaczenia
obliczeniowego współczynnika rezerwy
plastyczności określonego wzorem:

Mając wszystkie dane – wyznaczamy
nośność obliczeniową przekroju ze
względu na ścinanie.

)

1

(

2

1

pl

p











-w przypadku, gdy nasz przekrój jest
klasy 3 lub 4:

-ψ – współczynnik redukcyjny (dla
klasy 3 ψ=1), dla klasy 4 (ψ<1  wg

pkt 4.2.2.3 PN ψ=φ

p

).

-W

c

– wskaźnik wytrzymałości strefy

ściskanej;

d

c

R

f

W

M









Współczynnik redukcyjny ψ ustala się
według punktu 4.2.2.3 PN, który
pozwala nam przyjąć w stanie
krytycznym:

ψ=φ

p

Współczynnik niestateczności φ

p

należy

przyjmować w

zależności od smukłości

względnej

.



p



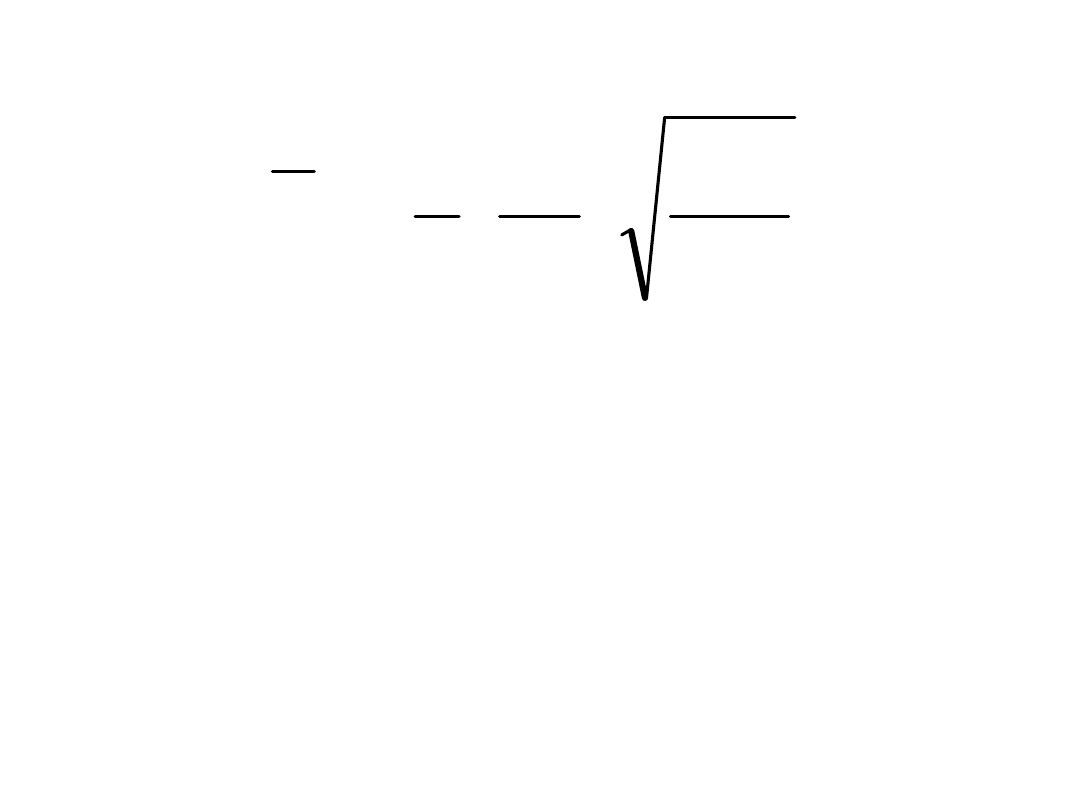
215

56

d

p

f

K

t

b









Smukłość względną ścianki przewiązki
dla zginania:

b, t – odpowiednio szerokość i grubość
ścianki przewiązki (wg tabeli 6 PN);

K – współczynnik podparcia i
obciążenia ścianki wg tabeli 8 PN;

W naszym przypadku ν = 0, ponieważ:

σ

g

= -σ

d

β – stosunek długości przewiązki do
wysokości;

g

d

g















2

Po obliczeniu współczynnika podparcia
i obciążenia K, obliczamy smukłość
względną w stanie krytycznym i
przyjmujemy współczynnik
niestateczności φ

p

.

Przyjmujemy ψ= φ

p

i obliczamy M

R

;

p



Następnym krokiem podczas
sprawdzania nośności przewiązki jest
konieczność ustalenia, czy występująca
siła poprzeczna Q (V) w przewiązce
wpływa na redukcję M

R,V

.

W tym celu musimy policzyć nośność
obliczeniową przy ścinaniu V

R

.

Jeżeli nasz przekrój spełnia warunek
określony w tablicy 7 (ścianka
kształtownika jest odporna na
miejscową utratę stateczności):

wówczas...









15

....

w

w

t

h

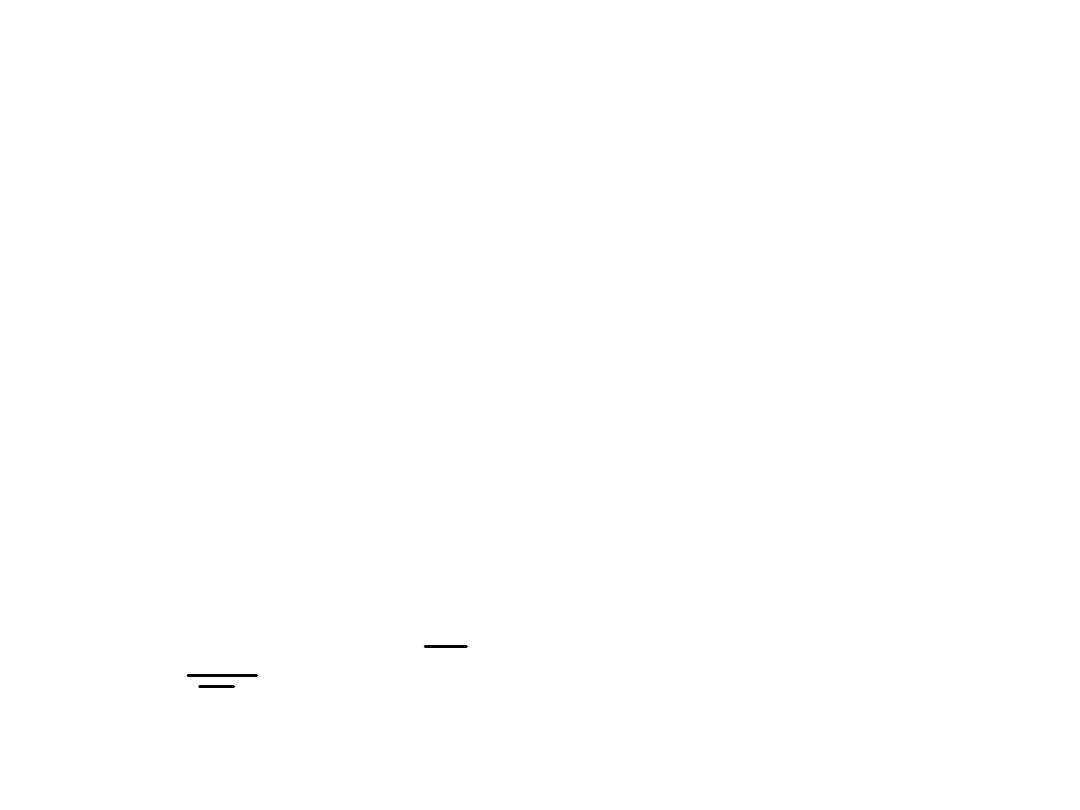
d

v

R

f

A

V





 58

,

0

gdzie:

A

ν

= 0,9·h·t

(tablica

7 PN)

Jeżeli przewiązka jest klasy 4,
wówczas:

d

v

pv

R

f

A

V











58

,

0

gdzie:

A

ν

= 0,9·h·t

(tablica

7 PN)

p

pv





1



smukłość względna
dla ścinania wg.
wzoru (7) PN



p



215

56

d

p

f

K

t

b











b, t – odpowiednio wysokość i grubość
przewiązki;

K – współczynnik podparcia i obciążenia
ścianki wyznaczany wg tabeli 8 dla ścinania;

dla β ≥ 1

dla β < 1

8

,

0

1

2

65

,

0













K















2

65

,

0

K

Jeżeli występująca siła poprzeczna

V

Q

>V

O

= 0,3 V

R

,

wówczas redukcję nośności

obliczeniowej ze zginania wykonuje się

według wzoru:



































2

)

(

,

1

R

Q

v

R

V

R

V

V

I

I

M

M



































2

)

(

,

1

R

Q

v

R

V

R

V

V

I

I

M

M

-gdzie:

I

(v)

– moment bezwładności części przekroju

czynnej przy ścinaniu względem osi obojętnej
(czynną część przekroju przy zginaniu
otrzymujemy z tabeli 7 PN odpowiednio do
rozpatrywanego przekroju);

I – moment bezwładności całego przekroju;

Zgodnie z tabelą 7 PN90/B-03200 pole
przekroju czynnego przy ścinaniu
wynosi: A

v

= 0,9·h·t

(h

,t – odpowiednio wysokość i grubość

elementu);

12

)

9

,

0

(

3

)

(

h

t

I







NOŚNOŚĆ PRZEWIĄZKI:

- w przypadku gdy nie uwzględniamy
sił poprzecznych:

1





R

L

M

M



M – obliczony moment (z wykresu sił poprzecznych);

M

R

– nośność obliczeniowa przekroju przy zginaniu;

φ

L

– współczynnik zwichrzenia wg. 4.5.4 PN (φ

L

= 1

ponieważ element przewiązki jest zabezpieczony przed
zwichrzeniem poprzez swoje niewielkie wymiary oraz
przyspawanie do konstrukcji)

NOŚNOŚĆ PRZEWIĄZKI:

-w przypadku gdy uwzględniamy siłę
poprzeczną:

M ≤ M

R, V

i

V ≤ V

R

M – obliczony moment

M

R, V

– zredukowana nośność obliczeniowa przekroju

przy zginaniu;

V – siła poprzeczna;

V

R

– nośność obliczeniowa przy ścinaniu;