Moment dipolowy
-
-
-
sposoby określania momentu dipoloweg
-
Moment dipolowy wiązana μ
[Cm]
Asymetryczny rozkład ładunku wywołuje
powstanie momentu dipolowego elektrycznego –
iloczyn (wektorowy) ładunku i odległości na
jaką ten ładunek jest przesunięty.
μ = q · l (q – cząstkowy ładunek elektryczny
[C] ,
l odległość miedzy środkami ciężkości ładunków
elektrycznych [m]
Jednostką momentu dipolowego jest
kulombometr [Cm] oraz debaj (1D = 3,333·10
-
30
Cm
Moment dipolowy wiązania – miara przesunięcia
elektronów tworzących wiązanie chemiczne w
kierunku jądra pierwiastka bardziej
elektroujemnego w heterocząsteczkach.
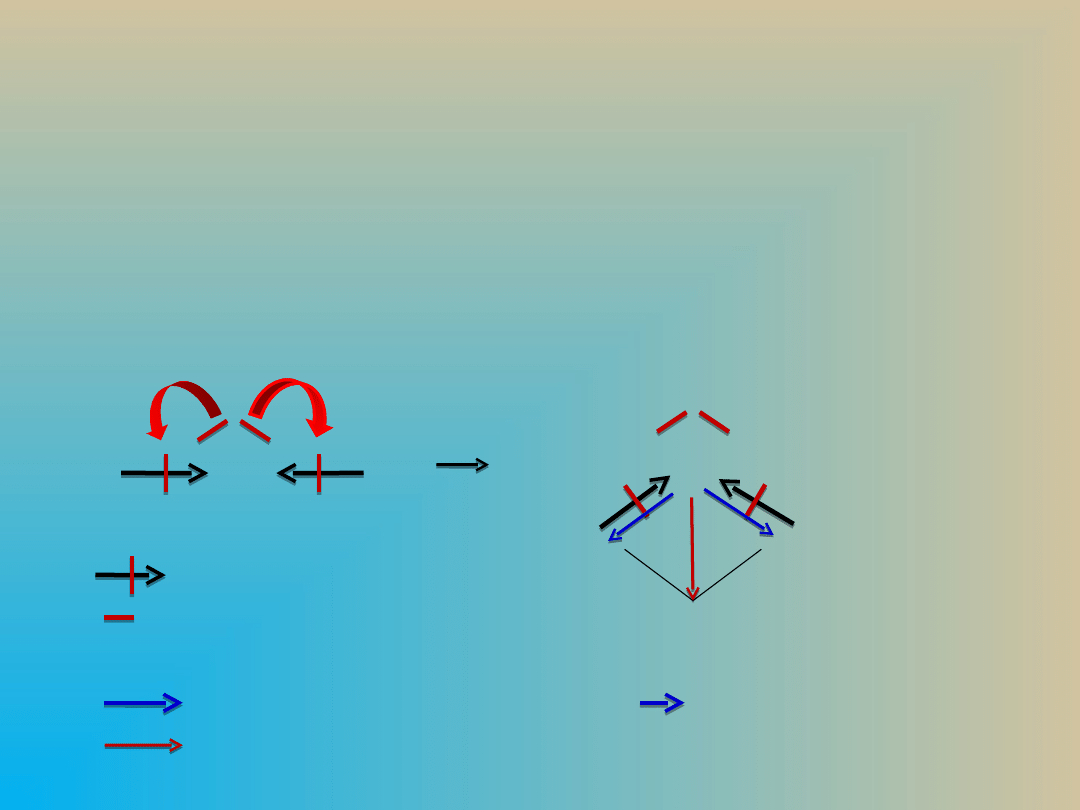
Moment dipolowy
cząsteczki μ
cz
Moment dipolowy cząsteczki –
suma wektorowa momentów
dipolowych poszczególnych wiązań.
:wiązanie kowalenc. polaryz.
:pary elektronowe niewiążące
δ+, δ- : cząstkowe ładunki elektryczne
: wektor momentu dipolowego (δ+ δ-)
: suma wektorów momentów dipolowych
O
δ-
δ+
H
H
δ+
O
δ-
H
δ
+
δ+
H
μ≠0
Sposób określania momentu dipolowego
wybranych cząsteczek
CCl
4
CO
2
CH
3
Cl
NH
3
μ = O
μ = O
μ ≠ O
μ ≠ O
C
δ+
Cl
δ
-
Cl
δ
-
Cl
δ
-
Cl
δ
-
C
Cl
Cl
C
l
Cl
C
δ+
H
δ
+
H
δ
+
H
δ
+
Cl
δ
-
C
H
H
H
Cl
N
δ-
H
δ
+
H
δ
+
H
δ
+
N
H
H
H
C
δ+
O
δ
-
O
δ
-
C
O
O
Cząsteczka polarna –
dipolowa
Moment dipolowy wiązania
nie jest równoznaczny z
momentem dipolowym cząsteczki:
Cząsteczki CO
2
, SO
3
, CH
4
, CCl
4
są apolarne
, chociaż
momenty dipolowe wiązań są różne od zera, jednak rozkład
ładunku elektrycznego jest symetryczny – momenty
dipolowe wiązań są przeciwnie skierowane i znoszą się.
Cząsteczki H
2
O, H
2
S
mają budowę kątową
– momenty
dipolowe wiązań nie znoszą się , cząsteczka ma
niesymetryczny rozkład ładunków elektrycznych
są
dipolami.
Cząsteczki dwuatomowe heterojądrowe
(
HF, HCl, HBr,
HI
) posiadają trwałe elektryczne momenty
dipolowe – są
dipolami
.
Cząsteczka NH
3
ma budową czworościanu, dzięki wolnej
parze elektronowej na atomie N rozkład ładunków
elektrycznych jest niesymetryczny a
suma momentów
dipolowych wiązań jest różna od zera
, a cząsteczka
jest
dipolem - cząsteczką polarną
.
Tu kliknij aby wrócić do
slajdu 1
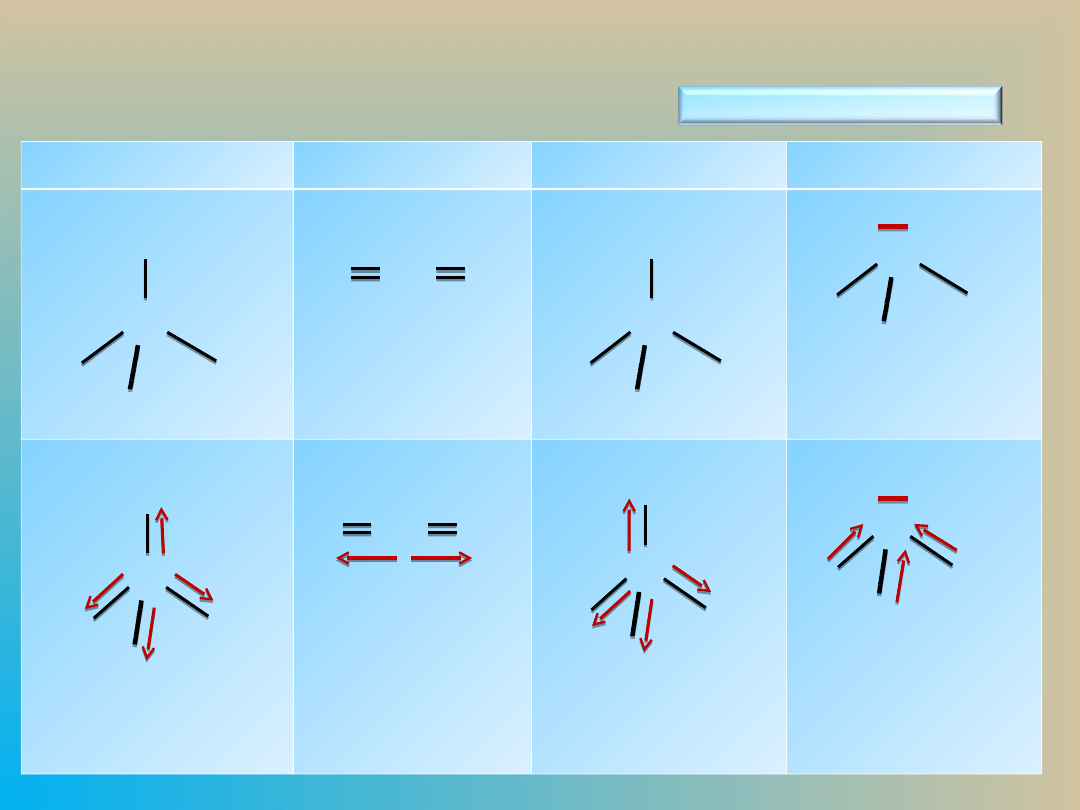
Ważniejsze rodzaje hybrydyzacji
Hybrydyza
cja atomu
Figura geomet.
określająca
położ. orbitali
zhybrydyz.
Stan
podstawowy
i
wzbudzony
atomu
Orbitale biorące udział
w hybrydyzacji
Przykład
y drobin
Diagonaln
a
Linia prosta
Be:1s
2
2s
2
1s
2
2s
1
2p
1
C: 1s
2
2s
2
p
2
1s
2
2s
1
2p
3
sp
: 2 orbitale sp, kąt =
180
o
sp
: 2 orbitale sp +
2 orbitale 2p
BeH
2
HC ≡
CH,
HC ≡ N
Trygonalna Trójkąt
równoboczny
B:1s
2
2s
2
2p
1
1s
2
2s
1
2p
2
C: 1s
2
2s
2
p
2
1s
2
2s
1
2p
3
sp
2
: 3 orbitale sp
2
,
kąt = 120
o
sp
: 3 orbitale sp
2
+
orbitale 2p
BCl
3
H
2
C = O
Tetraedryc
zna
Tetraedr
(czworościan)
P:
1s
2
2s
2
2p
6
3s
2
3
p
3
N:
1s
2
2s
2
2p
3
O: 1s
2
2
s
2
2p
4
S:
1s
2
2s
2
2p
6
3s
2
3
p
4
C:1s
2
2
s
2
p
2
1s
2
2s
1
2p
3
Si:
1s
2
2s
2
2p
6
3s
2
3
p
2
1s
2
2s
2
2p
6
3s
1
3
p
3
sp
3
: 4 orbitale sp
3
w
tym 1 orbital
obsadzony jest parą e
-
,
ok.93
o
< kąt < 109
o
28`
jw.
sp
3
: 4 orbitale sp
3
w
tym 2 orbitale
obsadzone parami e
-
sp
3
: 4 orbitale sp
3
jw.
PCl
3
, PH
3
NH
3
H
2
O
H
2
S
CH
4
,
CCl
4
SiH
4
Ważniejsze rodzaje
hybrydyzacji - cd
Hybrydyza
cja atomu
Figura geomet.
określająca
położ. orbitali
zhybrydyz.
Stan
podstawowy
i
wzbudzony
atomu
Orbitale biorące udział
w hybrydyzacji i przykłady
drobin
Kwadratow
a
Kwadrat
może dot. at.
pierw. okresu
3
i kolejnych
sp
2
d
- wymieszanie 1 orbitalu s
oraz 2-ch orbitali p i 1 orbitalu
d, orbitale są skierowanie do
narożników kwadratu,
kąty = 90
o
Bipiramida
lna
Bipiramida
trygonalna
P:
1s
2
2s
2
2p
6
3s
2
3p
3
1s
2
2s
2
2p
6
3s
1
3p
3
d
1
S:1s
2
2s
2
2p
6
3s
2
3p
4
1s
2
2s
2
2p
6
3s
2
3p
4
3d
1
Cl:
1s
2
2s
2
3s
2
3p
5
1s
2
2s
2
3s
2
3p
4
3d
1
sp
3
d
– pięć orbitali
sp
3
d,
trzy
orbitale skierowane są do
narożników trójkąta
równobocznego kąty = 120
o
, 2
orbitale są ┴ do płaszczyzny w
której leżą trzy orbitale – (kąty =
90
o
),
PCl
5
sp
3
d
- jeden z 5-ciu orbitali
sp
3
d
obsadza para e
-
, SF
4
sp
3
d
- dwa z 5-ciu orbitali
sp
3
d
obsadzają pary e
-
,
ClF
3
Oktaedrycz
na
Ośmiościan
foremny –
bipiramida
tetragonalna
S:1s
2
2s
2
2p
6
3s
2
3p
4
1s
2
2s
2
2p
6
3s
1
3p
3
3d
2
I:
[Kr]4d
10
5s
2
5p
5
I[Kr]4d
10
5s
2
5p
3
5d
2
sp
3
d
2
– 6 orbitali skierowanych
do narożników ośmiościanu
foremnego, SF
6
sp
3
d
2
– 6 orbitali, jeden z 6
orbitali obsadzony jest parą e
-
,
IF
5
Bipiramida
lno-
pentagonal
na
Bipiramida
pentagonalna
I:
[Kr]4d
10
5s
2
5p
5
I[Kr]4d
10
5s
1
5p
3
5d
3
sp
3
d
3
–siedem orbitali
skierowanych do narożników
bipiramidy pentagonalnej,
IF
7
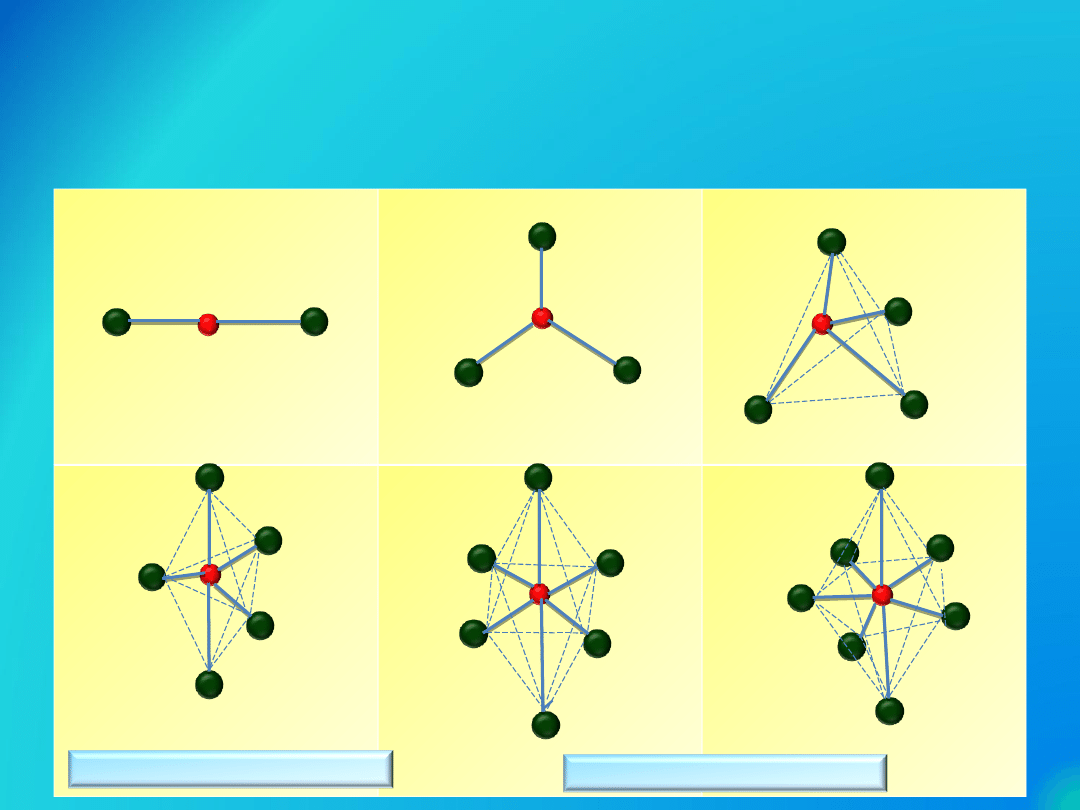
Przestrzenny rozkład wiązań
tworzonych przez orbitale
zhybrydyzowne
sp
sp
2
sp
3
sp
3
d
sp
3
d
2
sp
3
d
3
Tu kliknij aby wrócić do
slajdu 6
Tu kliknij aby wrócić do
slajdu 7