1

ATOM W POLU MAGNETYCZNYM cz. 

2

 

(wewnętrzne pola magnetyczne w atomie; 

poprawki na wzajemne oddziaływanie momentów 

magnetycznych elektronu; oddziaływanie spin-orbita)

 

 

2

Orbitalny (L) i spinowy (S) 

moment pędu elektronu; 

oddziaływanie związanych z nimi 

momentów magnetycznych

S

-

L

  

...

  

1,

-

S

L

  

,

S

L

J







Moment magnetyczny jest źródłem 

pola magnetycznego działającego na 

drugi moment magnetyczny; każdy z 

momentów magnetycznych elektronu 

powinien wykonywać precesję (ze 

względu na związany z nim moment 

pędu) wokół pola wytwarzanego przez 

drugi moment. 

Na wektor J = L + S nie działa 

zewnętrzny moment siły; oba momenty 

pędu L i S będą precesować wokół J 

przy czym:

a szybkość precesji (energia) będzie 

zależeć od J

 

 

3

Proton okrążający elektron wytwarza 

prąd:

generujący pole 

magnetyczne B

Oddziaływanie spin-orbita w atomie 

wodoru; model Bohra

r

2

v

Zq

T

Zq

e

e





które można obliczyć z prawa Biota-

Savarta:

L

r

m

c

4

Zq

dl

r

r

v

r

2

Zq

c

4

1

r

r

l

id

4

B

d

B

3

e

2

0

e

3

e

2

0

3

0















































v elektronu = -v protonu

 

 

4

gdzie                       

    i

Pole to oddziałuje z momentem 

magnetycznym związanym ze spinem 

elektronu; energia tego oddziaływania 

wyniesie:

s

l

r

m

c

8

h

g

Zq

L

r

m

c

4

Zq

S

m

2

g

q

B

E

3

2

e

2

0

2

s

2

e

3

e

2

0

e

e

s

e















































h

L

l







h

S

s



 

Po uwzględnieniu tzw. poprawki 

Thomasa, dla g

s

 = 2

otrzymamy ostatecznie:

 

 

5

Wyraz                 zależy od rozkładu 

radialnego (funkcji radialnej); wpływa 

na stałą a

s

l

a

s

l

r

m

c

8

h

Zq

E

3

2

e

2

0

2

2

e

























3

r



a –stała sprzężenia spin-orbita

dla atomów podobnych do atomu 

wodoru





1

l

2

1

l

l

n

Z

~

a

3

4















 



 

 

6

Energia oddziaływania spin-orbita 

wynosi:

s

l

a

E













s

l

j











Ponieważ:                     , podnosząc do 

kwadratu i wprowadzając kwadrat 

kwantowy, otrzymamy:



 

 



s

l

2

1

s

s

1

l

l

1

j

j

s

l

2

s

l

j

2

2

2









































 

 







1

s

s

1

l

l

1

j

j

2

1

s

l

















skąd:

i 

ostatecznie:



 

 







1

s

s

1

l

l

1

j

j

2

a

E















 

 

7

m

j

 = l + s, l + s – 1, … -l - 

s

s

l

j











Dla atomu wodoru l przyjmuje wartości 

0, 1, 2, 3 … (s, p, d, f …), a ponieważ s = 

1/2, możliwe są dwa przypadki:

s

l

j





i:

s

l

j





Kilka kolejnych 

stanów:

....

3d

 ,

3d

 ,

3p

 ,

3p

 ,

3s

 ,

2p

 ,

2p

 ,

2s

 ,

s

1

3/2

5/2

1/2

3/2

1/2

1/2

3/2

1/2

2

/

1

Można pokazać, że j

max

 = l + s;  j

min

 = l – s, 

z krokiem 1

 

 

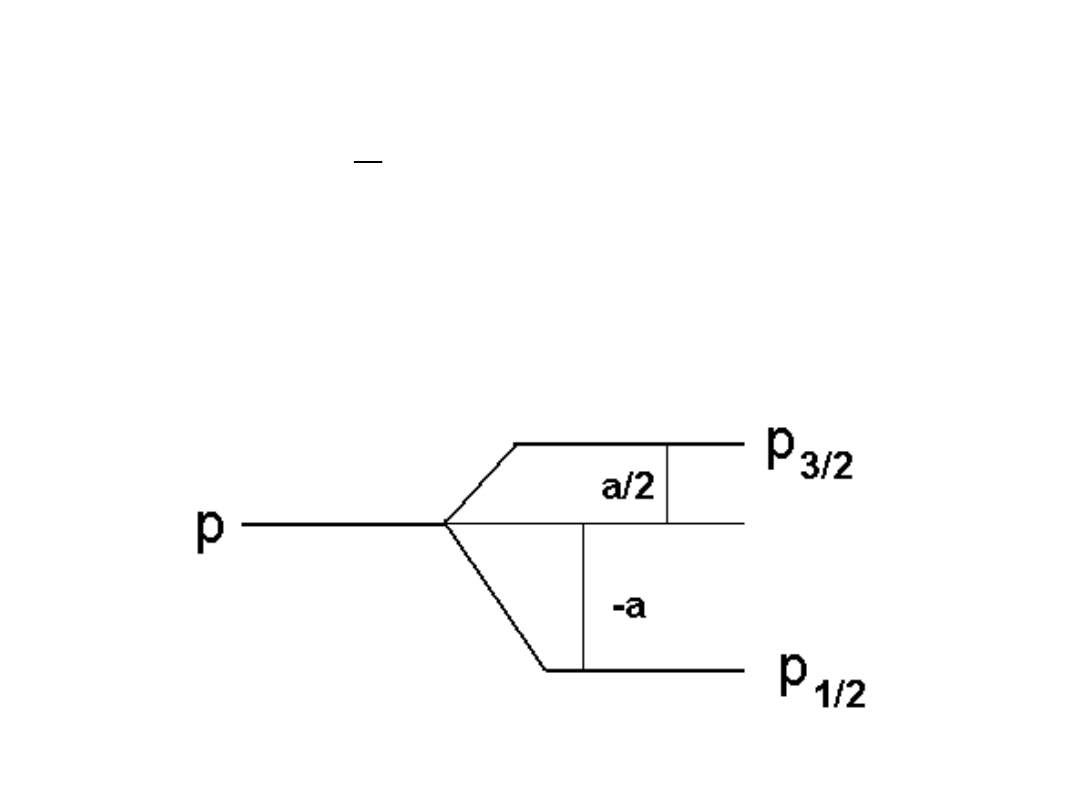
8



 

 







1

s

s

1

l

l

1

j

j

2

a

E















Przykład:  p

1/2

, p

3/2

ΔE

1/2

 = (1/2

.

3/2-1

.

2-1/2

.

3/2)a/2 = -a

ΔE

3/2

 = (3/2

.

5/2-1

.

2-1/2

.

3/2)a/2 = a/2

 

 

9

Teoria Diraca atomu wodoru

ss

n

j

,

l

,

n

E

E

E





2

2

n

ss

Z

n

4

3

2

1

j

1

n

E

E































gdzie:

c

h

e

c

h

4

q

2

0

2

e









to stała struktury subtelnej, równa 

około 1/137

poprawka E

ss

 

uwzględnia 

relatywistyczną 

zmianę mas i 

sprzężenie spin-

orbita

 

 

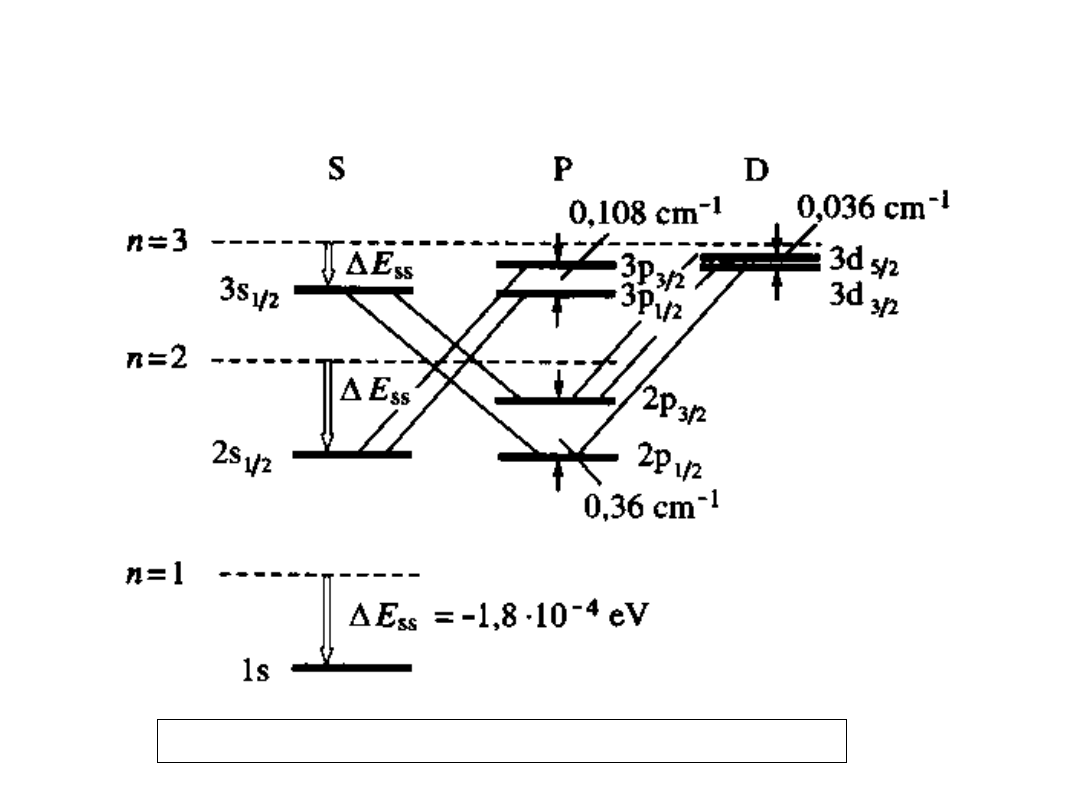
10

Struktura subtelna atomu wodoru 

(Dirac); poprawka zależy od j a nie od l

Copyright © Springer-Verlag, The Physics of Atoms and Quanta by Hermann Haken and 
Hans Christoph Wolf
Copyright © for the Polish edition by Wydawnictwo Naukowe PWN SA, Warszawa 2002

 

 

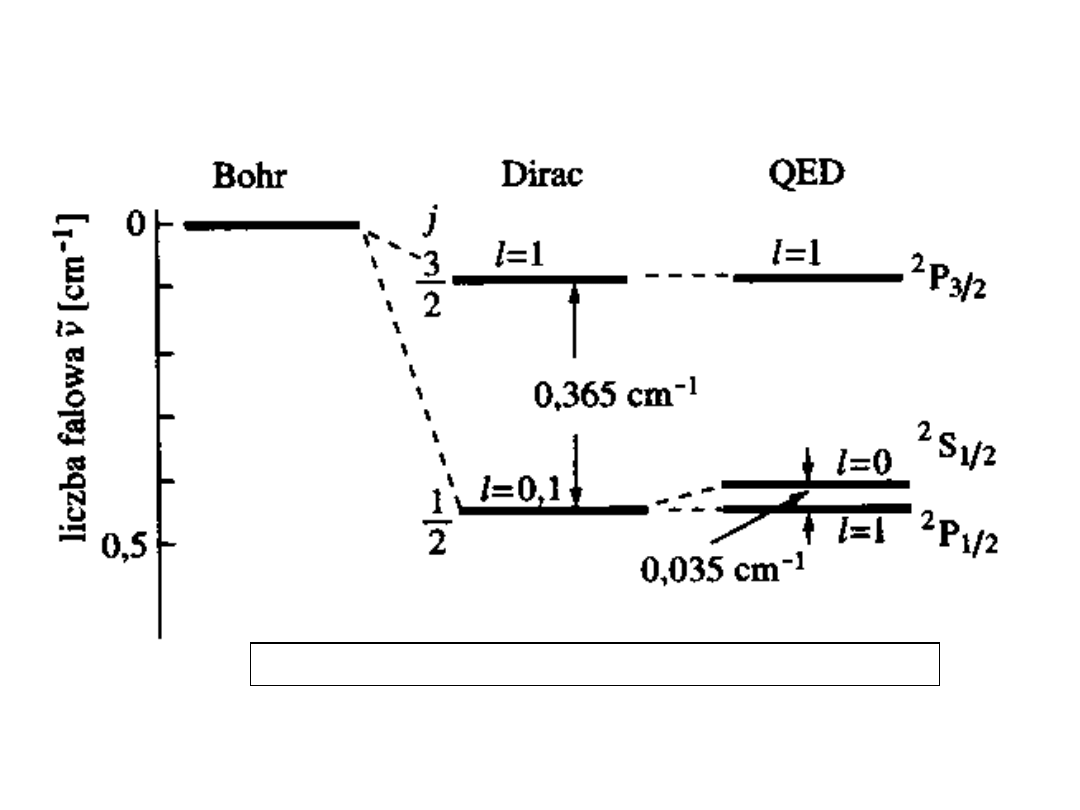
11

Przesunięcie Lamba (elektrodynamika 

kwantowa)

Copyright © Springer-Verlag, The Physics of Atoms and Quanta by Hermann Haken and 
Hans Christoph Wolf
Copyright © for the Polish edition by Wydawnictwo Naukowe PWN SA, Warszawa 2002

 

 

12

Reguły wyboru:

1

 

l 





1

 

 ,

 

0

j







0

s



zawsze spełniona dla 

stanów jednoelektronowych

J

1

S

2

L



Pełne oznaczenie 

spektroskopowe stanu:

Dla stanów jednoelektronowych L = l, J = 

j, S = s

 

 

13

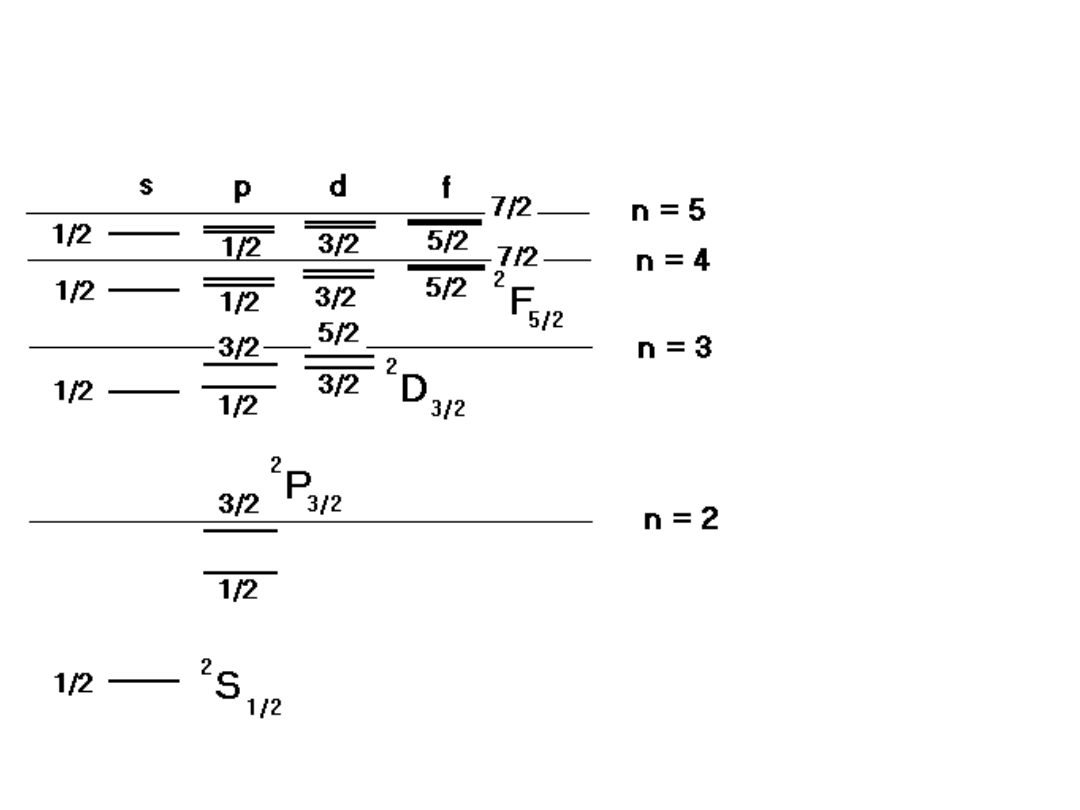
Układ jednoelektronowych stanów 

energetycznych dla atomów metali 

alkalicznych (Li, n = 2)

Bez 

zachowania 

skali. 

Rozszczepie

nie spin – 

orbita 

maleje z 

rosnącym n i 

l 

(człon z r

3

). 

Odstępstwa 

od wodoru 

maleją z 

rosnącym l i 

n

 

 

14

Linie serii głównej dla metali alkalicznych 

są dubletami 

(przejścia na nierozszczepione poziomy n 

2

S

1/2

)

Linie serii ostrej (II pobocznej) dla 

metali alkalicznych są dubletami 

(przejścia z nierozszczepionych wyższych 

poziomów  n’

2

S

1/2

 na najniższe poziomy 

p, n

2

P

1/2

 i n

2

P

3/2

)

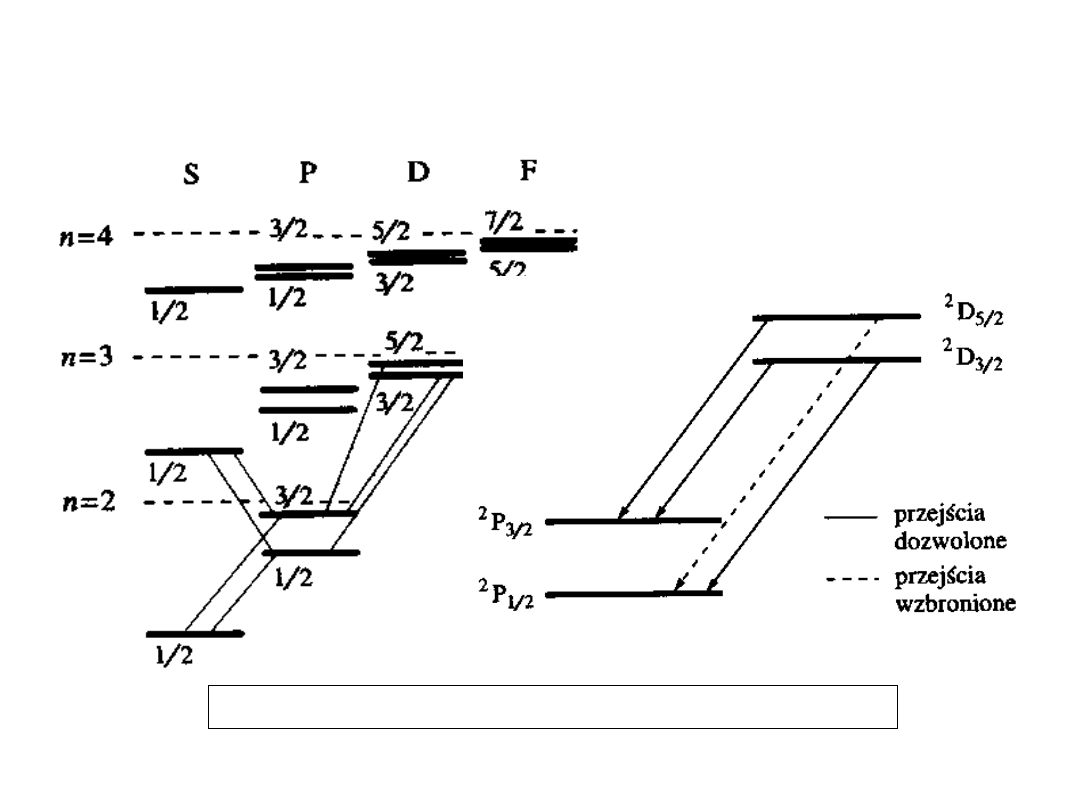
Linie serii rozmytej (I pobocznej) dla 

metali alkalicznych są trypletami 

(przejścia z wyższych poziomów  n’

2

D

3/2

 i 

n‘

2

D

5/2

 na najniższe poziomy p, n

2

P

1/2

 i 

n

2

P

3/2

), przejście 5/2 na 1/2 zabronione

 

 

15

Li, przejścia 3

2

D

3/2

 i 3

2

D

5/2

 na p, 2

2

P

1/2

 i 

2

2

P

3/2

), przejście 5/2 na 1/2 zabronione

Copyright © Springer-Verlag, The Physics of Atoms and Quanta by Hermann Haken and 
Hans Christoph Wolf
Copyright © for the Polish edition by Wydawnictwo Naukowe PWN SA, Warszawa 2002

 

 

16

Struktura nadsubtelna w atomie 

wodoru, sprzężenie spinu elektronu i 

spinu protonu

Spin S i I, dla obu s = 1/2 

S + I = F, 

o liczbie kwantowej f = 1 (tryplet) lub 

0 (singlet)

Przejście pomiędzy trypletem i 

singletem

1420 MHz, częstość radiowa

Obszerne omówienie struktury 

nadsubtelnej, z użyciem macierzy 

Pauliego, w III tomie Feynmana (rozdz. 

12)