1

SPRZĘŻENIE MOMENTÓW

PĘDU W ATOMACH

WIELOELEKTRONOWYCH;

SPRZĘŻENIE L-S, j-j.

REGUŁY WYBORU.

EFEKT ZEEMANA.

2

Sprzężenie L – S

Atom He: energia kulombowska (S, P, D…)

i wymiany (multipletowość); termy i

multiplety

Dwa elektrony: S = 0 (singlety), S = 1

(tryplety)

Trzy elektrony: S = 1/2 (dublety), S = 3/2

(kwartety)

Cztery elektrony: S = 0 (singlety), S = 1

(tryplety),

S = 2 (kwintety)

Pięć elektronów: S = 1/2 (singlety), S =

3/2 (kwartety),

S = 5/2 (sekstety), itd…

(mimo wzg. słabego oddziaływania spinów,

znaczenie części przestrzennej funkcji i

oddziaływania e

2

/r

12

)

3

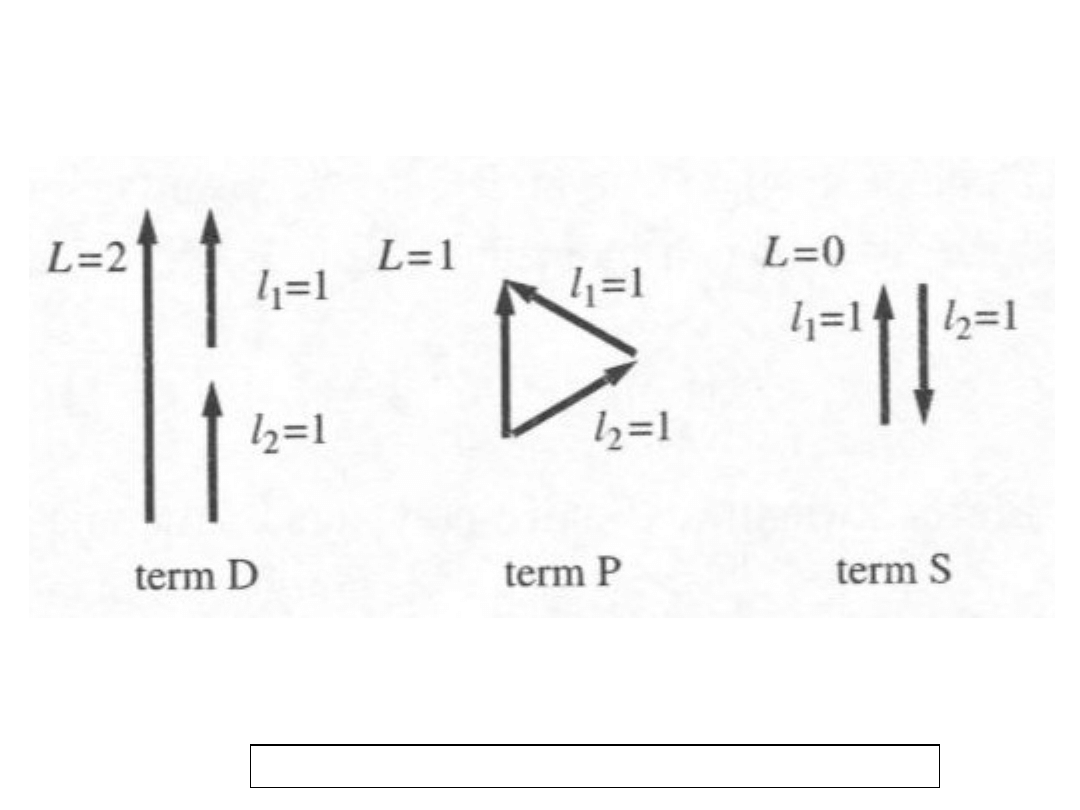
Składanie orbitalnych momentów pędu

dwóch elektronów p; model wektorowy

Copyright © Springer-Verlag, The Physics of Atoms and Quanta by Hermann Haken and
Hans Christoph Wolf
Copyright © for the Polish edition by Wydawnictwo Naukowe PWN SA, Warszawa 2002

4

Termy; nierozszczepione multiplety (bez

s – o)

J

1

S

2

L



Konfiguracja np. 1s2p (pole centralne)

Niecentralna część e

2

/r

12

(różne L)

Energia wymiany (termy)

Spin – orbita (różne J, multiplety: zbiory

poziomów)

Pole magnetyczne (różne m

J

, stany)

5

Oddziaływanie spin – orbita





S

L

h

1

S

,

L

'

H

2















S

-

L

...

1,

-

S

L

S,

L

J

L

i

S

dla

podobnie

,

h

1

J

J

J

S

L

J

























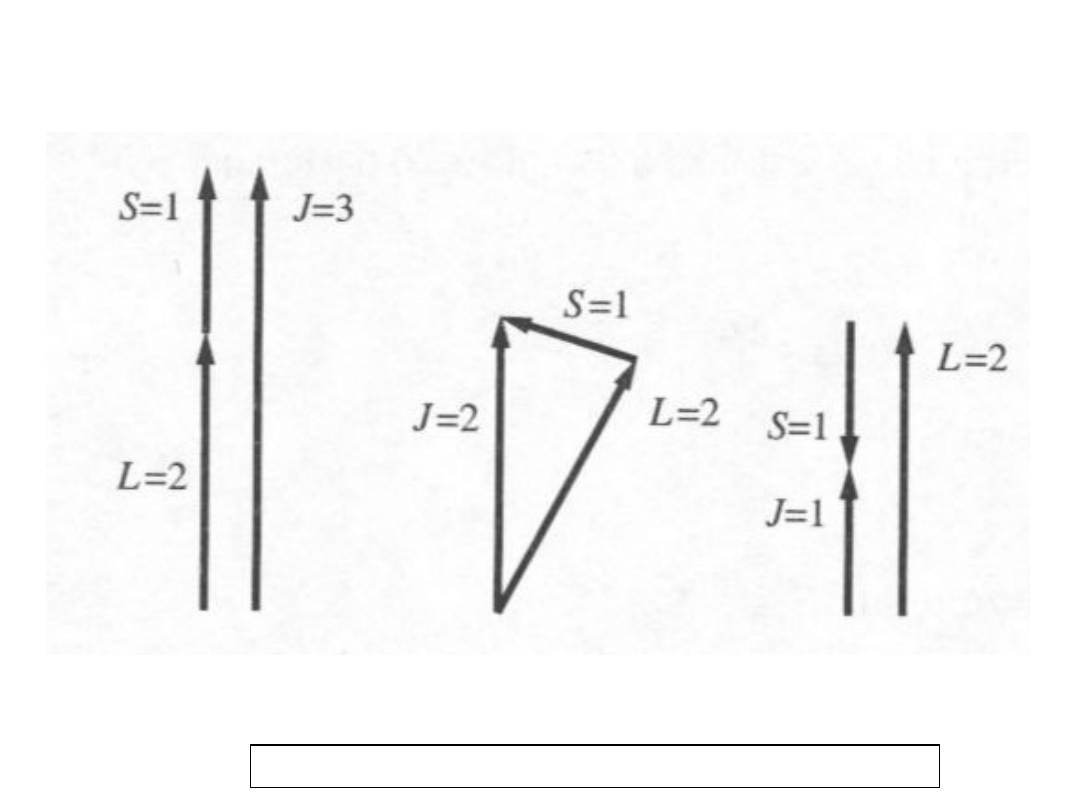
W modelu wektorowym:

Reguła trójkąta; ponieważ J = L + S, trzy

wektory tworzą trójkąt; trzeci bok nie

może być…

6

Składanie spinowego i orbitalnego

momentu pędu; model wektorowy

Copyright © Springer-Verlag, The Physics of Atoms and Quanta by Hermann Haken and
Hans Christoph Wolf
Copyright © for the Polish edition by Wydawnictwo Naukowe PWN SA, Warszawa 2002

7

Oddziaływanie spin – orbita





S

L

h

1

S

,

L

'

H

2

























 















1

S

S

1

L

L

1

J

J

S

,

L

2

1

E

S

L

2

1

S

S

1

L

L

1

J

J

S

L

J

J











































W modelu wektorowym:

8

A więc, dla prostych multipletów (J

wyżej od J – 1):



 































J

S

,

L

1

S

S

1

L

L

J

1

J

1

S

S

1

L

L

1

J

J

S

,

L

2

1

E

E

1

J

J









































Reguła interwałów Landégo; kryterium

na spełnienie przybliżenia Russela –

Saundersa

(sprzężenie L–S) przez atom

wieloelektronowy

9

Przykład; termy konfiguracji stanu

podstawowego atomu azotu, 2p

3

Ponieważ:

1

l

,

1

l

,

1

l

3

2

1







L = 3, 2, 1, 0

a S = 3/2 bądź 1/2, zatem wydawałoby

się, że dozwolone termy powinny być S, P,

D, F, dublety i kwartety.

ZAKAZ PAULIEGO!

Rozważymy rozkład elektronów 3p w

stanach jednoelektronowych,

scharakteryzowanych liczbami m

l

i m

s

,

taki, by był spełniony zakaz Pauliego

10

Znak + i – oznaczają m

s

= 1/2 i -1/2

m

l

dla elektronu p (l = 1) może być równe

1, 0, -1

plus 10 dodatkowych stanów z

zamienionymi + i –

m

l

m

S

1

+ + +

–

+

+

+

–

+

–

0

+ +

–

+ +

–

+

–

+

+

-1

+

–

+ +

+ +

–

+

–

+

11

Rozkład 20 stanów pomiędzy stany

wieloelektronowe

o określonej wartości M

L

i M

S

M

L

/M

S

-3/2 -1/2 +1/

2

+3/

2

2

1

1

1

2

2

0

1

3

3

1

-1

2

2

-2

1

1

Są to składowe następujących termów:

4

S,

2

P,

2

D

12

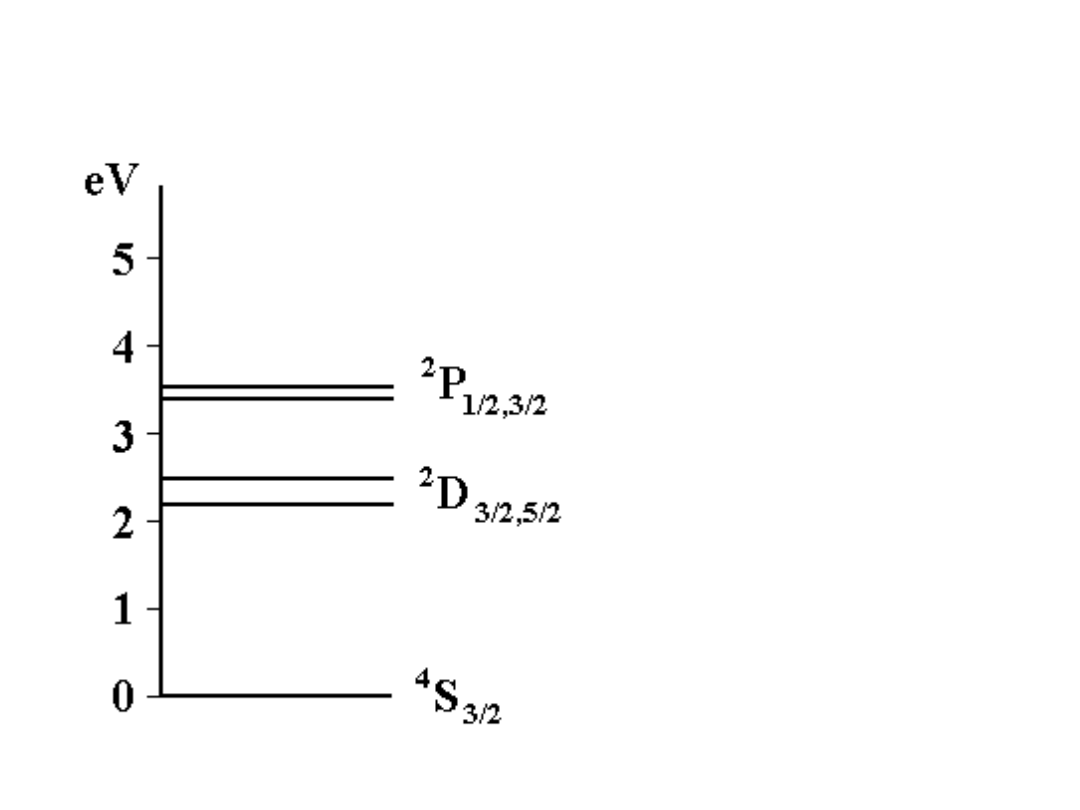
Układ poziomów zgodny z regułą Hunda

dla konfiguracji 2p

3

atomu azotu

/

Multiplety o

wyższej

multipletowości

niżej

Dla multipletów

o tej samej

multipletowości

niżej te z

większym L

Dla multipletów

prostych, niżej
leżą poziomy o

niższym J

13

Diagram termów dla atomu azotu (2p

3

)

/

Copyright © Springer-Verlag, The Physics of Atoms and Quanta by Hermann Haken and
Hans Christoph Wolf
Copyright © for the Polish edition by Wydawnictwo Naukowe PWN SA, Warszawa 2002

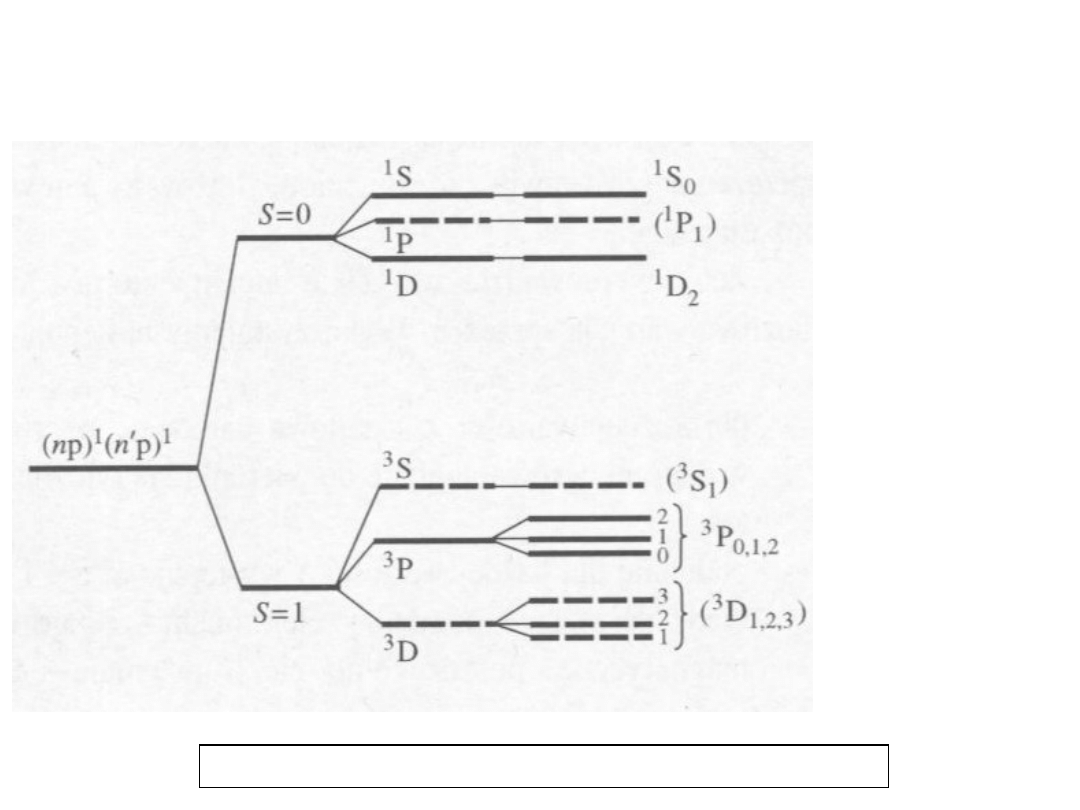
14

/

Sprzężenie dwóch elektronów p dla

konfiguracji (npnp) i (npn’p)

Copyright © Springer-Verlag, The Physics of Atoms and Quanta by Hermann Haken and
Hans Christoph Wolf
Copyright © for the Polish edition by Wydawnictwo Naukowe PWN SA, Warszawa 2002

Singlet,

antysymetrycz

na część

spinowa

(wymiana)

tryplet,

symetryczna

Całkowita

funkcja

falowa musi

być

antysymetrycz

na

15

Sprzężenie j – j

Stała sprzężenia spin – orbita dla

pojedynczego elektronu rośnie z Z:

s

l

a

s

l

r

m

c

8

h

Zq

E

3

e

2

0

2

2

e























zatem dla ciężkich atomów maleje

względne znaczenie energii wymiany;

maleje uporządkowanie

charakterystyczne dla sprzężenia L – S,

rośnie znaczenie sprzężenia s i l dla

pojedynczego elektronu

16

Musimy zastosować inny sposób składania

momentów pędu:





2

2

1

2

2

2

1

1

1

h

1

J

J

J

...

j

j

J

...

j

s

l

;

j

s

l









































Wartości j i J znajdujemy stosując model

wektorowy:

j

1

= l

1

+ s

1

, l

1

–

s

1

, j

2

= l

2

+ s

2

, l

2

– s

2

J = j

1

+ j

2

, j

1

+ j

2

–

1, … |j

1

–

j

2

|

Ale nie wszystkie tak znalezione stany

(j

1

,j

2

)

J

będą spełniać zakaz Pauliego

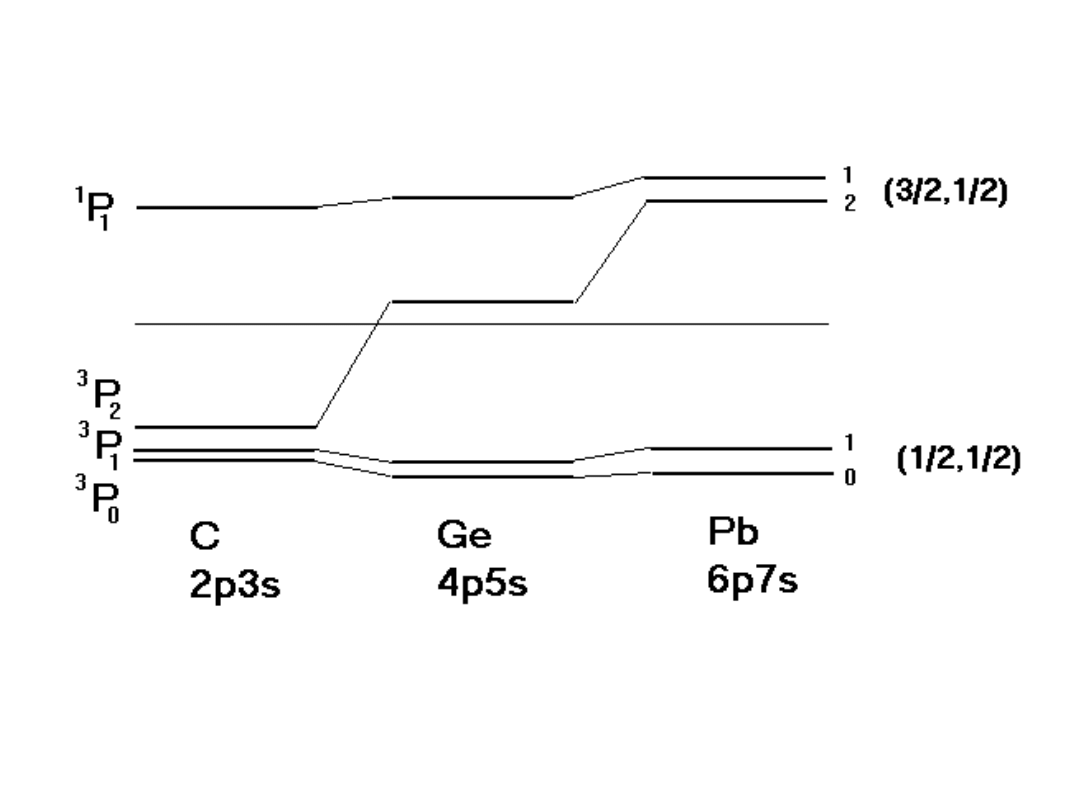
17

/

Przejście od sprzężenia L – S w atomach

lekkich do sprzężenia j – j w atomach

cięższych

Stany wzbudzone konfiguracji (np)

2

atomów

IV grupy układu okresowego (C, Si, Ge,

Sn, Pb)

1600 cm

-1

40 cm

-1

20 cm

-1

18

Reguły wyboru

(przejścia elektryczne – dipolowe)

ξ

= x, y, z dla światła spolaryzowanego

liniowo w kierunku x, y, z

= x + iy, x – iy, dla światła

spolaryzowanego

kołowo, rozchodzącego się w kierunku z

Całkowanie po współrzędnych

przestrzennych i spinowych

















d

d

H'

2

1

j

*

k

kj

element macierzowy

odpowiedzialny za

przejścia ze stanu j

do k

19

Moment dipolowy (q

ξ

), nie zależy od

współrzędnych spinowych, zatem:

atom

0

S

elektron

0

s









zabronione przejścia

interkombinacyjne

Funkcje falowe są zbudowane z funkcji

jednoelektronowych

Część spinowa funkcji falowej daje się

wyodrębnić

(w przybliżeniu Russela – Saundersa)

20

/

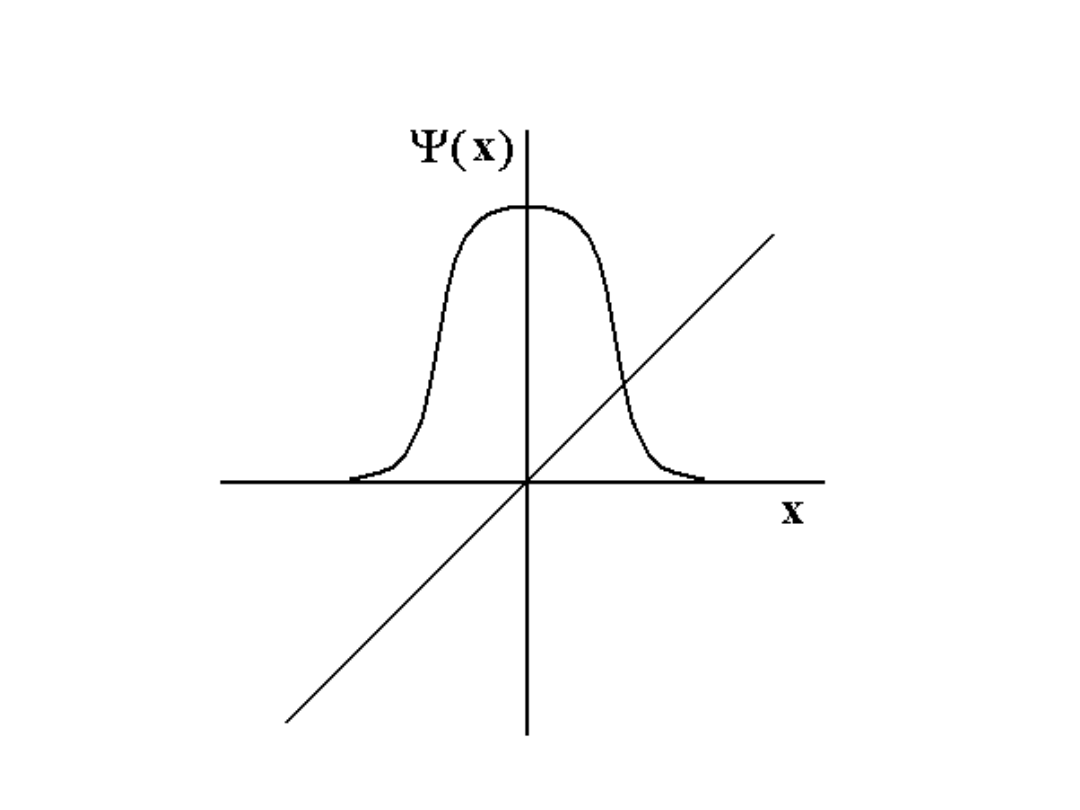
Całkowanie funkcji parzystych i

nieparzystych

 

0

dx

x

x















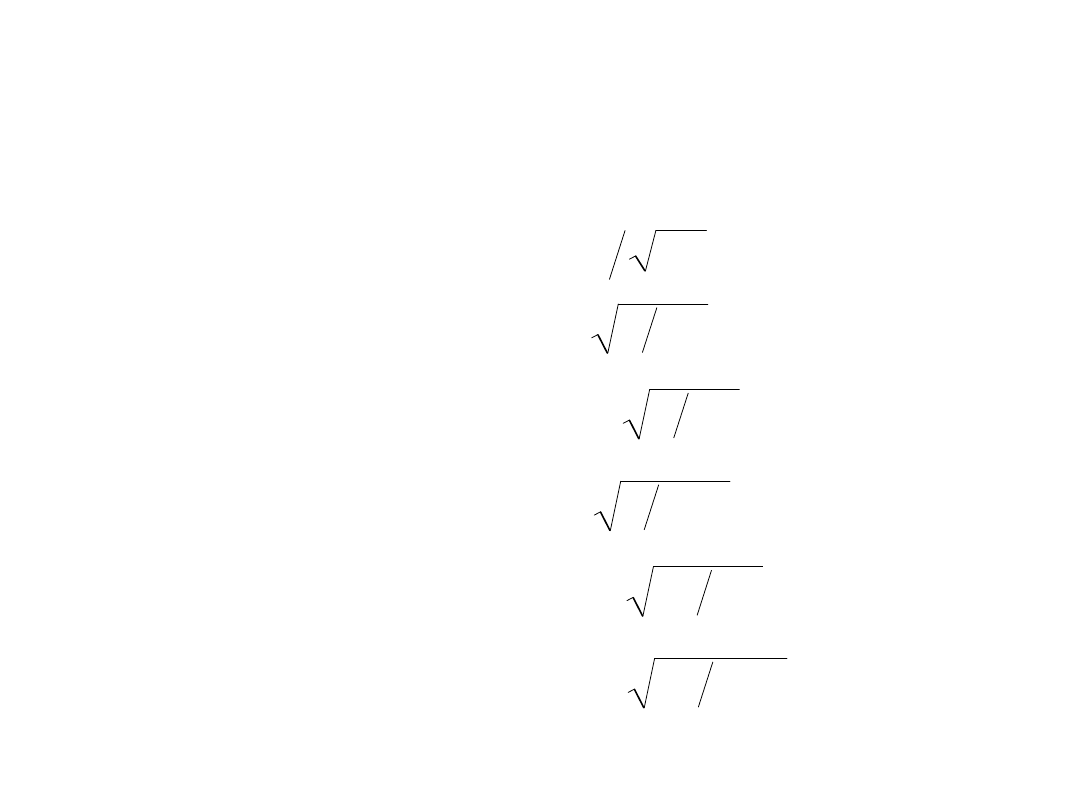
21

Radialna część funkcji falowej dla

wodoru:

 

l

1

































































i

2

2

2

,

2

i

1

,

2

2

20

i

1

,

1

10

00

e

sin

32

15

Y

e

sin

cos

8

15

Y

1

cos

3

16

5

Y

e

sin

8

3

Y

cos

4

3

Y

4

1

Y

parzystość









































lub

r

r





inwersja

22

Zatem:

Dla funkcji s l = 0, funkcje parzyste

Dla funkcji p l = 1, funkcje

nieparzyste

Dla funkcji d l = 2, funkcje parzyste

Dla funkcji f l = 3, funkcje

nieparzyste

Iloczyn funkcji parzystych, parzysty

Iloczyn funkcji nieparzystych, parzysty

A więc: Δl = ± 1

23

Kątowa zależność funkcji falowej wodoru

od kąta φ (kąt azymutalny)





 

















 

z

M

e

zd

e

d

,

zY

,

Y

z

M

e

,

Y

0

m

'

m

i

m

'

m

i

'

m

'

l

*

lm

im

lm







































M(z) dla światła spolaryzowanego wzdłuż

osi z, nie powinno zależeć od obrotu

wokół osi z.

Δm = 0

obrót o φ

0

24

/

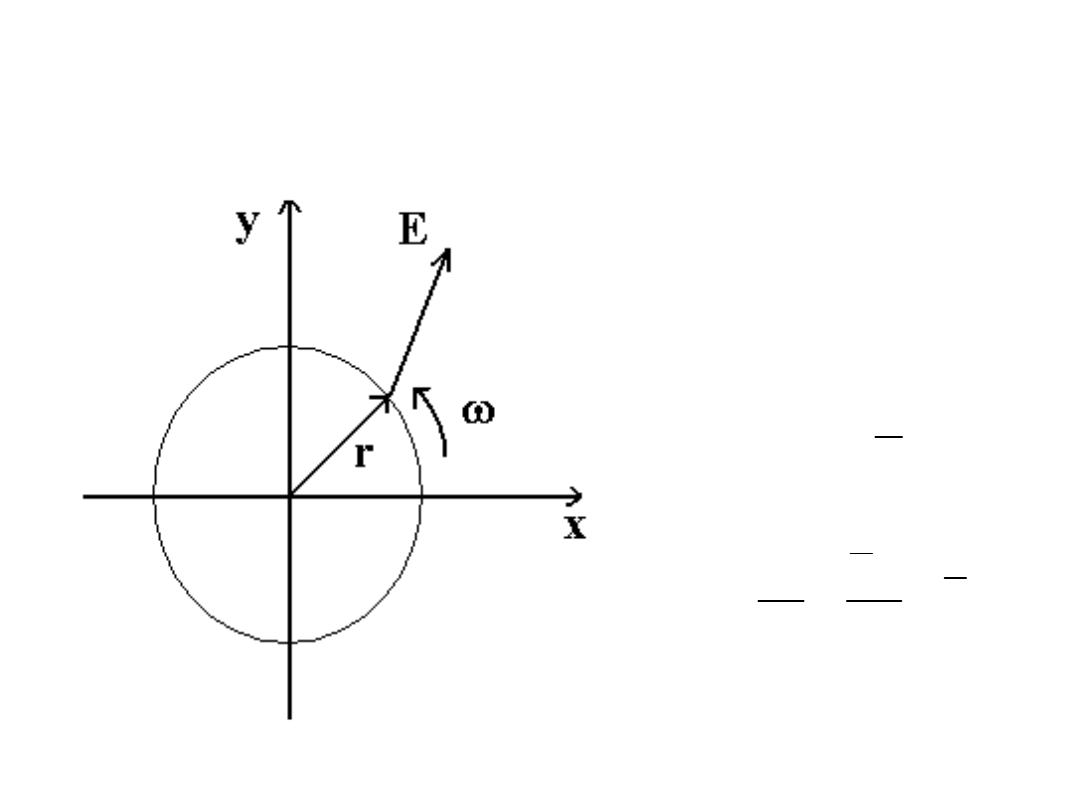
Moment pędu fotonu światła

spolaryzowanego kołowo

Elektron w ośrodku materialnym, pole

fali e-m spolaryzowanej kołowo w p-źnie

xy

E



h

h

W

M

t

M

t

t

r

v

r

F

vt

F

W

F

r

p

r

M

E

q

F

s

s





















































Porównujemy energię W i moment pędu

M przekazany elektronowi przez falę e-

m w czasie t

25

Moment pędu fotonu światła

spolaryzowanego kołowo, prawo- lub

lewoskrętnie, rozchodzącego się w

kierunku osi z jest równy:

±ħ

Z zasady zachowania momentu pędu,

moment pędu atomu musi się też zmienić

o tę samą wartość; więc, ponieważ:

J

z

= mħ

więc:

Δm = ±1

(polaryzacja lewo- lub prawoskrętna)

26

Reguły wyboru dla atomu w

sprzężeniu L–S:

1. przejścia elektryczno-dipolowe

zachodzą gdy jeden elektron

zmienia stan i Δl = ±1

2. Liczby kwantowe atomu

ΔS = 0

ΔL = ±1 lub 0

ΔJ = ±1 lub 0, ale 0 → 0 zabronione

Δm

J

= ±1 lub 0, ale Δm

J

= 0

zabronione

gdy ΔJ = 0

27

Reguły wyboru dla atomu w

sprzężeniu j–j:

1. przejścia elektryczno-dipolowe

zachodzą gdy jeden elektron zmienia

stan; dla tego elektronu:

Δl = ±1, ΔJ = ±1 lub 0,

dla pozostałych elektronów ΔJ = 0

2. Liczby kwantowe atomu

ΔJ = ±1 lub 0, ale 0 → 0 zabronione

Δm

J

= ±1 lub 0, ale Δm

J

= 0

zabronione

gdy ΔJ = 0

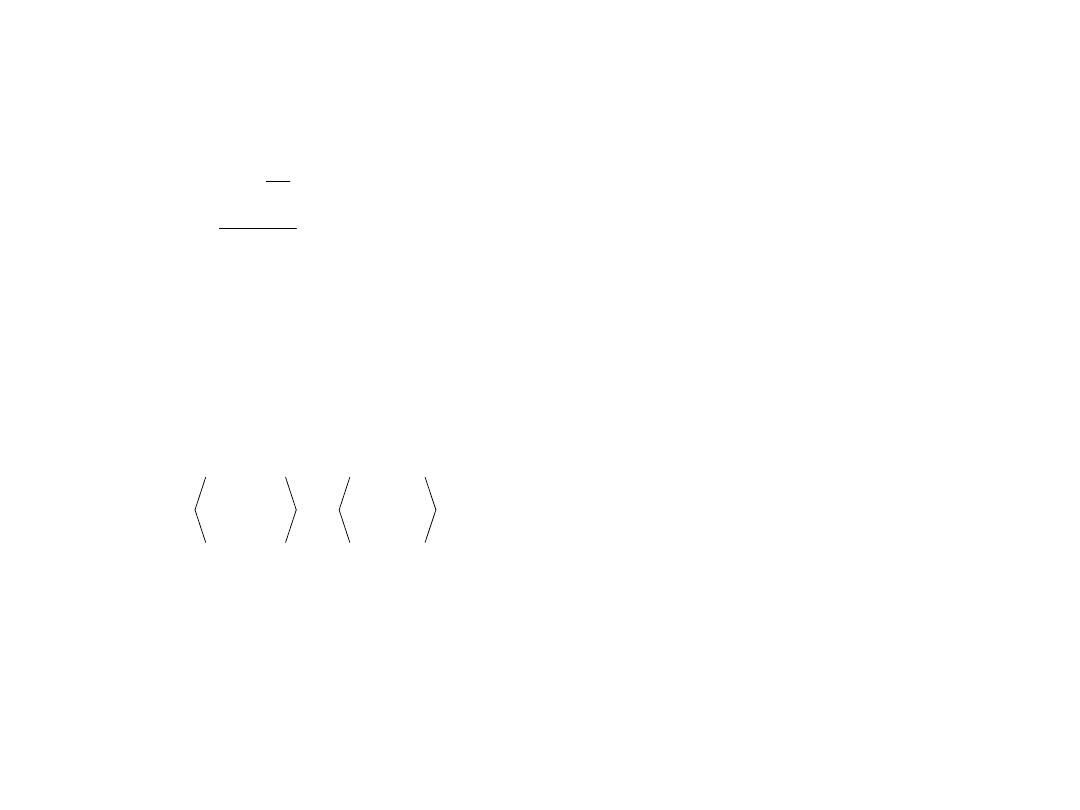
28

Atom wieloelektronowy w polu

magnetycznym; efekt Zeemana

gm

gm

m

2

h

q

B

e

e









mB

g

E

B







moment

magnetyczny w

kierunku pola B

energia w polu B





B

E

z

z

S

L











energia w polu B

Porównując oba wyrazy znajdujemy

efektywny czynnik Landego g

29

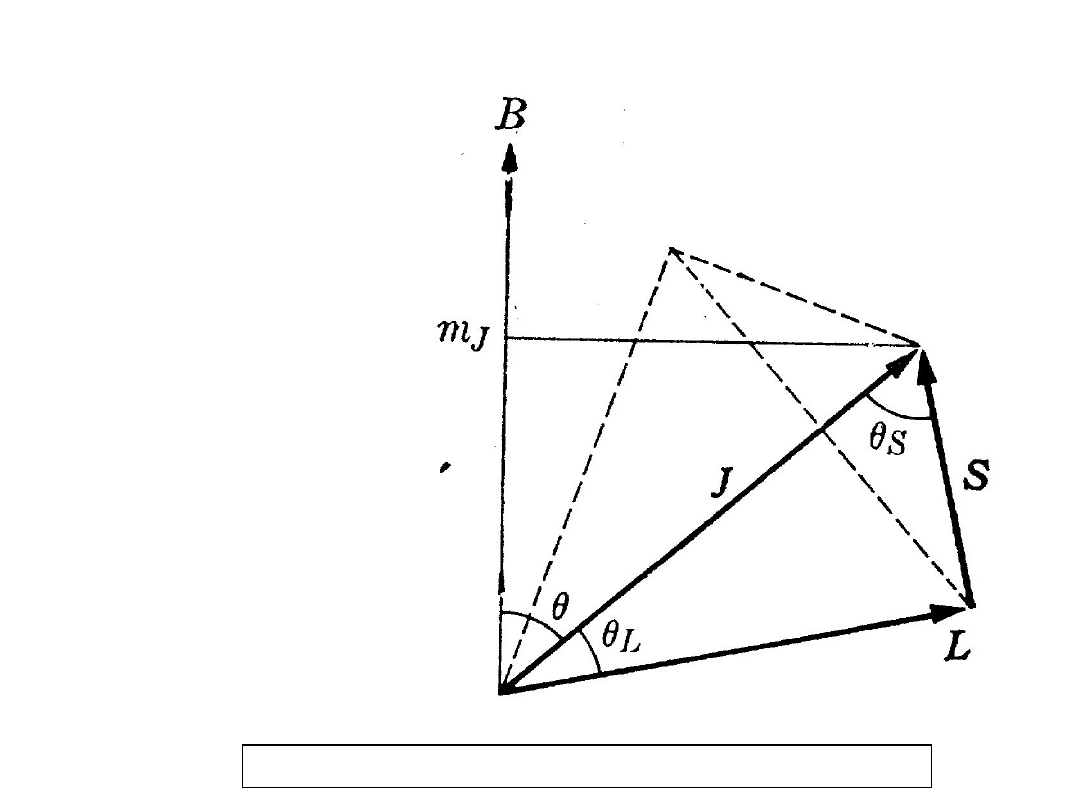
Obliczanie czynnika Landego g

Model

wektorowy

Sprzężenie L –

S

Słabe pole

magnetyczne

J, m

J

stałe,

wektor J

wykonuje

precesję

wokół B

L i S

wykonują

precesję

wokół J

Copyright © 1972 by Addison-Wesley Publishing Company, Inc, Introduction to Atomic
Physics by Harald A. Enge.
© Copyright for the Polish edition by Państwowe Wydawnictwo Naukowe, Warszawa
1983

30

gdzie θ

L

to kąt pomiędzy L i J, θ

S

to kąt

pomiędzy S i J, a θ to kąt pomiędzy J i B
Ponieważ:





























cos

cos

h

1

S

S

m

q

,

cos

cos

h

1

L

L

m

2

q

S

e

e

S

L

e

e

L

z

z

S

L

J











L

S

J

























 

















 



S

2

2

2

L

2

2

2

cos

1

S

S

1

J

J

2

1

S

S

1

J

J

S

J

2

S

J

1

L

L

L

cos

1

L

L

1

J

J

2

1

L

L

1

J

J

L

J

2

L

J

1

S

S

S

































































i

31

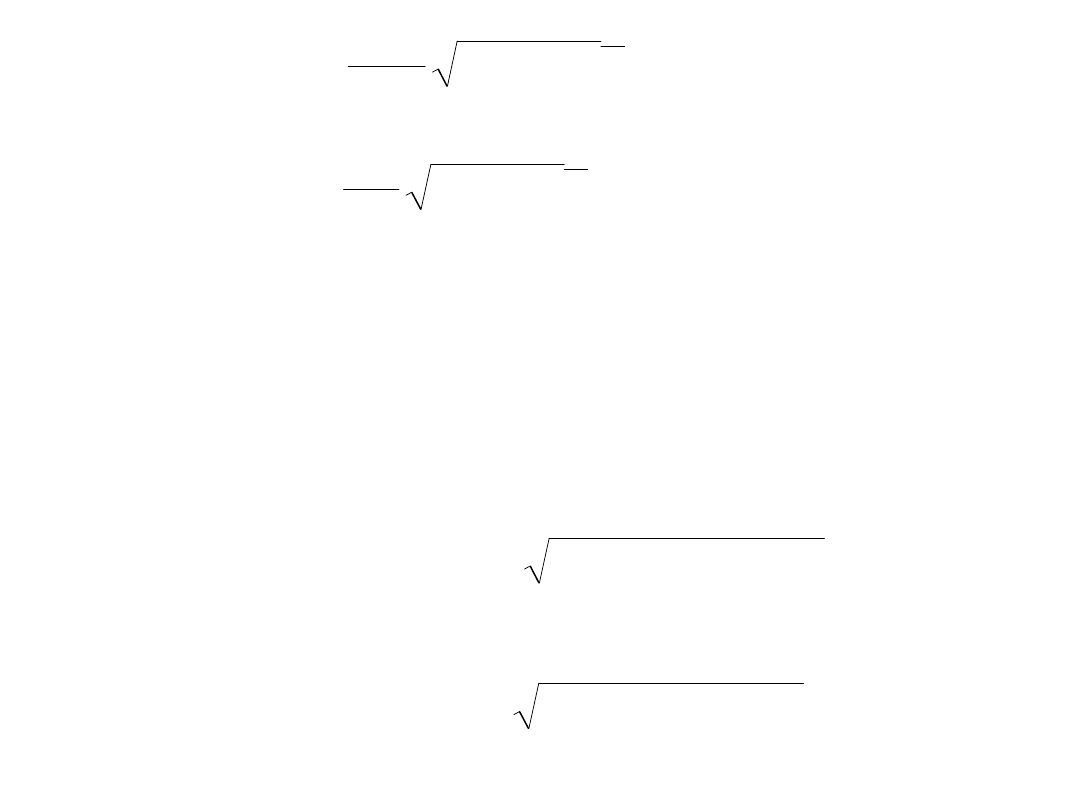
a także:

i z porównania odpowiednich

wyrażeń:





1

J

J

m

cos

J























B

m

1

J

J

2

1

L

L

1

S

S

1

J

J

1

m

2

h

q

E

J

e

e















































1

J

J

1

L

L

1

S

S

1

J

J

1

g

















Dla S = 0 mamy g = 1, tzw.

„normalne” zjawisko Zeemana, trzy

składowe nawet dla J > 1,

Δm

J

= 0, ±1

Dla S > 0, „anomalne” zjawisko

Zeemana

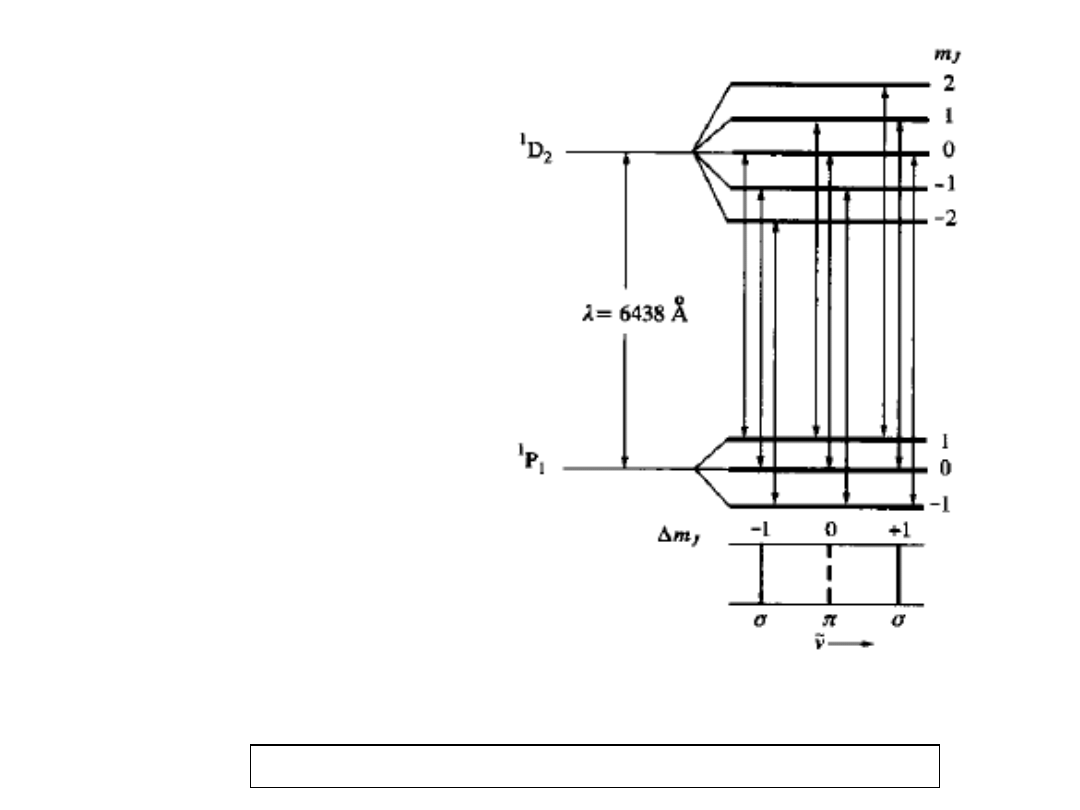
32

Normalne

zjawisko

Zeemana:

linia 643,8 nm

w Cd

(przejście

pomiędzy

wzbudzonymi

stanami

singletowymi

dla dwóch

konfiguracji,

5s5p i 5s5d):

1

P

1

→

1

D

2

Przypadek S =

0, trzy linie σ,

π, σ

Copyright © Springer-Verlag, The Physics of Atoms and Quanta by Hermann Haken and
Hans Christoph Wolf
Copyright © for the Polish edition by Wydawnictwo Naukowe PWN SA, Warszawa 2002

33

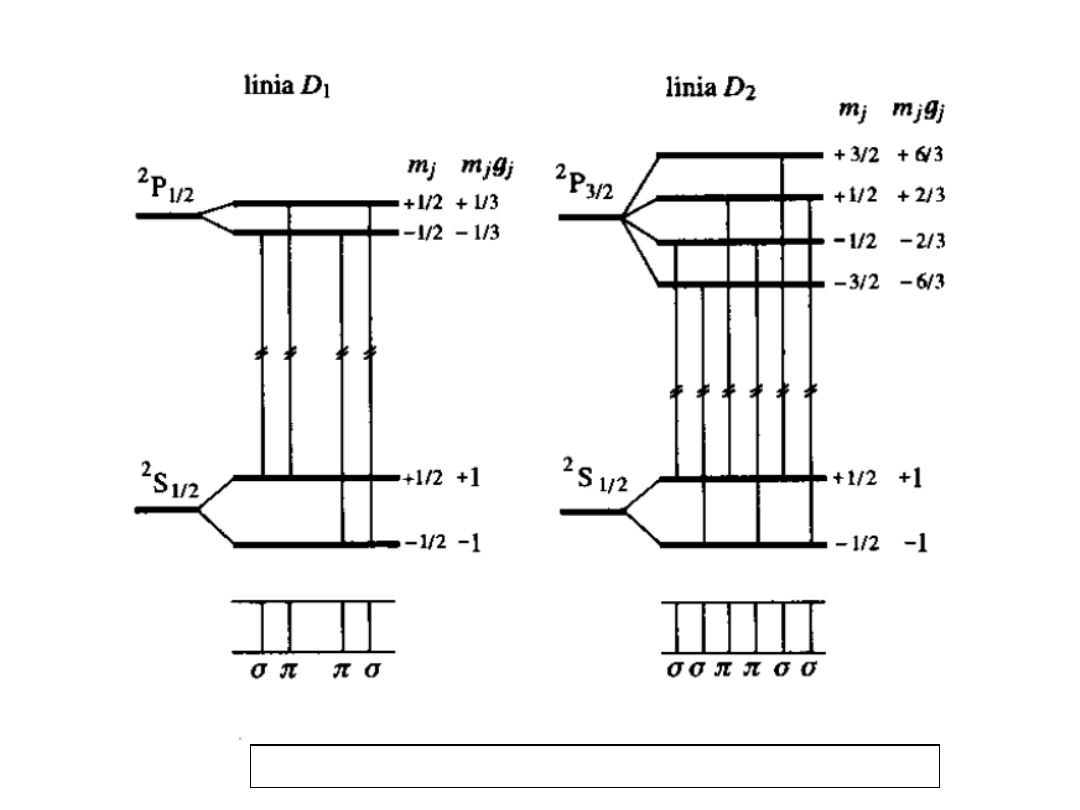
Anomalne zjawisko Zeemana,

rozszczepienie linii D

1

i D

2

sodu (3s-

3p):

2

S

1/2

→

2

P

1/2

(D

1

)

2

S

1/2

→

2

P

3/2

(D

2

)

Przypadek S > 0, σ,π,π,σ (D

1

)

σ,σ,π,π,σ,σ (D

2

)

34

Copyright © Springer-Verlag, The Physics of Atoms and Quanta by Hermann Haken and
Hans Christoph Wolf
Copyright © for the Polish edition by Wydawnictwo Naukowe PWN SA, Warszawa 2002