1

ATOM WODORU,

JONY WODOROPODOBNE;

PEŁNY OPIS

CZĘŚĆ II

2

Z protonów i jeden elektron:



























































































E

r

Ze

sin

r

1

sin

sin

r

1

r

r

r

r

1

m

2

2

2

2

2

2

2

2

2

2







   













,

Y

r

R

,

,

r

Podstawiając funkcję postaci:

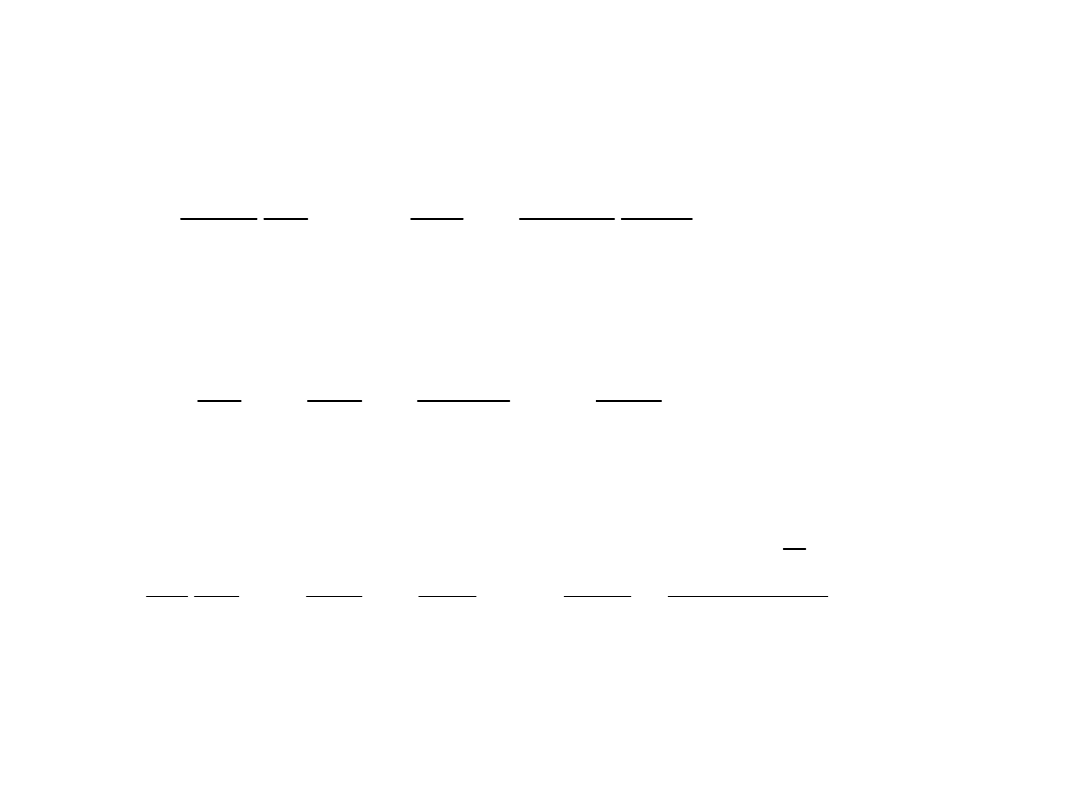
3

otrzymamy:





Y

1

Y

sin

1

Y

sin

sin

1

2

2

2





















































R

1

R

r

Ze

E

mr

2

dr

dR

r

dr

d

2

2

2

2











































0

R

mr

2

h

1

r

Ze

E

m

2

dr

dR

r

dr

d

r

1

2

2

2

2

2

2









































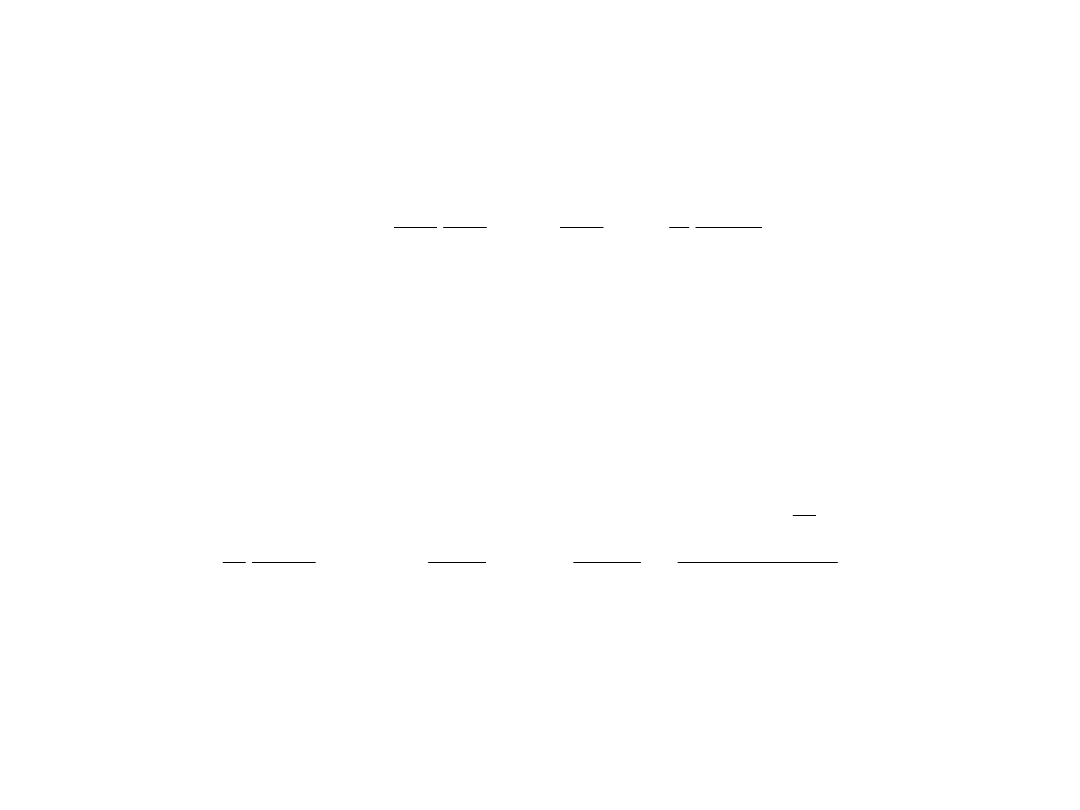
4

otrzymamy:

 





0

R

mr

2

h

1

r

Ze

E

m

2

rR

dr

d

r

1

2

2

2

2

2

2





























r

(

dr

d

r

1

dr

d

r

dr

d

r

1

2

2

2

2

2























Wykorzystując inną postać laplasjanu:

5

 

 

0

rR

r

Ze

E

m

2

rR

dr

d

2

2

2

2





















Rozpatrzymy najpierw przypadek ℓ

= 0 (funkcja Y

ℓ,m

stała, brak

zależności od kątów, symetria

kulistosymetryczna),

co oznacza brak wyrazu z energią

kinetyczną ruchu obrotowego:

6

Po podstawieniu:

promień Bohra Rydberg

otrzymamy:













0

2

2

a

mZe

r

















R

2

4

2

E

2

e

Z

m

E



 

 

0

R

2

R

d

d

2

2





























7

Przyjmiemy, że: oraz:

 

 

0

R

2

R

d

d

2

2





























 

 











R

f

 

 











g

e

f

 

 

 





























d

dg

e

g

e

d

df

Ponieważ:

8

oraz:

otrzymamy:

 

 

 

 

 

2

2

2

2

2

d

g

d

e

d

dg

e

d

dg

e

g

e

d

f

d

















































 

 

 

0

g

2

d

dg

2

d

g

d

2

2

2









































9

Możemy wykorzystać swobodę w

wyborze α

i przyjąć:

wówczas otrzymamy:

 

 

 

0

g

2

d

dg

2

d

g

d

2

2





























2

 













1

k

k

k

a

g

Szukamy rozwiązań w

postaci szeregu:

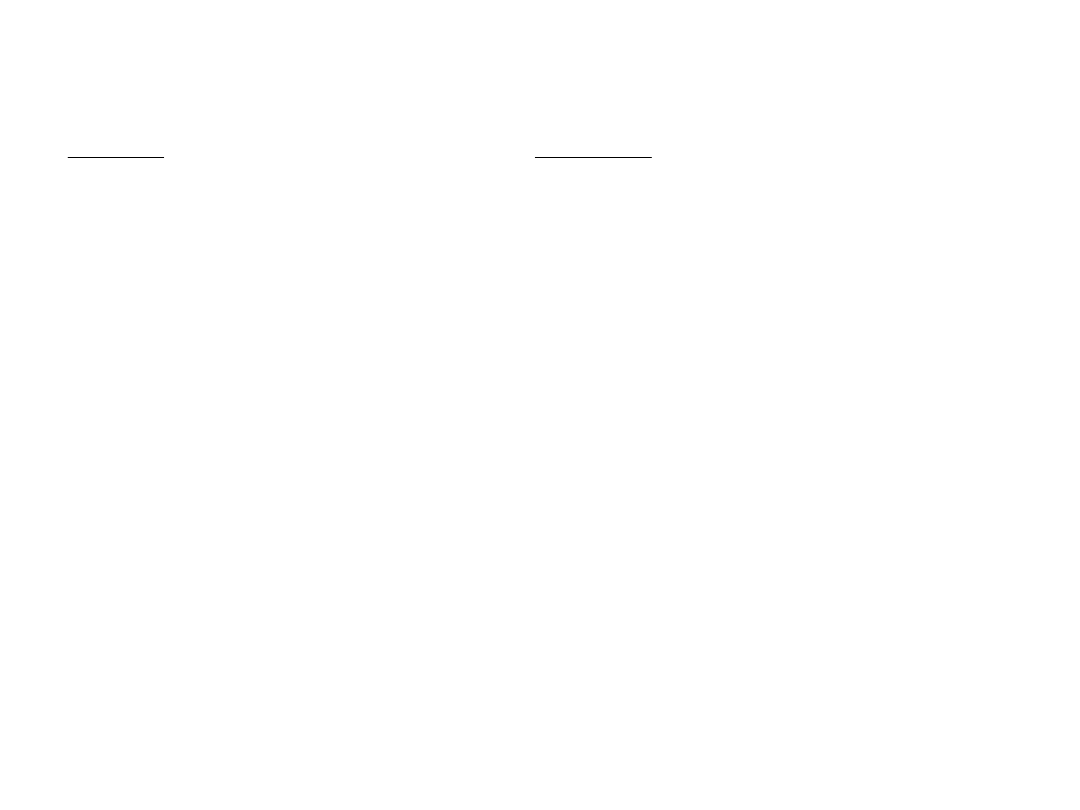
10

Wyliczamy pierwszą i drugą pochodną:

podstawiając otrzymamy:

Przenumerowujemy pierwszą sumę (za k

podstawiamy k+1):

 

















1

k

1

k

k

k

a

d

dg

 























1

k

2

k

k

2

2

1

k

k

a

d

g

d





0

a

2

k

a

2

1

k

k

a

1

k

1

k

k

1

k

1

k

k

1

k

2

k

k

















































0

a

2

ka

2

a

1

k

k

1

k

1

k

k

k

1

k























11

Skąd otrzymujemy rekurencyjny wzór

na współczynniki a

k

:

Szereg taki będzie równy 0 dla każdej

wartości ρ tylko wtedy, gdy:









0

a

1

k

2

a

1

k

k

k

1

k





















k

1

k

a

1

k

k

1

k

2

a











pozwalający wygenerować wszystkie

współczynniki a

k

(musimy tylko nadać

wartość współczynnikowi a

1

) a potem

otrzymać funkcję g, f, i na końcu R.

12

Dla dużych ρ (czyli dla dużych k):

Czy takie rozwiązanie jest fizycznie

prawidłowe?









k

k

1

k

a

k

2

a

1

k

k

1

k

2

a















czyli:

 

1

k

1

k

a

!

k

2

a







 

 



















2

1

k

1

k

k

1

e

a

!

k

2

a

g

i:

 















e

e

e

f

2

a funkcja f:

zmierza do nieskończoności dla dużych

odległości elektronu od jądra;

rozwiązanie niefizyczne

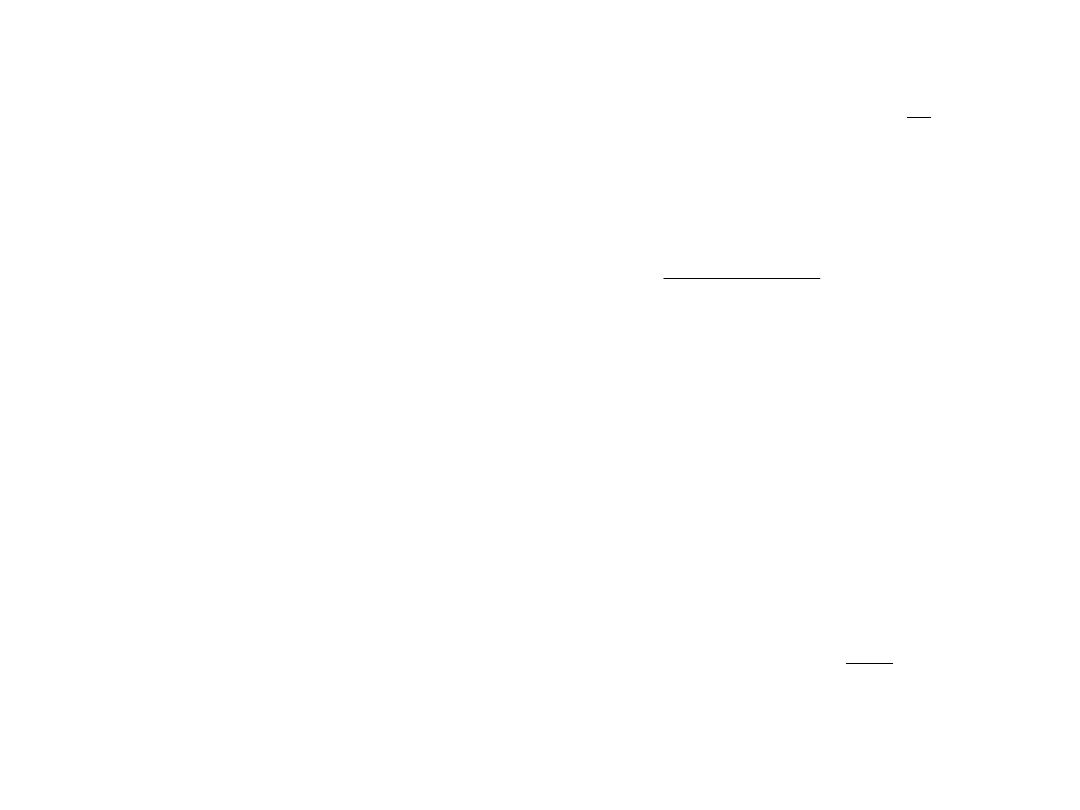
13

Sposobem na rozwiązanie

problemu jest przyjęcie

warunku, że:









.

0

a

1

n

n

1

n

2

a

n

1

n













.

n

1





Równe zeru będą także następne wyrazy i

dostaniemy wielomian o skończonym

rzędzie n, rosnący wolniej niż funkcja

eksponencjalna.

Mamy wówczas:

Mamy wówczas:

2

2

n

1











14

W konsekwencji:

 

eV

n

1

6

,

13

n

1

2

e

Z

m

E

E

2

2

2

4

2

R

n



















tzn. dopuszczone są tylko dyskretne

wartości energii, tak jak w teorii Bohra.

Wartości te odpowiadają kolejnym

wartościom liczby n, która, tak jak w

teorii Bohra, gra rolę głównej liczby

kwantowej

15

Natomiast część radialna funkcji falowej

wyrazi się:

gdzie:

 

 

 



















n

n

n

n

g

e

f

R

 











n

1

k

k

k

n

a

g





k

1

k

1

a

1

k

k

1

n

k

2

a

;

1

a













 







2

2

0

0

mZe

a

;

a

r









oraz:

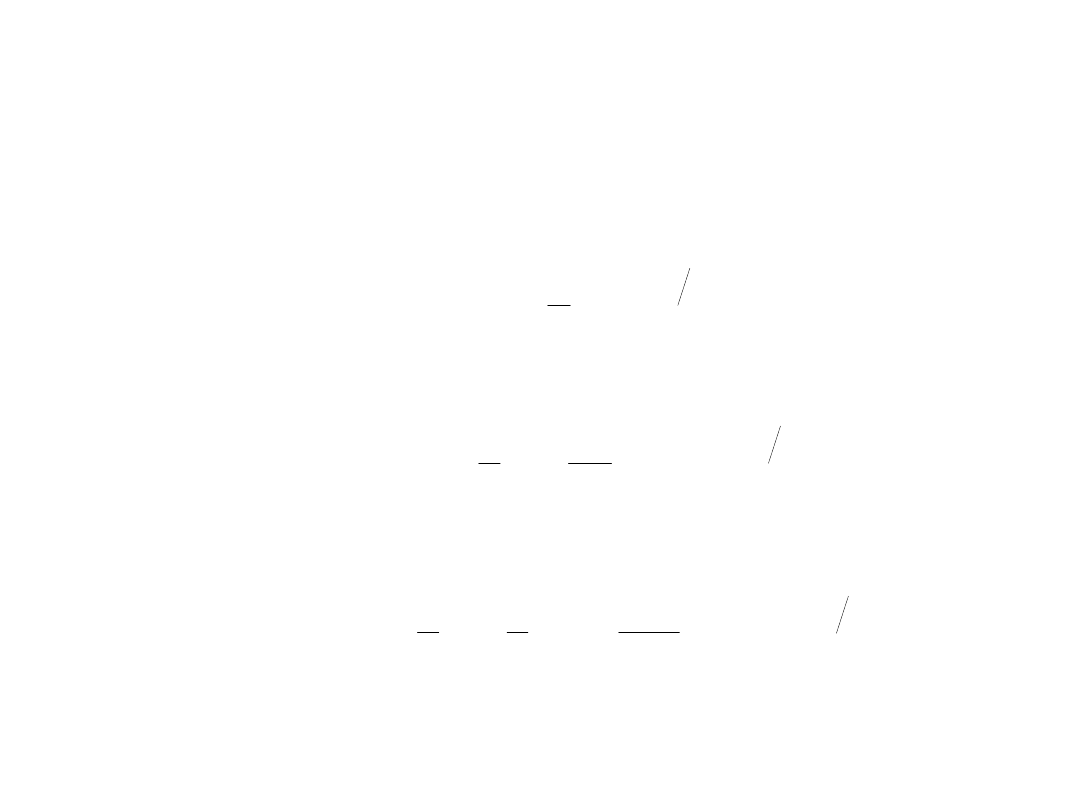
16

Kilka pierwszych funkcji radialnych dla ℓ

= 0:

 











e

1

R

1

 

2

2

e

2

1

R



























 

3

2

3

e

27

2

3

2

1

R































 

4

3

2

4

e

192

1

8

1

4

3

1

R



































17

Wracamy do pełnego równania

radialnego,

dopuszczamy zatem ℓ różne od zera:

 





 

0

rR

mr

2

h

1

r

Ze

E

m

2

rR

dr

d

2

2

2

2

2

2









































0

2

2

a

mZe

r

















R

2

4

2

E

2

e

Z

m

E



Po wykonaniu podstawień, takich samych

jak dla przypadku sferycznie

symetrycznego:

18

Otrzymujemy, podobnie jak poprzednio

równanie radialne (z dodatkowym

wyrazem):

Ten dodatkowy wyraz da dodatkowy wyraz

w rozwinięciu potęgowym funkcji g(ρ):

 



  

0

R

1

2

R

d

d

2

2

2











































 











1

k

2

k

k

a

1





19

Z wyrazu tego wydzielamy pierwszy wyraz

i przenumerowujemy całą sumę:







































1

k

1

k

1

k

1

a

a

1







 















0

a

1

a

2

ka

2

a

1

1

k

k

1

1

k

1

k

k

k

1

k









































Ponieważ ℓ jest różne od zera, a

1

musi być

równe zeru.

20

Zerowanie innych wyrazów zajdzie wtedy

gdy:

co stanowi zmodyfikowany związek

rekurencyjny na współczynniki

rozwinięcia funkcji g(ρ).







 



k

1

k

a

1

1

k

k

1

k

2

a



















Tak jak poprzednio, szereg musi się

urywać, co zajdzie dla k = n, gdy:

n

1





21

Ponieważ więc każdy kolejny
wyraz będzie równy 0, włącznie z
wyrazem k = ℓ.

0

a

1



Pierwszym wyrazem, który może być

różny od zera,

będzie wyraz a

ℓ+1

, ze względu na postać

wzoru rekurencyjnego (obecność wyrazu

ℓ(ℓ+1)).

Zatem, żeby nie okazało się, że wszystkie

wyrazy są równe zeru, musi zachodzić: ℓ

n



bo a

n+1

i następne wyrazy także muszą

być równe 0.

Dla danego n, k biegną od ℓ+1 do n.

Dozwolone wartości ℓ biegną od 0 do n –

1.

22

Dla małych ρ w funkcji R, równej:
dominować będzie wyraz z

A więc funkcje radialne R, dla większych

wartości ℓ, będą znacząco różnić się od

zera dalej od jądra.

 









g

e

.





Przykłady funkcji radialnych R dla kilku

wartości głównej (n) i pobocznej (ℓ)

liczby kwantowej:

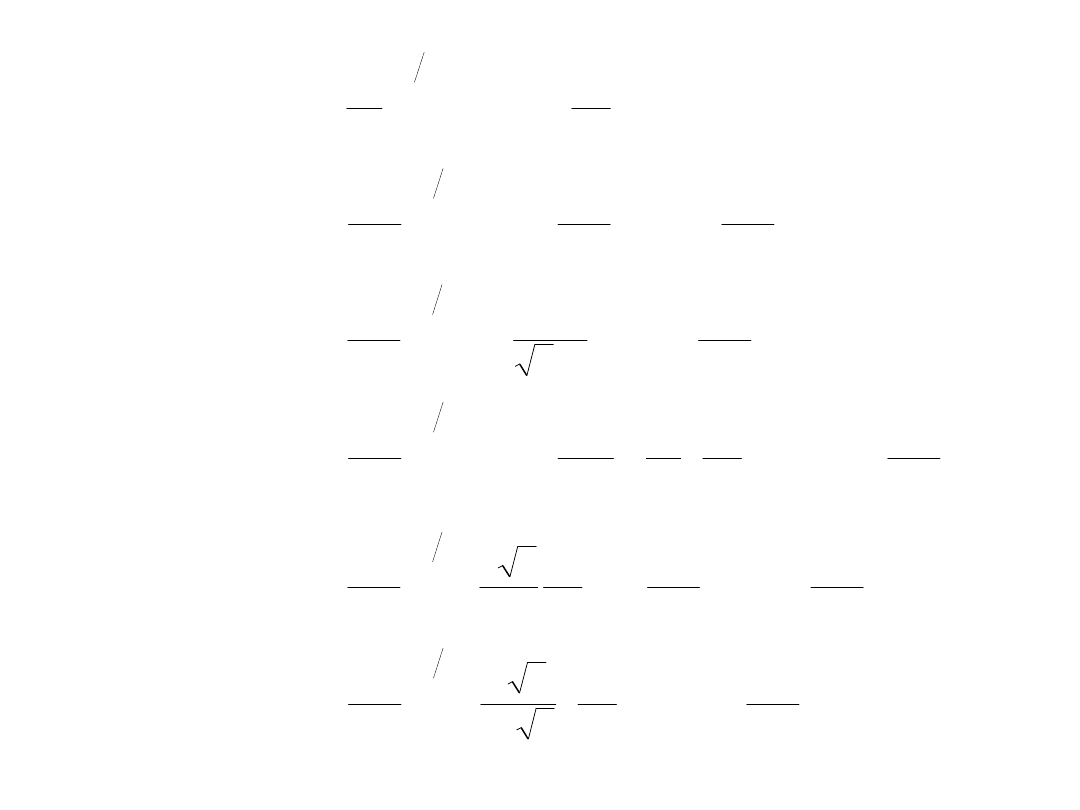
23

 

 

 

 

 

 







































































































































































































































































0

2

0

2

3

0

32

0

0

0

2

3

0

31

0

2

0

0

2

3

0

30

0

0

2

3

0

21

0

0

2

3

0

20

0

2

3

0

10

a

3

Zr

exp

a

Zr

5

27

2

2

a

3

Z

r

R

a

3

Zr

exp

a

6

Zr

1

a

Zr

3

2

4

a

3

Z

r

R

a

3

Zr

exp

a

Zr

27

2

a

3

Zr

2

1

2

a

3

Z

r

R

a

2

Zr

exp

a

3

Zr

2

a

2

Z

r

R

a

2

Zr

exp

a

2

Zr

1

2

a

2

Z

r

R

a

Zr

exp

2

a

Z

r

R

24

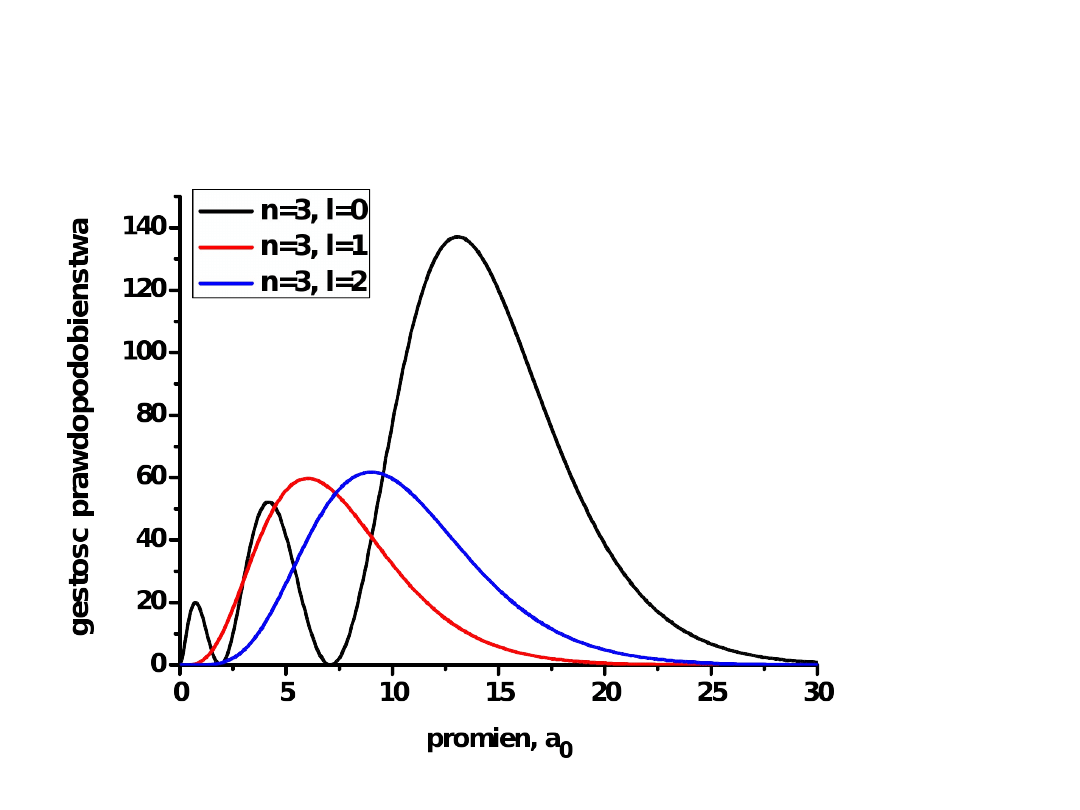
Radialna gęstość prawdopodobieństwa

dla elektronów 3s, 3p i 3d w atomie H

Choć średnio

elektron 3s jest

dalej od jądra,

prawdopodobień

stwo znalezienia

go w obszarze

bliskim jądra jest

większe niż dla

elektronu 3p i 3d

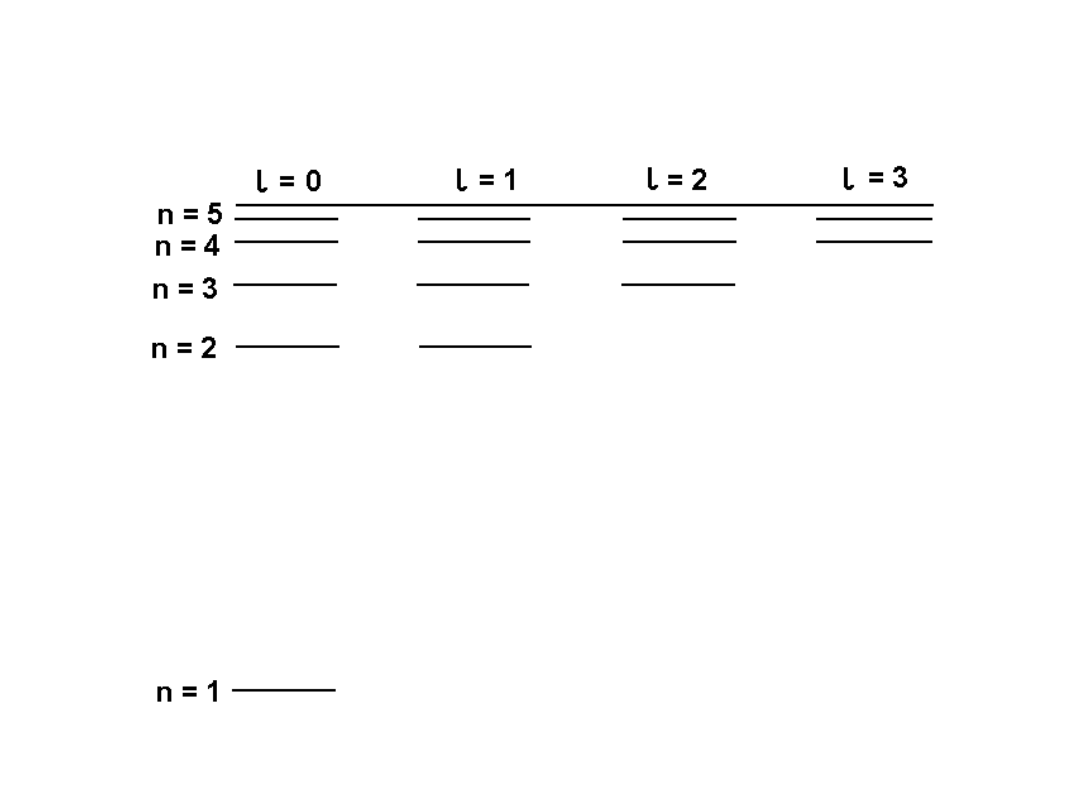
25

Schemat poziomów energetycznych

atomu wodoru;

diagram Grotriana

Dla jonów

wodoropodobnych

zmiana skali E ze

względu na Z

Degeneracja ze względu

na ℓ (degeneracja

orbitalna)