
Granica funkcji
Granica funkcji
Definicja Heine’go
Definicja Heine’go
i
i
Definicja Cauchy’ego
Definicja Cauchy’ego

Definicja Heine’go
Definicja Heine’go
Liczbę
Liczbę
a
a
nazywamy granicą funkcji
nazywamy granicą funkcji
y = f(x)
y = f(x)
w punkcie
w punkcie
x
x
0
0
jeśli dla każdego ciągu
jeśli dla każdego ciągu
(x
(x
n
n
)
)
argumentów funkcji zbieżnego do
argumentów funkcji zbieżnego do
x
x
0
0
o
o
wyrazach różnych od
wyrazach różnych od
x
x
0
0
, odpowiadający
, odpowiadający
mu ciąg
mu ciąg
(f(
(f(
x
x
n
n
))
))
wartości funkcji jest zbieżny
wartości funkcji jest zbieżny
do
do
a
a
.
.
Fakt, że granicą funkcji przy
Fakt, że granicą funkcji przy
x
x
dążącym do
dążącym do
x
x
0
0
jest liczba
jest liczba
a
a
zapisujemy:
zapisujemy:

Jeżeli
Jeżeli
f : X
f : X
R
R
i
i
g : X
g : X
R
R
(
(
X
X
-
- dziedzina
funkcji)
funkcji)
są dowolnymi funkcjami, to:
są dowolnymi funkcjami, to:
►
sumą funkcji
sumą funkcji
f
f
i
i
g
g
nazywamy
nazywamy
funkcję
funkcję
f + g : X
f + g : X
R
R
określoną wzorem:
określoną wzorem:

►
różnicą funkcji
różnicą funkcji
f
f
i
i
g
g
nazywamy funkcję
nazywamy funkcję
f – g : X
f – g : X
R
R
określoną wzorem:
określoną wzorem:
►
Iloczynem funkcji
Iloczynem funkcji
f
f
i
i
g
g
nazywamy
nazywamy
funkcję
funkcję
f
f
∙
∙
g : X
g : X
R
R
określoną wzorem:
określoną wzorem:

►
Ilorazem funkcji
Ilorazem funkcji
f
f
i
i
g
g
nazywamy
nazywamy
funkcje
funkcje
f/g : X
f/g : X
R
R
określoną wzorem:
określoną wzorem:
►
Iloczynem funkcji
Iloczynem funkcji
f
f
przez liczbę
przez liczbę
rzeczywistą
rzeczywistą
k
k
nazywamy funkcję
nazywamy funkcję
kf : X
kf : X
R
R
określoną wzorem:
określoną wzorem:

►
Jeśli funkcje
Jeśli funkcje
f
f
i
i
g
g
mają
mają
w punkcie
w punkcie
x
x
0
0
granice odpowiednio
granice odpowiednio
a
a
i
i
b
b
,
,
to istnieją w punkcie x
to istnieją w punkcie x
0
0
granice funkcji
granice funkcji
f + g, f – g, f
f + g, f – g, f
∙
∙
g, f/g : g
g, f/g : g
≠ 0
≠ 0
i zachodzą związki:
i zachodzą związki:
►
Jeżeli funkcja
Jeżeli funkcja
f
f
jest funkcją wymierną
jest funkcją wymierną
postaci
postaci
x
x
W
1
(x) / W
2
(x)
, gdzie
W
1
,
W
2
są wielomianami i punkt
x
2
nie jest
miejscem zerowym wielomianu
W
2
to:
)
(
)
(
lim
0
2
x
f
x
f
x

►
Liczbę
Liczbę
a
a
nazywamy granicą funkcji
nazywamy granicą funkcji
f : X
f : X
R
R
w punkcie
w punkcie
x
x
0
0
, gdy
, gdy
dla dowolnego otoczenia
dla dowolnego otoczenia
U
U
punktu
punktu
a
a
istnieje takie sąsiedztwo
istnieje takie sąsiedztwo
S
S
punktu
punktu
x
x
0
0
,
,
że jeśli
że jeśli
x
x
∈S∩X
∈S∩X
, to
, to
f(x)∈U
f(x)∈U

Definicje Heine’go dotyczące granic
Definicje Heine’go dotyczące granic
niewłaściwych funkcji w punkcie.
niewłaściwych funkcji w punkcie.
►
Funkcja
Funkcja
f : X
f : X
R
R
ma w punkcie
ma w punkcie
x0
x0
granicę niewłaściwą
granicę niewłaściwą
+
+
∞
∞
, jeśli dla
, jeśli dla
każdego ciągu (
każdego ciągu (
xn
xn
) argumentów
) argumentów
funkcji
funkcji
f
f
zbieżnego do
zbieżnego do
x0
x0
, o wyrazach
, o wyrazach
różnych od
różnych od
x0
x0
, odpowiadający mu ciąg
, odpowiadający mu ciąg
(
(
f(xn
f(xn
))
))
wartości funkcji jest rozbieżny
wartości funkcji jest rozbieżny
do
do
+∞
+∞
.
.

►
Funkcja
Funkcja
f : X
f : X
R
R
ma w punkcie
ma w punkcie
x
x
0
0
granicę niewłaściwą
granicę niewłaściwą
-
-
∞
∞
, jeśli dla
, jeśli dla
każdego ciągu
każdego ciągu
(
(
x
x
n
n
)
)
argumentów funkcji
argumentów funkcji
f
f
zbieżnego do
zbieżnego do
x
x
0
0
,
,
o wyrazach różnych od
o wyrazach różnych od
x
x
0
0
,
,
odpowiadający mu ciąg
odpowiadający mu ciąg
(f(x
(f(x
n
n
))
))
wartości funkcji jest rozbieżny do
wartości funkcji jest rozbieżny do
-∞
-∞
.
.

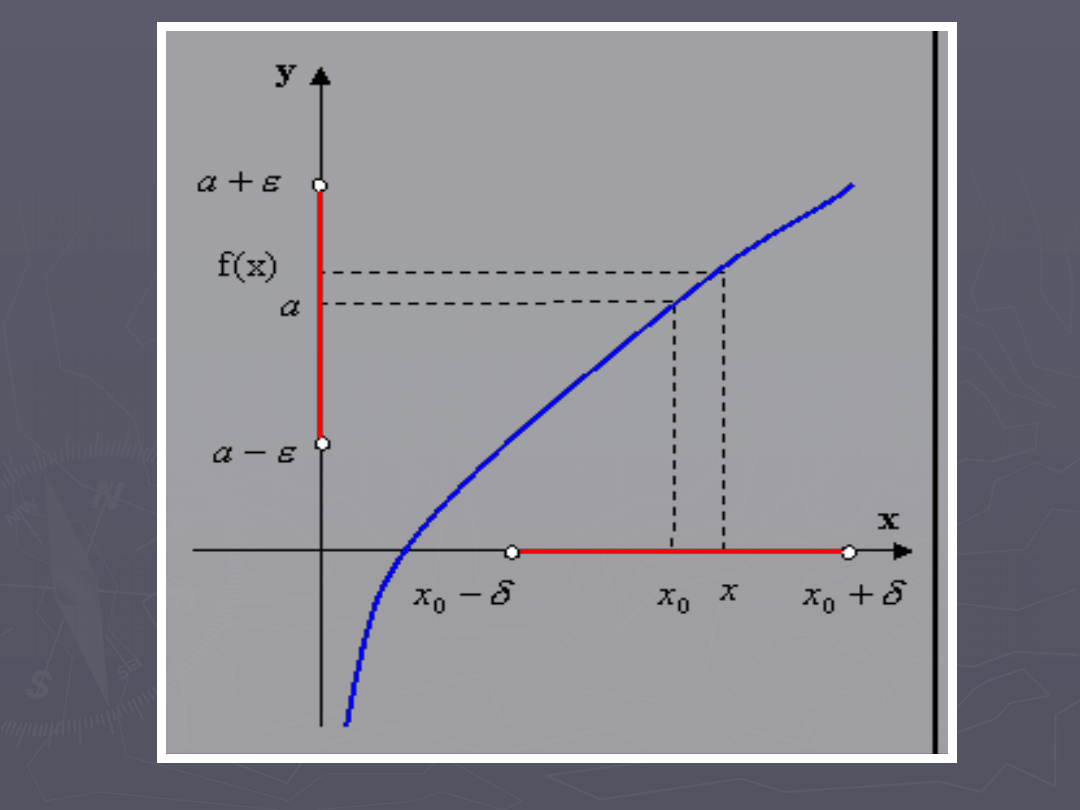
Definicja Cauchy’ego
Definicja Cauchy’ego
►
Liczbę
Liczbę
a
a
nazywamy granicą funkcji
nazywamy granicą funkcji
f : X
f : X
R
R
w punkcie
w punkcie
x
x
0
0
,
,
gdy dla każdej liczby
gdy dla każdej liczby
>0
>0
istnieje
istnieje
taka liczba
taka liczba
>0
>0
, że dla dowolnego
, że dla dowolnego
x
x
∈X
∈X
prawdziwa jest implikacja:
prawdziwa jest implikacja:
0
0
<
<
|x- x0|<
|x- x0|<
⇒
⇒
|f(x)-a| <
|f(x)-a| <

►
Możemy to zapisać jako:
Możemy to zapisać jako:

Definicje Cauchy’ego dotyczące
Definicje Cauchy’ego dotyczące
granic niewłaściwych funkcji w
granic niewłaściwych funkcji w
punkcie.
punkcie.
►
Funkcja
Funkcja
f : X
f : X
R
R
ma w punkcie
ma w punkcie
x
x
0
0
granicę niewłaściwą
granicę niewłaściwą
+
+
∞
∞
,
,
jeśli dla każdej liczby
jeśli dla każdej liczby
E>0
E>0
istnieje
istnieje
taka liczba
taka liczba
>0
>0
, że dla dowolnego
, że dla dowolnego
x
x
∈
∈
X
X
prawdziwa jest implikacja:
prawdziwa jest implikacja:
0<|x-x0|<
0<|x-x0|<
⇒f(x)>E
⇒f(x)>E

►
Możemy to zapisać jako:
Możemy to zapisać jako:
►
Funkcja
Funkcja
f : X
f : X
R
R
ma w punkcie
ma w punkcie
x
x
0
0
granicę niewłaściwą
granicę niewłaściwą
-
-
∞
∞
, jeśli dla każdej
, jeśli dla każdej
liczby
liczby
E>0
E>0
istnieje taka liczba
istnieje taka liczba
>0
>0
, że
, że
dla dowolnego
dla dowolnego
x
x
∈
∈
X
X
prawdziwa jest
prawdziwa jest
implikacja:
implikacja:
0<|x-x)|<
0<|x-x)|<
⇒
⇒
f(x)<-E
f(x)<-E

►
Możemy to zapisać jako:
Możemy to zapisać jako:

►
Granice funkcji
Granice funkcji
:
:


►
Przykłady:
Przykłady:
3
2
1
3
1
2
lim
2
sin
3
)
2
(
2
lim
2
sin
3
4
lim
.
3
4
7
3
1
6
1
lim
3
6
lim
.
2
26
15
2
24
7
8
lim
2
8
3
7
4
2
lim
2
2
3
7
2
2
lim
2
3
7
2
lim
.
1
0
0
0
1
4
4
1
2
2
3
2
2
3
2
2
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
Wyszukiwarka
Podobne podstrony:
(4078) granica funkcji semiiid 1050 ppt
granica funkcji zadania 1 plus 2
Analiza matematyczna Wykłady, GRANICE FUNKCJI
Matematyka cw5 Granice funkcji Ciaglosc funkcji Asymptoty
Granica funkcji(1), Prywatne
Granice funkcji - pochodne, Prywatne, matna
Granice funkcji
granice funkcji ciaglosc funkcji (1)
Analiza matematyczna. Wykłady GRANICE FUNKCJI
Granica funkcji, Granica funkcji
Kolokwium granice i funkcja
GRANICA FUNKCJI
Granice funkcji IMiR
więcej podobnych podstron