dr Mariola Chrzanowska

mariola_chrzanowska@sggw.pl

Wykład 1

PODSTAWY TEORII ESTYMACJI

1

METODY PROGNOZOWANIA WYKŁAD 1

Forecasting is the art of 
saying what will happen, and 
then explaining why it didn't!

    
 Anonymous 
(communicated by Balaji 
Rajagopalan)

2

METODY PROGNOZOWANIA WYKŁAD 1

ZASADY ZALICZEŃ

•

 Obecność na ćwiczeniach jest 

OBOWIĄZKOWA

•

 Koloqium 28.05.2012

•

 Koloqium poprawkowe 11.06.2012

•

 Warunkiem dopuszczenia do egzaminu 

jest zaliczenie ćwiczeń

•

 Egzamin zerowy 11.06.2012

•

 Egzamin I termin 18.06.2012 

3

METODY PROGNOZOWANIA WYKŁAD 1

TREŚCI KSZTAŁCENIA

•

 powtórzenie wiadomości z zakresu wnioskowania 

  statystycznego;

•

 modele regresji;

•

 ocena jakości modelu regresji;

•

 wybrane modele nieliniowe;

•

 modele zmiennych jakościowych

•

 prognozowanie na podstawie szeregów 

czasowych;

•

 modele wielorównaniowe

•

 analiza mnożnikowa

•

 sztuczne sieci neuronowe;

•

 modelowanie rozmyte

4

METODY PROGNOZOWANIA WYKŁAD 1

LITERATURA

•

 Cieślak Maria Prognozowanie gospodarcze,

  Wydawnictwo Naukowe PWN, Warszawa 2008
  (wersja elektroniczna na ibuk.pl);

•

 Witkowska Dorota Podstawy ekonometrii i 

  teorii prognozowania, Oficyna Ekonomiczna
  2006;

•

Zeliaś Aleksander, Pawełek Barbara, Wanat 

Stanisław

 Prognozowanie   ekonomiczne, Teoria,

 przykłady, zadania.   Wydawnictwo Naukowe 

PWN

 2008. 

5

METODY PROGNOZOWANIA WYKŁAD 1

Literatura uzupełniająca



Żółtowska Elżbieta, Sieczko Anna. 

Chrzanowska Mariola: Ekonometria. 
Wykład ilustrowany przykładami, 
Wydawnictwo Wyższej Szkoły Ekonomii i 
Prawa, Kielce 2009.



Lula Paweł: Jednokierunkowe sieci 

neuronowe w modelowaniu zjawisk 
ekonomicznych, Wydawnictwo Akademii 
Ekonomicznej w Krakowie, Kraków 1999. 

METODY PROGNOZOWANIA WYKŁAD 1

WPROWADZENIE

Przykład 1
Niech zmienna losowa X oznacza dzienne 
zapotrzebowanie na energię elektryczną gospodarstwa 
domowego. Przypuśćmy, że obserwując miesięczne 
zużycie pięciu gospodarstw otrzymano następujące 
realizacje zmiennej losowej X:
31,0  35,1  29,4  36,0  26,8  [KWh]
Na podstawie tych informacji  możemy wyznaczyć 
przeciętne miesięczne zużycie energii elektrycznej  
w badanych gospodarstwach domowych (31,66 KW/h)
Czy można w takiej  sytuacji uważać, że gospodarstwa 
domowe w Polsce zużywają  miesięcznie 61,66 kW/h?

7

METODY PROGNOZOWANIA WYKŁAD 1

WPROWADZENIE

Przykład 1 cd
Oczywiście nie można odpowiedzieć dokładnie, 
ile wynosi średnie zużycie gospodarstw 
domowych E(X). Można jedynie prawie 
wyznaczyć   jego wartość. 
Jakie warunki musi zatem spełniać próba, aby 
oszacowana wartość była jak najbardziej zbliżona 
do wartości prawdziwej?

8

METODY PROGNOZOWANIA WYKŁAD 1

DOBÓR PRÓBY DO BADAŃ 
CZĘŚCIOWYCH

próba reprezentatywna – 
odwzorowująca strukturę zbiorowości 
z przyjętą dokładnością,
dobór losowy: każda jednostka 
może wejść do próby z tym samym 
prawdopodobieństwem (wówczas 
próba jest nieobciążona),
próba reprezentatywna – 
nieobciążona i odpowiednio liczna

9

METODY PROGNOZOWANIA WYKŁAD 1

ESTYMACJA PARAMETRÓW ZBIOROWOŚCI 
GENENERALNEJ

Przykład 1 nawiązuje do problemów 
przybliżania nieznanych wartości 
parametrów,  który charakteryzuje rozkład 
pewnej zmiennej losowej. 
Estymacja, czy też ocena lub szacowanie to 
proces, który w badaniach częściowych 
umożliwia wnioskowanie o rozkładzie 
i podstawowych charakterystykach 
zbiorowości generalnej wykorzystując w tym 
celu metody wnioskowania statystycznego,

10

METODY PROGNOZOWANIA WYKŁAD 1

ESTYMACJA 

W ogólniejszym sformułowaniu chodzi tu o 

estymację nieznanego parametru, który 

charakteryzuje rozkład pewnej zmiennej 

losowej.

Rozróżnia się estymację punktową i 

estymację przedziałową. 

W pierwszym przypadku wynikiem estymacji 

jest jedna (konkretna) liczba. Wartość 

estymatora obliczana jest na podstawie n 

elementowej próby

W drugim przypadku wynik wyraża się w 

postaci przedziału. który z ustalonym 

prawdopodobieństwem zawiera nieznaną 

wartość szacowanego parametru zbiorowości 

generalnej.

11

METODY PROGNOZOWANIA WYKŁAD 1

PODSTAWOWE POJĘCIA

•

 Estymatorem nazywa się dowolną statystykę T

n

 

wyznaczoną na podstawie n-elementowej próby i służącą do 

oszacowania nieznanej wartości parametru w populacji 

generalnej 



. Inaczej mówiąc, estymatorem jest zmienna 

losowa (każdej próbie n-elementowej przypisujemy liczbę t

n

), 

której rozkład zależy od rozkładu szacowanego parametru. 

•

 Przez rozkład estymatora rozumie się rozkład 

prawdopodobieństwa zmiennej losowej T

n

, którego 

parametrami są wartość oczekiwana E(T

n

) oraz wariancja 

D

2

(T

n

). 

•

 Wartość liczbową t

n

, jaką przyjmuje estymator T

n

 

(parametru 



) dla określonej próby nazywa się oceną 

estymatora parametru 



. Oznacza to, że, wartość t

n,

 

będąca oceną estymatora parametru 



, jest realizacją 

zmiennej losowej T

n

.

 Statystyka to miara opisowa pochodząca z n-elementowej 

próby losowej, np. średnia arytmetyczna, odchylenie 

standardowe, wskaźnik struktury.

12

METODY PROGNOZOWANIA WYKŁAD 1

O wyborze takiego lub innego estymatora decydują 

jego własności. Szczególnie ważne są dwa kryteria:
Estymator Tn nazywamy nieobciążonym 

estymatorem parametru 



, jeśli jego wartość 

oczekiwana równa jest szacowanemu parametrowi, 

czyli jest spełniony warunek:

 
Wariancja D

2

(U) estymatora powinna być mała; im 

jest mniejsza, tym estymator ma większą 

efektywność. 
Stosowanie estymatora najbardziej efektywnego 

oznacza, że w trakcie estymacji popełnia się 

najmniejszy błąd szacunku.

13

 





n

T

E

WŁASNOŚCI

 

ESTYMATORÓW

METODY PROGNOZOWANIA WYKŁAD 1

WŁASNOŚCI ESTYMATORÓW

Estymator Tn nazywamy zgodnym z 

estymatorem parametru 



, jeśli jest on 

zbieżny według prawdopodobieństwa do  

wartości szacowanego parametru 



, tzn. gdy: 

Korzystanie z estymatora Tn posiadającego 

własności zgodności, nieobciążoności 

i będącego najbardziej efektywnym pozwala 

najlepiej oszacować nieznaną wartość 

parametr 



, ponieważ z dużym 

prawdopodobieństwem można przyjąć, że 

wyznaczona ocena estymatora Tn jest bliska 

rzeczywistej wartości 

14





0

 

lim

0





















n

n

T

P

METODY PROGNOZOWANIA WYKŁAD 1

W przypadku badania częściowego 
wartości parametrów zbiorowości 
generalnej są szacowane z pewnym 
błędem. 
Standardowy błąd szacunku jest 
odchyleniem standardowym, czyli 
pierwiastkiem kwadratowym z 
wariancji D

2

(T

n

) rozkładu estymatora 

T

n

, za pomocą którego szacuje się 

parametr 



 populacji generalnej. 

15

METODY PROGNOZOWANIA WYKŁAD 1

ESTYMACJA PRZEDZIAŁOWA

Wyznacza się przedział liczbowy, który z 

ustalonym prawdopodobieństwem zawiera 

nieznaną wartość szacowanego parametru 

zbiorowości generalnej. 

Prawdopodobieństwo to nosi nazwę 

współczynnika ufności i oznaczane jest 

jako 1-



, a znaleziony przedział nazywany 

jest przedziałem ufności. Innymi słowy, 

przedział ufności informuje, w jakich 

granicach należy spodziewać się wartości 

dla poszukiwanego parametru 



  z zadanym 

z góry prawdopodobieństwem. 

16

METODY PROGNOZOWANIA WYKŁAD 1

ESTYMACJA PRZEDZIAŁOWA

Konstruując przedział ufności jesteśmy w stanie 

określić prawdopodobieństwo, z jakim 

oszacowaliśmy przedział dla wartości 

nieznanego parametru, czego nie daje 

estymacja punktowa. Należy przy tym 

pamiętać, że:

•

przy zadanym poziomie ufności 1-



 im 

większa jest liczebność, tym krótszy przedział 

ufności,

•

przy ustalonej liczebności próby wraz ze 

wzrostem poziomu ufności rośnie rozpiętość 

(długość) przedziału ufności,

•

im krótszy przedział, tym mniejszy błąd 

szacunku, co oznacza większą dokładność 

oszacowania

17

METODY PROGNOZOWANIA WYKŁAD 1

ESTYMACJA PRZEDZIAŁOWA

Podstawowymi parametrami, które 
szacowane są dla populacji 
generalnej są: 

•

wartość oczekiwana (średnia) 

E(X)=



, wariancja D

2

(X)=



2

, 

•

odchylenie standardowe 



 

•

frakcja (wskaźnik struktury) p. 

METODY PROGNOZOWANIA WYKŁAD 1

18

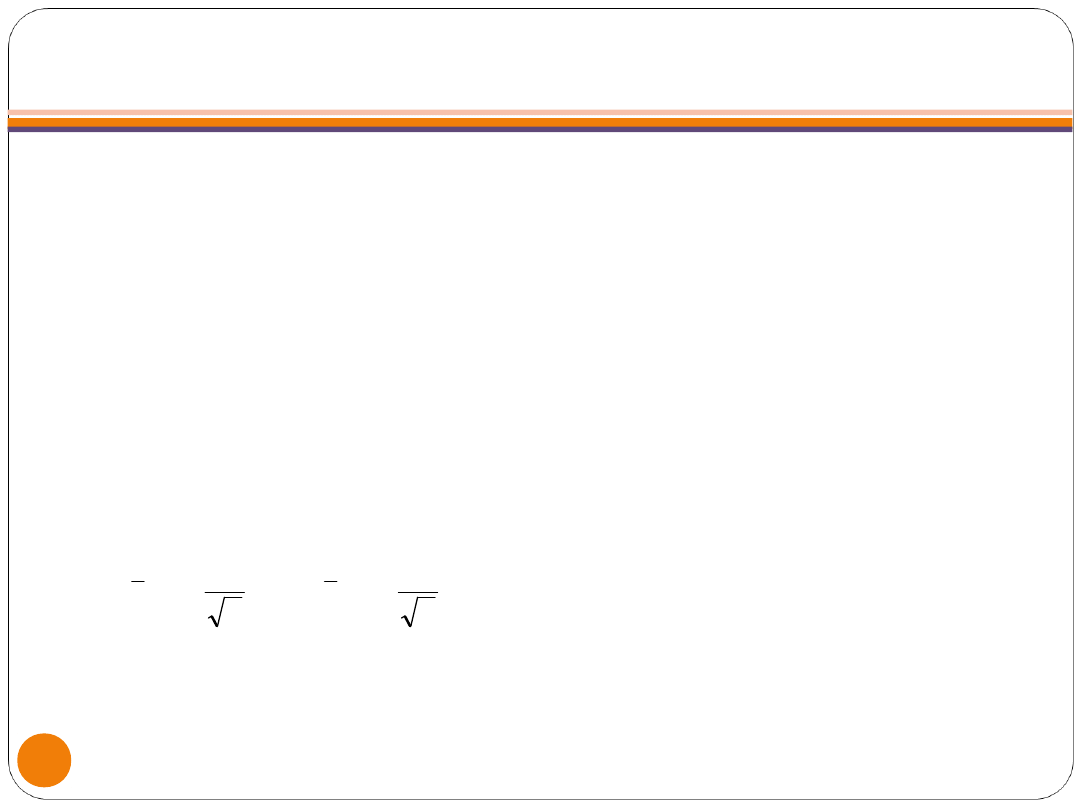
PRZYPADEK 1. PRZEDZIAŁ UFNOŚCI DLA 
WARTOŚCI OCZEKIWANEJ, GDY ZNANA JEST 
WARIANCJA 



2

Załóżmy, iż populacja generalna ma 
rozkład normalny i znamy jego 
zróżnicowanie mierzone 
odchyleniem standardowym (



). 

Wylosowano z niej  w sposób 
nieograniczony i niezależny próbę 
losową n-elementową. W tym 
przypadku przedział ufności jest 
postaci:

METODY PROGNOZOWANIA 2011/2012

19





































1

n

u

x

n

u

x

P

PRZYPADEK 1. PRZEDZIAŁ UFNOŚCI DLA 
WARTOŚCI OCZEKIWANEJ, GDY ZNANA JEST 
WARIANCJA 



2

gdzie: 



  - szacowana wartość oczekiwana (średnia) w 

populacji generalnej, 



  - znana wartość odchylenia standardowego w 

populacji generalnej, 
     - średnia arytmetyczna obliczona dla n-
elementowej próby statystycznej na podstawie 
jednej z  relacji
     -  wartość zmiennej losowej u odczytana z tablic 
dystrybuanty rozkładu normalnego 
standaryzowanego tak, aby spełniony był warunek 

20

x



















































1

u

n

x

P

u

u

P

u



METODY PROGNOZOWANIA 2011/2012

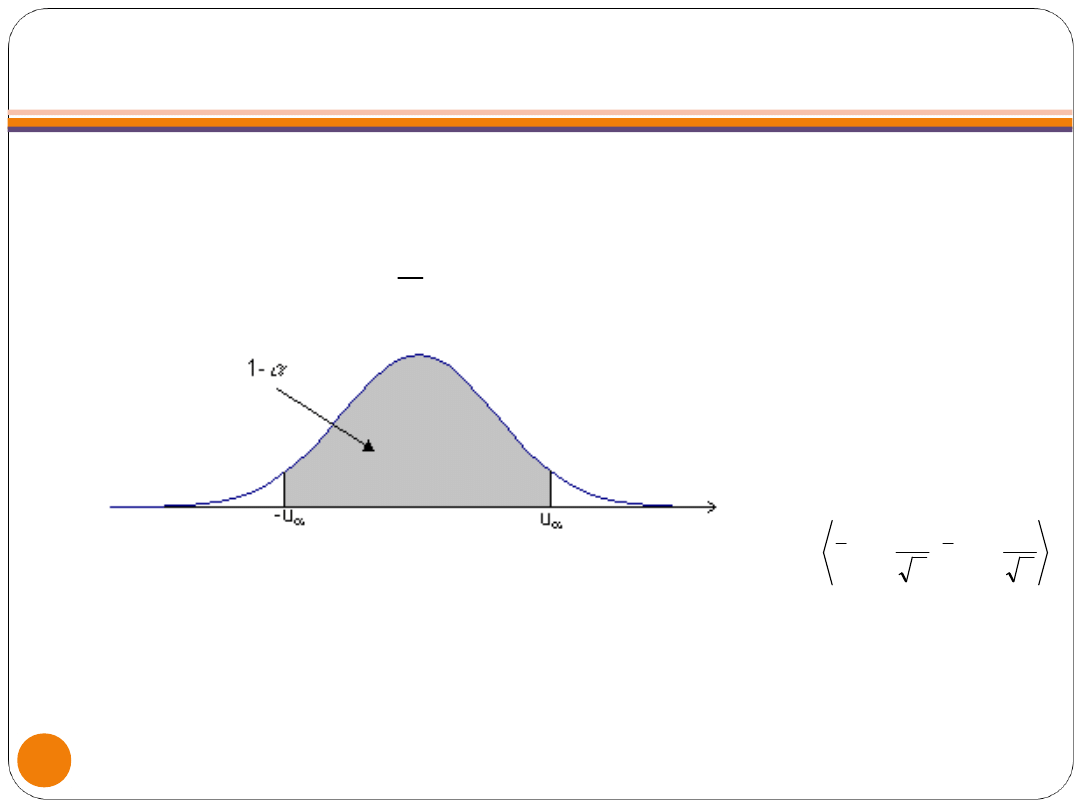
Innymi słowy z tablic dystrybuanty 

standaryzowanego rozkładu normalnego 

odczytujemy taką wartość       , która spełnia 

równanie: 

Przedziałem ufności dla parametru  jest 

przedział
który z prawdopodobieństwem  1-  pokrywa 

nieznaną wartość parametru .

21



u

 

2

1









 u

n

u

x

n

u

x













;

METODY PROGNOZOWANIA 2011/2012

PRZYKŁAD 2

W wyniku badania przeprowadzonego na 16-

elementowej próbie losowo wybranych 

pracowników firmy NORNIK, dotyczącego 

wieku okazało się, że przeciętny wiek 

pracownika to 27 lat. Wiadomo, że wielkość 

ta ma ona rozkład normalny. W wyniku tego 

badania stwierdzono, że zróżnicowanie 

wieku pracowników mierzone odchyleniem 

standardowym wynosiło 3. Z wiarygodnością 

95% wyznaczyć przedział ufności dla 

średniego wieku pracowników.

22

METODY PROGNOZOWANIA 2011/2012

PRZYKŁAD 2

W środku tablicy rozkładu normalnego szukamy prawdopodobieństwa o 

wartości 0,99:

Z prawdopodobieństwem 0,98 ,można twierdzić, że średni wiek 

pracowników zakładu NORNIK zawiera się między 25,2 a 28,7 lat

METODY PROGNOZOWANIA 2010/2011

23

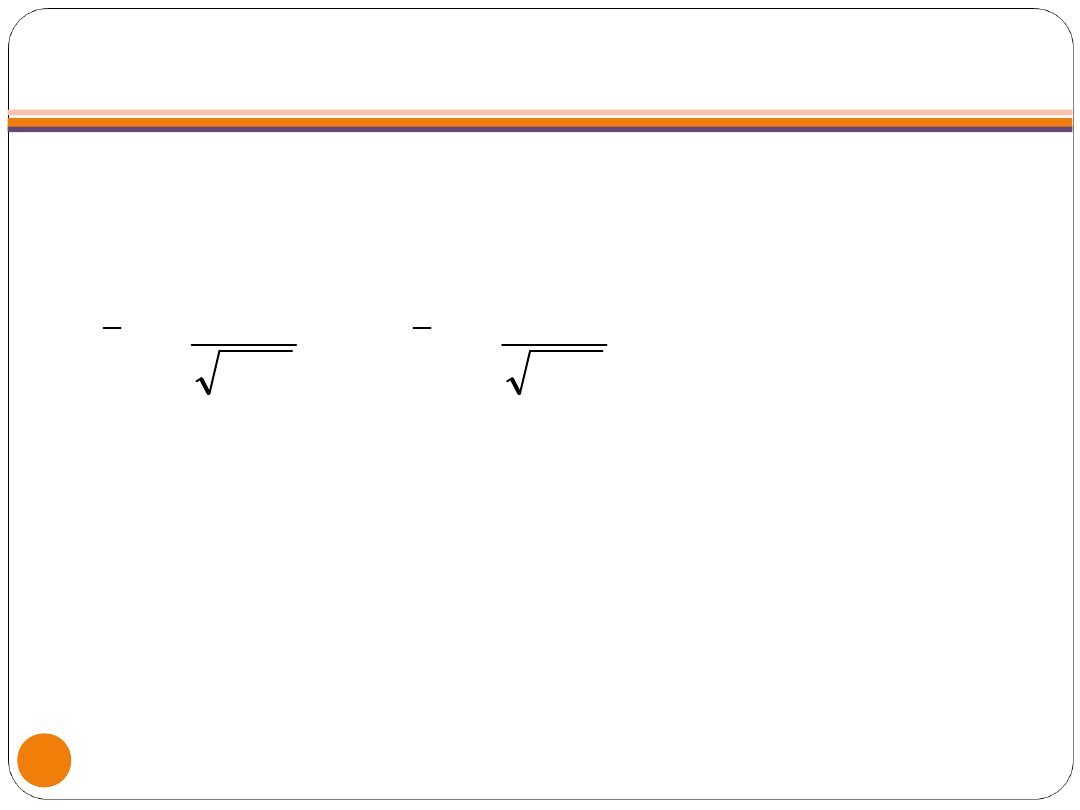
PRZYPADEK II. PRZEDZIAŁ UFNOŚCI DLA 
WARTOŚCI OCZEKIWANEJ, GDY NIEZNANA JEST 
WARIANCJA (MAŁA PRÓBA)

Estymator średniej ma wówczas 
rozkład 
t-Studenta, a przedział ufności jest 
postaci:

gdzie:
S - odchylenie standardowe obliczone 
dla n-elementowej próby. 

24

1

1













n

S

t

x

m

n

S

t

x





METODY PROGNOZOWANIA 2011/2012

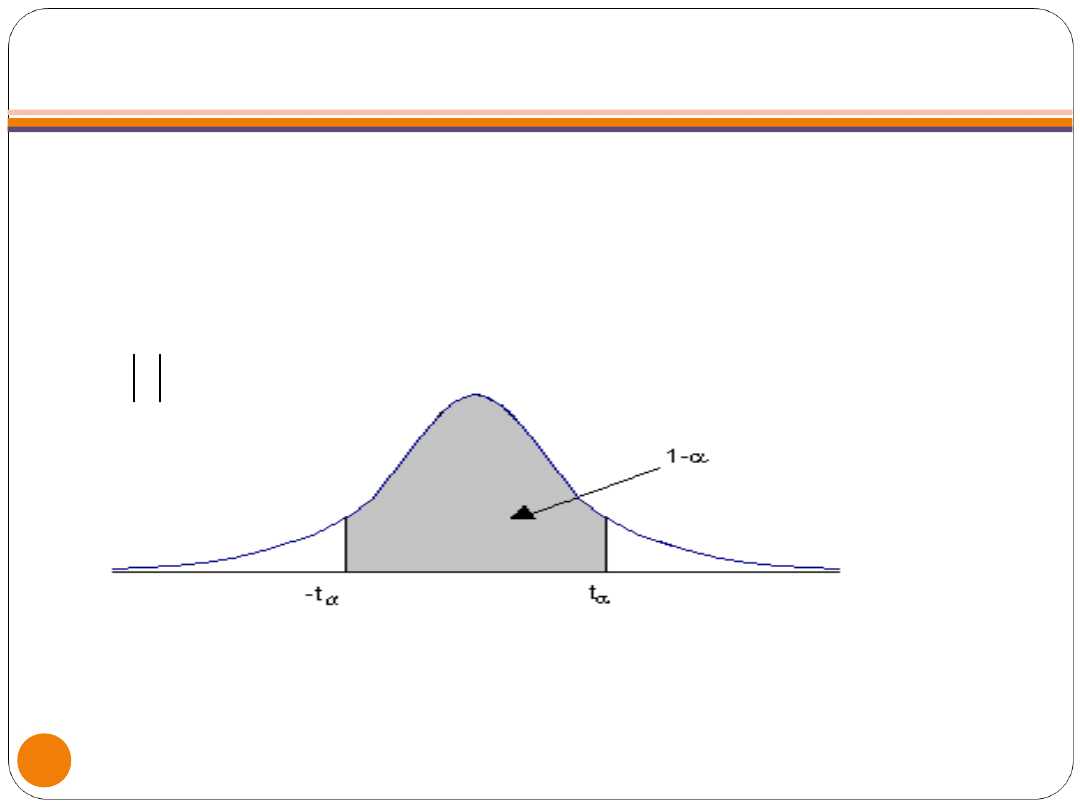
PRZYPADEK II. PRZEDZIAŁ UFNOŚCI DLA 
WARTOŚCI OCZEKIWANEJ, GDY NIEZNANA JEST 
WARIANCJA (MAŁA PRÓBA)

  - wartość zmiennej t odczytana z 
tablicy rozkładu t-Studenta dla n-1 
stopni swobody w taki sposób, aby 
spełniony był warunek:

25



t















1

t

u

P

METODY PROGNOZOWANIA 2011/2012

PRZYKŁAD 3

Oszacować żywotność (w godzinach) 

wyprodukowanej partii świetlówek. Wiadomo, 

że czas świecenia świetlówek ma rozkład 

normalny z odchyleniem standardowym 

s=129.7h. Wylosowana niezależnie w tej 

partii próba n=25 świetlówek dała 

następujące wyniki pomiarów czasu ich 

świecenia (w godzinach): 2630, 2820, 2900, 

2810, 2770, 2840, 2700, 2950, 2690, 2720, 

2800, 2970, 2680, 2660, 2820, 2580, 2840, 

3020, 2780, 2920, 3060, 2840, 2550, 2790, 

2850. Przyjmując współczynnik ufności 0,98 

oszacować metodą przedziałową średni czas 

świecenia świetlówek tej partii.

26

METODY PROGNOZOWANIA 2011/2012

PRZYKŁAD 3 - ROZWIĄZANIE

1-=0,98 stąd =0,02
N=25=n
S=129,7
Obliczamy parametry z próby:

Korzystamy ze wzoru II (n=25)

27

2799,6

25

6990

25

2850

2790

2550

....

2900

2820

2630



















x

METODY PROGNOZOWANIA 2011/2012

PRZYKŁAD 3 - ROZWIĄZANIE

Z prawdopodobieństwem 0,98 można twierdzić, że 
żywotność żarówek zawiera się między 2733,63 a 
2865,57 godzin

.

28

METODY PROGNOZOWANIA 2011/2012

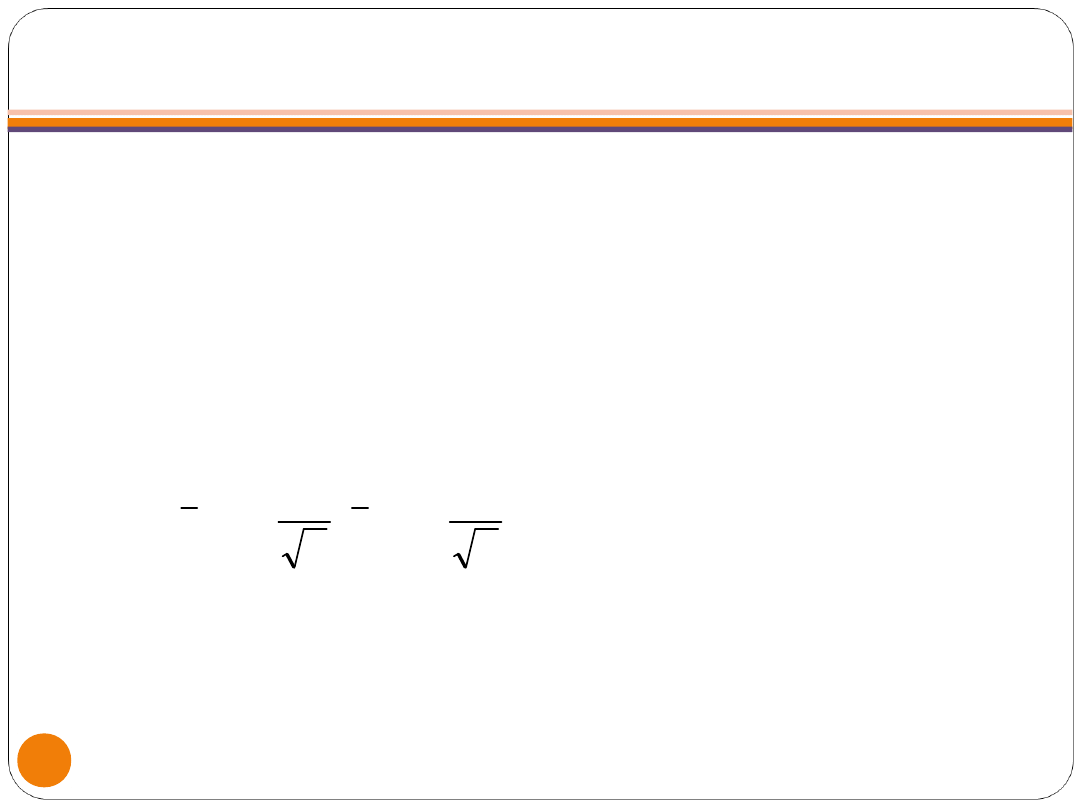
PRZYPADEK III. PRZEDZIAŁ UFNOŚCI DLA 
WARTOŚCI OCZEKIWANEJ, GDY NIEZNANA JEST 
WARIANCJA (DUŻA PRÓBA N>120)

W tym przypadku estymator  ma 
rozkład normalny. Przedział ufności  
wyznaczamy ze wzoru, w którym w 
miejsce nieznanego odchylenia 
standardowego w populacji 



 

wstawiamy oszacowaną z próby 
wartość S:

29



















n

S

u

x

n

S

u

x







;

METODY PROGNOZOWANIA 2011/2012

PRZYKŁAD 4

Dla ustalenia średniego wieku osób 
korzystających z pomocy finansowej 
Miejskiego Ośrodka Pomocy Społecznej 
w Tychach wylosowano niezależnie do 
próby 40 osób i uzyskano wyniki: 
średnia 44 lata oraz odchylenie 
standardowe s=11,58
Określ dla współczynnika ufności 0,9 
średnią wieku osób korzystających z 
pomocy finansowej MOPS w Tychach. 

30

METODY PROGNOZOWANIA 2011/2012

PRZYKŁAD 4 - ROZWIĄZANIE

METODY PROGNOZOWANIA 2010/2011

31

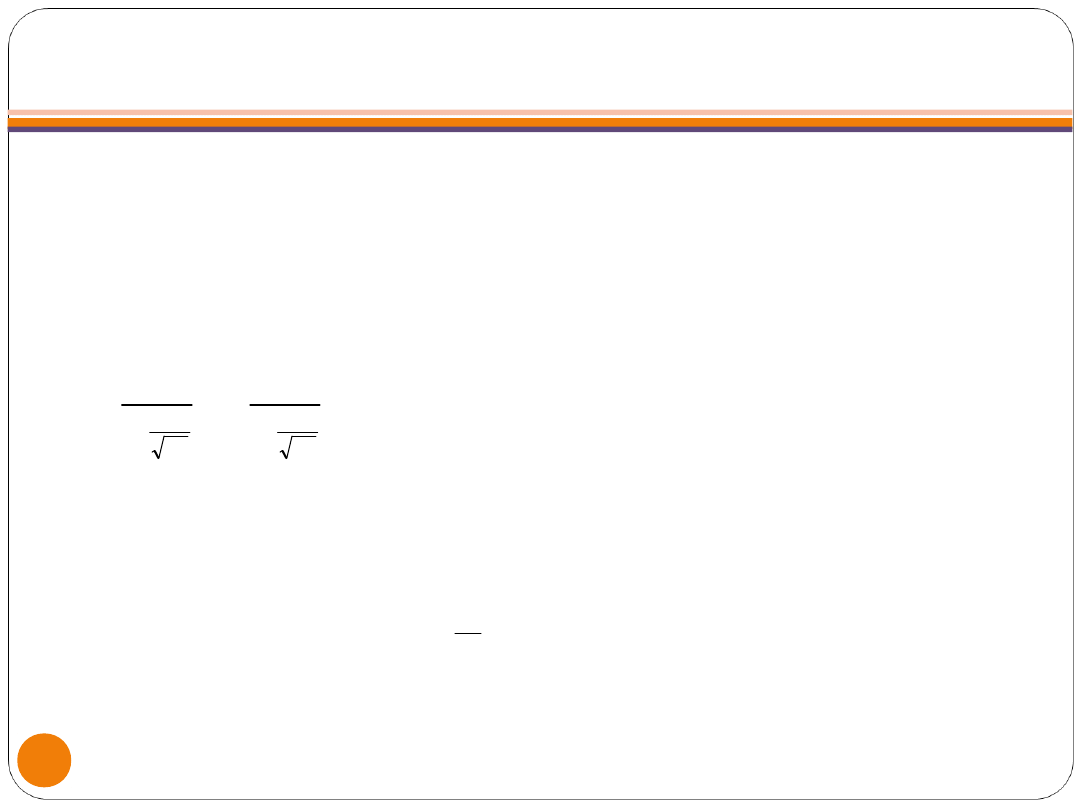
PRZEDZIAŁ UFNOŚCI DLA ODCHYLENIA 
STANDARDOWEGO

Jeżeli posiadamy dużą próbę losową, to 
przedział ufności dla nieznanej wartości 
odchylenia standardowego wyznaczamy 
za pomocą wzoru:

gdzie      odczytujemy z tablic rozkładu 
normalnego dla przyjętego poziomu 
ufności  1-



, aby spełniona była relacja:

32











































1

2

1

2

1

n

u

S

n

u

S

P

u



 

2

1









 u

METODY PROGNOZOWANIA 2011/2012

PRZEDZIAŁ UFNOŚCI DLA ODCHYLENIA 
STANDARDOWEGO

Przedziałem ufności dla parametru 



 

jest przedział:

który z prawdopodobieństwem 1-



 

pokrywa nieznana wartość 
parametru 



33































n

u

S

n

u

S

2

1

;

2

1







METODY PROGNOZOWANIA 2011/2012

WERYFIKACJA HIPOTEZ 

STATYSTYCZNYCH

METODY PROGNOZOWANIA wykład 1

34

WPROWADZENIE

Weryfikacja hipotez statystycznych ma 

na celu sprawdzenie sformułowanych 

hipotez statystycznych, czyli podjęcie 

określonych decyzji statystycznych.
Hipotezy dzielimy na dwie grupy:

•

 hipotezy parametryczne, tzn. sądy 

dotyczące parametrów rozkładu cechy 

w populacji generalnej,

•

 hipotezy nieparametryczne, tzn. 

sądy dotyczące kształtu rozkładu 

populacji generalnej.

35

METODY PROGNOZOWANIA 2011/2012

WPROWADZENIE

Procedura weryfikacji hipotez 

statystycznych opiera się zawsze na dwóch 

hipotezach: zerowej i alternatywnej. 
Hipoteza zerowa (H

0

) jest podstawową 

hipotezą statystyczną, która jest 

przedmiotem weryfikacji, tzn. proces 

weryfikacji może doprowadzić do jej 

odrzucenia bądź do stwierdzenia, że nie ma 

podstaw, by ją odrzucić. Hipoteza ta jest 

formułowana w taki sposób (czasem wbrew 

rozsądkowi), aby można ją było łatwo 

odrzucić. 

36

METODY PROGNOZOWANIA 2011/2012

WPROWADZENIE

Hipoteza alternatywna (H

1

) to 

hipoteza konkurencyjna w stosunku 
do hipotezy zerowej. Jest ona 
formułowana jako przypuszczenie, 
że rozkład nie posiada własności 
określonej w hipotezie zerowej 
(posiada ją w innym wariancie).

37

METODY PROGNOZOWANIA 2011/2012

WPROWADZENIE

•

 Jeżeli hipoteza zerowa jest parametryczna, to 

hipotezę alternatywną można sformułować 
dwustronnie (tzn. „jest różne”), prawostronnie 
(tzn. „jest większe od”) lub lewostronnie (tzn. „jest 
mniejsze od”), przy czym sposób formułowania 
hipotezy zależy nie tylko od celu badania, ale 
również od rodzaju informacji statystycznych 
uzyskanych z próby losowej,

•

 Jeżeli hipoteza zerowa jest nieparametryczna, to 

hipoteza alternatywna jest formułowana wyłącznie 
w postaci „jest różne” (wówczas nie ma problemu 
odmiennego podejścia do weryfikacji hipotezy 
zerowej).

38

METODY PROGNOZOWANIA 2011/2012

RODZAJE TESTÓW 
STATYSTYCZNYCH

Hipotezy statystyczne weryfikuje się za 
pomocą testów statystycznych, przy 
czym w zależności od rodzaju hipotezy 
rozróżniane są testy:

•

parametryczne (służą do weryfikacji 

hipotez parametrycznych); 

•

nieparametryczne (m.in. testy 

zgodności, testy losowości - służą do 
weryfikacji hipotez 
nieparametrycznych).

39

METODY PROGNOZOWANIA 2011/2012

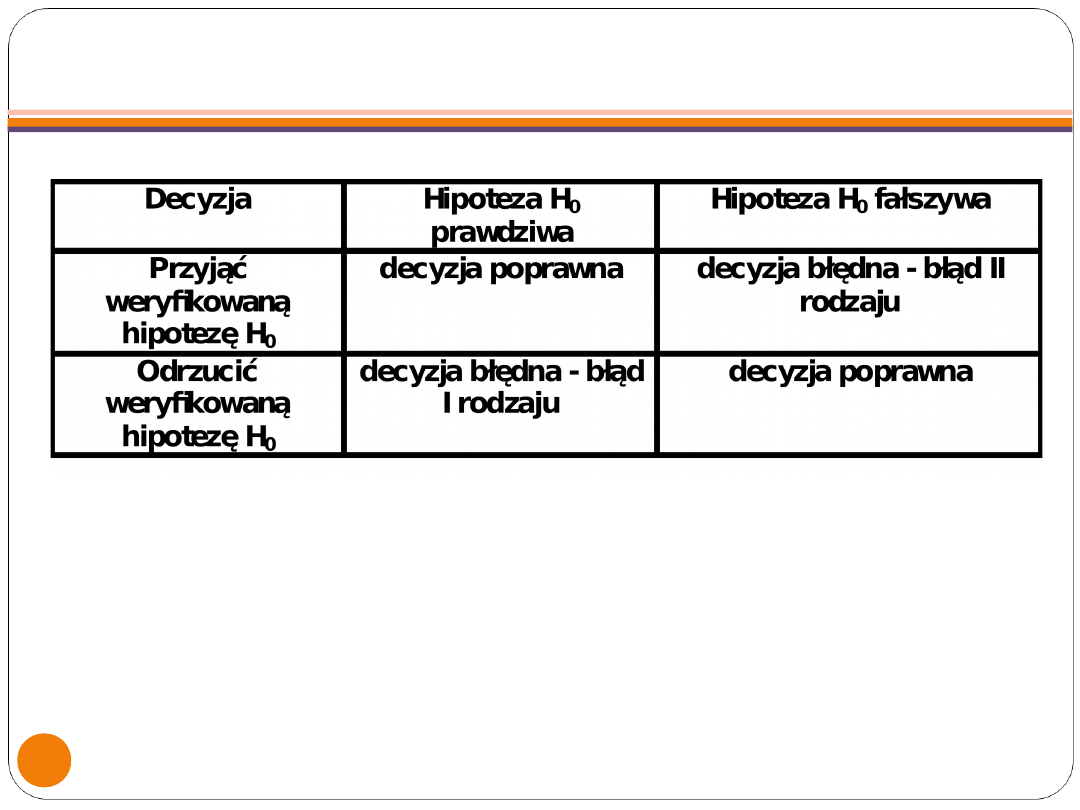
BŁĘDY POPEŁNIANE PRZY WERYFIKACJI HIPOTEZ 
STATYSTYCZNYCH

40

METODY PROGNOZOWANIA 2011/2012

BŁĘDY POPEŁNIANE PRZY WERYFIKACJI HIPOTEZ 
STATYSTYCZNYCH

Prawdopodobieństwo popełnienia błędu 
I  rodzaju 



 ustalone jest z góry jako 

dowolnie niskie prawdopodobieństwo 
odrzucenia prawdziwej hipotezy zerowej 
i nazwane jest poziomem istotności. 
W naukach technicznych 
prawdopodobieństwo błędu I  rodzaju 
przyjmuje się zazwyczaj z przedziału 
<0,001;0,1>, przy czym najczęściej 
=0,05.

41

METODY PROGNOZOWANIA 2011/2012

BŁĘDY POPEŁNIANE PRZY WERYFIKACJI HIPOTEZ 
STATYSTYCZNYCH

Wartość p jest to minimalna wartość 
poziomu istotności, dla którego może 
być odrzucona hipoteza H

0

 na 

podstawie wyników próby. Zatem H

0 

odrzucamy, gdy           .
Programy statystyczne zazwyczaj 
wyznaczają p 
(p-value) wraz z innymi wynikami 
testu statystycznego.

42





p

METODY PROGNOZOWANIA 2011/2012

ETAPY WERYFIKACJI HIPOTEZ 
STATYSTYCZNYCH

W procesie weryfikacji hipotez statystycznych 

można wyróżnić kilka etapów:

•

sformułowanie hipotezy zerowej (H

0

) oraz 

hipotezy alternatywnej (H

1

) (jednej lub kilku),

•

wybór testu statystycznego służącego do 

weryfikacji hipotezy zerowej,

•

wyznaczenie wartości sprawdzianu testu,

•

ustalenie poziomu istotności (1-) oraz 

wyznaczenie obszaru odrzucenia hipotezy 

zerowej,

•

podjęcie decyzji z określonym 

prawdopodobieństwem błędu.

43

METODY PROGNOZOWANIA 2011/2012

Test statystyczny to reguła postępowania, 

która na podstawie wyników z próby ma 

doprowadzić do odrzucenia - lub nie - 

postawionej hipotezy statystycznej. 

Najczęściej używanymi w praktyce są tzw. testy 

istotności, które umożliwiają odrzucenie 

hipotezy z ryzykiem równym poziomowi 

istotności 



, bez uwzględniania 

prawdopodobieństwa popełnienia błędu drugiego 

rodzaju. Stosując testy istotności podejmuje się 

decyzję odnośnie do odrzucenia hipotezy zerowej 

na rzecz hipotezy alternatywnej, albo decyzję o 

braku podstaw do odrzucenia hipotezy zerowej, 

co nie jest równoznaczne z jej przyjęciem. 

44

METODY PROGNOZOWANIA 2011/2012

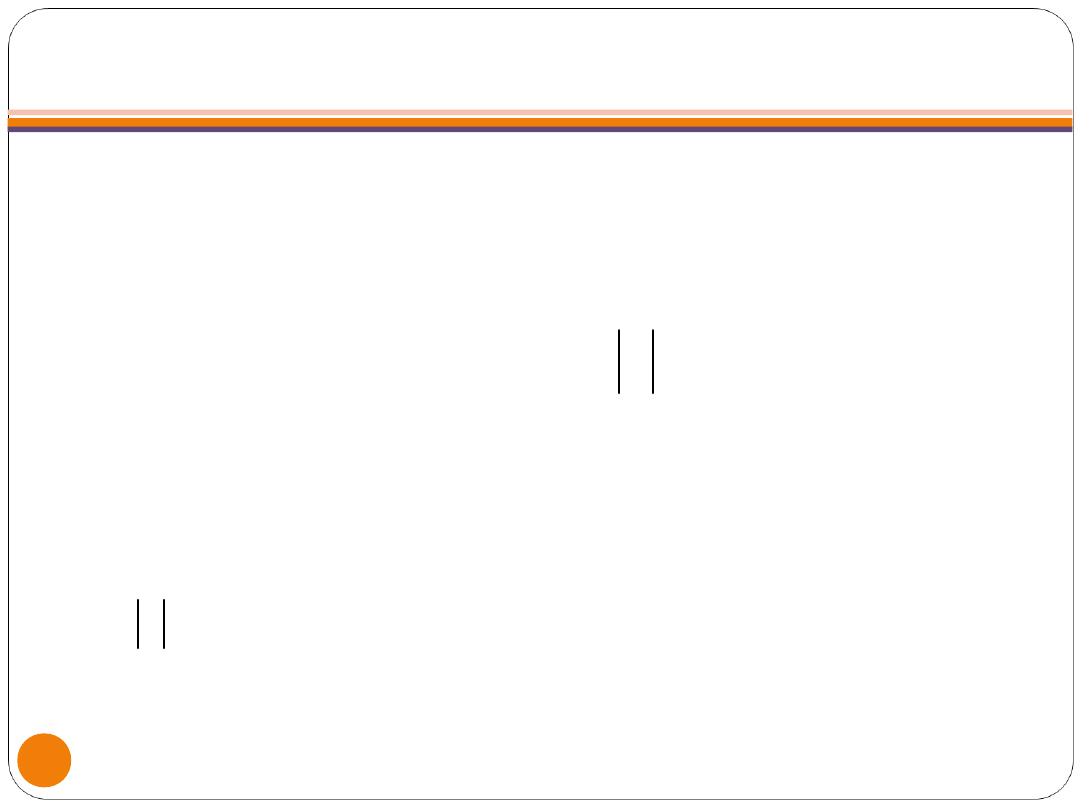
OBSZAR ODRZUCENIA HIPOTEZY 
ZEROWEJ

Obustronny (dwustronny) obszar 
odrzucenia hipotezy, który jest 
budowany, gdy H

1

 jest stawiana 

dwustronnie, to zbiór wszystkich wartości 
zmiennej losowej u takich, że 
gdzie 
     - wartość krytyczna odczytana z tablic 
dla ustalonego z góry poziomu istotności 
 taka, że
                        .

45



u

u 



u











u

u

P

METODY PROGNOZOWANIA 2011/2012

OBSZAR ODRZUCENIA HIPOTEZY 
ZEROWEJ

Jednostronny obszar odrzucenia 

hipotezy (jest budowany, gdy H

1

 jest 

stawiana jednostronnie) to zbiór wszystkich 

wartości zmiennej losowej u taka, że  
             (prawostronny obszar odrzucenia) 

lub 
             (lewostronny obszar odrzucenia), 

gdzie 
          - wartości krytyczne dla z góry 

zadanego poziomu istotności  takie, że  dla 

prawostronnego lub  dla lewostronnego 

obszaru odrzucenia .

46

1

u

u 

2

u

u 

2

1

,u

u

METODY PROGNOZOWANIA 2011/2012

Mocą testu nazywamy 
prawdopodobieństwo podjęcia słusznej 
decyzji, polegającej na odrzuceniu 
weryfikowanej hipotezy wtedy, gdy jest 
ona fałszywa. Wyznacza się ją jako 
M=1-



 gdzie 



 - prawdopodobieństwo 

popełnienia błędu II rodzaju.

47

METODY PROGNOZOWANIA 2011/2012

TESTY PARAMETRYCZNE

Weryfikacja hipotez może dotyczyć: 

•

jednej populacji generalnej - 

sprawdzenie, czy parametr ma 
określoną wartość,

•

dwóch lub więcej zbiorowości - 

weryfikacja hipotezy o równości 
parametru w obu zbiorowościach.

48

METODY PROGNOZOWANIA 2011/2012

Testy weryfikujące hipotezę o wartości 
oczekiwanej w populacji

Przypadek I. Populacja o rozkładzie 
normalnym ze znanym 
Z populacji losujemy n-elementową 
próbę. Jeżeli populacja ma rozkład N(



,), 

przy czym odchylenie standardowe 
populacji jest znane, to test istotności 
dla hipotezy H

0

: 



=



0 polega na 

podjęciu decyzji w oparciu 
o wyznaczoną wartość sprawdzianu 
testu:

49

n

x

u





0





METODY PROGNOZOWANIA 2011/2012

Testy weryfikujące hipotezę o wartości 
oczekiwanej w populacji

gdzie:
    - średnia arytmetyczna wyznaczona 
z próby,


0 

- z góry określona wartość średniej w 

populacji,
    - odchylenie standardowe dla populacji,
n  - liczebność próby.
Statystyka ta przy założeniu prawdziwości 
hipotezy H

0

 ma rozkład normalny N(0,1).

50

x



METODY PROGNOZOWANIA 2011/2012

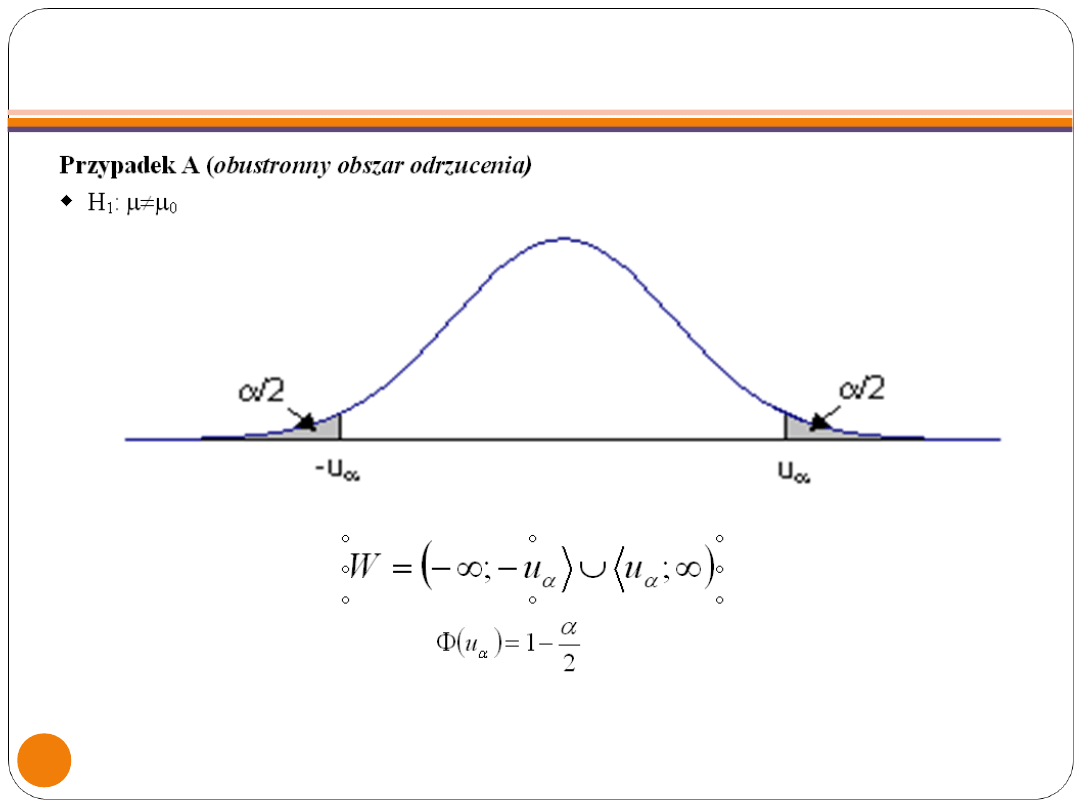
WARIANT 1. 

51

METODY PROGNOZOWANIA 2011/2012

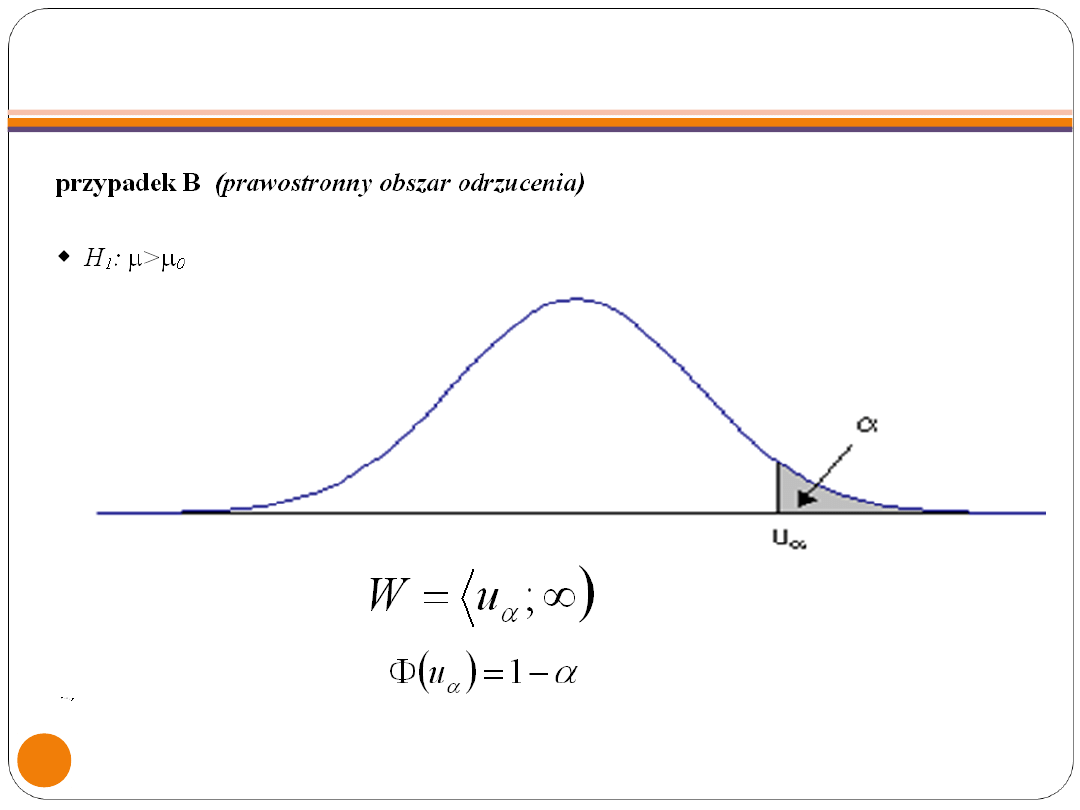
WARIANT 2

52

METODY PROGNOZOWANIA 2011/2012

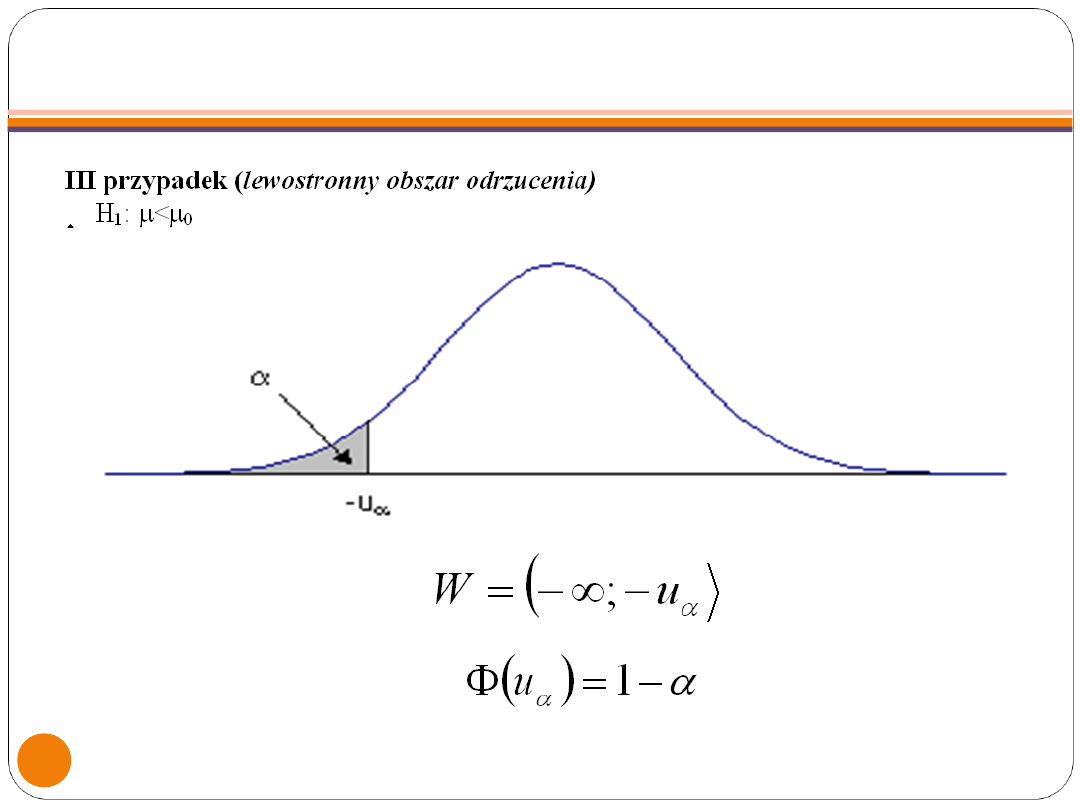
WARIANT 3

53

PRZYKŁAD 5

W stołówce studenckiej przeprowadzono 
wyrywkową kontrolę masy porcji obiadowej 
mięsa, która nominalnie powinna wynosić 120 
g. Losowo wybrano a następnie zważono 100 
porcji, uzyskując informację średnia=118,8 
oraz odchylenie standardowe= 3,9.
Na poziomie istotności =0,05 sprawdzić 

hipotezę, że studenci w badanej stołówce są 
żywieni zgodnie z recepturą. Zakłada się, że 
rozkład masy porcji mięsa w całej populacji 
jest rozkładem normalnym.

54

METODY PROGNOZOWANIA 2011/2012

PRZYKŁAD 5 - ROZWIĄZANIE

Dane:
=0,05

S=3,9
Stawiamy hipotezy:
H

0

: 



 = 120 (Studenci są żywieni 

zgodnie z recepturą)
H

0

: 



 



 120 (Studenci nie są żywieni 

zgodnie z recepturą)

55

8

,

118



x

METODY PROGNOZOWANIA 2011/2012

PRZYKŁAD 5 - ROZWIĄZANIE

Obliczamy wartość statystyki u

Ponieważ hipoteza alternatywna jest 
postaci: 



 



0

 

mamy obustronny obszar krytyczny 
W:

56

3,08

-

-

100

9

,

3

120

8

,

118







u

















;

;





u

u

W

METODY PROGNOZOWANIA 2011/2012

 

 Ponieważ u    W odrzucamy hipotezę zerową. Studenci nie są 

żywienie zgodnie z  recepturą.

57



PRZYKŁAD 5 - ROZWIĄZANIE

METODY PROGNOZOWANIA 2011/2012

Dziękuję za uwagę

58

METODY PROGNOZOWANIA 2011/2012