dr M. Chrzanowska

Wykład 5

Badanie własności składnika losowego

w modelu ekonometrycznym

1

METODY PROGNOZOWANIA Wykład 4

Założenia MNK dotyczące
struktury stochastycznej modelu
ekonometrycznego



Założenie 1: elementy macierzy są

ustalonymi liczbami rzeczywistymi (nie są
losowe);



Założenie 3 : ,



Założenie 4 :

gdzie I

n

jest macierzą jednostkową

stopnia n.



Założenie 5 (dodatkowe):

METODY PROGNOZOWANIA Wykład 4

2

0

ε 

)

(

E

n

I

ε

2

2

)

(

D





)

,

(

N

~

2

n

I

0

ε



Zakłócenia założenia 4



Przypuśćmy, że nie jest spełnione

Założenie 4 , czyli : .

( MNK – estymatory pozostają zgodne i

nieobciążone, ale nie są n



Możliwe są wówczas następujące

przypadki:

METODY PROGNOZOWANIA Wykład 4

3

Zakłócenia założenia 4



I przypadek - macierz wariancji i kowariancji
zakłóceń losowych (macierz wariancji i kowariancji
składnika losowego) jest macierzą diagonalną, ale
wariancje zakłóceń nie są stałe, czyli
najefektywniejsze w klasie estymatorów liniowych)



Gdzie i



Wówczas składnik losowy ma niejednorodną
wariancję czyli model jest heteroskedastyczny
(składnik losowy jest heteroskedastyczny)

METODY PROGNOZOWANIA Wykład 4

4

Ω

ε

2

2

1

2

2

2

2

2

1

2

0

0

0

0

0

0

0

0

0

0

0

0

0

0

)

(

D











































































n

n

























h

i

h

i





dla





n

I

Ω 

Zakłócenia założenia 4



II przypadek - macierz wariancji i kowariancji
zakłóceń losowych jest macierzą o stałych wariancjach,
ale kowariancje zakłóceń losowych są różne od zera,tj.



W tym przypadku wszystkie zmienne losowe ε

i

mają

taką samą wariancję, innymi słowy model jest
homoskedastyczny z autokorelacją składnika
losowego.

METODY PROGNOZOWANIA Wykład 4

5

n

i

i

,...,

2

,

1

,

const

)

(

D

2

2











h

i

h

i



 ,

0

)

,

cov(





















































1

1

1

1

)

(

D

3

2

1

3

1

2

2

1

1

1

2

1

2

2

















n

n

n

n

n

n



























ε

2

)

,

cov(









s

i

i

s





ρ

s

jest współczynnikiem

korelacji pomiędzy
składnikami losowymi,
odległymi o s okresów,
nazwany jest
współczynnikiem
autokorelacji.

Zakłócenia założenia 4



III przypadek

- model

heteroskedastyczny z autokorelacją
składnika losowego; żaden z warunków:

,

nie jest spełniony

METODY PROGNOZOWANIA Wykład 4

6

n

i

i

,...,

2

,

1

,

const

)

(

D

2

2











h

i

h

i



 ,

0

)

,

cov(





Uwaga



Niespełnienie założeń o

homoskedastyczności powoduje, że
estymatory są nadal nieobciążone i zgodne,
ale nie są najbardziej efektywne.



W praktyce oznacza to, że oszacowane

błędy standardowe estymatorów nie sa
optymalne (najmniejsze z możliwych).

7

METODY PROGNOZOWANIA Wykład 4

Uwaga



Heteroskedastyczność występuje modelach

oszacowanych na podstawie danych
przekrojowych.



Autokorelacja występuje zazwyczaj w

modelach opartych na szeregach
czasowych.

8

METODY PROGNOZOWANIA Wykład 4

Uwaga



Zaburzenie sferyczności zakłóceń jest na

tyle częstym zjawiskiem, że powstaje
pytanie jak silna jest autokorelacja czy
heteroskedastyczność

9

METODY PROGNOZOWANIA Wykład 4

Wniosek



Przy niewielkim zaburzeniu utrata

efektywności oszacowań jest nieznaczna,



przy silnych procesach autokorelacji lub

hetroskedastyczności może istotnie
podwyższać błędy standardowe
estymatorów, pogarszając tym samym
efektywność oszacowań.

10

METODY PROGNOZOWANIA Wykład 4

Konsekwencje zastosowania KMNK
przy heteroskedastyczności lub
autokorelacji



Estymator MNK jest nadal nieobciążony,

ale



Wariancja resztowa jest obciążona i w

przypadku autokorelacji dodatkowo
niedoszacowana.



W rezultacie testy hipotez oparte na

statystykach t − Studenta i F są
niepoprawne, co prowadzi do błędnych
wniosków wyprowadzanych na ich
podstawie.

11

METODY PROGNOZOWANIA Wykład 4

Wniosek



Należy zawsze sprawdzić, czy w modelu nie

występuje autokorelacji lub
heteroskedastyczność.



Jeśli w modelu występuje autokorelacja czy

heteroskedastyczność należy zamiast
KMNK stosować UMNK.

METODY PROGNOZOWANIA Wykład 4

12

Przypadek 1

heteroskedastyczność

METODY PROGNOZOWANIA Wykład 4

13

Testowanie
heteroskedastyczności



Test Golfelda-Quandta;



Test Breuscha-Pagana;



Test White’a

METODY PROGNOZOWANIA Wykład 4

14

Test Golfelda-Quandta

Testowanie stałości wariancji zakłóceń
realizuje się zgodnie z następującym
schematem:



uwzględniając wyżej opisane tendencje,
podzielić próbę na takie podpróby, dla
których można się spodziewać, że wariancje
zakłóceń losowych będą się istotnie różniły,



wyznaczyć wariancję zakłóceń losowych w
poszczególnych podpróbach,



testować, czy różnice między wyznaczonymi
wariancjami są statystycznie istotne.

METODY PROGNOZOWANIA Wykład 4

15

Testy heteroskedastyczności
Test Golfelda-Quandta



Stosowany w przypadkach, gdy

znana jest cecha wywołująca

niejednorodność wariancji. Innymi

słowy Test Goldfelda-Quandta nie

może być stosowany jeśli wariancja

błędu losowego jest zależna od

więcej niż jednej zmiennej,

(nie ma wówczas prostego sposobu

pogrupowania obserwacji)

16

METODY PROGNOZOWANIA Wykład 4

METODY PROGNOZOWANIA Wykład 4

17

Testy heteroskedastyczności
Test Golfelda-Quandta



Jest najprostszym testem testującym.



Stosujemy go jeśli jest możliwe podzielenie

obserwacji na dwie grupy taki sposób, że dla
prawdziwej hipotezy alternatywnej, wariancje
błędów losowych w tych dwóch grupach są
różne

17

Test Golfelda-Quandta
Algorytm postępowania



Wybieramy z próby losowej dwie podpróby; na
podstawie każdej z podprób szacujemy parametry
strukturalne modelu ekonometrycznego i
obliczamy wariancje resztowe.



Numerujemy podpróby tak, aby , gdzie

- wariancja resztowa w modelu oszacowanym

na podstawie i -tej podpróby, i=1,2.



Formułujemy hipotezy:

gdzie - wariancja zakłóceń losowych w
modelu oszacowanym na podstawie i - tej
podpróby , i=1,2.

METODY PROGNOZOWANIA Wykład 4

18

2

e

2

2

e

1

S

S 

2

e

i

S

2

2

2

1

0

:

H







2

2

2

1

1

:

H







2

i



Test Golfelda-Quandta
Algorytm postępowania



Sprawdzianem hipotezy zerowej jest statystyka

o rozkładzie F- Snedecora dla ustalonego α i

z liczbą stopni swobody r

1

=n

1

-k, r

2

=n

2

-k, gdzie

n

1

- liczba obserwacji w pierwszej podpróbie,

n

2

- liczba obserwacji w drugiej podpróbie,

k - ilość parametrów strukturalnych w modelu.



Prawostronny zbiór krytyczny jest postaci
,
gdzie F

kryt

to wartość odczytana z tablic rozkładu

F – Snedecora dla ustalonej wartości ustalonego α
i liczbą stopni swobody r

1

, r

2.

METODY PROGNOZOWANIA Wykład 4

19

2

e

2

2

e

1

S

F

S



α

r

,

r

2

1

F











,

F

Z

kryt

kryt

Test Golfelda-Quandta
Algorytm postępowania



Jeżeli wartość F

*

statystyki należy do

zbioru krytycznego Z

kryt

, to odrzucamy

hipotezę H

0

o homoskedastyczności

zakłóceń losowych na poziomie istotności
α , na rzecz hipotezy H

1

; stwierdzamy

heteroskedastyczność zakłóceń losowych.



Jeżeli F

*

nie należy do zbioru Z

kryt

, to nie

ma podstaw do odrzucenia hipotezy H

0

.

METODY PROGNOZOWANIA Wykład 4

20

Testy heteroskedastyczności
Test Breuscha Pagana (BP)



Jest stosowany w sytuacjach, gdy wariancja

zależy od kilku zmiennych

METODY PROGNOZOWANIA Wykład 4

21

Testy heteroskedastyczności
Test Breuscha-Pagana

i

n

n

i

x

x

x

y





















...

2

2

1

1

0

METODY PROGNOZOWANIA Wykład 4

22



Za pomocą KMNK szacujemy

równanie postaci:

n

e

n

i

i







1

2

2







Wyznaczamy wariancję resztową
korzystając ze wzoru



Konstruujemy nową
zmienną:

2

2





i

i

e

p 

Testy heteroskedastyczności
Test Breuscha-Pagana

i

k

k

i

u

z

z

z

p



















...

2

2

1

1

0

METODY PROGNOZOWANIA Wykład 4

23



Szacujemy model pomocniczy:









n

i

i

i

p

p

ESS

1

2

)

ˆ

(



Na podstawie równania regresji
pomocniczej wyznaczamy sumę kwadratów

ESS,

gdzie

:

Testy heteroskedastyczności
Test Breuscha-Pagana

k

H













...

:

2

1

0

METODY PROGNOZOWANIA Wykład 4

24



Definiujemy statystykę testową

:

BP=0,5·ESS

2

1



k





Statystyka testowa ma rozkład o k-1
stopniach swobody



Formułujemy hipotezę zerową

:

(

zaburzenia

losowe są homoskedastyczne

)

Testy heteroskedastyczności
Test Breuscha-Pagana



Jeżeli odrzucamy hipotezę

o homoskedastyczności. W modelu
występuje heteroskedastyczność

.



Niska wartość statystyki testowej

może być zarówno efektem braku
heteroscedastyczności, jak i źle
wyspecyfikowanej alternatywy.

2

1





k

BP



METODY PROGNOZOWANIA Wykład 4

25

METODY PROGNOZOWANIA Wykład 4

26

TEST BREUSCHA-PAGANA



Regresja pomocnicza sprawdza silę związku

miedzy kwadratem reszt a wektorem
zmiennych z

i

. Jeżeli wariancja rzeczywiście

zależy od zmiennych zawartych w macierzy
Z to wyjaśniona suma kwadratów regresji
pomocniczej będzie duża i statystyka
wpadnie do obszaru krytycznego wskazując
na heteroscedastyczność składnika
losowego.

26

Testy heteroskedastyczności
Test White’a



Jest stosowany w sytuacji, gdy nie

wiemy, która ze zmiennych
objaśniających wywołuje
heteroskedastyczność



Sprawdza, czy postać regresji jest

poprawna

METODY PROGNOZOWANIA Wykład 4

27

Testy heteroskedastyczności
Test White’a



Jest stosowany w sytuacji, gdy nie

wiemy, która ze zmiennych
objaśniających wywołuje
heteroskedastyczność



Sprawdza, czy postać regresji jest

poprawna

28

METODY PROGNOZOWANIA Wykład 4

METODY PROGNOZOWANIA Wykład 4

29

HETEROSKEDASTYCZNOŚĆ-
TEST WHITE’A

29

UWAGA



Uwzględnienie heteroskedastyczności

wymusza znajomość macierzy . W

praktyce modelowania brak jest
jednoznacznych wzorców do stosowania.
Zatem eliminacja heteroskedastyczności
jest możliwa tylko w przypadku znacznego
poziomu tego zjawiska.

METODY PROGNOZOWANIA Wykład 4

30

Przypadek 2 Autokorelacja

METODY PROGNOZOWANIA Wykład 4

31

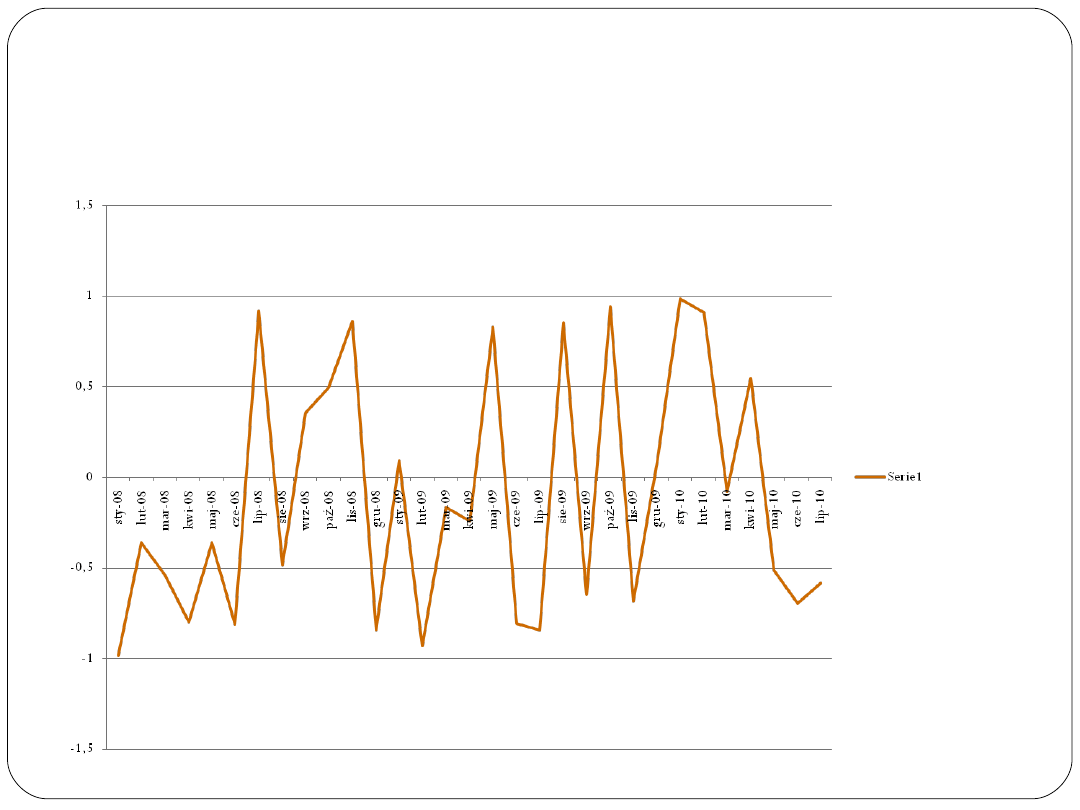
Wykres reszt spełniających
założenia KMNK

32

METODY PROGNOZOWANIA Wykład 4

Zaburzenia składnika
losowego -autokorelacja



Najczęściej spotykaną formą autokorelacji jest

autokorelacja dodatnia. Dodatnio skorelowane

zaburzenia losowe nie zachowują sie całkowicie

chaotycznie. Jeśli w okresie t błąd losowy był

dodatni, to prawdopodobieństwo, że w okresie

t + 1 będzie on także dodatni jest wyższe niż

prawdopodobieństwo, że w okresie tym będzie

on ujemny.



Autokorelacja dodatnia występuje często w

modelach szacowanych na szeregach

czasowych. Spowodowana jest ona zwykle

rozciągnięciem na dłużej niż jeden okres

skutków zdarzeń losowych wpływających na

poziom zmiennej objaśniane

33

METODY PROGNOZOWANIA Wykład 4

Zaburzenia składnika
losowego



Rzadziej spotykaną formą autokorelacji

jest autokorelacja ujemna. W takim
przypadku prawdopodobieństwo
wystąpienia po dodatnim błędzie
losowym ujemnego błędu jest wyższa niz.
prawdopodobieństwo wystąpienia
dodatniego błędu.



UWAGA

Autokorelacja ujemna zdarza się
wyjątkowo w modelach ekonomicznych
szacowanych na szeregach czasowych

34

METODY PROGNOZOWANIA Wykład 4

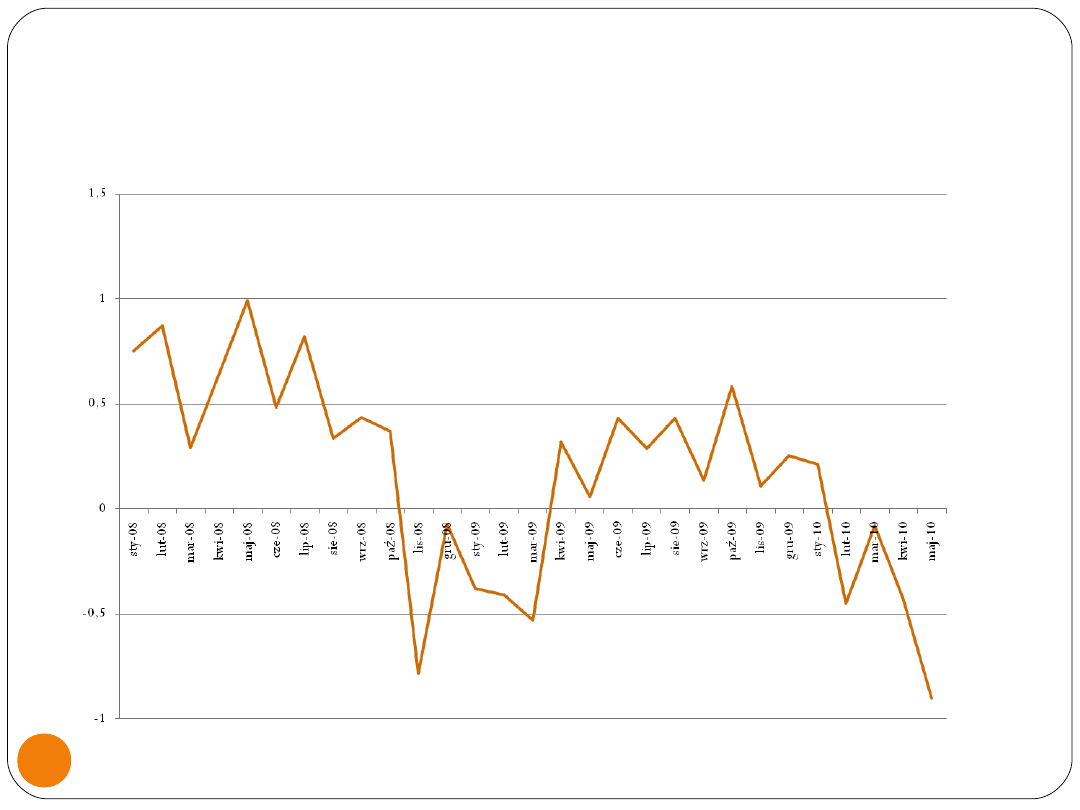
Zaburzenia składnika
losowego-korelacja dodatnia

35

METODY PROGNOZOWANIA Wykład 4

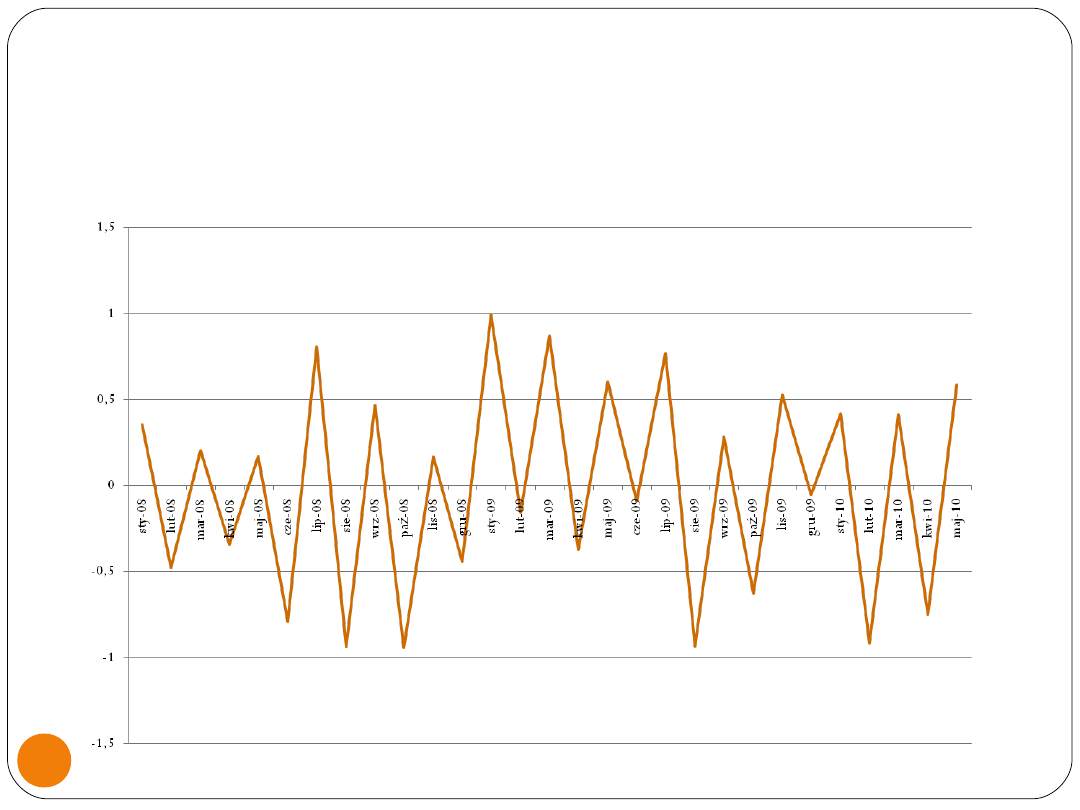
Zaburzenia składnika
losowego-korelacja ujemna

36

METODY PROGNOZOWANIA Wykład 4

37

Autokorelacja - testy



Durbina Watsona



Breuscha-Godfreya



Ljunga-Boxa



Berenblutta – Webba



Walda

Dla modeli z opóźnioną zmienną objaśnianą:



h Durbina



LM

METODY PROGNOZOWANIA Wykład 4

Test Durbina Watsona



Jest jednym z najpopularniejszych testów
weryfikujących nieskorelowanie czynników
losowych. Statystyka DW jest standardowo
umieszczana na wydrukach z wynikami
pochodzącymi ze pakietów ekonometrycznych.



Podstawową zaletą statystyki DW jej jest prostota
i fakt, że istnieją tablice wartości krytycznych dla
tej statystyki w próbach skończonych.



Jej wadą jest to, że ma ona niestandardowy
rozkład



Test Durbina-Watsona ma tę wadę, że pozwala
jedynie na badanie autokorelacji pierwszego
rzędu

38

METODY PROGNOZOWANIA Wykład 4

Test Durbina Watsona

Aby poprawnie stosować ten test,

rozpatrywany model ekonometryczny musi
posiadać następujące własności:



model ma wyraz wolny,



składnik losowy ma rozkład normalny,



w modelu nie występuje opóźniona zmienna

objaśniana jako zmienna objaśniająca.

METODY PROGNOZOWANIA Wykład 4

39

Test Durbina-Watsona

Weryfikuje się jeden z dwóch zestawów

hipotez.



(A)

(B)



Sprawdzianem hipotezy H

0

jest statystyka

która ma rozkład Durbina – Watsona na

przedziale <0,4>

METODY PROGNOZOWANIA Wykład 4

40

0

:

H

0

:

H

1

0









0

:

H

0

:

H

1

0













 

















n

i

i

n

i

i

i

e

e

e

1

2

2

2

1

W

-

D

d

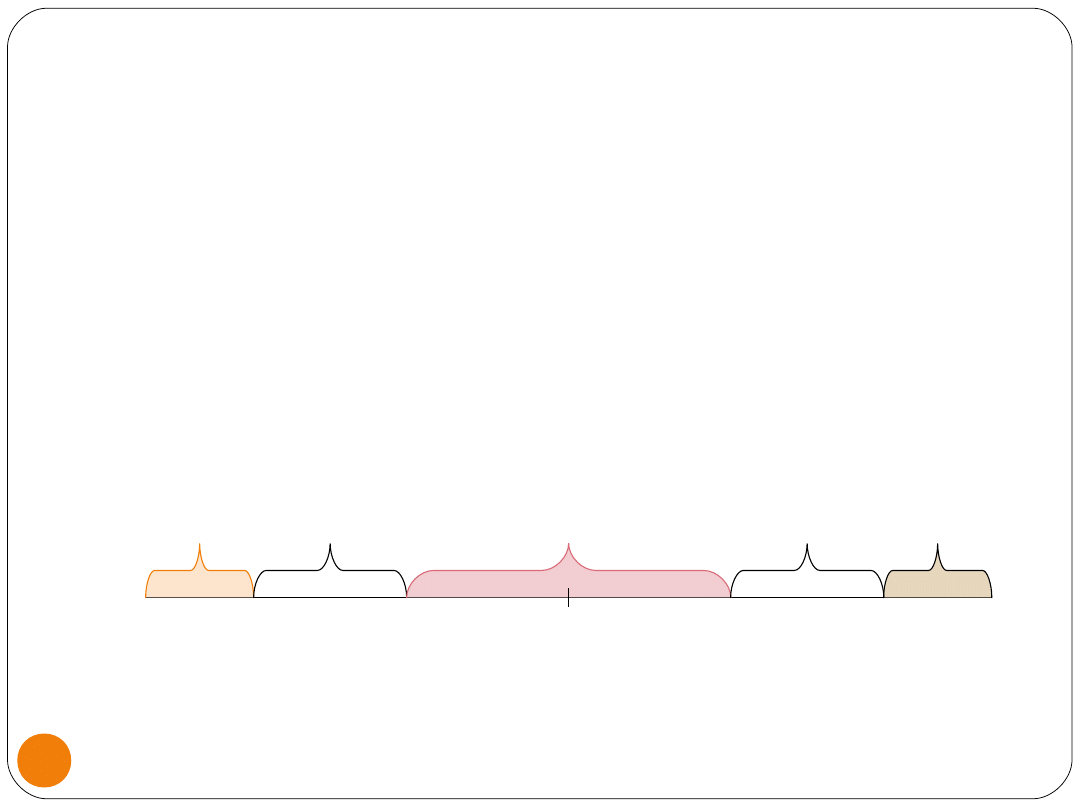
Test Durbina-Watsona



Z tablic rozkładu Durbina – Watsona

odczytuje się dwie wartości krytyczne:
wartość dolną d

l

i wartość górną d

u

,

które zależą od ustalonego poziomu
istotności α, liczebności próby losowej n
i liczby k-1 ( k ilość parametrów
strukturalnych w modelu)

METODY PROGNOZOWANIA Wykład 4

41

autokorelacja brak
autokorelacja
dodatnia ? autokorelacji ?
ujemna

0

d

L

d

U

2

4-d

U

4-

d

L

4

Wady testu Durbina-Watsona



Test daje tylko odpowiedzi poprawne tylko

w przypadku, gdy zmienne objaśniające są

stałe w powtarzalnych próbach a nie

losowe, co jest często spotykane.



Test jest bardzo czuły na założenie

normalności rozkładu zaburzeń lososwych i

zawodzi, gdy zaburzenia nie mają tego

rozkładu

42

METODY PROGNOZOWANIA Wykład 4

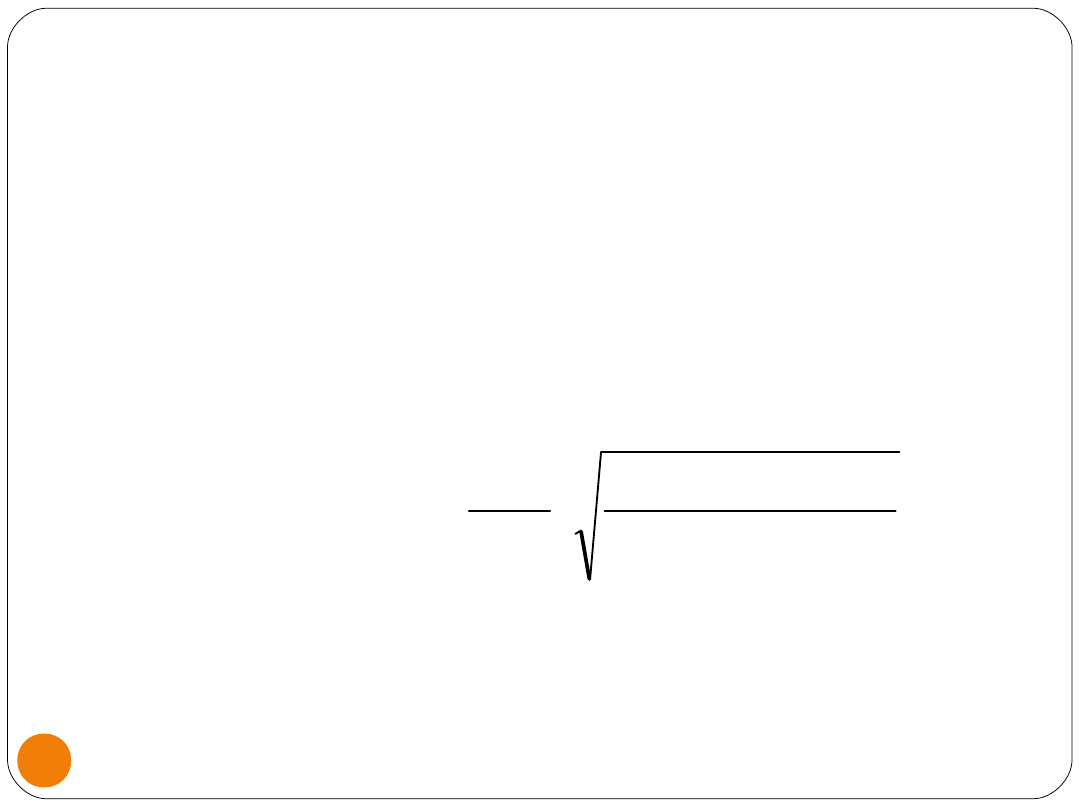
Test h-Durbina

43

Odpowiedź Durbina na zarzut, że test DW
jest zbyt skłonny nie wykrywać
autokorelacji, gdy regresorem jest
opóźniona zmienna objaśniana.

(Nerlove, Wallis 1966)





)

1

(

ˆ

1

2

1

















 



t

y

Var

n

n

DW

d



Wysokie wartości d świadczą o autokorelacji.

d~N(0,1).

43

METODY PROGNOZOWANIA Wykład 4

Test Breuscha-Golfrey’a
mnożnika Lagrange’a (LM)

44







X

y

Szacujemy podstawowe równanie
regresji:

...i drugie pomocnicze równanie, w
którym składnik losowy uzależniamy
dodatkowo od jego P poprzednich
wartości:

P

t

P

K

t

K

t

K

t

t

x







































...

2

2

1

1

'

0





T

X

jeżeli nie ma autokorelacji, poprzednie
wartości nie objaśnią bieżącej

wniosek: R

2

pomocniczego modelu powinno

być niewielkie

~

2

nR

LM

)

(

2

P



UWAGA!
test
asymptotycz
ny

44

METODY PROGNOZOWANIA Wykład 4

Test Breuscha-Golfrey’a

p

H













...

:

2

1

0



Formułujemy hipotezę zerową (w

modelu nie występuje autokorelacja):

2

nR

LM

2

p





Weryfikujemy hipotezę zerową za
pomocą statystyki LM



Statystyka LM ma rozkład

45

METODY PROGNOZOWANIA Wykład 4

Test Breuscha-Golfrey’a

2
p

LM







Jeżeli odrzucamy hipotezę zerową.
W modelu występuje autokorelacja.

46

METODY PROGNOZOWANIA Wykład 4

Test Breuscha-Golfrey’a
UWAGI



Test BG nie nakłada żadnych ograniczeń

na zmienne objaśniające.



Istotną wadą testu jest brak wskazówek

co do wyboru wartości rzędu
autokorelacji (wartości p). Niekiedy jest
to ilość obserwacji w cyklu sezonowym.
W praktyce jako wartość p zostaje
wybrana wyższa wartość niż
postulowana wiedzą ekonomiczną

47

METODY PROGNOZOWANIA Wykład 4