Metody prognozowania

Wprowadzenie do teorii prognozowania

Dr Krystyna Melich-Iwanek

Katedra Ekonometrii

[e-mail]

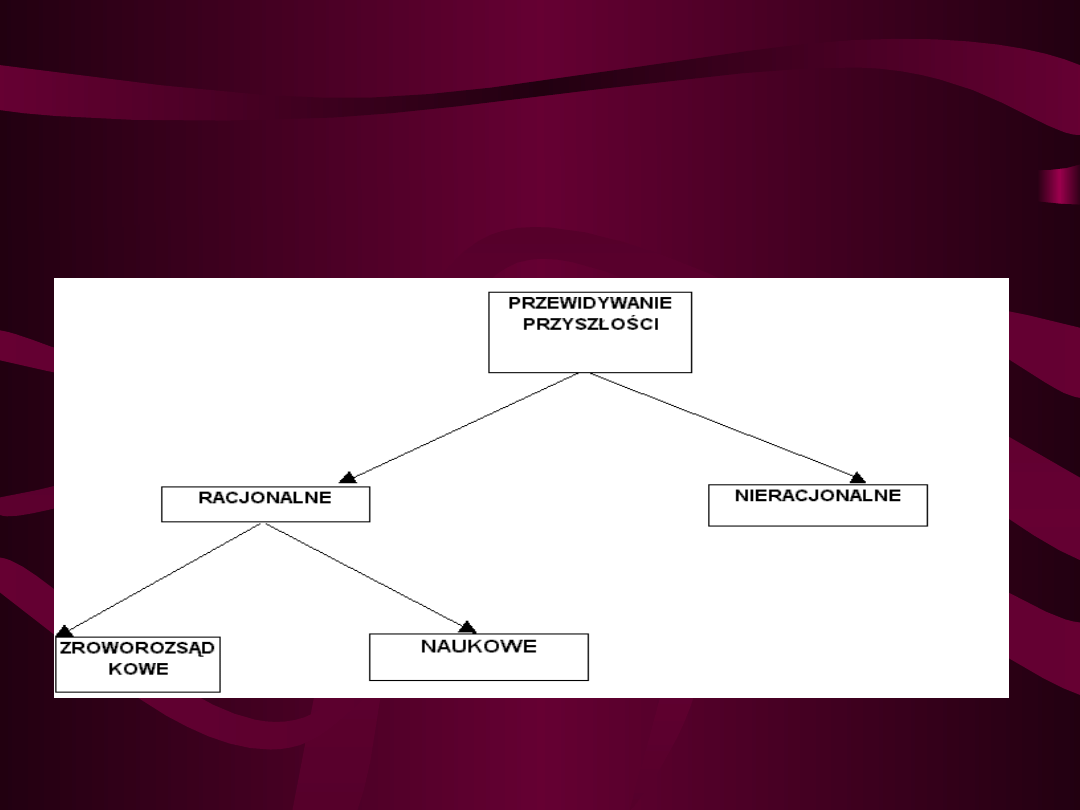
Pojęcia podstawowe

PRZEWIDYWANIE - TO WNIOSKOWANIE

O

ZDARZENIACH NIE ZNANYCH NA

PODSTAWIE

ZDARZEŃ ZNANYCH

Przewidywanie przyszłości wg. M.
Cieslak

PROGNOZOWANIE - TO RACJONALNE,
NAUKOWE PRZEWIDYWANIE PRZYSZŁYCH
ZDARZEŃ (WG. M. CIEŚLAK)

(WG. A. ZELIASIA, A. GRABIŃSKIEGO, CZ. WYDYMUSA) -
PROGNOZA JEST NAUKOWO UZASADNIONYM
WYOBRAŻENIEM PRZYSZŁOŚCI, UTRWALAJĄCYM W
POJĘCIACH WŁAŚCIWYCH DANEJ DZIEDZINIE WIEDZY
ZDARZENIE NIE PODLEGAJĄCE OBSERWACJI

.

PROGNOZA (WG. Z. CZERWIŃSKIEGO) - SĄD O ZAJŚCIU
OKREŚLONEGO ZDARZENIA W CZASIE OKREŚLONYM Z
DOKŁADNOŚCIĄ DO MOMENTU (PUNKTU) LUB OKRESU
(PRZEDZIAŁU) CZASU, NALEŻĄCEGO DO PRZYSZŁOŚCI

.

Wynikiem procesu prognozowania
jest prognoza.

CECHY PROGNOZY:

•PODSTAWA NAUKOWA.

•DOTYCZY PRZYSZŁOŚCI.

•MOŻNA JĄ WERYFIKOWAĆ EMPIRYCZNIE I
OKREŚLAĆ JEJ DOKŁADNOŚĆ

Podstawowe funkcje prognoz

:

1. Preparacyjna- zadaniem prognozy jest stworzenie dodatkowych

przesłanek w procesie podejmowania decyzji.

2. Aktywizująca - pobudzanie do podejmowania działań.

sprzyjających (gdy prognoza korzystna) lub przeciwdziałających
( gdy niekorzystna) realizacji prognozy.

3. Informacyjna – zapowiadanie spodziewanych zmian.

(wg.A.Zeliaś, B.Pawełek,S.Wanat)

RODZAJE PROGNOZ

KRYTERIUM

RODZAJ PROGNOZY

1.OKREŚLANIA
ZDARZENIA
PROGNOZOWANEGO

1. ILOŚCIOWA
2. JAKOŚCIOWA

2. SPOSÓB OKREŚLANIA
ZMIENNEJ
ROGNOZOWANEJ

1. PUNKTOWA
2. PRZEDZIAŁOWA

3. HORYZONT CZASOWY 1. KRÓTKOTREMINOWE

2. ŚREDNIOTERMINOWE
3. DŁUGOTERMINOWE
LUB
OPERACYJNE I

STRATEGICZNE

4. STOPIEŃ
SZCZEGÓŁOWOŚCI

1. OGÓLNE
2. SZCZEGÓŁOWE

5. STRUKTURA
PROGNOZY I BADANYCH
ZJAWISK

1. PROSTA
2. ZŁOŻONA

6. ZAKRES UJĘCIA

1. CAŁOŚCIOWE
2. CZĘŚCIOWE

7. ZASIĘG TERENOWY

1. ŚWIATOWE
2. MIĘDZYNARODOWE
3. KRAJOWE
4. REGIONALNE

8. METODA
OPRACOWANIA

1. INDUKCYJNA
2. DEDUKCYJNA

9. WARIANTOWOŚĆ
PROGNOZ

1. MINIMALNA
2. ŚREDNIA
3. MAKSYMALNA

10. CEL LUB FUNKCJA
PROGNOZY

1. OSTRZEGAWCZA
2. BADAWCZA
3. NORMATYWNA

11. STOPIEŃ AGREGACJI
GOSPODARKI

1. MIKROEKONOMICZNE
2. MAKROEKONOMICZNE

9. WARIANTOWOŚĆ
PROGNOZ

1. MINIMALNA
2. ŚREDNIA
3. MAKSYMALNA

10. CEL LUB FUNKCJA
PROGNOZY

1. OSTRZEGAWCZA
2. BADAWCZA
3. NORMATYWNA

11. STOPIEŃ AGREGACJI
GOSPODARKI

1. MIKROEKONOMICZN

E

2. MAKROEKONOMI
CZNE

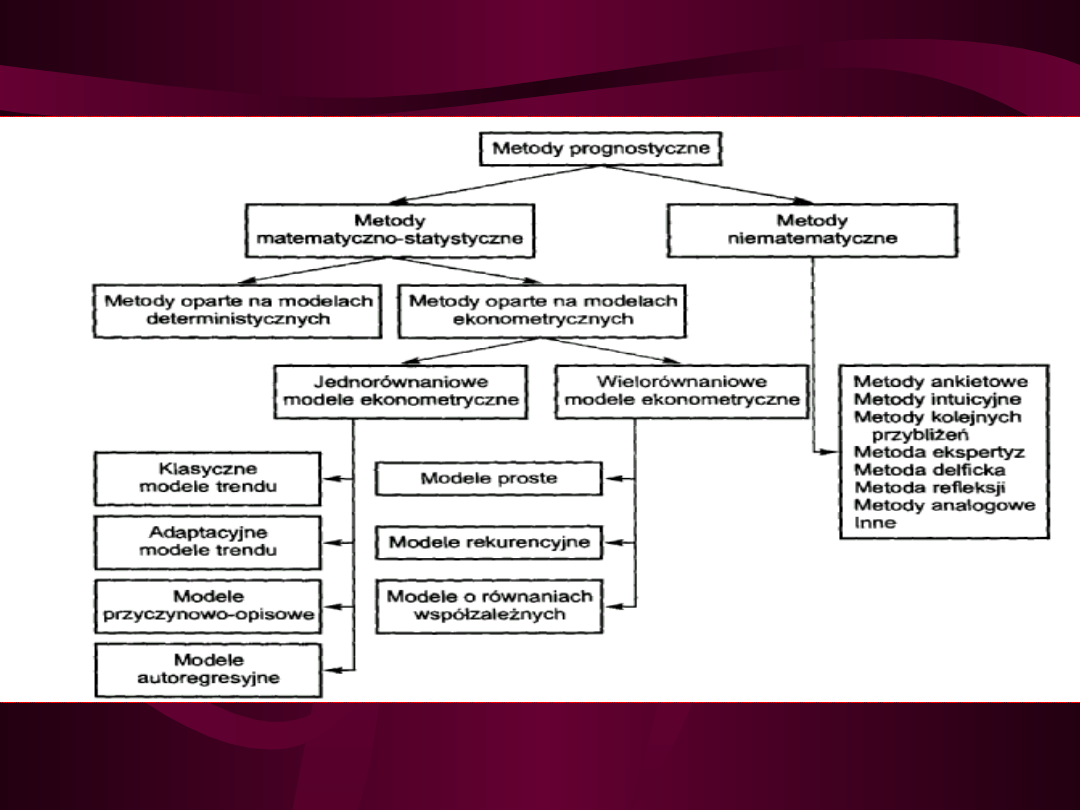
Modele prognostyczne - Metody
prognozowania

Źródło: Prognozowanie ekonomiczne. Teoria, przykłady, zadania, A.
Zeliaś,
B. Pawełek. S. Wanat, Wydawnictwo Naukowe PWN, Warszawa 2003

Metody prognozowania można podzielić na

cztery grupy, z których każda reprezentuje
odmienny sposób podejścia do prognozowania:



metody statystyczne opierają prognozowanie

na

prawidłowościach z przeszłości, bez wnikania w przyczyny ich
powstania; podstawowe informacje mają postać tzw.
szeregów czasowych;



metody modelowania przyczynowo-skutkowego

opierają prognozowanie na modelach zmian prognozowanych
zmiennych

przy

wykorzystaniu

tzw.

zmiennych

objaśniających, które opisują mechanizm ich zmiany

;



metody analogowe

opierają wnioskowanie o

przyszłości obiektu prognozowanego na informacjach o
obiektach do niego podobnych

;



metody heurystyczne

polegają na wykorzystaniu

opinii ekspertów opartej na intuicji i doświadczeniach

.

PODSTAWOWE ZAŁOŻENIA KLASYCZNEGO
EKONOMETRYCZNEGO (PREDYKCJI EKONOMETRYCZNEJ)
WNIOSKOWANIA W PRZYSZŁOŚĆ

1.

ZNANY JEST MODEL EKONOMETRYCZNY WYJAŚNIAJĄCY

KSZTAŁTOWANIE SIĘ ZMIENNEJ, DLA KTÓREJ NALEŻY
ZBUDOWAĆ PROGNOZĘ,

2

. STRUKTURA OPISYWANYCH PRZEZ MODEL ZJAWISK

JEST STABILNA W CZASIE, TZN, ŻE MODEL JEST AKTUALNY
RÓWNIEŻ W OKRESIE PROGNOZOWANYM „T”,

3. ROZKŁAD SKŁADNIKA LOSOWEGO MODELU NIE ULEGA
ZMIANOM W CZASIE

,

4.ZNANE SĄ DLA OKRESU PROGNOZOWANEGO „ T”
WARTOŚCI ZMIENNYCH OBJAŚNIAJĄCYCH WYSTĘPUJĄ
-CYCH W MODELU BĘDĄCYM PODSTAWĄ PREDYKCJI,

5. DOPUSZCZALNA JEST EKSTRAPOLACJA MODELU POZA
ZAOBSERWOWANY W PRÓBIE OBSZAR ZMIENNOŚCI
ZMIENNYCH OBJAŚNIAJĄCYCH.

PREDYKCJA EKONOMETRYCZNA – OGÓŁ ZASAD I METOD
WNIOSKOWANIA W PRZYSZŁOŚĆ NA PODSTAWIE
ODPOWIEDNIEGO MODELU EKONOMETRYCZNEGO

PROGNOZA EKONOMETRYCZNA, (y

Tp

) - WYNIK PROCESU

PREDYKCJI, PRZY PRZYJĘTYCH Z GÓRY ZAŁOŻENIACH,









k

i

,

iT

x

i

a

Tp

y

1

i= 1, 2, ... ,k
a

i

– oszacowanie i – tego parametru strukturalnego

modelu,
x

iT

– wartość i-tej zmiennej objaśniającej modelu w

okresie prognozowanym T.

Prognoza ta obliczana jest zgodnie z zasadą tzw. predykcji

nieobciążonej, czyli na

poziomie wartości nadziei zmiennej prognozowanej w okresie

prognozowanym, przy założonych wartościach zmiennych
objaśniających.

Ocena stopnia dokładności prognoz

MIARY DOKŁADNOŚCI PROGNOZ

 

MIERNIKI EX ANTE – MIARY TE INFORMUJĄ, JUŻ W

MOMENCIE BUDOWANIA PROGNOZY, JAKI BĘDZIE RZĄD
DOKŁADNOŚCI
PRZEWIDYWANIA.



  MIERNIKI EX POST – CHARAKTERYSTYKI OBLICZANE NA

PODSTAWIE REALIZACJI BŁĘDÓW PROGNOZ LUB
CZĘSTOŚCI WZGLĘDNE REALIZACJI TRAFNYCH PROGNOZ

Błąd prognozy

:

u

T

= y

T

– y

Tp

y

T

– realizacja zmiennej Y

t

w okresie T,

y

Tp

– prognoza dla okresu T .

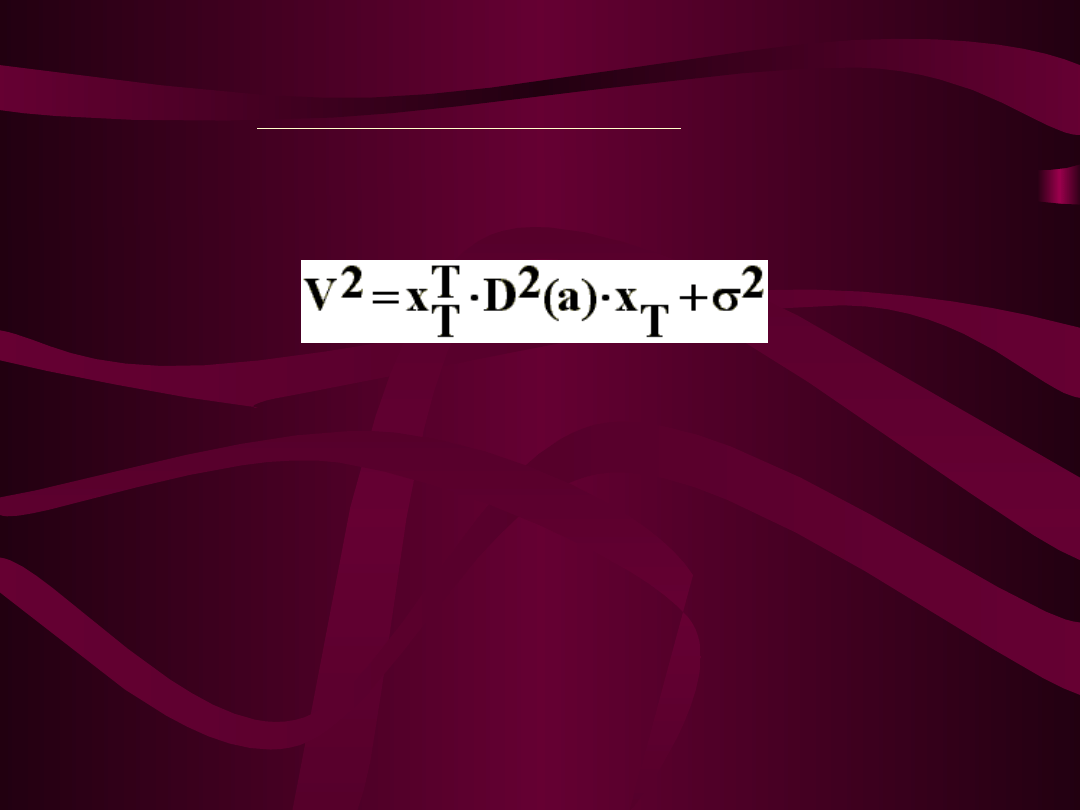
Miary ex ante

WARIANCJA PREDYKCJI

Podstawowy miernik ex ante w warunkach predykcji
nieobciążonej i powtarzalnej, opartej na modelu liniowym
oszacowanym MNK

.

 
 

gdzie:
X

T

T

– transponowany wektor założonych, dla okresu

prognozowanego T, wartości zmiennych objaśniających,
D

2

(a) – macierz wariancji i kowariancji estymatorów,



2

– wariancja składnika losowego modelu

.  

V

2

-

•

mierzy rząd dokładności predykcji przy założeniu, że

mierzy rząd dokładności predykcji przy założeniu, że

przyjęte przy obliczaniu prognozy wartości zmiennych

przyjęte przy obliczaniu prognozy wartości zmiennych

objaśniających faktycznie się zrealizują,

objaśniających faktycznie się zrealizują,

•

zależy od wielkości próby,

zależy od wielkości próby,

•

jest nie mniejsza od wariancji składnika losowego

jest nie mniejsza od wariancji składnika losowego

.

.

Średni błąd predykcji

Średni błąd predykcji

-

błąd średni predykcji, informuje o ile średnio rzecz

biorąc, w długim ciągu predykcji, rzeczywiste
realizacje Y

T

będą się odchylać (in plus i in minus) od

wartości obliczonej prognozy

.

2

V

V

Średni względny błąd predykcji

Średni względny błąd predykcji

Tp

y

V

d

wyraża stosunek średniego błędu
predykcji do jej wartości

W przypadku modelu trendu liniowego błąd prognozy ex ante
dany jest następująco

:

S

n

n

t

t

t

t

T

T

V















































1

1

1

2

)

(

2

)

(

gdzie:
s - jest odchyleniem resztowym,
t – zmienna czasowa t=1,2,…,n,
T - okres prognozowany

Średni błąd predykcji ex ante

(trend liniowy)

1. ŚREDNI BŁĄD PROGNOZY

gdzie:

m – długość okresu empirycznej weryfikacji prognoz,
liczba okresów prognozowanych,
y

T

– realizacja zmiennej Y

t

w okresie T,

y

Tp

– prognoza dla okresu T.

 













m

T

Tp

T

T

y

y

m

u

1

1

MIERNIKI EX POST

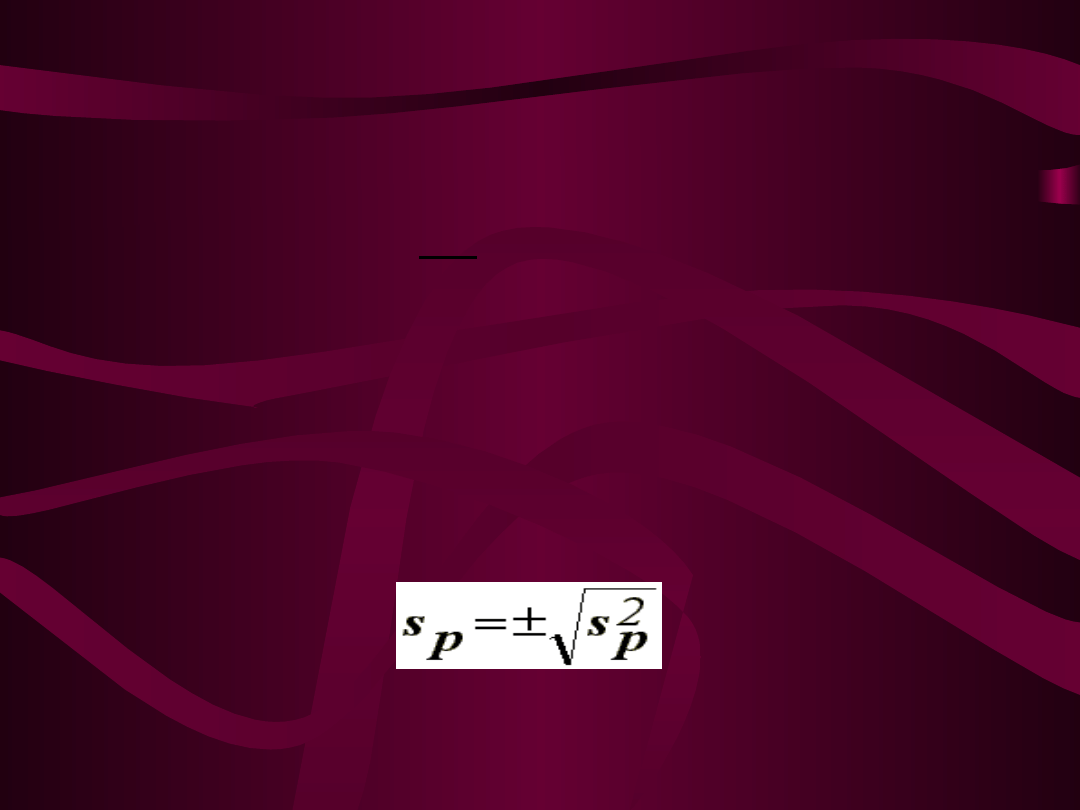
2. EMPIRYCZNA WARIANCJA PREDYKCJI

s

2

p

= MSE – MEAN SQUARE ERROR,

s

p

– ŚREDNI EMPIRYCZNY BŁĄD PROGNOZY

s

p

– RMSE





2

1

2

1









m

T

Tp

T

y

y

m

s

p

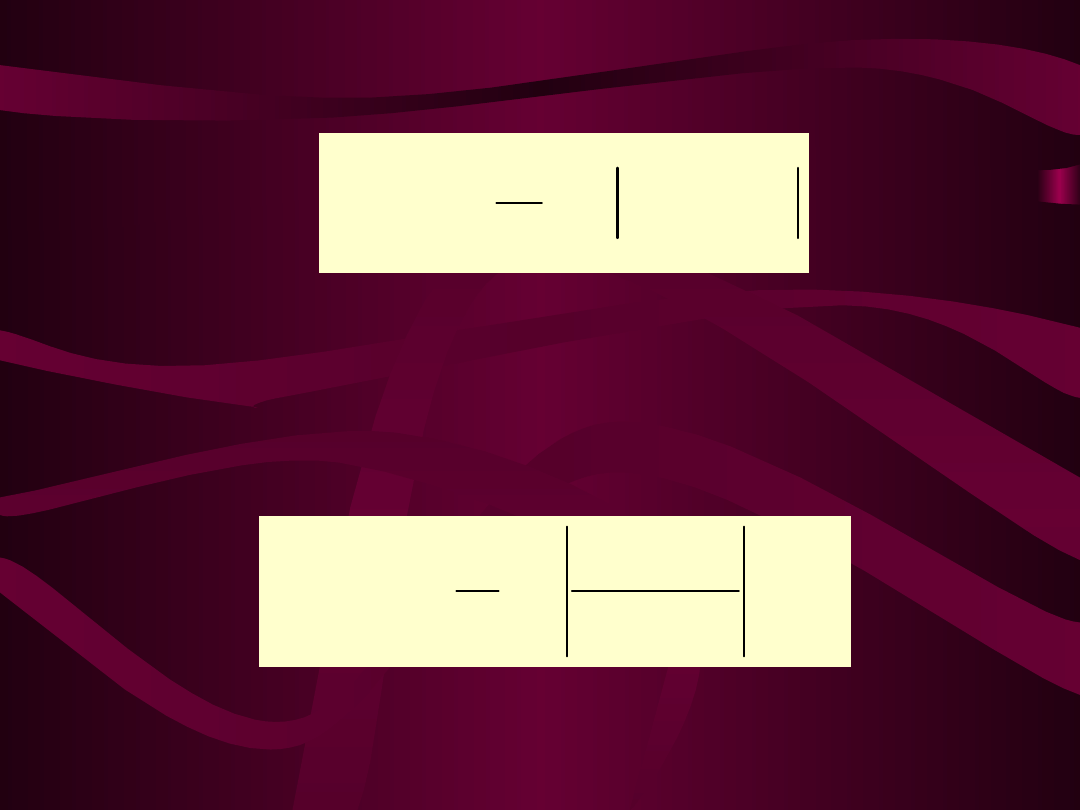
3. ŚREDNI ABSOLUTNY BŁĄD PROGNOZY

MAE – MEAN ABSOLUTE ERROR

,

4. PROCENTOWY ŚREDNI BŁĄD ABSOLUTNY

MAPE – MEAN ABSOLUTE PERCENTAGE ERROR,









m

T

Tp

T

y

y

m

MAE

1

1

100

1

1











m

T

T

Tp

T

y

y

y

m

MAPE

Prognozy dopuszczalne

Gdy nie ma indywidualnych kryteriów

dopuszczalności prognoz to przyjmuje się, że jeżeli
względny miernik D dokładności prognoz (ex ante lub ex
post ) spełnia nierówność;

D  



to prognozy są bardzo dobre,

3%< D  



to prognozy uznaje się za dobre,

5%< D 





to prognozy mogą być dopuszczalne,

10%< D, to prognozy sa niedopuszczalne

PRZYKŁAD

PRZYKŁAD

DANY JEST OSZACOWANY MODEL POZIOMU
SPRZEDAŻY W PRZEDSIĘBIORSTWIE „Q”:
(Źródło” prognozowanie gospodarcze, red. E. Nowak,
Placet, Warszawa 1998)

Y

t

= ,4 X

t

+ 6 X

2t

+ ,8 + u

t,

 gdzie:

 

Y

t

– WARTOŚĆ SPRZEDAŻY, w tys. zł , w roku t,

X

1t

–WYDATKI NA REKLAMĘ , w tys. zł , w roku t,

X

2t

–NAKŁADY INWESTYCYJNE, w tys. zł , w roku t,

t= 1984, 1995, ..., 1997, czyli t = 1, 2, ...,14

WIEMY PONADTO, ŻE







































12.96

0.4

1.6

-

0,4

2.56

2.8

1,6

-

2.8

4.84

(a)

2

D

s

2

= 4,

R

2

= ,92,

DW = ,72

MODEL MOŻE BYĆ WYKORZYSTANY DLA CELÓW
PROGNOZOWANIA PONIEWAŻ:

•PARAMETRY SĄ ISTOTNE STATYSTYCZNIE,

•DOPASOWANIE DO DANYCH EMPIRYCZNYCH JEST
WYSOKIE,

•NIE WYSTĘPUJE AUTOKORELACJA RESZT,

•ZNAKI PARAMETRÓW SĄ POPRAWNE MERYTORYCZNIE

ZADANIE:
OBLICZYĆ PROGNOZĘ SPRZEDAŻY NA ROK 1998,
DYSPONUJĄC FUNKCJAMI TRENDÓW ZMIENNYCH
OBJAŚNIAJĄCYCH

 

X

1t

*

=0,2 t +2

X

2t

*

= 0,3 t +3,5 

ABY OBLICZYĆ PROGNOZĘ SPRZEDAŻY
NALEŻY USTALIĆ WARTOŚCI ZMIENNYCH
OBJAŚNIAJĄCYCH W ROKU 1998 tj. dla T=15

 

X

X

1T

1T

*

*

=0,2

=0,2





15 +2 = 5

15 +2 = 5

 

 

X

X

2T

2T

*

*

= 0,3

= 0,3





15 +3,5 = 8 

15 +3,5 = 8 

Prognoza na rok 1998, przy założeniu, że

X

1T

= 5 tys. zł., X

2T

= 8 tys. zł.,

  

Y

Y

TP

TP

= ,4

= ,4









 + 6

 + 6





8 + ,8 = 28,8 tys. zł

8 + ,8 = 28,8 tys. zł

WARIANCJA PREDYKCJI,

WARIANCJA PREDYKCJI,

ŚREDNI WZGLĘDNY BŁĄD PREDYKCJI

ŚREDNI WZGLĘDNY BŁĄD PREDYKCJI











2

s

T

x

(a)

2

D

T

T

x

2

V

68,2

4

1

8

12.96

0.4

1.6

-

0,4

2.56

2.8

1,6

-

2.8

4.84

1

8

5

5































































































V ≈ 8,26 tys. zł,

V ≈ 8,26 tys. zł,

6,4%

100%

128,8

8,26

Tp

y

V





