Decyzje

w

zarządzaniu

Decyzje

w

zarządzaniu

zapasami

zapasami

Funkcjonalny

Funkcjonalny

podział

podział

zapasów

zapasów

1.

1.

Zapas bieżący

Zapas bieżący

(cykliczny)

(cykliczny) – jest to część zapasów

zużywanych w toku normalnej sprzedaży i
odtwarzanych w rutynowym procesie zamawiania. Odnosi
się również do produktów, które firma regularnie zużywa w
toku normalnej działalności gospodarczej.

2.

2.

Zapasy w produkcji

Zapasy w produkcji – zapasy te, czasami nazywane

produkcją w toku, produktami
przetwarzanymi lub półproduktami, są ważne
w sferze wytwarzania. Termin „zapas w drodze” odnosi się
to zapasu transportowanego przez przewoźnika do
nabywcy.

3.

3.

Zapas bezpieczeństwa

Zapas bezpieczeństwa – nazywany także zapasem

buforowym. Chroni on przed niepewnością w dynamice
popytu

lub

czasie

dostawy.

Utrzymanie

zapasu

bezpieczeństwa pomaga firmie uniknąć negatywnych dla
klientów skutków wyczerpania zapasu w przypadku
nieoczekiwanego wzrostu popytu.

4.

4.

Zapas sezonowy

Zapas sezonowy – gromadzony i utrzymywany przez

przedsiębiorstwo przed sezonem, w którym będzie go
potrzebować (przemysł spożywczy, odzieżowy, artykułów
sportowych, zabawkowy).

5.

5.

Zapas promocyjny

Zapas promocyjny – utrzymywany po to, aby system

logistyczny firmy mógł sprawnie zareagować na promocję
marketingową lub ofertę cenową.

6.

6.

Zapas spekulacyjny

Zapas spekulacyjny – kojarzony z materiałami

potrzebnymi firmom produkcyjnym i montażowym. Chroni
przed zwyżką ceny lub ograniczeniem dostępności
produktów.

7.

7.

Zapas martwy

Zapas martwy – nie ma wartości z punktu widzenia

normalnych celów gospodarczych. Firma może wysłać
zapas martwy do miejsca, w którym ma on wartość
ekonomiczną, sprzedać go lub przekazać do dystrybucji na
rynkach zagranicznych, albo pozbyć się go zgodnie z
wymogami ochrony środowiska naturalnego.

Kontrola poziomu zapasów typu

„pchania” i „ssania”

Zarządzanie zapasami opiera się w zasadzie na dwóch

podstawowych koncepcjach:

• „pchania” – zmierza ona do rozdysponowania dostaw

o rozmiarach wynikających z tzw. korzyści
skali (produkcji i zakupu) do
poszczególnych punktów gromadzenia zapasów,

• „ssania” - polegająca na stałym uzupełnianiu zapasu w

miarę występujących potrzeb.

I. Kontrola poziomu zapasów typu

„pchania”

Firma produkcyjna X posiada 3 magazyny, zaopatrujące sieć

sklepów. Każdy z tych magazynów obsługuje ok. 200
sklepów.

Firma wyprodukowała 6000 kalkulatorów (zapas przekroczył

bieżące potrzeby). Podjęto taką decyzję, ponieważ
produkcja w tym okresie była najekonomiczniejsza, a
zakład jest pewny, że znajdzie zbyt na ten produkt.
Wszystkie wyprodukowane kalkulatory powinny być
rozesłane do poszczególnych magazynów stosowanie do
przewidywanego popytu w każdym z nich.

Przy obliczeniach należy także uwzględnić aktualny poziom

zapasów tych kalkulatorów w każdym z magazynów.
Należy więc obliczyć sposób alokacji dostawy 6 000 sztuk
kalkulatorów naukowych.

Magazyn

A

B

C = A - B

D

E = D + C

Miesięczn

a

prognoza

sprzedaż

y

Ilość

aktualne

go

zapasu

Potrzeby

netto

Przydział

nadmiaru

Przydział

1

3 700

1 500

2

2 100

700

3

1 300

300

Razem

7 100

 

Obliczenia

Przydział nadmiaru obliczamy ze wzory:

nadmierna ilość zakupu

(dokonany zakup – suma potrzeb

netto)

x potrzeby netto / całkowite

zaopatrzenie systemu

(suma potrzeb netto)

Rozwiązanie:

Dokonany zakup: 6 000

Nadmierna ilość zakupu: 1 400

(1) 1 400 x 2 200 / 4 600 = 670

(2) 1 400 x 1 400 / 4 600 = 426

(3) 1 400 x 1 000 / 4 600 = 304

Magazyn

A

B

C = A - B

D

E = D + C

Miesięczn

a

prognoza

sprzedaż

y

Ilość

aktualne

go

zapasu

Potrzeby

netto

Przydział

nadmiaru

Przydział

1

3 700

1 500

2 200

670

2 870

2

2 100

700

1 400

426

1 826

3

1 300

300

1 000

304

1 304

Razem

7 100

 

4 600

1400

6 000

II. Kontrola zapasów typu „ssanie”

II. Kontrola zapasów typu „ssanie”

1. Metoda stałej wielkości zamówienia

Firma „AE” sprzedaje 160 sztuk produktu „EDUKACJA”

tygodniowo. W celu uzupełnienia zapasów musi
składać zamówienia u dostawcy z
dwutygodniowym wyprzedzeniem. Czasami zdarza się, że
tygodniowe zapotrzebowanie klientów na produkt wzrasta
do 200 sztuk tygodniowo, a okres dostawy wydłuża się do
3 tygodni. Wartość produktu „EDUKACJA” wynosi 20 zł a
koszty złożenia zamówienia 400 zł, natomiast koszty
utrzymania zapasów 30% wartości produktu w skali roku.
Celem kontroli poziomu zapasów jest utrzymanie
optymalnej ilości zapasów.

Wyznaczanie punktu zamówienia (ROP)

Punkt zamówienia jest to moment, w którym należy złożyć

zamówienie uzupełniające zapasy tak, aby do momentu
dostawy aktualny zapas nie uległ wyczerpaniu.

ROP = 2 tygodnie x 160 sztuk/tydzień = 320 sztuk

Oznacza to, że jeżeli aktualny zapas produktu „EDUKACJA”

obniży się do poziomu 320 sztuk, należy złożyć ponowne
zamówienie u dostawcy.

Jeśli stosunkowo często pojawiają się opóźnienia w realizacji

dostaw a popyt na produkt „EDUKACJA” ma tendencje
zwyżkowe, to punkt zamawiania należy wyznaczyć na
podstawie wielkości maksymalnych:

ROP = 3 tygodnie x 200 sztuk/tydzień = 600 sztuk

W ten sposób redukujemy możliwość przedwczesnego

wyczerpania się zapasów.

Wyznaczanie optymalnej

Wyznaczanie optymalnej

(ekonomicznej) wielkości dostawy –

(ekonomicznej) wielkości dostawy –

EOQ

EOQ

Optymalna partia (wielkość) dostawy jest to taka partia,

której łączne koszty zakupu i utrzymania zapasów są
najmniejsze. Łączny koszt uzyskania rocznych dostaw
składa się z następujących elementów:

 kosztów zakupu
 kosztów magazynowania
 wartości zakupionego towaru

Koncepcja kosztu całkowitego

Koncepcja kosztu całkowitego

Koszt zakupu (K

Z

) oblicza się jako:

K

Z

= (koszt pojedynczego zamówienia K

d

) x roczne

zaopatrzenie D / wielkość dostawy Q

Koszt magazynowania (K

m

) oblicza się jako:

K

m

= (jednostkowy koszt składowania K

s

) x (cena

jednostkowa C) x wielkość dostawy Q / 2

Wartość (W) zakupionego towaru w ciągu roku wynosi:

W = (cena jednostkowa c) x (roczne zapotrzebowanie

D)

Tak więc równanie łącznego kosztu uzyskania rocznych

dostaw można zapisać w następujący sposób:

D

C

2

Q

C

K

Q

D

K

K

s

d

c















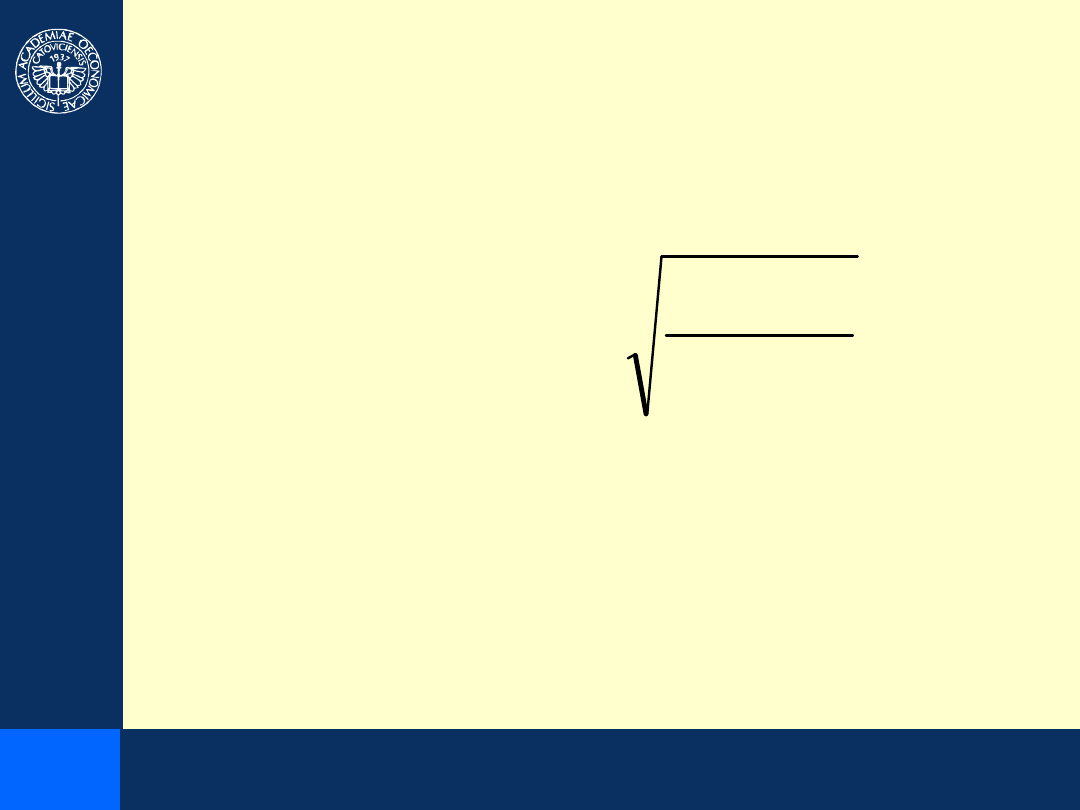
Wyznaczanie optymalnej wielkości

dostawy

Wielkość optymalnej partii dostawy obliczamy ze wzoru:

gdzie:
K

D

– koszt pojedynczego zamówienia

K

S

– jednostkowy koszt składowania

D – roczne zapotrzebowania
C – cena jednostkowa

C

K

D

K

Q

EOQ

S

D









2

2. Metoda stałego okresu zamawiania

POQ

Polega ona na ustaleniu równych okresów przeglądu (kontroli)

stanu zapasu określonego produktu (zamiast stałej
kontroli).

D

EOQ

n

POQ





Po okresowej kontroli zapasów zamawia się taką

ilość produktu, która uzupełni jego zapas do

poziomu maksymalnego.

Należy wyznaczyć maksymalny poziom zapasu produktu:

normalne zapotrzebowanie · POQ (stały okres zamawiania)

+ (max. zapotrzebowanie · max. okres dostawy)

.



Z

MAX

3. Wielkość optymalnej partii dostawy

przy upustach cenowych

Otrzymujemy dodatkowe dane, wynikające z aktualnej stawki

transportowej:

Ilość w sztukach

Stawka

transportowa za

sztukę

> 700

0,35 zł

700 – 1100

0,28 zł

< 1100

0,26 zł

W celu obliczenia tej partii dostawy, której łączny koszt
będzie najniższy, należy sprawdzić koszty tych wszystkich
wielkości partii dostawy, które mogą wiązać się ze zmianami.

Otrzymujemy dodatkowe dane, wynikające z aktualnej stawki
transportowej:

D

St

2

Q

C

K

Q

D

K

K

s

d

c















• dla 699

K

C

= 400 x (160 x 52 / 699) + (0,3 x 20 x 699 / 2) +

(0,35 x 160 x 52) = 9 770 zł

• dla 1053

K

C

= 400 x (160 x 52 / 1053) + (0,3 x 20 x 1053 / 2) +

(0,28 x 160 x 52) = 8 649 zł

• dla 1101

K

C

= 400 x (160 x 52 / 1101) + (0,3 x 20 x 1101 / 2) +

(0,26 x 160 x 52) = 8 489 zł

• dla 1200

K

C

= 400 x (160 x 52 / 1200) + (0,3 x 20 x 1200 / 2) +

(0,26 x 160 x 52) = 8 537 zł

Koszty

Wielkość partii

699

1053

1101

1200

Transport

u

2 912 zł

2 330 zł

2 163 zł

2 163 zł

Zakupów

4 761 zł

3 160 zł

3 023 zł

2 773 zł

Utrzymani

a

zapasów

2 097 zł

3 159 zł

3 303 zł

3 600 zł

Razem

9 770 zł

8 649 zł

8 489 zł

8 537 zł

Mając możliwość skorzystania z niższych stawek

transportowych stwierdzamy, że obecnie optymalną
partią dostawy jest partia 1101 sztuk produktu.

4. Wielkość optymalnej serii

produkcyjnej 

Firma produkujący wyroby higieniczne produkuje pieluchy

jednorazowe, których zbyt wynosi rocznie 1 000 000 sztuk.
Koszt ustawienia linii produkcyjnej wynosi 180 zł, a
tygodniowa wielkość produkcji tych pieluch 22 000 sztuk.

Jeżeli koszt produkcji pieluchy wynosi 0,45 zł / szt., a roczny

koszt utrzymania zapasu 0,10 zł, to ile pieluch powinna
wytwarzać firma w czasie jednej serii produkcyjnej?

Jeżeli firma produkuje 1 144 000 sztuk pieluch
jednorazowych rocznie (22 000 x 52), a sprzedaje
tylko 1 000 000,

to wskaźnik sprzedaży (zużycia)

wynosi:

87

,

0

1144000

1000000







p

d

W

Z

gdzie:
d – wielkość popytu w danym okresie
p – wielkość produkcji w danym okresie

Wskaźnik sprzedaży (zużycia) wynosi 87%, pozostała
część – 13% jest utrzymywana w zapasie.

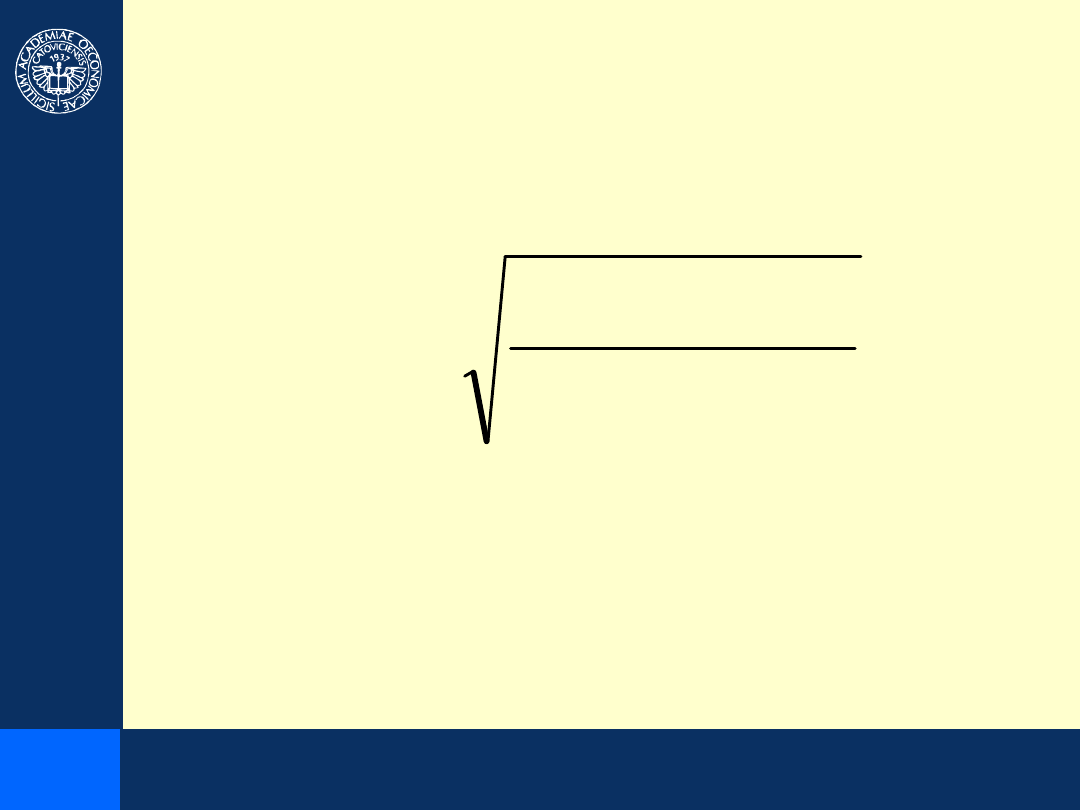
Wielkość optymalnej serii produkcyjnej

będzie więc

równa:

gdzie:
C

PP

– koszt jednorazowego przestawienia produkcji

)

1

(

2

Z

S

PP

O

W

K

D

C

S











Wielkość optymalnej serii produkcyjnej będzie więc
równa:

166410



0,87)

(1-

*

0,10

1000000

*

180

*

2

=

S

O

Długość optymalnej serii produkcyjnej pieluszek
jednorazowych wynosi 166 410 sztuk, co przy
tygodniowej wielkości produkcji sprawia, że każda
seria będzie produkowana przez około 7,5 tygodnia.
Oznacza to, że firma będzie uruchamiała produkcję raz
na dwa miesiące.

Zadanie 1.

Zakłady meblarskie ze Świdnicy, które produkują głównie
komody, posiadają 3 magazyny. Magazyny te mają za
zadanie obsługiwać sieć 11 sklepów firmowych. Zakłady w
ostatnim czasie wyprodukowały 7 000 komód. Podjęto taką
decyzję, ponieważ produkcja w tym okresie była
najekonomiczniejsza, a zakład jest pewny, że znajdzie zbyt na
komody (obserwuje się w ostatnim czasie zwiększone
zainteresowanie rynku na ten właśnie produkt). Poniżej w
tabeli zestawiono prognozę miesięcznej sprzedaży oraz ilość
aktualnego zapasu.

Magazyn 1

Magazyn 2

Magazyn 3

Razem

Miesięczny przewidywany
zbyt

3 000

2 500

1 000

6 500

Wielkość aktualnego zapasu

600

400

150

Potrzeby netto

Przydział nadmiaru

Przydział całkowity

Produkcja tygodniowa komód wymaga dostarczania do
zakładu 6 000 sztuk odpowiednich desek. W celu
uzupełnienia zapasów zakłady meblarskie muszą zamawiać
deski z tartaku z dwutygodniowym wyprzedzeniem. Często
bywa jednak (np. gdy firma produkuje w
nadmiarze), że zapotrzebowanie na deski wzrasta do 9 000
sztuk tygodniowo, a czas dostawy wydłuża się aż do 3
tygodni. Wartość jednostkowa (koszt jednej deski) wynosi 8
zł, a jednorazowy koszt złożenia zamówienia 300 zł,
natomiast koszty utrzymania zapasów wynoszą aż 32%
wartości produktu (w skali roku).

Zakłady mają podpisaną stałą umowę na dostawę
wspomnianych desek z tartaku. Tartak sam dostarcza deski
do zakładu, a w umowie uwzględnił upusty cenowe na stawce
transportowej, które uzależnione są oczywiście od wielkości
przewożonych desek, upusty te przedstawia tabela poniżej:

Do produkcji komód niezbędne są rączki do szuflad, które
przytwierdza się po jednej do każdej z nich (1 komoda = 4
rączki). Zakład stworzył specjalną linię do ich produkcji, a ich
zużycie wynosi 240 000 sztuk rocznie. Koszty ustawienia linii
produkcyjnej wynoszą 1 500 zł, a tygodniowa wielkość
produkcji 5 700 rączek.

Ilość w sztukach

Stawka transportowa

za sztukę

do 6 000

0,20 zł

6 000 – 9 000

0,13 zł

powyżej 9 000

0,11 zł

1. Oblicz potrzeby netto i dokonaj alokacji nadmiaru dla

każdego z magazynów wyznaczając jednocześnie
przydział całkowity dla każdego z nich.

2. Wyznacz punkt ponownego zamówienia dla dostaw

terminowych i normalnej produkcji oraz dostaw
wydłużonych i zwiększonej produkcji komód.

3. Wyznacz ekonomiczną wielkość dostawy (EOQ).
4. Wyznacz maksymalny poziom zapasu desek w stałym

cyklu zamawiania (POQ).

5. Dokonaj wyboru wielkości partii dostaw (tych, które będą

wiązały się ze zmianami) i określ, która z rozważanych
partii dostaw będzie najbardziej optymalna.

6. Oblicz wskaźnik zużycia i wielkość optymalnej serii

produkcyjnej dla rączek produkowanych w zakładzie,
wiedząc, że koszt wyprodukowania jednej rączki wynosi
1,25 zł a jednostkowy koszt utrzymania zapasu 0,25 zł/szt.

1. Oblicz potrzeby netto i dokonaj alokacji nadmiaru dla

każdego z magazynów wyznaczając jednocześnie
przydział całkowity dla każdego z nich.

Przydział nadmiaru obliczamy ze wzory:

nadmierna ilość zakupu

(dokonany zakup – suma potrzeb

netto)

x potrzeby netto / całkowite

zaopatrzenie systemu

(suma potrzeb netto)

Rozwiązanie:

Dokonany zakup: 7000

Nadmierna ilość zakupu: 1650

1 650 · 2 400 / 5 350 = 740 szt.
1 650 · 2 100 / 5 350 = 648 szt.

1 650 · 850 / 5 350 = 262 szt.

Magazy

n 1

Magazy

n 2

Magazy

n 3

Razem

Miesięczny
przewidywany zbyt

3 000

2 500

1 000

6 500

Wielkość
aktualnego zapasu

600

400

150

Potrzeby netto

Przydział nadmiaru

Przydział całkowity

Magazy

n 1

Magazy

n 2

Magazy

n 3

Razem

Miesięczny
przewidywany zbyt

3 000

2 500

1 000

6 500

Wielkość
aktualnego zapasu

600

400

150

Potrzeby netto

2 400

2 100

850

5 350

Przydział nadmiaru

740

648

262

1 650

Przydział całkowity

3 140

2 748

1 112

7 000

2. Wyznacz punkt ponownego zamówienia dla dostaw

terminowych i normalnej produkcji oraz dostaw
wydłużonych i zwiększonej produkcji komód.

ROP

I

= 2 tygodnie · 6 000 szt. / tydzień = 12 000 sztuk

ROP

II

= 3 tygodnie · 9 000 szt. / tydzień = 27 000 sztuk

Przy dostawach terminowych i normalnej wielkości produkcji

ponowny punkt zamawiania wynosi 12 000 sztuk, a w
sytuacji wydłużających się w czasie dostaw oraz
zwiększonego zapotrzebowania na deski do produkcji
(zwiększonej produkcji) wyniesie on 27 000 sztuk.

3. Wyznacz ekonomiczną wielkość dostawy (EOQ).

C

K

D

K

Q

EOQ

S

D









2

8551

73125000

56

,

2

187200000

8

32

,

0

52

6000

300

2

















Q

Ekonomiczna wielkość dostawy będzie wynosiła
8551 sztuk desek.

4. Wyznacz maksymalny poziom zapasu desek w stałym

cyklu zamawiania (POQ).

D

EOQ

n

POQ





43

,

1

312000

444652

6000

52

8551

52











POQ

Wyznaczamy maksymalny poziom zapasu desek:

35580

3

9000

43

,

1

6000











Z

MAX



Z

MAX

Oznacza to, że poziom zapasu desek powinien być
kontrolowany co półtorej tygodnia, a wielkość partii
dostawy

powinna

odpowiadać

różnicy

pomiędzy

aktualnym zapasem desek, a jego maksymalnym
zapasem, który wynosić 35 580 sztuk.

normalne zapotrzebowanie · POQ (stały

okres zamawiania)

+ (max. zapotrzebowanie · max. okres

dostawy)

5. Dokonaj wyboru wielkości partii dostaw (tych, które będą
wiązały się ze zmianami) i określ, która z rozważanych partii
dostaw będzie najbardziej optymalna. (5999, 8551, 9001 oraz
10000)

T

M

Z

C

K

K

K

K







- dla wielkości dostawy 5 999:

zł

K

C

3

,

85681

62400

7

,

7678

6

,

15602

)

52

6000

20

,

0

(

)

2

5999

8

32

,

0

(

)

5999

52

6000

(

300





























- dla wielkości dostawy 8 551 (ekonomiczna wielkość
dostawy):

zł

K

C

4

,

62451

40560

3

,

10945

1

,

10946

)

52

6000

13

,

0

(

)

2

8551

8

32

,

0

(

)

8551

52

6000

(

300





























- dla wielkości dostawy 9001:

- dla wielkości dostawy 10000:

zł

K

C

1

,

56240

34320

3

,

11521

8

,

10398

)

52

6000

11

,

0

(

)

2

9001

8

32

,

0

(

)

9001

52

6000

(

300





























zł

K

C

56480

34320

12800

9360

)

52

6000

11

,

0

(

)

2

10000

8

32

,

0

(

)

10000

52

6000

(

300





























Mając

możliwość

skorzystania

z

niższych

stawek

transportowych stwierdzamy, że obecnie optymalną partią
dostawy jest partia 9 001 sztuk desek.

6. Oblicz wskaźnik zużycia i wielkość optymalnej serii
produkcyjnej dla rączek produkowanych w zakładzie,
wiedząc, że koszt wyprodukowania jednej rączki wynosi
1,25 zł a jednostkowy koszt utrzymania zapasu 0,25 zł/szt.

Obliczanie wskaźnika zużycia:

81

,

0

296400

240000







p

d

W

z

Obliczanie optymalnej serii produkcyjnej:

)

1

(

2

Z

S

PP

O

W

K

D

C

S











sztuk

S

O

123117

)

81

,

0

1

(

25

,

0

240000

1500

2













Wskaźnik zużycia wynosi 0,81, a wielkość optymalnej serii
produkcyjnej dla rączek to 123 117 sztuk. Oznacza to, że
przy tygodniowej wielkości produkcji 5 700 rączek każda
seria produkcyjna będzie produkowana przez około 21
tygodni (około 5 miesięcy).