DLACZEGO PIENIĄDZ TRACI NA WARTOŚCI

1.

Polityka banku centralnego

2.

Pieniądze będące wcześniej do dyspozycji mogą być zainwestowane

3.

Naturalna preferencja podmiotów – chęć posiadania rzeczy wcześniej

4.

Obietnicy otrzymania sumy pieniędzy w przyszłości towarzyszy ryzyko

faktycznego jej otrzymania

INFLACJA

WARTOŚCI PRZYSZŁA

informuje z jaką wartością nominalnie ustalonej kwoty będziemy mieli do czynienia po

upływie określonego czasu. Proces przechodzenia od wartości aktualnej do wartości

przyszłej to

kapitalizacja.

Polega ona na arytmetycznym ustaleniu ostatecznej wartości

przepływu (lub przepływów) środków pieniężnych, przy zastosowaniu odsetek składanych.

FV

n

= PV • (1+r)

n

FV

n

– wartość przyszła

PV – wartość teraźniejsza

r – stopa procentowa (dla jednego okresu)

n – liczba okresów

FVIF

r,n

Future Value Interest

Factor

PRZYKŁAD:

Do banku został złożony

depozyt

o wartości 1000 zł na 3 lata. Oprocentowanie depozytu wynosi 10%

rocznie. Określ wartość depozytu na koniec 3 okresu.

1000

1100

1210

1331

FV

3

= 1000 • (1 +0,10)

3

= 1000 • 1,331 = 1331 zł

r = 10%

0

1

2

3

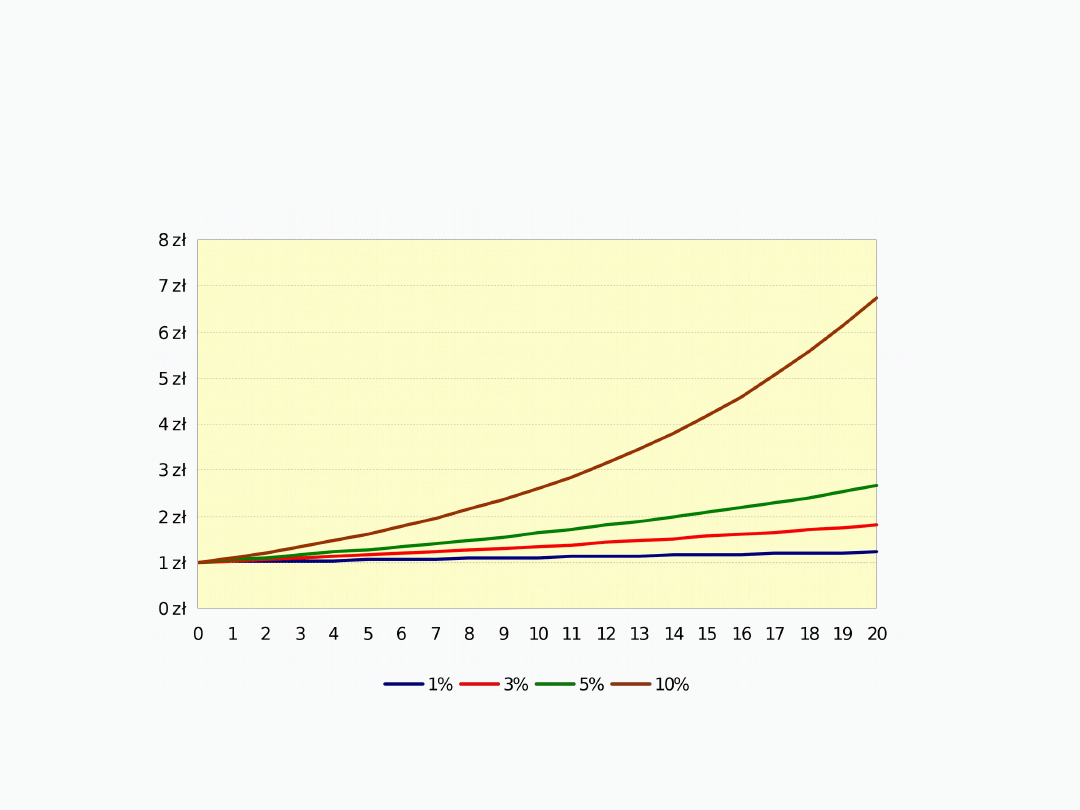
ZALEŻNOŚĆ WARTOŚCI PRZYSZŁEJ

OD STOPY PROCENTOWEJ I LICZBY OKRESÓW

Wartość przyszła 1 złotego złożonego na

n

okresów i

r

procent

1%

3%

5%

10%

PV

n

= FV •

PV

n

– wartość bieżąca przyszłej płatności

FV – wartość przyszła na koniec n-tego okresu

r – stopa dyskontowa (reprezentuje utratę wartości pieniądza w czasie)

n – okres z końca którego sprowadzamy przyszłą wartość na początek okresu bieżącgo

WARTOŚCI BIEŻĄCA

(TERAŹNIEJSZA, ZAKTUALIZOWANA)

określa teraźniejszą wartość przyszłych przepływów środków pieniężnych. W celu obliczenia

wartości zaktualizowanej posługujemy się metodą dyskonta.

Dyskontowanie

to proces

odwrotny do kapitalizacji. Polega na obliczeniu, jaką wartość w dniu dzisiejszym ma kwota,

którą otrzymamy po n okresach przy założeniu, że stopa procentowa reprezentująca utratę

wartości pieniądza wynosi r.

PVIF

r,n

Present Value Interest

Factor

PRZYKŁAD:

Pod koniec 3 roku otrzymuje kwotę 1000 zł.

Stopa dyskontowa wynosi 10% rocznie. Określ wartość

bieżącą przyszłej kwoty

751

826

909

1000

FV

3

= 1000 • 1/(1 + 0,10)

3

= 1000 • 0,751 = 751 zł

1

(1+r

)

n

r = 10%

0

1

2

3

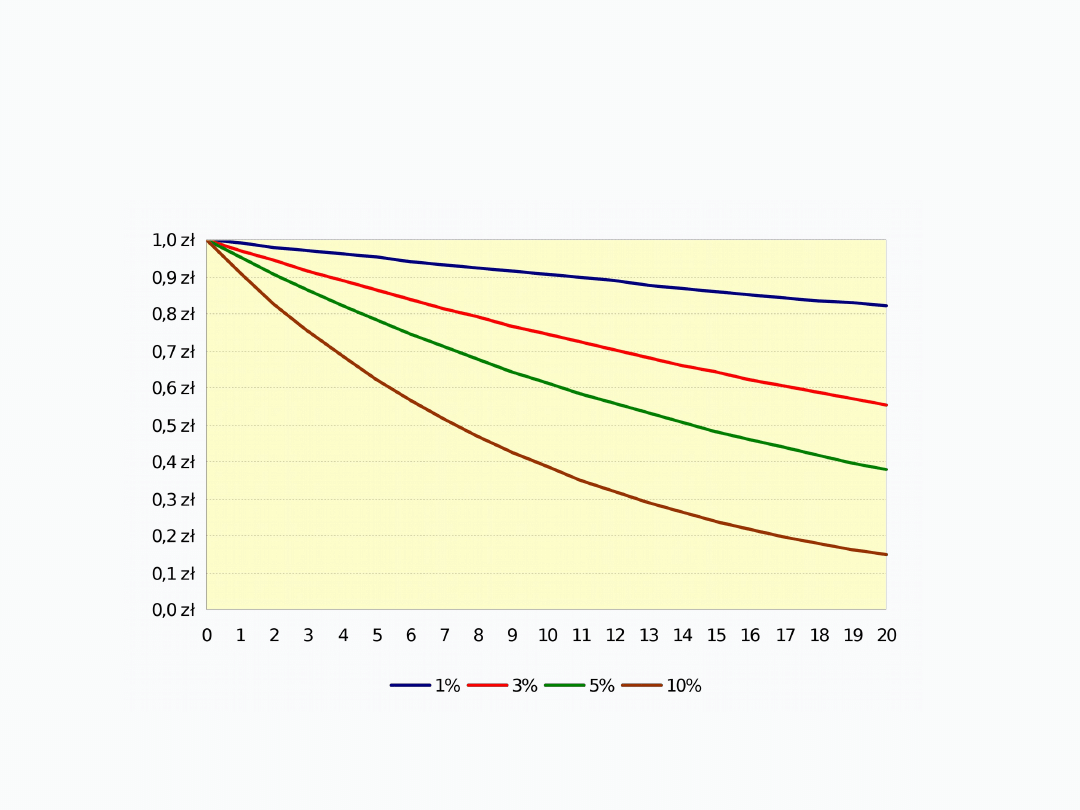
ZALEŻNOŚĆ WARTOŚCI BIEŻĄCEJ

OD STOPY DYSKONTOWEJ I LICZBY OKRESÓW

Wartość bieżąca 1 złotego złożonego na

n

okresów i

r

procent

1%

3%

5%

10%

PŁATNOŚĆ ANNUITETOWA - RENTA

Seria

stałych

płatności (PMT) dokonywanych w ciągu n okresów,

w

równych

odstępach czasu,

przy niezmiennej stopie r

Przykłady:

• spłata rat kredytu bankowego

• opłaty leasingowe

• płatności wynikające z umowy dzierżawy i najmu

• płatności ubezpieczeniowe

• płatności na fundusze emerytalne

WARTOŚCI BIEŻĄCA ANNUITY

1. PŁATNEJ Z DOŁU

PV(A

r,n

) – wartość przyszła annuity na koniec n-tego okresu dla n płatności okresowych

r – stopa procentowa (dla jednego okresu)
n – liczba płatności równa liczbie okresów
PMT – wielkość annuity realizowanej na

koniec

każdego okresu

PVIFA

r,n

Present Value Interest Factor of

Annuity

PV(A

r,n

) = PMT •

1 - (1 + r)

-n

r

2. PŁATNEJ Z GÓRY

PV(A

r,n

) = PMT •

1 - (1 + r)

-n

• (1 + r)

r

PMT – wielkość annuity realizowanej na

początek

każdego okresu

WARTOŚCI PRZYSZŁA ANNUITY

1. PŁATNEJ Z DOŁU ( = renta zwykła)

FV(A

r,n

) – wartość przyszła annuity na koniec n-tego okresu dla n płatności okresowych

r – stopa procentowa (dla jednego okresu)
n – liczba płatności równa liczbie okresów
PMT – wielkość annuity realizowanej na

koniec

każdego okresu

FVIFA

r,n

Future Value Interest Factor of

Annuity

FV(A

r,n

) = PMT •

(1 + r)

n

- 1

r

2. PŁATNEJ Z GÓRY (= renta należna)

FV(A

r,n

) = PMT •

(1 + r)

n

- 1

• (1 + r)

r

PMT – wielkość annuity realizowanej na

początek

każdego okresu

EFEKTYWNA ROCZNA STOPA PROCENTOWA

EAR (Effective Annual Rate) – jest uzależniona od nominalnej stopy procentowej oraz

okresów, w jakich następuje kapitalizacja odsetek (częstotliwość odsetek).

r

ear

– efektywne roczne oprocentowanie

r

nom

– nominalne oprocentowanie roczne

m – liczba kapitalizacji w roku

r

ear

= (1+

r

nom

)

m

- 1

m

EAR to problem typu 

jakie jest efektywne roczne oprocentowanie lokaty bankowej, jeśli

nominalna stopa roczna wynosi 5%, a kapitalizacja odsetek jest np. miesięczna

EFEKTYWNA ROCZNA STOPA PROCENTOWA – przykład

Wybierz najkorzystniejszy wariant ulokowania 1000 zł w banku

1.

na 10,0 % rocznie przy rocznej kapitalizacji odsetek,

2.

na 9,9 % rocznie przy półrocznej kapitalizacji odsetek

3.

na 9,8 % rocznie przy kwartalnej kapitalizacji odsetek

4.

na 9,7 % rocznie przy miesięcznej kapitalizacji odsetek,

5.

na 9,6 % rocznie przy dziennej kapitalizacji odsetek

(zakładamy, że rok ma 360 dni),

O co tak naprawdę

jesteśmy pytani?

EAR

NOMINALNE

OPROCENTOWANIE

ROCZNE [%]

LICZBA KAPITALIZACJI

W ROKU

EFEKTYWNE ROCZNE

OPROCENTOWANIE

10,0

1

10,00

9,9

2

10,15

9,8

4

10,17

9,7

12

10,14

9,6

360

10,07