WARTOŚCI PRZYSZŁA

informuje z jaką wartością nominalnie ustalonej kwoty będziemy mieli do czynienia po

upływie określonego czasu. Proces przechodzenia od wartości aktualnej do wartości

przyszłej to

kapitalizacja.

Polega ona na arytmetycznym ustaleniu ostatecznej wartości

przepływu (lub przepływów) środków pieniężnych, przy zastosowaniu odsetek składanych.

FV

n

= PV • (1+r)

n

FV

n

– wartość przyszła

PV – wartość teraźniejsza

r – stopa procentowa (dla jednego okresu)

n – liczba okresów

PRZYKŁAD:

Do banku został złożony

depozyt

o wartości 1000 zł na 3 lata. Oprocentowanie depozytu wynosi 10%

rocznie. Określ wartość depozytu na koniec 3 okresu.

1000

1100

1210

1331

FV

3

= 1000 • (1 +0,10)

3

= 1000 • 1,331 = 1331 zł

r = 10%

0

1

2

3

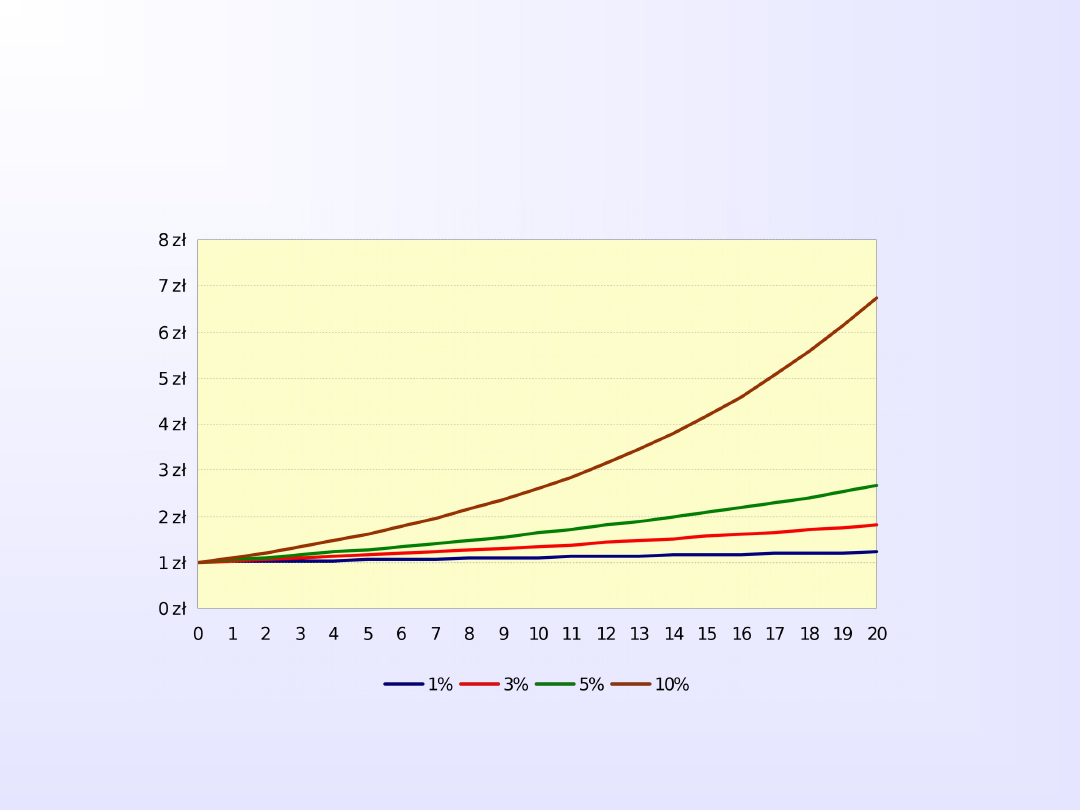
ZALEŻNOŚĆ WARTOŚCI PRZYSZŁEJ

OD STOPY PROCENTOWEJ I LICZBY OKRESÓW

Wartość przyszła 1 złotego złożonego na

n

okresów i

r

procent

1%

3%

5%

10%

PV

n

= FV •

PV

n

– wartość bieżąca przyszłej płatności

FV – wartość przyszła na koniec n-tego okresu

r – stopa dyskontowa (reprezentuje utratę wartości pieniądza w czasie)

n – okres z końca którego sprowadzamy przyszłą wartość na początek okresu bieżącgo

WARTOŚCI BIEŻĄCA

(TERAŹNIEJSZA, ZAKTUALIZOWANA)

określa teraźniejszą wartość przyszłych przepływów środków pieniężnych. W celu obliczenia

wartości zaktualizowanej posługujemy się metodą dyskonta.

Dyskontowanie

to proces

odwrotny do kapitalizacji. Polega na obliczeniu, jaką wartość w dniu dzisiejszym ma kwota,

którą otrzymamy po n okresach przy założeniu, że stopa procentowa reprezentująca utratę

wartości pieniądza wynosi r.

PRZYKŁAD:

Pod koniec 3 roku otrzymuje kwotę 1000 zł.

Stopa dyskontowa wynosi 10% rocznie. Określ wartość

bieżącą przyszłej kwoty

751

826

909

1000

FV

3

= 1000 • 1/(1 + 0,10)

3

= 1000 • 0,751 = 751 zł

1

(1+r

)

n

r = 10%

0

1

2

3

PŁATNOŚĆ ANNUITETOWA - RENTA

Seria

stałych

płatności (PMT) dokonywanych w ciągu n okresów,

w

równych

odstępach czasu,

przy niezmiennej stopie r

Przykłady:

• spłata rat kredytu bankowego

• opłaty leasingowe

• płatności wynikające z umowy dzierżawy i najmu

• płatności ubezpieczeniowe

• płatności na fundusze emerytalne

WARTOŚCI BIEŻĄCA ANNUITY

1. PŁATNEJ Z DOŁU

PV(A

r,n

) – wartość przyszła annuity na koniec n-tego okresu dla n płatności okresowych

r – stopa procentowa (dla jednego okresu)

n – liczba płatności równa liczbie okresów

PMT – wielkość annuity realizowanej na

koniec

każdego okresu

PVIFA

r,n

Present Value Interest Factor of

Annuity

PV(A

r,n

) = PMT •

1 - (1 + r)

-n

r

2. PŁATNEJ Z GÓRY

FV(A

r,n

) = PMT •

1 - (1 + r)

-n

• (1 + r)

r

PMT – wielkość annuity realizowanej na

początek

każdego okresu

rata kredytu

w ratach równych

WARTOŚCI PRZYSZŁA ANNUITY

1. PŁATNEJ Z DOŁU ( = renta zwykła)

FV(A

r,n

) – wartość przyszła annuity na koniec n-tego okresu dla n płatności okresowych

r – stopa procentowa (dla jednego okresu)
n – liczba płatności równa liczbie okresów
PMT – wielkość annuity realizowanej na

koniec

każdego okresu

FVIFA

r,n

Future Value Interest Factor of

Annuity

FV(A

r,n

) = PMT •

(1 + r)

n

- 1

r

2. PŁATNEJ Z GÓRY (= renta należna)

FV(A

r,n

) = PMT •

(1 + r)

n

- 1

• (1 + r)

r

PMT – wielkość annuity realizowanej na

początek

każdego okresu

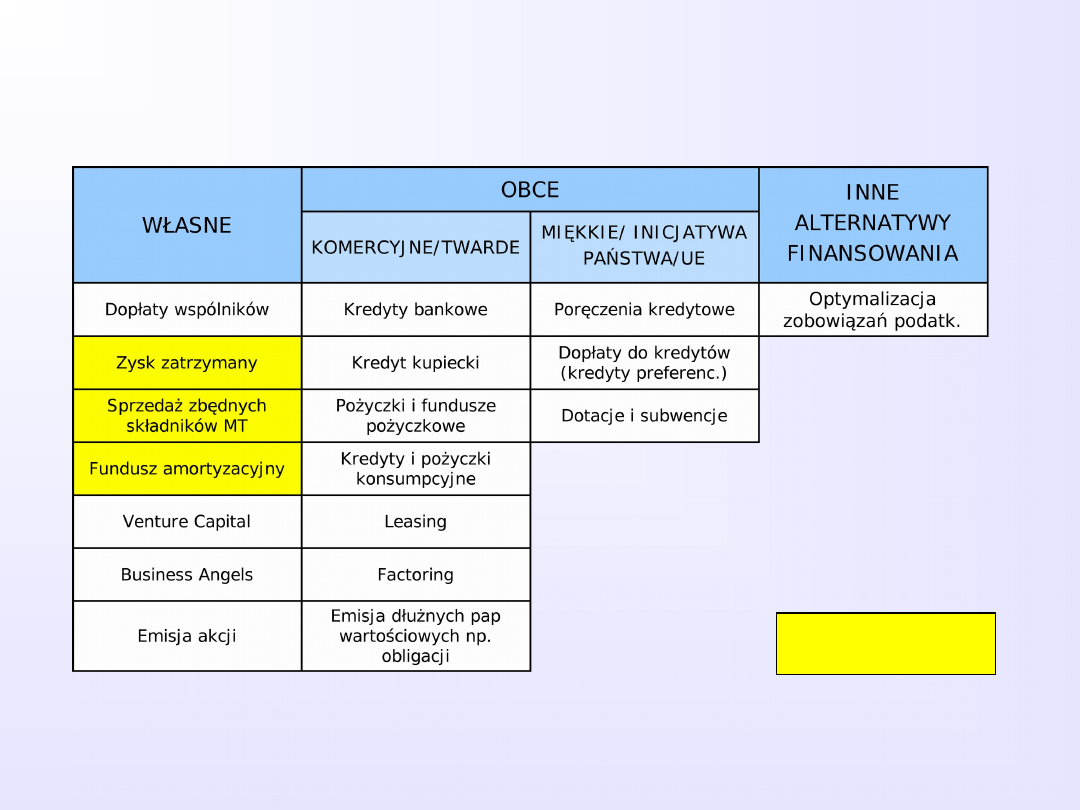
ŹRÓDŁA FINANSOWANIA PRZEDSIĘBIORSTW

Finansowanie

wewnętrzne

KOSZT KAPITAŁU

KOSZT KAPITAŁU – oczekiwana stopa zwrotu z zainwestowanego

kapitału

OCZEKIWANA STOPA ZWROTU uzależniona jest od:

- realnej stopy zwrotu (z pewnych inwestycji rynkowych)

- stopy inflacji

- poziomu ryzyka

KOSZT KAPITAŁU – można także wyznaczyć poprzez odniesienie do innych

alternatywnych inwestycji

W JAKICH JEDNOSTKACH

MIERZYMY KOSZT

KAPITAŁU??

KOSZT KAPITAŁU - KALKULACJA

Odsetki są wliczane w ciężar kosztów finansowych

 zmniejszają podstawę

opodatkowania (jeśli przedsiębiorstwo wypracowało zysk operacyjny)

Koszt długu

k

def

= (1 – T) • k

dnom

k

def

– koszty długu efektywny (po opodatkowaniu)

k

dnom

– koszty długu nominalny (przed opodatkowaniem), oprocentowanie w banku

T – stopa podatku dochodowego

Koszt kapitału własnego

k

kw

= dochód z pewnych inwestycji + premia za ryzyko

brak osłony podatkowej !!!!

WEWNĘTRZNA STOPA ZWROTU (IRR)

– najlepszy sposób kalkulacji kosztu kapituła

– warunek

 trzeba znać przepływy pieniężne

IRR (ang. Internal Rate of Return) – wartość stopy dyskontowej dla której suma zdyskontowanych

płatności związanych ze spłatą źródła finansowania jest równa wartości pozyskanego kapitału

I

0

=

CF

1

+

CF

2

+ … +

CF

n

1 + r

(1 + r)

2

(1 + r)

n

Wartość poszukiwana IRR

I

0

– wartość środków uzyskana z danego źródła finansowania

CF

i

- płatności związane ze spłatą danego źródła finansowania

Przykład

Jakie oprocentowanie będzie miała pożyczka wartości 100 tys. zł jeżeli dłużnik będzie ją

spłacał w ratach rocznych, na koniec każdego roku po 25 tys. zł.

100=

25

+

25

+

…

+

25

1 + IRR

(1 + IRR)

2

(1 + IRR)

5

IRR = 7,931%

Zadanie 1

12

Jeden z otwartych fundusz emerytalny na dziesięciolecie swojej

działalności ogłosił, że stopa zwrotu w z jego jednostek uczestnictwa w

ciągu 10 lat wyniosła 195%. Stosownych wyliczeń dokonano przy

założeniu, że w 1999 roku jednostka uczestnictwa kosztowała 10 PLN,

a w 2009 roku 29,5 PLN.

Odpowiedz jaka jest roczna stopa zwrotu z tej inwestycji??

Jaka jest roczna stopa zwrotu jeśli uwzględnimy 4% prowizje pobieraną

od wniesionych środków

W domu

 policz jaka jest średnia stopa zwrotu na GPW z ostatnich 15 lat,

biorąc pod uwagę zmianę wartości wskaźnika WIG

RODZAJE KREDYTÓW

oprocentowanie STAŁE

oprocenotwanie

ZMIENNE

>

CZYNNIK ZMIENNY

•

WIBOR, LIBOR

CZYNNIK STAŁY

•

MARŻA BANKU

+

RATA KREDYTU =

CZĘŚĆ KAPITAŁOWA + ODSETKI

CONSTANS

CONSTANS

RATY MALEJĄCE

RATY STAŁE

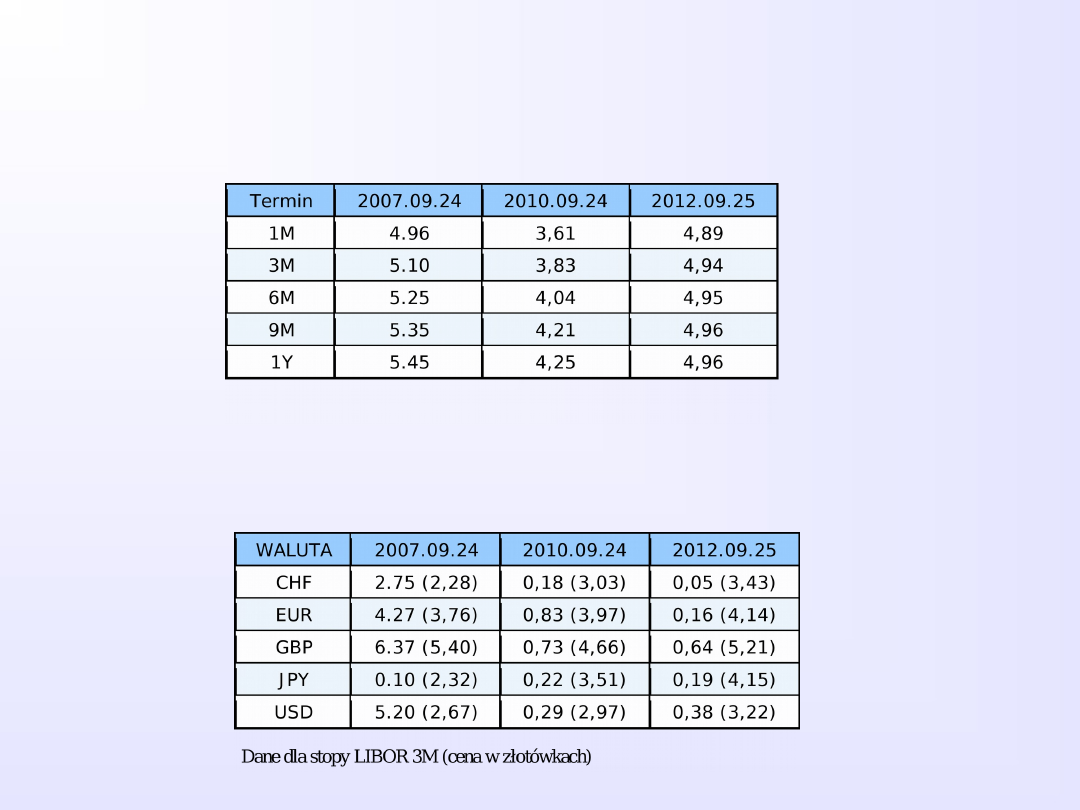
WIBOR

-

Warsaw Interbank Offered Rate – wysokość oprocentowania pożyczek na polskim

rynku międzybankowym

LIBOR

- London Interbank Offered Rate – stopa procentowa kredytów oferowanych na rynku

międzybankowym przez 4 główne banki