Modelowanie i symulacja

WYKŁAD 5,6

Ogólna postać układu
równań różniczkowych

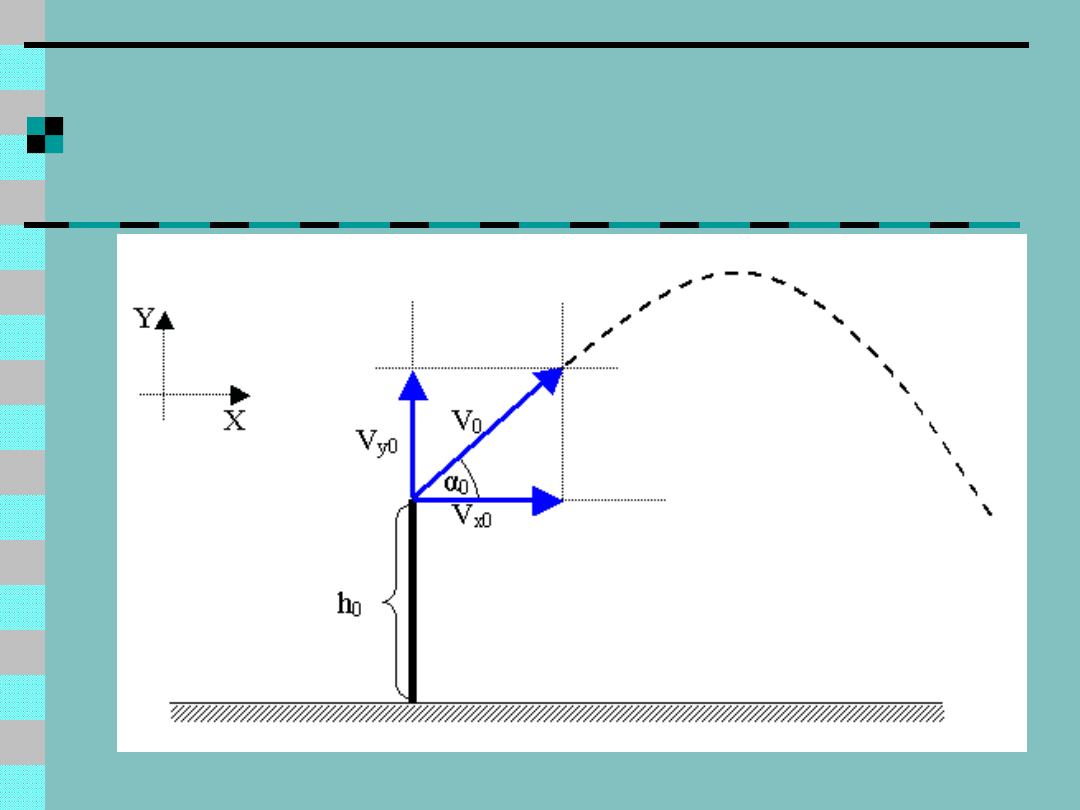
Formułowania ODE -
przykład

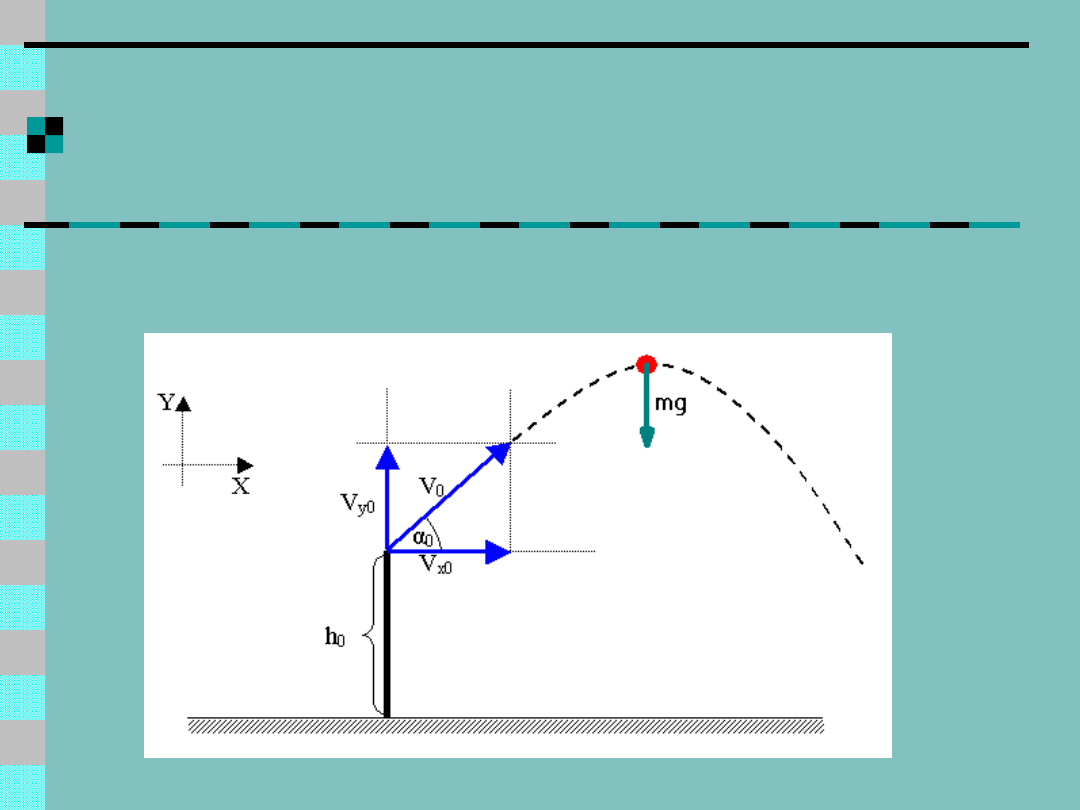
Formułowania ODE -
przykład



II zasada dynamiki Newtona:
F=ma

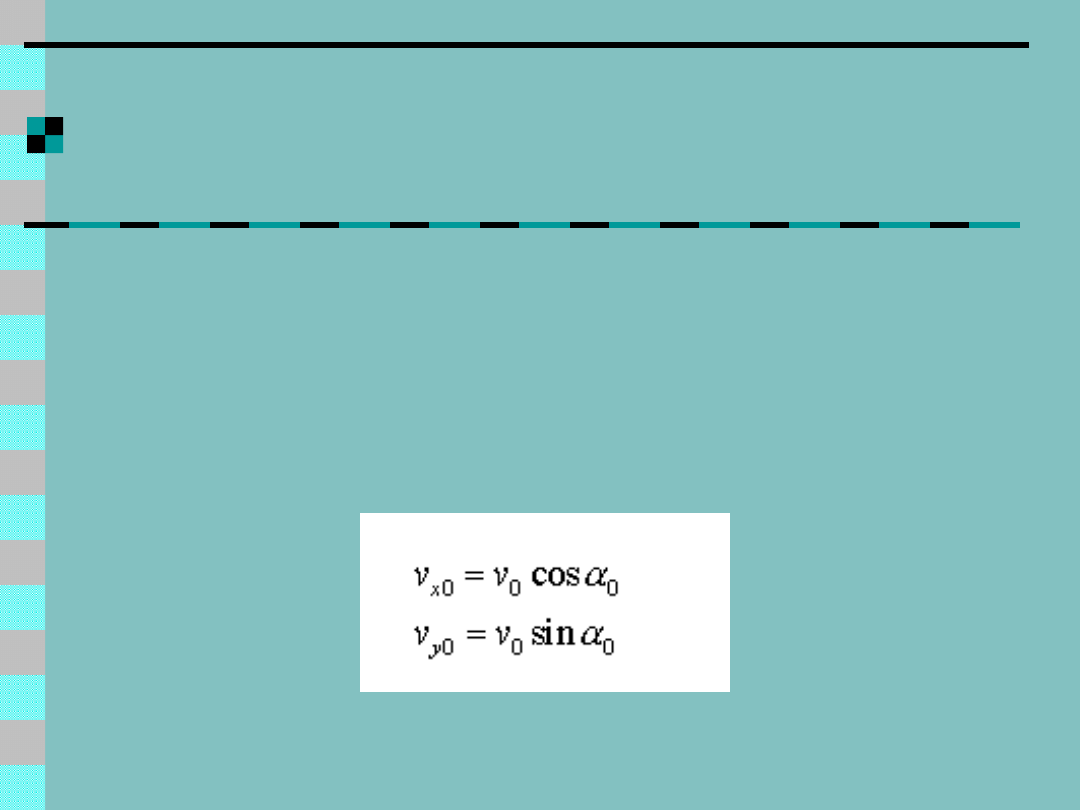
Formułowania ODE -
przykład



Zasada Galileusza: składowe
ruchu w ortogonalnych kierunkach
x,y można rozpatrywać niezależnie

Formułowania ODE -
przykład



Chcemy znać trajektorię, a więc
współrzędne x, y w
poszczególnych chwilach czasu t



Przejście do zrealizowania: siły 

przyspieszenia  prędkości 

położenia



Z definicji:

Formułowania ODE -
przykład



Z definicji



Potrzebne jest podwójne całkowanie

dt

dy

v

dt

dx

v

dt

dv

a

dt

dv

a

dt

ds

v

dt

dv

a

y

x

y

y

x

x













Formułowania ODE -
przykład



W kierunku x:

 

 

xo

x

x

t

t

x

x

x

x

x

v

C

v

v

v

t

dla

C

d

d

dt

dv

t

v

dt

dv

a

F



























0

0

0

0

0

cos

,

0

0

0

0

0









Formułowania ODE -
przykład

 

 

 

 

 

t

v

t

x

C

x

t

dla

C

t

v

d

v

d

v

d

dt

dx

t

x

x

x

t

x

t

t

x

0

0

0

0

0

0

0

0

0

,

0







































Formułowania ODE -
przykład

 

 

yo

y

y

t

t

y

y

y

y

y

v

C

v

v

v

t

dla

C

gt

gd

d

dt

dv

t

v

dt

dv

g

a

mg

F





































0

0

0

0

0

sin

,

0

0









Formułowania ODE -
przykład

 

 

 





 

 

2

0

0

0

0

0

2

0

0

0

0

2

1

0

,

0

2

1

gt

t

v

h

t

y

h

C

h

y

t

dla

C

t

v

gt

d

v

gt

d

v

d

dt

dy

t

y

y

y

t

y

t

t

y



















































Formułowania ODE -
przykład



Bardziej realistyczne zjawisko:



zamiast rzutu ukośnego – wystrzał
rakiety



oprócz siły ciążenia – działa siła ciągu
silnika



działa także siła oporu powietrza



masa rakiety zmienia się w czasie lotu

 

t

T

 

 

2

t

sv

c

t

D





 

 





 

 

 





 

 

g

t

m

t

t

D

t

T

F

t

t

D

t

T

F

y

x















sin

cos

Formułowania ODE -
przykład



Sposób postępowania jest analogiczny,

jednak całkowanie symboliczne, w

zależności od zależności siły ciągu i

masy od czasu może być

skomplikowane

 

 





 

 

 





 

 

g

t

m

t

t

D

t

T

F

t

t

D

t

T

F

y

x















sin

cos

Całkowanie numeryczne -
schemat Eulera

Leonhard Euler (1707-1783)

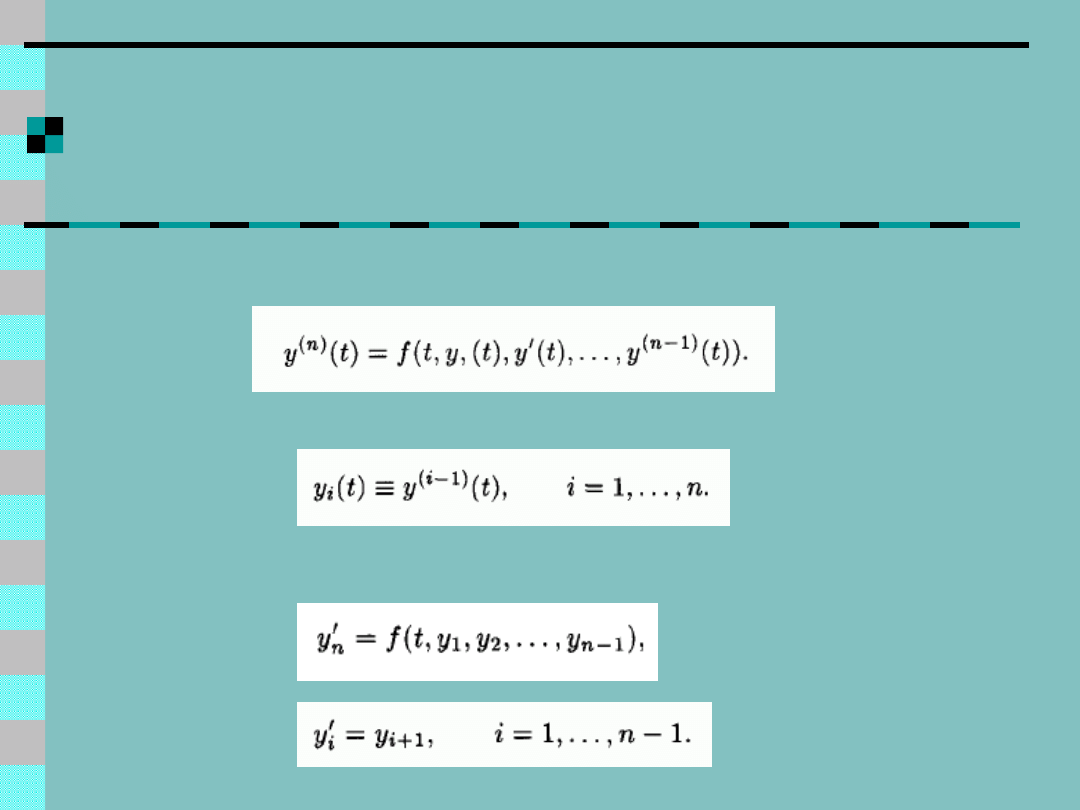
Redukcja równania
wyższego rzędu do
niższego rzędu



Pierwotne równanie:



Podstawienie:



Powstaje układ równań:

Schemat Eulera



Równanie różniczkowe w postaci
normalnej:



Rozwinięcie Taylora:

 

 





t

t

y

f

t

y

,







    



  

 





t

t

t

y

f

t

y

t

t

y

t

t

y

t

y

t

t

y





















0

0

0

0

0

0

0

,



Schemat Eulera



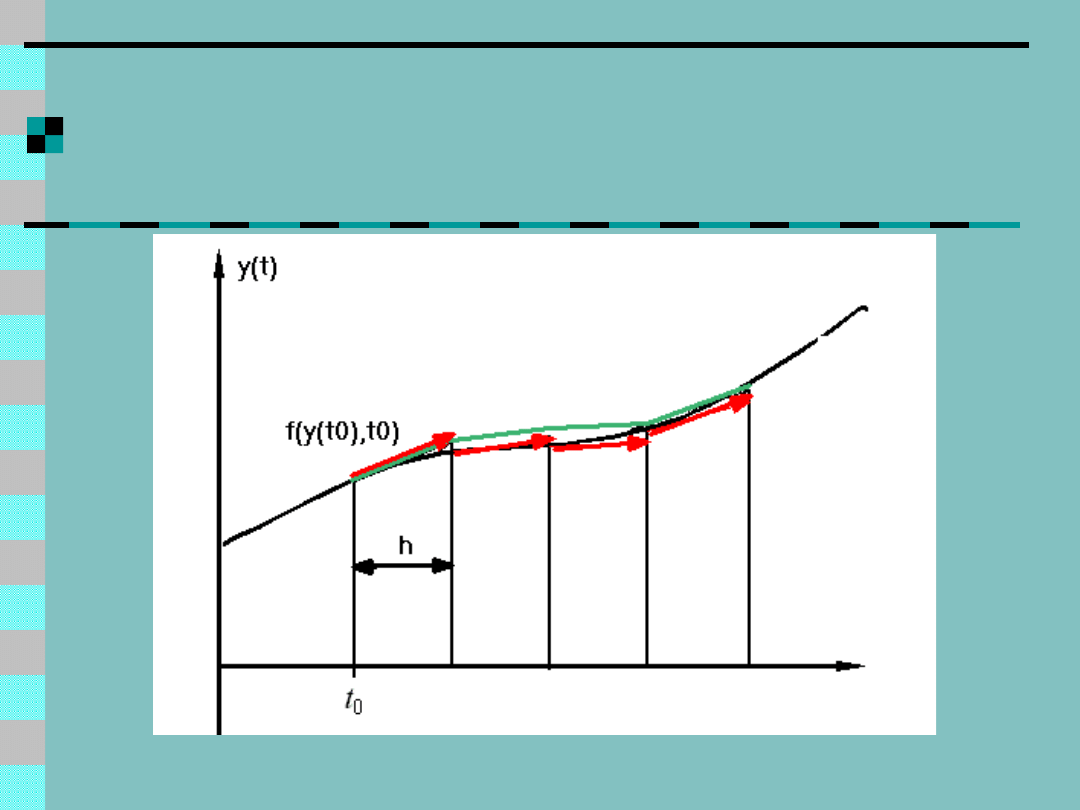
Jeżeli znana jest wartość szukanej trajektorii
y(t

0

) w pewnym momencie czasu t

0

, to

można w przybliżeniu obliczyć wartość
trajektorii dla niedalekiej chwili czasu t

0

+h



Potrzebna jest do tego znajomość pochodnej
trajektorii w chwili t

0

, czyli wartość funkcji

f(y(t

0

),t

0

)



Ta informacja dana jest przez równanie
różniczkowe

Schemat Eulera



Trzeba zacząć od pewnego znanego
punktu np. y(0)



Przedział, w którym ma być
wyznaczona trajektoria, to np. [0,t

k

]



Przedział ten jest dzielony
równomiernie na ciąg
podprzedziałów o długości h (krok
całkowania)

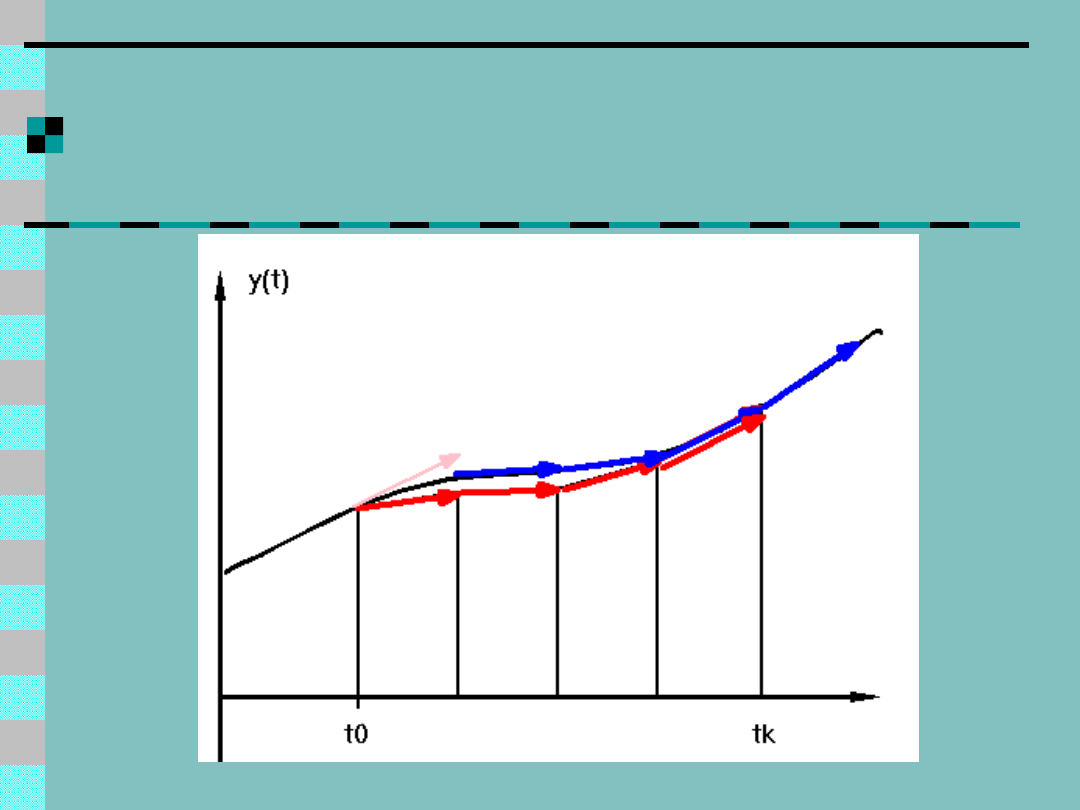
Schemat Eulera



Zaczynając od znanej wartości y(0)
powtarza się iteracyjnie przepis:

dochodząc wreszcie do punktu

końcowego t

k



Zapis oznacza przybliżoną
wartość y(t

i

)



  

 





h

t

t

y

f

t

y

h

t

y

i

i

i

i

,

ˆ

ˆ

ˆ







 

i

t

yˆ

Schemat Eulera



Cały proces nazywany jest
całkowaniem numerycznym



Rozwiązanie równania
różniczkowego polega na jego
scałkowaniu

Schemat Eulera

Schemat Eulera



Przybliżenie:

jest tym lepsze, im mniejsze jest h



  

 





h

t

t

y

f

t

y

h

t

y

i

i

i

i

,







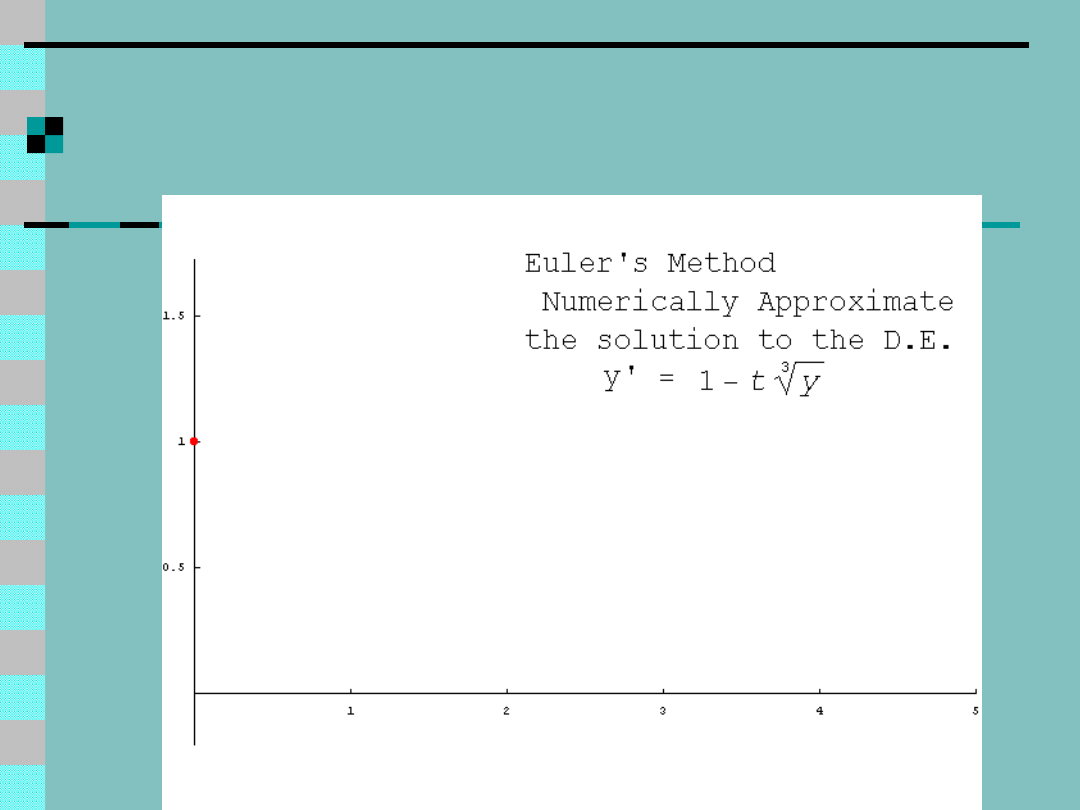
Schemat Eulera

Schemat Eulera

Schemat Eulera



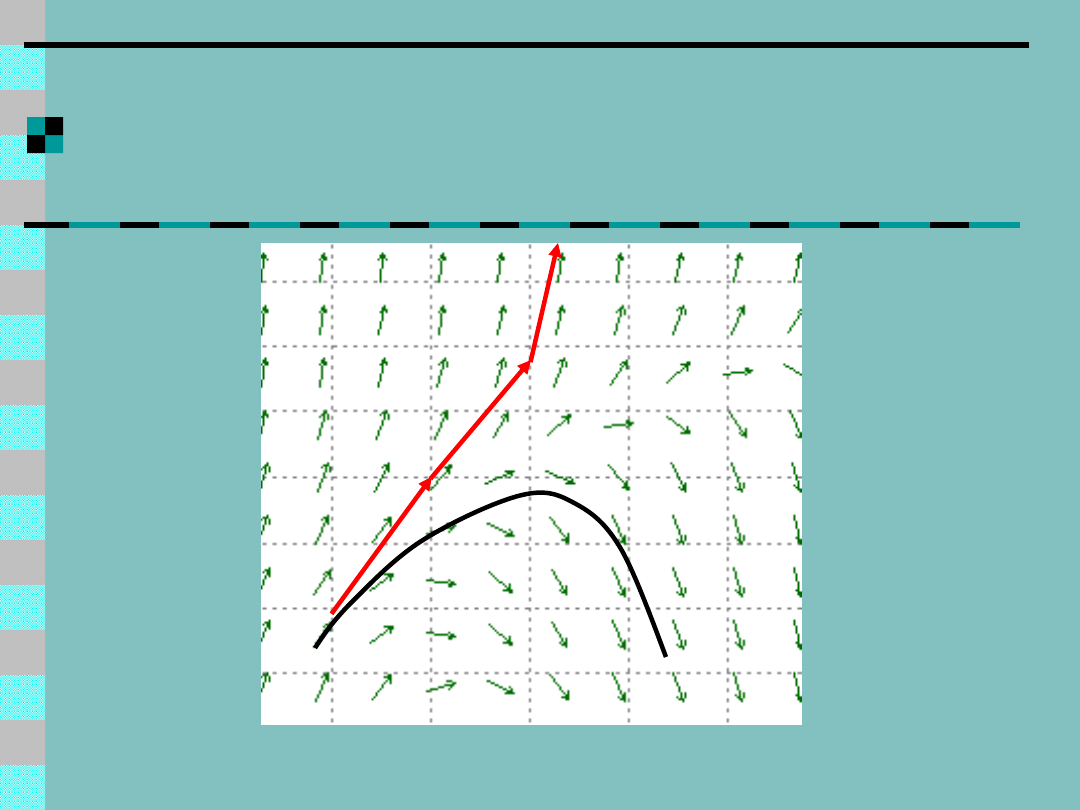
Pole kierunkowe – ilustracja
informacji podanej przez równanie
różniczkowe



Prezentacja DField i PPlane

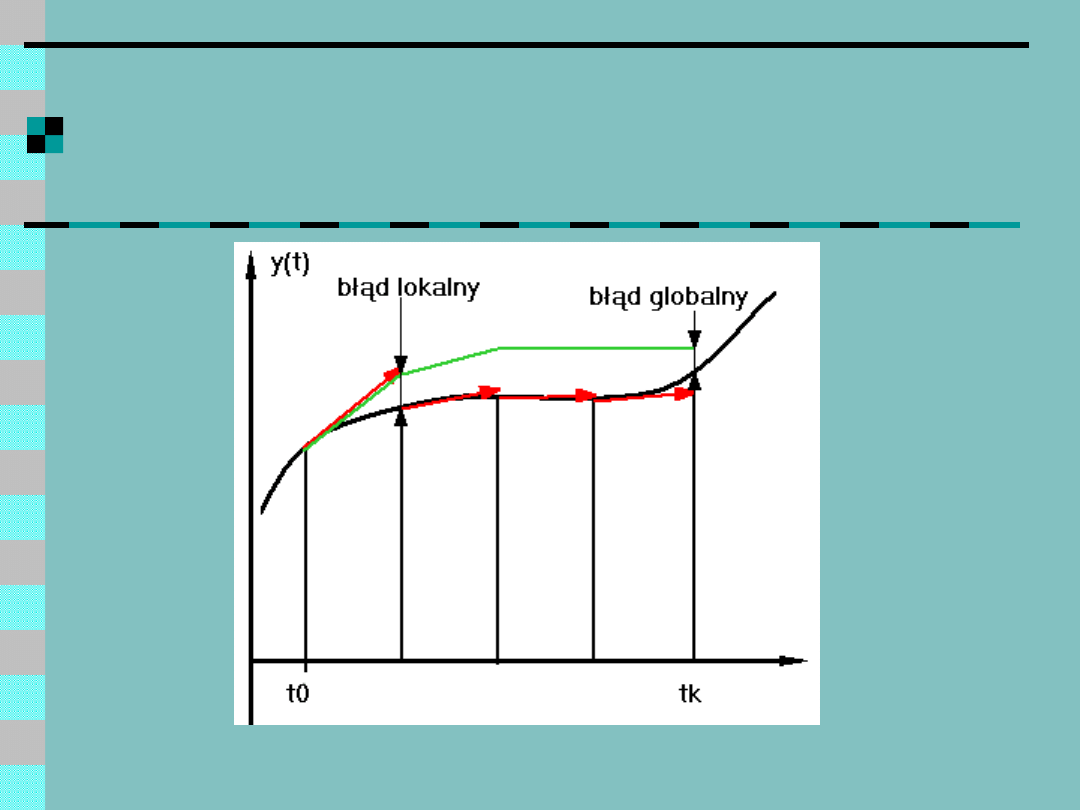
Błędy schematu Eulera

Błąd lokalny (obcięcia)



Wynika z obciętego rozkładu
Taylora



  

 





 



  

 





h

t

t

y

f

t

y

h

t

y

h

O

h

t

t

y

f

t

y

h

t

y

i

i

i

i

i

i

i

i

,

ˆ

ˆ

ˆ

,

2















Błąd lokalny (obcięcia)



Wynika z aproksymacji liniowej, czy też

różnicowego oszacowania pochodnej:



Błąd lokalny jest rzędu



Dwukrotne zmniejszenie kroku

zmniejsza błąd o 75%



  

 





 







  

h

t

y

h

t

y

t

t

y

f

h

t

t

y

f

t

y

h

t

y

i

i

i

i

i

i

i

i

ˆ

ˆ

,

ˆ

,

ˆ

ˆ

ˆ













2

h

Błąd globalny



Nie jest po prostu sumą błędów lokalnych



Błędem jest obarczona także informacja o
pochodnej, ponieważ jest wyznaczana na
podstawie przybliżonego rozwiązania
cząstkowego



Dla schematu Eulera globalny błąd jest
rzędu O(h)



  

 





h

t

t

y

f

t

y

h

t

y

i

i

i

i

,

ˆ

ˆ

ˆ







Zagrożenie rozbieżności

Zagadnienie zbieżności



Czy jeśli h dąży do zera, to błąd
dąży do zera?



A jeśli błąd dąży do zera, to jaka
szybka jest zbieżność, tzn. na ile
mały musi być krok, żeby osiągnąć
pożądany poziom błędu?

Modyfikacja schematu
Eulera



Zamiast:



Stosujemy:



Czyli pochodna jest brana z końca
przedziału całkowania

  

  

 





   

 





h

t

t

y

f

t

y

t

y

h

t

t

y

f

t

y

h

t

y

t

y

i

i

i

i

i

i

i

i

i

1

1

1

1

1

1

1

,

ˆ

ˆ

ˆ

,

ˆ

ˆ

ˆ

ˆ





























  

 





h

t

t

y

f

t

y

h

t

y

i

i

i

i

,

ˆ

ˆ

ˆ







Modyfikacja schematu
Eulera

Modyfikacja schematu
Eulera



Te same oszacowania błędów



Jednak odwrócony schemat Eulera
jest zwykle bardziej stabilny i
dokładniejszy



Odwrócony schemat Eulera nie jest
metodą bezpośrednią – wyznaczana
wartość
występuje po obu stronach przepisu

 

1

ˆ



i

t

y

Poprawa schematu Eulera



Prosty schemat Eulera –

„reprezentantem” pierwszej

pochodnej w całym przedziale jest

wartość z początku przedziału



Odwrócony schemat Eulera –

„reprezentantem” pierwszej

pochodnej w całym przedziale jest

wartość z końca przedziału



Twierdzenie o wartości pośredniej:

Poprawa schematu Eulera



Twierdzenie o wartości pośredniej



Równość jest dokładna! Trzeba tylko

wiedzieć, jaka jest wartość p



Wartość pochodnej wyznaczona w

odpowiednim punkcie przedziału

umożliwiłaby osiągnięcie zerowego

błędu



   



1

,

0

,











p

h

ph

t

y

t

y

h

t

y

i

i

i



Poprawa schematu Eulera

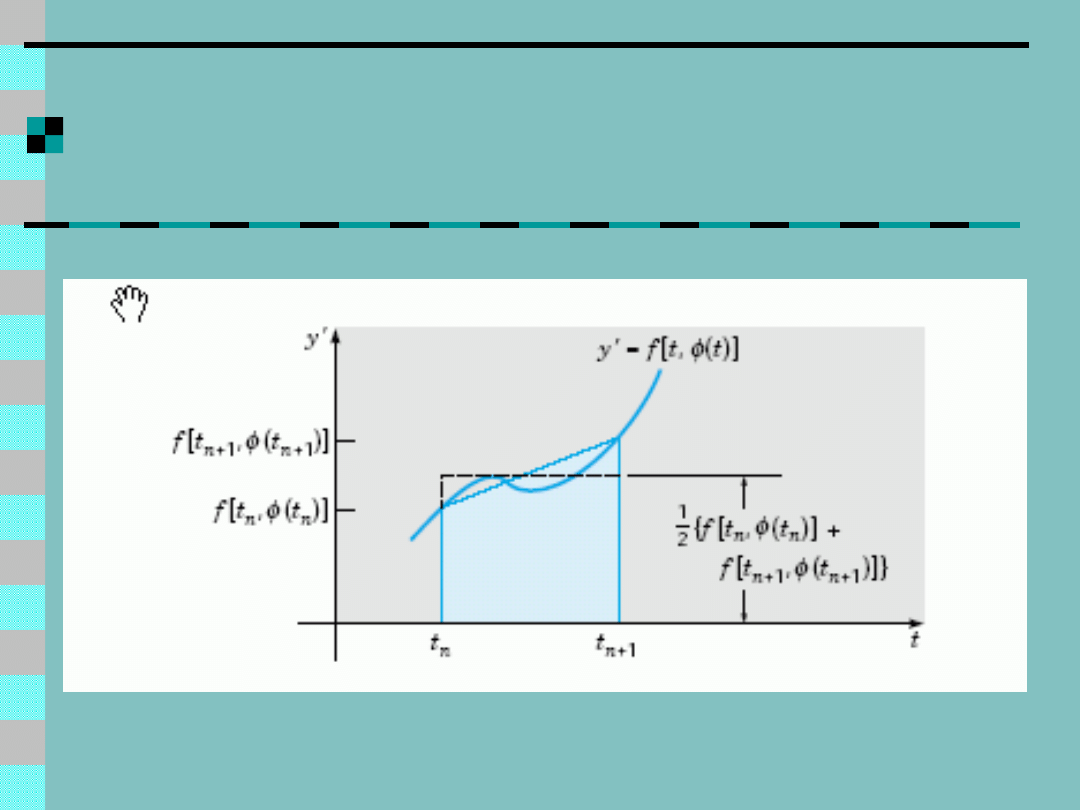
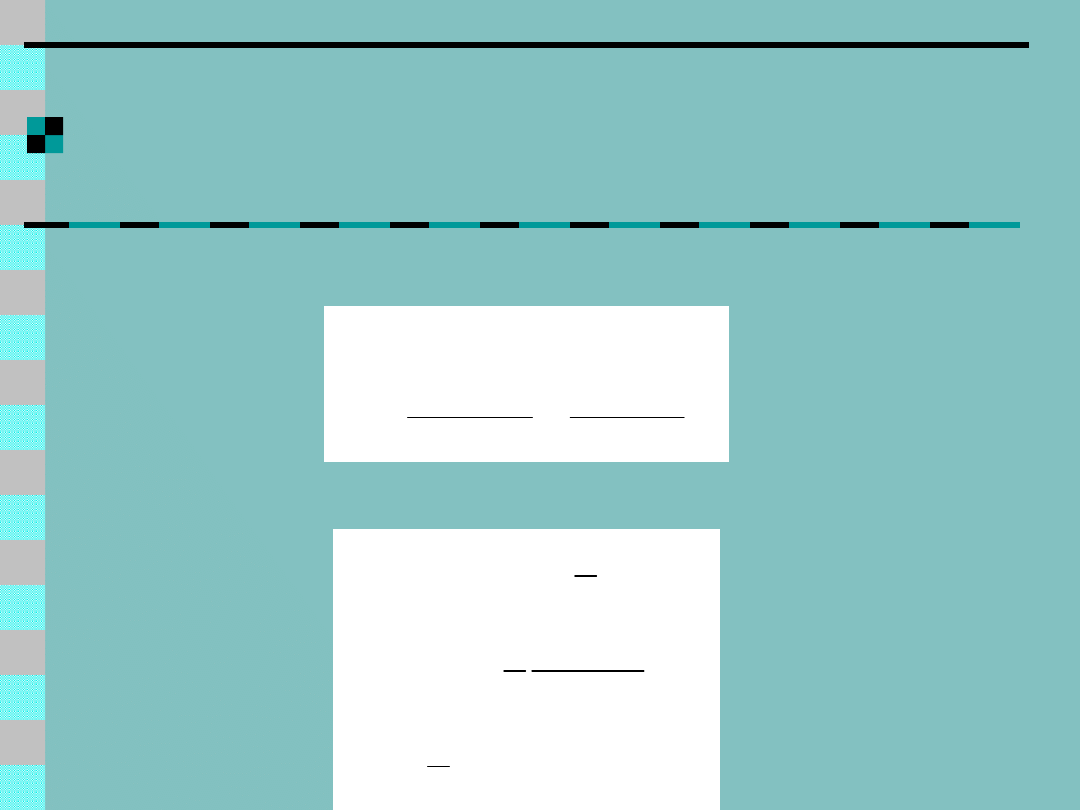
Schemat Heuna

Schemat Heuna



Błąd lokalny – proporcjonalny do
h

3



Błąd globalny – do h

2

Metoda konstruowania
schematów wyższych
rzędów



Różnicowe przybliżenie drugiej
pochodnej



Rozwinięcie Taylora drugiego
rzędu:

 

 





h

f

f

h

y

y

y

f

y

t

t

y

f

t

y

i

i

i

i

i

i

i

i

i

i

1

1

'

ˆ

'

ˆ

''

ˆ

'

ˆ

,

'

ˆ

'

ˆ





















1

2

1

2

1

3

2

1

ˆ

2

1

ˆ

''

ˆ

2

1

'

ˆ

ˆ

ˆ































i

i

i

i

i

i

i

i

i

i

i

f

f

h

y

h

h

f

f

h

f

y

h

y

h

y

y

y

Runge-Kutta

Martin Wilhelm Kutta (1867 – 1944)

Carl David Runge (1856 – 1927)

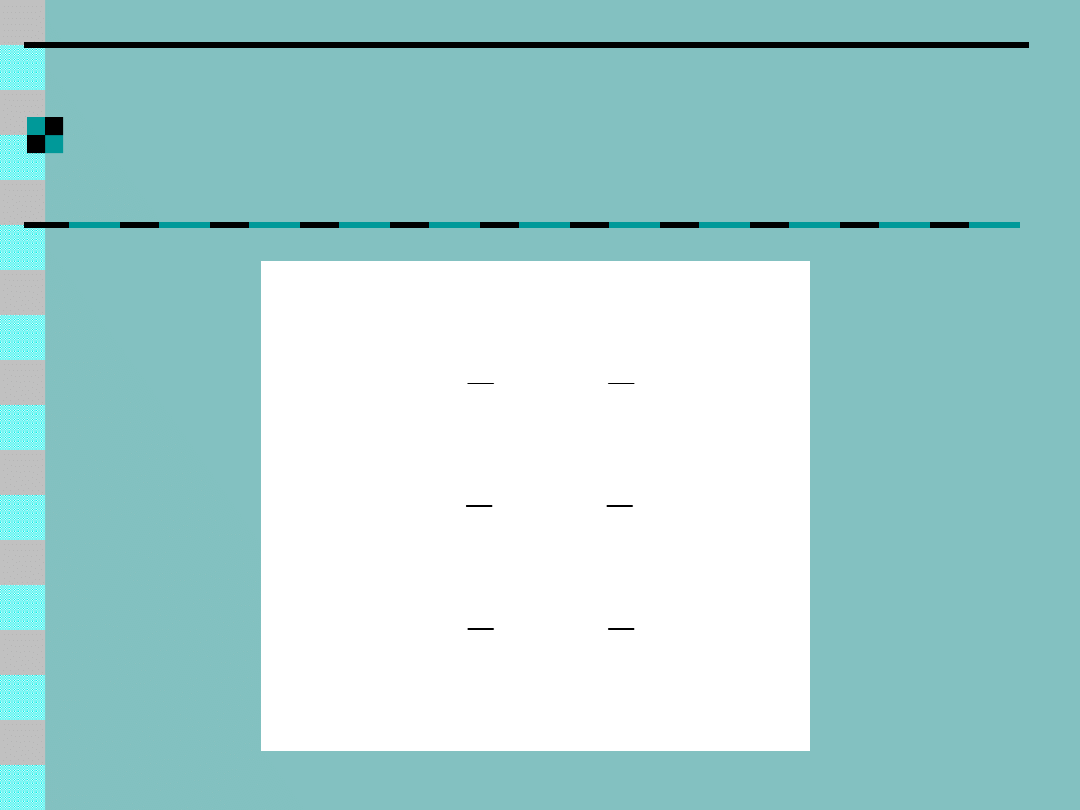
Metoda Runge-Kutta 4-
tego rzędu









6

/

2

2

ˆ

ˆ

2

1

ˆ

,

2

1

2

1

ˆ

,

2

1

2

1

ˆ

,

2

1

ˆ

,

4

3

2

1

1

3

4

2

3

1

2

1

k

k

k

k

y

y

k

y

h

t

hf

k

k

y

h

t

hf

k

k

y

h

t

hf

k

y

t

hf

k

i

i

i

i

i

i

i

i

i

i



































































