Rozkład Gaussa

Zjawiska Losowe

Np. Liczba wypadków drogowych

Kurs Akcji na giełdzie

Rachunek Prawdopodobieństwa

Doświadczenie Losowe

Zdarzenia Elementarne

Przestrzeń Zdarzeń Elementarnych

Zdarzenie losowe

Zdarzenia losowe oznaczamy dużymi literami A, B, C

Każde doświadczenie składa się z najprostszych, nierozkładalnych

zdarzeń (wyników doświadczeń)

Zbiór wszystkich zdarzeń e. powiązanych z doświadczeniem to PZE

Elementy przestrzeni oznaczamy symbolem e

i

a przestrzeń z.e. jako E.

Każdy podzbiór przestrzeni zdarzeń elementarnych to zdarzenia losowe

Przestrzeń z.e. może być zbiorem skończonym lub nieskończonym

Prawdopodobieństwo i jego własności

Zdarzenia Elementarne

Przestrzeń Zdarzeń Elementarnych

Zdarzenie losowe

Zdarzenia losowe oznaczamy dużymi literami A, B, C

Zbiór wszystkich zdarzeń e. powiązanych z doświadczeniem to PZE

Elementy przestrzeni oznaczamy symbolem e

i

a przestrzeń z.e. jako E.

Każdy podzbiór przestrzeni zdarzeń elementarnych to zdarzenia losowe

Przestrzeń z.e. może być zbiorem skończonym lub nieskończonym

Skończona przestrzeń zdarzeń elementarnych

Przykład: Ze skończoną przestrzenią zdarzeń elementarnych mamy do czynienia np. w doświadczeniu

polegającym na jednokrotnym rzucie kostką do gry. Zdarzeniami losowymi mogą być tutaj:

A - Wypadła parzysta liczba oczek

B - Wypadła liczba oczek większa od 3

C - Wypadła liczba oczek będąca liczbą pierwszą

W tym doświadczeniu zbiór zdarzeń elementarnych jest 6-o elementowy E={e1,e2,e3,e4,e5,e6}, gdzie

e

i

(i=1,2,…,6) oznaczają zdarzenia elementarne: wypadło i oczek.

Zdarzeniem A określamy podzbiór {e2,e4,e6}

Zdarzeniem B określamy podzbiór {e4,e5,e6}

Zdarzeniem C określamy podzbiór {e2,e3,e5}

Jeśli zdarzenie elementarne należy do zdarzenia losowego (zbioru) A to sprzyja ono zdarzeniu A.

Jeśli nie mówimy o zdarzeniu przeciwnym (niesprzyjającym).

Zdarzenie pewne – Zdarzenie A jest zdarzeniem pewnym jeśli każde zdarzenie elementarne ze zbioru E

sprzyja zdarzeniu A.

Zdarzenie niemożliwe – Zdarzenie A jest zdarzeniem niemożliwym, jeśli żadne zdarzenie elementarne ze

ze zbioru E nie sprzyja zdarzeniu A

Zdarzenia Elementarne

Przestrzeń Zdarzeń Elementarnych

Zdarzenie losowe

Zdarzenia losowe oznaczamy dużymi literami A, B, C

Zbiór wszystkich zdarzeń e. powiązanych z doświadczeniem to PZE

Elementy przestrzeni oznaczamy symbolem e

i

a przestrzeń z.e. jako E.

Każdy podzbiór przestrzeni zdarzeń elementarnych to zdarzenia losowe

Przestrzeń z.e. może być zbiorem skończonym lub nieskończonym

Skończona przestrzeń zdarzeń elementarnych

Jeśli przestrzeń zdarzeń elementarnych jest zbiorem n-elementowym, to liczba jego podzbiorów
jest równa . Ze zbioru E = {e1, e2, e3, e4, e5, e6} można zatem utworzyć 64 podzbiory (zdarzenia):

1. 2 podzbiory niewłaściwe: , E;
2. 6 podzbiorów jednoelementowych: {e1}, …, {e6}
3. 15 podzbiorów dwuelementowych: {e1,e2},{e1,e3},…{e1,e6}
4. 20 podzbiorów trzyelementowych: {e1,e2,e3},…{e4,e5,e6}
5. 15 podzbiorów czteroelementowych: {e1,e2,e3,e4}…{e3,e4,e5,e6}
6. 6 podzbiorów pięcioelementowych: {e1,e2,e3,e4,e5},…,{e2,e3,e4,e5,e6}

n

2



Zdarzenia Elementarne

Przestrzeń Zdarzeń Elementarnych

Zdarzenie losowe

Zdarzenia losowe oznaczamy dużymi literami A, B, C

Zbiór wszystkich zdarzeń e. powiązanych z doświadczeniem to PZE

Elementy przestrzeni oznaczamy symbolem e

i

a przestrzeń z.e. jako E.

Każdy podzbiór przestrzeni zdarzeń elementarnych to zdarzenia losowe

Przestrzeń z.e. może być zbiorem skończonym lub nieskończonym

Skończona przestrzeń zdarzeń elementarnych

Na zdarzeniach losowych, podobnie jak na zbiorach możemy wykonywać działania, a mianowicie:

1) Zdarzenia A i B nazywamy identycznymi (A = B), jeżeli zdarzenie A zachodzi wtedy i tylko wtedy gdy

zachodzi zdarzenie B. Zdarzeniom tym sprzyjają te same zdarzenia elementarne

2) Zdarzenie A pociąga za sobą (implikuje) zdarzenie B ( ), jeśli zdarzenie elementarne sprzyjające

zdarzeniu A sprzyja również zdarzeniu B (jeśli zaszło zdarzenie A to zaszło również zdarzenie B)

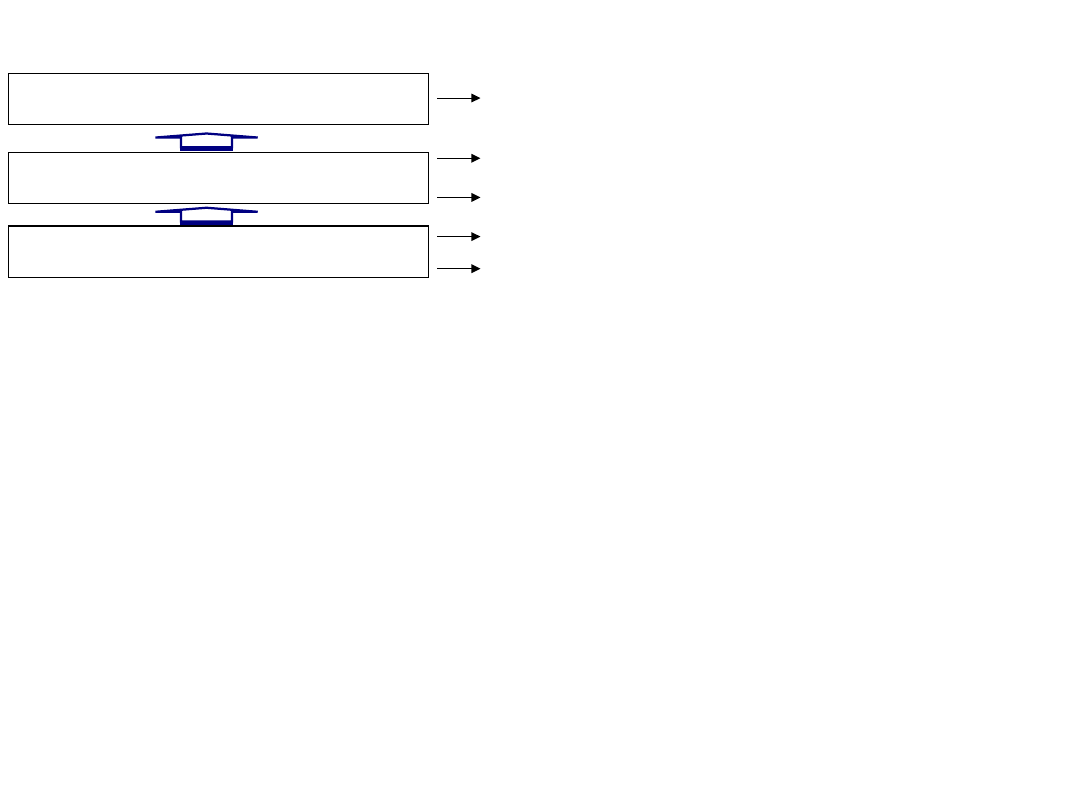
3) Sumą (alternatywą) zdarzeń A i B ( ) nazywamy takie zdarzenie C, które zachodzi wtedy i tylko wtedy

gdy zachodzi zdarzenie A lub zdarzenie B.

Niech A oznacza zdarzenie polegające na tym, że w rzucie kostką wypadła nieparzysta liczba oczek, a B –
zdarzenie polegające na otrzymaniu liczby mniejszej od 4. Mamy zatem:

B

A

B

A

}

,

,

,

{

}

,

,

{

}

,

,

{

5

3

2

1

3

2

1

5

3

1

e

e

e

e

e

e

e

e

e

e

B

A

C











Zdarzenia Elementarne

Przestrzeń Zdarzeń Elementarnych

Zdarzenie losowe

Zdarzenia losowe oznaczamy dużymi literami A, B, C

Zbiór wszystkich zdarzeń e. powiązanych z doświadczeniem to PZE

Elementy przestrzeni oznaczamy symbolem e

i

a przestrzeń z.e. jako E.

Każdy podzbiór przestrzeni zdarzeń elementarnych to zdarzenia losowe

Przestrzeń z.e. może być zbiorem skończonym lub nieskończonym

Skończona przestrzeń zdarzeń elementarnych

Na zdarzeniach losowych, podobnie jak na zbiorach możemy wykonywać działania, a mianowicie:

4) Iloczynem (koniunkcją, częścią wspólną) zdarzeń A i B nazywamy takie zdarzenie C, które zachodzi

wtedy i tylko wtedy, gdy zachodzi zdarzenie A i zdarzenie B tj.

Niech A oznacza zdarzenie polegające na wylosowaniu z listy mężczyzny, a B – na wylosowaniu osoby
palącej papierosy. Wtedy oznacza zdarzenie polegające na wylosowaniu mężczyzny palącego
papierosy.
Jeżeli iloczyn zdarzeń A i B tworzy zbiór pusty , to zdarzenia A i B nazywamy
wykluczającymi się (wyłączającymi się). Np. w rzucie kostką do gry zdarzeniami wykluczającymi się
są: zdarzenie A – wyrzucenie liczby oczek mniejszej od 2 i zdarzenie B – otrzymanie więcej niż 4 oczek

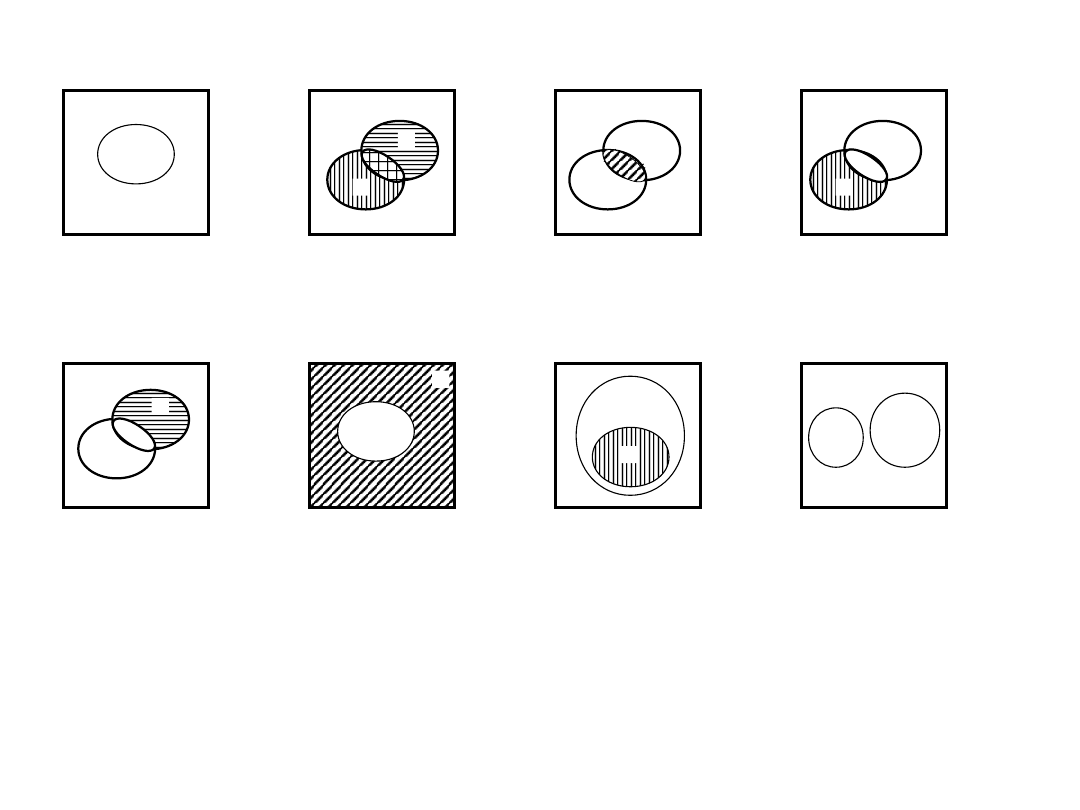
5) Różnicą zdarzeń A i B (A – B) nazywamy takie zdarzenie C, które zachodzi wtedy i tylko wtedy, gdy

zachodzi zdarzenie A i nie zachodzi zdarzenie B

Niech A oznacza zdarzenie polegające na wyrzuceniu w rzucie kostką parzystej liczby oczek, a B oznacza
wyrzucenie liczby oczek większej od 3. Wówczas:

B

A

C





B

A





 B

A

}

{

}

,

,

{

}

,

,

{

2

6

5

4

6

4

2

e

e

e

e

e

e

e

B

A

C











Skończona przestrzeń zdarzeń elementarnych

A

A

B

E

E

E

E

E

E

E

A

B

A

A

A

A

B

B

A

B

B

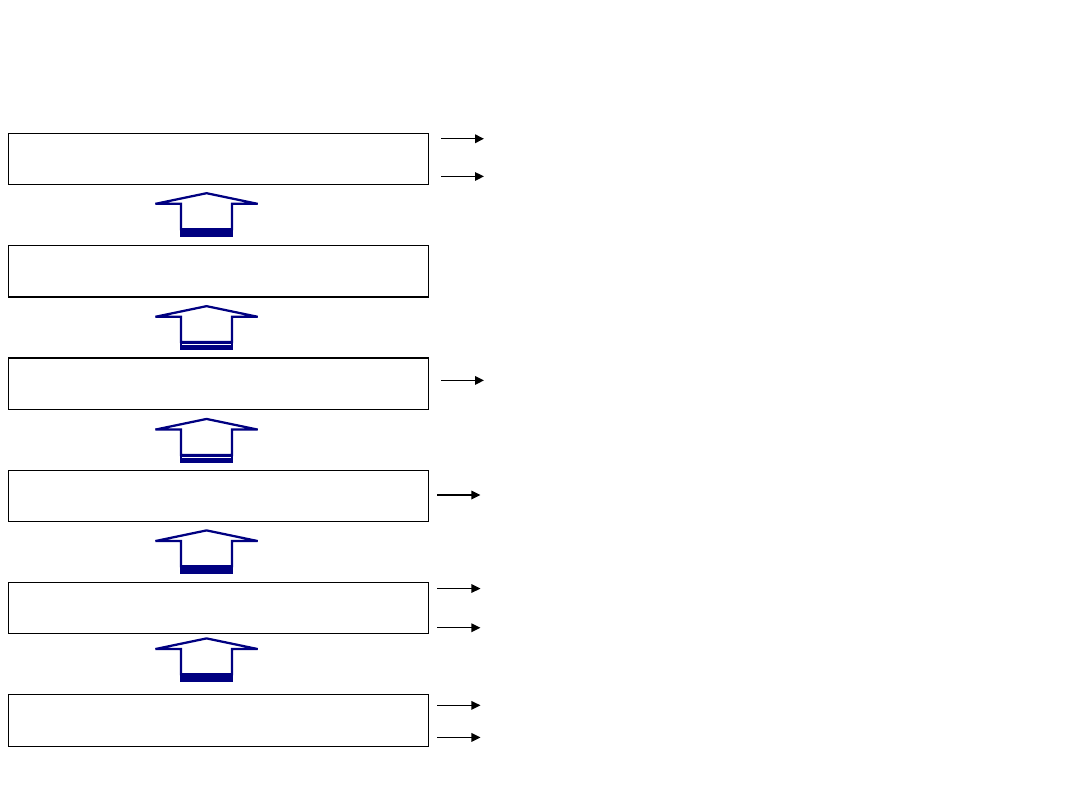
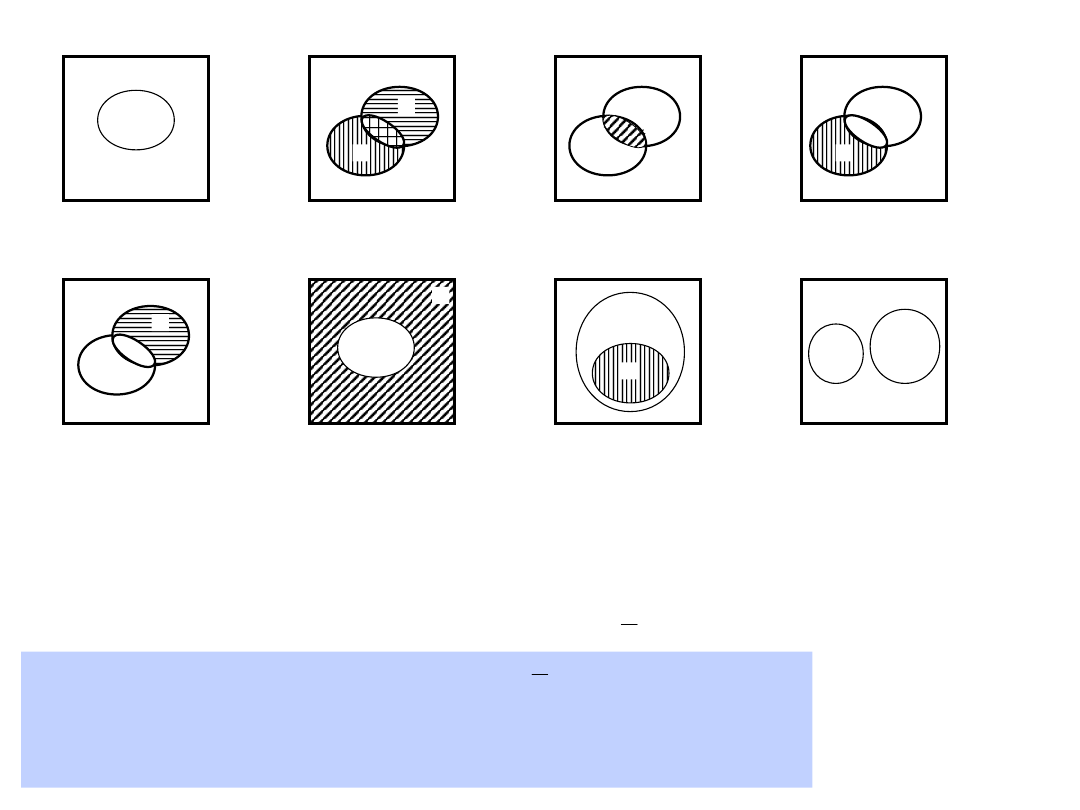
a) Zdarzenie A w

przestrzeni E

E

b) Suma zdarzeń

przestrzeni E

a) Iloczyn zdarzeń

a) Różnica zdarzeń

a) Różnica zdarzeń

a) Zdarzenie przeciwne

do A lub dopełnienie

zdarzenia A

a) Zdarzenie A

zawiera się w

zdarzeniu B

a) Zdarzenie A i B

wykluczają się

B

A

B

A

A

B

B

A





 B

A

Ćwiczenie 1

A

A

B

E

E

E

E

E

E

E

A

B

A

A

A

A

B

B

A

B

B

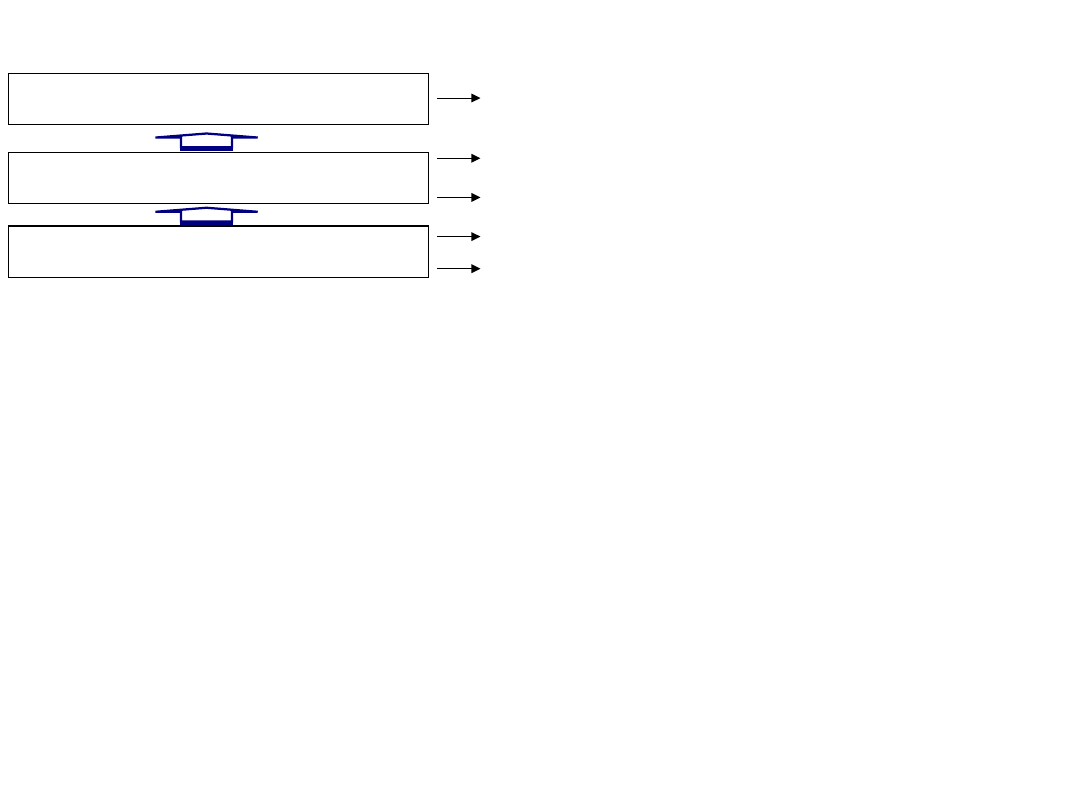
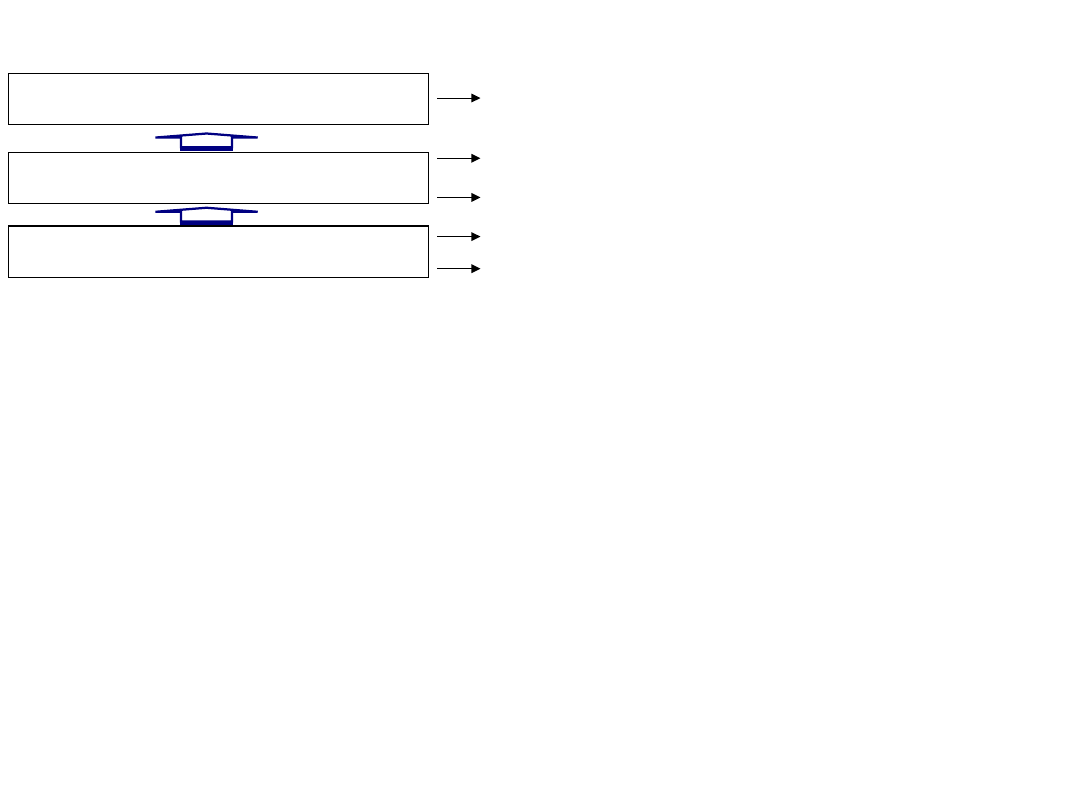
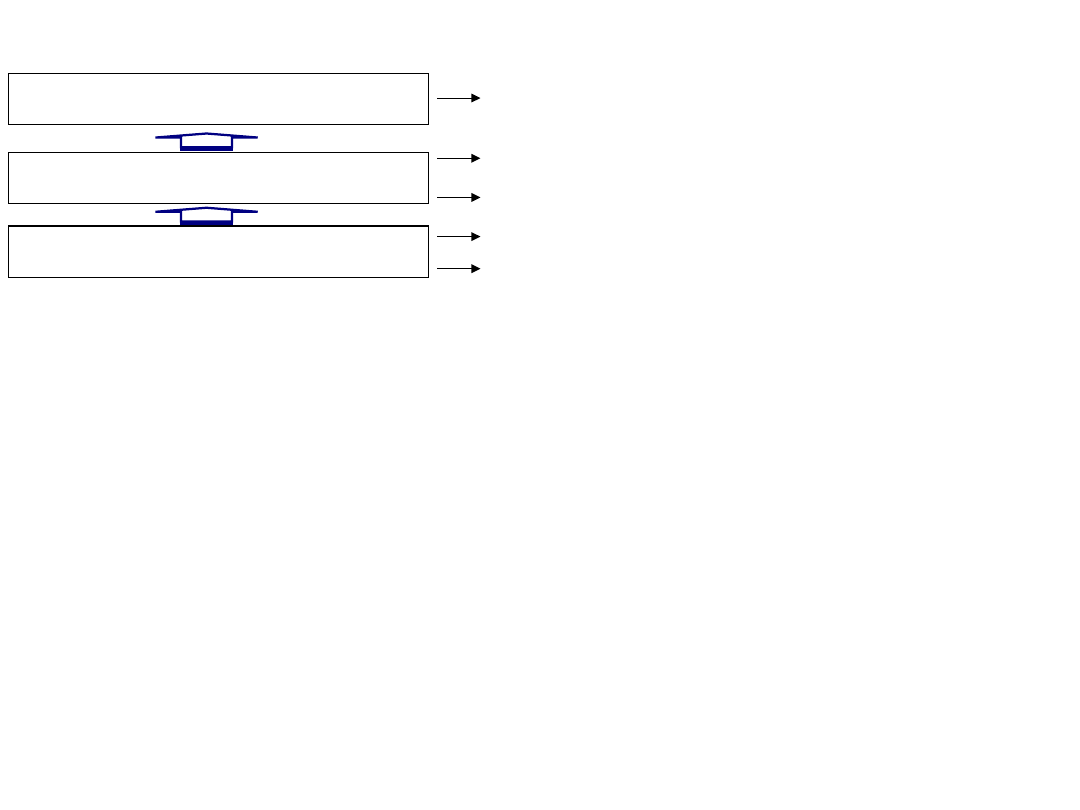
a) Zdarzenie A w

przestrzeni E

E

b) Suma zdarzeń

przestrzeni E

a) Iloczyn zdarzeń

a) Różnica zdarzeń

a) Różnica zdarzeń

a) Zdarzenie przeciwne

do A lub dopełnienie

zdarzenia A

a) Zdarzenie A

zawiera się w

zdarzeniu B

a) Zdarzenie A i B

wykluczają się

B

A

B

A

A

B

B

A





 B

A

Przestrzeń zdarzeń elementarnych jest określona następująco:
Niech zdarzenie A oznacza podzbiór
a zdarzenie B – podzbiór

Określ podzbiory zdarzeń:

}

,

,

,

,

{

4

3

2

1

0

e

e

e

e

e

}

,

,

,

{

5

4

3

2

e

e

e

e

}

,

,

,

,

,

{

5

4

3

2

1

0

e

e

e

e

e

e

E 

B

A

B

A

B

A

,

,

}

{

}

,

,

{

5

4

3

2

e

B

A

e

e

e

B

A

E

B

A













B

A

Odpowiedź:

A

,

}

,

{

1

0

e

e

A 

Zmienna Losowa

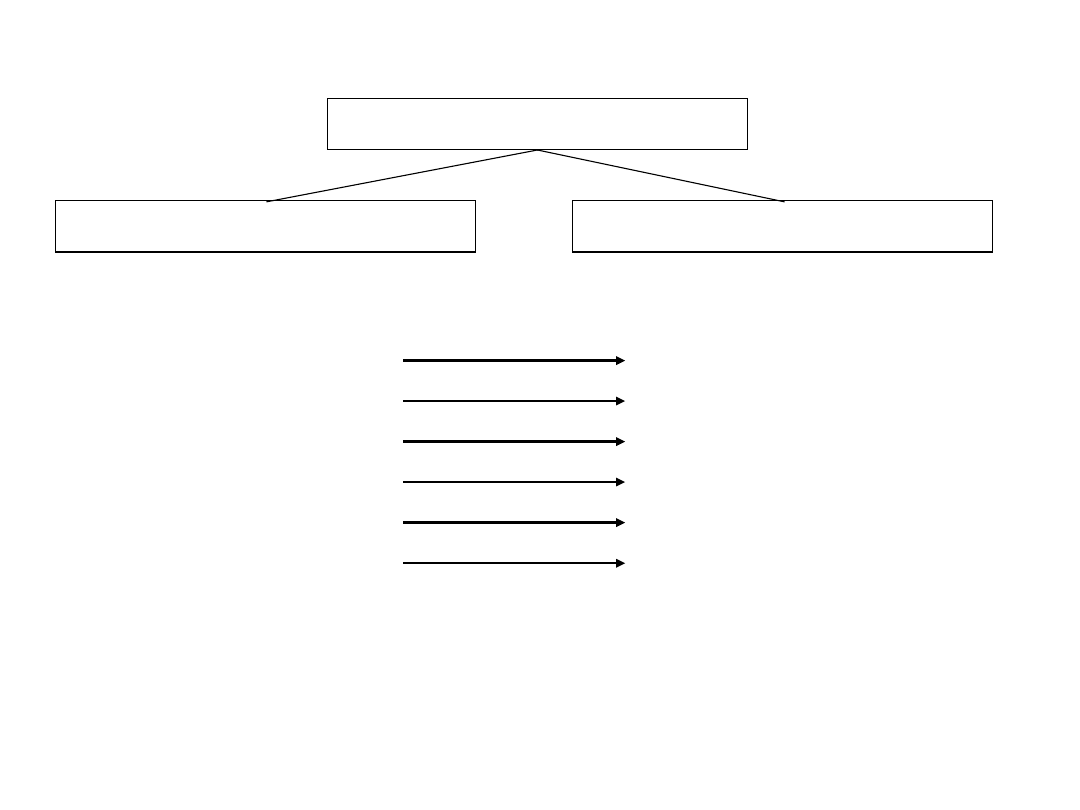
Zmienna Losowa

Opisowa

Matematyczna

Opis statystyczny
Cechy zmienne
Warianty cech
Częstości empiryczne
Rozkłady empiryczne
Parametry opisowe

Wnioskowanie statystyczne
Zmienne losowe
Realizacje zmiennych losowych
Prawdopodobieństwa teoretyczne
Rozkłady teoretyczne
Statystyki

Ćwiczenie wyjaśniające - Zmienna Losowa

Rozważmy doświadczenie polegające na 3-krotnym rzucie monetą. Możliwe zdarzenia losowe to

E1;

E2;

E3;

E4;

E5;

E6;

E7;

E8;

Orzeł

Orzeł

Orzeł

Reszka

Orzeł

Reszka

Reszka

Reszka

Orzeł

Reszka

Orzeł

Orzeł

Reszka

Orzeł

Reszka

Reszka

Orzeł

Orzeł

Reszka

Orzeł

Reszka

Reszka

Orzeł

Reszka

Jeśli poszczególnym zdarzeniom przypiszemy określone liczby, np. każdemu wyrzuceniu
orła odpowiada zapłata 10 $, a każdemu wyrzuceniu reszki odpowiada wypłata 10 $,
to otrzymujemy następujące wartości zmiennej losowej:

-30

-10

-10

-10

10

10

10

30

Zmienna losowa jest przekształceniem zdarzenia losowego w wartość

liczbową. Definiuje się ją jako funkcję rzeczywistą opisaną na zbiorze

zdarzeń elementarnych.

Ćwiczenie wyjaśniające - Zmienna Losowa

Jeśli uporządkujemy wszystkie możliwe wyniki w opisanej wyżej grze, to widać że zmienna losowa,
zdefiniowana jako wielkość wygranej, przyjmuje jedynie wartości: -30, -10, 10, 30.

Zbiór tych liczb nosi nazwę przestrzeni prób

Wystąpienie każdej z tych liczb jest uzależnione od rezultatu trzykrotnego rzutu monetą. Każdy
z rezultatów ma określoną szansę wystąpienia, opisaną przez prawdopodobieństwo zdarzenia
losowego. Zachodzą zatem następujące relacje:

8

/

1

)

30

(

)

(

8

/

1

)

10

(

)

(

8

/

1

)

10

(

)

(

8

/

1

)

10

(

)

(

8

/

1

)

10

(

)

(

8

/

1

)

10

(

)

(

8

/

1

)

10

(

)

(

8

/

1

)

30

(

)

(

8

7

6

5

4

3

2

1

























































X

P

E

P

X

P

E

P

X

P

E

P

X

P

E

P

X

P

E

P

X

P

E

P

X

P

E

P

X

P

E

P

Po uporządkowaniu tych wartości otrzymujemy układ

X=x

i

-30

-10

10

30

Pi=P(X=

x

i

)

1/8

3/8

3/8

1/8

Układ ten nosi nazwę rozkładu prawdopodobieństwa
zmiennej losowej X. Nazywa się tak bo określa sposób
rozłożenia całej masy prawdopodobieństwa (równej 1)
na poszczególne wartości zmiennej.

Zmienna Losowa - charakterystyka

Rozkład zmiennej losowej

Skokowa (dyskretna)

Ciągła

• Funkcja prawdopodobieństwa

• Dystrybuanta

• Parametry Rozkładu

• Funkcja gęstości

• Dystrybuanta

• Parametry Rozkładu

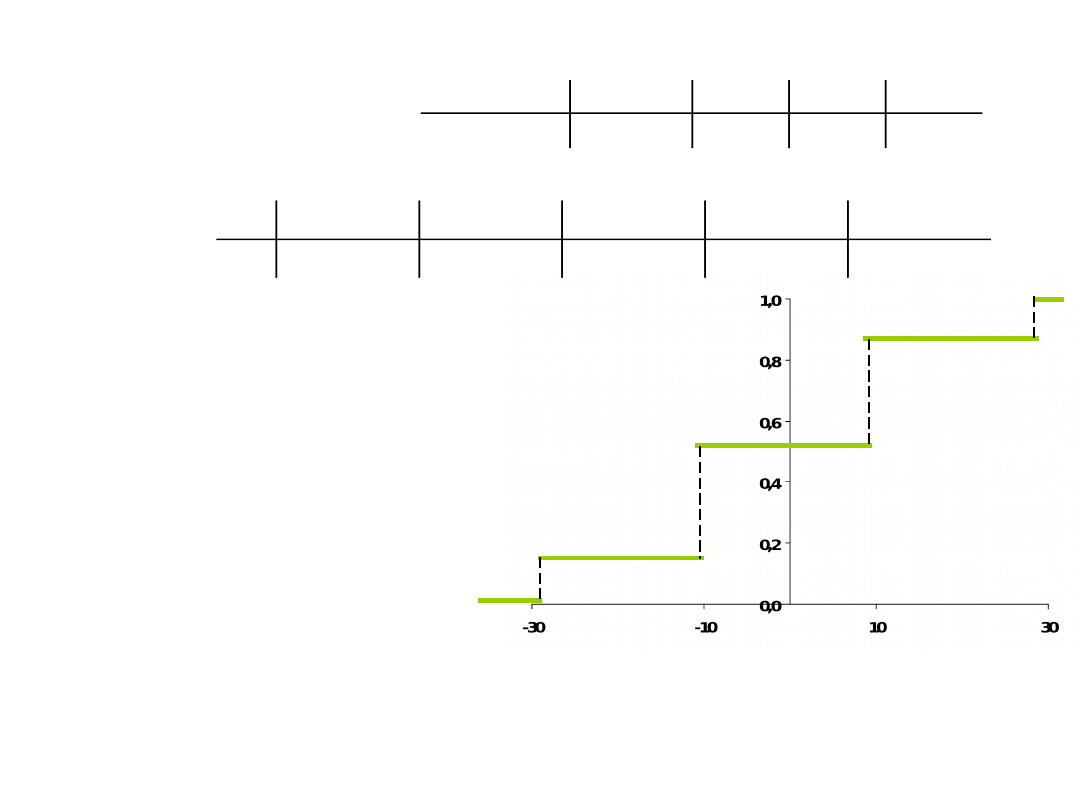
Zmienna Losowa Skokowa (Dyskretna) -
charakterystyka

np

X

E



)

(

)

1

(

)

(

2

p

np

X

D





X=x

i

-30

-10

10

30

Pi=P(X=x

i

)

0,125

0,375

0,375

0,125

• Funkcja prawdopodobieństwa

• Dystrybuanta

X

( ,

-30)

<-30, -10)

<-10,10)

<10,30)

<30,

)

F(x

)

0

0,125

0,500

0,875

1,000



















































.

30

000

,

1

,

30

10

875

,

0

,

10

10

500

,

0

,

10

30

125

,

0

,

30

000

,

0

)

(

x

dla

x

dla

x

dla

x

dla

x

dla

x

F

• Parametry rozkładu

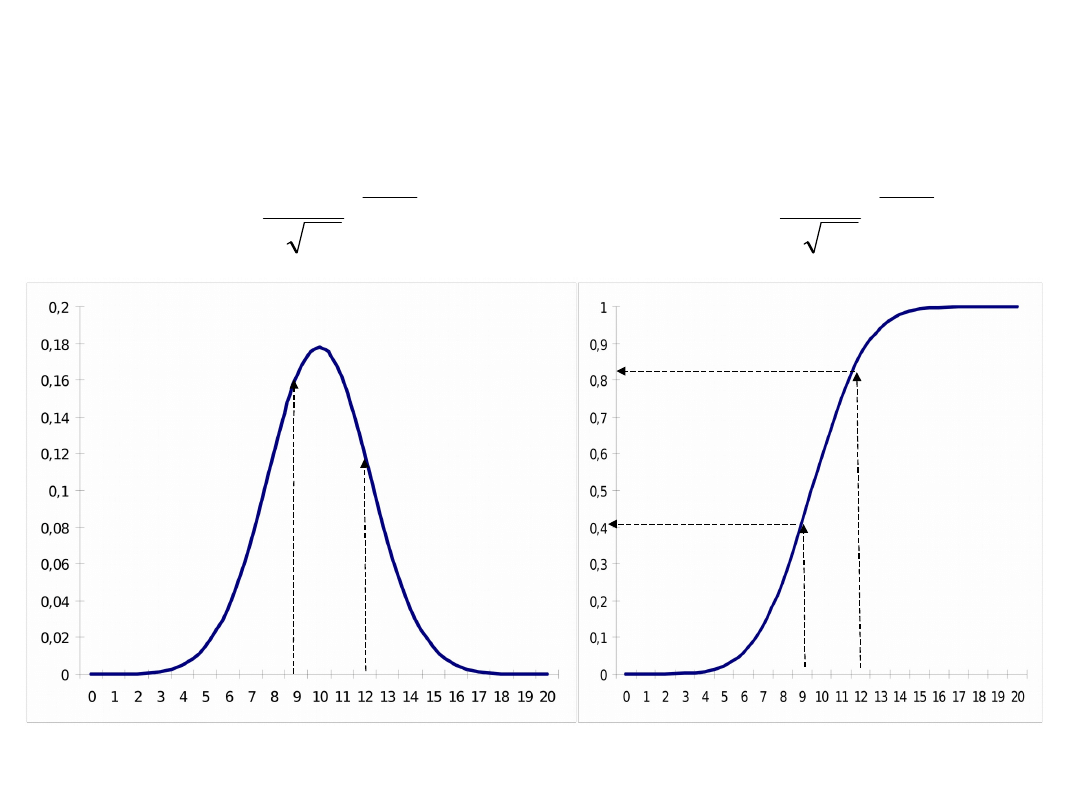
Funkcja gęstości

Funkcja gęstości

prawdopodobieństwa i dystrybuanta

prawdopodobieństwa i dystrybuanta

 





2

2

2

2

1













x

e

X

f

 















x

x

dx

e

X

F

2

2

2

2

1









 

12

F

 

9

F





 

 

9

12

12

9

F

F

x

P









 

x

F





x

x

F





x

x 



x

Gęstość prawdopodobieństwa

Gęstość prawdopodobieństwa

Funkcja gęstości jest pochodną dystrybuanty

 

 





 

x

x

F

x

x

F

lim

X

F

X

f

x

'

















0

1. Przyjmuje wartości nieujemne
2. Wartość funkcji gęstości informuje o tempie przyrostu dystrybuanty
3. Nie jest prawdopodonieństwem i może przyjmować wartości >1
4. Pole pod wykresem funkcji gęstości = 1

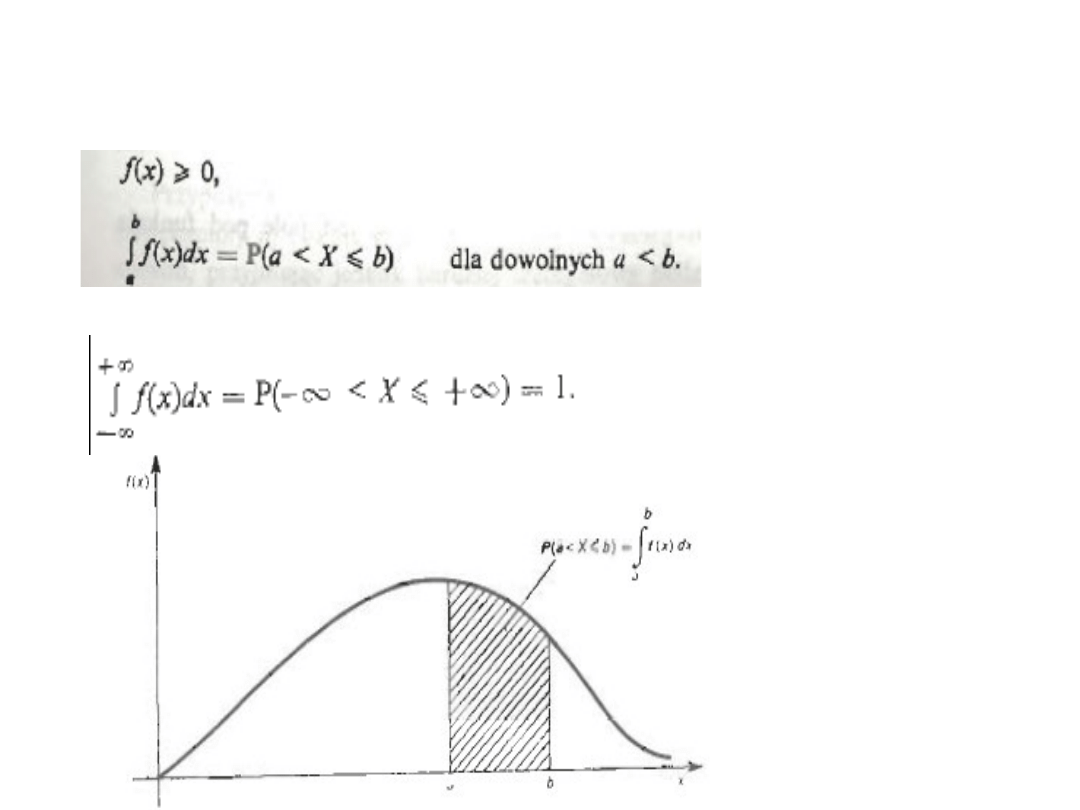
Funkcją gęstości prawdopodobieństwa zmiennej losowej typu ciągłego nazywamy
funkcję f(x), określoną na zbiorze liczb rzeczywistych o następujących własnościach

Z własności tej funkcji wynika, że spełnia ona warunek:

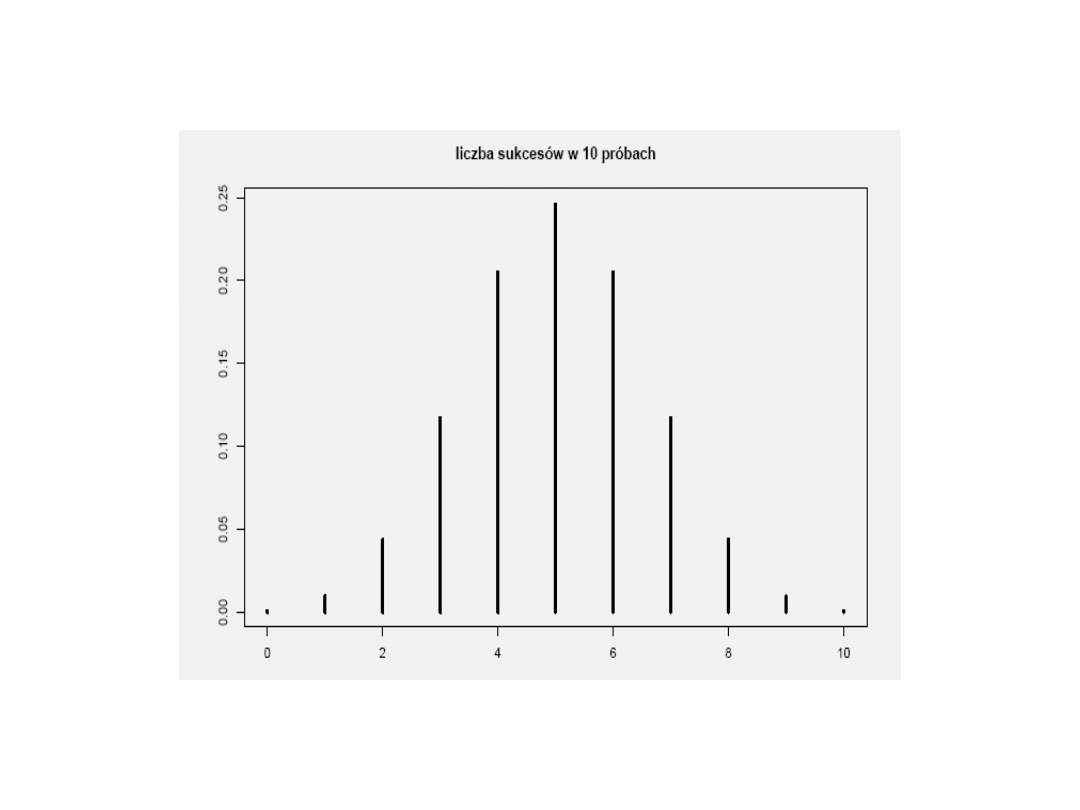
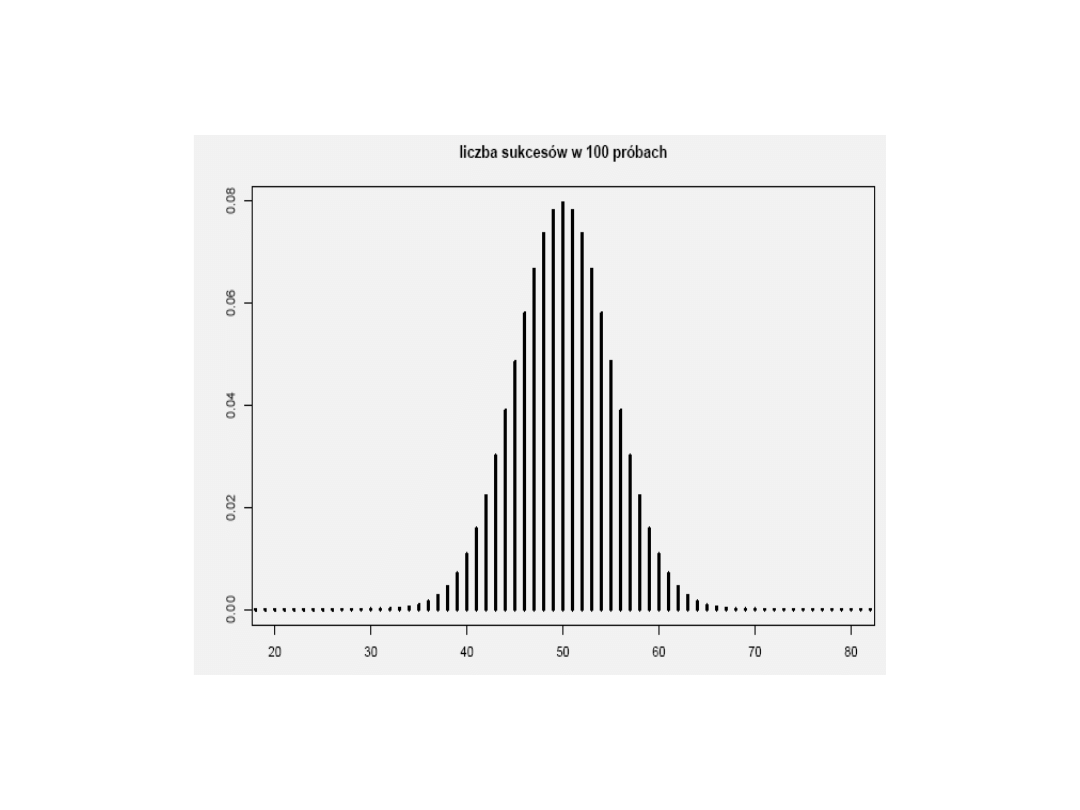
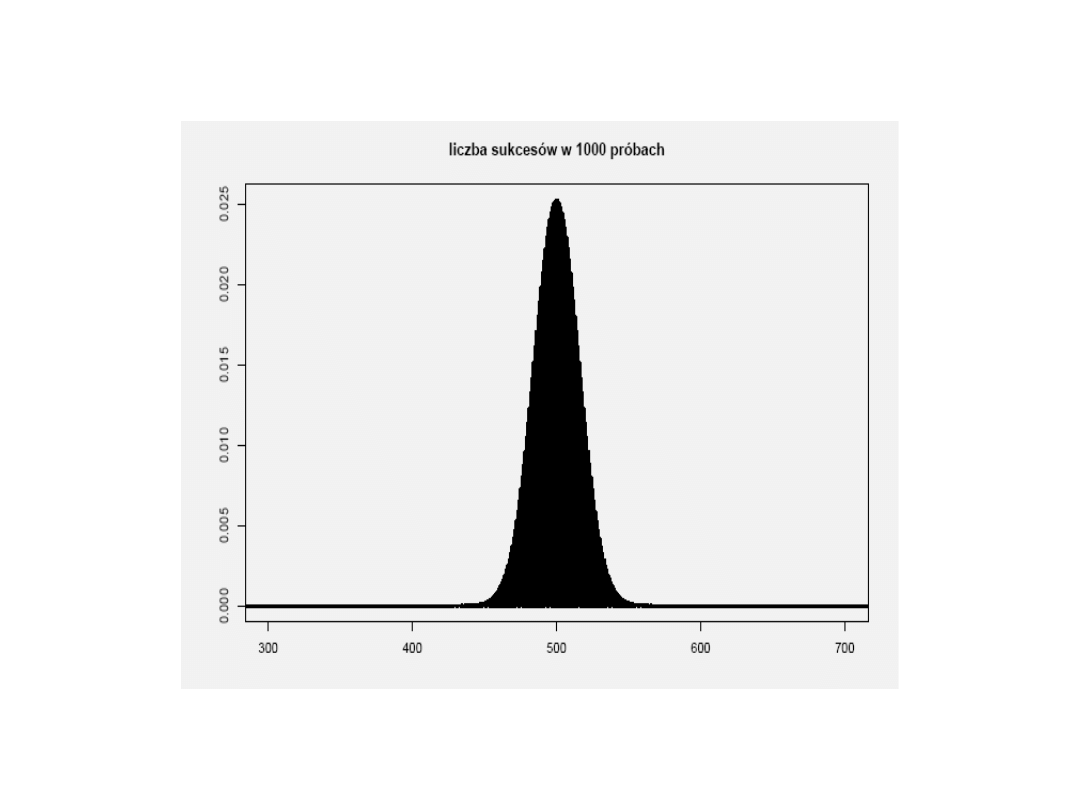
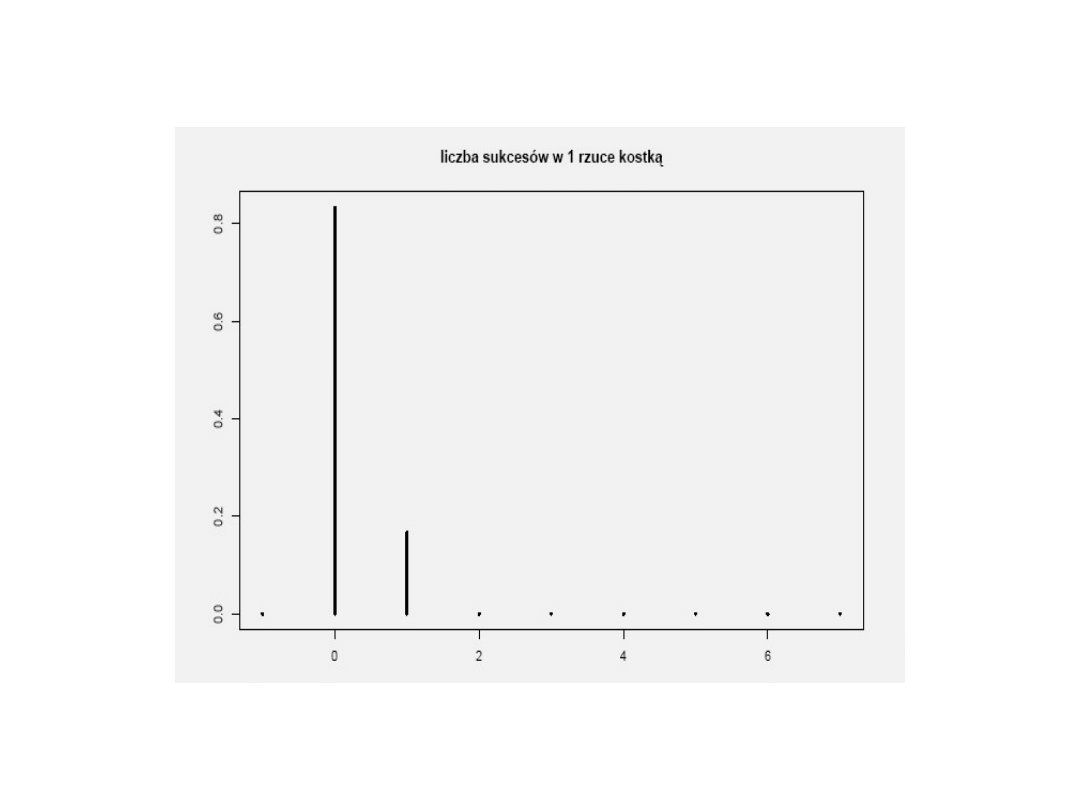
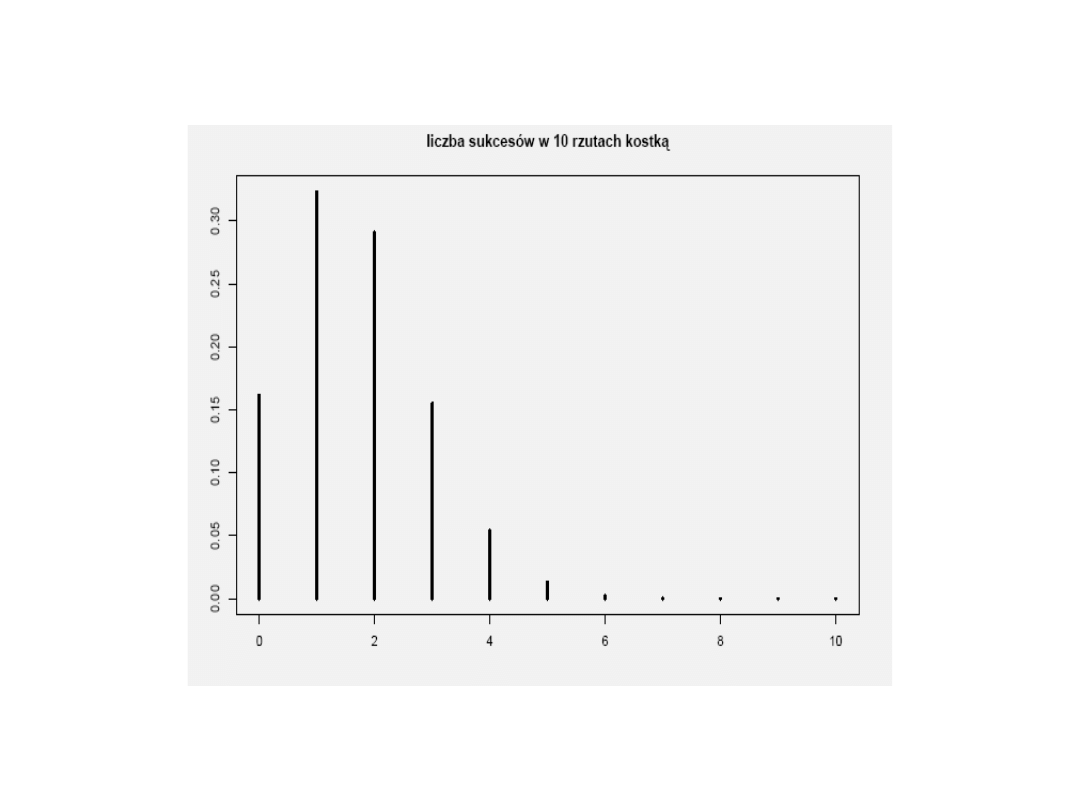
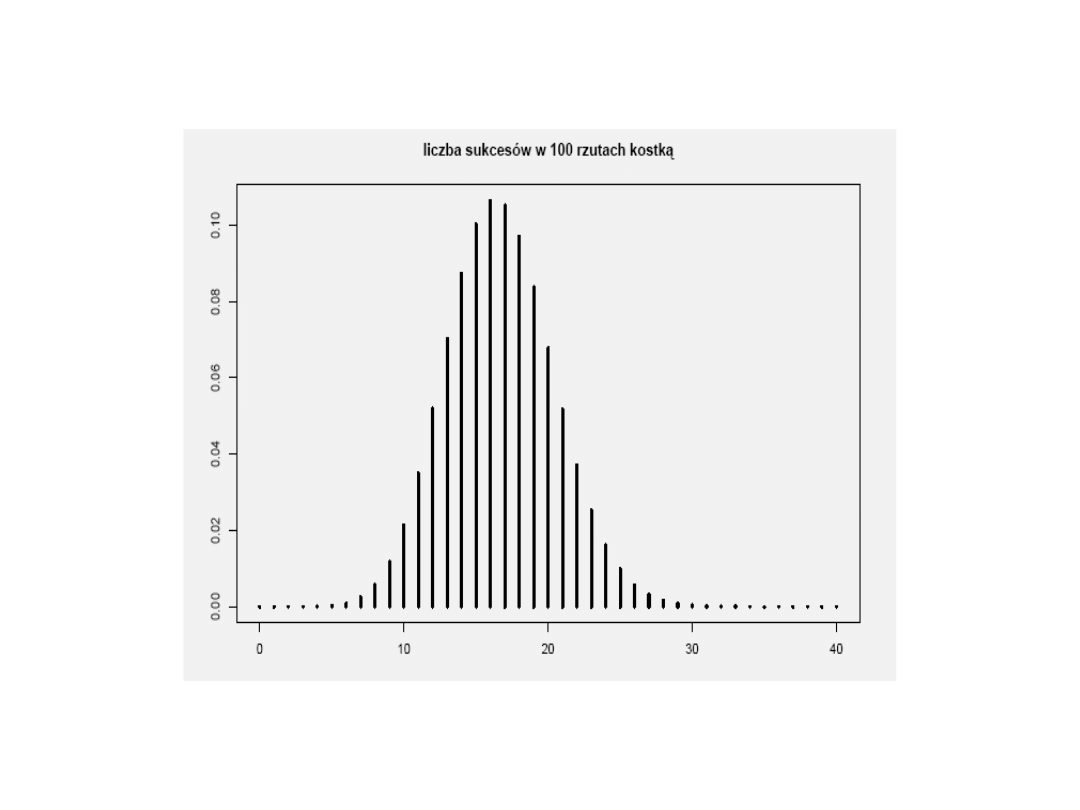
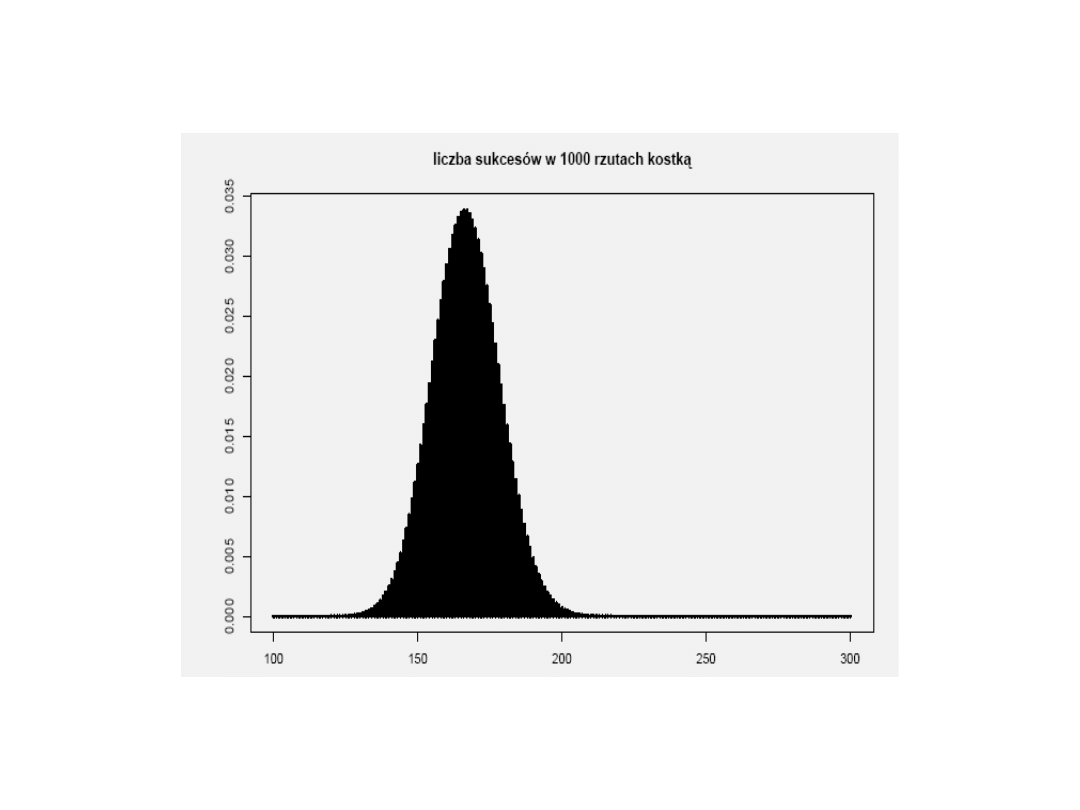
Rozkład Gaussa

Rozkład Gaussa

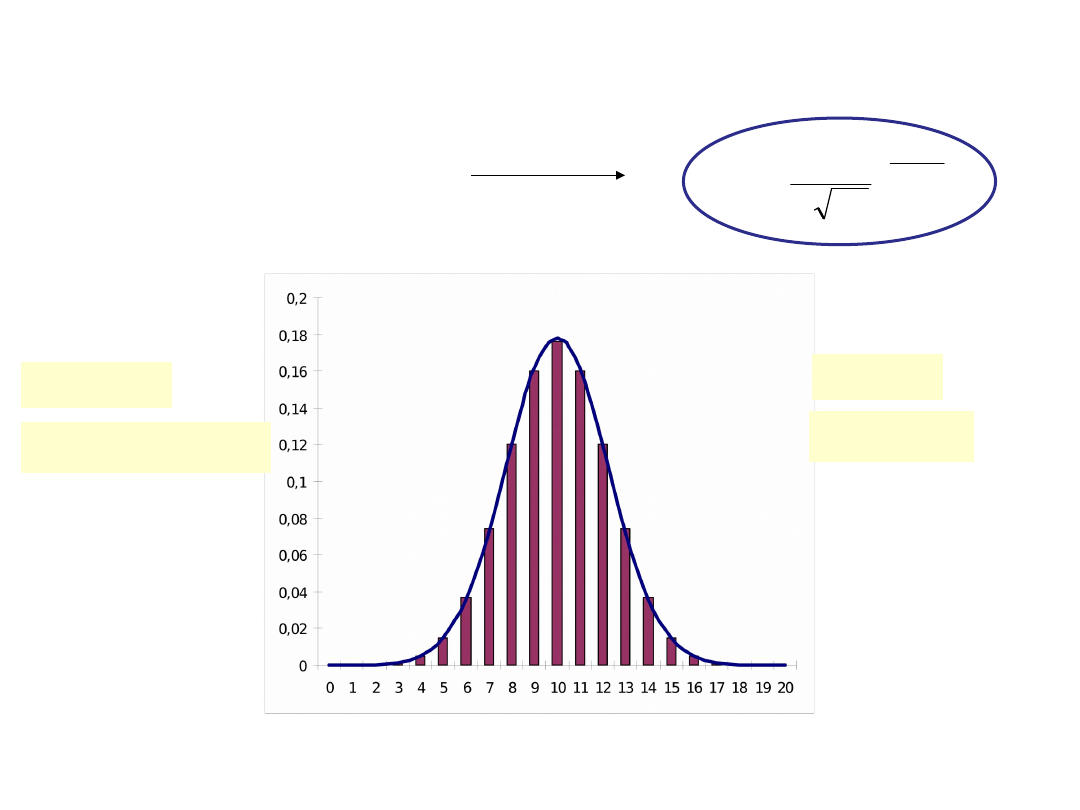
Rozkład normalny Gaussa

Rozkład normalny Gaussa

k

n

k

p)

(1

p

k

n

p)

n,

(k;

B



















n=20
p=0,5

 





2

2

2

2

1













x

e

X

f

Np

(X)

E



p)

-

Np(1

(X)

D

2



(X)

E





(X)

D

2



2



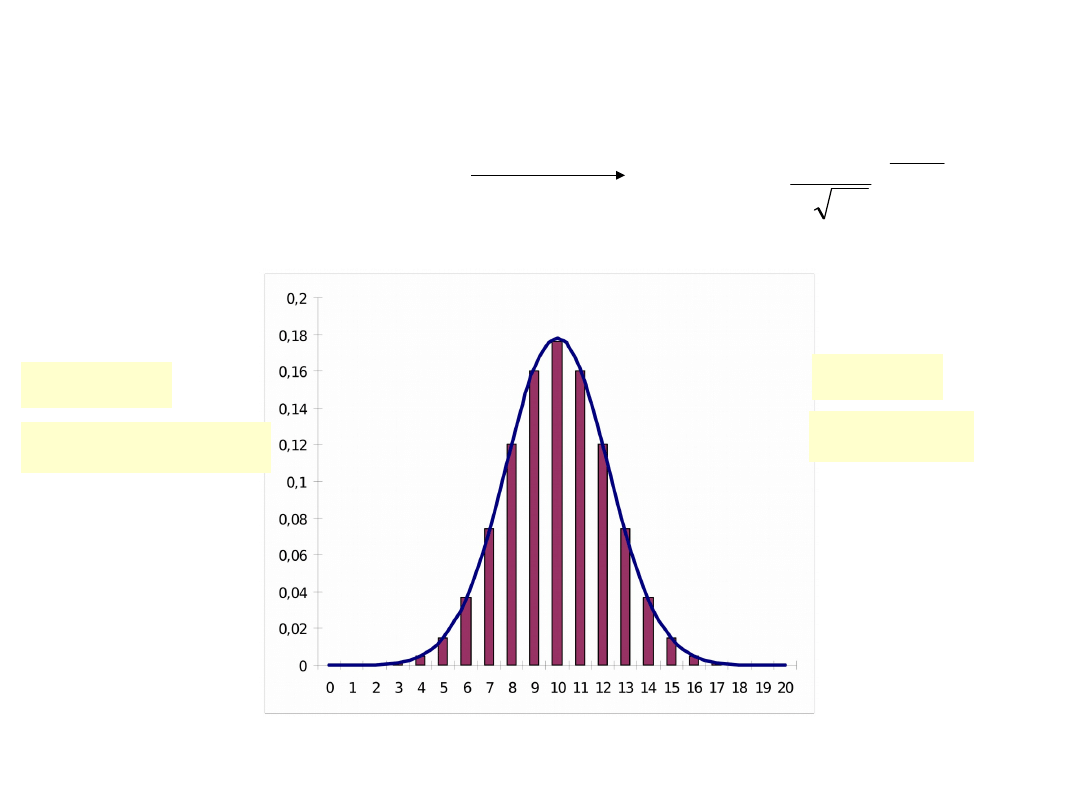
Rozkład normalny Gaussa

Rozkład normalny Gaussa

k

n

k

p)

(1

p

k

n

p)

n,

(k;

B



















n=20
p=0,5

 





2

2

2

2

1













x

e

X

f

Np

(X)

E



p)

-

Np(1

(X)

D

2



(X)

E





(X)

D

2



2



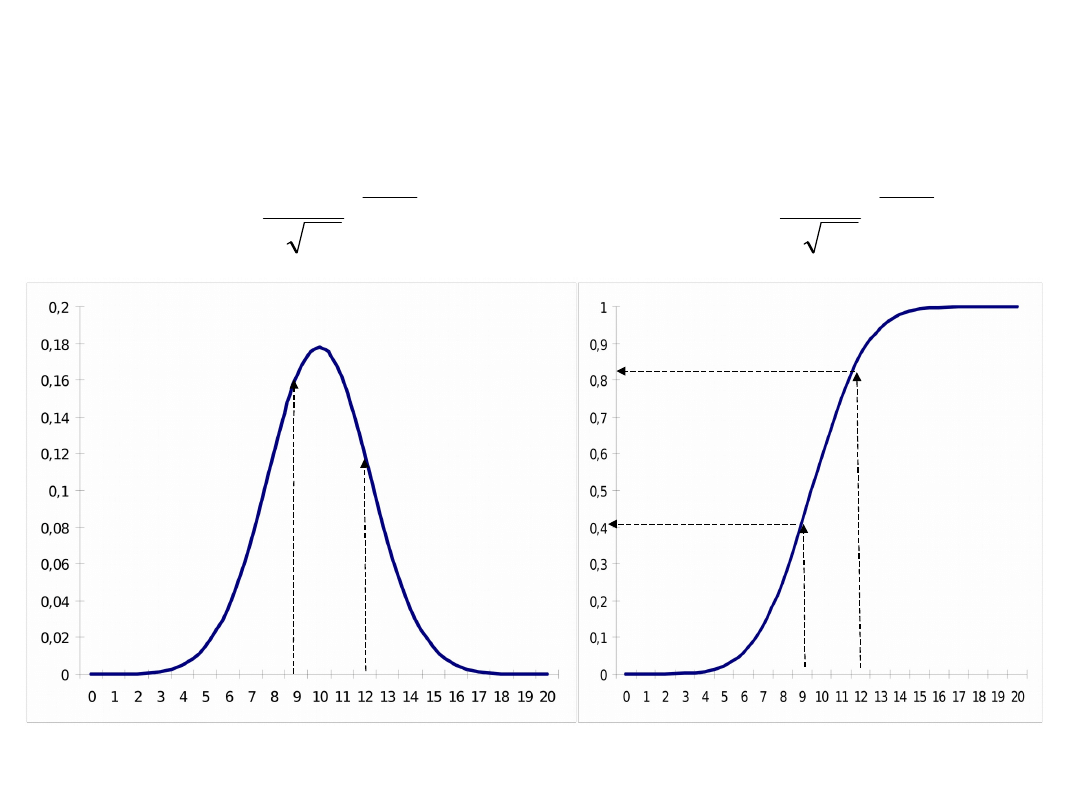
Funkcja gęstości

Funkcja gęstości

prawdopodobieństwa i dystrybuanta

prawdopodobieństwa i dystrybuanta

 





2

2

2

2

1













x

e

X

f

 















x

x

dx

e

X

F

2

2

2

2

1









 

12

F

 

9

F





 

 

9

12

12

9

F

F

x

P









 

x

F





x

x

F





x

x 



x

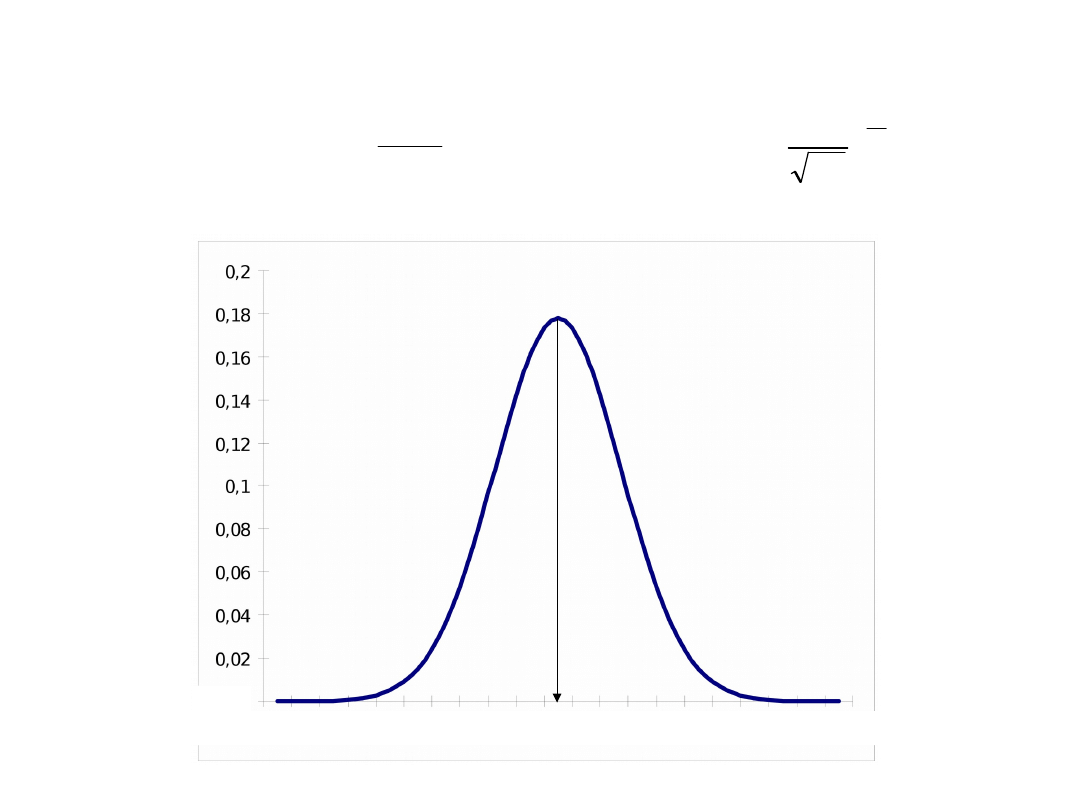
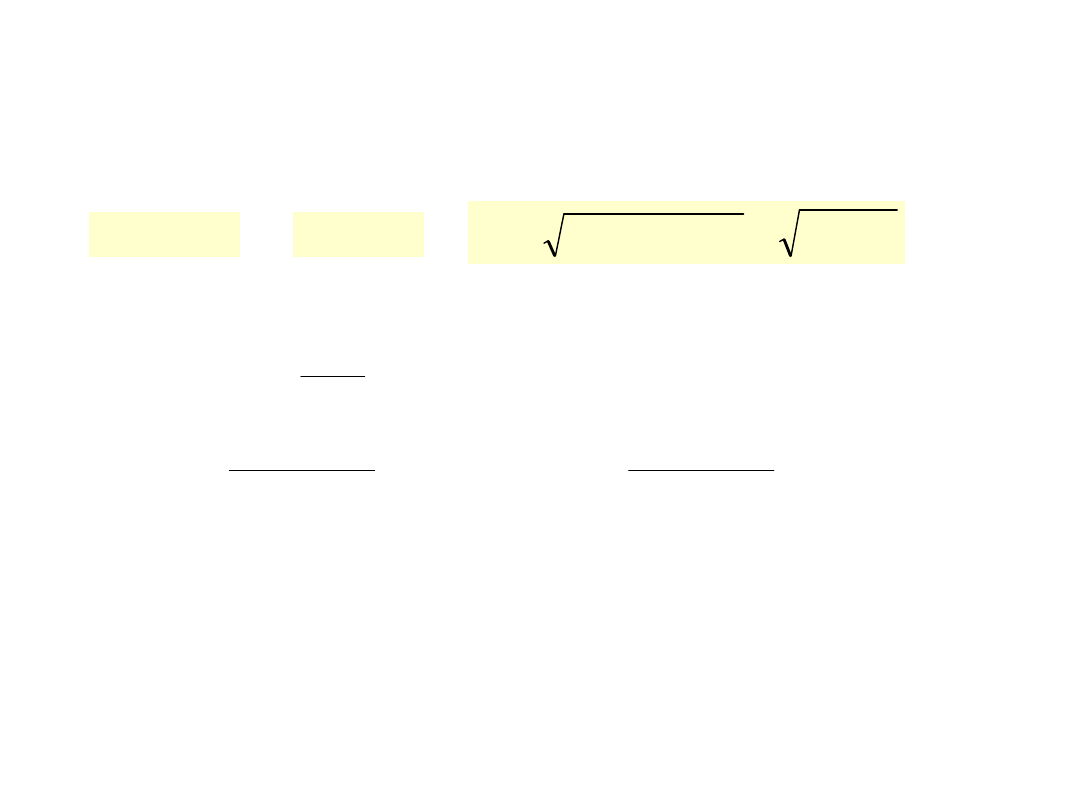
Rozkład znormalizowany N(0,1)

Rozkład znormalizowany N(0,1)

 

2

2

2

1

x

e

z

f





Normalizacja









x

z

0









Przykład

Przykład

Rzucamy 10000 razy monetą. Przyjmując, że prawdopodobieństwo wyrzucenia
Orła wynosi ½, oblicz prawdopodobieństwo tego, że liczba wyrzuconych orłów
Zawiera się w granicach 5050 do 5100.

Normalizacja









x

z

Np

(X)

E



(X)

E





)

(

)

1

(

*

*

2

X

D

p

p

n









5000

5000

50





1

50

5000

5050

5050

1







t





2

50

5000

5100

5100

2







t

1360

,

0

)

2

1

(





T

P

 

4773

,

0

2



 t

 

3413

,

0

1



 t

1360

,

0

)

5100

5050

(

)

(

2

1













X

P

x

X

x

P

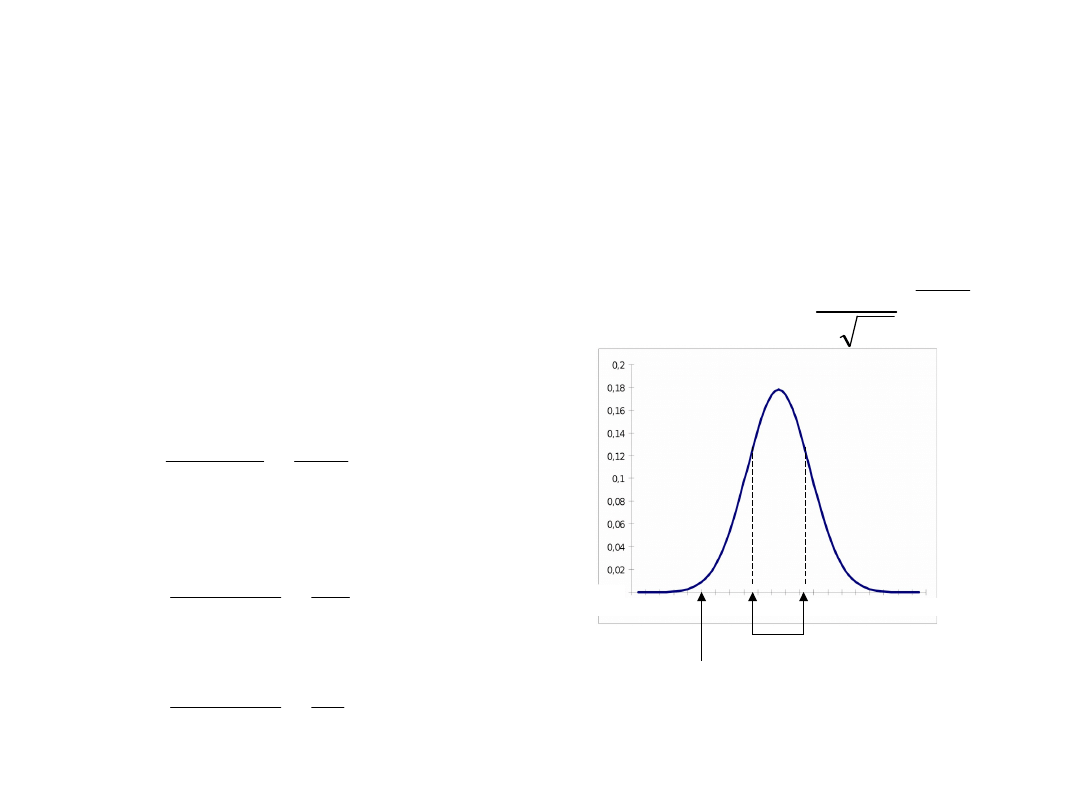
Tablice dystrybuanty N(0,1)

Tablice dystrybuanty N(0,1)

W populacji B zmierzono poziom IQ i otrzymano średnią 125
punktów i odchylenie standardowe 25. Rozkałd IQ jest
normalny. Jaki procent badanych ma inteligencję nie wyższą
od 80 punktów, a jaki procent badanych ma inteligencję w
przedziale 120-130 punktów

Normalizacja

 

8

1

25

45

25

125

80

80

,

z













 

2

0

25

5

25

125

120

120

,

z













 

2

0

25

5

25

125

130

130

,

z









0









8

1,



2

0,



2

0,

 





2

2

2

2

1













x

e

X

f

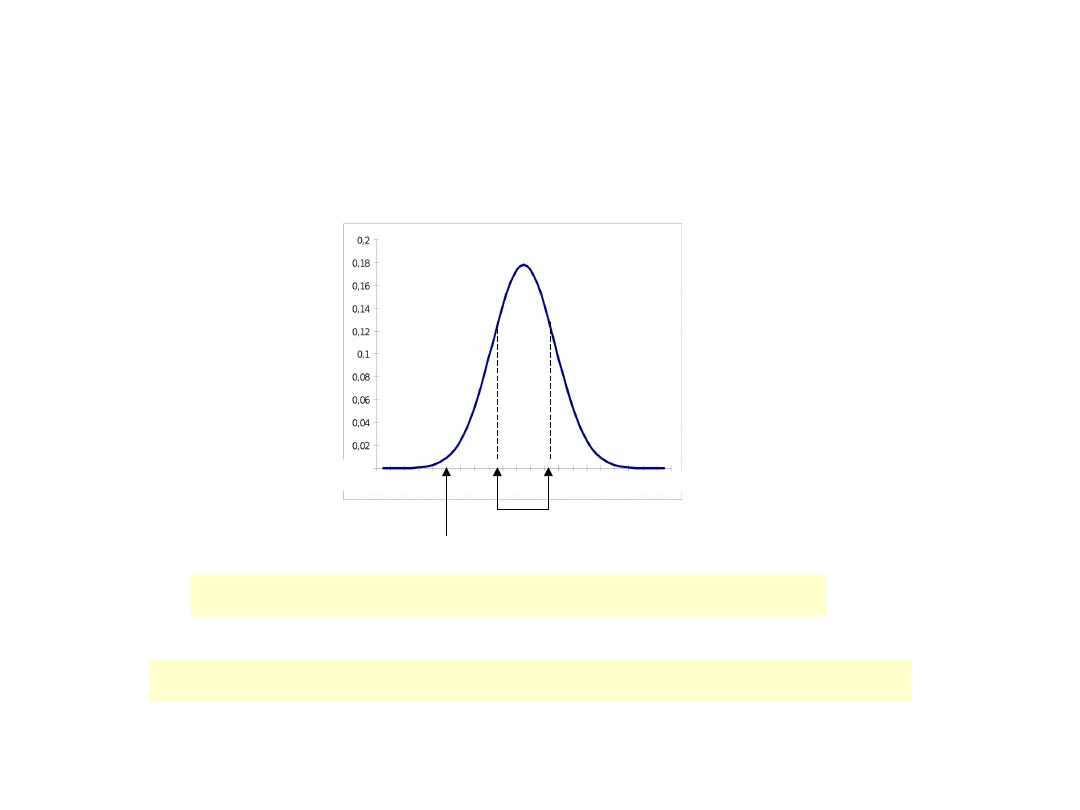
Tablice dystrybuanty N(0,1)

Tablice dystrybuanty N(0,1)

W populacji B zmierzono poziom IQ i otrzymano średnią 125 punktów i wariancję 25. Rozkałd IQ jest
normalny. Jaki procent badanych ma inteligencję nie wyższą od 80 punktów, a jaki procent badanych ma
inteligencję w przedziale 120-130 punktów

0









8

1,



2

0,



2

0,









 

0359

0

9641

0

1

8

1

1

8

1

80

,

,

,

F

,

F

IQ

P





















 





1594

0

4203

0

5797

0

2

0

2

0

130

120

,

,

,

,

F

,

F

IQ

P

















Przykładowe zadanie

Przykładowe zadanie

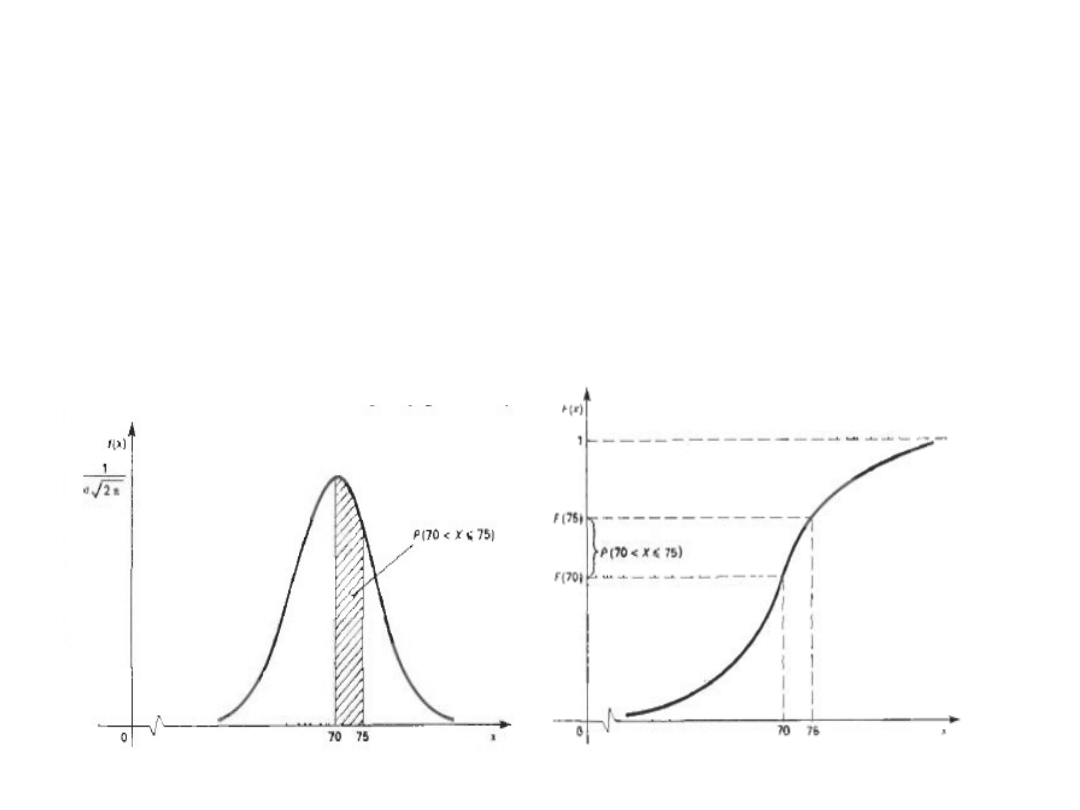
Zadanie 1

Zadanie 1

Waga mężczyzn (w kg) w pewnej populacji ma rozkład N (70;6). Sporządzimy
wykres funkcji gęstości i dystrybuanty wagi mężczyzn w populacji. Zilustrujemy
na tych wykresach prawdopodobieństwo tego, że wybrany przypadkowo
mężczyzna będzie miał wagę z przedziału (70,75). Symboliczny zapis X: N(70;6)
oznacza, że waga mężczyzn jest zmienną losową o rozkładzie normalnym ze
średnią m=70 kg i odchyleniem standardowym d=6 kg.

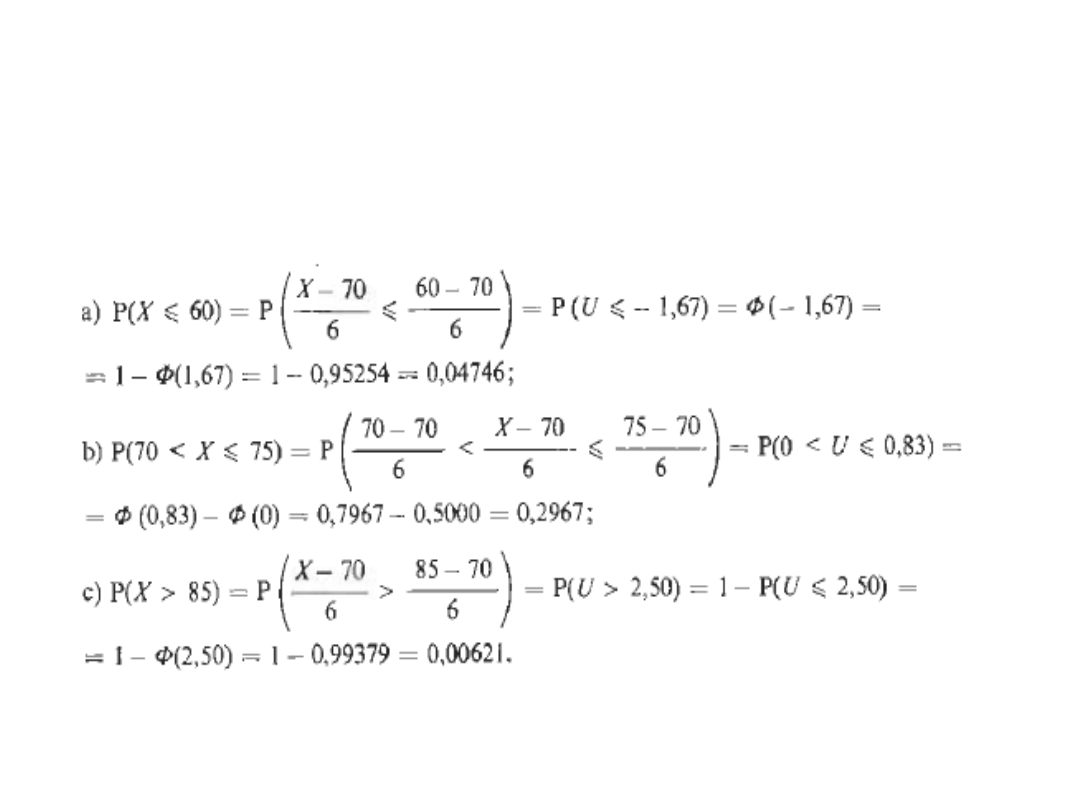
Zadanie 1 cd…

Zadanie 1 cd…

Korzystając z danych, w których stwierdza się, że waga mężczyzn

(w kg) ma rozkład N(70;6) obliczymy udział w populacji

mężczyzn o wadze:

a) Mniejszej od 60 kg

b) W przedziale od 70 kg do 75 kg,

c) wyższej od 85 kg

Uzyskane wyniki oznaczają, że około 7,7% mężczyzn w populacji

ma wagę poniżej 60 kg, około 29,7% mężczyzn – wagę od 70 kg

do 75 kg, około 0,6% mężczyzn – wagę powyżej 85 kg.

zadanie

zadanie

Zadanie 1

Zadanie 1

Przyjmijmy że wyniki testu IQ przeprowadzonego w grupie 500 osób
mają rozkład normalny ze średnią arytmetyczna = 100 i
odchyleniem standardowym = 15. Oszacuj ile osób z tej grupy
uzyskało wynik testu:

a) między 85 a 115

b )większy od 115

c) większy od 130

 





2

2

2

2

1













x

e

X

f

 

1

15

15

15

100

85

85













z

 

1

15

15

15

100

115

115









z

 

0

,

2

15

30

15

100

130

130









z









 

0359

0

9641

0

1

8

1

1

8

1

80

,

,

,

F

,

F

IQ

P





















 





1594

0

4203

0

5797

0

2

0

2

0

130

120

,

,

,

,

F

,

F

IQ

P

























x

z

(X)

E





(X)

D

2



2



Zadanie 1

Zadanie 1

Korzystając

z

tablic

standaryzowanego

rozkładu normalnego odczytać dystrybuanty:
a) F(-2,58)=
b) F(-1,96)=
c) F(-1,68)=
d) F(0)=
e) F(1,68)=
f) F(1,96)=
g) F(2,58)=

Zadanie 1

Zadanie 1

Korzystając

z

tablic

standaryzowanego

rozkładu normalnego odczytać dystrybuanty:
a) F(-2,58)= 0,00494
b) F(-1,96)= 0,025
c) F(-1,68)= 0,04648
d) F(0)= 0,50
e) F(1,68)= 0,95352
f) F(1,96)= 0,97500
g) F(2,58)= 0,99506

Zadanie 2

Zadanie 2

Korzystając

z

tablic

standaryzowanego

rozkładu normalnego odczytać wartość :
a) F( )=0,9999
b) F( )=0,95
c) F( )=0,90
d) F( )=0,68
e) F( )=0,05
f) F( )=0

Zadanie 3a

Zadanie 3a

Iloraz inteligencji ma w populacji rozkład normalny =100;

=15. Znaleźć prawdopodobieństwo, że z populacji

wylosujemy osobę z IQ:

a) nie większym niż 70

b) nie większym niż 120

c) większym niż 140

d) pomiędzy 70 i 130









x

z









 

0359

0

9641

0

1

8

1

1

8

1

80

,

,

,

F

,

F

IQ

P





















 





1594

0

4203

0

5797

0

2

0

2

0

130

120

,

,

,

,

F

,

F

IQ

P

















Zadanie 3b

Zadanie 3b

Liczba elementów jakie osoba jest w stanie przechowywać w pamięci

krótkotrwałej ma w populacji

uczniów rozkład normalny =7; =1,5. Obliczyć prawdopodobieństwo,

że z tej populacji wylosujemy osobę, która jest w stanie zapamiętać po

jednorazowym przeczytaniu:

a) numer nie dłuższy niż 6 cyfrowy

b) numer dłuższy niż 8 cyfrowy

Zadanie 4

Zadanie 4

W dużej populacji mężczyzn wzrost ma rozkład
normalny o średniej wartości 170 cm i odchyleniu
standardowym 5 cm.
Jaki procent populacji odpowiada przedziałowi
1) od 170 cm do 190 cm
2)poniżej 160 cm
3) powyżej 200 cm?









 

0359

0

9641

0

1

8

1

1

8

1

80

,

,

,

F

,

F

IQ

P





















 





1594

0

4203

0

5797

0

2

0

2

0

130

120

,

,

,

,

F

,

F

IQ

P

















Zadanie 5

Zadanie 5

Pewien

zakład

produkcyjny

zatrudnia

100

pracowników, których staż pracy jest zgodny z
rozkładem normalnym N(10 lat, 5 lat). Obliczyć ilu
pracowników miało staż:
a) krótszy niż 3 lata,
b) dłuższy niż 15 lat,









 

0359

0

9641

0

1

8

1

1

8

1

80

,

,

,

F

,

F

IQ

P





















 





1594

0

4203

0

5797

0

2

0

2

0

130

120

,

,

,

,

F

,

F

IQ

P

























x

z

Zadanie 6

Zadanie 6

Wiedząc, że rozkład wagi zawartości paczki kawy jest
zgodny z rozkładem normalnym z wartością
oczekiwaną równą 250g i odchyleniem standardowym
równym 4g.
Obliczyć

prawdopodobieństwo,

że

zakupione

opakowanie kawy będzie ważyło:

a)poniżej 246g,
b)poniżej 244g,
c)powyżej 257g,
d)od 246 do 254g,
e)równo 249g?

Zadanie 7

Zadanie 7

Żywotność żarówek produkowanych przez pewną firmę ma
rozkład normalny. Średnia żywotność żarówek wynosi 1000 h, a
odchylenie standardowe czasu świecenia żarówki wynosi 200 h.
Pewna firma zakupiła 25 żarówek. Obliczyć prawdopodobieństwo,
że:

a) średni czas świecenia kupionych żarówek jest dłuższy niż 1100
h
b) średni czas świecenia kupionych żarówek jest krótszy od 1100
h