Kinematyka prosta

Kinematyka prosta

Macierze

Macierze

Mnożenie macierzy

Mnożenie macierzy

nie jest

nie jest

przemienne,

przemienne,

i aby można było mnożyć macierze

i aby można było mnożyć macierze

ilość kolumn 1 macierzy musi być

ilość kolumn 1 macierzy musi być

równa ilości wierszy 2 macierzy

równa ilości wierszy 2 macierzy

Macierz A mnożymy przez macierz B

Macierz A mnożymy przez macierz B



























p

o

n

m

l

k

j

i

h

g

f

e

d

c

b

a

A



























8

7

6

5

4

3

2

1

z

y

x

w

u

t

s

r

B

A*B=C

A*B=C



























16

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

C

Tak więc aby uzyskać wynik np. „x10”

Tak więc aby uzyskać wynik np. „x10”

mnożymy pierwszą liczbę 3 wiersza

mnożymy pierwszą liczbę 3 wiersza

macierzy A z pierwszą liczbą 2 kolumny

macierzy A z pierwszą liczbą 2 kolumny

macierzy B następie dodajemy do tego

macierzy B następie dodajemy do tego

iloczyn drugiej liczby 3 wiersza

iloczyn drugiej liczby 3 wiersza

macierzy A i drugiej liczby 2 kolumny

macierzy A i drugiej liczby 2 kolumny

macierzy B potem znów dodajemy

macierzy B potem znów dodajemy

iloczyn trzeciej liczby 3 wiersza

iloczyn trzeciej liczby 3 wiersza

macierzy A i trzeciej liczby 2 kolumny

macierzy A i trzeciej liczby 2 kolumny

macierzy B i znów dodajemy iloczyn

macierzy B i znów dodajemy iloczyn

czwartej liczby 3 wiersza macierzy A i 4

czwartej liczby 3 wiersza macierzy A i 4

liczby 2 kolumny macierzy B i tak

liczby 2 kolumny macierzy B i tak

otrzymujemy wynik w macierzy C

otrzymujemy wynik w macierzy C

będący przecięciem 3 wiersza i 2

będący przecięciem 3 wiersza i 2

kolumny (tj. x10).

kolumny (tj. x10).

W przypadku innych wyników mnożenia

W przypadku innych wyników mnożenia

postępujemy analogicznie, co widać na

postępujemy analogicznie, co widać na

następnym slajdzie.

następnym slajdzie.

Rozpisanie wyników mnożenia

Rozpisanie wyników mnożenia

macierzy :

macierzy :

5

*

1

*

*

*

13

5

*

1

*

*

*

9

5

*

1

*

*

*

5

5

*

1

*

*

*

1

p

o

s

n

r

m

x

l

k

w

j

r

i

x

h

g

w

f

r

e

x

d

c

w

b

r

a

x

































7

*

3

*

*

*

16

7

*

3

*

*

*

11

7

*

3

*

*

*

7

7

*

3

*

*

*

*

3

p

o

y

n

t

m

x

l

k

y

j

t

i

x

h

g

y

f

t

e

x

d

c

y

b

t

a

x































6

*

2

*

*

*

14

6

*

2

*

*

*

10

6

*

2

*

*

*

6

6

*

2

*

*

*

2

p

o

x

n

s

m

x

l

k

x

j

s

i

x

h

g

x

f

s

e

x

d

c

x

b

s

a

x

































8

*

4

*

*

*

16

8

*

4

*

*

*

*

12

8

*

4

*

*

*

8

8

*

4

*

*

*

4

p

o

z

n

u

m

x

l

k

z

j

u

i

x

h

g

z

f

u

e

x

d

c

z

b

u

a

x































Proste zadanie kinematyki

Proste zadanie kinematyki

–

–

polega ono na obliczeniu pozycji i

polega ono na obliczeniu pozycji i

orientacji chwytaka względem

orientacji chwytaka względem

nieruchomej podstawy

nieruchomej podstawy

manipulatora.

manipulatora.

Aby tego dokonać niezbędna jest notacja

Aby tego dokonać niezbędna jest notacja

Denavita-Hartenberga i notacja Eulera

Denavita-Hartenberga i notacja Eulera

.

.

Notacja

Notacja

Denavita-Hartenberga

Denavita-Hartenberga

jest to

jest to

zagadnienie analizy względnego

zagadnienie analizy względnego

położenia ciała, znajdującego się w

położenia ciała, znajdującego się w

jednym układzie, w stosunku do jego

jednym układzie, w stosunku do jego

położenia w innym układzie.

położenia w innym układzie.

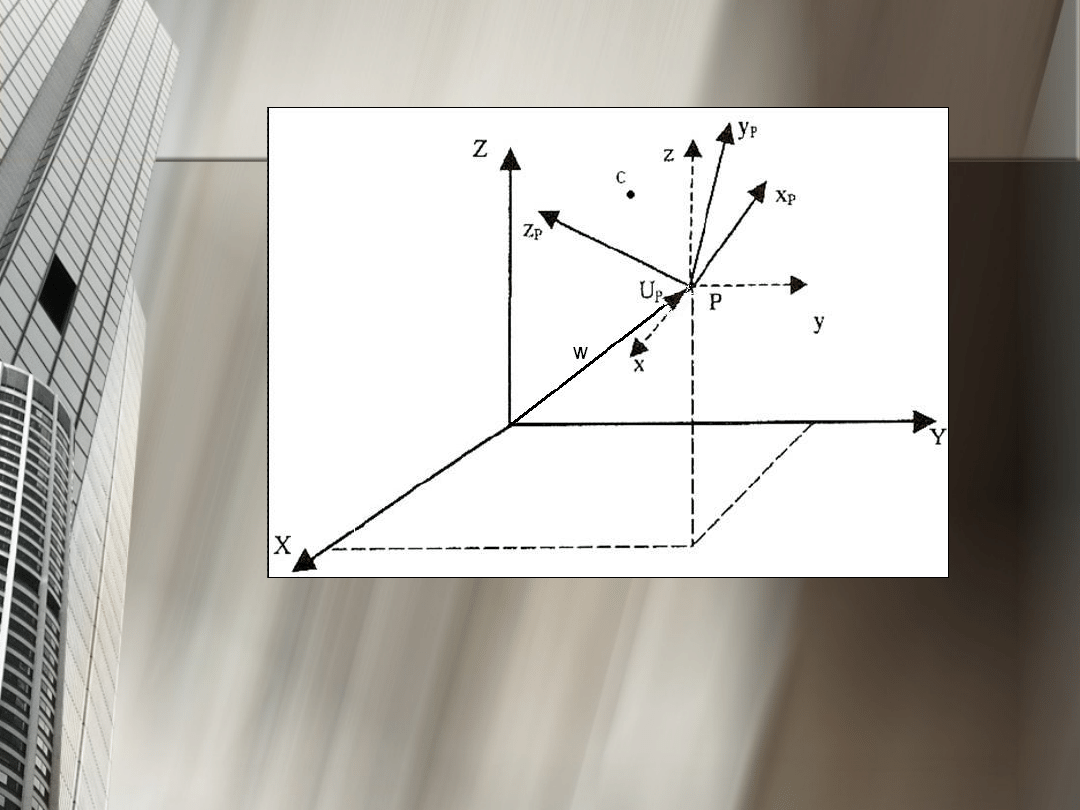
Chcąc znaleźć położenie punktu C (leżącego w

Chcąc znaleźć położenie punktu C (leżącego w

układzie Up) względem głównego układu

układzie Up) względem głównego układu

współrzędnych należy wpierw znaleźć

współrzędnych należy wpierw znaleźć

orientację układu Up względem układu

orientację układu Up względem układu

głównego

głównego

Układ współrzędnych Up jest obrócony

Układ współrzędnych Up jest obrócony

względem układu głownego

względem układu głownego

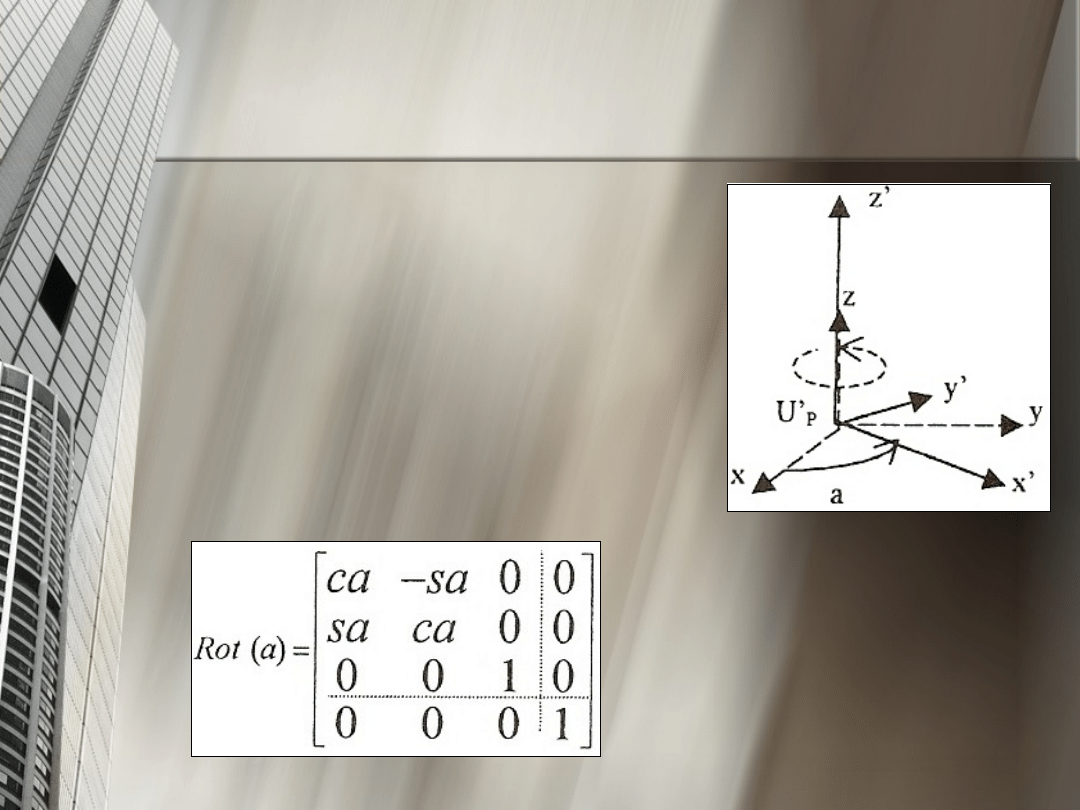
1. układ Up jest obrócony wokół osi Z głównego

1. układ Up jest obrócony wokół osi Z głównego

układu o kąt „a” i powstaje

układu o kąt „a” i powstaje

układu U’p

układu U’p

Obrót ten

Obrót ten

zapisujemy jako

zapisujemy jako

macierz

macierz

gdzie:

gdzie:

c – kosinus kąta

c – kosinus kąta

s – sinus kąta

s – sinus kąta

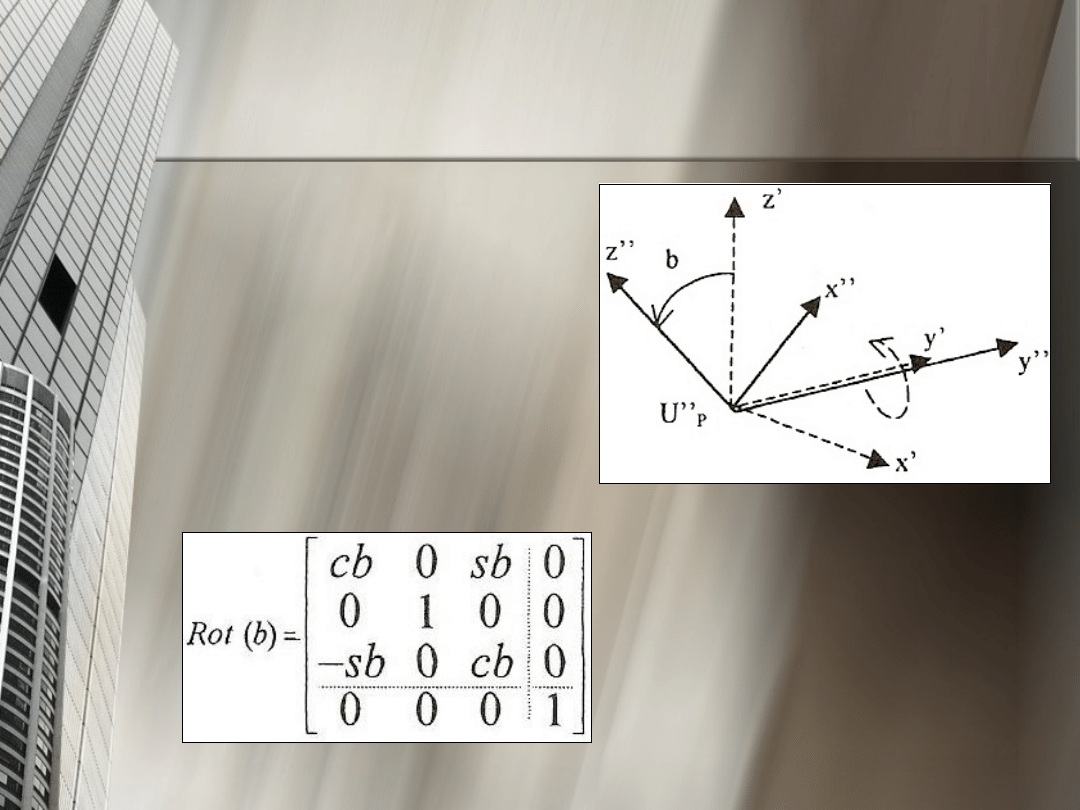
2. układ U’p jest obrócony wokół osi Y’ układu

2. układ U’p jest obrócony wokół osi Y’ układu

U’p o kąt „b” i powstaje

U’p o kąt „b” i powstaje

układu U’’p

układu U’’p

Obrót ten

Obrót ten

zapisujemy jako

zapisujemy jako

macierz

macierz

gdzie:

gdzie:

c – kosinus kąta

c – kosinus kąta

s – sinus kąta

s – sinus kąta

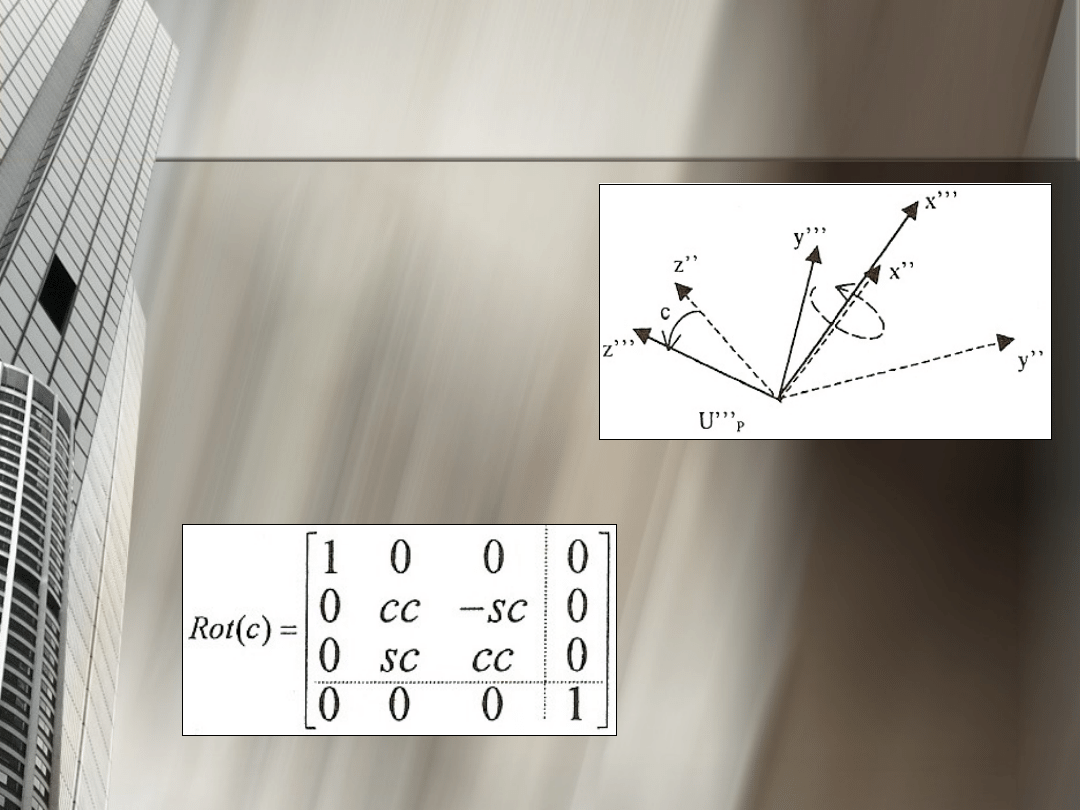
3. układ U’’p jest obrócony wokół osi X’’’ układu

3. układ U’’p jest obrócony wokół osi X’’’ układu

U’’p o kąt „c”

U’’p o kąt „c”

i powstaje układu U’’’p

i powstaje układu U’’’p

Obrót ten

Obrót ten

zapisujemy jako

zapisujemy jako

macierz

macierz

gdzie:

gdzie:

c – kosinus kąta

c – kosinus kąta

s – sinus kąta

s – sinus kąta

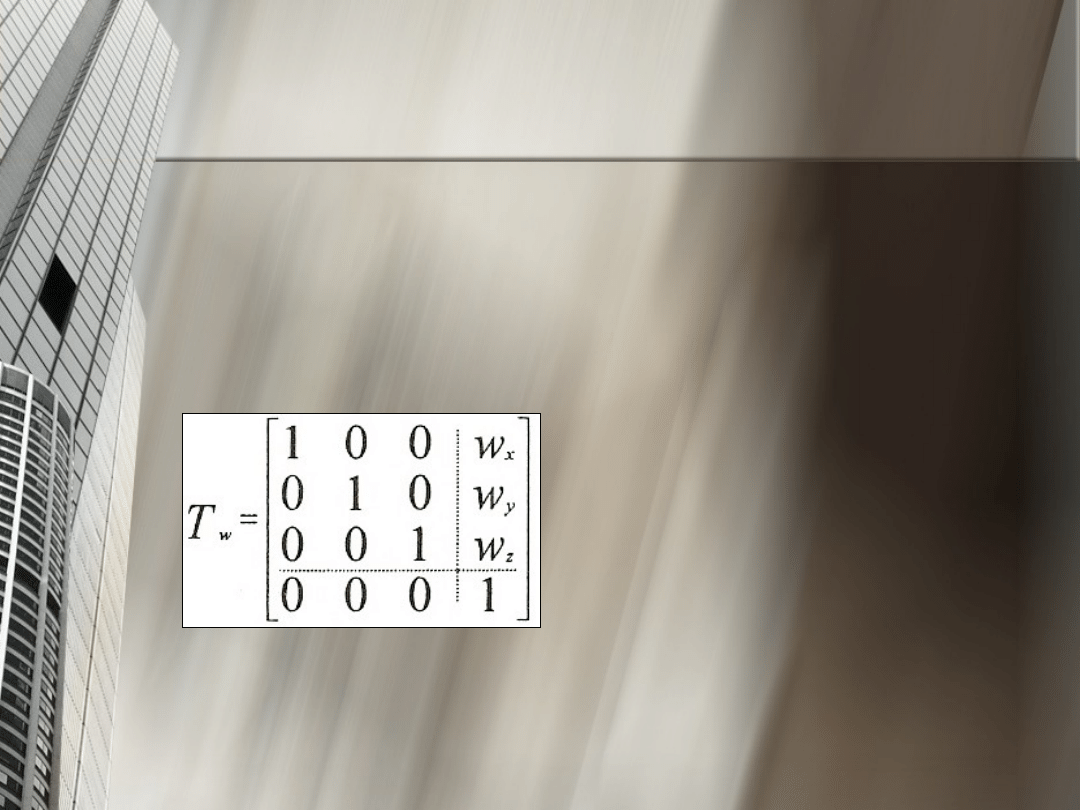
Przy obrotach układów Up, U’p, i U’’p i początek

Przy obrotach układów Up, U’p, i U’’p i początek

tych układów współrzędnych nie zmienia się i

tych układów współrzędnych nie zmienia się i

jest wciąż taki sam, czyli pozostaje nim punkt P

jest wciąż taki sam, czyli pozostaje nim punkt P

Układ U’’’p jest przesunięty o wektor względem

Układ U’’’p jest przesunięty o wektor względem

układu głównego.

układu głównego.

Wektor ten można zapisać w postaci macierzy:

Wektor ten można zapisać w postaci macierzy:

Wartości „1” i „0” w macierzach dotychczas

Wartości „1” i „0” w macierzach dotychczas

przedstawionych są stałe i nie ulegają zmianie

przedstawionych są stałe i nie ulegają zmianie

Tak więc orientacja układu U’’’p względem

Tak więc orientacja układu U’’’p względem

układu głównego jest iloczynem macierzy

układu głównego jest iloczynem macierzy

obrotu i translacji

obrotu i translacji

czyli:

czyli:

Tp = Rot(a)*Rot(b)*Rot(c)*Tw

Tp = Rot(a)*Rot(b)*Rot(c)*Tw

Wynikiem tego iloczynu jest macierz

Wynikiem tego iloczynu jest macierz

gdzie:

gdzie:

a, b, c, d, e, f, g, h, i –

a, b, c, d, e, f, g, h, i –

to orientacja układu

to orientacja układu

U’’’p względem układu

U’’’p względem układu

głównego (tj. jak

głównego (tj. jak

poszczególnego osie

poszczególnego osie

zostały obrócone

zostały obrócone

x, y, z, - to

x, y, z, - to

współrzędne początku

współrzędne początku

układu U’’’p w

układu U’’’p w

układzie głównym

układzie głównym

Aby obliczyć położenie punktu C względem

Aby obliczyć położenie punktu C względem

głównego układu należy macierz Tp przemnożyć

głównego układu należy macierz Tp przemnożyć

przez macierz punktu C (Tc)

przez macierz punktu C (Tc)

T

T

gł

gł

= Tp*Tc

= Tp*Tc

gdzie:

gdzie:

X

X

gł

gł

, Y

, Y

gł

gł

, Z

, Z

gł –

gł –

współrzędne

współrzędne

punktu C w

punktu C w

układzie

układzie

głównym

głównym

Gdy mamy do czynienia z większą ilością

Gdy mamy do czynienia z większą ilością

układów to postępujemy w analogiczny sposób.

układów to postępujemy w analogiczny sposób.

Przyjmując, że punkt C jest początkiem

Przyjmując, że punkt C jest początkiem

kolejnego układu współrzędnych a położenie i

kolejnego układu współrzędnych a położenie i

orientacja układu U’’’p względem układu

orientacja układu U’’’p względem układu

głównego jest macierzą A. Potem należy

głównego jest macierzą A. Potem należy

policzyć orientację i położenie układu Uc

policzyć orientację i położenie układu Uc

względem U’’’p z czego otrzymalibyśmy

względem U’’’p z czego otrzymalibyśmy

macierz B. Tak więc chcąc znać orientacje i

macierz B. Tak więc chcąc znać orientacje i

położenie układu Uc względem głównego

położenie układu Uc względem głównego

trzeba macierz A przemnożyć przez macierz B

trzeba macierz A przemnożyć przez macierz B

Copyright by Wojdas

Copyright by Wojdas

®

®