Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
WITAJ !!!!!!!!!
JESTEM SZALONYM NAUKOWCEM.
PO OSTATNICH ODKRYCIACH Z
CHEMII I FIZYKI ZOSTAŁO PO MNIE
TYLKO TYLE:
ALE NIE MARTW SIĘ!!! Matematyka nie
jest taka groźna, więc nic nie
ryzykujesz (oprócz wiedzy) gdy
pouczysz się ze mną o funkcjach

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
FUNKCJA TO BARDZO WAŻNE POJĘCIE W
MATEMATYCE DLATEGO KONIECZNE JEST, ABYŚ
DOBRZE JE POZNAŁ I ZROZUMIAŁ. WIADOMOŚCI
O FUNKCJI MOŻESZ UZYSKAĆ NA PRZYKŁAD
TAK
LUB
TAK
•
JEDNAK ZAMIAST UCZENIA SIĘ KSIĄŻKI NA PAMIĘĆ
CZY PRACOWITEGO WBIJANIA WIEDZY MŁOTKIEM
DO GŁOWY PROPONUJĘ CI ZABAWĘ I NAUKĘ
Z KOMPUTEREM

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
Zastanów się teraz co już wiesz o funkcji i wybierz jedną z
możliwości:
Jeżeli funkcje stanowią
dla ciebie zaklęty i
tajemniczy świat kliknij
na ufoludka.
Jeżeli w krainie funkcji
czujesz się jak jak ryba
w wodzie i chcesz tylko
uzupełnić oraz
sprawdzić swoje
wiadomości kliknij na
rybkę.

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
NIC NIE
WYBRAŁEŚ !!!!!!
WRÓĆ

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
Matematyka to nie tylko obliczenia, rysowanie figur,
wyznaczanie pól i objętości. Matematyka to potężne
narzędzie, którym ludzie posługują się opisując świat i
rządzące nim zależności...Opis matematyczny używa
wielu pojęć, niektóre są dość trudne i rzadko
używane, bez innych nie można wyobrazić sobie
jakiejkolwiek matematyzacji. Takim ważnym pojęciem
jest
przyporządkowanie
. Typowe przykłady
przyporządkowania to:
1. Każdemu prostokątowi przyporządkowujemy jego pole
2. Każdy uczeń w danej klasie ma swój numer w
dzienniku.
Zauważ, że nie istnieje prostokąt, który nie ma pola.
Nie zdarzy się również prostokąt, który będzie miał
dwa różne pola. Również uczeń może mieć w danej
klasie tylko jeden numer w dzienniku i na pewno w
waszej klasie nie ma ucznia bez przyporządkowanego
mu numeru. Takie przyporządkowania to właśnie
funkcje. Sądzę, że przyszedł czas na poznanie definicji
funkcji.

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
DEFINICJA FUNKCJI
Jeśli dane są dwa zbiory X i Y i jeśli
każdemu
elementowi zbioru X zostanie
przyporządkowany
dokładnie jeden
element
ze zbioru Y, to takie
przyporządkowanie nazywamy funkcją
określoną na zbiorze X o wartościach w
zbiorze Y.
Zbiór X nazywamy
dziedziną
funkcji, jego elementy to
argumenty
funkcji. Zbiór Y to zbiór
wartości
funkcji, jego
elementy to wartości funkcji.

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
Zastanówmy się teraz nad przykładami
przyporządkowań, które są funkcjami:
każdemu dziecku przyporządkowujemy jego mamę –
dziedziną tej funkcji jest zbiór dzieci, zbiorem wartości są mamy,
natomiast przyporządkowanie odwrotne tzn mamie – dziecko, nie
jest funkcją bo są mamy, które mają więcej niż jedno dziecko.
słowu w języku polskim – literę, która znajduje się na końcu
–
dziedziną są słowa, zbiorem wartości są litery
każdemu uczniowi twojej klasy – liczbę jego rodzeństwa
(nawet gdy ktoś jest jedynakiem to ma przyporządkowaną
liczbę 0)
dziedziną jest zbiór uczniów a zbiorem wartości jest zbiór
liczb, określających ilość rodzeństwa

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
FUNKCJĘ OKREŚLAMY PODAJĄC JEJ
DZIEDZINĘ I SPOSÓB W JAKI
ARGUMENTOM
PRZYPORZĄDKOWYWANE SĄ JEJ
WARTOŚCI. MOŻEMY TO ZROBIĆ PRZY
POMOCY:
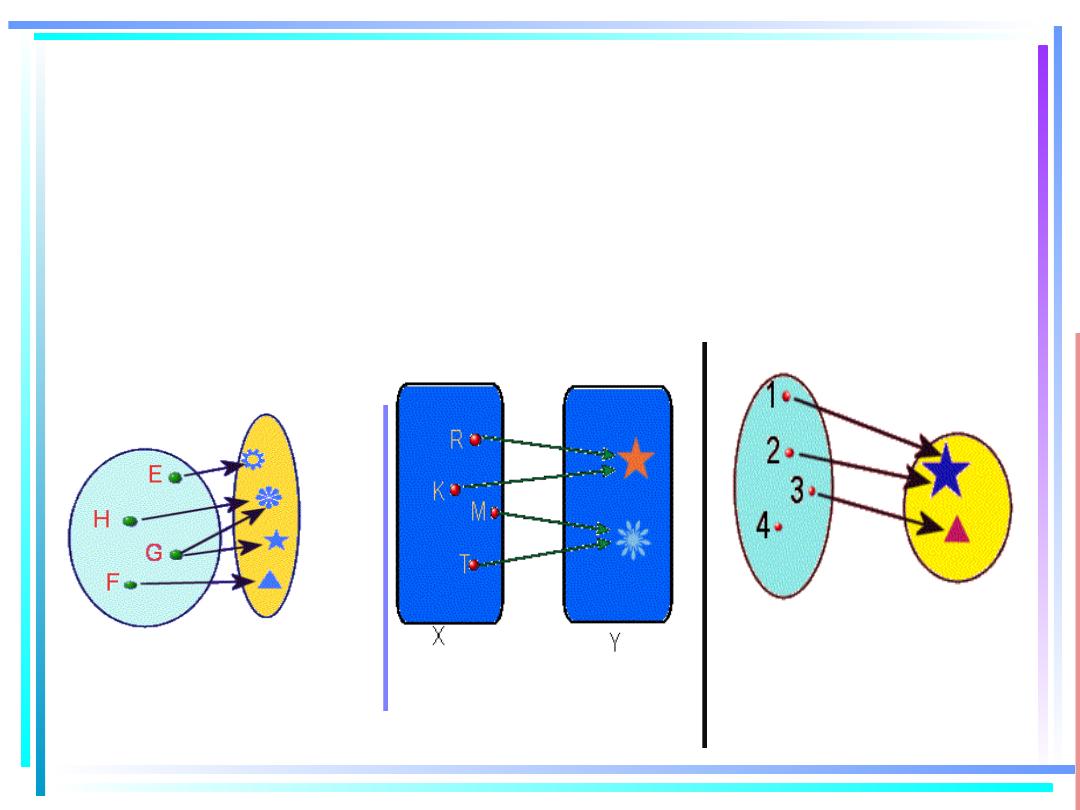
Opisu słownego
Grafu
Tabelki
Wykresu
Wzoru

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
ZOBACZ, JEDNĄ I TĘ SAMĄ FUNKCJĘ PRZEDSTAWIMY TERAZ
NA PIĘĆ RÓŻNYCH SPOSOBÓW
OPIS SŁOWNY
KAŻDEJ LICZBIE CAŁKOWITEJ WIĘKSZEJ
OD -3 ORAZ MNIEJSZEJ OD 7,
PRZYPORZĄDKOWUJEMY LICZBĘ O DWA
MNIEJSZĄ
WZÓR FUNKCJI
y = x – 2, dla
7
x
3
i
C
x
Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
TO JEST TABELKA NASZEJ
FUNKCJI
x -2 -1 0 1 2 3 4 5 6
y -4 -3 -2 -1 0 1 2 3 4
Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
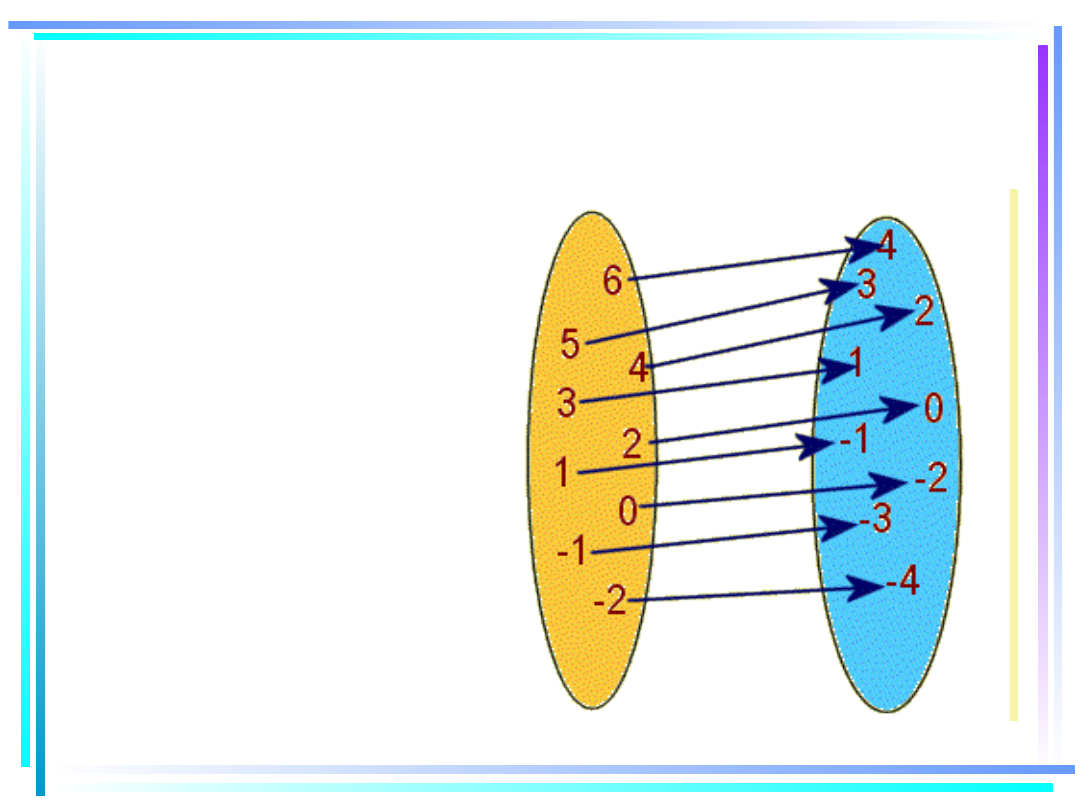
GRAF FUNKCJI
Argumentami tej
funkcji są liczby:
-2, -1, 0, 1, 2, 3,
4, 5, 6.
Wartościami tej
funkcji są liczby:
-4, -3, -2, -1, 0, 1,
2, 3, 4,
Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
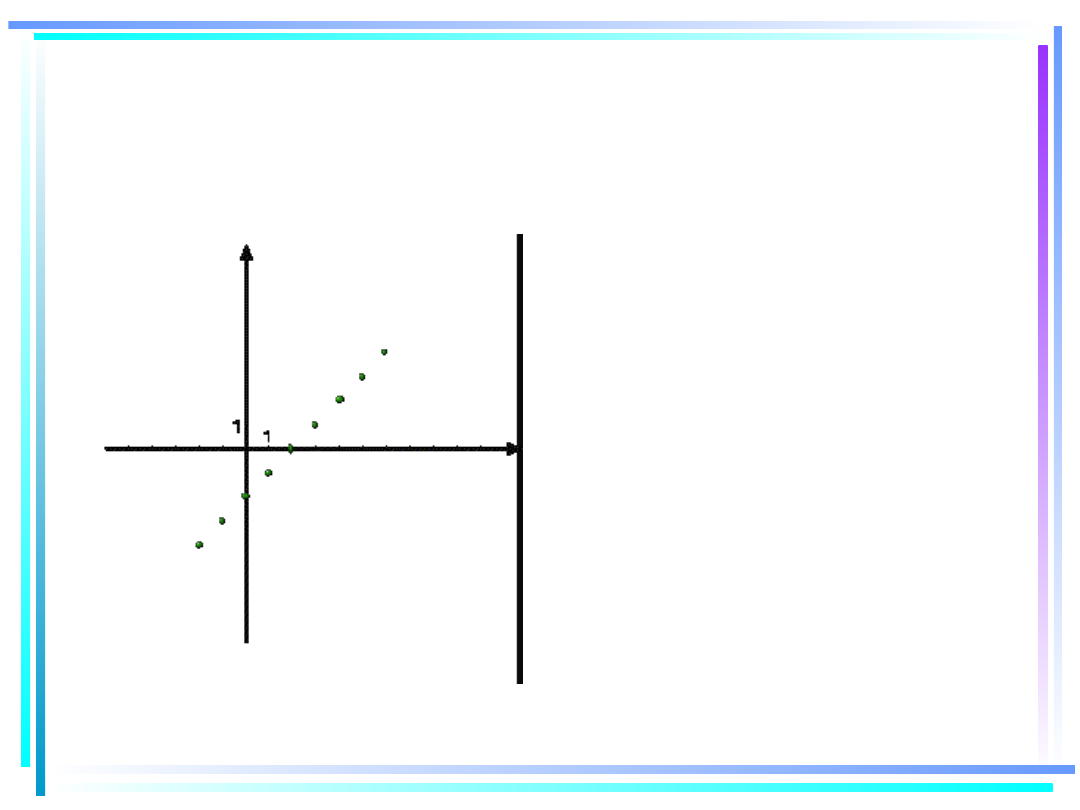
TO JEST WYKRES NASZEJ
FUNKCJI
Argumentami tej
funkcji są liczby:
-2, -1, 0, 1, 2, 3,
4, 5, 6.
Wartościami tej
funkcji są liczby:
-4, -3, -2, -1, 0, 1,
2, 3, 4,
y
x

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
Bardzo ważna jest
umiejętność odczytywania
wartości funkcji dla danego
jej argumentu x, oraz
argumentów, dla których
funkcja przyjmuje określoną
wartość.
Uważnie przeczytaj poniższe
przykłady!!!!!!!!!!!

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
Funkcja dana wzorem np.
y=x+5
•
Aby policzyć wartość tej funkcji dla argumentu x=2, wstawiamy liczbę 2 do wzoru funkcji i
obliczamy y: y=2+5
y=7
•
Obliczając wartość argumentu dla którego funkcja będzie miała wartość 10, wstawiamy w miejsce y
liczbę 10 i obliczamy x: 10=x+5
x=5
Zapis f(2)=7 oznacza, że wartość funkcji dla argumentu 2 wynosi 7
Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
Dla funkcji
określonych grafem
znajdujemy w
odpowiednim
zbiorze interesujący
nas argument i
odczytujemy wartość
odpowiadającą temu
argumentowi np.
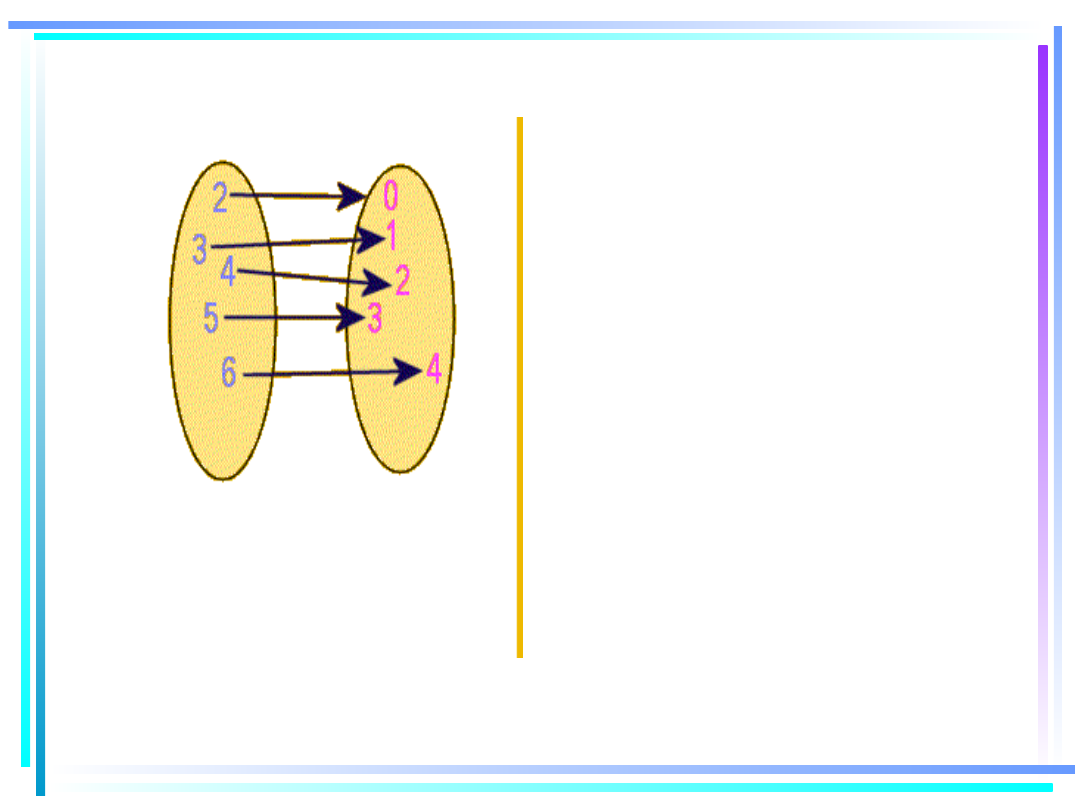
f(2)=0.
TO JEST
ZBIÓR
ZWIERAJĄC
Y
ARGUMENT
Y FUNKCJI
TO JEST ZBIÓR
ZAWIERAJĄCY
WARTOŚCI
FUNKCJI
Funkcja dana grafem
Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
Dla
funkcji
określonych
tabelką
znajdujemy w
odpowiedniej kolumnie
interesujący nas
argument i w drugim
wierszu odczytujemy
wartość odpowiadającą
temu argumentowi np.
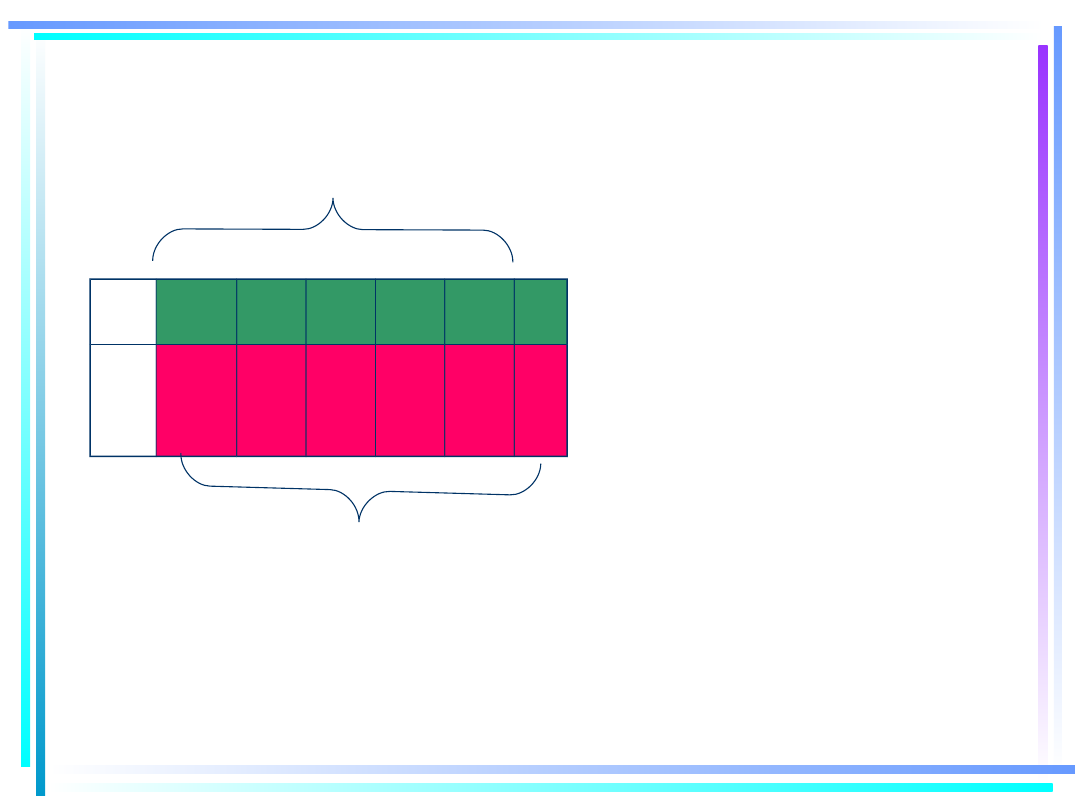
f(2)=5.
•
dla podanej wartości
funkcji np. y=6
szukamy w drugi
wierszu liczby 6 i
odczytujemy
odpowiadający jej
argument
x 1 2 3 4 5 6
y 3 5 1
0
6 2 1
TO SĄ ARGUMENTY
FUNKCJI
TO SĄ WARTOŚCI
FUNKCJI
Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
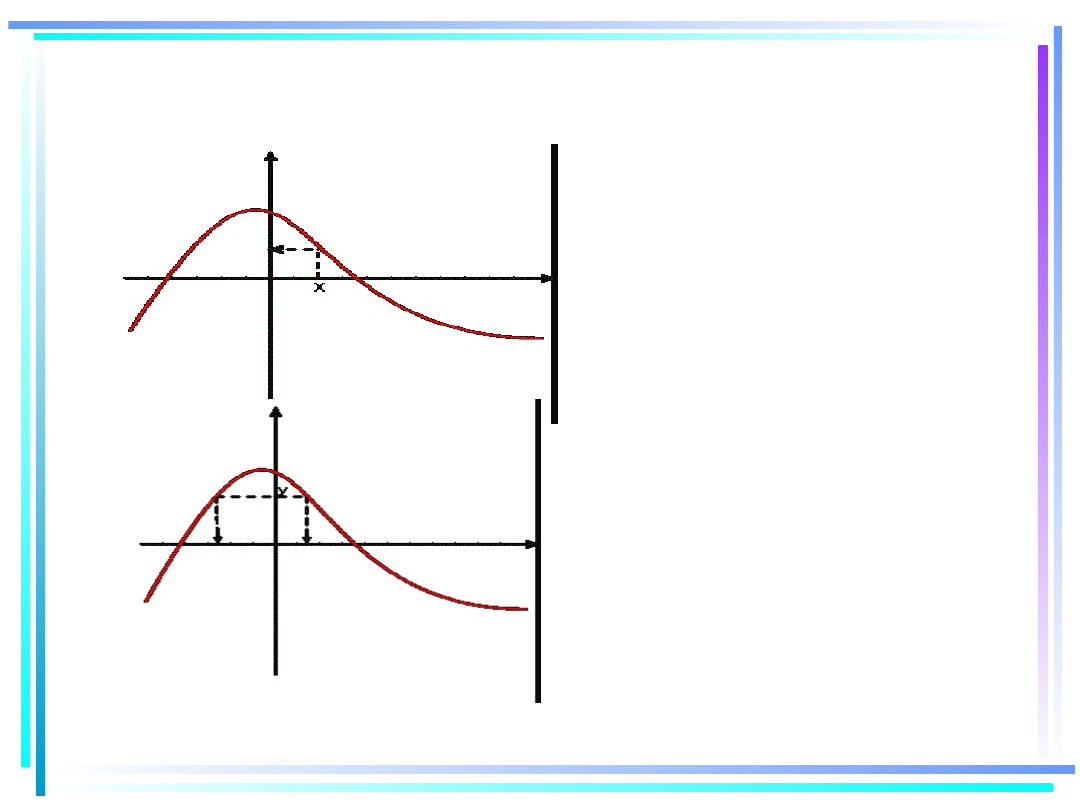
Funkcja dana wykresem
•
Tak znajdujemy
wartość funkcji dla
danego argumentu
x.
•
A tak argumenty, dla
których funkcja
przyjmuje daną
wartość y.

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
OCH !!!!!
WIDZĘ, ŻE NIE
MOŻESZ SIĘ
DOCZEKAĆ,
ABY
SPRAWDZIĆ
SWOJE
UMIEJĘTNOŚCI !

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
ZACZYNAMY!!!!!!!!!!!
•
W każdym zadaniu masz do
wyboru dwie możliwości, wybierz
tę, którą uważasz za poprawną.
Zastanów się dobrze!!!!!
•
Chcesz przejść do następnego
zadania? Kliknij „dalej”.
Życzę powodzenia!!!

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
Czy poniższe przyporządkowania
są funkcjami?
Liczbie- jej dwukrotność
Kontynentom - państwa
Liczbom - ich dzielniki
Rzekom - ich długość w km
Wielokątom – liczby określające
ich obwód
Tak
Państwom - ich stolice
Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
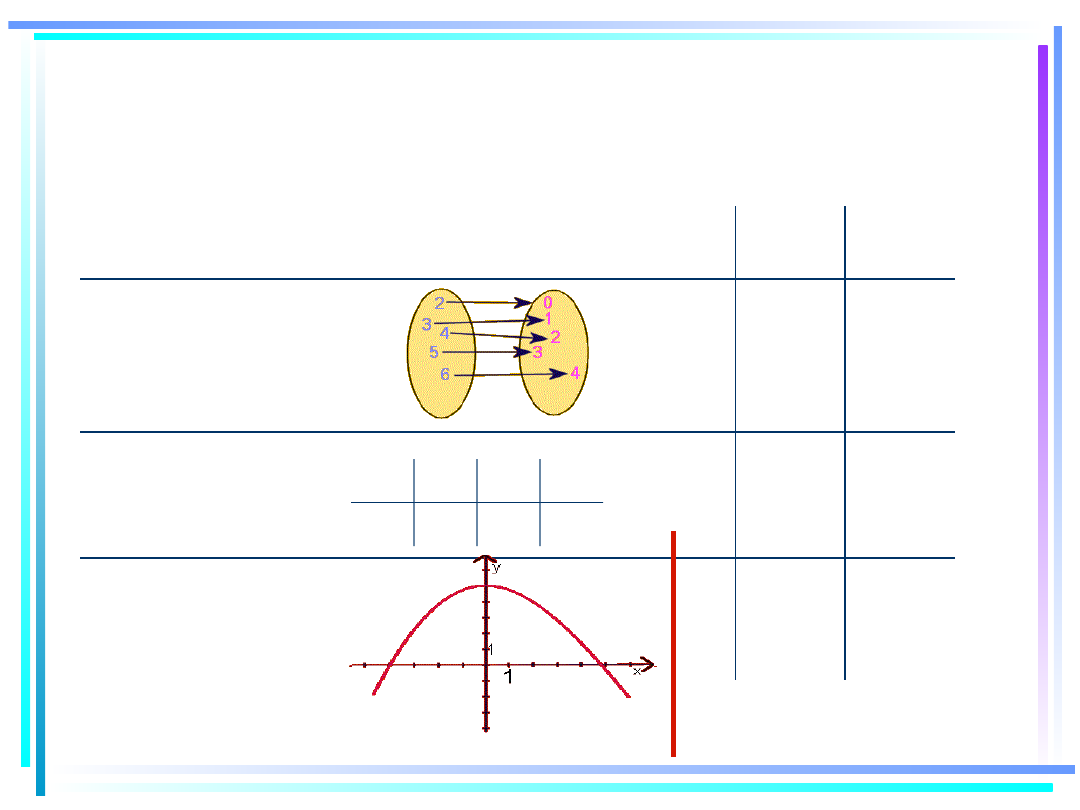
Zaznacz jakie wartości przyjmują poniższe
funkcje dla argumentu 2 ? Funkcja dana
jest:
wykresem
tabelką
4
5
0
grafem
6
wzorem y=4+x
x
1
3
2
y
6
7
5
Dalej

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
Teraz się pożegnamy !!!!!!!!!!!!
Dziękuję za
współpracę !
!!!

Monika Korzeniowska
INFORMATYKA NOWY SĄ
CZ
KONIEC
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 36
- Slide 37
Wyszukiwarka
Podobne podstrony:
Rozwój multimediów zaczyna zmieniać sposób funkcjonowania tradycyjnych środków przekazu, media w edu
BANK CENTRALNY I JEGO FUNKCJE
Zaburzenia funkcji zwieraczy
Genetyka regulacja funkcji genow
BYT 2005 Pomiar funkcjonalnosci oprogramowania
Diagnoza Funkcjonalna
Insulinoterapia funkcjonalna
Postać kanoniczna funkcji kwadratowej
Wpływ choroby na funkcjonowanie rodziny
LAB PROCEDURY I FUNKCJE
STRUKTURA I FUNKCJONOWANIE GN
Maszynoznawstwo prezentacja multimedialna
układ pokarmowy budowa i funkcja
15 Fizjologiczne funkcje nerek
więcej podobnych podstron