ZARZĄDZANIE RYZYKIEM

STÓP PROCENTOWYCH

Stopa procentowa

• Koszt pożyczenia pieniędzy

• Wartość pieniądza w czasie wyrażona

w procentach w stosunku rocznym

Stopa procentowa na rynku

międzybankowym wyrażona jest w

postaci

• Kursu kupna – gotowość przyjęcia
depozytów

• Kursu sprzedaży – gotowość
udzielania kredytów

• K.S. > K.K. dla stopy procentowej
• K.S. < K.K. dla stopy dyskontowej

K.S. – K.K. = marża bankowa

Stopy na rynku

międzybankowym

• Kwotowanie - określanie stóp na

rynku międzybankowym

• BOR (Banking Offered Rate) – kredyt
• BID (Banking Interesed Rate) –

depozyt

• WIBOR, WIBID – w Warszawie
• LIBOR, LIBID – w Londynie
• EURIBOR, EURIBID – rynek europejski

Stopy międzybankowe ustalane są

w trzech obszarach

• Przedmiotowym – depozyty i kredyty
• Terminowym – O/N, T/N, 1W – 1Y
• Walutowym:
- Wibor, Wibid – w złotych
- Euribor, Euribid – w euro
- Libor, Libid – w: funtach, dolarach
amer., frankach szw.,
euro, jenach

Pojęcie ryzyka stopy

procentowej



Niebezpieczeństwo negatywnego
wpływu zmiany rynkowej stopy
procentowej (RSP) na sytuację
finansową banku



Może dotyczyć:

–

pozycji bilansowych

–

pozycji pozabilansowych

Rodzaje ryzyka stopy

procentowej

• Stałej stopy procentowej

• Zmiennej stopy procentowej

DYNAMIKA MARŻY

ODSETKOWEJ

• Stała stopa procentowa – stawka procentowa, która nie ulega zmianie aż

do nadejścia terminu płatności

• Zmienna stopa procentowa – stawka procentowa, która przed upływem

terminu płatności ulega zmianie wraz ze zmianą:

warunków rynkowych (automatyczne przeszacowanie wynikające ze
wzrostu inflacji)

stóp procentowych banku centralnego

Ryzyko stopy zmiennej

• Ryzyko utraty klientów (wzrost ceny

kredytów, zbyt niskie oprocentowanie
depozytów)

• Konieczność spisania na straty części

należności w wyniku utraty przez klientów
zdolności do ich spłaty

• Zagrożenie niewielkie
• Zmiana stóp przez bank centralny

wykorzystywana do zwiększania marży

Ryzyko stopy stałej

• Ryzyko niedopasowania terminów

przeszacowania stóp procentowych

• Tworzy się luka czasowa

• Ryzyko zmniejszenia różnicy między

odsetkami otrzymanymi a zapłaconymi

Czynniki ryzyka zmiennej stopy

procentowej

• Struktura aktywów

• Struktura pasywów

• Różnica między oprocentowaniem aktywów i

pasywów

• Wielkość i rodzaj luki

• Kierunek i poziom zmiany stóp procentowych

banku centralnego

Zarządzanie ryzykiem stopy

procentowej

• Analiza luki – metoda GAP

• Analiza czasu trwania - duration

Sterowanie luką obejmuje

koordynowanie wszystkich kategorii

bilansowych w taki sposób, by

maksymalnie zwiększyć wartość

majątku akcjonariuszy.

W praktyce sterowanie luką

koncentruje się przede wszystkim na

zależności między aktywami o

zmiennych stopach procentowych i

pasywami o zmiennych stopach

procentowych.

pozycja luki zerowej

Aktywa o

zmiennych stopach

procentowych

Zobowiązania o

zmiennych stopach

procentowych

Aktywa o stałych

stopach

procentowych

Zobowiązania o

stałych stopach

procentowych

pozycja luki dodatniej

Aktywa o

zmiennych

stopach

procentowych

Aktywa o

stałych stopach

procentowych

Zobowiązania o

zmiennych

stopach

procentowych

Zobowiązania o

stałych stopach

procentowych

pozycja luki ujemnej

Aktywa o

zmiennych

stopach

procentowych

Aktywa o

stałych

stopach

procentowych

Zobowiązania

o zmiennych

stopach

procentowych

Zobowiązania

o stałych

stopach

procentowych

Analiza luki

• Różnica między aktywami i

pasywami, których przeszacowanie
odbywa się w różnym terminie

• Luki czasowe powstają w sytuacji

niedopasowania tych terminów

Zarządzanie luką polega na:

• niedopuszczeniu do tego, aby różnica

między oprocentowaniem pasywów i
aktywów nie zmniejszyła się
nadmiernie

•
• wykorzystaniu sytuacji rynkowej tak,

aby luka była jak największa i w
odpowiednim kierunku

SYTUACJA 1

WSZYSTKIE PRODUKTY MAJĄ ZMIENNĄ STOPĘ PROCENTOWĄ

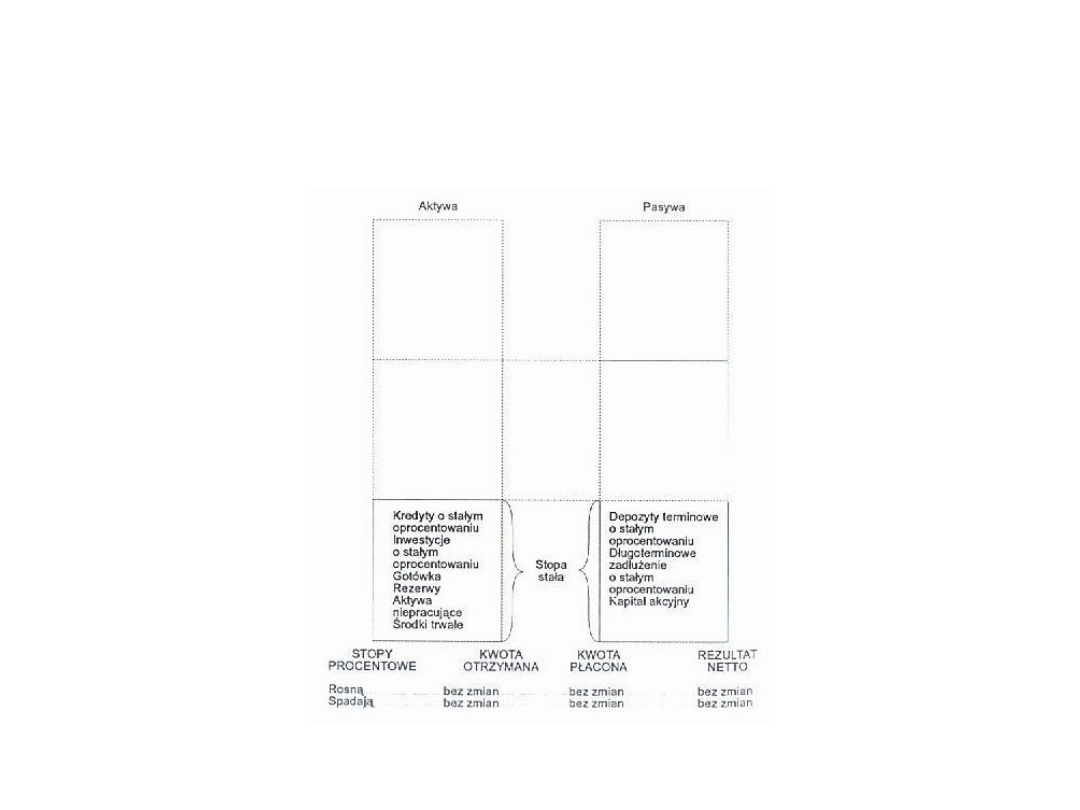
SYTUACJA 2

WSZYSTKIE PRODUKTY MAJĄ STAŁĄ STOPĘ PROCENTOWĄ

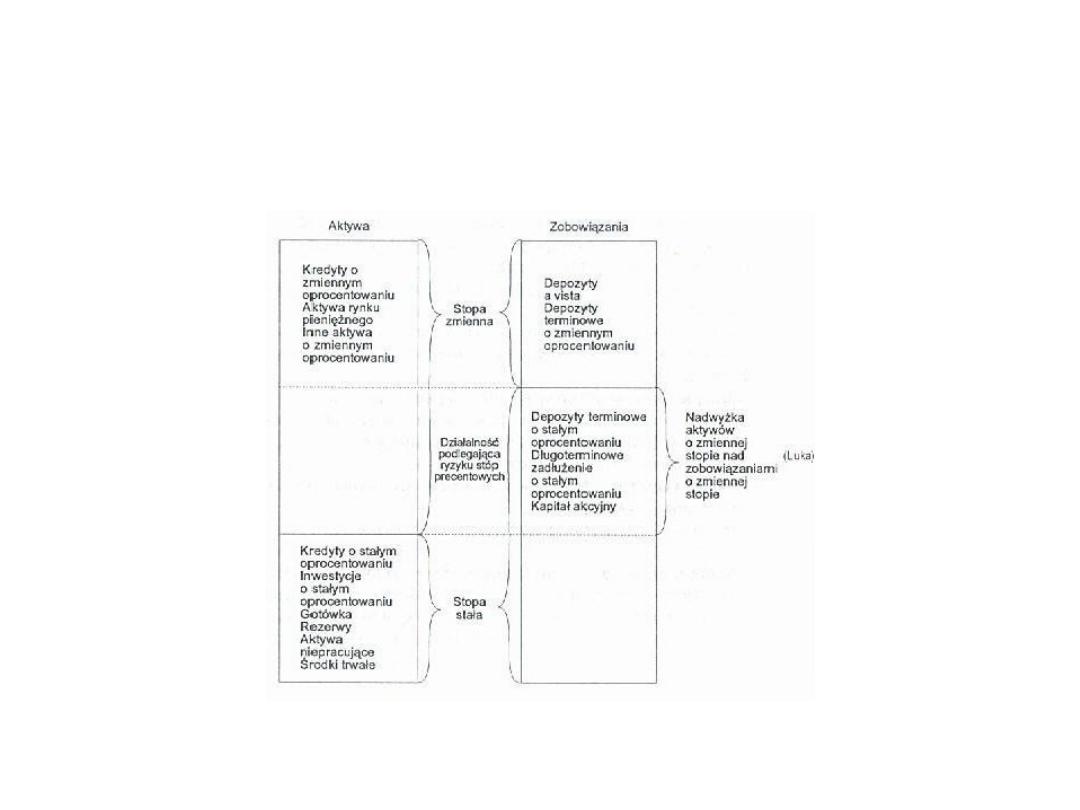
SYTUACJA 3

WIĘKSZOŚĆ AKTYWÓW MA STAŁE OPROCENTOWANIE,

A PASYWÓW ZMIENNE

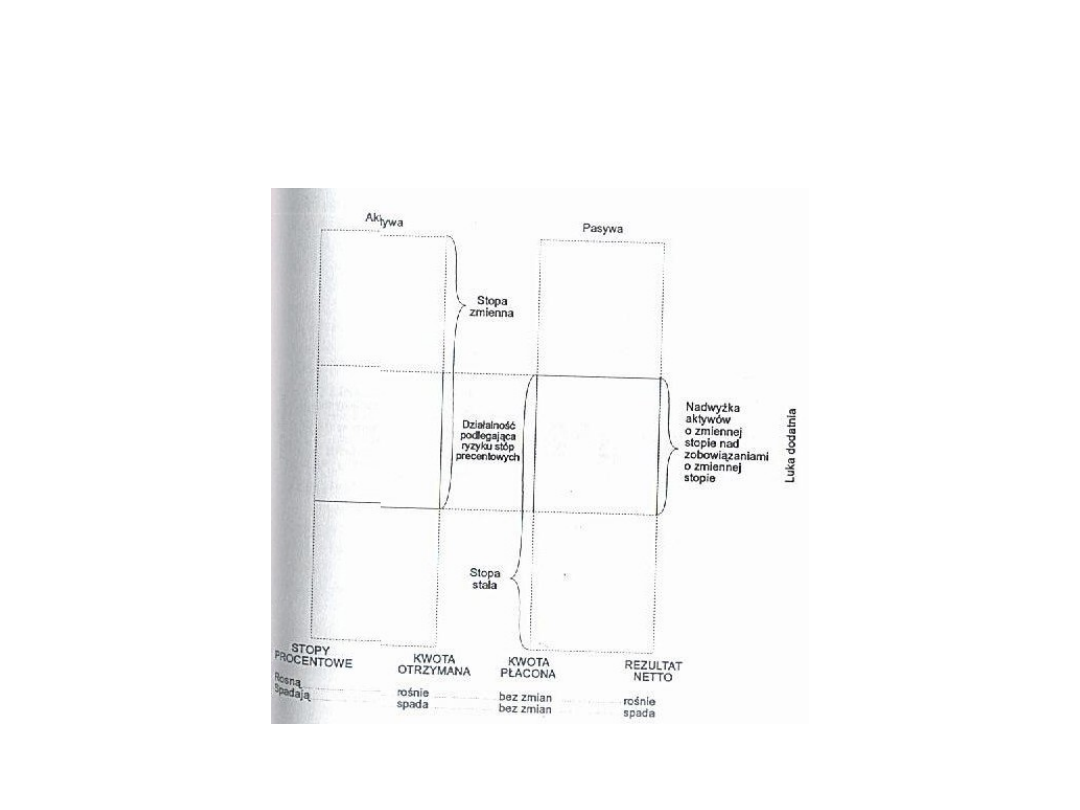
SYTUACJA 4

WIĘKSZOŚĆ AKTYWÓW MA ZMIENNE OPROCENTOWANIE,

A PASYWÓW STAŁE

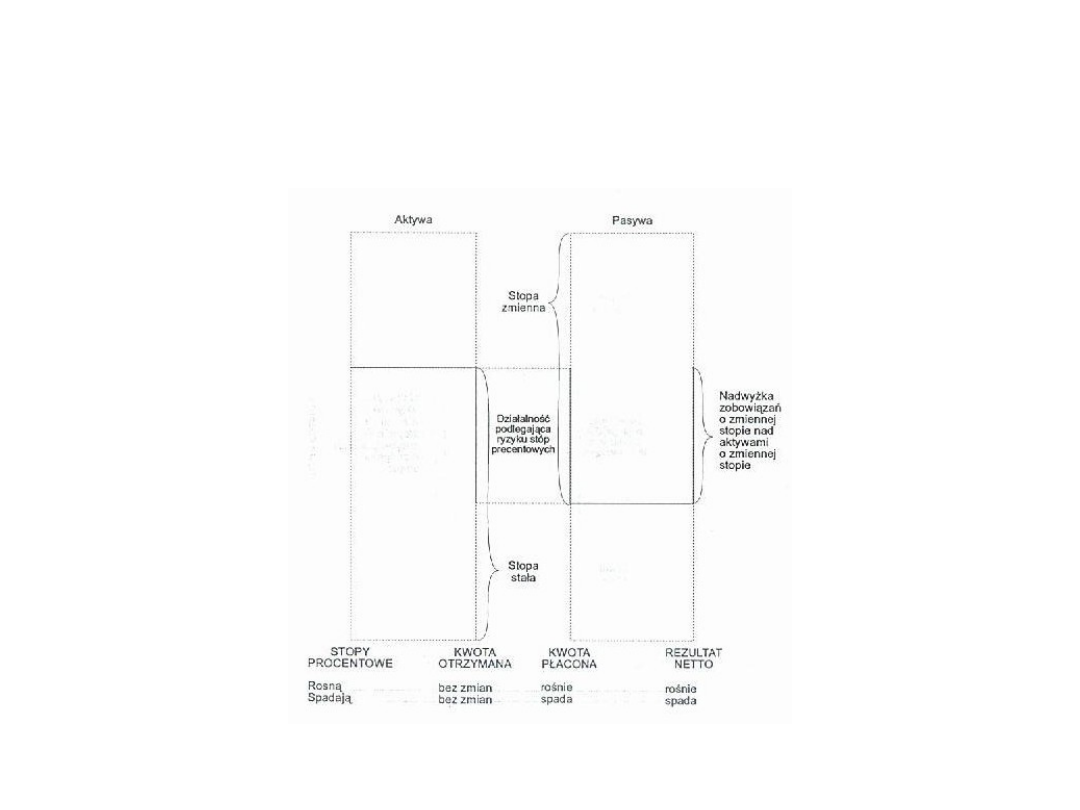
SYTUACJA 5

WIĘKSZOŚĆ AKTYWÓW MA STAŁE OPROCENTOWANIE,

A PASYWÓW ZMIENNE

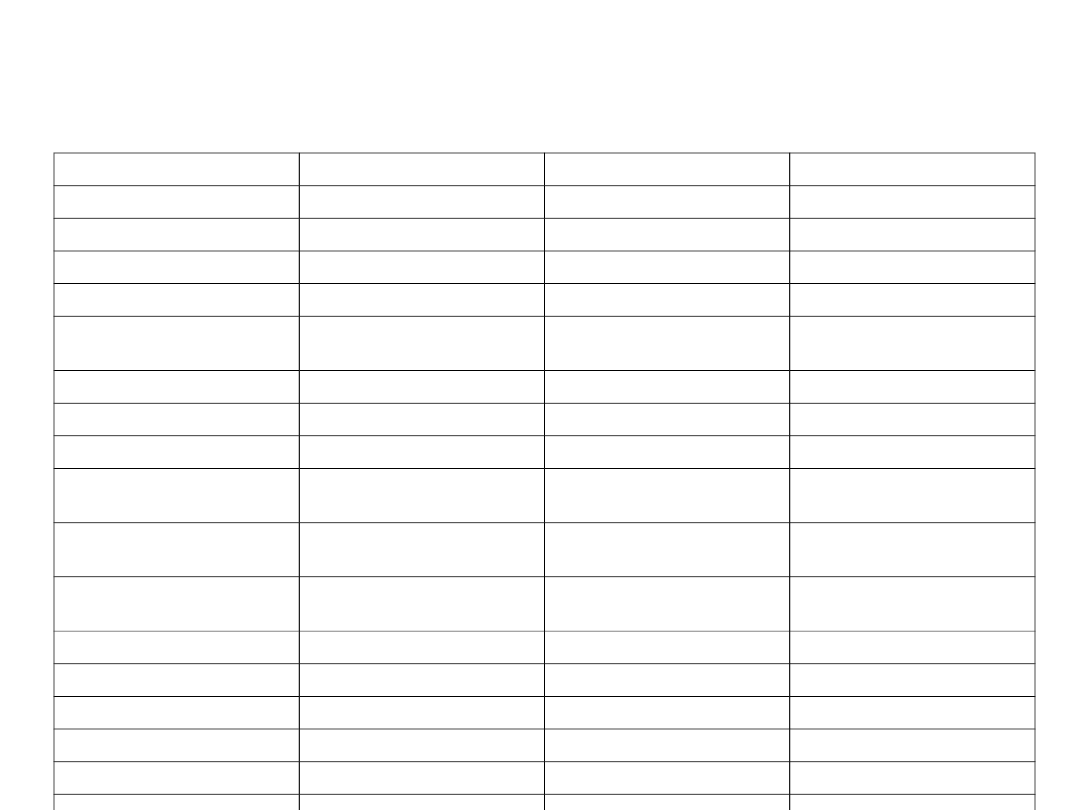
ANALIZA WRAŻLIWOŚCI OPROCENTOWANIA

BILANS – STRUKTURA PODSTAWOWA

Stopa zmienna

Stopa stała

Łączna

Aktywa dochodowe

50.000.000 zł

100.000.000 zł

Zmiana w aktywach

Aktywa łącznie

50.000.000 zł

100.000.000 zł

Zobowiązania

50.000.000 zł

100.000.000 zł

Zmiana w

zobowiązaniach

Zobowiązania łącznie

50.000.000 zł

100.000.000 zł

Luka

Stopa na aktywach

12%

10%

Stopa na

zobowiązaniach

Stopa na nowych

aktywach

Stopa na nowych

zobowiązaniach

Dochody odsetkowe

6.000.000 zł

5.000.000 zł

11.000.000 zł

Koszty odsetkowe

4.500.000 zł

3.500.000 zł

8.000.000 zł

Zysk odsetkowy netto

1.500.000 zł

3.000.000 zł

Stawka otrzymana

12%

10%

11%

Stawka płacona

Rozpiętość procentowa

Różne strategie zarządzania

aktywami i zobowiązaniami

Faza niskiej stopy

• Zweryfikować linie kredytowe
• Wydłużyć terminy płatności zasobów

finansowych

• Skrócić terminy płatności inwestycji
• Zwiększyć zadłużenie długoterminowe
• Ograniczyć kredyty o stałej stopie

procentowej

• Zweryfikować politykę kalkulacji cen
• Sprzedać inwestycje

Faza przejściowa - rosnąca

• Skracać terminy płatności zasobów finansowych
• Wydłużać terminy płatności inwestycji
• Rozszerzać kredyty o stałych stopach

procentowych

• Pozyskiwać inwestycje

Faza wysokiej stopy

• Uzupełnić linie kredytowe
• Skrócić terminy płatności zasobów finansowych
• Wydłużyć terminy płatności inwestycji
• Podwyższyć jakość inwestycji
• Rozszerzyć kredyty o stałej stopie procentowej
• Zaplanować sprzedaż inwestycji
• Pozyskać inwestycje

Faza przejściowa -

spadająca

• Wydłużać terminy płatności zasobów finansowych
• Skracać terminy płatności inwestycji
• Ograniczać kredyty o stałych stopach

procentowych

• Sprzedawać inwestycje

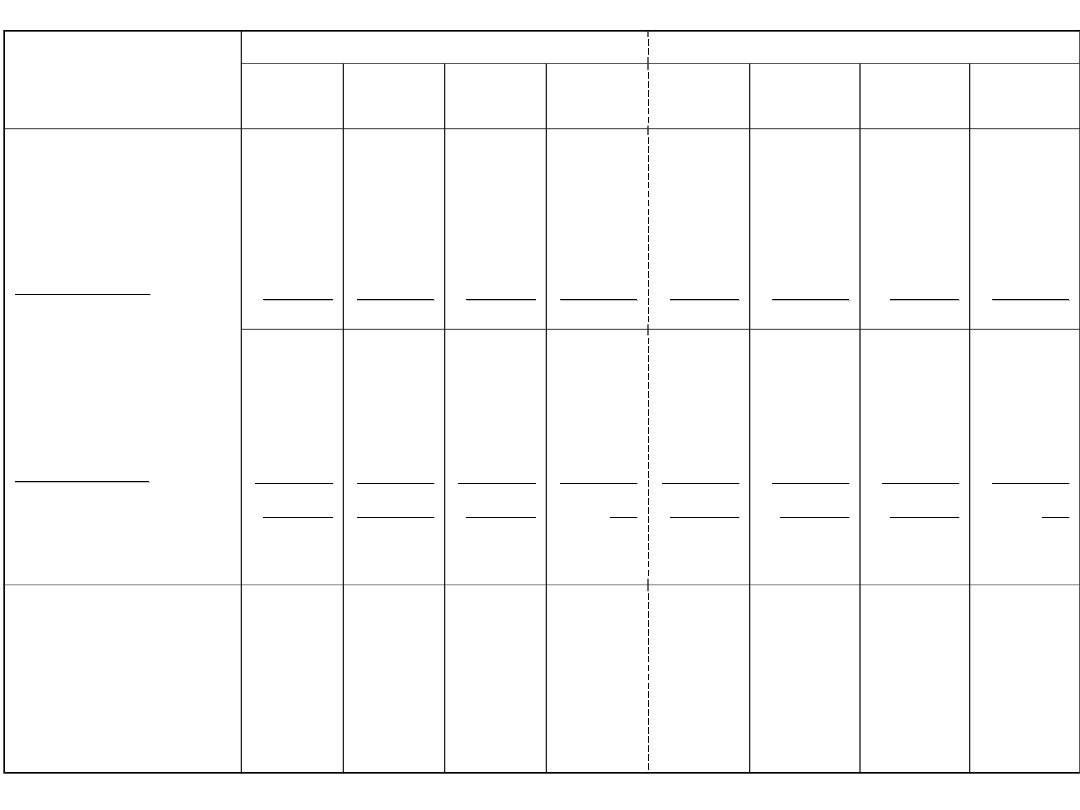
Źródła pochodzenia i

sposoby wykorzystania

zasobów finansowych

Rok 2005

Rok 2006

Stopa

zmienna

Stopa

stała

Stopa

zerowa

łącznie

Stopa

zmienna

Stopa

stała

Stopa

zerowa

łącznie

Sposoby wykorzystania

Kredyty

Portfel papierów

wartościowych

Inwestycje krótkoterminowe

Gotówka i inne aktywa

AKTYWA RAZEM

Żródła pochodzenia

Środki nie oprocentowane

Depozyty terminowe

Środki pożyczone

Inne zobowiązania i kapitał

akcyjny

PASYWA RAZEM

Luka zasobów finansowych

50.876.200

15.241.200

7.394.000

0.00

73.511.400

174.882.400

53.508.800

0,00

228.391.200

0.00

61.120.400

225.758.600

68.750.000

7.394.000

61.120.400

363.023.000

55.015.600

19.189.000

4.785.400

0.00

78.990.000

154.838.000

49.093.200

0.00

203.931.200

0.00

46.560.200

46.560.000

209.853.600

68.282.600

4.785.400

46.560.200

329.481.400

0.00

112.884.800

11.469.400

0.00

125.354.200

50.842.800

0.00

108.901.000

0.00

74.816.000

116.382.600

112.008.600

77.662.000

0.00

44.624.200

122.286.200

61.165.800

77.662.000

221.785.800

11.469.400

52.105.800

363.023.000

0.00

102.711.800

11.900.000

0.00

114.611.800

35.621.800

0.00

105.998.000

0.00

7.428.800

113.416.800

90.514.400

68.169.800

0.00

33.283.000

101.452.800

54.892.000

68.169.800

208.699.800

11.900.000

40.711.800

329.481.400

0.00

Współczynnik luki zasobów

Aktywa o zmiennych

stopach do aktywów

dochodowych

Zasoby finansowe o

zmiennych stopach do

aktywów dochodowych

0.59

24.35%

41.19%

0.68

27.92%

40.51%

Współczynnik aktywa o zmiennych stopach

350.000.000

luki zasobów = = =

0.7

finansowych zobowiązania o zmiennych stopach

500.000.000

Aktywa o zmiennych stopach procentowych

Zobowiązania o zmiennych stopach procentowych

Krótkoterminowe

papiery wartościowe 150.000.000

Rachunki

oszczędnościowe 400.000.000

Kredyty

o zmiennych stopach procentowych 200.000.000

Pożyczki

krótkoterminowe 100.000.000

Łącznie 350.000.000

Łącznie 500.000.000

Luka zasobów

aktywa o zobowiązania

finansowych w = zmiennych - o zmiennych =

350.000.000 – 500.000.000 = -150.000.000

wymiarze łącznym stopach stopach

Elastyczność

oprocentowania

Metoda elastyczności stopy procentowej, w przeciwieństwie do

metody gap, pozwala na oszacowanie ryzyka stopy
procentowej, związanego z pozycjami, których
dochodowość (koszt) związana jest ze zmiennymi stopami
procentowymi.

Elastyczność dopasowania się stóp procentowych aktywów

oraz pasywów do zmian rynkowej stopy procentowej
definiowana jest jako iloraz procentowej zmiany stopy
procentowej danej pozycji aktywów lub pasywów do zmiany
rynkowej stopy procentowej

Wrażliwość na zmiany stóp

procentowych

• Stopa procentowa aktywów i

pasywów ma tę samą elastyczność

• Stopa procentowa aktywów reaguje

silniej niż stopa pasywów

• Stopa procentowa pasywów reaguje

silniej niż stopa aktywów

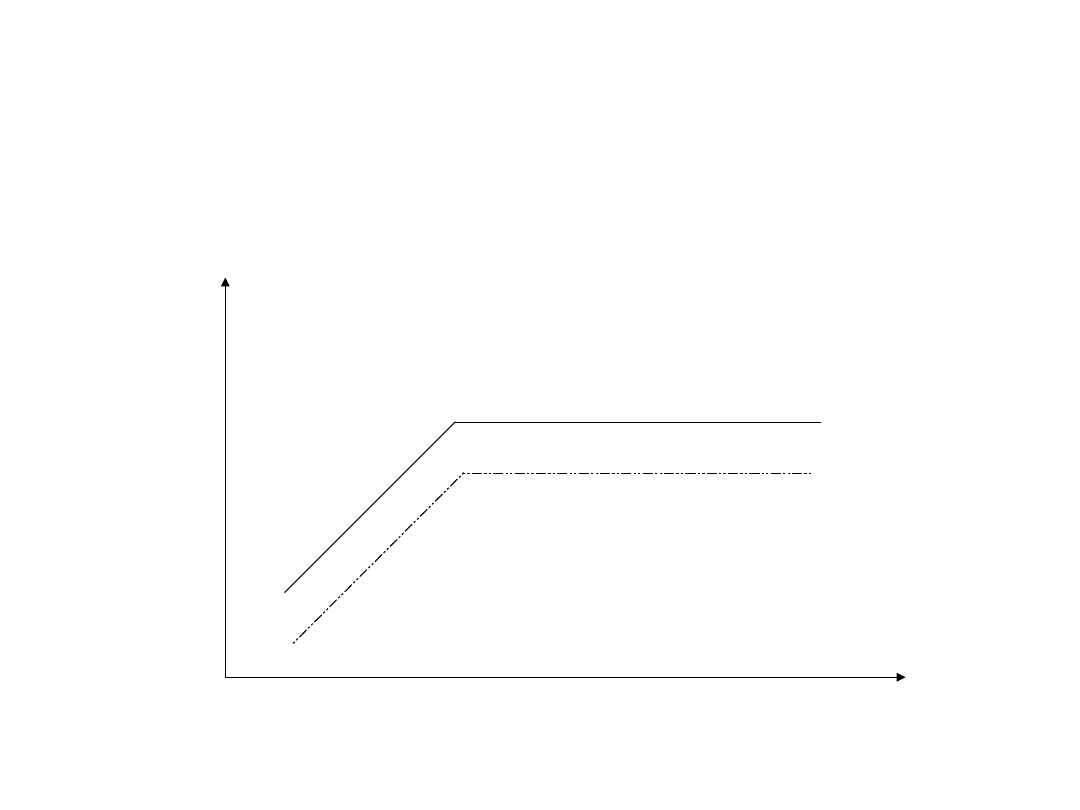
Elastyczność aktywów = elastyczność pasywów

oprocentowanie
Aktywów/pasywów

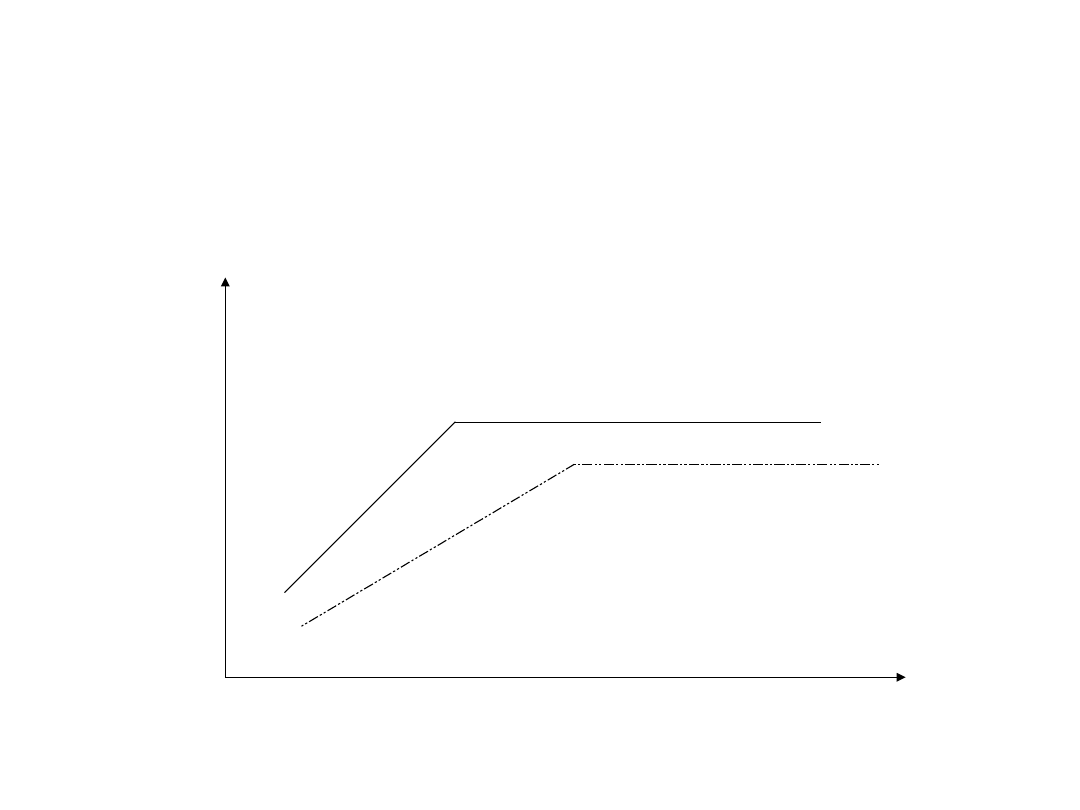
Elastyczność aktywów > elastyczność pasywów

oprocentowanie
Aktywów/pasywów

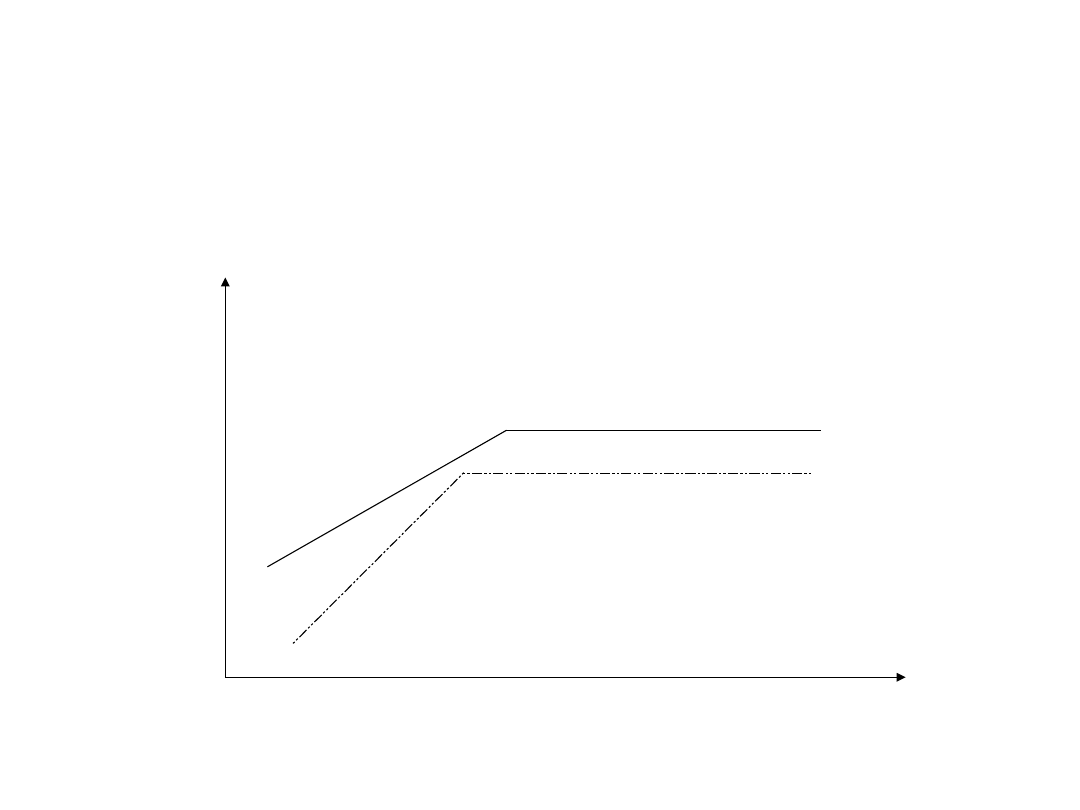
Elastyczność aktywów < elastyczność pasywów

oprocentowanie
Aktywów/pasywów

Obligacja z 5 procentowym kuponem Obligacja z 10 procentowym kuponem

Bieżąca wartość przy bieżąca wartość przy

ROK strumień gotówki 9% 10% 11% strumień gotówki 9% 10% 11%

1 5 zł 5,585 4,545 4,505 10 zł 9,17 9,09 9,01

2 5 zł 4,21 4,135 4,06 10 zł 8,42 8,27 8,21

3 5 zł 3,86 3,755 3,655 10 zł 7,72 7,51 7,31

4 5 zł 3,54 3,415 3,295 10 zł 7,08 6,83 6, 59

5 105 zł 68,25 65,205 62,37 110 zł 71,5 68,3 65,34

skumulowana bieżąca 84,45 81,06 77,89 103,89 100 94,46

wartość lub cena

elastyczność oprocentowania

10 na 9% 10 na 11%

5% kupon - 0,42 - 0,39

10% kupon - 0,39 - 0,35

Analiza okresowa

Metoda duracji

Metoda duracji (czasu trwania) służy
analizie operacji długoterminowych.
Podstawowym założeniem jest to, że
wpływy z długoterminowych operacji
są reinwestowane, więc faktyczny
termin zapadalności instrumentu jest
krótszy niż nominalny.

• Przez durację rozumie się

średnioważony okres oczekiwania na
wpływy środków pieniężnych z
danego instrumentu finansowego.

• Durację oblicza się w oparciu o

wartość rynkową instrumentu.

• Wartość rynkowa instrumentu

finansowego to zdyskontowana suma
wszystkich przyszłych przepływów
środków pieniężnych z tego
instrumentu do terminu jego
zapadalności.

Przyszła wartość dla okresu t:

FV= PV x (1+r)

Teraźniejsza wartość:

PV = ∑FV / (1+r)

gdzie:

r – stopa dyskontowa

t - czas

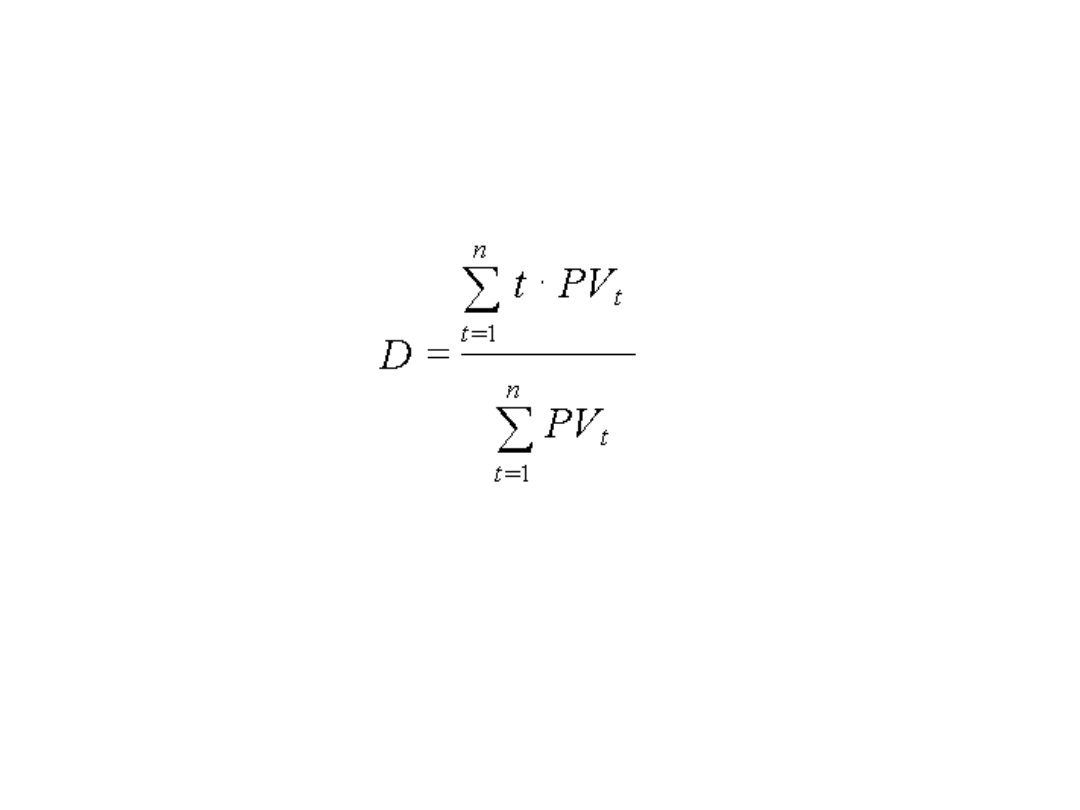
Duration to iloraz sumy wartości bieżących

ważonych czasem oraz sumy nieważonych
wartości bieżących.

gdzie:
n – liczba okresów do terminu

zapadalności

Przykład

Instrument finansowy na 100 zł, termin

3 lata, oprocentowanie 10%

Z wzoru na PV otrzymujemy 100 zł.
Natomiast duration wynosi 2,74.

Z powyższych obliczeń wynika, że czas

oczekiwania na wpływy z tego

instrumentu wynosi około 2,7 lat.

Wskaźnik duration jest tym niższy, im:

- wyższa jest nominalna stopa

procentowa,

- wyższa jest rentowność,
- wcześniej rozpoczynają się płatności.

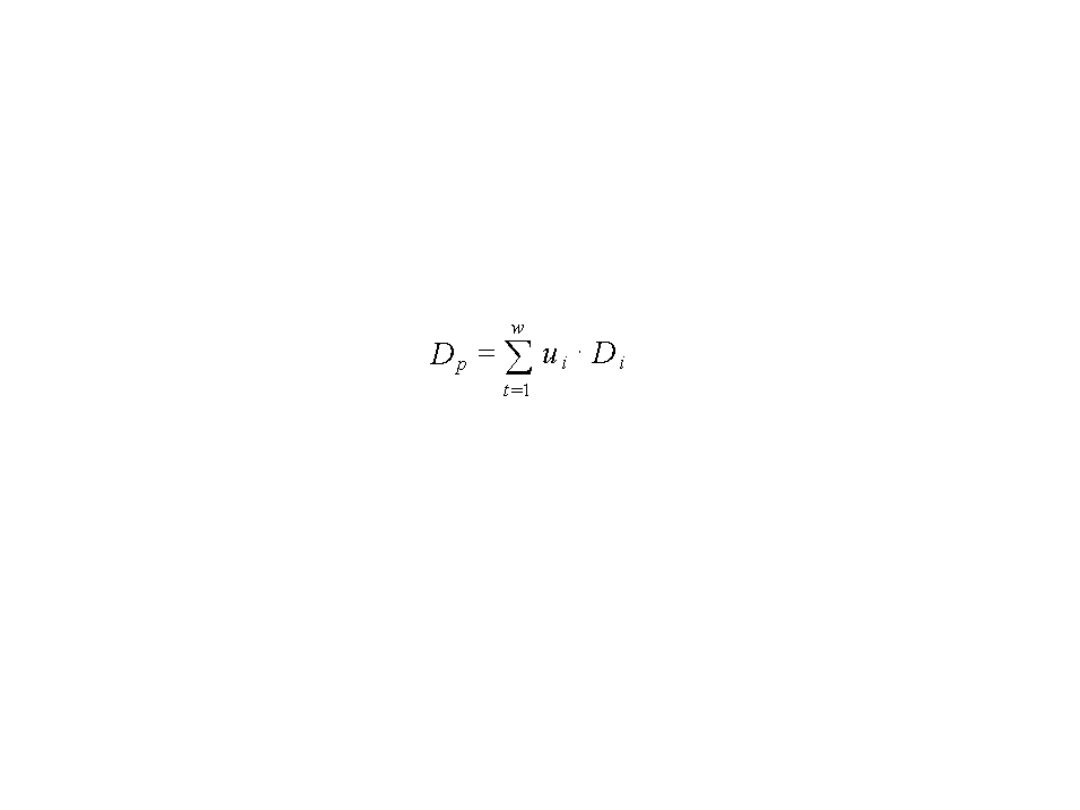
Duration dla portfela papierów

wartościowych oblicza się

następująco:

gdzie:
w – liczba papierów wartościowych w portfelu
u

– udział i-tego papieru w portfelu,

– wskaźnik duration dla i-tego papieru

– duration portfela

Duration wykorzystuje się również do

obliczenia wrażliwości instrumentu

finansowego (aktywów lub pasywów,

papierów wartościowych, portfeli) na

zmiany stopy procentowej:

Procentowa zmiana ceny instrumentu

finansowego = (-) duration x zmiana
rynkowej stopy procentowej

Analizę duration można przeprowadzić

dla aktywów i pasywów o stałej stopie

procentowej

ryzyko stopy procentowej = duration x

zmiany stopy procentowej

duration = aktywa x D

– pasywa x D

Zarządzanie luką okresu

Banki zarządzając luką okresu nie chcą

jej wyeliminować, tylko tak kreować,
aby przyniosła im zyski

Lukę okresu można wyrazić w

następujący sposób

Luka okresu = okres aktywów –

depozyty / aktywa razem x okres
depozytów

Bank kreuje

• ujemną lukę – w przypadku wzrostu

stóp procentowych

• dodatnią lukę – w przypadku spadku

stóp procentowych

Aby dokonać pomiaru i prawidłowo

zarządzać okresem aktywów i

zobowiązań bank zbiera informacje o:

• Terminach płatności
• Stopach procentowych
• Wcześniejszych płatnościach
• Możliwościach wcześniejszych wypłat
• Możliwościach opóźnień w spłacie

kredytu

Innym sposobem ochrony banku przed

ryzykiem stopy procentowej są

instrumenty pochodne, w

szczególności:

• Forward
• FRA

Forward

• Forward to porozumienie między

dwiema stronami, w którym jedna ze
stron zobowiązuje się kupić w
przyszłości aktywa o stałym
oprocentowaniu, a druga
zobowiązuje się je sprzedać.

• Cena jest ustalana między obiema

stronami kontraktu.

FRA

• FRA jest bardzo podobny do Forward,

z wyjątkiem sposobu rozliczania.

• Forward ma bilansowy charakter

natomiast FRA jest rozliczany jako
różnica pomiędzy ceną kontraktu FRA
a bieżącą rynkową stopą procentową

Document Outline

Slide 1
Slide 2
Slide 3
Slide 4
Slide 5
Slide 6
Slide 7
Slide 8
Slide 9
Slide 10
Slide 11
Slide 12
Slide 13
Slide 14
Slide 15
Slide 16
Slide 17
Slide 18
Slide 19
Slide 20
Slide 21
Slide 22
Slide 23
Slide 24
Slide 25
Slide 26
Slide 27
Slide 28
Slide 29
Slide 30
Slide 31
Slide 32
Slide 33
Slide 34
Slide 35
Slide 36
Slide 37
Slide 38
Slide 39
Slide 40
Slide 41
Slide 42
Slide 43
Slide 44
Slide 45
Slide 46
Slide 47
Slide 48
Slide 49
Slide 50
Slide 51
Slide 52
Slide 53
Slide 54
Slide 55
Slide 56

Ryzyko stopy procentowej

Document Outline