Dyfuzja w roztworach

polimerów

Proces dyfuzji opisują dwa prawa Ficka

i

c

grad

D

i

J









I prawo
Strumień składnika jest proporcjonalny do gradientu stężenia,
lecz kierunki strumienia i gradientu stężenia są przeciwne.

Dyfuzja to migracja cząsteczek w kierunku przeciwnym do gradientu stężenia

Szybkości dyfuzji określa strumień składnika J

i

:

jest to ilość składnika (wyrażoną w molach) przepływająca w
jednostce czasu przez jednostkową powierzchnię, prostopadłą do
kierunku strumienia:

dt

dn

S

1

i

i

J







II prawo
Strumień składnika zmienia stężenie składnika w czasie i przestrzeni





































2

i

2

2

i

2

2

i

2

i

i

z

c

y

c

x

c

D

t

c



































z

c

y

c

x

c

D

i

i

i

i

i

J

WSPÓŁCZYNNIK
DYFUZJI D

 charakteryzuje wielkość strumienia dla jednostkowego
gradientu stężenia.

 zależy od właściwości układu,
tzn. zarówno od właściwości substancji rozpuszczonej,
jak i od właściwości
rozpuszczalnika.

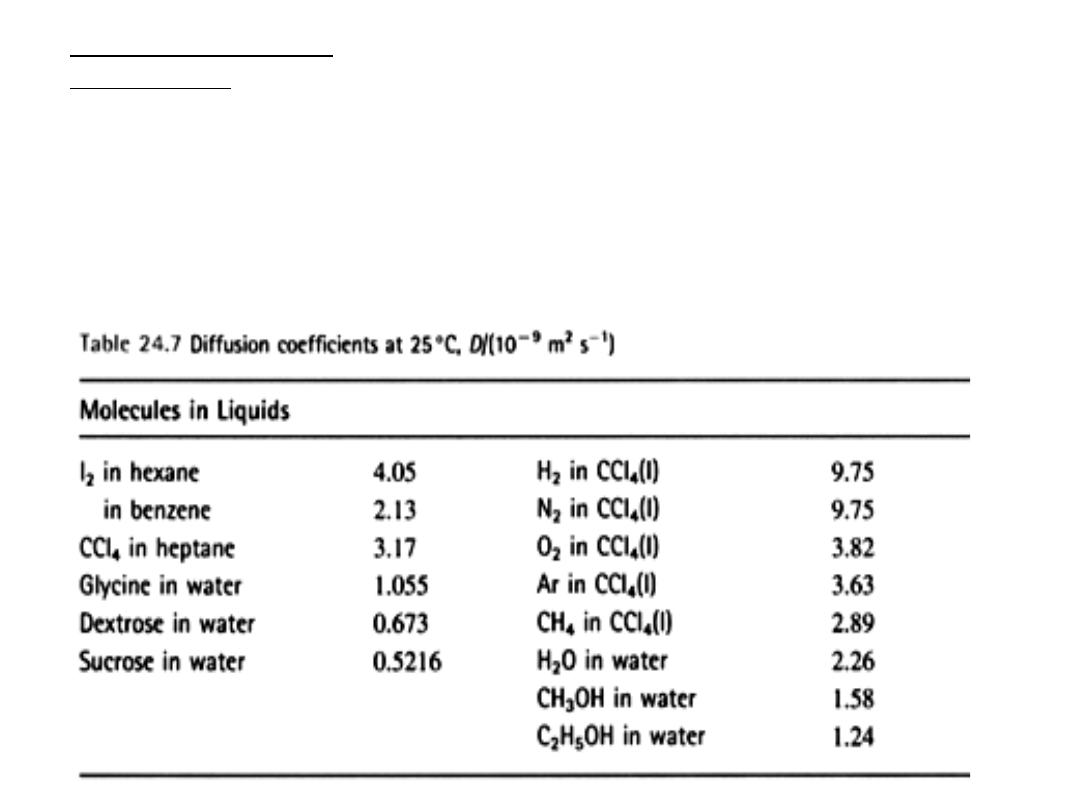
Współczynniki dyfuzji w temperaturze 25

0

C [ D / (10

-9

m

2

s

-1

) ]

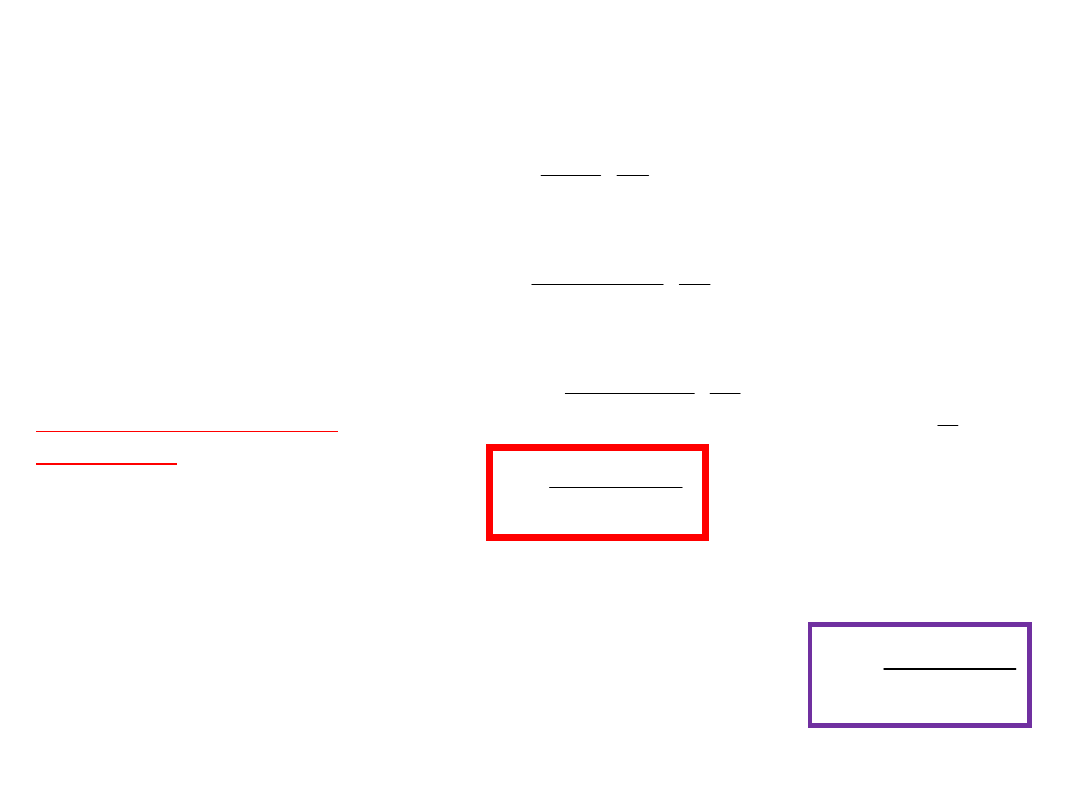
Współczynnik dyfuzji D

Jednostajny ruch (v=
const) cząsteczki o
promieniu r, w
roztworze o lepkości η,
zachodzi w stanie
zrównoważenia się siły
napędowej dyfuzji i siły
oporu lepkiego

v

r

η

6π

x

c

N

c

RT

A



















v

c

x

c

N

r

η

6π

RT

A



















dx

dc

D

J







I prawo Ficka

J

x

c

N

r

η

6π

RT

A

















A

N

r

η

6π

RT

D









Równanie Stokesa –
Einsteina

przedstawia

zależność współczynnika
dyfuzji cząsteczki od jej
rozmiaru (r) i lepkości
rozpuszczalnika 

h

0

R

η

6π

T

k

D

B







W roztworze polimeru współczynnik dyfuzji
translacyjnej makrocząsteczki zależy od jej
promienia hydrodynamicznego R

h

i lepkości

rozpuszczalnika η

0

Hydrodynamiczny promień makrocząsteczki R

h



charakteryzuje ruch makrocząsteczki w rozpuszczalniku

 obejmuje promień sztywnej cząstki kulistej wraz z warstewką
rozpuszczalnika, na jej powierzchni i wewnątrz, poruszającą się razem
z cząstką w jej ruchu dyfuzyjnym

 w przypadku makrocząsteczek giętkich zależy od stopnia
przepuszczalności kłębka i od oddziaływań hydrodynamicznych
segmentów.

 

1/2

2
G

0

R

η

5,1

T

k

D

B











h

0

R

η

6π

T

k

D

B







Współczynnik dyfuzji makrocząsteczek można
eksperymentalnie wyznaczyć z pomiarów dynamicznego
rozpraszania światła (DSL)

Promień hydrodynamiczny R

h

jest związany z promieniem bezwładności makrocząsteczki

W pomiarach dynamicznego rozpraszania światła (DSL) obserwuje się



fluktuacje intensywności światła rozproszonego



przesunięcia częstości fali rozproszonej względem fali padającej

zachodzące podczas ruchu cząstki rozpraszającej.

W metodzie DSL badany jest kształt funkcji autokorelacji , z
której otrzymuje się informacje o dynamice ruchu
makrocząsteczek.

Dynamiczne rozpraszanie światła

 funkcja autokorelacji pola
elektrycznego, G

(1)

():

charakteryzuje szybkość zmian pola
elektrycznego fali rozproszonej związaną z
dynamiką ruchu cząsteczek ośrodka.

 

 

  



τ

t

E

t

E

τ

G

S

S

1







 funkcja autokorelacji natężenia, G

(2)

():

jest związana ze zmianami widma światła rozproszonego

 

  



τ

t

I

t

I

τ

G

S

S

(2)







Ruchy termiczne makrocząsteczek wytwarzają fluktuacje przenikalności
elektrycznej ośrodka rozpraszającego światło. Jeśli fluktuacje ulegają
szybkim zmianom w czasie, to w wiązce światła rozproszonego pojawiają
się przesunięcia częstości.
Zależność kątowa światła rozproszonego, I

S

(), oraz rozkład widmowy

I

S

() dostarczają informacji o przestrzennych i czasowych fluktuacjach

przenikalności elektrycznej, które zależą od dynamiki ruchu cząsteczek.

E

S

wektor elektryczny fali rozproszonej

E

S

* wielkość zespolona

I

S

natężenie światła rozproszonego

I

S

* wielkość zespolona

 

 

τ

2Dq

2

2

be

1

τ

g







Współzależność funkcji autokorelacji podaje wzór Siegerta:

gdzie g

(1)

() i g

(2)

() są znormalizowanymi funkcjami autokorelacji G

(1)

()

i G

(2)

().

 

 

 

 

2

1

2

τ

g

1

τ

g





Dla monodysperyjnych
sferycznych cząsteczek o
rozmiarach mniejszych od
długości padającego światła
współczynnik dyfuzji można
wyznaczyć z zależności















2

θ

sin

λ

n

4π

q

0

0

b – stała
aparaturowa

 

 





τ

Dq

exp

τ

g

2

1





q- wektor fali rozproszonej

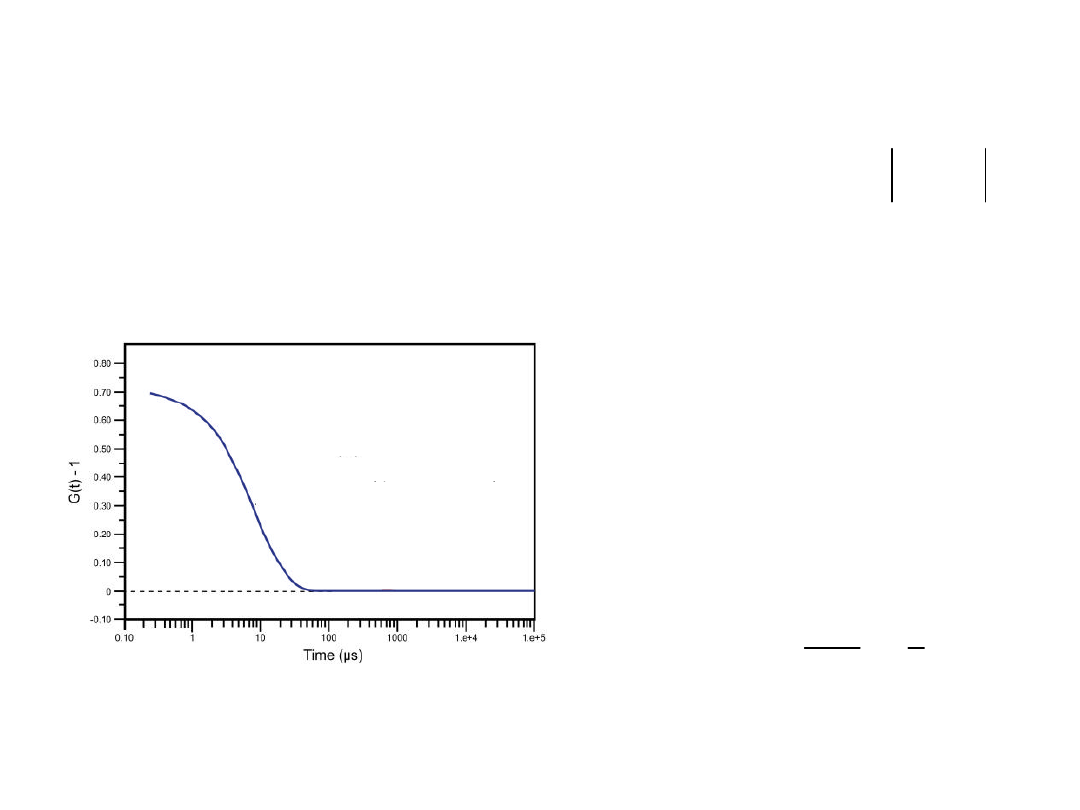
Po wyznaczeniu funkcji g

(2)

(τ) dla określonego

kąta rozpraszania θ,
z wykresu ln[g

(2)

(τ)-1]=f(τ) wyznacza się wartość

2Dq

2

Dynamiczne rozpraszanie światła

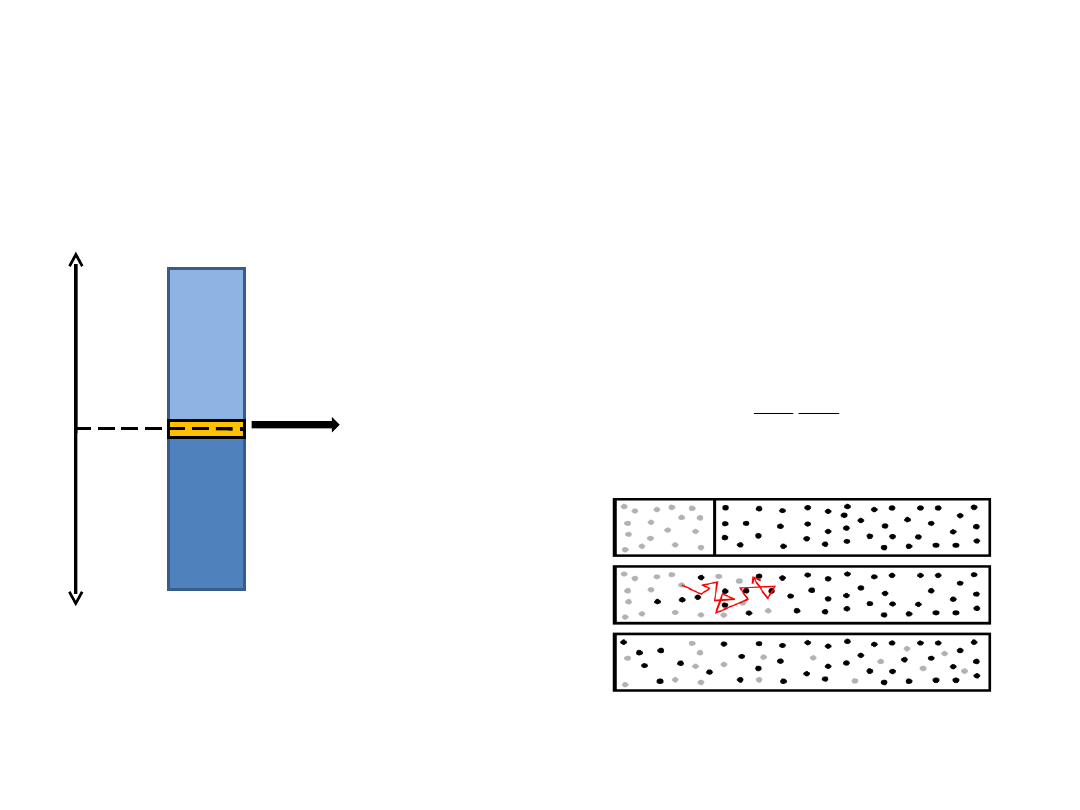
+x

-x

rozpuszczalnik

roztwór

ruchoma membrana

Po usunięciu ruchomej
przegrody następuje wzajemna
dyfuzja makrocząsteczek i
cząsteczek rozpuszczalnika

.

Pomiar współczynnika dyfuzji metodą swobodnej granicy

Współczynnik dyfuzji w roztworach polimerów określa się jako
stosunek szybkości przemieszczania się makrocząsteczek w
roztworze do szybkości przemieszczania się cząsteczek
rozpuszczalnika

W roztworze polimeru współczynnik
dyfuzji wzajemnej D’ zależy od
współczynnika samodyfuzji D i
ciężaru cząsteczkowego M
dyfundujących cząsteczek oraz
gradientu ciśnienia osmotycznego

c

Π

RT

M

D

D'







Cela pomiarowa
dyfuzjometru











 



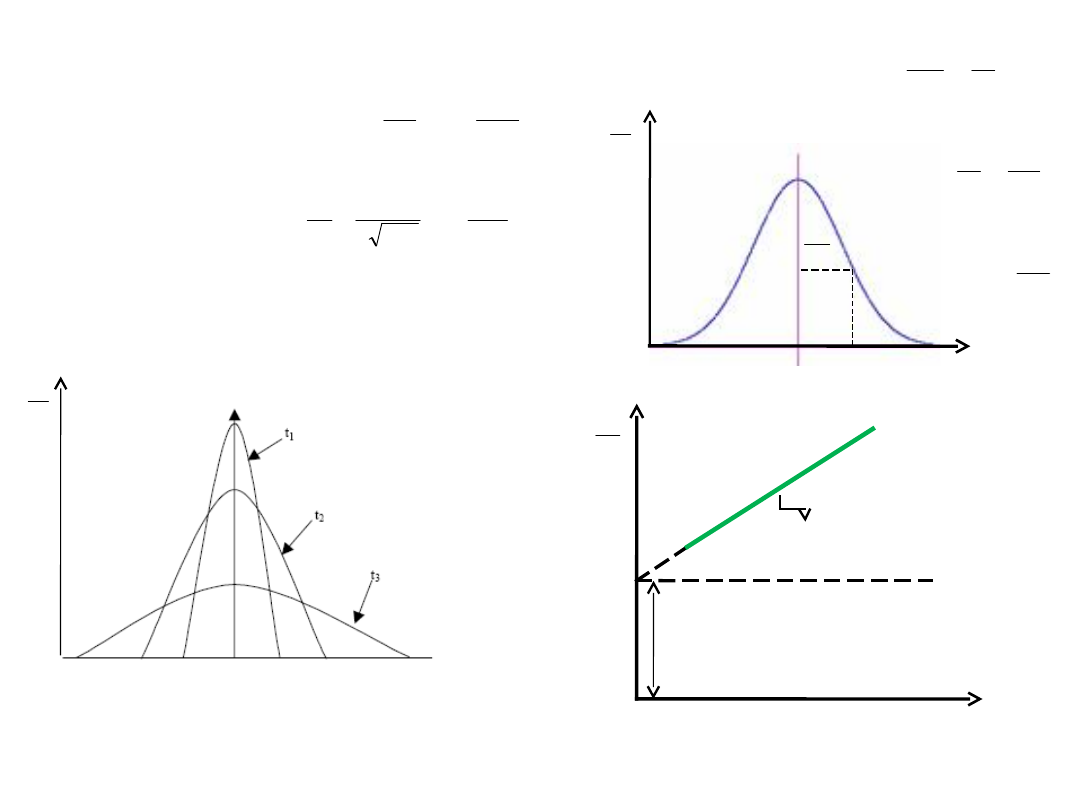
4Dt

x

exp

πDt

2

Δc

dx

dc

2

x = 0

dx

dc

Rozkład gradientu stężenia dla
różnych czasów dyfuzji opisany
jest funkcją Gaussa o odchyleniu
standardowym σ

2

= 2Dt

Rozwiązanie II prawa
Ficka

dla dyfuzji
jednokierunkowej

2

i

2

i

i

x

c

D

t

c













x

Wyznaczanie współczynnika dyfuzji

Szybkość dyfuzji

i

i

x

D

dt

dx



t

0

x

i

i

i

x

2D

t

x



dt

dx

i

dc

dx

odległość od granicy rozdziału

2t

x

D

2
i



c

dt

dx

nachylenie =
stała
szybkości
dyfuzji

D

0

Zależność szybkości dyfuzji od stężenia polimeru

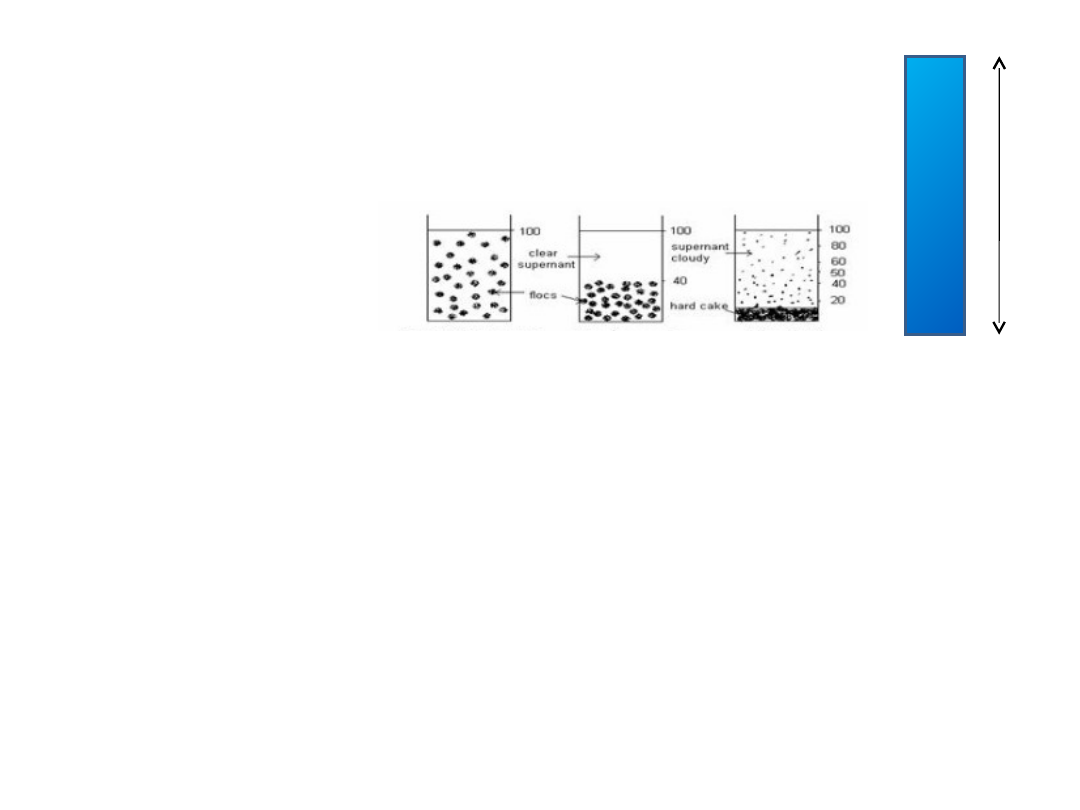
SEDYMENTACJA w roztworach polimerów

h

Zjawisko sedymentacji polega na opadaniu
składnika rozproszonego w polu grawitacyjnym.

W roztworach polimerów energia potencjalna
makrocząsteczek jest mała w porównaniu z energią ruchu
cieplnego k

B

T i sedymentacji nie obserwuje się.

Sedymentacja w roztworach polimerów zachodzi w polu dużych sił odśrodkowych.

W ultrawirówkach otrzymuje się przyśpieszenie odśrodkowe w
zakresie od 500 g do 10

6

g (przyśpieszenie ziemskie)

W ultrawirówce analitycznej można wyznaczyć wielkość cząstek,
średni ciężar cząsteczkowy, rozkład ciężarów cząsteczkowych oraz
parametry oddziaływania P-R w roztworze.

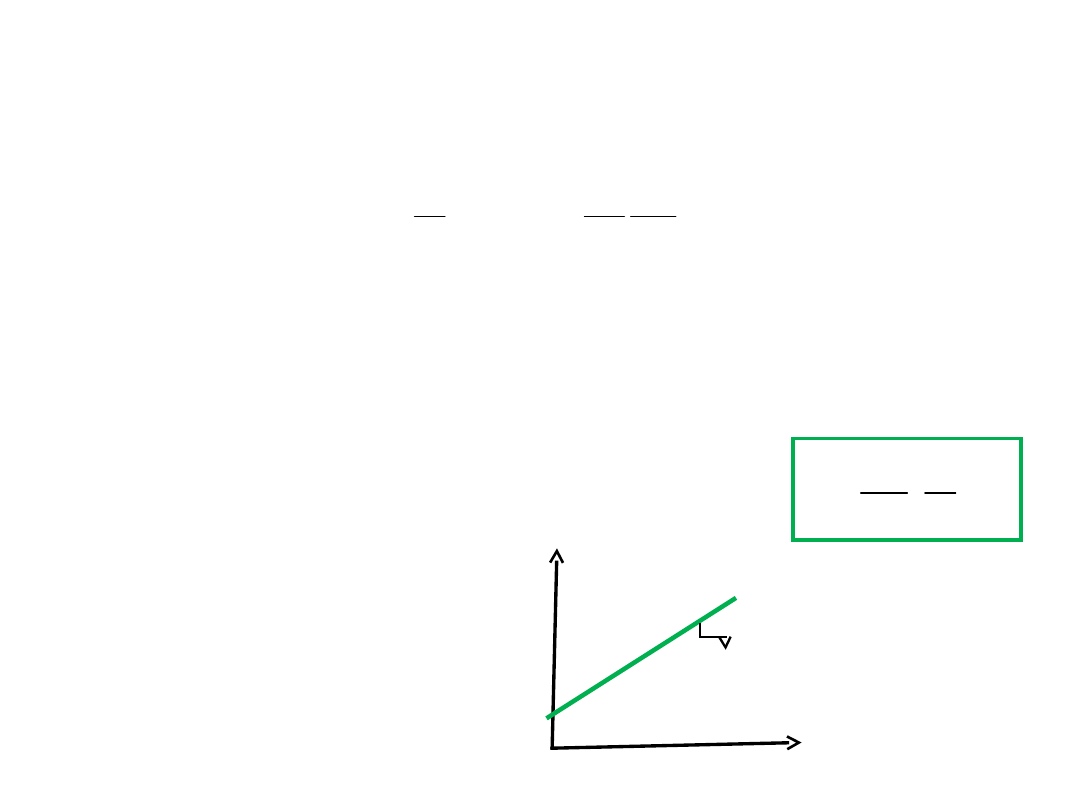
Równowaga sedymentacji

w wirówce

dt

dr

r

ω

1

S

2





Szybkość sedymentacji w wirówce określa

współczynnik sedymentacji S

, który jest ilorazem

szybkości przesuwania się granicy sedymentacji i
natężenia pola sił odśrodkowych

W stanie równowagi w doskonałym roztworze polimeru (w
warunkach θ) o ciężarze cząsteczkowym M

i

po odwirowaniu w

wirówce siła sedymentacji jest równa sile dyfuzji.

r

c

c

RT

r

ω

M

d

d

1

i

i

2

i

i





















d- gęstość roztworu,
d

i

- gęstość frakcji o ciężarze cząsteczkowym M

i

(d

i

-1

= v

i

cząstkowa objętość właściwa składnika o ciężarze

cząsteczkowym M

i

),

ω = 2πν prędkość kątowa wirnika (ν-liczba obrotów wirnika na sekundę ),
r- odległość od osi obrotu.

Sω

2

t = lnr + const

Czas t, s

lnr

S

ω

2

Jednostką współczynnika
sedymentacji jest 1 svedberg
1S= 10

-13

s

Oznaczanie ciężaru cząsteczkowego polimeru
metodą pomiaru szybkości sedymentacji.



















p

r

0

0

z

d

d

1

RT

D

S

M

limS

0

c

0

S





limD

0

c

0

D





Równanie Svedberga











n

1

i

2
i

i

n

1

i

3

i

Z

M

N

M

N

M

i

Theodor Svedberg
(1884-1971)

Skonstruował ultrawirówkę
(1922),
stworzył podstawy jej
zastosowanie do oznaczeń
ciężarów cząsteczkowych
polimerów
Nagroda Nobla w zakresie
chemii (1926)