1

Wykład 3

MECHANIKA TEORETYCZNA

Studia stacjonarne I stopnia – rok akademicki 2013/14

Autor:

Henryk Laskowski

Katedra Podstaw Mechaniki Ośrodków Ciągłych
Instytut Mechaniki Budowli
Wydział Inżynierii Lądowej

TEORIA RÓWNOWAŻNOŚCI UKŁADÓW SIŁ

Część 1

SIŁY I UKŁADY SIŁ

3

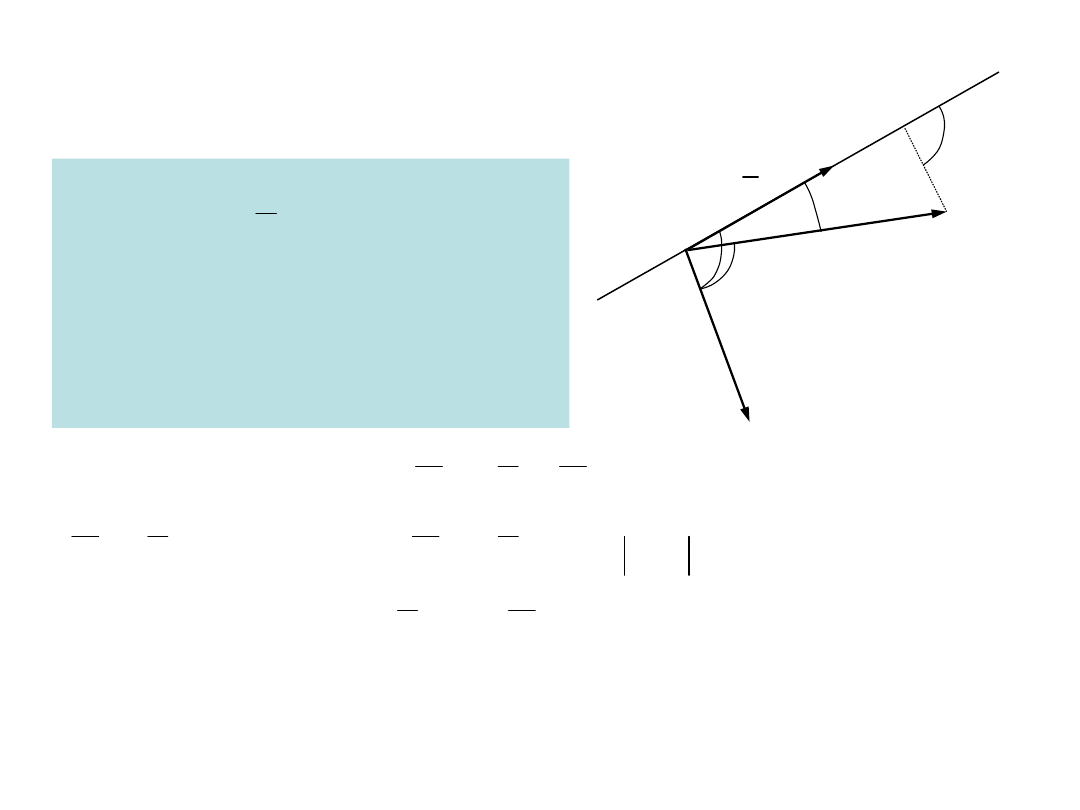
1.1. Moment siły względem punktu

Definicja

Momentem siły względem punktu
nazywamy wektor równy
iloczynowi
wektorowemu siły i wektora
wyznaczone-go przez punkt zaczepienia
siły i punkt, względem którego moment
jest liczony

































ną

prawoskręt

trójkę

stanowią

:

zwrot

:

wartość

:

kierunek

B

B

B

B

df

B

M

AB

F

AB

F

M

AB

M

F

M

AB

F

M

,

,

α

sin

|

|

|

|

|

|

:

____

____

____

____

B

M

___

____

AB

r

F

B

A

α

.

B

M

___

F

B

4

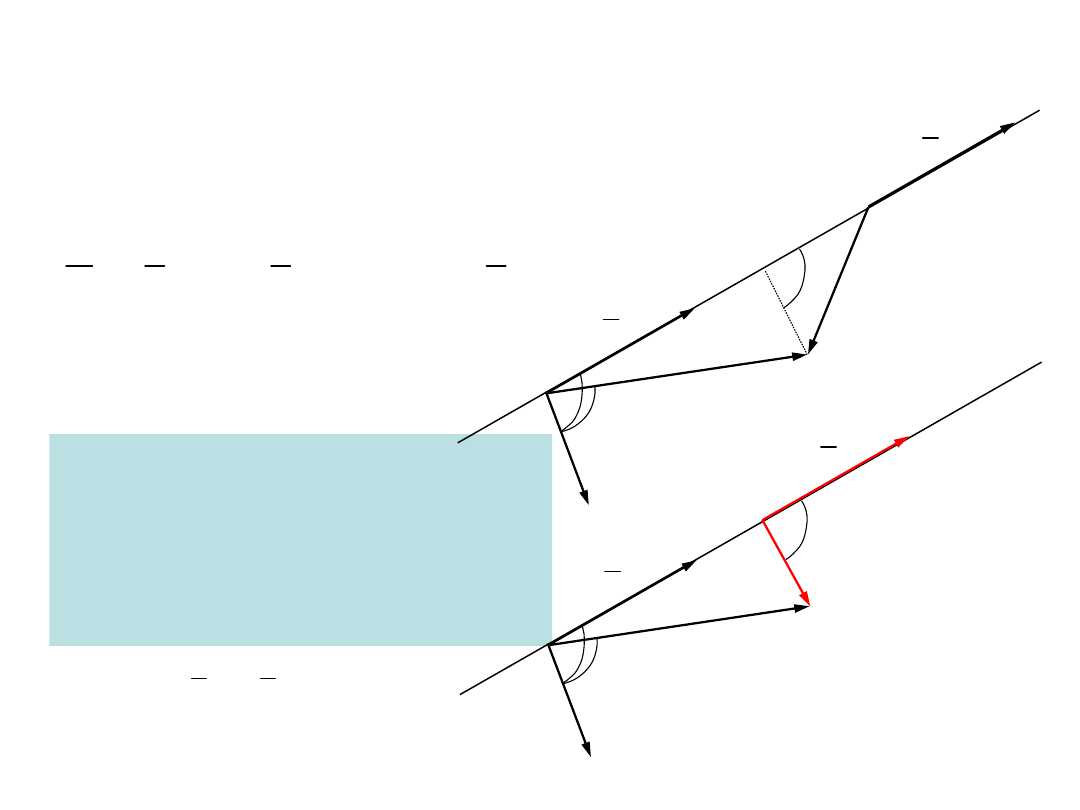
Przesunięcie siły wzdłuż jej kierunku działania

Przesunięcie siły wzdłuż jej kierunku działania nie
wpływa na zmianę wartości momentu siły względem
punktu

Ramię działania siły

Jest to wektor prostopadły do prostej
działania siły, którego początek leży na
tej prostej a koniec w punkcie,
względem którego liczony jest moment
siły

_______

____

____

____

____

const

BR

F

BR

AB

F

AR

F

M

R

















)

(

R

M

___

____

AR

r

F

R

A

.

B

F

____

BR

'

R

____

R

M

F R' R

= �

R

M

___

____

AR

F

R

A

.

F

____

' R

R

'

R

5

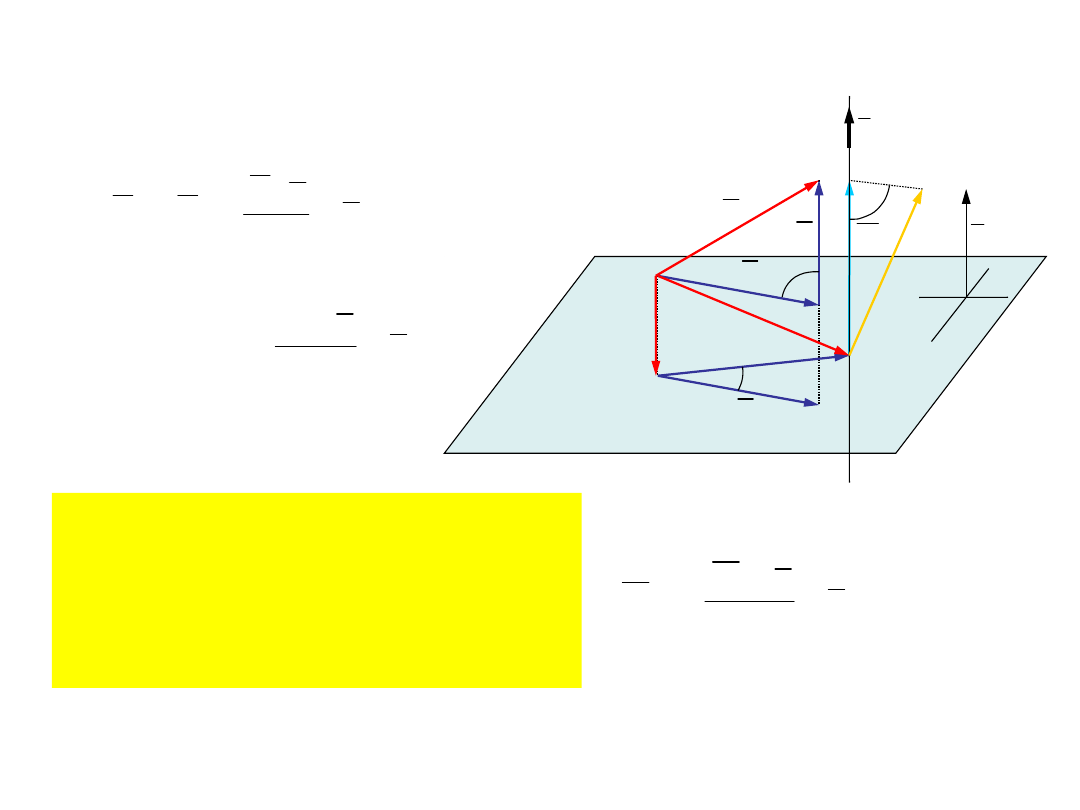
1.2. Moment siły względem prostej

Definicja

Momentem siły względem prostej
nazywamy iloczyn wektorowy rzutu
siły na płaszczyznę prostopadłą do
tej prostej względem punktu
przebicia płaszczyzny przez tę
prostą.

A

n

____

____

π

π

____

π

||

' :

|

| |

| | ' | sinα

,

' ,

l

df

l

l

l

kierunek: M l

M F A O wartość: M

F

A O

zwrot: F A O M stanowią trójkę prawoskrętną

�

�

�

= �

=

�

�

�

�

�

�

l

M

'

A

π

F

O



α

____

'O

A

F

l

e

6

Twierdzenie

Moment siły względem prostej jest równy
rzutowi momentu siły względem
dowolnego punktu prostej na tę prostą.
Dowód pominięto

Twierdzenie o momencie siły względem prostej

l

M

n

α



____

'O

A

O

'

A

π

F

F

A

l

e

O

M

___

π

F

l

F

n

n

n

F

F

F













 





2

π

n

n

n

AO

AO

O

A





























2

____

____

_____

'

n

n

n

M

M

O

l



















2

7

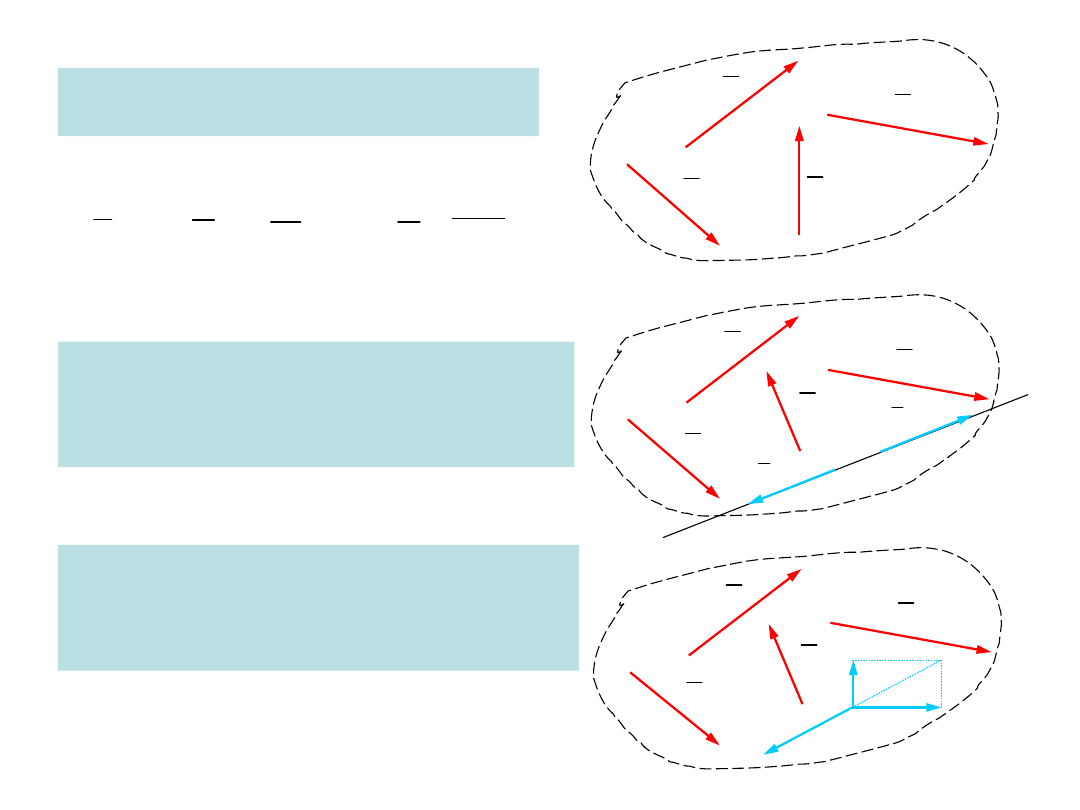
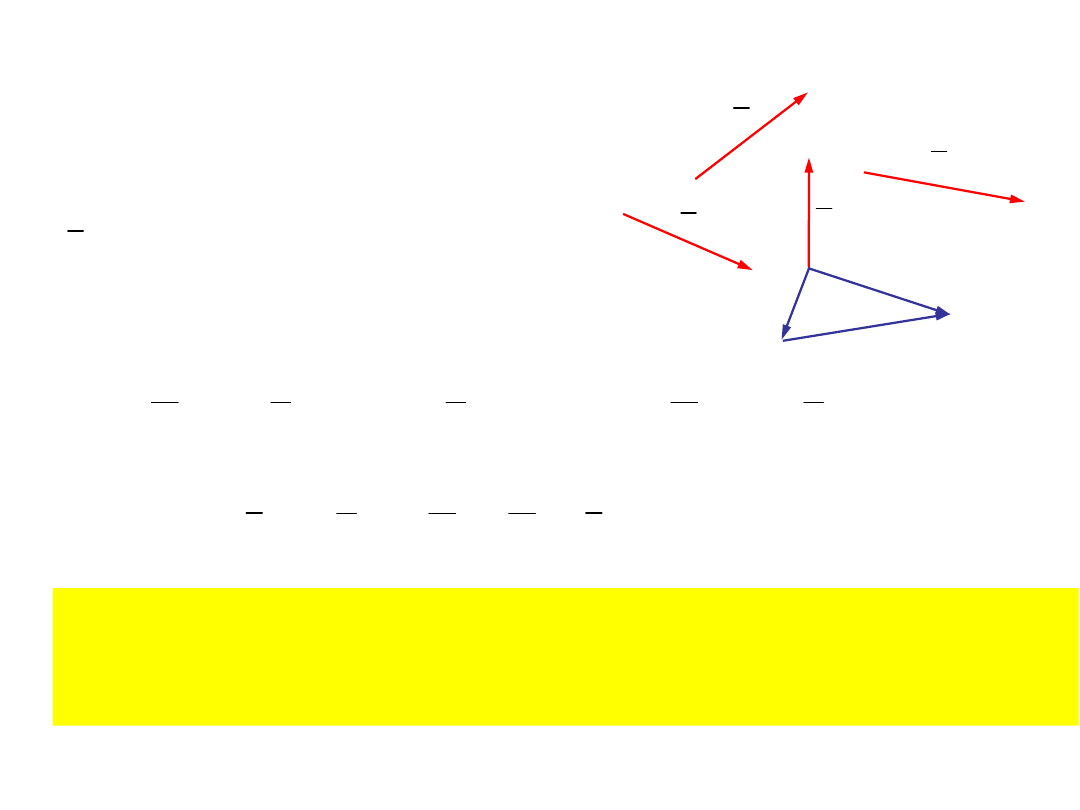
Układ sił
Zbiór sił wraz z punktami zaczepienia

Przekształcenie elementarne I-go
rodzaju
Dodanie do układu lub odjęcie dwóch sił
przeciwnych działających wzdłuż prostej

Przekształcenie elementarne II-go
rodzaju
Dodanie do układu lub odjęcie układu sił
zbieżnych o sumie równej 0

Przekształcenia elementarne nie
zmieniają sumy i momentu układu

Suma
układu sił

Moment
układu sił

n

A

2

F

1

A



i

A

2

A

i

F

1

F

n

F







n

A

2

F

1

A



i

A

2

A

i

F

1

F

n

F







n

A

2

F

1

A



i

A

2

A

i

F

1

F

n

F











F

-

0



F

0





i

i

F

S







i

i

i

R

R

A

F

M

8

1.3. Twierdzenie o zmianie bieguna

Układ n sił

- punkt zaczepienia siły

- siła
- biegun redukcji
- nowy biegun redukcji

Twierdzenie
Moment układu sił względem nowego bieguna jest równy sumie momentu tego
układu względem starego bieguna i iloczynu wektorowego sumy układu i wektora
łączącego stary biegun z nowym.

____

____

____

____

BR

F

M

BR

B

A

F

R

A

F

M

n

i

i

B

n

i

i

i

n

i

i

i

R









































1

1

1

)

(

i

A

n

A



2

F

1

A



i

A

2

A

B

R

i

F

1

F

n

F

B

R

i

F







n

i

i

df

F

S

1

____

BR

S

M

M

B

R







9

Wniosek 1
Jeżeli suma układu jest równa 0 to moment układu jest stały, tzn. nie
zależy od bieguna, względem którego jest liczony

Wnioski z twierdzenia o zmianie bieguna

Z: Suma układu jest równa 0

T: Moment układu jest
stały

D:

S =0

M const

=

____ S

B

A

B

A

M

M

S AB

M

M

=

=

+ �

�

=

0

10

Wniosek 2
Jeżeli momenty układu liczone względem trzech niewspółliniowych
punktów są równe to suma układu jest równa 0

Z: Punkty A, B, C są niewspółliniowe

oraz

T: Suma jest równa
0

D:

Wniosek 3
Iloczyn skalarny sumy i momentu liczonego
względem dowolnego punktu jest dla danego
układu sił wielkoś-cią stałą i nosi nazwę parametru
układu sił

D:

0





____

____

AC

AB

C

B

A

M

M

M





0



S

0

0

0











































S

AC

S

AB

S

AC

S

M

M

AB

S

M

M

A

C

A

B

____

____

____

____

const

S

M

K

O

df







S

M

OA

S

S

S

M

S

OA

S

M

S

M

O

O

O

A

























)

(

)

(

____

____

11

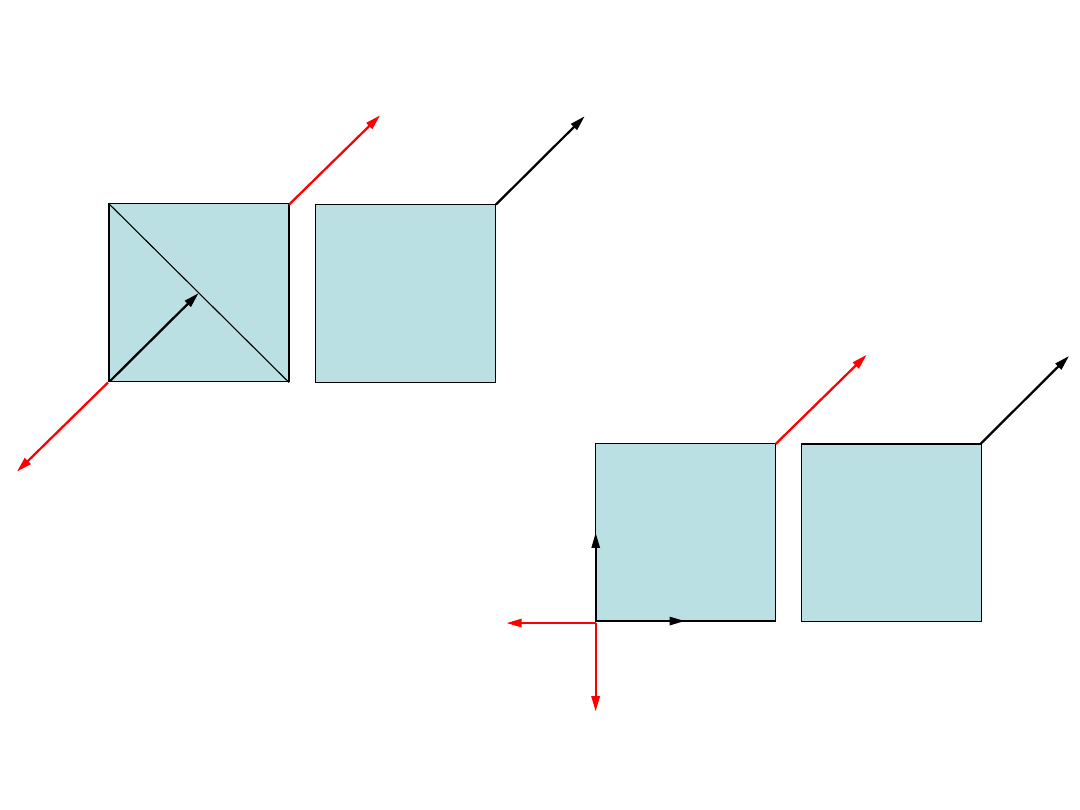
1.4. Równoważność układów sił

O równoważności układu wektorów (sił) można mówić wyłącznie w odniesieniu
do rozważanego problemu. W mechanice teoretycznej rozważa się
równoważność układów sił w odniesieniu do problemu redukcji.

Dwa układy

i

są równoważne, jeżeli można, wykonując na jednym z nich skończoną liczbę
przekształceń I-go i II-go rodzaju, przekształcić jeden układ w drugi.

Definicja równoważności układów sił

punkt

dowolny

)

(

)

(

)

(

)

(

O

O



















O

M

M

S

S

df

B

A

B

A

B

A

:















n

i

n

i

A

A

A

A

F

F

F

F

...

...

...

...

2

1

2

1

A















m

i

m

i

B

B

B

B

R

R

R

R

...

...

...

...

2

1

2

1

B

12

Równoważne układy sił

Równoważne układy sił

Przekształcenie elementarne
I–go rodzaju

Przekształcenie elementarne
II–go rodzaju

13

Twierdzenia o równoważności układów sił

Twierdzenie 1
Dwa układy są równoważne, gdy mają równe sumy i równe momenty liczone
względem jednego (ustalonego) punktu.

Z:

oraz

T:

D:

Dowód

)

)

B

A

(

(

O

O

M

M



)

)

B

A

(

(

S

S



B

A 

)

(

)

(

OO'

)

(

)

(

)

(

OO'

)

(

)

(

)

(

O'

O'

O

O'

O

O'

B

A

B

B

B

A

A

A

M

M

S

M

M

S

M

M

























____

____

14

Twierdzenie 2
Dwa układy są równoważne, gdy mają (odpowiednio) równe momenty liczone
względem trzech niewspółliniowych punktów.

oraz

T:

D:

Dowód

Z: Punkty O, O’, O” są niewspółliniowe

czyli

)

)

B

A

(

(

O

O

M

M



)

)

B

A

(

(

S

S



B

A 

____

____

____

____

OO"

)

(

)

(

)

(

OO"

)

(

)

(

)

(

OO'

)

(

)

(

)

(

OO'

)

(

)

(

)

(

O

O"

O

O"

O

O'

O

O'





























B

B

B

A

A

A

B

B

B

A

A

A

S

M

M

S

M

M

S

M

M

S

M

M

)

)

B

A

(

(

O'

O'

M

M



)

)

B

A

(

(

O"

O"

M

M











0

)

(

-

)

(

OO"

do

równoległy

jest

nie

OO'

0

OO"

)

(

-

)

(

0

OO'

)

(

-

)

(























B

A

B

A

B

A

S

S

S

S

S

S

____

____

____

____

15

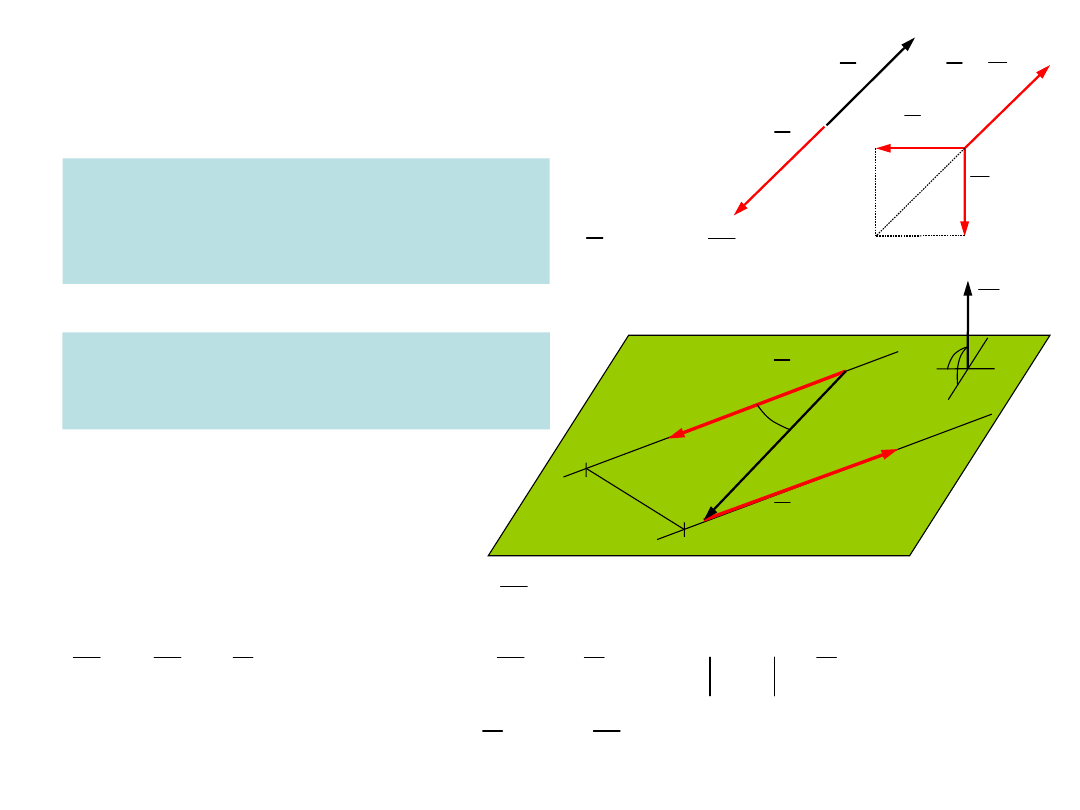
1.5. Zerowy układ sił i para sił

Zerowy układ sił
Układ sił, którego suma i moment
liczony względem dowolnego punktu
jest wektorem zerowym.

Para sił
Układ dwóch niezerowych sił przeciw-
nych nie leżących na jednej prostej.

0

0







M

S

F

F



F

G

)

(

G

F 

































ne

prawoskręt

:

zwrot

:

wartość

:

kierunek

O

O

O

B

O

M

AB

F

d

F

AB

F

M

M

AB

F

M

M

,

,

|

|

α

sin

|

|

|

|

|

|

Π

:

____

____

____

F

A

B

F



O

M

0



d

Π

α

Część 2

REDUKCJA UKŁADU SIŁ

17

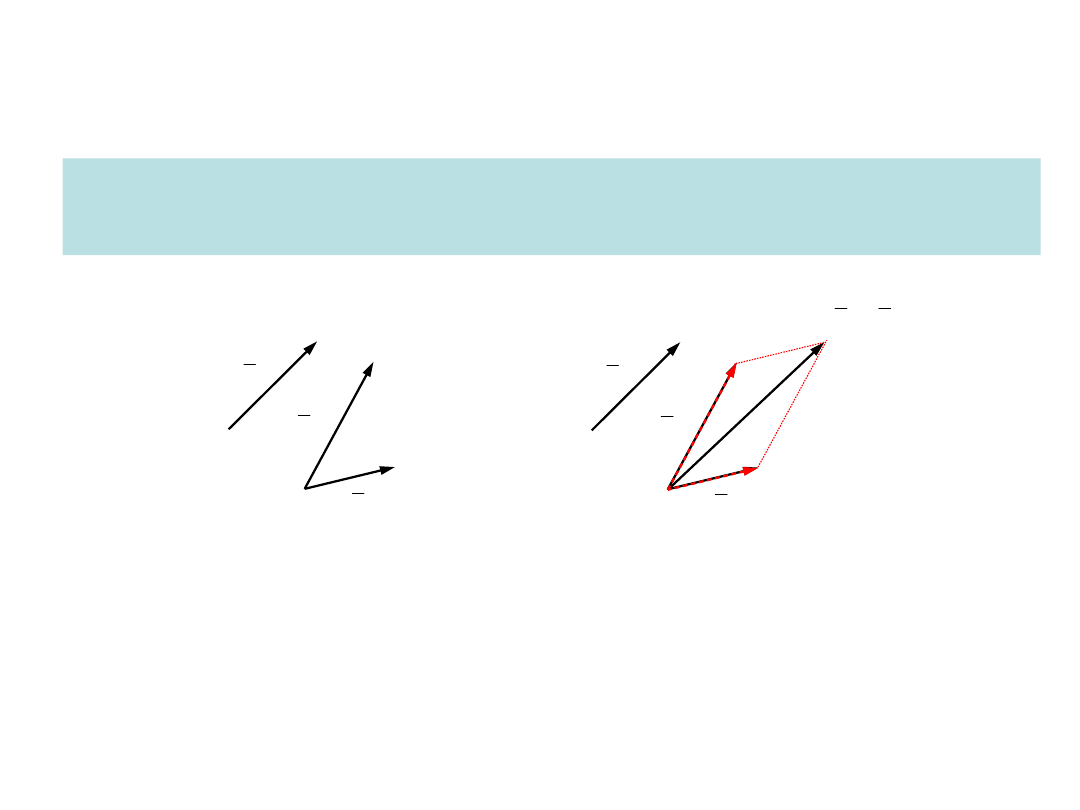
2.1. Redukcja układu sił w punkcie

Redukcja układ sił
Przekształcenie polegające na zastąpieniu danego układu sił równoważnym
układem prostszym, tj. złożonym z mniejszej liczby sił

Układ trzech sił

Układ równoważny,
zredukowany do dwóch sił

F

1

F

2

F

3

F

1

F

F

+

2

3

F

2

F

3

F

2

F

3

18

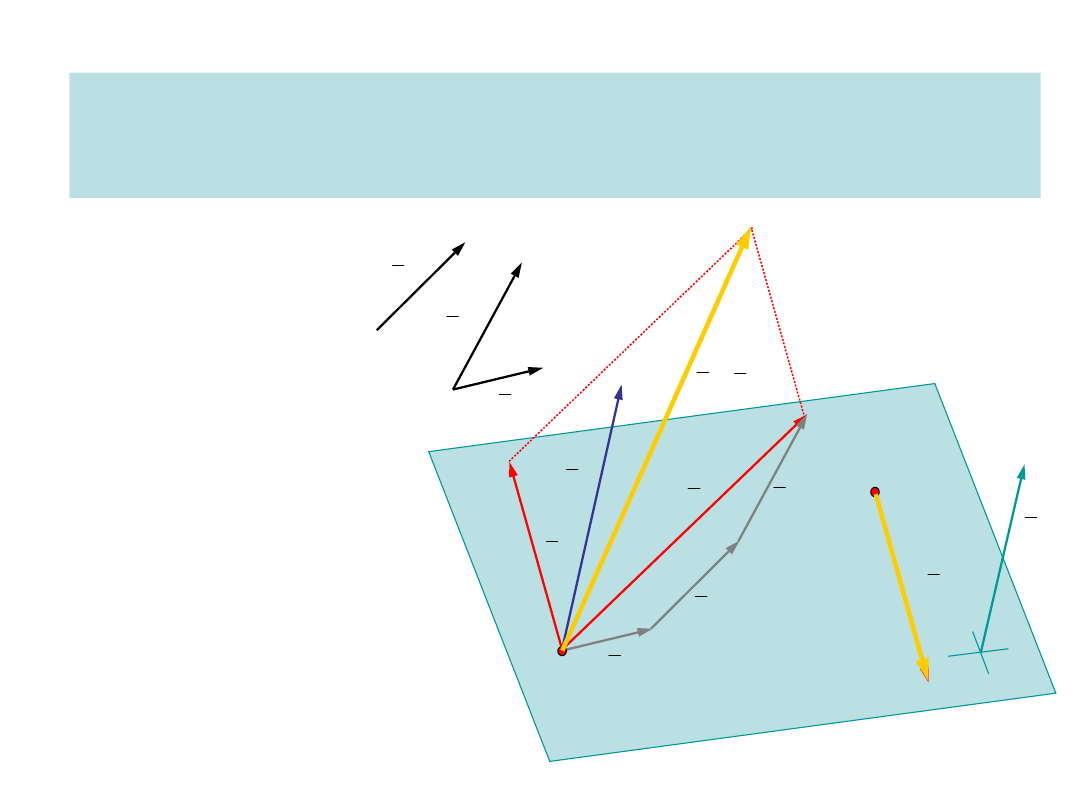
Redukcja w punkcie (w biegunie redukcji)
Zastąpienie danego układu układem równoważnym, złożonym z wektora
równego sumie układu i pary sił o momencie równym momentowi układu sił
względem bieguna redukcji

Tok
postępowania:

1. Wybór bieguna redukcji O

2. Wyznaczenie

wektora

zaczepionego w punkcie O

równego sumie układu

3. Wyznaczenie

momentu

układu sił względem bieguna
O

4. Wyznaczenie

pary sił o momencie

równym momentowi układu
względem bieguna redukcji, z
których jedna jest zaczepiona w
biegunie redukcji

5. Redukcja układu do dwóch sił
skośnych poprzez dodanie sił
zaczepionych w O

n

π

F

1

F

2

F

3

S

F

3

F

1

F

2

O

F

F

-

G

O

M

S F

+

19

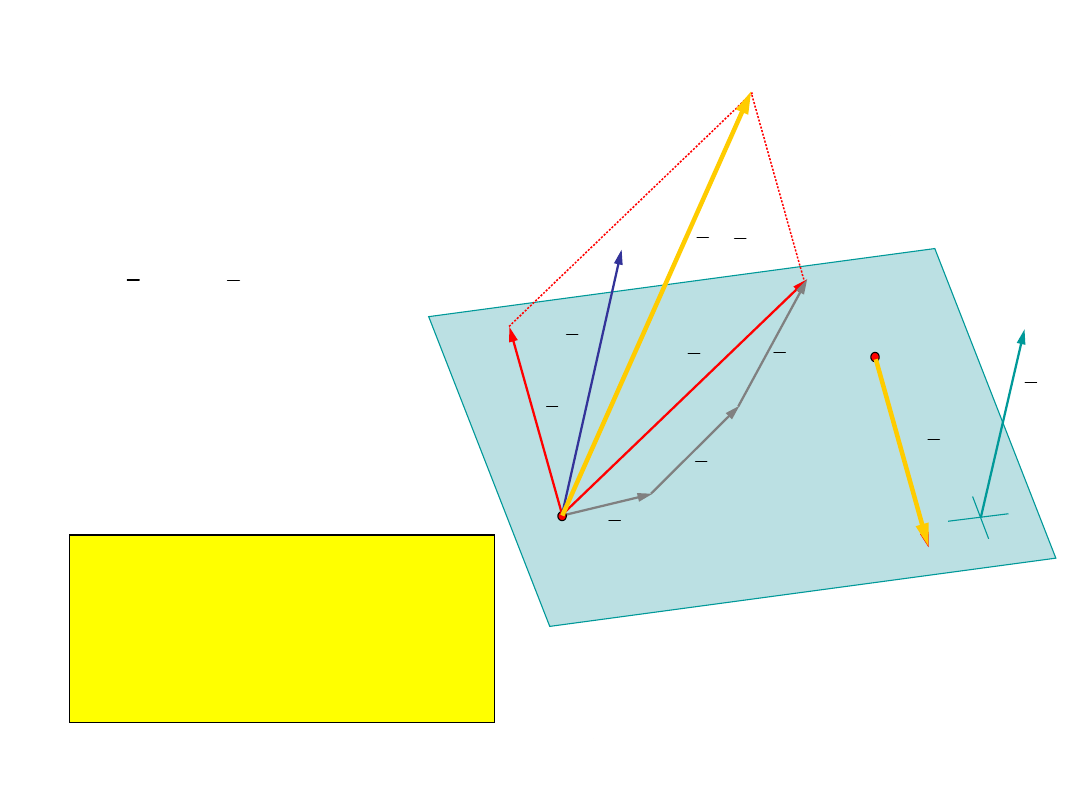
Cztery przypadki redukcji w punkcie

Przypadek 1 (ogólny):

Układ sił redukuje się do wektora
b = S zaczepionego w punkcie
redukcji oraz pary sił o
momencie M

O

równym

momentowi układu sił względem
punktu redukcji

n

π

S

F

3

F

1

F

2

O

F

F

-

G

O

M

S F

+

S

M

�ǹ

0

0

20

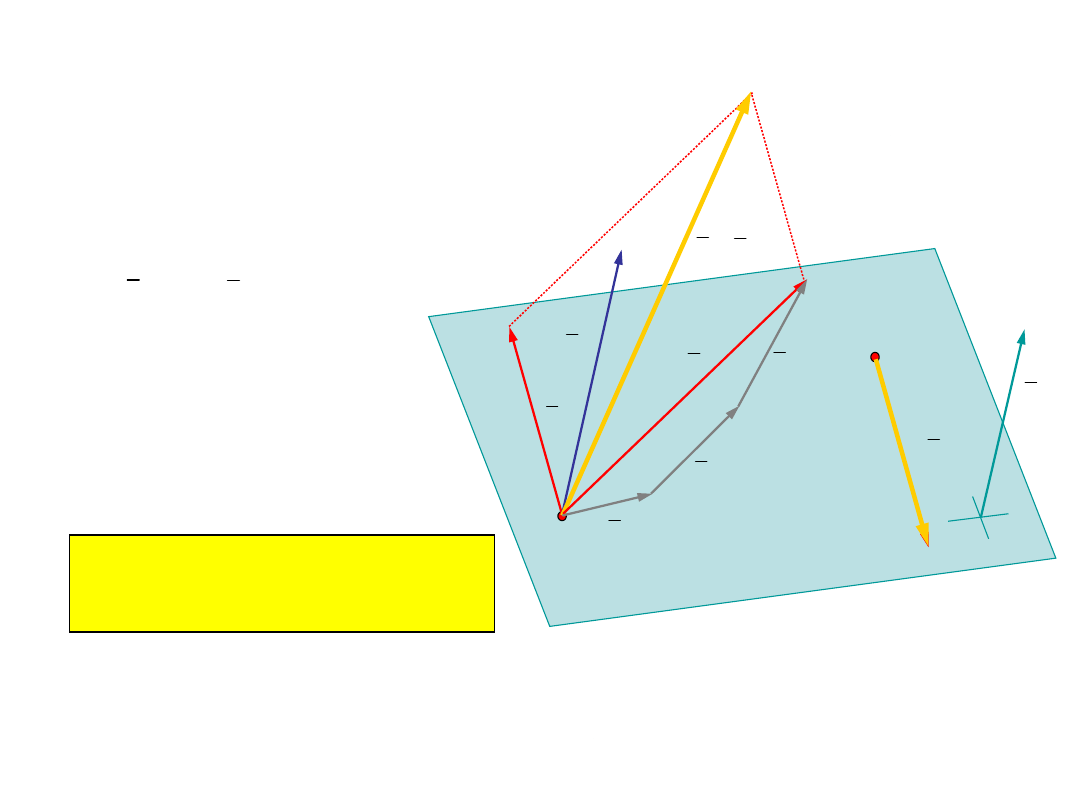
Cztery przypadki redukcji w punkcie - cd

Przypadek 2:

Układ sił redukuje się do wektora
b = S zaczepionego w punkcie
redukcji

S

M

� �

=

0

0

n

π

O

F

F

-

G

O

M

S F

+

S

F

3

F

1

F

2

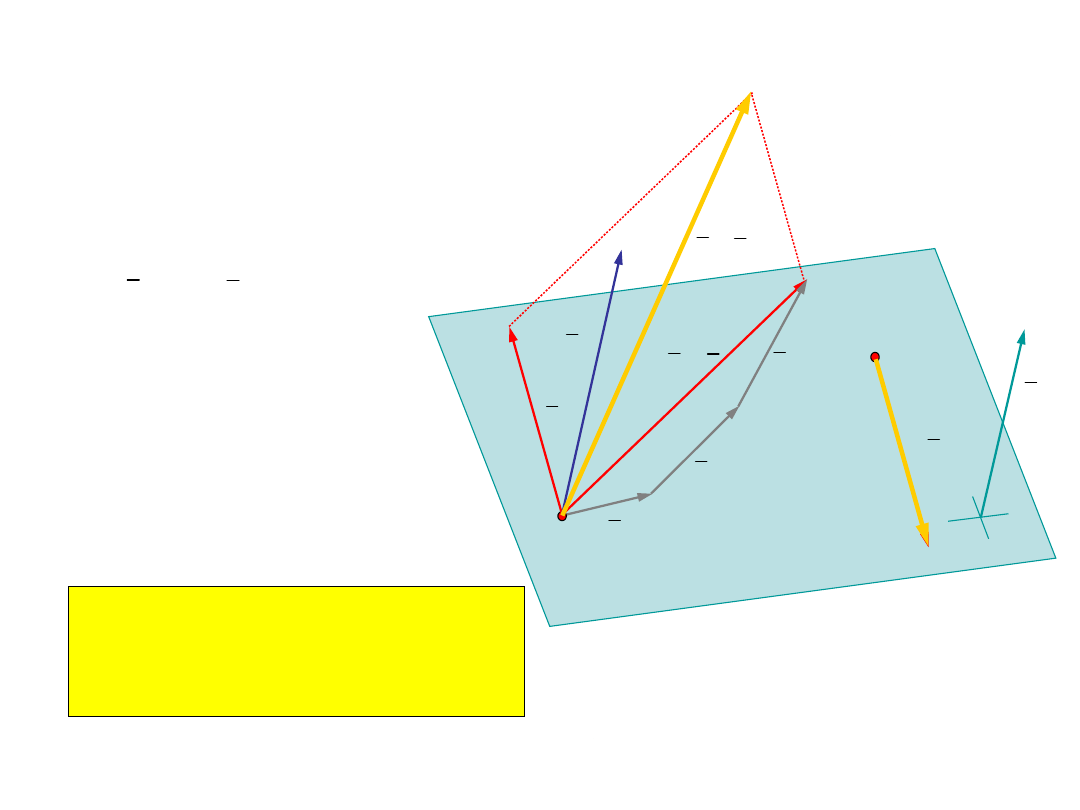
21

Cztery przypadki redukcji w punkcie - cd

Przypadek 3:

Układ sił redukuje się do pary sił
o momencie M

O

równym

momentowi układu sił względem
punktu redukcji

S

M

= ǹ

0

0

n

π

b S

=

F

3

F

1

F

2

O

F

F

-

G

O

M

S F

+

22

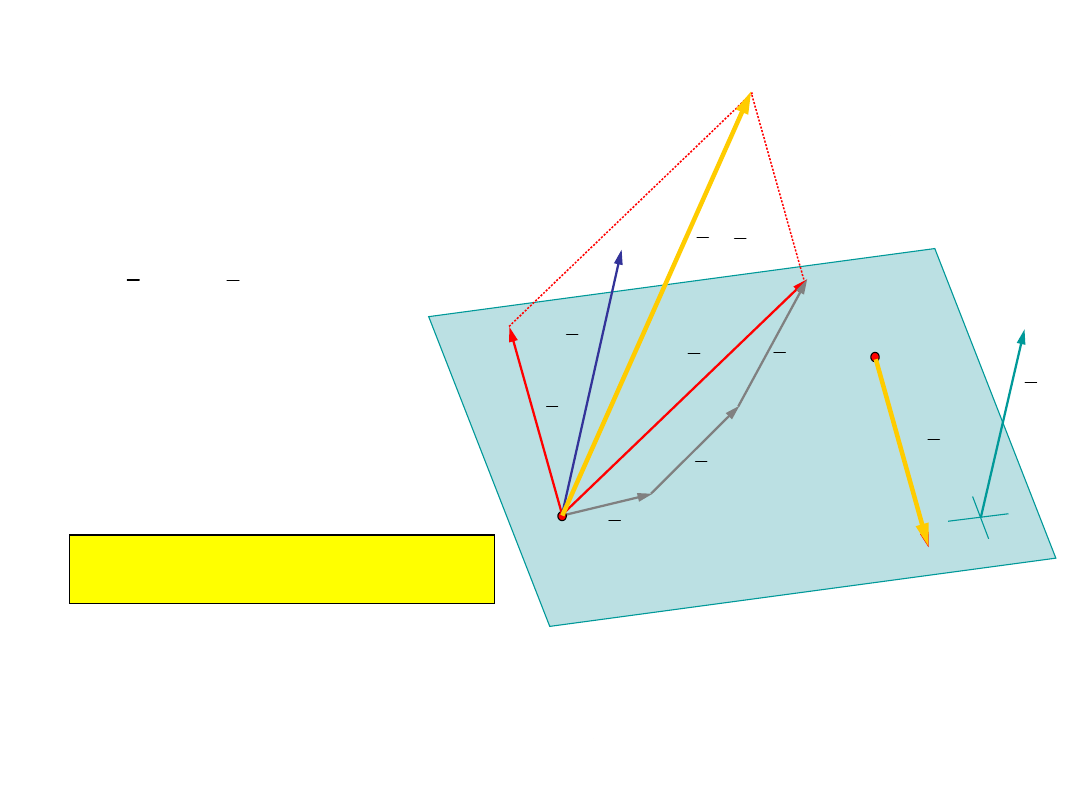
Cztery przypadki redukcji w punkcie - cd

Przypadek 4:

Układ sił redukuje się do układu
zerowego

S

M

= �

=

0

0

n

π

S

F

3

F

1

F

2

O

F

F

-

G

O

M

S F

+

23

2.2. Redukcja układu sił do najprostszej
postaci

Redukcja układ sił do najprostszej postaci
Przekształcenie polegające na zastąpieniu danego układu sił układem
równoważnym złożonym z najmniejszej liczby sił

Redukcja w punkcie a redukcja do najprostszej postaci

W problemie redukcji w punkcie biegun redukcji jest znany (wybrany lub
zadany) natomiast w problemie redukcji do najprostszej postaci poszukuje się
położenia takich punktów, w których układ sił redukuje się do najprostszej
postaci

24

Przypadek 1:
Jeżeli w wybranym lub zadanym biegunie redukcji układ sił redukuje się do układu
zerowego to układ zerowy jest najprostszym zredukowanym układem tego układu
sił

Układ sił w każdym punkcie
redukuje się do

układu

zerowego

Szczególne przypadki redukcji do najprostszej postaci

Przypadek 2:
Jeżeli w wybranym lub zadanym biegunie redukcji układ sił redukuje się do pary sił
o momencie równym momentowi układu sił względem bieguna redukcji to
para sił jest najprostszym zredukowanym układem tego układu sił

Układ sił w każdym punkcie
redukuje się do

pary sił

O

S

M

O

= �

=

-

0

0

wybrany punkt

O

S

M

O

= ǹ

-

0

0

wybrany punkt

25

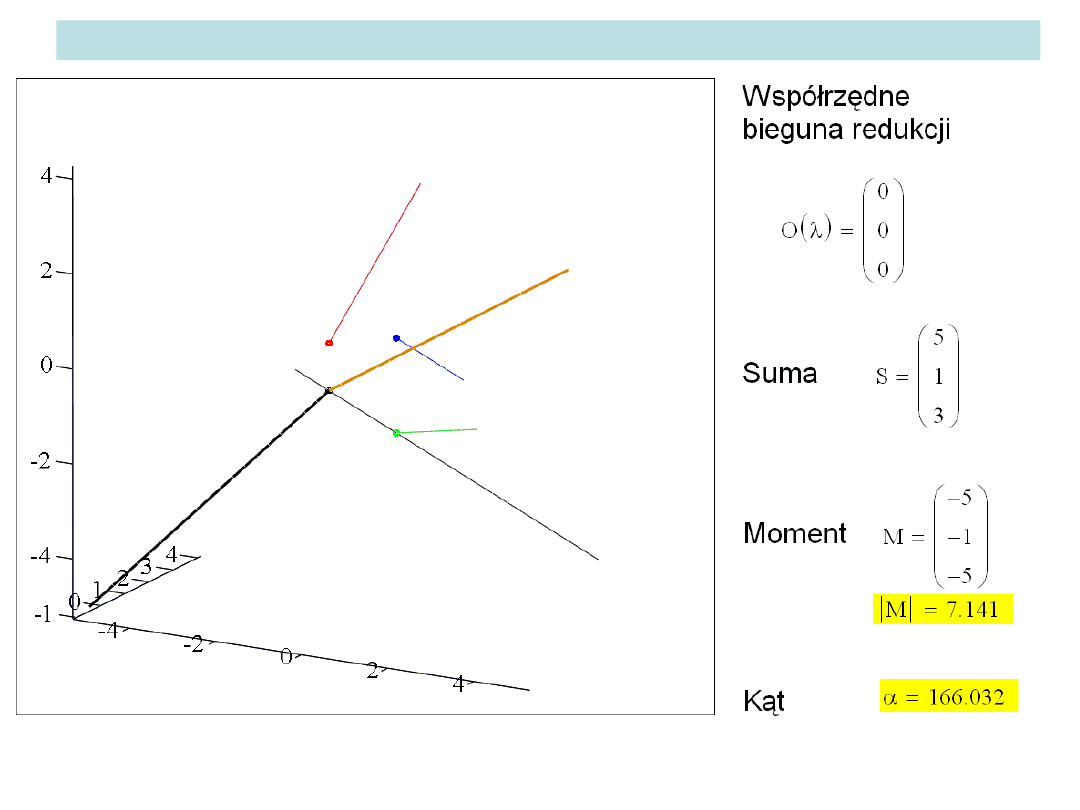
Przypadek ogólny: parametr układu jest różny od 0 – przykład:

Dany jest układ trzech sił:

Suma układu:

Moment układu
względem punktu
(0, 0, 0):

Parametr układu:

Zadanie:
Jak zmienia się równoważny układ zredukowany w biegunie redukcji
poruszającym się wzdłuż wybranej prostej.

Równanie parametryczne
przypadkowo wybranej prostej:

(

)

(

)

(

)

(

)

(

)

(

)

a

b

c

A

B

C

�

�

=

=

-

=

-

�

�

�

�

-

�

�

1 2 3

1 1

1

3

2 1

0 0 1

1 1 1

1 1

1

(

) (

) (

) (

)

S =

+

- +

-

=

1 2 3

1 1

1

3

2 1

5 1 3

(

)

(

)

(

)

(

)

(

)

(

) (

)

O

M

-

-

=

+

+

= -

-

-

-

-

-

-

-

-

�

�

�

1 2 3

1 1

1

3

2 1

5

1

5

0 0

1

1

1

1

1

1 1

(

) (

)

O

K S M

= � =

-

-

-

=-

5 1 3

5

1

5

41

o

xλ , y λ , z

λ

=

=

=-

26

Rozwiązanie zadania przy l zmieniającym się w sposób ciągły od 0 do 3

27

Przypadek ogólny: parametr układu jest różny od 0 – rozważania teoretyczne

Punkty, w których układ sił o parametrze K różnym od 0 redukuje się do sumy i
pary sił o momencie równoległym do sumy leżą na prostej zwanej

osią

środkową

Układ sił w punktach osi środkowej redukuje się do

skrętnika

(

)

O

O

O

K S M

S M cos

S,M

const

=

= �

�

=

o

S

(

)

O

O

K

M

S cos

S,M

=

� S

(

)

O

O

M

min

S,M

π

�

ۮ�

�

�

0

S

(

)

O

O

O

O

S

M

M

S

S,M

K

M

S

�

=

�

�

�

=

�

�

=

�

�

0

S

:

O

K

M

S

S

=

�

2

(

)

O

O

O

O

S

M

M

S

S,Mπ

K

M

S

�

=-

�

�

�

=

�

�

=-

�

�

S

:

O

K

M

S

S

=

�

2

28

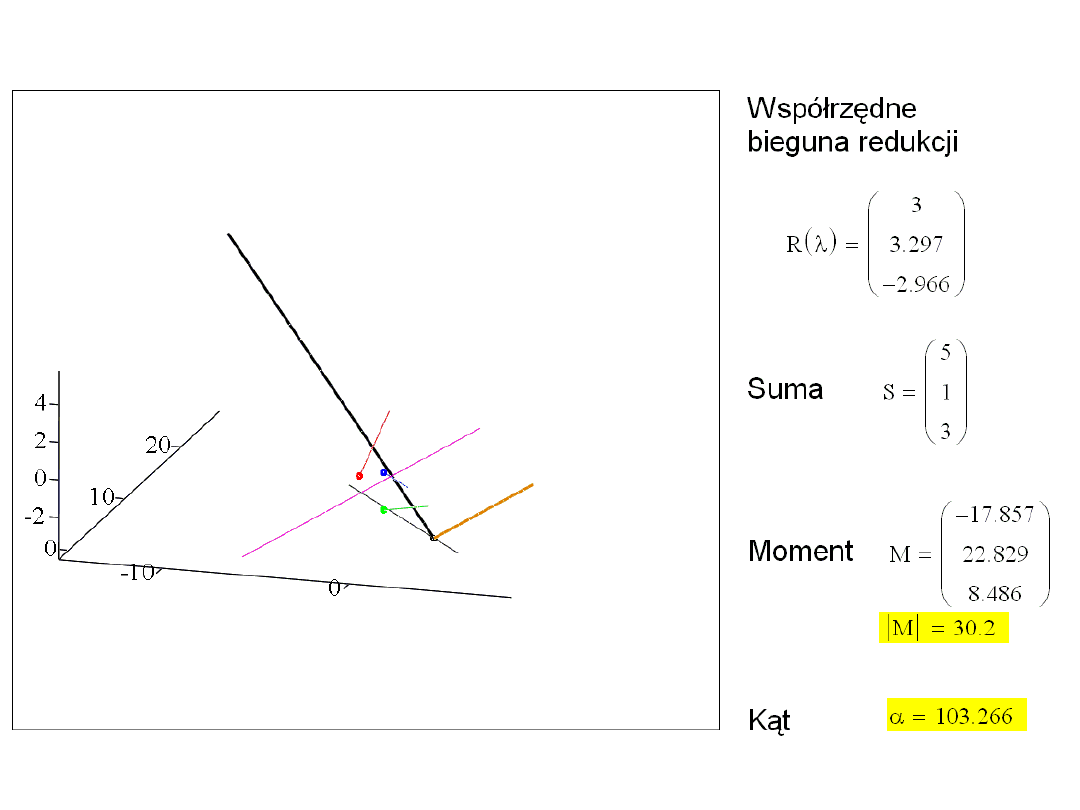
Przypadek ogólny: parametr układu jest różny od 0 – przykład:

Zadanie:
Wyznaczyć oś środkową układu sił z poprzedniego przykładu a następnie
zilustrować zmiany równoważnego układu zredukowanego gdy punkt redukcji
porusza się po prostej przecinającej się z osią środkową

W osi środkowej układ redukuje się do sumy i pary sił o
momencie równoległym do sumy i osiąga minimalną wartość
(skrętnik):

Przyrównując odpowiednie współrzędne wyznacza się równanie krawędziowe
lub parametryczne osi środkowej

Wykorzystując twierdzenie o zmianie bieguna formułuje się wektorowe
równanie osi środkowej:

- punkt leżący na osi środkowej

R

K

M

S

S

=

�

2

(

)

(

)

z

y

d

, gdzie d

x

z

d

� -

-

+ =

�

=

�

-

-

+ =

�

�

3

5 1

0

41

3

5

1

0

35

(

)

(

)

xλ

yλ

d

zλ

d

�

�

=

�

� = -

+

�

�

�

=

-

+

�

�

1

26

1

5

15

3

1

1

5

5

(

)

R

O

K

M

S M

S OR , R x,y,z

S

=

� =

+ �

2

29

30

Przypadek 3:
Suma układu jest różna od zera a parametr jest równy 0

Trzeci szczególny przypadek redukcji do najprostszej postaci

Definicja wypadkowej:
Wypadkowa to układ sił równoważny danemu złożony z jednego wektora

Układ sił w każdym punkcie osi środkowej
redukuje się do jednego wektora

-

wypadkowej

(moment układu jest zawsze prostopadły do
sumy)

Wypadkowa działa wzdłuż ściśle określonej prostej (prosta działania
wypadkowej, oś środkowa) o tej własności, że moment układu względem
punktów tej prostej jest równy 0

O

K

M

S

S

=

� =

2

0

S

K

� � =

0

0