Metody pomiaru i

zarządzania ryzykiem

Obszary zarządzania ryzykiem

• Ryzyko płynności -

korelacja terminów

zapadalności aktywów i wymagalności pasywów

• Ryzyko stopy procentowej -

określenie

terminów przeszacowania aktywów i pasywów

• Ryzyko inwestycji –

wybór instrumentu,

ocena emitenta, strategia doboru instrumentów do
portfela)

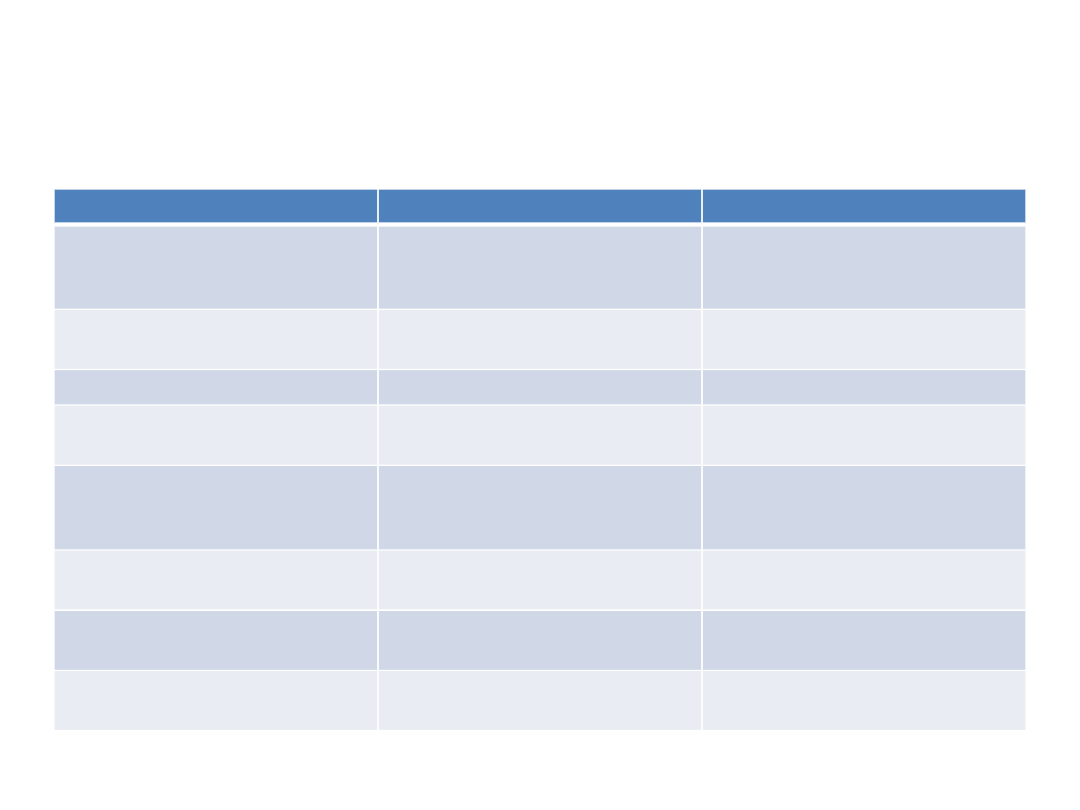
Zestawienie metod pomiaru ryzyka zarządzania aktywami i

pasywami

Metoda pomiaru

Zastosowanie

Stopień trudności

Luka płynności

Ocena dopasowania
przepływów środków
pieniężnych

Niski dla terminów
kontraktowych, średni dla
terminów urealnionych

Ocena depozytów
rdzennych

Ocena struktury pasywów

Niski

Ocena aktywów płynnych

Ocena płynności aktywów

Niski

Luka stopy procentowej

Ocena pozycji o stałym
oprocentowaniu

Niski

Duration

Ocena pozycji o stałym
oprocentowaniu oraz
inwestycji w papiery dłużne

Średni

Analiza wrażliwości

Ocena pozycji o stałym i
zmiennym oprocentowaniu

Wysoki – niezbędne dane
historyczne

Modele VaR

Ocena pozycji o stałym i
zmiennym oprocentowaniu

Wysoki – niezbędne dane
historyczne

Analiza portfelowa

Ocena portfela
inwestycyjnego

Średni

Luka płynności

•

Konstrukcja luki obejmuje zestawienie terminów
zapadalności aktywów i wymagalności pasywów

•

Sprawozdanie luki powinno być urealnione

•

Szczególną wagę należy przywiązywać do
najkrótszych okresów

•

W tych okresach należy zapewnić nadwyżki
środków

Ocena depozytów rdzennych

• Depozyty rdzenne stanowią depozyty

długoterminowe i osady we wkładach

• Depozyty rdzenne wyznaczane są

indywidualnie dla poszczególnych
banków

• Ich miarą jest relacja depozytów

rdzennych do wartości aktywów
ogółem

Wzór

• Wysoka wartość wskaźnika oznacza stabilne

źródła finansowania

• Obliczany na podstawie obserwacji zachowania

klientów w przeszło

ści

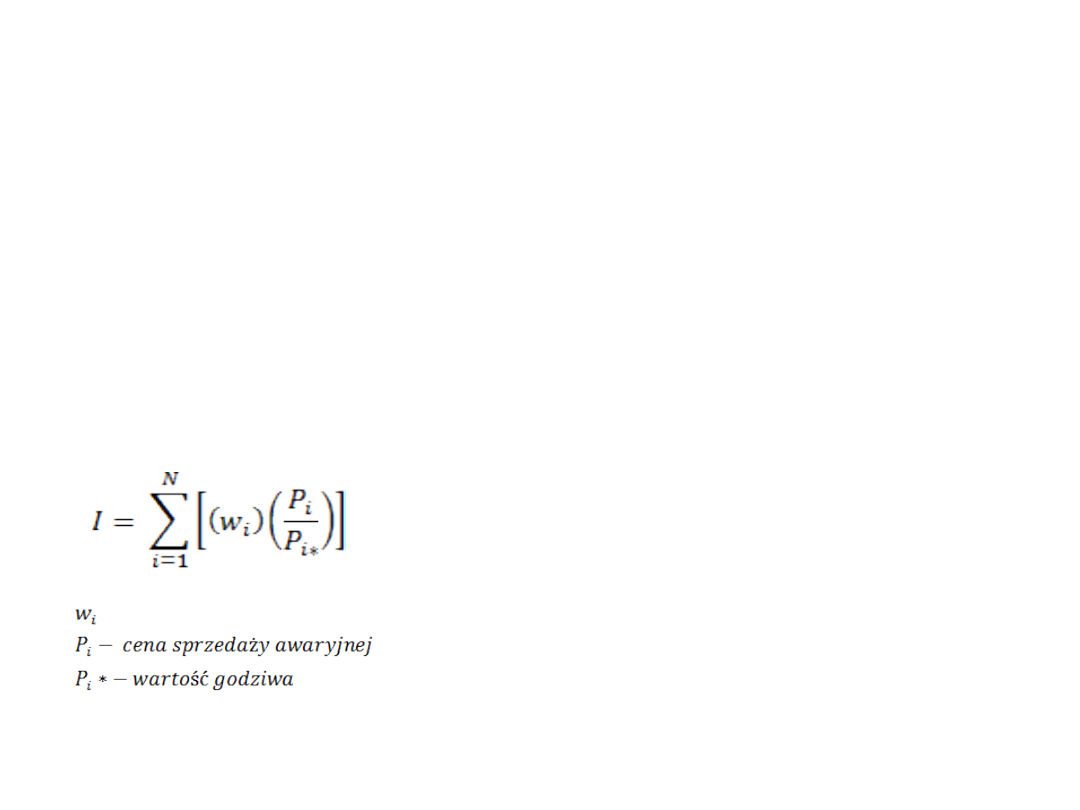
Ocena aktywów płynnych

•

Aktywa płynne ocenia się indeksem
płynności

•

Wysoki poziom wskaźnika świadczy o
wysokiej jakości aktywów płynnych –
możliwości ich sprzedaży po dobrej cenie

•

Wzór:

Gdzie:
udział poszczególnych pozycji w portfelu

Luka stopy procentowej

• Luka bada niedopasowanie terminów

przeszacowania oprocentowania
aktywów i pasywów

• Ocena udziału aktywów i pasywów o

stałej i zmiennej stopie procentowej
w strukturze bilansu (w sumie
bilansowej)

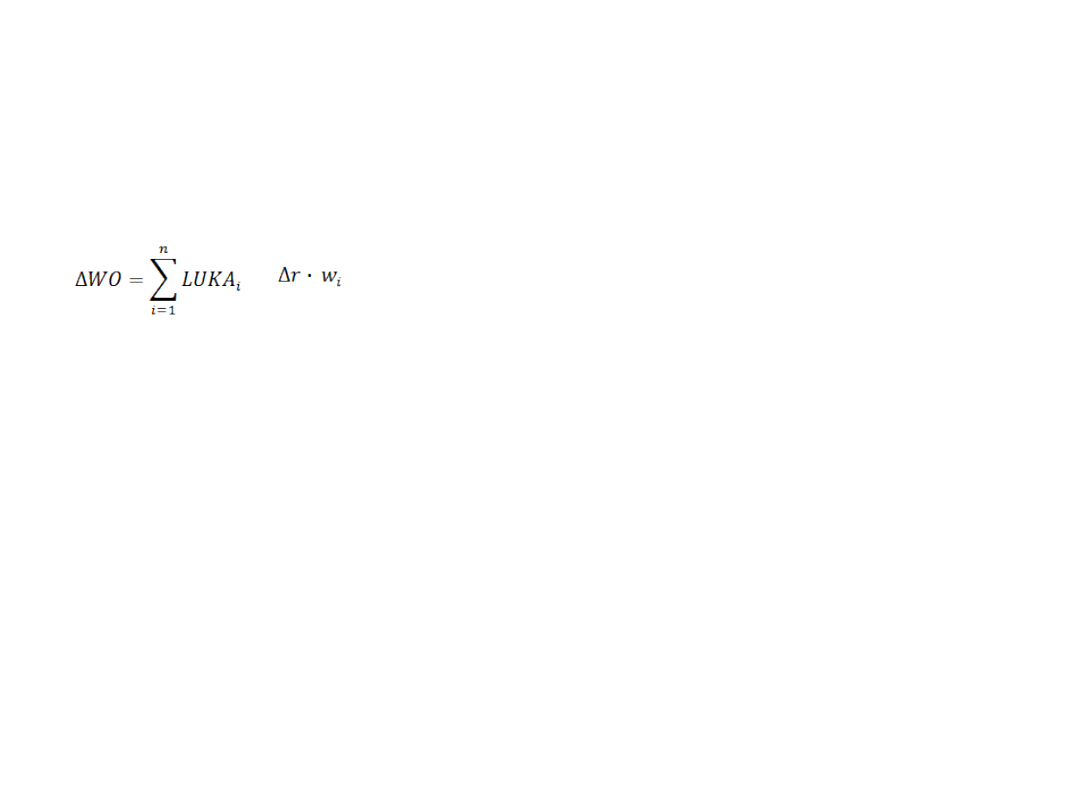
Wpływ stopy procentowej

na wynik finansowy

• Wzór:

x

• gdzie:

ΔWO – zmiana wyniku odsetkowego banku
LUKAi - wielkość luki okresowej w i-tym okresie
Δr – przewidywana zmiana stopy procentowej
Wi - waga mierząca długość okresu, dla którego
zmieni się oprocentowanie
n – liczba wyodrębnionych pasm luki
i – numer okresu

Duration

•

Analiza czasu trwania

•

Pozwala na ocenę wpływu zmian rynkowych stóp
procentowych na wartość rynkową banku, w tym
zmianę wartości inwestycji w dłużne papiery
wartościowe księgi handlowej

•

Średni okres pozostający do wykupu danego
instrumentu finansowego (średni okres
odzyskania środków z inwestycji – zamrożenia
oprocentowania aktywów i pasywów)

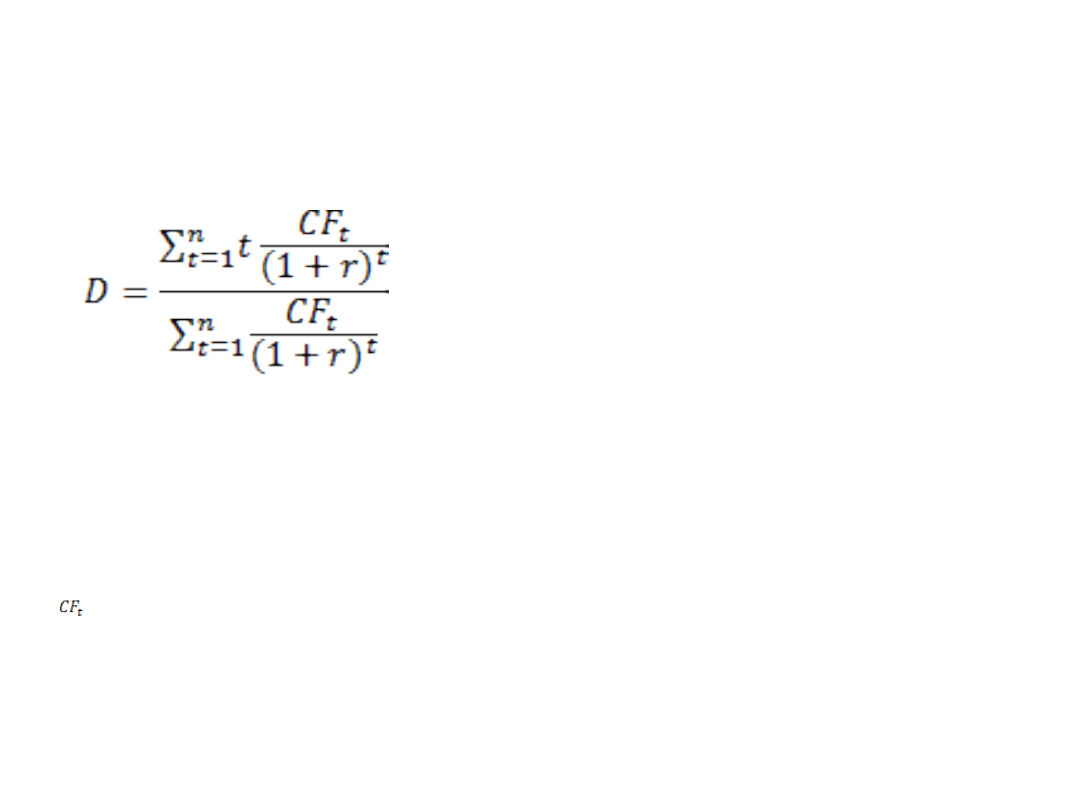
Duration - wzór

gdzie:
n – liczba okresów wypłaty dochodu (kuponów)
t - numer okresu
r – stopa procentowa (dyskonta)
- wpływy z tytułu odsetek i spłaty kapitału w okresie t

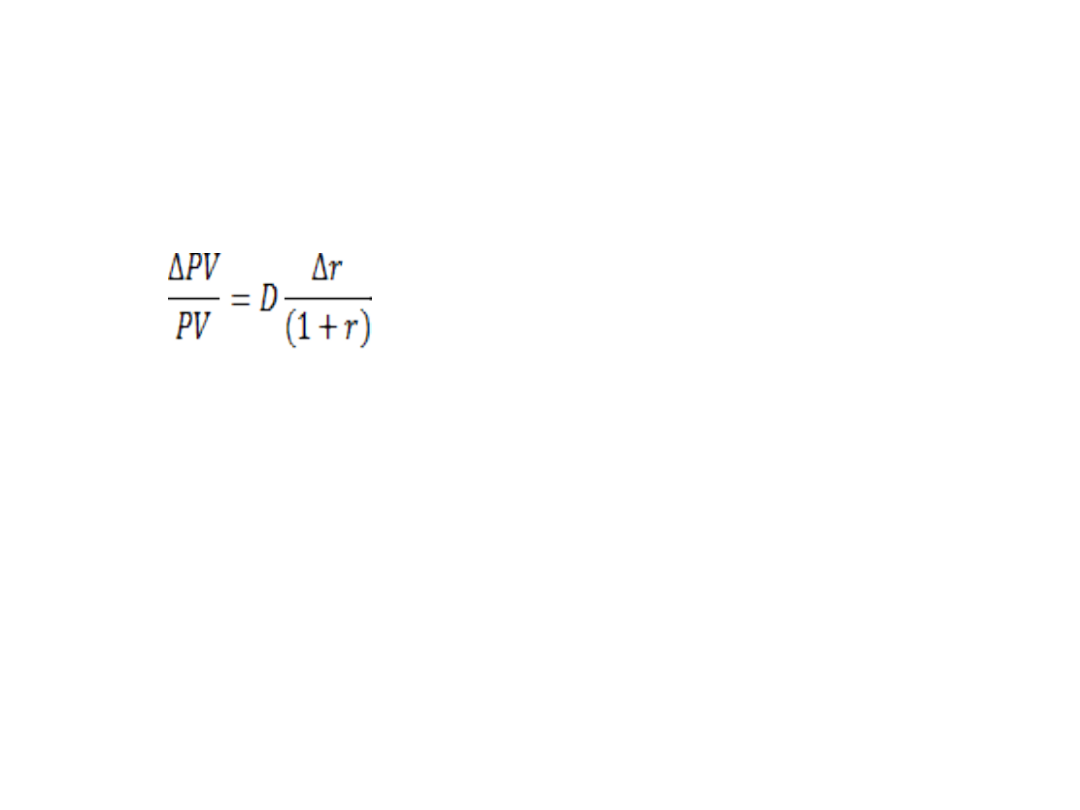
Wpływ zmian stóp procentowych na

wartość inwestycji

gdzie:
PV – wartość instrumentu
r – stopa dyskonta

Luka duration

• Stosowana do analizy ryzyka stopy

procentowej całego banku

• Bada wpływ zmian stóp procentowych

na rynkową wartość kapitału własnego

• DGAP = D

A

- D

p

k

Gdzie:
DGAP – luka duration

D

A

- duration aktywów

D

p

- duration zobowiązań

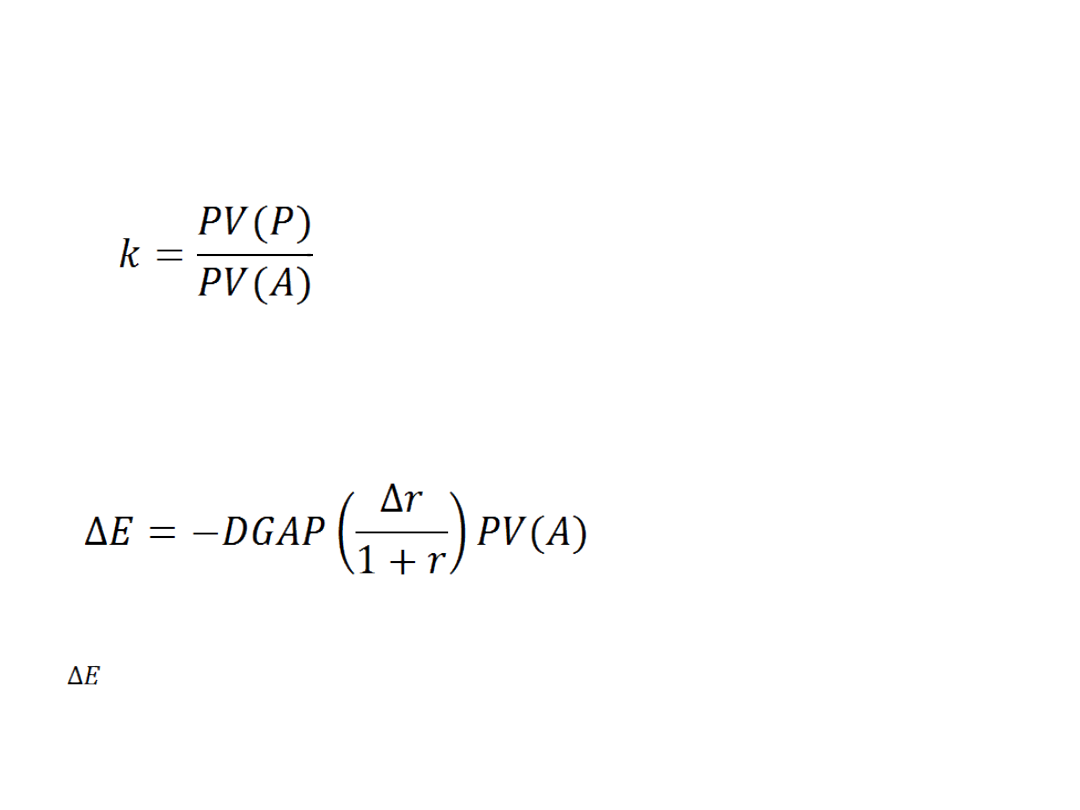
Wzór

• Stosunek wartości rynkowej zobowiązań do wartości rynkowej

aktywów

gdzie:

-- zmiana wartości rynkowej kapitału własnego

PV(A)

– wartość bieżąca aktywów

Analiza wrażliwości

•

Pozycje o zmiennym oprocentowaniu tworzą
ryzyko bazy

•

Każda pozycja o zmiennym oprocentowaniu
otrzymuje określony współczynnik elastyczności
informujący o zmianie oprocentowania danej
pozycji w relacji do zmiany oprocentowania
rynkowego

•

Współczynnik elastyczności obliczany jest na
podstawie danych historycznych

Miary wrażliwości

• Badają odchylenie od wartości

docelowej powstające na skutek
jednostkowej zmiany parametru
rynkowego

• Należą do nich wariancja i odchylenie

standardowe in plus i in minus

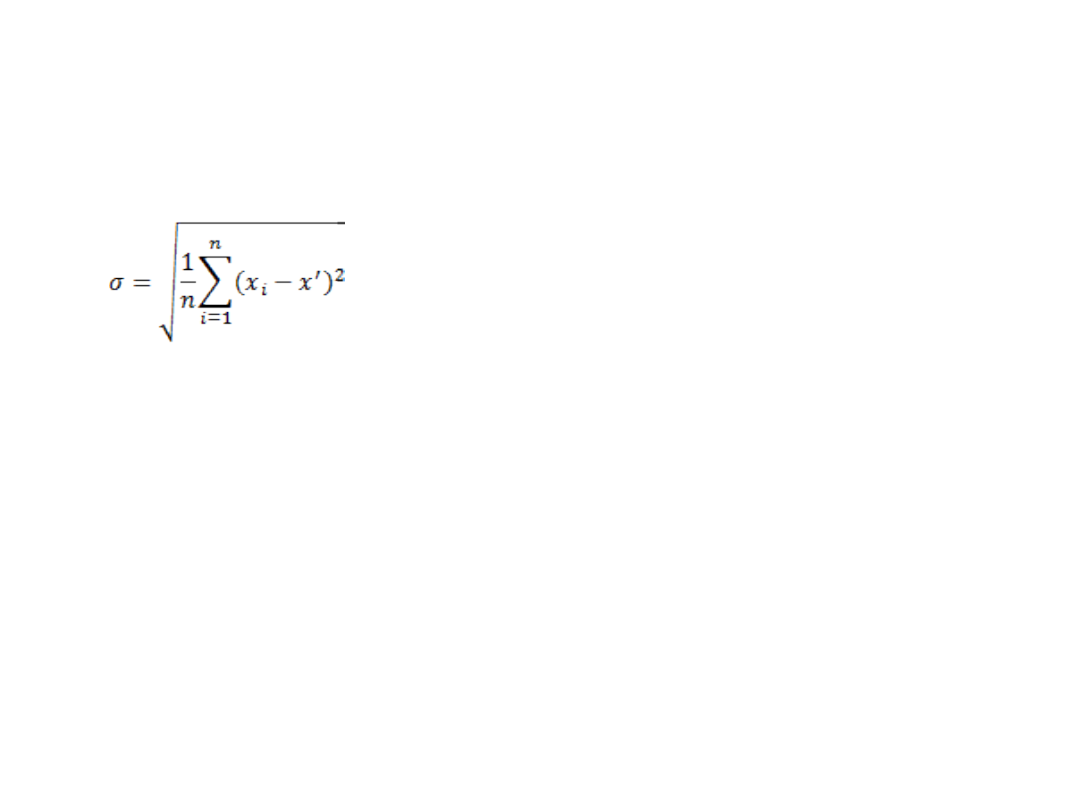
Odchylenie standardowe - wzór

Gdzie:
n - liczba obserwacji (dla małej próby n -1)
x – analizowana zmienna
x’ – średnia z obserwacji analizowanej zmiennej

Modele wartości zagrożonej VaR

• Syntetyczna miara skali ryzyka

• Kwotowe wyrażenie poziomu ryzyka z

zastosowaniem metod statystycznych

• Możliwość porównania różnych rodzajów

ryzyka, w tym:

- Kredytowego
- Stopy procentowej
- Inwestycji
- Rynkowego
- Operacyjnego

var

• Jest miarą strat oczekiwanych i

nieoczekiwanych

• Koncentruje się na odchyleniach negatywnych

• Jej kompleksowość wynika z połączenia oceny

zmienności i wrażliwości

• Wymaga oceny rozkładu prawdopodobieństwa

Formuła var

• Gdzie:

-

wartość początkowa portfela

-

stopa zwrotu z inwestycji

-

poziom istotności

-

wartość oczekiwana stopy zwrotu

- współczynnik wynikający z rozkładu normalnego, którego
wartość zależy od poziomu istotności
- odchylenie standardowe

Współczynnik c

• Dla rozkładu jednostronnego wynosi

VaR = oczekiwana strata (zysk) – maksymalna strata przy danym α
Lub
VaR (absolutny) = maksymalna strata przy danym α

α(%)

c

5

1,65

1

2,33

0,13

3,0

0,03

3,43

Analiza portfelowa

• Pozwala na analizę, oczekiwanych

stóp zwrotu i ryzyka inwestycji
łącznie dla instrumentów
wchodzących w skład portfela

• Ryzyko portfela wyrażone jest

odchyleniem standardowym i
korelacją między poszczególnymi
aktywami (instrumentami)

• Im mniejsza korelacja, tym mniejsze

ryzyko portfela

Wzór na ryzyko portfela

• Portfel składa się z dwóch aktywów

Gdzie:
- ryzyko portfela
- udział aktywu 1 w portfelu
- udział aktywu 2 w portfelu ( )
- ryzyko aktywu 1 mierzone odchyleniem standardowym
- ryzyko aktywu 2 mierzone odchyleniem standardowym
- korelacja między stopami zwrotu aktywu 1 i aktywu 2
- kowariancja (łączna zmienność) aktywów 1 i 2