PROJEKTOWANIE
DYSKRETNYCH UKŁADÓW
MECHANICZNYCH - SYNTEZA

Szymon Kraut

Informacje na temat:

•

stanów rezonansowych maszyn i

urządzeń

•

tłumienia

•

metod wyznaczania charakterystyki

dynamicznej oraz dalszej

syntezy

układów

dyskretnych

21-12-1

2

Wstęp teoretyczny

Ważne pojęcia

Synteza

– zadanie poszukiwania parametrów

oraz struktury układów, spełniających zadane
własności dynamiczne w postaci widma
częstości.

21-12-1

3

Stany rezonansowe maszyn i urządzeń

Stany rezonansowe są to częstotliwości w
których w urządzeniu powstają
największe drgania. Ze względu na ich
szkodliwe działanie, pożądany jest taki
dobór częstotliwości drgań własnych, aby
były one poza zakresem częstotliwości
drgań generowanych przez urządzenie
podczas prawidłowej pracy. Istnieją także
przypadki, w których stany rezonansowe
działają pozytywnie.

21-12-1

4

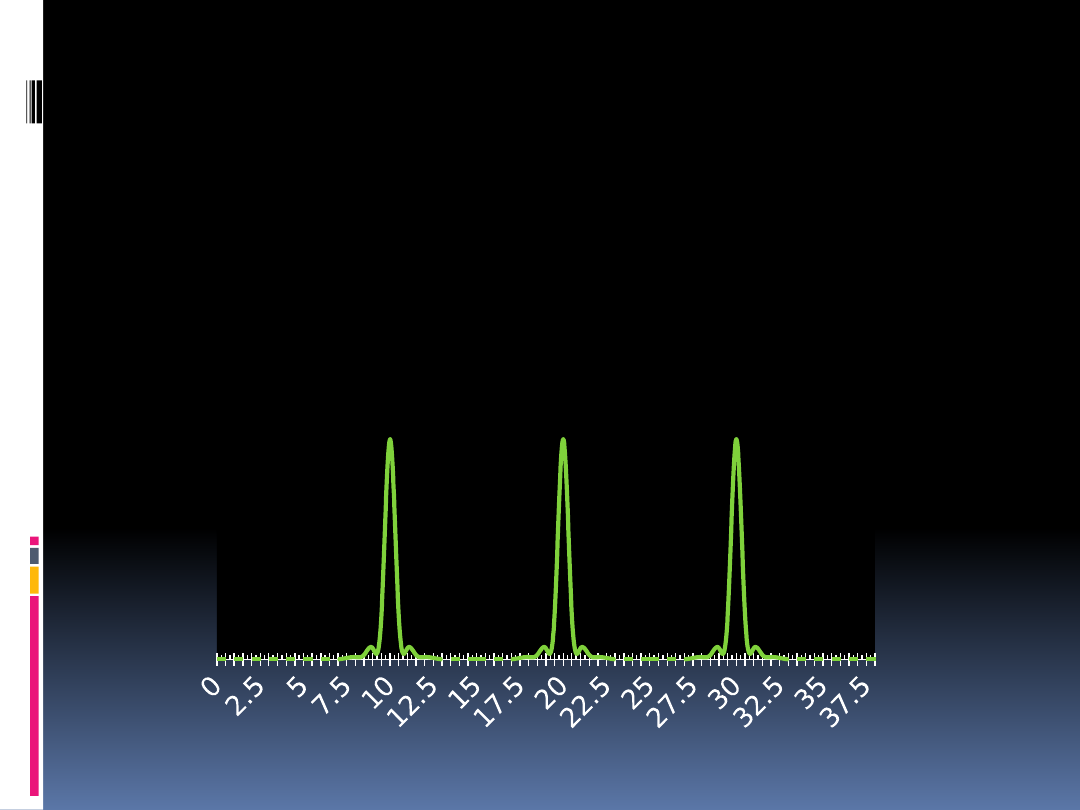
Tłumienie a stany rezonansowe

Tłumienie obniża amplitudę drgań,
co pozwala maszynie na wyjście ze
stanu rezonansu. W maszynie
pojawia się wiele częstotliwości
drgań własnych.

21-12-1

5

Hz

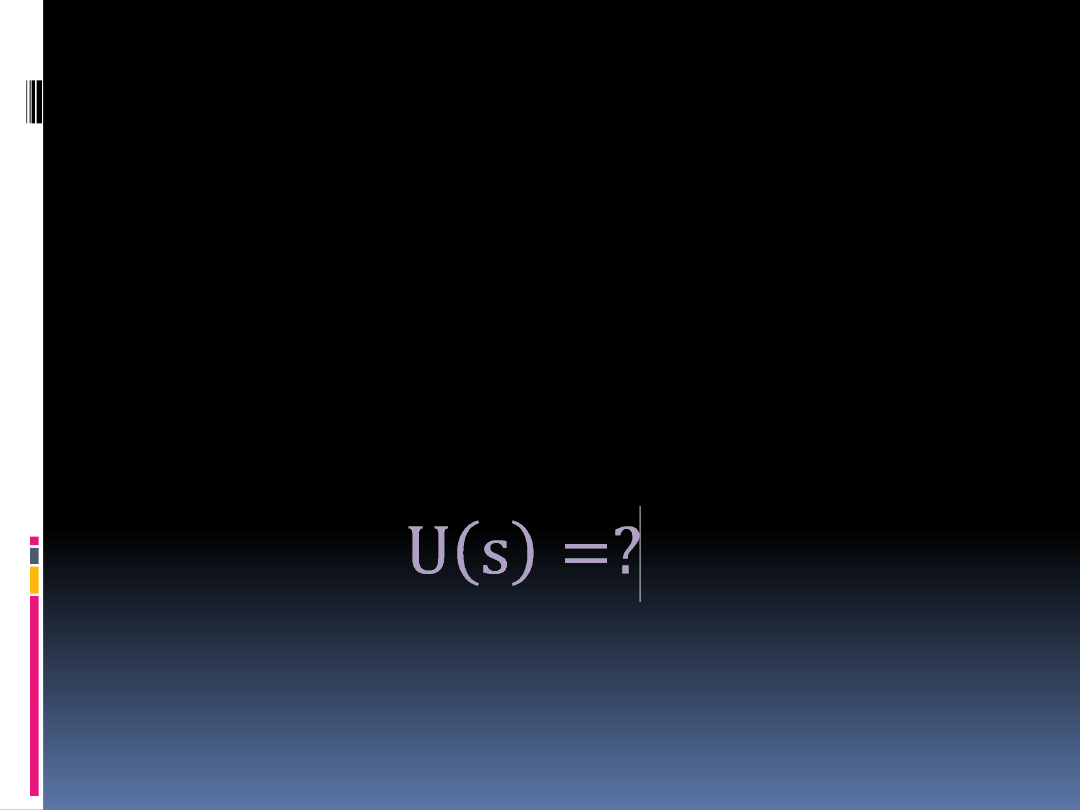
Problem syntezy układów

Aby dokonać syntezy układu
mechatronicznego, należy najpierw
wyznaczyć

charakterystykę

dynamiczną

.

21-12-1

6

3 kroki wyznaczania charakterystyki dynamicznej

1.

Przyjąć rodzaj syntezowanej funkcji,
czyli określić czy dana funkcja
będzie ruchliwością V(s), czy też
powolnością U(s).

2.

Przyjąć wymagania odnośnie
tłumienia.

3.

Wyznaczyć charakterystykę
dynamiczną V(s) [U(s)] w postaci
funkcji wymiernej z dokładnością do
stałej H.

21-12-1

7

Synteza charakterystyki

Istnieje wiele możliwości syntezy
charakterystyki zgodnie z
założeniami. Liczba możliwych
struktur zależy od częstości
rezonansowych i nałożonych na
układ utwierdzeń.

21-12-1

8

Synteza powolności układów
przytwierdzonych.

21-12-1

9

Przykład rozwiązania zadania

Wymagania

Wymagania, jakie spełnić ma układ
podane są w postaci ciągu częstości
rezonansowych i
antyrezonansowych:

21-12-1

10

























zera

s

rad

s

rad

s

rad

bieguny

s

rad

s

rad

s

rad

25

,

15

,

0

30

,

20

,

10

4

2

0

5

3

1













1

Założenia

1.

Poszukiwana funkcja
charakterystyczna jest powolnością
U(s).

2.

Przyjmuje się wymagania do
tłumienia dla dwóch przypadków:

1.

Tłumienie jest proporcjonalne do elementu
inercyjnego

2.

Tłumienie jest proporcjonalne do elementu
sprężystego

21-12-1

11

s

1

8

0

się

przyjmuje

,

m

Ns

2

,

h

hm

b

i

i





s

01

0

się

przyjmuje

,

s

1

2

,

m

Ns

2

,

λω

h

c

b

n

n

i

i











2

3

Charakterystyka dynamiczna

1.

Gdy spełnione jest założenie (

11.2

)

21-12-1

12

 















2

4

2

2

2

2

2

5

2

2

3

2

2

1

2

2

2

2

2

2

































hs

s

hs

s

s

hs

s

hs

s

hs

s

H

s

U

 

s

s

s

s

s

s

s

s

s

s

s

H

s

U

140625

6800

914

16

36000000

3920000

579600

22912

1529

24

2

3

4

5

2

3

4

5

6























4

4

Charakterystyka dynamiczna

2.

Gdy spełnione jest założenie (

11.3

)

21-12-1

13

 















2

4

4

2

2

2

2

2

2

5

5

2

2

3

2

2

2

1

1

2

2

2

2

2

2

































s

h

s

s

h

s

s

s

h

s

s

h

s

s

h

s

H

s

U

 

s

s

s

s

s

s

s

s

s

s

s

H

s

U

140625

14062

6

,

1201

5

,

42

36000000

5400000

760000

53500

2625

70

2

3

4

5

2

3

4

5

6























5

5

Charakterystyka dynamiczna

Przeprowadzając syntezę charakterystyk (

12.4

)

i (

13.5

), należy podać syntezie powolność,

opisującą drgania nie tłumione w postaci:

a następnie uwzględnić założenia dotyczące
tłumienia (

11.2

) i (

11.3

)

21-12-1

14

 















2

4

2

2

2

2

2

5

2

2

3

2

2

1

2























s

s

s

s

s

s

H

s

U

 

s

s

s

s

s

s

s

s

s

s

s

H

s

U

140625

14062

6

,

1201

5

,

42

36000000

5400000

760000

53500

2625

70

2

3

4

5

2

3

4

5

6























6

6

Wstęp do właściwej syntezy

Sprecyzowane wcześniej wymagania
w postaci charakterystyk
dynamicznych (

10.1-14.6

) poddaje

się syntezie jedną z metod:



rozkładu na ułamek łańcuchowy



rozkładu na ułamki proste



metodą mieszaną



wykorzystując algorytm wyznaczania
elementu sprężystego

21-12-1

15

Przystępując do syntezy rozpatrywanych
funkcji (

12.4

) i (

13.5

) określa się liczbę

nałożonych na układ utwierdzeń. Przy
wyznaczaniu p elementów typu c/s należy
rozpatrywaną charakterystykę w postaci
(

14.6

) przy założeniach (

11.2

) i (

11.3

),

pomnożyć przez, która w przypadku
powolności (

14.6

) nie powinna przekroczyć

p=3, ponieważ liczba częstości
rezonansowych (biegunów) jest równa 3.

21-12-1

16

Synteza powolności z zastosowaniem algorytmu
wyznaczania elementu sprężystego

1

1





p

p

s

s

Zakłada się, że liczba nałożonych na
układ utwierdzeń n=2. Zatem funkcja
charakterystyczna (.) przyjmuje postać:

Dzieląc współczynnik stojący przy
najniższej potędze licznika przez
współczynnik stojący przy najniższej
potędze mianownika otrzymuje się
wartość górnej granicy przedziału, z
której wyznacza się dwójnik typu
sprężystego, czyli:

21-12-1

17

 

2

4

6

3

5

7

140625

850

36000000

490000

1400

'

s

s

s

s

s

s

s

H

s

U

















s

N

256

,

0

1



c

7

-

W następnym kroku mianownik powolności
(

17.7

) zapisuje się jako:

Otrzymany w ten sposób wielomian mnoży się
przez wartość przyjętej sztywności w następujący
sposób:

Odejmując wielomian (.

9

) od licznika rozważanej

powolności (

17.7

), otrzymuje się następujące

wyrażenie:

21-12-1

18





s

s

s

s

140625

850

3

5









s

s

s

140625

850

180

3

5









s

s

s

s

10687500

337000

1220

3

5

7







8

9

1

0

Po wykonaniu powyższych działań powolność
(

17.7

) można zapisać jako:

gdzie:

Z (.

11

) wynika, że pierwszym wyznaczonym

elementem jest dwójnik typu sprężystego, czyli:

21-12-1

19

 

 

s

U

s

s

U

1

180

'





 

2

4

6

3

5

7

140625

850

10687500

337000

1220

'

s

s

s

s

s

s

s

s

U













s

s

c

180

1



1

1

1

2

-

Wyznaczoną powolność U1(s) poddaje się
rozkładowi na ułamek łańcuchowy. Ostatecznie
otrzymuje się charakterystykę dynamiczną w
następującej postaci ułamka łańcuchowego:

Uwzględniając założenie (

11.2

), wyznacza się

wartości dwójników typu tłumiącego:

21-12-1

20

 

s

m

s

c

c

s

s

m

c

s

s

m

s

c

s

U

3

4

3

2

2

1

1

1

1

1

1

1















m

Ns

762

.

1

m

Ns

854

.

1

m

Ns

600

.

1

3

2

1







b

b

b

1

3

1

4

Otrzymany układ dyskretny

21-12-1

21

n=3, p=2

m

1

m

2

m

3

c

1

b

1

c

2

c

3

c

4

b

3

b

2

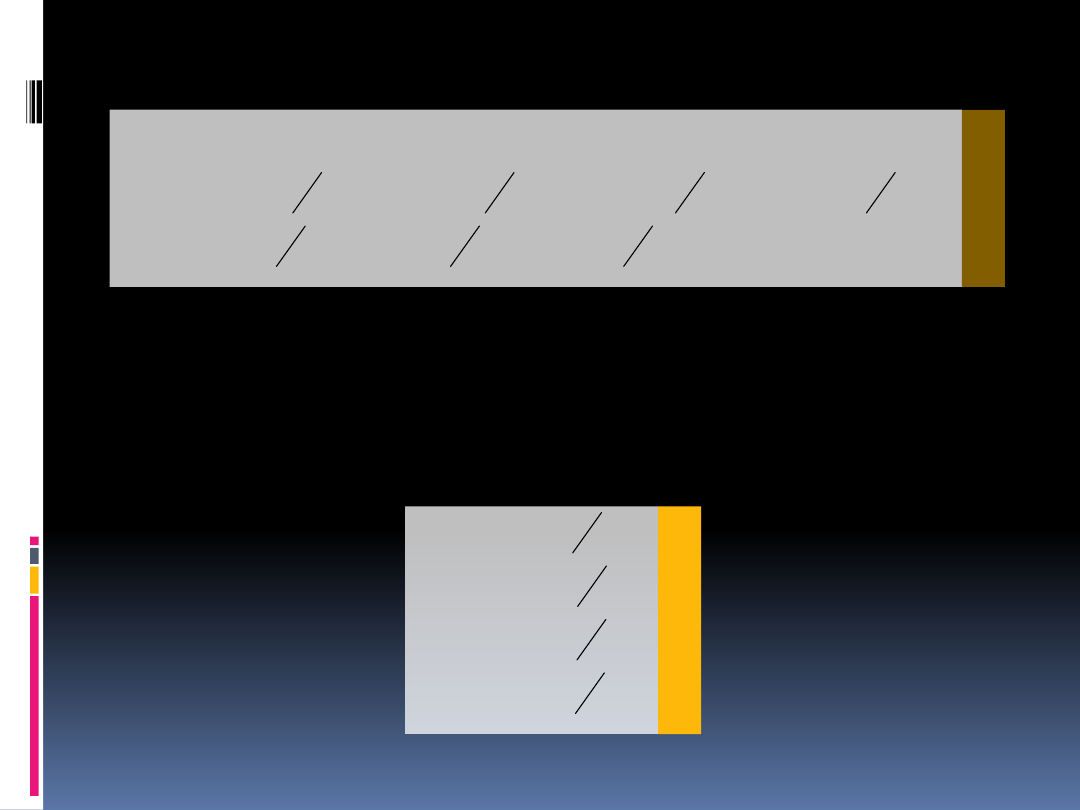
Wartości otrzymanych dwójników są
następujące:

Rozpatrując drugie założenie (

11.3

) dotyczące

tłumienia, warunek proporcjonalności wartości
tłumienia do wartości dwójników typu
sprężystego, otrzymuje się:

21-12-1

22

m

Ns

762

.

1

,

m

Ns

854

.

1

,

m

Ns

600

.

1

m

N

017

.

176

,

m

N

471

.

209

,

m

N

000

.

370

,

m

N

000

.

180

kg

101

.

1

,

kg

159

.

1

,

kg

000

.

1

3

2

1

4

3

2

1

3

2

1





















b

b

b

c

c

c

c

m

m

m

m

Ns

760

.

1

m

Ns

095

.

2

m

Ns

700

.

3

m

Ns

800

.

1

4

3

2

1









b

b

b

b

-

1

5

Otrzymany układ dyskretny

21-12-1

23

n=3, p=2

m

1

m

2

m

3

c

1

b

1

c

2

c

3

c

4

b

3

b

2

b

3

Otrzymane w ten sposób elementy mają
następujące wyniki:

21-12-1

24

m

Ns

760

.

1

,

m

Ns

095

.

2

,

m

Ns

700

.

3

,

m

Ns

800

.

1

m

N

017

.

176

,

m

N

471

.

209

,

m

N

000

.

370

,

m

N

000

.

180

kg

101

.

1

,

kg

159

.

1

,

kg

000

.

1

4

3

2

1

4

3

2

1

3

2

1























b

b

b

b

c

c

c

c

m

m

m

-

Liczba możliwości

n=3 – liczba częstotliwości rezonansowych

21-12-1

25

3

Bibliografia:



Buchacz A., Dymarek A., Dzitkowski T.: Projektowanie i badanie
wrażliwości ciągłych i dyskretno-ciągłych układów mechanicznych
o żądanym widmie częstotliwości w ujęciu grafów i liczb
strukturalnych. Monografia, Politechnika Śląska, Gliwice 2005.



Dymarek A.: Odwrotne zadanie dynamiki tłumionych
mechanicznych układów drgających w ujęciu grafów i liczb
strukturalnych. Politechnika Śląska, Gliwice 2001.

21-12-1

26

KONIEC