Agnieszka Kozub

Zad 72.

Napisać program rozwiązujący równanie f(x)=0 metodą
, gdzie n
,
-dany punkt oraz
. W implementacji tej metody musi być podana funkcja
. Wprowadzi ograniczenie na ilość iteracji i zwiększa gdy iteracji jest za mało. Drukowa ilość faktycznie wykonanych iteracji. Zastosować ten program do wyznaczenia najmniejszej wartości danej funkcji w przedziale [a,b]. Rozważy przynajmniej dwie rożne funkcje.

1. Rozwiązanie problemu i opis programu

Aby tą metodą znaleźć rozwiązanie równania f(x) = 0 należy na początku wyznaczyć punkt
. Polegała na badaniu dla jakich argumentów wartości
i
mają różne znaki dla a=-0.05 , r=0.1 , i=0,1,2… (lub
i
- aby zbadać całą prostą a nie tylko
). Punkt
jest wtedy środkiem odcinka
, a jego wartość to
(podobnie
=
). Procedura ta została wykonana w funkcji x1. Ponieważ funkcja log(x) jest określona jedynie na wartościach
stworzyłam funkcję x2 szukającą wartość
na dodatniej półosi.

Funkcja zero szuka rozwiązania równania f(x)=0 szukając punktu x według zadanej metody, tj. (po uproszczeniu)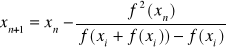
.Użyta zmienna it to licznik wykonanych iteracji.

Najmniejszą wartość funkcji w przedziale [a,b] (w programie [0.5,10]) wyznaczyłam metodą : porównałam ze sobą wartości na krańcach przedziału oraz w miejscu, w którym pochodna spełnia
i wybrałam wartość najmniejszą.

2.Opracowanie wyników

Dla funkcji
pochodna

A otrzymany wynik to:

dla x=1

to wartość najmniejsza na podanym przedziale.

Położenie tych punktów przedstawione jest na wykresie:

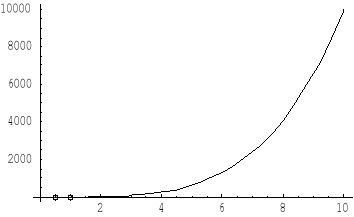
Oraz w przybliżeniu:

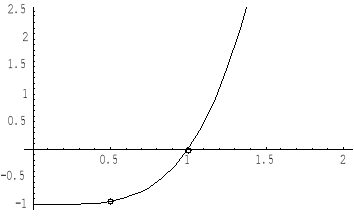
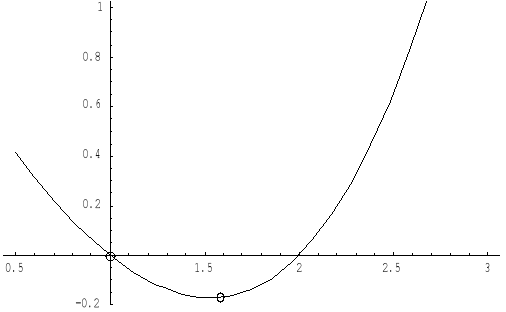
Dla drugiej funkcji
pochodna

dla x=1 , natomiast
jest wartością najmniejszą w tym przedziale.

Zarówno wykres funkcji jak i wyznaczone punkty przedstawiają wykresy:

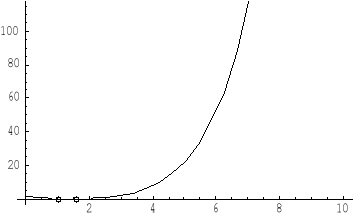
Kod Programu

//Agnieszka Kozub zad.72

#include <stdio.h>

#include <iostream.h>

#include <math.h>

#define r 0.1

//funkcja f1

double f1(double x){

return pow(x,4)-1;

}

//funkcja f2

double f2(double x){

return pow(2,x)-2*x;

}

//pochodna funkcji f1

double f11(double x){

return 4*pow(x,3);

}

//pochodna funkcji f2

double f21(double x){

return -2+pow(2,x)*log10(x)/log10(2);

}

//funkcja wyznaczająca x0

double x1(double f(double x)) {

double pom1, pom2;

pom1=-0.05; pom2=-0.05+r;

while ( (f(pom1))*(f(pom2))>=0 && (f(-pom1))*(f(-pom2))>=0){

pom1 +=r;

pom2 +=r;

}

if((f(pom1))*(f(pom2))<0)

return (pom1+pom2)/2;

else

return (-pom1-pom2)/2;

}

//funkcja wyznaczające x0 dla f21

double x2() {

double pom1, pom2;

pom1=0.05; pom2=0.05+r;

while ( f21(pom1)*f21(pom2)>=0 ){

pom1 +=r;

pom2 +=r;

}

return (pom1+pom2)/2;

}

//szukanie x dla którego f(x)=0

double zero(double x1, int ilosc, double f(double)){

double xn;

int it = 0; //licznik iteracji

xn=x1;

while (it<ilosc && f(xn)!=0 ){ //ilość to ograniczenie ilości wykonywanych iteracji

xn= xn- pow(f(xn),2)/(f(xn + f(xn)) - f(xn));

it++;

}

cout << "ilosc wykonanych iteracji: " << it << endl;

return xn;

}

int main(){

double wynik1, wynik2, min1,xm1, min2,xm2;

double pomocnicza;

cout << "Program rozwiazuje rownanie f(x)=0 metoda Steffensena dla dwoch funkcji:"<<endl;

cout << "(1) f(x)= x^4-1" << endl;

cout << "(2) f(x) = 2^x - 2*x" << endl;

cout <<"Oraz szuka najmniejszej wartosci kazdej z funkcji na przedziale [0.5,10]."<<endl << endl;

cout << "Dla funkcji (1): "<< endl ;

wynik1 = zero(x1(f1),10,f1);

cout << "f(x)=0 dla x=" << wynik1 << endl << endl;

//szukanie minimum funkcji f1

min1=f1(0.5);

xm1=0.5;

if(min1>f1(10)){

min1=f1(10);

xm1=10; }

pomocnicza=zero(x1(f11),10,f11);

if(pomocnicza>0.05 && pomocnicza <10){

if(min1>f1(pomocnicza)){

min1=f1(pomocnicza);

xm1=pomocnicza; }

}

cout<< "funkcja przyjmuje minimum w punkcie xmin=" << xm1 << ", f(xmin)=" << min1 << endl;

cout <<endl<< endl << "Dla funkcji (2): "<< endl ;

wynik2 = zero(x1(f2),10,f2);

cout << "f(x)=0 dla x=" << wynik2 << endl << endl;

//szukanie minimum dla funkcji f2

min2=f2(0.5);

xm2=0.5;

if(min2>f2(10)){

min2=f2(10);

xm2=10; }

pomocnicza=zero(x2(),16,f21);

if(pomocnicza>0.05 && pomocnicza <10){

if(min2>f2(pomocnicza)){

min2=f2(pomocnicza);

xm2=pomocnicza; }

}

cout <<"funkcja przyjmuje minimum w punkcie xmin=" << xm2 << ", f(xmin)=" << min2 << endl;

return 0;

}

---