
Politechnika Śląska
Gliwice, 2006/2007
Wydział: Automatyki, Elektroniki i Informatyki
Semestr: 6 (letni)
Kierunek: Automatyka i robotyka
Podstawy Automatyki
– laboratorium
Ćw 2. Podstawowe elementy automatyki.
Data ćwiczeń laboratoryjnych:
28.02.2007
Grupa: 1
Sekcja: 3
Skład osobowy sekcji:
Zięba Andrzej
Bojko Marcin
Pawliczek Krystian

1. Cel ćwiczenia:
Celem ćwiczenia jest zapoznanie się z charakterystykami podstawowych elementów
dynamicznych oraz metodami identyfikacji ich parametrów. Dostarczone dane pomiarowe, w
postaci odpowiednich wektorów, pozwalają na wykreślenie przebiegów czasowych, charakterystyk
amplitudowo-fazowych oraz charakterystyk Bodego wybranych elementów. Wykreślony komplet
charakterystyk jednoznacznie określa typ elementu oraz pozwala na wyznaczenie parametrów
opisujących poszczególne elementy.
2. Program ćwiczenia:
1. Na podstawie otrzymanych danych wykreślić:
a. odpowiedź czasową badanego elementu
b. charakterystykę amplitudowo-fazową
c. charakterystyki Bodego
2. Ocenić typ badanego elementu na podstawie otrzymanych charakterystyk.
3. Wyznaczyć parametry elementu.
4. Wprowadzić do Matlab-a transmitancję elementu z wyznaczonymi parametrami.
5 Porównać charakterystyki otrzymanej transmitancji z charakterystykami z p.1.
6. Sprawdzić poprawność wyznaczonych stałych.
Czynności te należy powtórzyć dla czterech zadań dostarczonych przez prowadzącego.
3. Kod źródłowy programu:
Z uwagi na występujące podobieństwa w źródłach dla zadań zamieszczono tylko kod
źródłowy programu dla zadania 1 i kod źródłowy funkcji rysowania wykresów.
Kod źródłowy funkcji rysowania wykresów zapisany w pliku „rysuj.m”:
function rysuj(t,y,w,re,im);
w_min=10^(-3.5);
w_max=10^2;
subplot(3,2,1);
plot(t,y,'r');
xlabel('Czas t (sek)','Position',[max(xlim) min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Wyjscie y(t)','Position',[min(xlim) max(ylim)],'Horizontal','Right','Vertical','Top');
xlim(xlim);
ylim(ylim);
grid on;
subplot(3,2,2);
plot(re,im);
xlabel('Re K(jw)','Position',[max(xlim) min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Im K(jw)','Position',[min(xlim) max(ylim)],'Horizontal','Right','Vertical','Top');
xlim(xlim);
ylim(ylim);
grid on;
mag=(re.^2+im.^2).^0.5;
subplot(3,2,3);
semilogx(w,mag);
xlabel('Pulsacja w (rad/sek)','Position',[w_max
min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Modul |K(jw)|','Position',[w_min max(ylim)],'Horizontal','Right','Vertical','Top');
xlim([w_min w_max]);
grid on;
subplot(3,2,4);
semilogx(w,re);

xlabel('Pulsacja w (rad/sek)','Position',[w_max
min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Re K(jw)','Position',[w_min max(ylim)],'Horizontal','Right','Vertical','Top');
xlim([w_min w_max]);
grid on;
fi=atan2(im,re)*180/pi;
subplot(3,2,5);
semilogx(w,fi);
xlabel('Pulsacja w (rad/sek)','Position',[w_max
min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Faza fi(w) (st)','Position',[w_min max(ylim)],'Horizontal','Right','Vertical','Top');
xlim([w_min w_max]);
grid on;
subplot(3,2,6);
semilogx(w,im);
xlabel('Pulsacja w (rad/sek)','Position',[w_max
min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Im K(jw)','Position',[w_min max(ylim)],'Horizontal','Right','Vertical','Top');
xlim([w_min w_max]);
grid on;
Kod źródłowy programu dla zadania 1 zapisany w pliku „Zad1.m”:
close all;
clear all;
clc;
w_min=10^(-3.5);
w_max=10^2;
% Wczytanie danych pomiarowych:
load('cw_2_gr_1_sek_3_zad_1.mat');
% Wyrysowanie charakterystyk:
rysuj(t,y,w,re,im);
% Z wyrysowanych charakterystyk stwierdzono ze badanym elementem jest
% element proporcjonalno-calkujacy { K(s)=(1+s*T)/(1+s*alpha*T), alpha>1 }
% Identyfikacja parametrow (alpha,T) z charakterystyki odpowiedzi skokowej:
disp('Identyfikacja parametrow (alpha,T) z charakterystyki odpowiedzi skokowej:');
figure;
plot(t,y,'r'); % przebieg odpowiedzi skokowej
xlim([0 150]);
ylim([0.6 1.2]);
hold on;
plot([0 150],[1 1],'b'); % prosta o rownaniu y=1
a=(y(2)-y(1))/(t(2)-t(1));
b=y(1)-t(1)*(y(2)-y(1))/(t(2)-t(1));
plot([0 50],[b 50*a+b],'b'); % prosta styczna do char. dla t=0
xlabel('Czas t (sek)');
ylabel('Wyjscie y(t)');
grid on;
% Odczytujemy zaznaczone na charakterystyce wartosci (1/alpha, alpha*T):
disp('Odczytane dane:');
alphaT=24.1121
alpha_inv=0.6821
% Wyznaczamy wspolczynniki transmitancji:
disp('Wyznaczone parametry:');
alpha=1/alpha_inv
T=alphaT*alpha_inv
% Zbudawanie transmitancji K(s):
disp('Wyznaczona transmitancja:');
s=tf('s');
K1=(1+s*T)/(1+s*alpha*T)
% Wykonanie charakterystyk obrazujacych dokladnosc wyznaczenia:
% (Kolor czerwony dla charakterystyk z danych pomiarowych, kolor niebieski dla char. uzyskanych)
figure;
subplot(2,1,1);
plot(t,y,'r');
hold on;
[y1,t1]=step(K1);
plot(t1,y1,'b');
xlabel('Czas t (sek)','Position',[max(xlim) min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Wyjscie y(t)','Position',[min(xlim) max(ylim)],'Horizontal','Right','Vertical','Top');
xlim(xlim);
ylim(ylim);
grid on;

hold off;
subplot(2,1,2);
plot(re,im,'r');
hold on;
[RE,IM]=nyquist(K1,w);
for i=1:length(w);
re1(i)=RE(:,:,i);
im1(i)=IM(:,:,i);
end
plot(re1,im1,'b');
xlabel('Re K(jw)','Position',[max(xlim) min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Im K(jw)','Position',[min(xlim) max(ylim)],'Horizontal','Right','Vertical','Top');
xlim(xlim);
ylim(ylim);
grid on;
hold off;
% Identyfikacja parametrow (alpha,T) poprzez okreslenie pulsacji w1 dla ktorej ImK(jw) osiaga
minimum:
disp('Identyfikacja parametrow (alpha,T) poprzez okreslenie w1:');
% Wyznaczenie w1,re_w1,im_w1
i=1;
while im(i)~=min(im)
i=i+1;
end
disp('Wyznaczono:');
w1=w(i)
re_w1=re(i)
im_w1=im(i)
% Wizualizacja wyznaczenia:
figure;
subplot(2,1,1);
semilogx(w,re);
xlabel('Pulsacja w (rad/sek)','Position',[w_max
min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Re K(jw)','Position',[w_min max(ylim)],'Horizontal','Right','Vertical','Top');
xlim([w_min w_max]);
hold on;
semilogx([w1 w1],[0.6 1],'k');
semilogx([w_min w_max],[re_w1 re_w1],'k');
hold off;
subplot(2,1,2);
semilogx(w,im);
xlabel('Pulsacja w (rad/sek)','Position',[w_max
min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Im K(jw)','Position',[w_min max(ylim)],'Horizontal','Right','Vertical','Top');
xlim([w_min w_max]);
hold on;
semilogx([w1 w1],[-0.2 0],'k');
semilogx([w_min w_max],[im_w1 im_w1],'k');
hold off;
% Wyznaczenie parametrow transmitancji:
disp('Wyznaczono parametry transmitancji:');
alpha=1/(2*re_w1-1)
T=1/(w1*alpha)
% Zbudawanie transmitancji K(s):
disp('Wyznaczona transmitancja:');
K2=(1+s*T)/(1+s*alpha*T)
% Wykonanie charakterystyk obrazujacych dokladnosc wyznaczenia:
% (Kolor czerwony dla charakterystyk z danych pomiarowych, kolor niebieski dla char. uzyskanych)
figure;
subplot(2,1,1);
plot(t,y,'r');
hold on;
[y1,t1]=step(K2);
plot(t1,y1,'b');
xlabel('Czas t (sek)','Position',[max(xlim) min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Wyjscie y(t)','Position',[min(xlim) max(ylim)],'Horizontal','Right','Vertical','Top');
xlim(xlim);
ylim(ylim);
grid on;
hold off;
subplot(2,1,2);
plot(re,im,'r');
hold on;
[RE,IM]=nyquist(K2,w);
for i=1:length(w);
re1(i)=RE(:,:,i);
im1(i)=IM(:,:,i);
end

plot(re1,im1,'b');
xlabel('Re K(jw)','Position',[max(xlim) min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Im K(jw)','Position',[min(xlim) max(ylim)],'Horizontal','Right','Vertical','Top');
xlim(xlim);
ylim(ylim);
grid on;
hold off;
% Identyfikacja parametrow (alpha,T) poprzez okreslenie pulsacji w0 dla ktorej fi(w) osiaga minimum:
disp('Identyfikacja parametrow (alpha,T) poprzez okreslenie w0:');
% Wyznaczenie w0,fi_min:
fi=atan2(im,re)*180/pi;
i=1;
while fi(i)~=min(fi)
i=i+1;
end
disp('Wyznaczono:');
w0=w(i)
fi_min_st=fi(i) % bo rysujemy w stopniach a liczymy w radianach
fi_min_rad=fi_min_st*pi/180
% Wizualizacja:
figure;
subplot(2,1,1);
plot(re,im);
xlim([-0.1 1.1]);
ylim([-0.2 0.1]);
xlabel('Re K(jw)','Position',[max(xlim) min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Im K(jw)','Position',[min(xlim) max(ylim)],'Horizontal','Right','Vertical','Top');
xlim([-0.1 1.1]);
ylim([-0.2 0.1]);
hold on;
plot([0 1],[0 im(i)/re(i)],'k');
grid on;
hold off;
subplot(2,1,2);
semilogx(w,fi);
xlabel('Pulsacja w (rad/sek)','Position',[w_max
min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Faza fi(w) (st)','Position',[w_min max(ylim)],'Horizontal','Right','Vertical','Top');
xlim([w_min w_max]);
hold on;
semilogx([w0 w0],[0 -15],'k');
semilogx([w_min w_max],[fi_min_st fi_min_st],'k');
hold off;
% Wyznaczenie parametrow transmitancji:
disp('Wyznaczono parametry transmitancji:');
alpha=(tan((pi/4)-(fi_min_rad/2)))^2
T=1/(w0*sqrt(alpha))
% Zbudawanie transmitancji K(s):
disp('Wyznaczona transmitancja:');
K3=(1+s*T)/(1+s*alpha*T)
% Wykonanie charakterystyk obrazujacych dokladnosc wyznaczenia:
% (Kolor czerwony dla charakterystyk z danych pomiarowych, kolor niebieski dla char. uzyskanych)
figure;
subplot(2,1,1);
plot(t,y,'r');
hold on;
[y1,t1]=step(K3);
plot(t1,y1,'b');
xlabel('Czas t (sek)','Position',[max(xlim) min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Wyjscie y(t)','Position',[min(xlim) max(ylim)],'Horizontal','Right','Vertical','Top');
xlim(xlim);
ylim(ylim);
grid on;
hold off;
subplot(2,1,2);
plot(re,im,'r');
hold on;
[RE,IM]=nyquist(K3,w);
for i=1:length(w);
re1(i)=RE(:,:,i);
im1(i)=IM(:,:,i);
end
plot(re1,im1,'b');
xlabel('Re K(jw)','Position',[max(xlim) min(ylim)],'Horizontal','Right','Vertical','Bottom');
ylabel('Im K(jw)','Position',[min(xlim) max(ylim)],'Horizontal','Right','Vertical','Top');
xlim(xlim);
ylim(ylim);
grid on;
hold off;
4. Realizacja zadań:
4.1 Realizacja zadania 1:
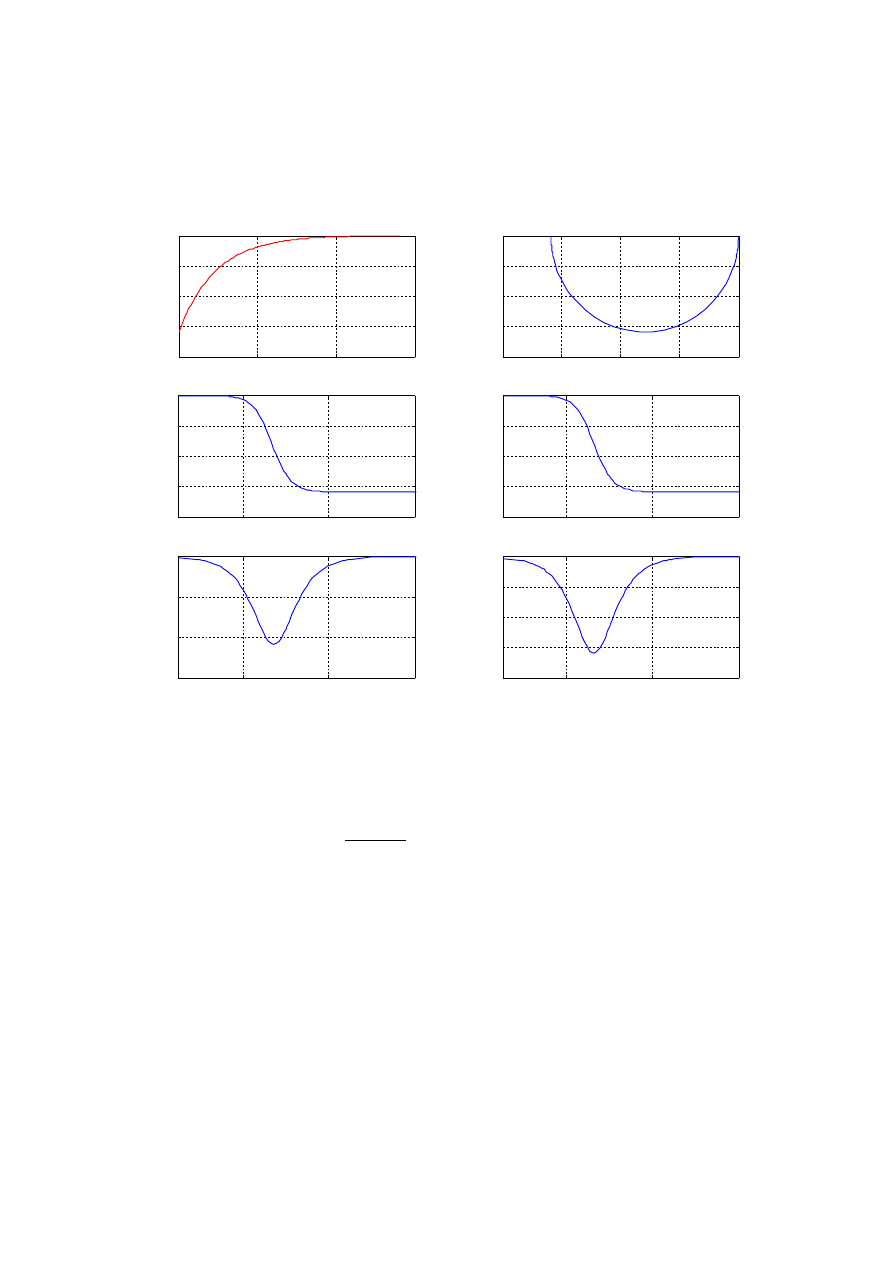
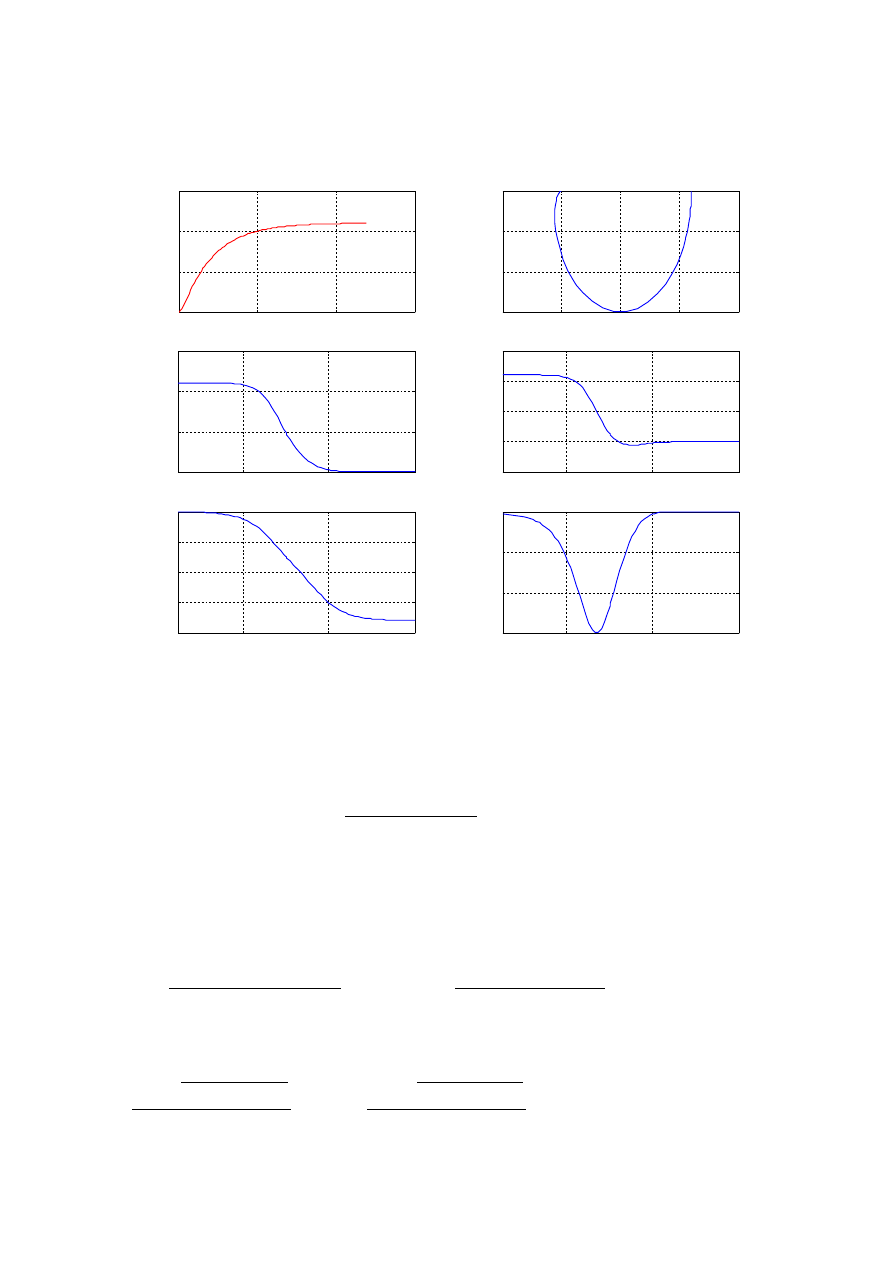
Wyrysowanie zadanych charakterystyk:
Rozpoznanie typu badanego obiektu:
Element proporcionalno-całkujący:
Transmitancja:
K s=
1sT
1s T
Parametry do wyznaczenia: , T .
W zadaniu pierwszym wyznaczono parametry przy użyciu zamieszczonych w obowiązującym
skrypcie metod (w kolejnych zadaniach tylko wybranej). Kolejne metody obrazują sposób
wyznaczenia parametrów oraz przedstawione są przebiegi porównawcze (charakterystyka
odpowiedzi na skok jednostkowy i charakterystyka amplitudowo-fazowa) na których to naniesione
są kolorem czerwonym przebiegi z punktów pomiarowych dostarczonych przez prowadzącego,
natomiast kolorem niebieski przebiegi uzyskane ze zbudowanej transmitancji na podstawie
otrzymanych parametrów.
0
5 0
1 0 0
1 5 0
0 . 7
0 . 8
0 . 9
1
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
0 . 7
0 . 8
0 . 9
1
- 0 . 2
- 0 . 1 5
- 0 . 1
- 0 . 0 5
0
R e K ( j w )
Im
K
(j
w
)
1 0
- 2
1 0
0
1 0
2
0 . 6
0 . 7
0 . 8
0 . 9
1
P u l s a c j a w ( r a d / s e k )
M
o
d
u
l
|K
(j
w
)|
1 0
- 2
1 0
0
1 0
2
0 . 6
0 . 7
0 . 8
0 . 9
1
P u l s a c j a w ( r a d / s e k )
R
e
K
(j
w
)
1 0
- 2
1 0
0
1 0
2
- 1 5
- 1 0
- 5
0
P u l s a c j a w ( r a d / s e k )
F
a
z
a
f
i(
w
)
(s
t)
1 0
- 2
1 0
0
1 0
2
- 0 . 2
- 0 . 1 5
- 0 . 1
- 0 . 0 5
0
P u l s a c j a w ( r a d / s e k )
Im
K
(j
w
)
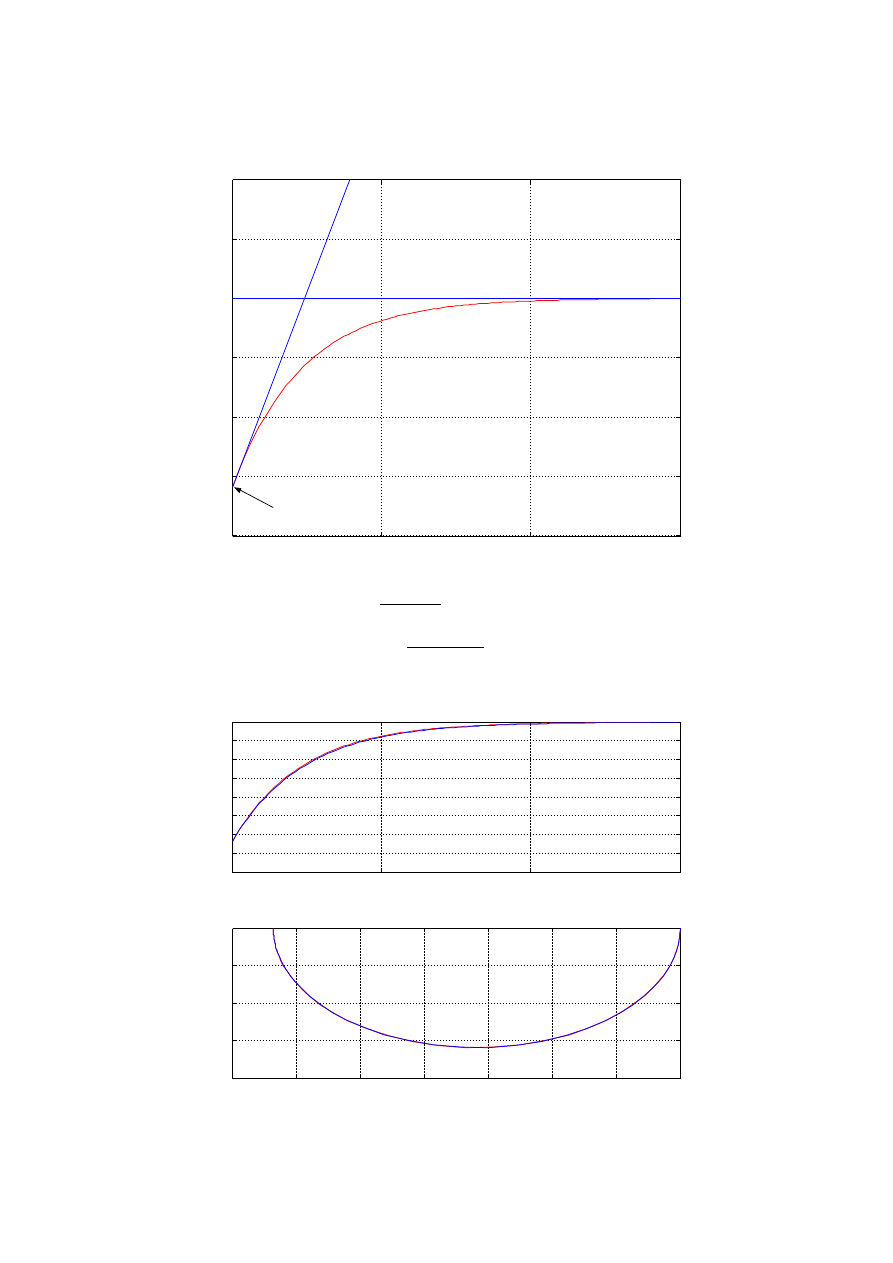
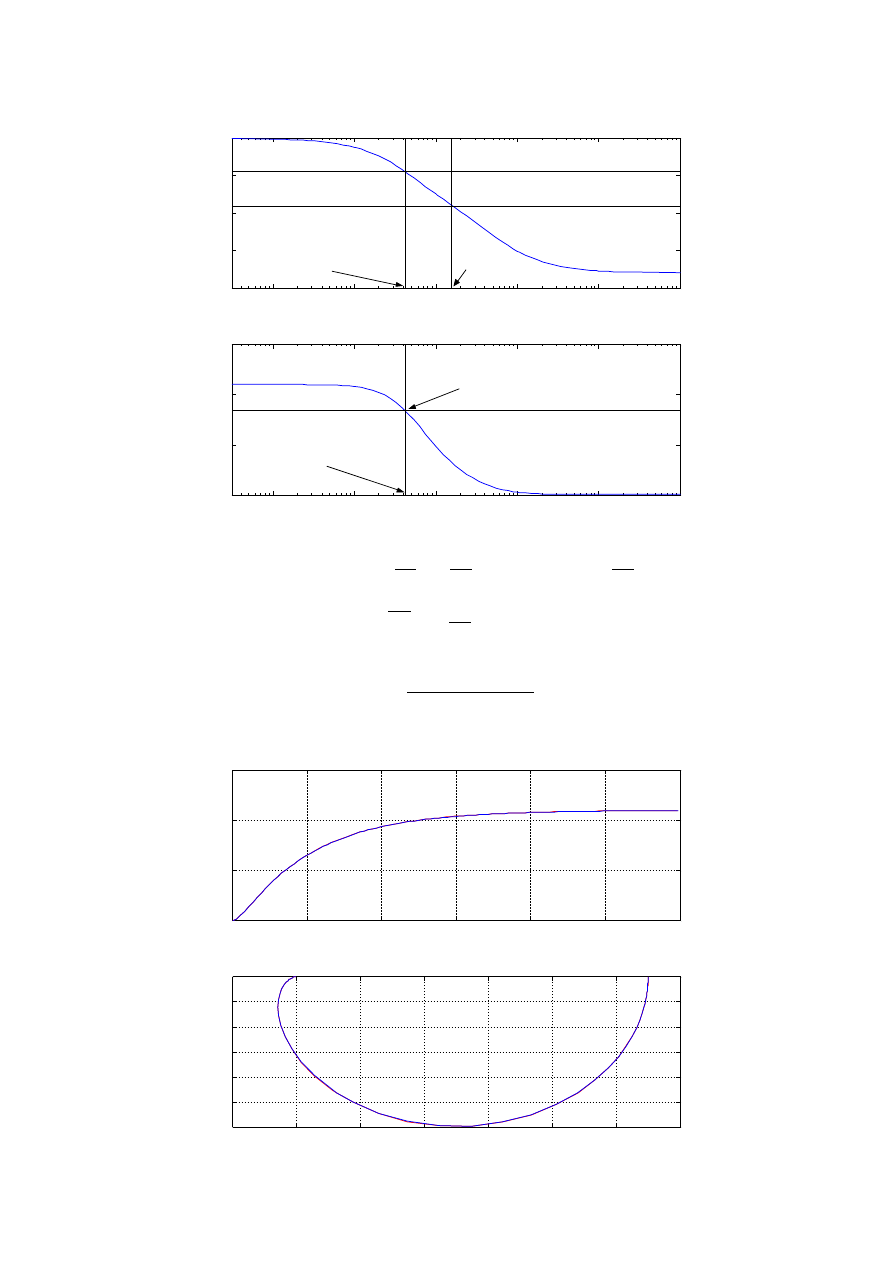
a) Wyznaczenie parametrów na podstawie przebiegu odpowiedzi na skok jednostkowy:
Idea wyznaczenia parametrów:
Wyznaczone parametry:
=
1
1/alpha
=
1.4661 , T =alpha∗T⋅1/alpha=16.4469
Zbudowana transmitancja:
K s=
16.45 s1
24.11 s1
Przebiegi porównawcze:
0
5 0
1 0 0
1 5 0
0 . 6
0 . 7
0 . 8
0 . 9
1
1 . 1
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
1 / a l p h a = 0 . 6 8 2 1
a l p h a * T =
= 2 4 . 1 1 2 1
0
5 0
1 0 0
1 5 0
0 . 6 5
0 . 7
0 . 7 5
0 . 8
0 . 8 5
0 . 9
0 . 9 5
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
0 . 6 5
0 . 7
0 . 7 5
0 . 8
0 . 8 5
0 . 9
0 . 9 5
1
- 0 . 2
- 0 . 1 5
- 0 . 1
- 0 . 0 5
0
R e K ( j w )
Im
K
(j
w
)
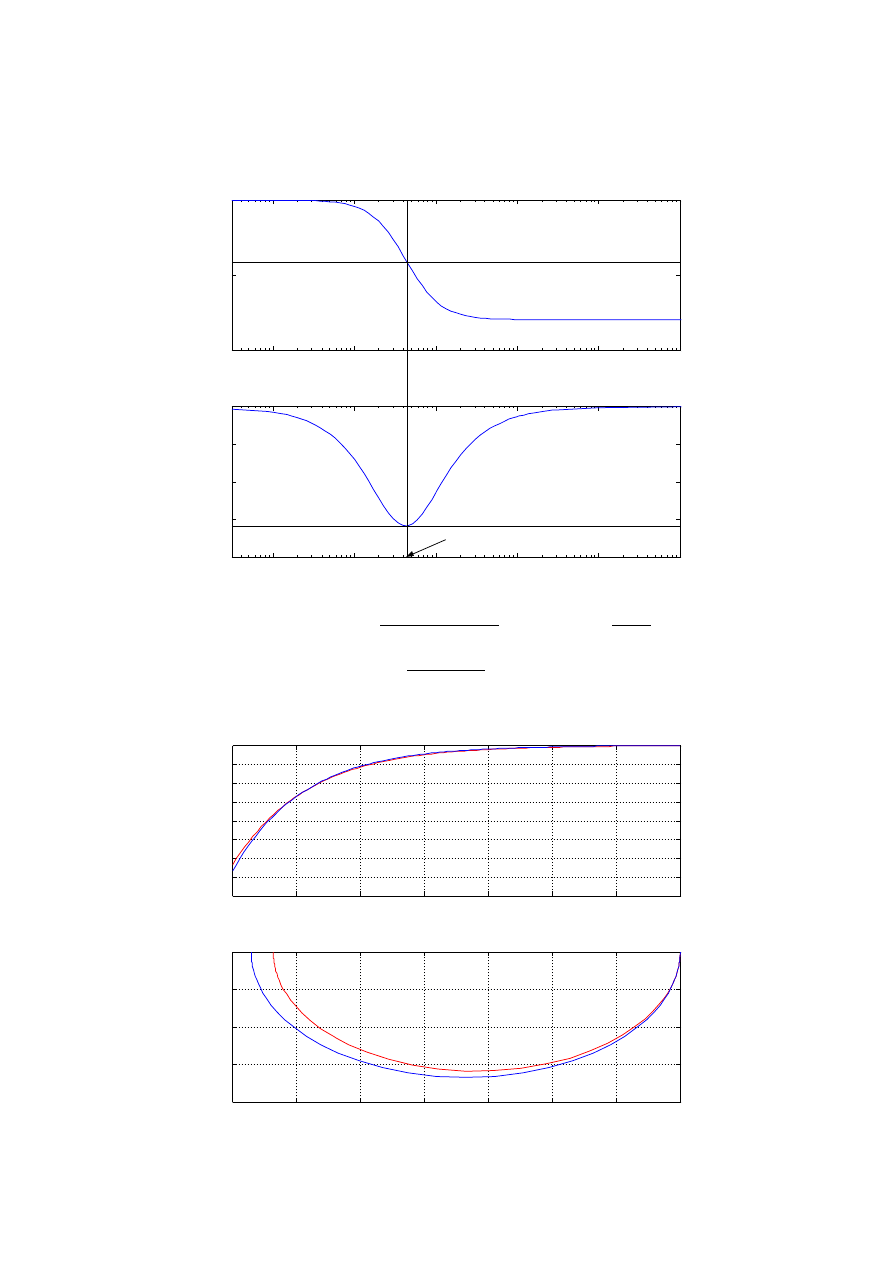
b) Wyznaczenie parametrów poprzez określenie pulsacji ω
1
przy której Im K(jω) osiąga
minimum:
Idea wyznaczenia parametrów:
Wyznaczone parametry:
=
1
2⋅ℜ K j
1
−
1
=
1.5044 , T =
1
1
⋅
=
14.7658
Zbudowana transmitancja:
K s=
14.77 s1
22.21 s1
Przebiegi porównawcze:
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0 . 6
0 . 8
1
P u l s a c j a w ( r a d / s e k )
R
e
K
(j
w
)
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
- 0 . 2
- 0 . 1 5
- 0 . 1
- 0 . 0 5
0
P u l s a c j a w ( r a d / s e k )
Im
K
(j
w
)
w 1 = 0 . 0 4 5 0
R e K ( j w ) = 0 . 8 3 2 4
I m K ( j w ) = - 0 . 1 5 8 7
0
2 0
4 0
6 0
8 0
1 0 0
1 2 0
1 4 0
0 . 6 5
0 . 7
0 . 7 5
0 . 8
0 . 8 5
0 . 9
0 . 9 5
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
0 . 6 5
0 . 7
0 . 7 5
0 . 8
0 . 8 5
0 . 9
0 . 9 5
1
- 0 . 2
- 0 . 1 5
- 0 . 1
- 0 . 0 5
0
R e K ( j w )
Im
K
(j
w
)
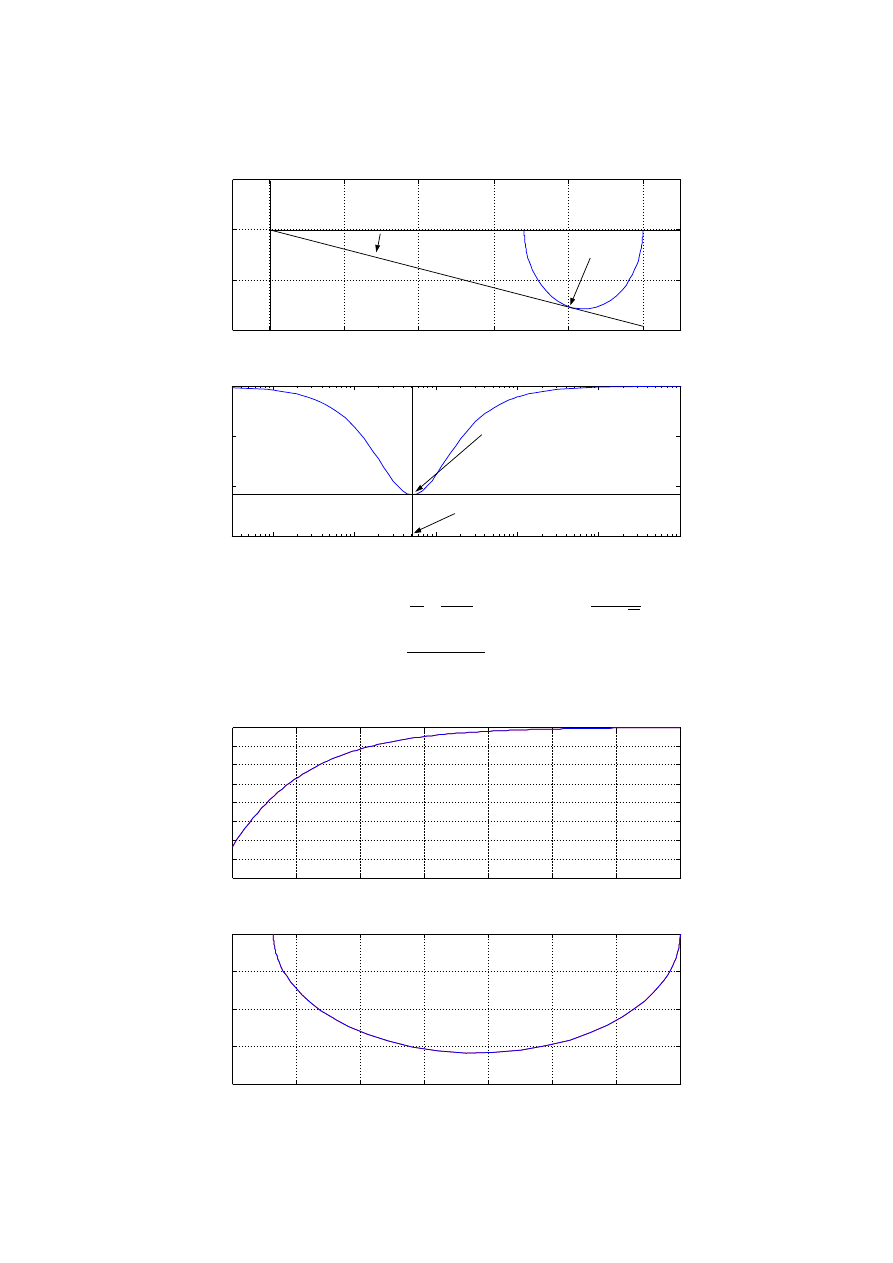
c) Wyznaczenie parametrów poprzez określenie pulsacji ω
0
dla której φ(ω) osiąga minimum:
Idea wyznaczenia parametrów:
Wyznaczone parametry:
=
tg
2
4
−
min
2
=
1.4662 , T =
1
0
⋅
=
16.0000
Zbudowana transmitancja:
K s=
16 s1
23.46 s1
Przebiegi porównawcze:
0
0 . 2
0 . 4
0 . 6
0 . 8
1
- 0 . 2
- 0 . 1
0
0 . 1
R e K ( j w )
Im
K
(j
w
)
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
- 1 5
- 1 0
- 5
0
P u l s a c j a w ( r a d / s e k )
F
a
z
a
f
i(
w
)
(s
t)
w 0
f i
m in
w 0 = 0 . 0 5 1 6
f i
m in
= - 1 0 . 8 9 5 7
o
=
= - 0 . 1 9 0 2 r a d
0
2 0
4 0
6 0
8 0
1 0 0
1 2 0
1 4 0
0 . 6 5
0 . 7
0 . 7 5
0 . 8
0 . 8 5
0 . 9
0 . 9 5
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
0 . 6 5
0 . 7
0 . 7 5
0 . 8
0 . 8 5
0 . 9
0 . 9 5
1
- 0 . 2
- 0 . 1 5
- 0 . 1
- 0 . 0 5
0
R e K ( j w )
Im
K
(j
w
)
4.2 Realizacja zadania 2:
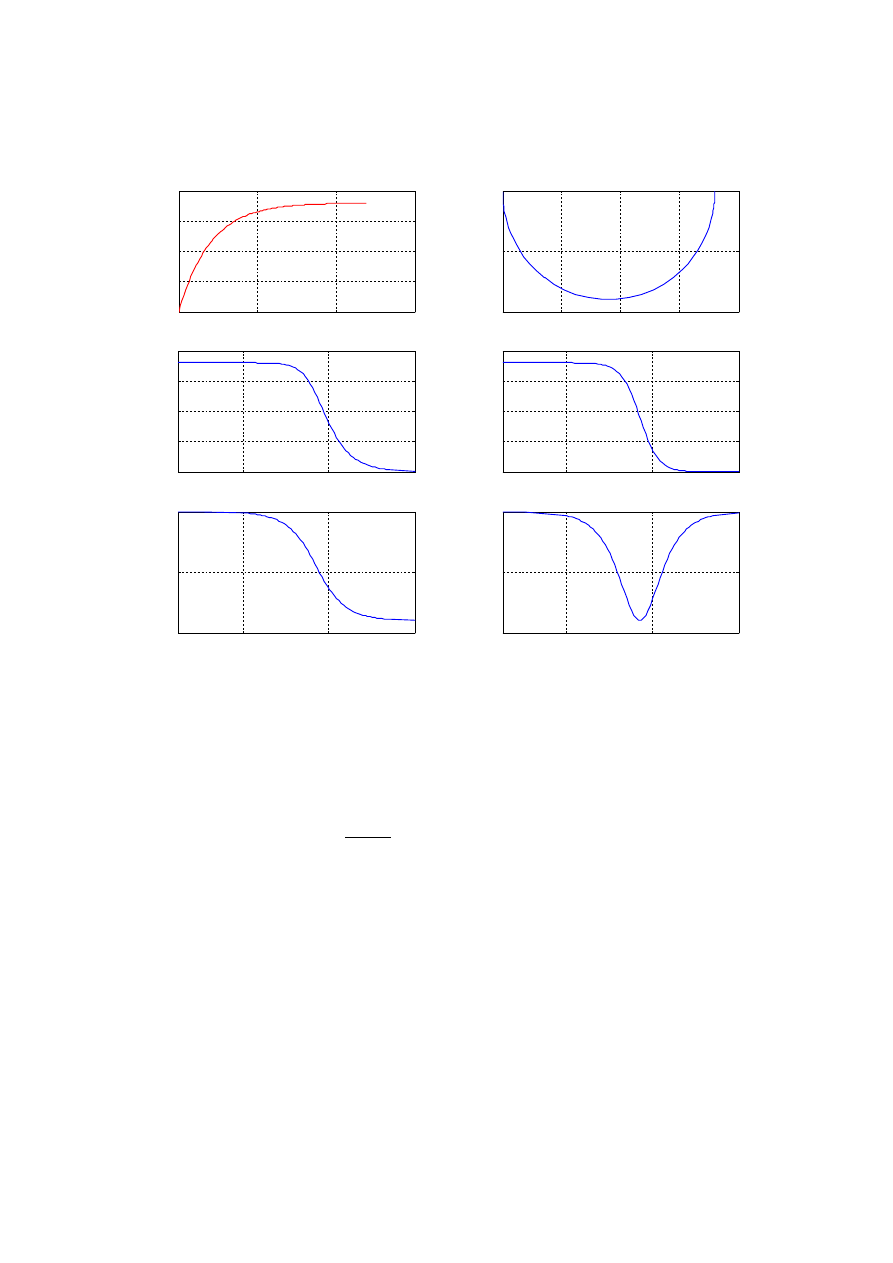
Wyrysowanie zadanych charakterystyk:
Rozpoznanie typu badanego obiektu:
Element inercyjny rzędu II:
Transmitancja: K s=
k
1sT
1
⋅
1sT
2
Parametry do wyznaczenia:
k , T
1
, T
2
.
Wyznaczenie parametrów poprzez określenie ω
1
i ω
2
dla których φ(ω
1
)=-π/4 i φ(ω
2
)=-π/2:
Zależności pomiędzy T
1
' i T
2
', a T
1
i T
2
:
K j =
k
1 j T
1
⋅
1 jT
2
i
K j =
k
1−
2
⋅
T
2
'
2
j T
1
'
czyli :
T
1
' =T
1
T
2
i T
2
'=T
1
⋅
T
2
Po rozwiązaniu układu równań :
T
1
=
T
1
'
T
1
'
2
−
4⋅T
2
'
2
2
i T
2
=
T
1
'−
T
1
'
2
−
4⋅T
2
'
2
2
0
5 0
1 0 0
1 5 0
0
5
1 0
1 5
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
- 5
0
5
1 0
1 5
- 6
- 4
- 2
0
R e K ( j w )
Im
K
(j
w
)
1 0
- 2
1 0
0
1 0
2
0
5
1 0
1 5
P u l s a c j a w ( r a d / s e k )
M
o
d
u
l
|K
(j
w
)|
1 0
- 2
1 0
0
1 0
2
- 5
0
5
1 0
1 5
P u l s a c j a w ( r a d / s e k )
R
e
K
(j
w
)
1 0
- 2
1 0
0
1 0
2
- 2 0 0
- 1 5 0
- 1 0 0
- 5 0
0
P u l s a c j a w ( r a d / s e k )
F
a
z
a
f
i(
w
)
(s
t)
1 0
- 2
1 0
0
1 0
2
- 6
- 4
- 2
0
P u l s a c j a w ( r a d / s e k )
Im
K
(j
w
)
Idea wyznaczenia parametrów:
Wyznaczone parametry T
1
' i T
2
':
T
1
' =
1
1
1−
1
2
2
2
=
22.0252 , T
2
' =
1
2
=
6.3245
Wyznaczone parametry:
k =
2⋅1−
1
2
2
2
⋅
∣
K j
1
∣
=
10.9942 ,
T
1
=
20.0280 , T
2
=
1.9972
Zbudowana transmitancja:
K s=
10.99
40 s
2
22.03 s1
Przebiegi porównawcze:
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
- 2 0 0
- 1 5 0
- 1 0 0
- 5 0
0
P u l s a c j a w ( r a d / s e k )
F
a
z
a
f
i(
w
)
(s
t)
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
5
1 0
1 5
P u l s a c j a w ( r a d / s e k )
M
o
d
u
l
|K
(j
w
)|
w 1 = 0 . 0 4 2 2
w 2 = 0 . 1 5 8 1
f i = 4 5
o
f i = 9 0
o
w 1 = 0 . 0 4 2 2
| K ( j w 1 ) | = 8 . 3 6 9 5
0
2 0
4 0
6 0
8 0
1 0 0
1 2 0
0
5
1 0
1 5
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
- 2
0
2
4
6
8
1 0
1 2
- 6
- 5
- 4
- 3
- 2
- 1
0
R e K ( j w )
Im
K
(j
w
)
4.3 Realizacja zadania 3:
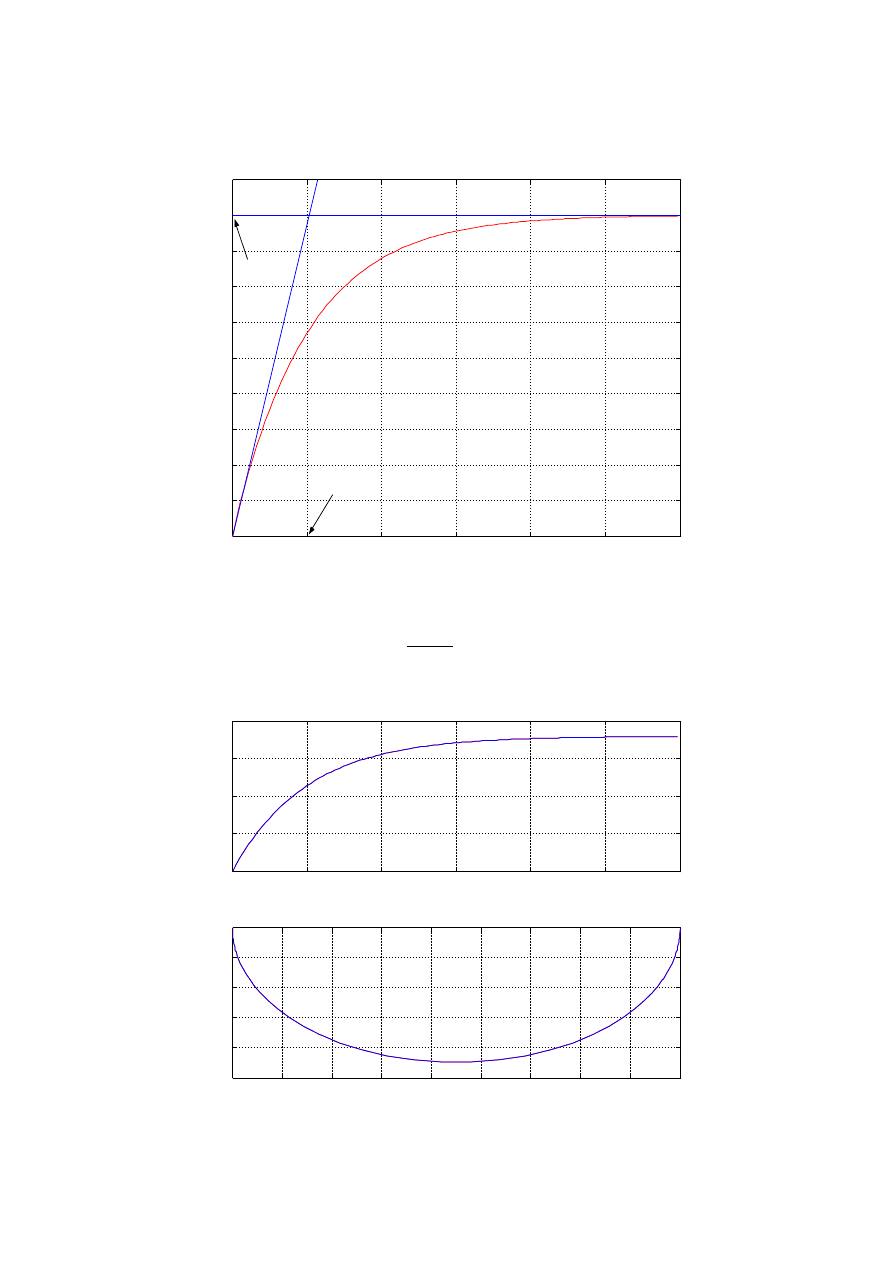
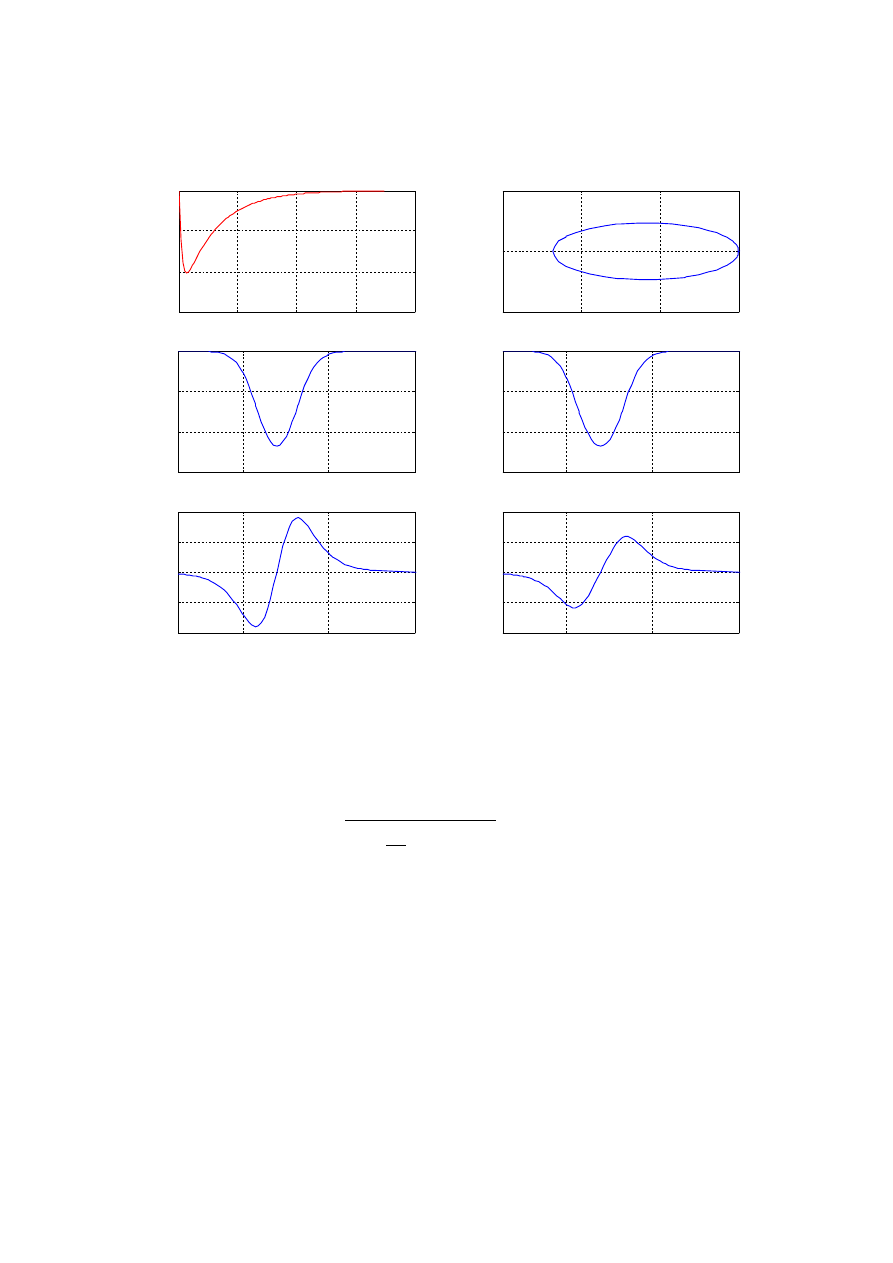
Wyrysowanie zadanych charakterystyk:
Rozpoznanie typu badanego obiektu:
Element inercyjny rzędu I:
Transmitancja: K s=
k
1sT
Parametry do wyznaczenia:
k , T
.
0
5
1 0
1 5
0
5
1 0
1 5
2 0
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
0
5
1 0
1 5
2 0
- 1 0
- 5
0
R e K ( j w )
Im
K
(j
w
)
1 0
- 2
1 0
0
1 0
2
0
5
1 0
1 5
2 0
P u l s a c j a w ( r a d / s e k )
M
o
d
u
l
|K
(j
w
)|
1 0
- 2
1 0
0
1 0
2
0
5
1 0
1 5
2 0
P u l s a c j a w ( r a d / s e k )
R
e
K
(j
w
)
1 0
- 2
1 0
0
1 0
2
- 1 0 0
- 5 0
0
P u l s a c j a w ( r a d / s e k )
F
a
z
a
f
i(
w
)
(s
t)
1 0
- 2
1 0
0
1 0
2
- 1 0
- 5
0
P u l s a c j a w ( r a d / s e k )
Im
K
(j
w
)
Wyznaczenie parametrów na podstawie przebiegu odpowiedzi na skok jednostkowy:
Idea wyznaczenia parametrów:
Odczytane parametry:
k =18 , T =2
Zbudowana transmitancja:
K s=
18
2 s1
Przebiegi porównawcze:
Uzyskane przebiegi całkowicie pokrywają przebiegi uzyskane z punktów pomiarowych!
0
2
4
6
8
1 0
1 2
0
2
4
6
8
1 0
1 2
1 4
1 6
1 8
2 0
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
T = 2
k = 1 8
0
2
4
6
8
1 0
1 2
0
5
1 0
1 5
2 0
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
0
2
4
6
8
1 0
1 2
1 4
1 6
1 8
- 1 0
- 8
- 6
- 4
- 2
0
R e K ( j w )
Im
K
(j
w
)
4.4 Realizacja zadania 4:
Wyrysowanie zadanych charakterystyk:
Rozpoznanie typu badanego obiektu:
Element proporcjonalno-całkująco-różniczkujący:
Transmitancja:
K s=
1sT
1
⋅
1sT
2
1s
T
1
⋅
1sT
2
Parametry do wyznaczenia: , T
1
, T
2
.
0
1 0 0
2 0 0
3 0 0
4 0 0
0 . 4
0 . 6
0 . 8
1
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
0 . 4
0 . 6
0 . 8
1
- 0 . 5
0
0 . 5
R e K ( j w )
Im
K
(j
w
)
1 0
- 2
1 0
0
1 0
2
0 . 4
0 . 6
0 . 8
1
P u l s a c j a w ( r a d / s e k )
M
o
d
u
l
|K
(j
w
)|
1 0
- 2
1 0
0
1 0
2
0 . 4
0 . 6
0 . 8
1
P u l s a c j a w ( r a d / s e k )
R
e
K
(j
w
)
1 0
- 2
1 0
0
1 0
2
- 2 0
- 1 0
0
1 0
2 0
P u l s a c j a w ( r a d / s e k )
F
a
z
a
f
i(
w
)
(s
t)
1 0
- 2
1 0
0
1 0
2
- 0 . 4
- 0 . 2
0
0 . 2
0 . 4
P u l s a c j a w ( r a d / s e k )
Im
K
(j
w
)
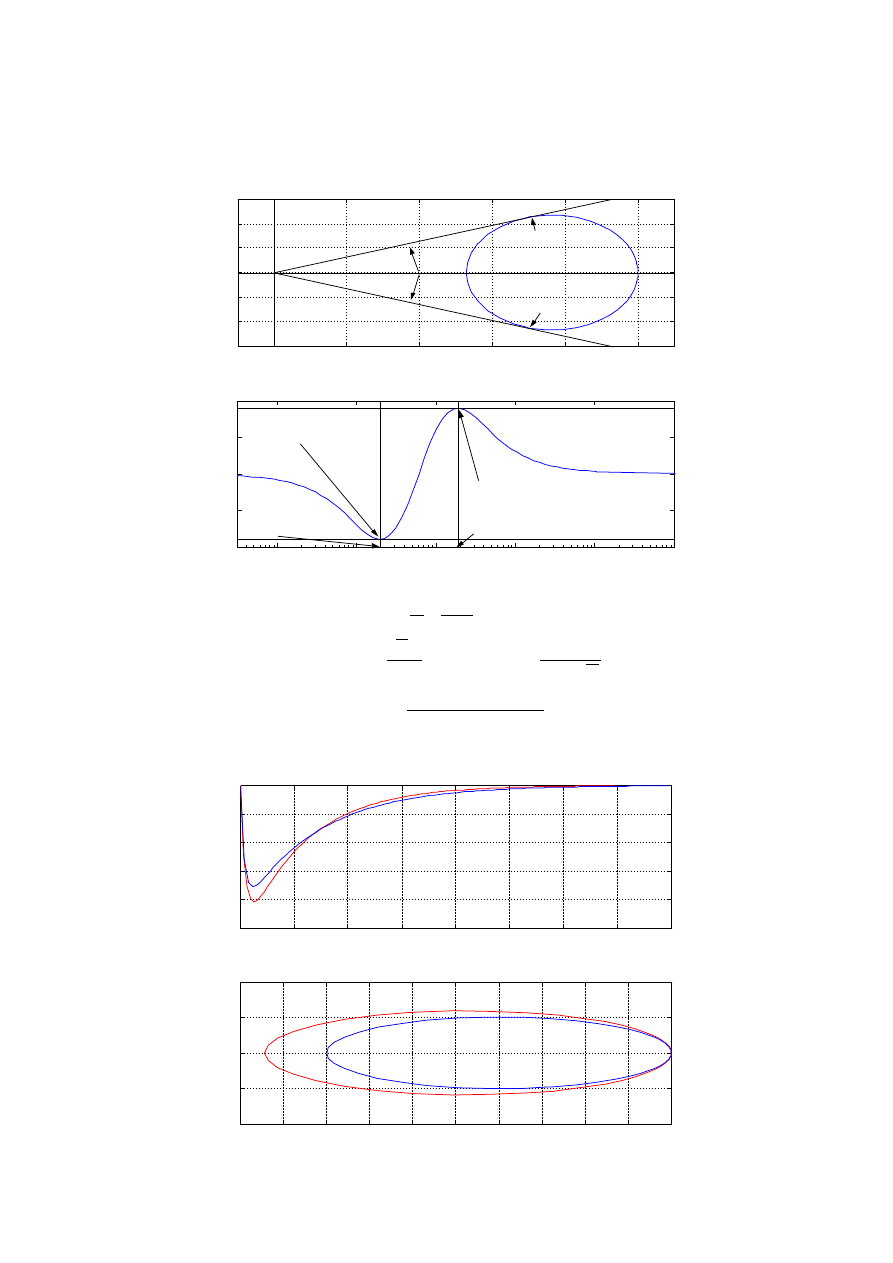
Wyznaczenie parametrów poprzez określenie ω
max
i ω
min
dla których φ(ω
max
) osiąga
maksimum i φ(ω
min
) osiąga minimum:
Idea wyznaczenia parametrów:
Wyznaczone parametry:
=
tg
2
4
−
min
2
=
1.8920 ,
T
1
=
max
=
7.3229 , T
2
=
1
min
⋅
=
36.8705
Zbudowana transmitancja:
K s=
270 s
2
44.19 s1
270 s
2
73.63 s1
Przebiegi porównawcze:
0
0 . 2
0 . 4
0 . 6
0 . 8
1
- 0 . 2
- 0 . 1
0
0 . 1
0 . 2
0 . 3
R e K ( j w )
Im
K
(j
w
)
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
- 2 0
- 1 0
0
1 0
2 0
P u l s a c j a w ( r a d / s e k )
F
a
z
a
f
i(
w
)
(s
t)
fi
m a x
fi
m in
w
m a x
w
m in
w
m in
= 0 . 0 1 9 7
w
m a x
= 0 . 1 8 7 8
f i
m in
= - 1 7 . 9 6 4 9
o
f i
m a x
= 1 7 . 9 6 4 9
o
0
5 0
1 0 0
1 5 0
2 0 0
2 5 0
3 0 0
3 5 0
4 0 0
0 . 5
0 . 6
0 . 7
0 . 8
0 . 9
1
C z a s t ( s e k )
W
y
js
c
ie
y
(t
)
0 . 5
0 . 5 5
0 . 6
0 . 6 5
0 . 7
0 . 7 5
0 . 8
0 . 8 5
0 . 9
0 . 9 5
1
- 0 . 4
- 0 . 2
0
0 . 2
0 . 4
R e K ( j w )
Im
K
(j
w
)

5. Wnioski:
●
Im bardziej złożony jest element badany tym trudniej jest określić jego parametry.
Przykładowo dla elementu inercyjnego pierwszego rzędu uzyskano całkowitą zgodność
przebiegów kontrolnych, a dla korektora PID występują stosunkowo duże niedokładności.
●
Wybór metody wyznaczenia parametrów jest uwarunkowany charakterami przebiegów z
tego względu w pewnych warunkach lepiej jest analizować na przykład przebieg
odpowiedzi na skok jednostkowy a w innych na przykład charakterystykę amplitudowo-
fazową. Warunki te to przede wszystkim dokładność z jaką możemy określić na przykład
punkty przegięcia (o ile występują) czy ekstrema przebiegów.
●
Najkorzystniej jest przeprowadzić analizę kilkoma metodami i wybrać tą która zwraca
wyniki najbliższe rzeczywistym (dokonać porównania przebiegów porównawczych).
Przykładowo w zadaniu jeden najkorzystniej będzie wybrać metodę oznaczoną jako c.
Wynika to z faktu że styczne poprowadzone w otoczeniu minimum funkcji φ(ω) mają
stosunkowo duże nachylenie. Najbardziej niekorzystna metoda z omawianych to metoda
oznaczona jako b, ponieważ styczne poprowadzone w otoczeniu minimum funkcji Im K(ω)
mają stosunkowo małe nachylenie (identyfikacja minimum jest trudniejsza).
●
Na wyznaczenie parametrów mają również wpływ metody numerycznego wyznaczania
wartości oraz błędu odczytu z charakterystyk.
●
Jeżeli identyfikowanym obiektem będzie element rzeczywisty należy poprawnie określić
warunki przy których zdejmowane będą punkty pomiarowe. Niestety niemożliwe jest wtedy
całkowite wyeliminowanie wpływu zakłóceń.
Document Outline
Wyszukiwarka
Podobne podstrony:
Ćw 2 Podstawowe elementy automatyki
Zadania Podstawowe Elementy Automatyki
Podstawowe elementy automatyki charakterystyki czasowe
Podstawowe elementy automatyki DOC
07 Badanie charakterystyk częstotliwościowych i przebiegów nieustalonych podstawowych elementów auto
Podstawowe elementy logiczne AUTOMATYKA
Podstawowe elementy logiczne AUTOMATYKA
smalec,podstawy automatyzacji L,?dania symulacyjne elementów automatyki w środowisku Matlab Simulink
cw 3?danie dynamiki podstawowych czlonow automatyki
Modelowanie i badanie podstawowych elementów liniowych automatyki – symulacja
Wybrane elementy automatyki instalacyjnej
cw 2 podstawy biostatystyki seminarium z teorii
Spr 1, AGH IMIR Mechanika i budowa maszyn, III ROK, Elementy automatyki przemysłowej, EAP lab1
Elementy automatyki1
Elementy automatyki
Podstawowe elementy planowania i podejmowania decyzji
Cw 26 Elementy kontrolne
więcej podobnych podstron