Odpowiedzi z Teorii Pola

1. Prawo Gaussa i Stoke’sa w zastosowaniu teorii pola elektromagnetycznego (przykłady)

∫

⋅

)

Równanie to przedstawia prawo Gaussa: Strumie

elektryczny przez powierzchni

zamkni

równa si

ładunkowi zawartemu we wn

trzu tej powierzchni. Oznacza to,

e pole elektryczne

jest polem

ródłowym, a

ródłem pola elektrycznego jest ładunek.

ródłem linii pola elektrycznego s

ładunki, przy czym linie pola zaczynaj

na ładunkach dodatnich, a ko

na ładunkach

ujemnych. Linie pola elektrycznego maja zatem pocz

tek oraz koniec i nie s

liniami zamkni

tymi.

Przykład:

Ładunek punktowy:

(

)

cos

sin

−

∫

∫ ∫

∫

Twierdzenie Stokesa

Całka liniowa wektora pola wzdłu

krzywej zamkni

tej równa si

strumieniowi rotacji tego wektora

przez powierzchni

, której brzegiem jest wspomniana krzywa:

∫

⋅

)

( S

rotA

Twierdzenie to mo

na zinterpretowa

jako przekształcenie całki liniowej na całk

powierzchniow

. Pole wektorowe jest polem bezwirowym lub potencjalnym w obszarze, gdy rotacja

wektora jest równa zeru w ka

dym punkcie tego obszary. Zgodnie z twierdzeniem Stokesa, w polu

bezwirowym całka liniowa wektora pola wzdłu

dowolnej krzywej zamkni

tej równa si

zeru. Pole

wektorowe jest polem wirowym, gdy rotacja wektora pola jest ró

na od zera w tym obszarze.

2. Poda

ró

niczkow

posta

równa

Maxwella i ich interpretacj

Podstawowymi równaniami pola elektromagnetycznego s

równania Maxwella; posta

ró

niczkowa

tych równa

dotycz

cych

rodowisk nieruchomych:

rot

∂

Z równania 1. wynika,

e ka

dy pr

d wywołuje pole magnetyczne.

Po obustronnym obliczeniu dywergencji















∂

div

rot

div

otrzymujemy prawo ci

gło

ci wektora g

sto

ci pr

du:















∂

div

gdy

divrot ka

dego wektora =0. Jest to pierwsze prawo Kirchoffa w postaci wektorowej.

d mo

e mie

ró

natur

Gdy zjawisko przepływu pr

du zachodzi w przewodniku wyst

puje pr

d przewodzenia

przew

gdzie

to konduktywno

ść

rodka. Zale

ść

ta jest wektorow

postaci

prawa Ohma.

W ogólnej postaci (ciała poruszaj

ce si

z pr

dko

w polu o indukcji

)

(

)

przew

gdzie

to składowa nat

ęż

enia pola elektrycznego nazwana obc

lub

postronn

. Spowodowana ona mo

e by

obcymi siłami elektromotorycznymi pochodzenia

nieelektrycznego (np. w skutek nierównomiernej koncentracji ładunków)
W ka

dym dielektryku wyst

puje pr

d przesuni

cia wywołany zmiennym polem elektrycznym:

przes

∂

gdzie

- wektor polaryzacji cz

stek dielektryka. Pr

przesuni

cia płynie tylko pod wpływem zmiennego w czasie pola elektrycznego. Składnika

∂

jest

zwi

zany ze zmian

wektora indukcji pola elektrycznego w pró

ni, a składnik

∂

ze zmian

polaryzacji cz

stek.

W przestrzeni zawieraj

cej ładunki swobodne płynie pr

d konwekcji

kon

gdzie

-g

sto

ść

obj

ciowa ładunku poruszaj

cego si

z pr

dko

Podsumowanie:
Na podstawie I równania Maxwella stwierdzamy,

e pr

d elektryczny (niezale

nie od

rodowiska i

sposobu powstania) jest to takie zjawisko, któremu towarzyszy pole magnetyczne.

rot

∂

−

Z równania 2. wynika,

e zmiennemu polu magnetycznemu towarzyszy pole elektryczne.

Znak minus wyra

a reguł

bezwładno

ci elektromagnetycznej Lenza: W obwodach elektrycznych

istnieje tendencja do zachowania w stanie niezmiennym strumieni skojarzonych z tymi obwodami.
Przy wszelkiej próbie zmiany strumienia w obwodach powstaj

siły elektromagnetyczne działaj

ce w

kierunku przeciwstawienia si

tym zmianom.

div

Równanie 3. opisuje ci

gło

ść

wektora indukcji

. Wynika z niego,

e nie istniej

oddzielnie ładunki

magnetyczne, a jedynie dipole. Oznacza to,

e pole magnetyczne jest polem bez

ródłowym, a linie

pola magnetycznego s

liniami zamkni

tymi.

eli b

dziemy operowa

strumieniem magnetycznym zamkni

tej powierzchni to otrzymamy

równanie

div

Z równania 4. wynika,

e w obszarach zawieraj

cych ładunek wektor indukcji elektrycznej jest

nieci

gły. Linie wektora

zaczynaj

na ładunkach dodatnich (

ródłach) i ko

na ładunkach

ujemnych (odbiornikach). Linie pola elektrycznego nie s

liniami zamkni

tymi.

3. Poda

całkow

posta

równa

Maxwella i ich interpretacj

∫

⋅

∂

⋅

)

(

I równanie Maxwella w postaci całkowej jest znane pod nazw

prawa Amper’a. Interpretacja:

Napi

cie magnetyczne wzdłu

krzywej zamkni

tej jest równe pr

dowi całkowitemu, czyli sumie pr

przewodzenia i pr

du przesuni

cia przez powierzchni

, której brzegiem jest ta krzywa.

∫

⋅

∂

−

⋅

)

(

II równanie Maxwella w postaci całkowej przedstawia prawo indukcji elektromagnetycznej Faradaya:
Napi

cie wzdłu

krzywej zamkni

tej jest równe sile elektromotorycznej wzniecanej wskutek

zmian czasowych strumienia magnetycznego przenikaj

cego powierzchni

, której brzegiem

jest ta krzywa.

∫

⋅

)

Równanie to przedstawia prawo Gaussa: Strumie

elektryczny przez powierzchni

zamkni

równa si

ładunkowi zawartemu we wn

trzu tej powierzchni. Oznacza to,

e pole elektryczne

jest polem

ródłowym, a

ródłem pola elektrycznego jest ładunek.

ródłem linii pola elektrycznego s

ładunki, przy czym linie pola zaczynaj

na ładunkach dodatnich, a ko

na ładunkach

ujemnych. Linie pola elektrycznego maja zatem pocz

tek oraz koniec i nie s

liniami zamkni

tymi.

)

(

⋅

∫

Na podstawie tego wzoru stwierdzamy,

e strumie

magnetyczny przez dowoln

powierzchni

zamkni

równa si

zeru. Oznacza to,

e pole magnetyczne jest polem bez

ródłowym, a linie

pola magnetycznego s

liniami zamkni

tymi.

4. Warunki graniczne : opis, rodzaje, interpretacja

Warunki graniczne pozwalaj

na jednoznaczne rozwi

zanie problemu, stawiane naszej funkcji np.

V(P) lub jej pochodnej na brzegu obszaru

Ω

( w którym ta funkcja jest okre

lona, zadana ) w danej

chwili czasu.
Szczególne przypadki warunków brzegowych :
a) warunki pocz

tkowe - warunki stawiane poszukiwanej funkcji V(P) w obszarze

Ω

dla t=t

b) warunki brzegowe - warunki stawiane poszukiwanej funkcji V(P) na brzegu S obszaru

Ω

Istnienie jedynej funkcji holomorficznej V(P) spełniaj

cej dowolne równanie ró

niczkowe cz

stkowe II

du dowodzi si

za pomoc

tw. Cauchy’ego.

1 Zagadnienie brzegowe pierwszego rodzaju - zagadnienie Dirichleta

V(P) =

(P) dla P

∈

S gdzie V(P) - szukana funkcja

lub V(P,t) =

(P,t)

Jest zadana funkcja

(P),

(P,t) w punktach P na brzegu S obszaru

Ω

w których jest poszukiwane

rozwi

zanie r.r.

Zastosowanie : Warunki graniczne na zewn

trz solenoidu ( np. B=0 )

2 Zagadnienie brzegowe drugiego rodzaju - zagadnienie Neumanna

=>

)

(

)

(

)

V(P,

∂

Zadana jest funkcja pochodna

(P) lub

(P,t) w punktach P na brzegu S obszaru

Ω

w których jest

poszukiwanie rozwi

zania r.r. Jest ona pochodn

normaln

funkcji V(P) w punktach P na brzegu S

obszaru

Ω

Zastosowanie : warunki graniczne wewn

trz solenoidu (dB/dn=const lub An+C)

3 Zagadnienie brzegowe trzeciego rodzaju - zagadnienie Henkela ( tylko wspomniane )
W szczególnym przypadku, gdy zadane na brzegu funkcje s

równe 0, wyst

puj

jednorodne

warunki brzegowe. Na granicy o

rodków nale

y uwzgl

dni

warunki ci

gło

ci skalarów i wektorów.

5. Metody numeryczne rozwi

zywania problemów brzegowych w zagadnieniach polowych :

podstawy, krótki opis

Dostajemy gotowe zale

ci w postaci wykresów lub tabel, s

to rozwi

zania przybli

one.

1. Metoda ró

nic sko

czonych

Równania ró

niczkowe zast

pujemy równaniami ró

nicowymi. Zagadnienie brzegowe sprowadza si

do układu liniowych równa

algebraicznych, a po ich rozwi

zaniu otrzymuje si

przybli

one

rozwi

zanie problemu.

Tworzymy siatk

, któr

pokrywamy cały obszar. Liczymy potencjały w ka

dym w

ęź

le siatki

(rozwijaj

c funkcj

potencjału w szereg Taylora mo

emy wyznaczy

i,j

zale

ne od potencjałów

siednich w

złów, gdy przyjmiemy równomiern

siatk

i,j

=[-f

i-1,j

i+1,j

i,j-1

i,j+1

]/4 ). Równanie mo

na napisa

dla ka

dego w

zła wewn

trznego,

przy czym warto

ci funkcji V w w

złach poło

onych na granicy obszary zast

puje si

przez warto

wynikaj

ce z warunku brzegowego. W rezultacie otrzymuje si

ukł. rów. algebraicznych, które po

rozwi

zaniu daj

warto

ci funkcji V w w

złach wewn

trznych.

Mamy dwie metody rozwi

zywania :

a) metoda macierzowa - [K][V]=[B] obliczmy [V] odwracaj

c macierz [K] (

mudna robota) przy czym

w macierzy [B] siedz

warunki graniczne

b) metoda relaksacyjna - (iteracyjna) polega na obliczaniu kolejnych potencjałów siatki w p

tli (

numerycznie ) dopóki zadana warto

ść

bł

∆

>max d

i,j

gdzie d

i,j

-V

i,j

k-1

( k - nr iteracji ).

Dokładno

ść

metody polega na odpowiednim ustaleniu bł

du ( jak najmniejszy ). W zale

ci czy

bierzemy pod uwag

nowe warto

ci w tej samej iteracji rozró

niamy metod

Jacobiego i Gaussa-

Siedla. MRS jest prosta pod wzgl

dem matematycznym, łatwa w u

yciu i charakteryzuj

żą

ogólno

. Jej wad

jest stosunkowo mała dokładno

ść

i trudno

ść

w oszacowaniu bł

du.

2. Metoda elementów sko

czonych

MES znajduje zastosowanie przy rozwi

zywaniu zagadnie

brzegowych dla równa

typu

eliptycznego sprowadzaj

c problem do ukł. rów. algebraicznych, z których po rozwi

zaniu

otrzymujemy rozwi

zanie przybli

one. Metoda ta pozwala znale

źć

równie

przybli

one rozwi

zanie

r.r. cz. typu parabolicznego sprowadzaj

c problem do ukł. rów. ró

niczkowych zwyczajnych I rz

du.

MES powi

zana jest z metodami wariacyjnymi, mo

na bowiem otrzyma

równania dla rozwi

zania

przybli

onego w drodze minimalizacji funkcjonału. Obszar dzielimy na elementy, ich wielko

ść

nale

dopasowa

do kształtu obszaru jest to tak zwana dyskretyzacja obszaru S ( cz

stkowe obszary s

zwane elementami ). Nast

pnie dobieramy funkcj

, która opisuje potencjał w jednym punkcie ( w

jednym elemencie naszego obszaru ). Kolejnym etapem jest utworzenie globalnego układu równa

który obejmuje cały obszar. Ostatni

czynno

jest rozwi

zanie tego układu równa

)

(

)

(

dla

)

(

)

(

∂

∈

∂

6. Metoda ró

nic sko

czonych - zało

enia, wyprowadzenie podstawowych zale

ci dla

równania Poissone’a

Rozwijamy w szereg Taylora potencjały s

siednich w

złów w stosunku do V

i,j

Równanie mo

na napisa

dla ka

dego w

zła wewn

trznego, przy czym warto

ci funkcji V w w

złach

poło

onych na granicy obszary zast

puje si

przez warto

ci wynikaj

ce z warunku brzegowego. W

rezultacie otrzymuje si

ukł. rów. algebraicznych, które po rozwi

zaniu daj

warto

ci funkcji V w

złach wewn

trznych.

Mamy dwie metody rozwi

zywania :

a) metoda macierzowa - [K][V]=[B] obliczmy [V] odwracaj

c macierz [K] (

mudna robota) przy czym

w macierzy [B] siedz

warunki graniczne

b) metoda relaksacyjna - (iteracyjna) polega na obliczaniu kolejnych potencjałów siatki w p

tli (

numerycznie ) dopóki zadana warto

ść

bł

∆

>max d

i,j

gdzie d

i,j

-V

i,j

k-1

( k - nr iteracji ).

Dokładno

ść

metody polega na odpowiednim ustaleniu bł

du ( jak najmniejszy ). W zale

ci czy

bierzemy pod uwag

nowe warto

ci w tej samej iteracji rozró

niamy metod

Jacobiego i Gaussa-

Siedla. MRS jest prosta pod wzgl

dem matematycznym, łatwa w u

yciu i charakteryzuj

żą

ogólno

. Jej wad

jest stosunkowo mała dokładno

ść

i trudno

ść

w oszacowaniu bł

du.

)

(

oraz

)

(

dla

icznie

log

ana

)

(

)

(

)

(

)

(

...

)

(

)

(

)

(

)

(

)

(

...

)

(

)

(

)

(

)

(

)

(

∂

−

∂

⇒

−

∂

−

∂

−

∂

−

)

(

gdy

)

(

)

(

)

(

)

(

otrzymujem

Poissone

rownania

dla

oraz

gdy

)

(

)

(

)

(

−

∂

−

∂

⇒

7. Opisa

metode ró

nic sko

czonych w zastosowaniu do obliczania pola wokół obiektu o

zadanym potencjale

W metodzie tej zagadnienie brzegowe sprowadza sie do ukladu liniowych rowna

matematycznych,a po ich rozwi

zaniu otrzymuje si

przybli

one rozwi

zanie zagadnienia.

Załózmy

e zagadnienie brzegowe jest okreslone w obszarze plaskim.Rysujemy siatk

której kształt zale

y od układu współrzednych.W przypadku układu prostok

tnego przyjmujemy

siatke regularn

o skoku = h.W

zły siatki sa równe Xi = X0 + ih Yj = Y0 +jh

Brzeg obszaru aproksymuje si

lini

łaman

przechodz

przez w

zły siatki.

Potencjał w punkcie Xi Yj obliczamy wg nast

puj

cego równania:

1/4 V(Xi,Yj) –V(Xi-1,Yj-1)- V(Xi+1,Yj-1)- V(Xi-1,Yj+1)- V(Xi+1,Yj+1)=0
Po obliczeniu potencjałów dla wszystkich punktów obszaru cał

operacje powtarzamy od pocz

tku

dopóki w kolejnej iteracji ró

nica mi

dzy poprzednim a aktualnym potencjałem b

dzie

znikoma....

8. Podział o

rodkow materialnych,opis i scharakteryzowa

własno

ci.

Wyró

nia si

nast

pujace o

rodki materialne:

- Jednorodny: ma on takie same własno

ci fizyczne w ka

dym punkcie.

- Izotropowy: ma takie same własno

ci fizyczne w trzech kierunkach przestrzeni.

- Liniowy:stałe fizyczne charakteryzuj

ce ten o

rodek nie zale

a ani od nat

ęż

enia

pola elektrycznego ani od nat

ęż

enia pola magnetycznego(stłe te to przenikalno

ść

magnetyczna,elektryczna i konduktywno

ść

- Przewodz

cy: wyst

puje zjawisko przewodzenia pr

du elektrycznego jako

uporz

dkowanego ruchu ładunków elektrycznych pow wpływem działania

pola elektrycznego.(J =

- Nieprzewodz

cy(dielektryk): brak zjawiska przewodzenia,wektory D i E s

proporcjonalne(D =

- Bianizotropowy: wktor indukcji D zale

y od nat

ęż

enia pola elektrycznego i

magnetycznego (D =

E +

- Diamagnetyczny: przenikalno

c magnetyczna

=const.<1 i jest to linia

Przechodz

ca przez

rodek układu wsp.(B=

H )

- Paramagnetyczny:j.w.

- Ferromagnetyczny: przenikalno

ść

zale

y od nate

enia pola magnetycznego(

(H)).

Jest to o

rodek nieliniowy,wyst

puje zjawisko histerezy.

9. Opisa

natur

du przewodzenia,przesuni

cia i konwekcji.

d przewodzenia jest utworzony przez poruszajace sie ładunki pod wpływem

działania pola elektrycznego
W metalach tworzy go strumie

elektronów ,charakteryzuje go gesto

ść

J=dI/dS przy dS---0

dem przesuni

cia nazywa sie wystepuj

cy w całkowej postaci równa

Maxwella

człon

Jednostk

jest amper.Stanowi on przedłu

enie przepływu pr

du np.miedzy okladkami

kondensatora gdzie nie wyst

puje pr

d przewodzenia.W ten sposób realizuje sie

przepływ pr

du wzdlu

drogi zamkni

tej.Przybiera on znaczne rozmiary przy bardzo

szybkich zmiana czasowych pola elektromagnetycznego

d konwekcji wyst

puje wówczas gdy ruch elektryczno

ci odbywa sie w wyniku

ruchu materii obdarzonej ładunkiem .Jego g

sto

ść

J =

V, gdzi

to przestrzenna

gesto

ść

ładunku, a V-pr

dko

ść

unoszenia.

10. Poda

i zinterpretowa

równania Poissone’a i Laplace’a. Poda

przykłady wykorzystania

tych równa

Pole trójwymiarowe:

=const

Podstawiaj

c do wzoru:

div

otrzymujemy

div

a po podstawieniu

gradV

−

mamy:

−

divgradV

czyli

−

∇

(równanie Poissona).

gdzie

∇

jest laplasjanem.

eli w pewnym obszarze pola elektrostatycznego nie ma ładunku (

=0) w punktach tego

obszaru potencjał spełnia równanie Laplace’a

∇

Wyznaczenie potencjału w polu elektrostatycznym sprowadza si

do rozwi

zania równania

Poissona lub Laplace’a, przy spełnieniu okre

lonych warunków brzegowych, czyli do rozwi

zania

zagadnienia brzegowego.

∫

)

(

V(x,

πε

gdzie:

)

spełnia równanie Poissona w punktach obszaru V, którym

istnieje ładunek przestrzenny o g

sto

, a równanie Laplace’a – na zewn

trz tego obszaru, gdzie

nie ma ładunku przestrzennego. Z tego powodu powy

sze wyra

enie nazywa si

rozwi

zaniem

podstawowym równa

Poissona i Laplace’a.

Pole dwuwymiarowe:
W obszarze ograniczonym powierzchni

walcow

o tworz

cych równoległych do osi z ukł

współrz

dnych prostok

tnych znajduje si

ładunek przestrzenny o g

sto

, która nie zale

y od

współrz

dnej z. Przy zało

eniu,

e długo

ść

w kierunku osi z jest niesko

czenie du

a, rozpatrywane

pole nie zale

y od współrz

dnej z i jest takie samo w ka

dej płaszczy

nie prostopadłej do osi z.

Otrzymujemy w tym przypadku pole dwuwymiarowe, zale

ne tylko od współrz

dnych x, y, nazywane

sto polem płaskim. We wn

trzu obszaru, gdzie znajduje si

ładunek przestrzenny, potencjał

spełnia dwuwymiarowe równanie Poissona:

−

a na zewn

trz tego obszaru – dwuwymiarowe równanie Laplace’a:

11. Poda

i zinterpretowa

prawo Jule’a–Lenza w postaci ró

niczkowej.

Przy przepływie pr

du w

rodowisku przewodz

cym wyst

puje zjawisko przekształcania si

energii elektrycznej w ciepło. Zjawisko to ma charakter przestrzenny i zachodzi w całym obszarze
pola przepływowego. Niech

∆

oznacza moc przekształcan

w ciepło w obszarze

∆

pola

przepływowego. Wielko

ść

lim

∆

→

∆

(*)

nazywa si

sto

obj

ciow

mocy przetwarzanej na ciepło.

Rozpatrzmy odcinek rurki pola przepływowego mi

dzy dwiema powierzchniami ekwipotencjalnymi

oraz

. Niech dS oraz dn oznaczaj

odpowiednio pole poprzecznego przekroju oraz długo

ść

rozpatrywanego odcinka rurki, a du – napi

cie wzdłu

tego odcinka. Pr

d płyn

cy w rurce wyra

a si

wzorem: di=JdS zgodnie z prawem J-L, moc przetwarzana na ciepło w odcinku rurki jest równa:
dP=R(di)

, =>

gdzie rezystancja odcinka rurki wynosi:

- konduktywano

ść

rodowiska

Po wykonaniu elementarnych przekształce

otrzymujemy:

, gdzie

dV=dSdn – obj

ść

odcinka rurki

Zgodnie ze wzorem (*) g

sto

ść

obj

ciowa mocy wynosi:

lub

⋅

12. Poda

definicj

i opisa

poj

cie: „Dywergencja pola wektorowego” dla wybranego układu

współrz

dnych.

W obszarze V okre

lone jest pole wektorowe, a wektor

(x,

jest funkcj

ró

niczkowaln

tym obszarze. Niech S oznacza powierzchnie w rozpatrywanym obszarze. Element dS tej

powierzchni przedstawiamy w postaci wektora

normalnego wzgl

dem tego elementu. Warto

(miar

) wektora

jest pole powierzchni elementu dS.

Wielko

ść

Acos

⋅

przedstawia strumie

elementarny wektora

przez powierzchnie

dS. Strumie

wektora

przez powierzchnie S nazywamy całk

powierzchniow

⋅

∫

. Strumie

wektora przez powierzchni

jest skalarem. Strumie

wektora

przez powierzchni

zamkni

przedstawiamy w postaci

∫

⋅

Zakładamy przy tym,

e wektor

ma zwrot normalnej zewn

trznej. Strumie

wektora wypływaj

na zewn

trz przez brzeg obszaru jest dodatni, a strumie

wpływaj

cy ujemny.

Dywergencj

lub rozbie

div

wektora

nazywamy granic

, do której d

ąż

y strumie

wektora

przez powierzchnie zamkni

S, b

brzegiem obszary

∆

, podzielony przez obj

ść

tego

obszaru, gdy ta obj

ść

ąż

y do zera, czyli dywergencja jest wielko

skalarn

div

lim

∆

⋅

∫

→

∆

Dywergencja jest operacj

przekształcaj

wektor

pola na wielko

ść

skalarn

div

. Okre

lenie

dywergencji nie zale

y od przyj

tego układu współrz

dnych, jednak

e posta

wzoru dla div

zale

od rodzaju układu.
współrz

dne prostok

tne

Strumie

wektora

przez obie rozpatrywane

ciany wynosi:

∆

−

∆

)]

(

)

(

Zgodnie ze wzorem Taylora. Strumienie wektora A przez prostopadłe

ciany prostopadło

cianu s

równe:

∆

oraz

∆

Wobec tego przez wszystkie

ciany wynosi on

∆













∆

, wi

c otrzymujemy

div

13. Rodzaje i klasy równa

ró

niczkowych stosowanych przy opisie pól

elektromagnetycznych.

Równania ró

niczkowe:

eliptyczne (Laplace’a, Poissona, Helmholtza)

paraboliczne (równanie przewodnictwa)

hiperboliczne (równanie falowe)

I. Równanie eliptyczne

równanie Laplace’a

skalarne:

∇

wektorowe:

∆

V - funkacja skalarna lub składowa wektora

∇

- nabla

∇

- laplasjan skalarny

∆

- laplasjan wektorowy

równanie Poissona

skalarne:

−

∇

wektorwe:

−

∆

f – funkcja opisuj

ca przestrzenny rozkład

ródeł wzbudzaj

cych pole

równanie Helmholtza

skalarne jednorodne:

∇

skalarne niejednorodne:

−

∇

wektorowe jednorodne:

∆

wektorowe jednorodne:

−

∆

II. Równanie paraboliczne:
przewodnictwa (np.dyfuzji,Fouriera)

skalrne:

⋅

∇

wektorowe:

⋅

∆

; h

– współczynnik rzeczywisty

14. Poda

definicje i opisa

poj

cie: „Rotacja pola wektorowego” dla wybranego układu

współrz

dnych.

Def.
F – pole wektorowe

)

rotF

'
x

'
y

−

F=(P,Q,R)

Rotacj

pola wektorowego F nazywamy pole wektorowe

)

rotF

'
x

'
y

−

rotF

(*)

(Dla pola potencjalnego rotacja równa jest zero)

rot

∇

Istot

rotacji najłatwiej wytłumaczy

na przykładzie jakiej

wielko

ci fizycznej. We

my ruch

obrotowy cieczy (w miejscu tworzenia si

wirów). Pr

dko

ść

liniowa cz

steczek płynu jest równa

rsin

- pr

dko

ść

towa

⋅

Po wykorzystaniu (*) otrzymamy rotv=2

⇒

rotv

co oznacza,

e wektor pr

dko

ci k

towej jest

równy połowie rotacji wektora pr

dko

ci liniowej.

15. Metoda rozdzielenia zmiennych – zastosowanie na przykładzie rozwi

zania równania

Laplace’a w układzie kartezja

skim na płaszczy

nie.

Równanie Laplace’a w układzie kartezja

skim w R

∇

V=(X(x),Y(y),Z(z))

V=(X,Y,Z)

Równanie Laplace’a w układzie kartezja

skim w R

(na płaszczy

nie)

równanie wyj

ciowe

→

V=(X,Y)

(*)

Stosujemy podstawienie:

p-stała rozdzielenia zmiennych

Aby została zachowana równo

ść

(*)

−

Po rozdzieleniu zmiennych równanie wyj

ciowe zast

pujemy układem równa












−

16. Zestawi

i scharakteryzowa

wielko

ci wyst

puj

ce w obwodach elektrycznych i

magnetycznych.

Strumie

elektryczny

∫

DdS

Strumie

magnetyczny

∫

BdS

. Nazywa si

go inaczej strumieniem indukcji. Jednostk

strumienia jest 1 weber (Wb)

1Wb = 1T

∗

= 1

Ze wzgl

du na to,

e linie pola magnetycznego (linie indukcji) s

krzywymi zamkni

tymi, strumie

przez powierzchni

zamkni

jest równy zero:

∫

Bds

*10

-7

=1.25663706144*10

-6

V*s*A

-1

Indukcja magnetyczna B jest to wektor o kierunku pola. Jednostk

indukcji magnetycznej jest 1 Tesla

1T = 1

Indukcja elektryczna to wielko

ść

któr

mierzy si

w takich samych jednostkach jak polaryzacj

C/m

D =

E + P.

Nat

ęż

enie pola magnetycznego oznaczamy liter

H i okre

lamy wzorem

Jednostk

nat

ęż

enia pola magnetycznego jest A*m

-1

. Nat

ęż

enie pola jest wektorem (osiowym).

Potencjał elektryczny okre

la si

wzorem

πε

E=-gradV

∫

∞

Edr

Potencjał magnetyczny przypisujemy do pola magnetycznego i okre

lamy wzorem

∫

∞

Hdr

H=-gradV

17. Poda

definicj

i opisa

poj

cie: “Strumie

pola wektorowego“ dla wybranego układu

współrz

dnych.

Strumie

pola skalarnego

∫

udS

Skalarny strumie

pola wektorowego opisany jest wzorem

∫

wdS

nazywany jest strumieniem wektora w.
Wektorowy strumie

pola wektorowego

∫

18. Wyznaczy

rozkład pola elektrostatycznego wokół ładunku punktowego.

Niech ładunek punktowy q znajduje si

rodowisku jednorodnym i izotropowym o przenikalno

elektrycznej

.Wokół tego ładunku zakre

lamy umy

lon

powierzchni

kulist

o powierzchni S i

promieniu r. Z twierdzenia Gaussa wynika,

e strumie

wektora indukcji elektrycznej przez

powierzchni

zamkni

= D4

= q

Uwzgl

dniaj

c zale

ść

E otrzymujemy

πε

Nat

ęż

enie pola elektrycznego jest odwrotnie proporcjonalne do kwadratu odległo

ci od rozpatrywanej

powierzchni do punktu, w którym jest umieszczony ładunek. Linie nat

ęż

enia pola elektrycznego

rozchodz

promieniowo we wszystkich kierunkach. Ze wzgl

du na symetri

kulist

powierzchnie

ekwipotencjalne s

sferami koncetrycznymi.

19. Poda

analogie pomi

dzy polem elektrycznym pr

du stałego i polem elektrostatycznym

Pole elektrostatyczne jest poj

ciem fikcyjnym i w rzeczywistych warunkach nie istnieje ,

bowiem nie ma takich układów, w których ładunki byłyby niezmienne i nieruchome. Okazuje si

jednak,

e wyniki otrzymane dla pola elektrostatycznego mo

na równie

stosowa

w przypadku pól

zmieniaj

cych si

powoli. Z tego powodu rezultaty uzyskane dla pól elektrostatycznych znajduj

zastosowanie praktyczne .

Pole elektryczne

Pole elektrostatyczne

20. Zdefiniowa

współczynniki potencjałowe własne i wzajemne oraz wyja

ich sens w

aspekcie obliczania pojemno

ci.

Dla dwóch jednakowych przewodów o niesko

czonej długo

ci , równoległych do ziemi

ziemia

2’

1’

∫

−

→

div

rot

∫

−

→

Gaussa

div

rot

Współczynniki potencjalne:
-własne

-wzajemne

Przy obliczaniu pojemno

a) Podczas obliczania pojemno

ci linii napowietrznej otrzymujemy wzór na jej potencjał

Natomiast pojemno

ść

b) Dla dwóch przewodów jak na pocz

tku

Pojemno

ść

linia pierwsza-ziemia

Pojemno

ść

linia druga ziemia

Pojemno

ść

linia pierwsza – linia druga

21. Poda

podstawowe zale

ci opisuj

ce pole elektrostatyczne

∗

−

divD

rotE

∫

)

(

DdS

Edl

22. Pojemno

ść

linii 2 przewodowej

Dwa jednakowe, bardzo długie, naładowane przewody s

równoległe do powierzchni ziemii. 1.

Przewody przedstawiamy w postaci ładunków liniowych o g

sto

τ.

2. zakładamy

=−τ

3. Stosuj

c metod

odbi

zwierciadlanych przedstawimy układ z rys. 1 jak na rys 2 (w ten sposób

realizuje si

warunek V=0 w punktach powierzchni ziemii)

rys.1

rys. 2

4. Potencjały V1 i V2 przewodów 1 i 2 wyznaczamy na podstawie zasady superpozycji, przy
wykorzystaniu wzoru

C11

C12

C22

Rys. 3

Rys. 4

23. Wyznaczy

potencjał i pole elektryczne w układzie składaj

cym si

z kuli o promieniu r

umieszczonej w polu jednorodnym o nat

ęż

eniu E

Kula wykonana z dielektryka o przenikalno

ci elektrycznej

1 i umieszczona w niesko

cz. dielektryku

o przenikalno

ci elektrycznej

W ka

dej płaszczy

nie równoległej do linii pola i przechodz

cej przez

rodek kuli pole jest

jednakowe. W tych warunkach pole zale

y tylko od r i

(układ wsp. sferycznych), nie zale

y od wsp.

. Wewn

trz i na zewn

trz kuli potencjał spełnia równanie Laplace’a

∇

V=0, które dla wsp.

sferycznych przybiera posta

sin













∂













∂

Przyjmujemy rozwi

zanie tego

równania w postaci:

−

cos

)

(

, 0

≤

−

cos

)

(

, r

≥

gdzie A

, A

= const.

Składowe nat

ęż

enia pola elektrycznego wynosz

dla 0

≤

−

∂

−

cos

)

(

−

∂

−

sin

)

(

dla r>r

∂

−

cos

)

(

−

∂

−

sin

)

(

Wstawiaj

c do powy

szych warunki brzegowe (wykorzystujemy ci

gło

ść

składowej stycznej wektora

oraz ci

gło

ść

składowej normalnej wekt.

otrzymujemy:

−

sin

)

(

sin

)

(

−

cos

)

(

cos

)

(

Rozwi

zuj

c te równania otrzymamy :

−

wstawiamy to do wzorów na V

i V

(z pocz

tku):

−

cos

, 0

≤













−

cos

, r>r

Nat

ęż

enie pola elektromagnetycznego we wn

trzu kuli o promieniu r

wynosi:

−

Po wstawieniu A

otrzymujemy:

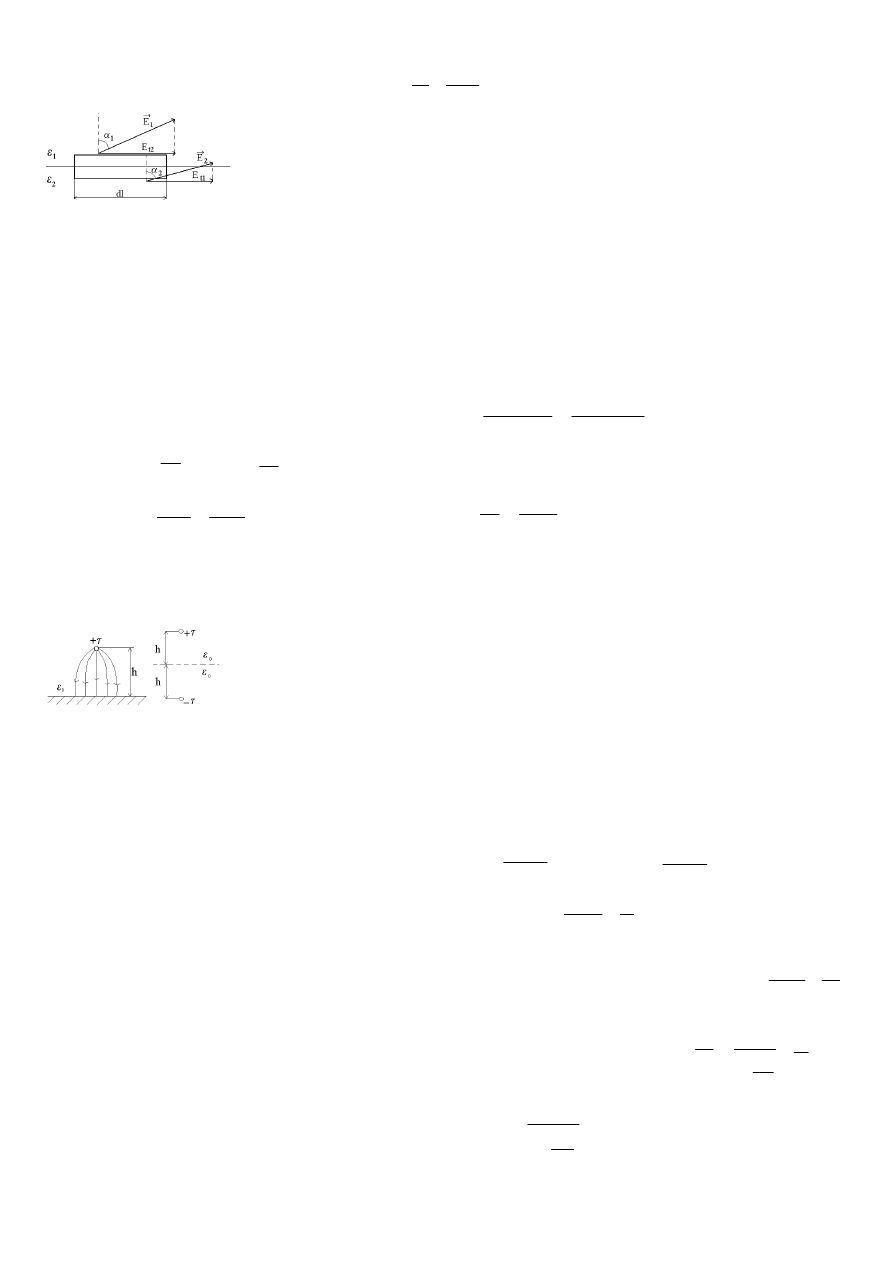
24. Wykaza

e w polu elektrostatycznym na granicy dwóch o

rodków zachodzi zwi

zek:

, E

– składowe styczne nat

ęż

enia pola elektr. b. blisko powierzchni granicznej, odpowiednio w

rodowisku górnym i dolnym.

Napi

cie wzdłu

rozpatrwanej krzywej zamkni

tej wynosi: E

dl-E

dl=0 poniewa

napi

cie wzdłu

krzywej zamkni

tej równa si

zero. Otrzymujemy: E

, czyli:

sin

Dla pola elektrycznego składowa styczna wektora nat

ęż

enia pola elektrycznego jest zawsze ci

gła w

punktach powierzchni granicznej. Je

eli na pow. granicznej

rodowisk nie ma ładunku elektr. , to

składowa normalna wektora indukcji elektr. jest ci

gła w punktach tej powierzchni :

cos

Ostatnie dwa równania dzielimy przez siebie stronami:

cos

sin

cos

sin

wiemy,

oraz

otrzymujemy:

a ostatecznie:

wzór ten wyra

a prawo załamania linii pola elektrycznego w punktach powierzchni granicznej.

25. Wyznaczy

pojemno

ść

linii jednoprzewodowej zawieszonej nad ziemi

wykorzystuj

metod

odbi

zwierciadlanych.

Rzeczywisty układ zast

pujemy układem równowa

nym stosuj

c tzw. metod

odbi

zwierciadlanych.

Bardzo długi przewód o promieniu r

umieszczony jest na wysoko

ci h nad powierzchni

ziemi. Na

przewodzie znajduje si

ładunek o stałej g

sto

ci liniowej

. Przyjmujemy,

e potencjał powierzchni

ziemi równy jest zeru. W tym celu rozpatrzymy dwa ładunki liniowe przeciwnego znaku umieszczone
w

rodowisku o przenikalno

ci elektrycznej

wzdłu

dwóch linii równoległych oddalonych od siebie

o 2h. Potencjał w punkcie P pola wyznaczamy za pomoc

metody superpozycji:

∫

)

(

)

(

)

(

)

(

−

– odległo

ść

od pkt. P w której potencjał równy jest zeru.

W celu wyznaczenia potencjału górnego przewodu przyjmujemy,

e punkt P le

y na jego

powierzchni, zatem r

, r

=2h-r

≈

2h (bo r

<<2h). Zatem potencjał górnego przewodu:

Układ ten (przewód nad ziemi

) mo

emy traktowa

jako kondensator, jedna okładka- pow.

przewodu, druga – pow. ziemi. Obliczamy pojemno

ść

na jednostk

długo

ci:









Pojemno

ść

odcinka przewodu o długo

ci l wynosi:

27. Algorytm wyznacz. pojemno

ci uwarstwionego kondensatora płaskiego.

dzy okładkami uwarstwionego kondensatora płaskiego istnieje n- warstw dielektryków o

przenikalno

ciach elektrycznych

,...,

. Gdy suma d

+...d

odległo

ci mi

dzy płytkami jest

nieznaczna w porównaniu z rozmiarami płytek, wówczas mo

emy przyj

ąć

e w obszarze mi

dzy

płytkami pole jest równomierne. Powierzchnia graniczna dwóch dielektryków jest powierzchni

ekwipotencjaln

. W zwi

zku z tym kondensator n – warstwowy mo

emy przedstawi

w postaci

poł

czenia szeregowego n – kondensatorów, przy czym w obszarze mi

dzy płytkami ka

dego

kondensatora znajduje si

dielektryk o stałej przenikalno

ci elektrycznej. Pojemno

ci kondensator.:

....

S – pole powierzchni jednej okładki.
Pojemno

ść

C kondens. uwarstwionego równa si

pojemno

ci zast

pczej poł

czenia szeregowego

kondensator. o pojemno

ciach C

,...C

, wobec czego:

...

Zatem

∑

...

28. Wyznaczanie pojemno

ci kondensatora walcowego.

Zakładamy,

e na ka

dej powierzchni walcowej o długo

ci l i promieniu R

i R

znajduje si

ładunek

q. Mi

dzy tymi powierzchniami znajduje si

dielektryk.

Na podstawie twierdzenia Gaussa: q = DS =

E 2

wobec czego nat

ęż

enie pola elektrycznego:

Πε

Korzystaj

c z zale

ci mi

dzy nat

ęż

eniem pola elektrycznego a napi

ciem mi

dzy okładkami

kondensatora

⌠



⌡

otrzymamy

Πε

R2
R1

po podstawieniu tego wyra

enia do wzoru C = q/U otrzymamy

Πε

R2
R1

W przypadku gdy znany jest wektor nat

ęż

enia pola el. E oraz indukcji elektrycznej D mi

dzy

okładkami dwóch ciał metalowych (o promieniach R

i R

i długo

ci l ) na których jest umieszczony

ładunek q , pojemno

ść

na wyznaczy

z zale

ci: C = q / U przy czym:

⌠



⌡

R 2

⌠



⌡

c po podstawieniu

⌠



⌡

R 1

R 2

⌠



⌡

29. Wyznaczy

potencjał i nat

ęż

enie pola elektrycznego wokół i w walcu przewodz

cym o

konduktywno

γγγγ

i promieniu R

, znajduj

cym si

rodowisku o konduktywno

γγγγ

= const. .W

rodowisku tym istnieje równomierne pole elektryczne o nat

ęż

eniu E

Przyjmuj

e potencjał w kierunku osi z jest stały. Równanie Laplace’a dla współrz

dnych

walcowych ma posta

∇

(

)

∂

= 0

Wyra

am potencjał jako iloczyn dwóch funkcji: R = f(r),

= f(

), czyli V = R*

Po podstawieniu do powy

szego równania otrzymujemy:

(

)

∂

= 0

Równanie Laplace’a posiada rozwi

zanie w układzie współrz

dnych walcowych w postaci :

V(r,

) =

(

)(

)

A r

−

∞

∑

sin

cos

Stałe A

, A

’

, B

’

oraz n wyznaczamy z warunków brzegowych . Linie pola elektrycznego s

prostopadłe do osi walca (z) ,z symetrii pola wzgl

dem osi x wynika ,

e potencjał skalarny V w

punkcie (r,

) jest taki sam jak w punkcie (r ,-

).Warunek ten spełniaj

funkcje parzyste wi

c B

= 0.

Przyjmuj

e potencjał osi y = 0 dlatego rozwi

zanie ogólne nie mo

e zawiera

funkcji

wielokrotno

ci k

, s

spełnione warunki :

( )

V r,

(

)

V r,

−

Z powy

szych warunków wynika ,

e stała n = 1.

Funkcja potencjału przyjmuje posta

(

)

A r

cos

Po wprowadzeniu nowych zmiennych

A B

Funkcja potencjału przyjmie posta

(

)

K r

cos

Aby wyznaczy

musimy dysponowa

układem dwóch równa

,w tym celu obliczamy

nat

ęż

enie pola elektrycznego E = - grad V .

(

)

(

)

= −

−

cos

sin

W odległo

ci r =

∞

przy k

cie

= 0 , E = E

.Po podstawieniu tego warunku do powy

szego

równania otrzymujemy K

= -E

Dla r = R

potencjał V = 0, st

d otrzymujemy K

, dla dowolnego k

. K

= E

Ostatecznie :

( )

E r

= −

−

cos

oraz nat

ęż

enie

( )

[

]

− −

cos

sin

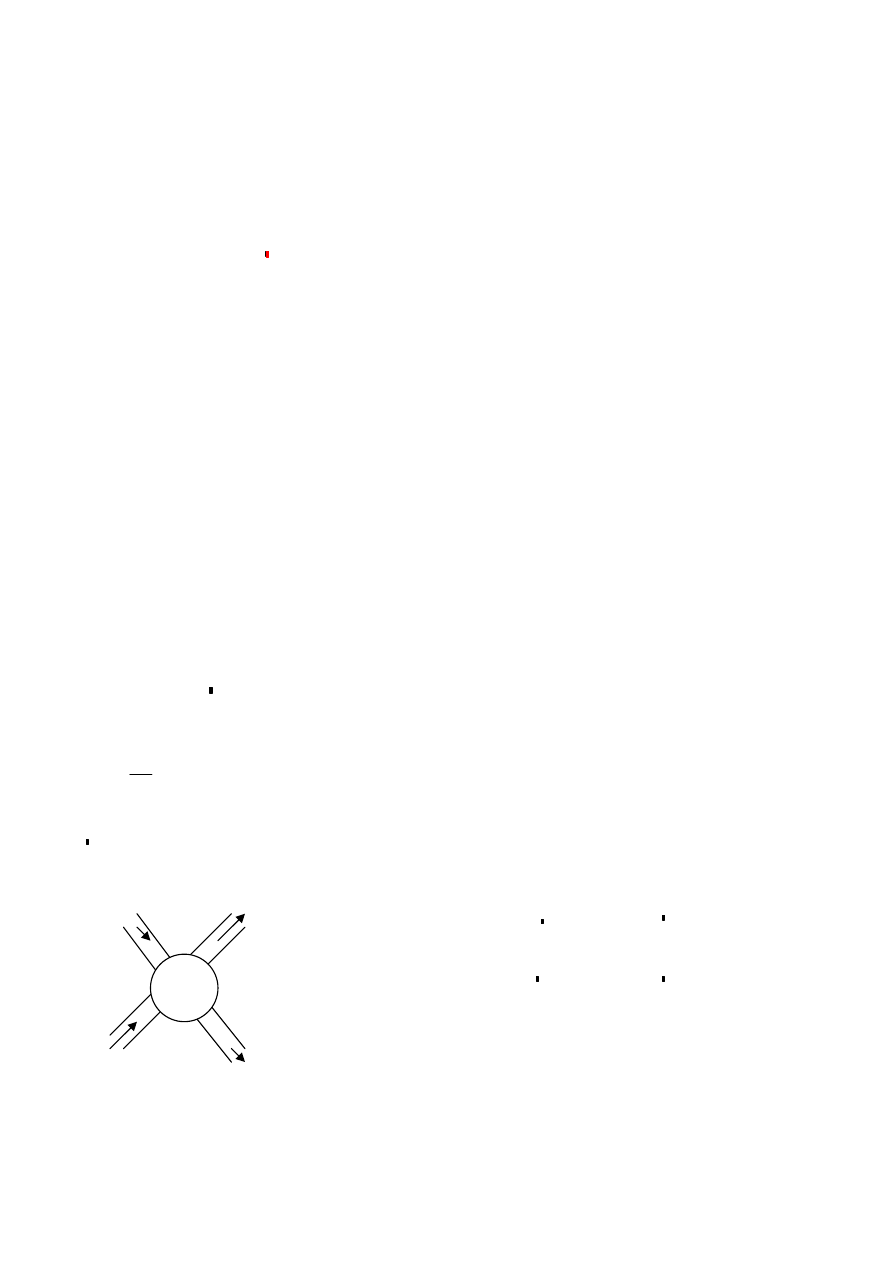
30. Podstawowe prawa opisuj

ce pole przepływowe pr

du stałego

Polem przepływowym nazywamy pole elektryczne w

rodowisku przez które przepływa pr

d elektryczny. W

szczególnym przypadku przepływu pr

du stałego, pole elektryczne nazywamy statycznym polem przepływowym.

Podstawowe prawa opisuj

ce statyczne pole przepływowe to: prawo Ohma, Kirchhoffa oraz Joule’a – Lenza. Prawa

te mog

wyra

one w postaci wektorowej.

1. Prawo ohma w postaci wektorowej.

W przypadku wyst

powania pola elektrycznego o nat

ęż

eniu E w

rodowisku przewodz

cym, napi

cie mi

dzy punktami

A i B wyra

a si

wzorem:

UAB

⌠



⌡

eli nat

ęż

enie pola elektrycznego wewn

trz elementu przewodz

cego o długo

∆

l przekroju

∆

s i konduktancji

oznaczymy przez E to zmiana potencjału na długo

∆

l wynosi

∆

U = E

∆

Nat

ęż

enie pr

du elektrycznego o g

sto

ci J wynosi :

∆

I = J

∆

Z prawa Ohma w postaci skalarnej
R =

∆

U /

∆

I , wtedy R = E

∆

l / J

∆

S , a poniewa

rezystancja rozpatrywanego elementu wynosi R =

∆

l /

s to po

porównaniu stronami otrzymamy :
E / J =

lub J =

Prawo Ohma w postaci wektorowej wyra

a zwi

zek mi

dzy nat

ęż

eniem pola elektrycznego w przewodniku a g

sto

du elektrycznego.

2. Prawo Joule’a Lenza.

Prawo to umo

liwia obliczenie mocy która zostanie przekształcona na ciepło w elemencie o konduktywno

i obj

V, przy nat

ęż

eniu pola elektrycznego E w tym elemencie.

∆

P =

∆

I = ( E

∆

l)(J

∆

S) = EJ

∆

V, przy czym

∆

V to elementarna obj

ść

Po uwzgl

dnieniu wzoru J =

E elementarna moc wydzielona w elemencie przewodz

cym o elementarnej obj

∆

wynosi:
dP =

dV , st

P =

⌠



⌡

sto

ść

obj

ciowa wynosi :

⋅

3. Pierwsze i drugie prawo Kirchhoffa.

⌠



⌡

= 0

oznacza,

e wektor g

sto

ci pr

du stałego J jest bez

ródłowy, oraz tzw. zasad

gło

ci pr

elektrycznego. I

, S

⌠



⌡

⌠



⌡

, S

S I

, S

⌠



⌡

−

⌠



⌡

−

⌠



⌡

⌠



⌡

⌠



⌡

⌠



⌡

⌠



⌡

czyli I

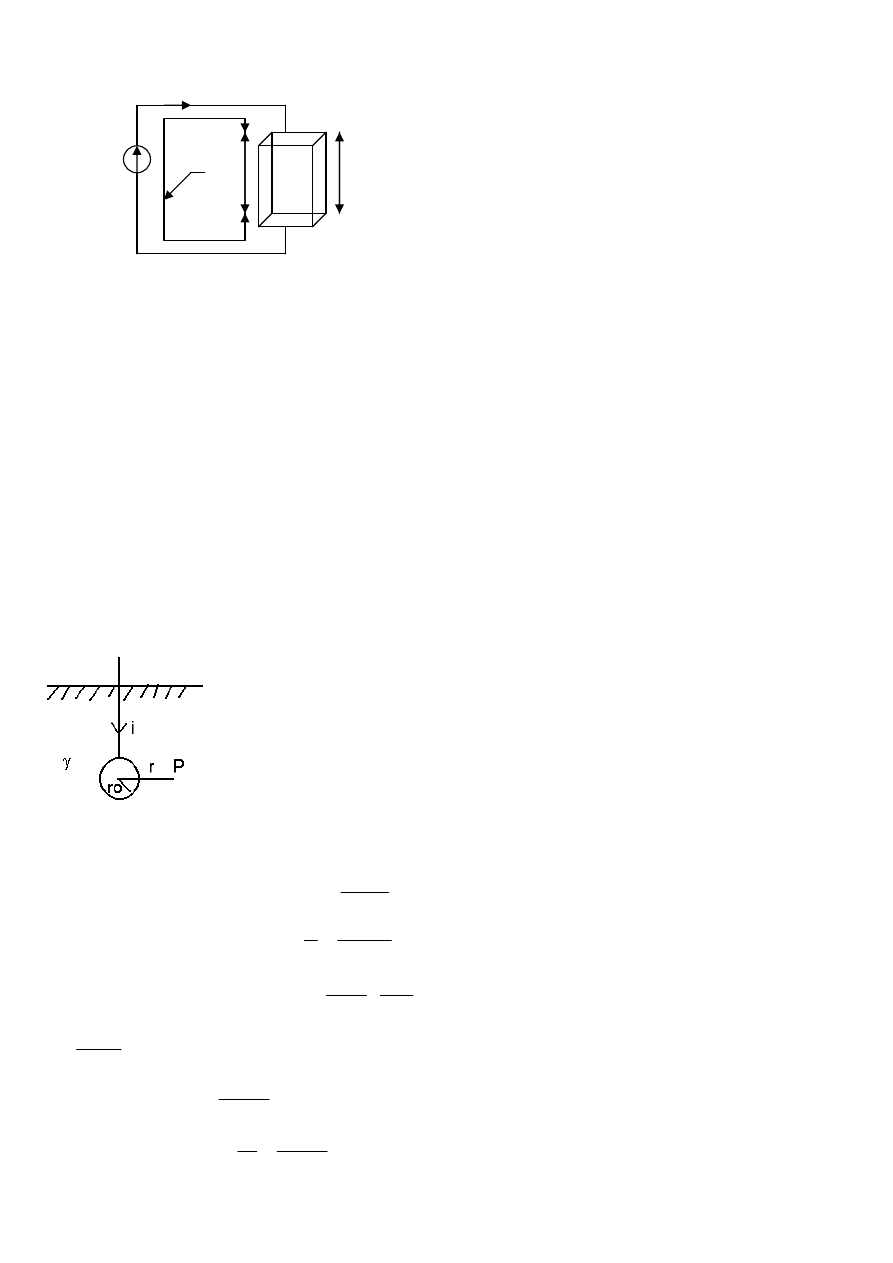
Równanie to wyra

a pierwsze prawo Kirchhoffa w postaci wektorowej. Div J = 0

Drugie prawo Kirchhoffa w postaci wektorowej dotyczy bilansu napi

ęć

I

E

Napi

cie

ródłowe wywołane na drodze l

wynosi:

U zr

l 1

E g

⌠



⌡

l 1

Napi

cie na drodze l

l 2

⌠



⌡

l 2

Bilans napi

ęć

na wyrazi

w postaci wektorowej

⌠



⌡

⌠



⌡

Równanie to nazywamy drugim prawem Kirchh. w postaci wektorowej.

31. Opisa

sposób i wyprowadzi

zale

noci noezb

dnych do obliczania rezystancji uziomu

kulistego

Uziom to elektroda umieszczona w ziemi. Pr

d przepływaj

cy przez uziom wytwarza w okół niego

pole przepływowe

-konduktywno

ść

gruntu

ro- promie

uziomu

r odległo

ść

P od

rodka uziomu

sto

ść

powierzchniowa pr

du :

∏

Nat

ęż

enie pola w punkcie P

∏

Potencjał w punkcie P

∫

∞

−

∏

−

Edr

∏

Potencjał uziomu

∏

Rezystancja uziomu

∏

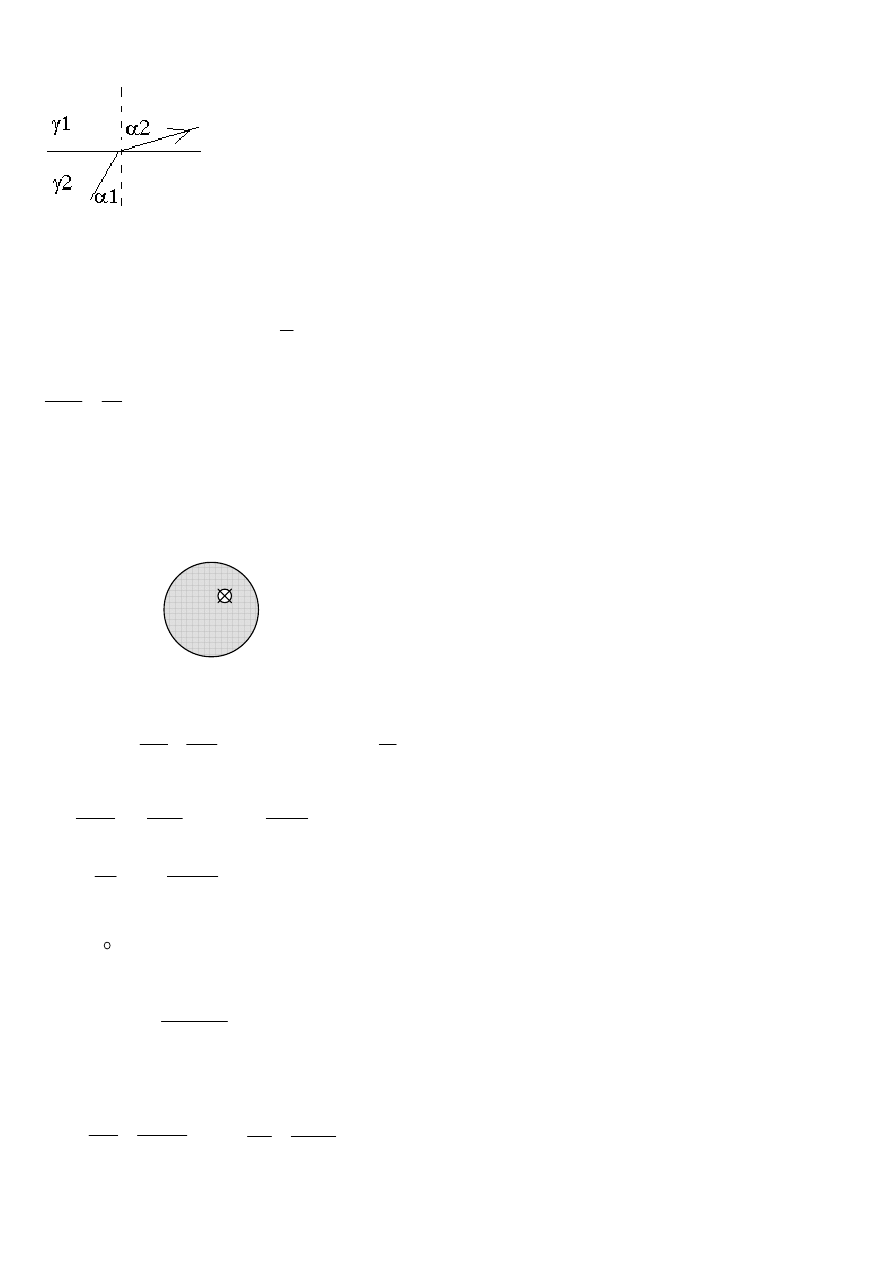
33. Wykaza

e w polu przepływowym na granicy dwuch o

rodków zachodzi zwi

zek

Na granicy dwuch o

rodków nast

puje ci

gło

ść

składowej normalnej wektora g

sto

ci pr

oraz ci

gło

ść

składowej stycznej wektora nat

ęż

enia pola elektyrycznego

a wi

zachodz

zale

cos

sin

gdzie

dziel

c te równania stronami otrzymujemy:

34. Zdefiniowa

poj

cia: indukcyjno

ść

wewn

trzna i zewn

trzna, oraz poda

algorytm ich

wyznaczania.

Je

eli podzielimy obszar w którym istnieje pole magnetyczne na dwa podobszary

Obszar 1 jest ograniczony, obszar 2 ma

e by

ale nie musi.

Obszar 1 nazywamy wewn

trznym, a 2 zewn

trznym. Zakładamy

dany jest niesk. długi przewód wiod

cy pr

Całkowit

indukcyjno

ść

dzielimy na wewn

trzn

i zewn

trzn

L= L

+ L

Na podstawie wzoru na indukcyjno

ść

wzajemn

dzy konturami i, k:

iki

na napisa

Indukcyjno

ść

własna wynosi:

Ω

∫ ∫

Ω Ω

Ω

∫ ∑ ∫

Ω =

Zakładaj

e wszystkie pr

dy s

skupione mo

na napisa

∫

Ω

Idl

Wykorzystuj

c definicj

indukcyjno

ci wzajemnej i własnej:

∑ ∑

Dla pojedynczego konturu powy

szy wzór ma posta

=LI

/2, L=2W

Podział indukcyjno

ci na wewn

trzn

i zewn

trzn

jest zwi

zany z podziałem strumienia

skojarzonego i energii pola:

2
I=0

1
I

≠

Podział strumienia na wewn

trzny i zewn

trzny nie zawsze jest mo

liwy, gdy

nie wen

wszystkich przypadkach mo

na wyodr

bni

linie wektora B przenikaj

ce tylko przez jeden

obszar.

Obszary 1 i 3 s

wewn

trzne, 2,4 zewn

trzne. W obszarze 4 nie ma pola

magnetycznego poniewa

I+I’=0 a wi

c B=0.

Indukcyjno

ść

kabla:

, gdzie

Wówczas gdy nie mo

na całego pola podzieli

na wewn

trzne i zewn

trzne, obliczamy indukcyjno

ść

z pewn

niedokładno

35. Poda

i opisa

prawa Kirchhoffa dla obwodów magnetycznych

Zgodnie z prawem przepływu całka liniowa wektora nat

ęż

enia pola magnetycznego H po krzywej

zamkni

tej l równa si

dowi przenikaj

cemu przez powierzchni

ograniczon

krzyw

∑

∫

Hdl

∫

lśś

Hdl

W praktyce całka mo

e by

zast

piona sum

iloczynów H

, gdzie k to numer kolejnego odcinka

obwodu magnetycznego, wzdłu

którego nat

ęż

enie pola magnetycznego H

i przenikalno

ść

magnetyczna

pozostaj

niezmienne.

∑

-siła magnetomotoryczna

-przepływ pr

∑

, gdzie U

- napi

cie magnetyczne

Prawa Kirhchoffa stosuje si

dla obwodów magnetycznych rozgał

zionych. Dla w

zła obwodu

magnetycznego o b gał

ziach suma algebraiczna strumieni magnetycznych jest równa zeru.

∑

Dla oczka obwodu magnetycznego suma algebraiczna napi

ęć

magnetycznych wszystkich

elementów oczka jest równa sumie algebraicznej sił magnetomotorycznych zawartych w tym
oczku:

∑

oraz

∑

1 I 2 3 4
I’

36. Wykaza

e w polu magnetostatycznym na granicy dwóch o

rodków zachodzi zwi

zek

Mamy dwa o

rodki w obu jest pole magnetyczne, na granicy o

rodków nast

puje załamanie linii

wektora indukcji i wektora nat

ęż

enia:

Granic

dzy o

rodkami otaczamy dostatecznie małym prostok

tem abcd. W obszarze

bezpr

dowym jest spełnione równanie rotH=-rotgradV

=0, które w postaci całkowej ma posta

całka(H*dl)=0; V

-potencjał skalarny.

Kontur abcd mo

na wybra

tak, aby na odcinkach ab i cd pole było równomierne.

Przy tych zało

eniach równanie całka(H*dl)=0 ma posta

sin

ab-H

sin

cd=0; H

sin

bo ab=cd

Z tego wynika,

e składowa styczna wektora nat

ęż

enia pola magnetycznego jest ci

gła.

eli na granicy o

rodków wyodr

bnimy prostopadło

cian, w ka

dym punkcie pola magnetycznego

jest spełnione równanie divB=0, posta

całkowa całka(B*ds.)=0.

Zawsze mo

na wybra

tak

dowolnie mał

powierzchni

zamkni

e wewn

trz pole b

dzie

równomierne. Zakładamy,

e powierzchnie bc i da s

wielokrotnie mniejsze od powierzchni ab i cd.

Poniewa

przez powierzchnie równoległe do płaszczyzny rysunku nie przenika wektor indukcji.

Z postaci całkowej otrzymamy

–B

cos

s+B

cos

s=0

;

cos

1=B

cos

Na tej podstawie stwierdzamy,

e składowa normalna wektora indukcji magnetycznej jest ci

gła.

Dziel

c otrzymane równania otrzymamy:

, prawo załamania pola magnetycznego.

37. Siła i energia.

Jednym z przejawów istnienia pola magn. jest siła działaj

ca na magnesy trwałe lub przewody z

dem. G

sto

ść

obj. siły działaj

cej w polu magn. na przewód z pr

dem:

Ω

(ze wzoru Loretza)

po podstawieniu:

Idl

Siła działaj

ca na element a obj.

Ω

∫

Ω

li pr

dy s

liniowe to siła działaj

ca:

∫

Energia
G

sto

ść

obj

ciowa energii:

Gdy

rodowisko izotrobowe:

′

Energia zgromadzona w obj.

Ω

⋅

∫

Ω

rotA

eli uwzgl

dnimy

∫

Ω

−

Ω

⋅

−

⋅

≡

div

rotHd

rot

div

)

(

)

(

zgodnie z tw. Gaussa:

div

∫

Ω

)

(

rozci

gni

te na niesko

czon

ilo

ść

obj. -> 0

Ω

∫

Ω

rotH

po uwzgl

dnieniu rów. Maxwella I:

∫

⋅

Ω

⋅

Ω

poniewa

∫

⋅

Jds

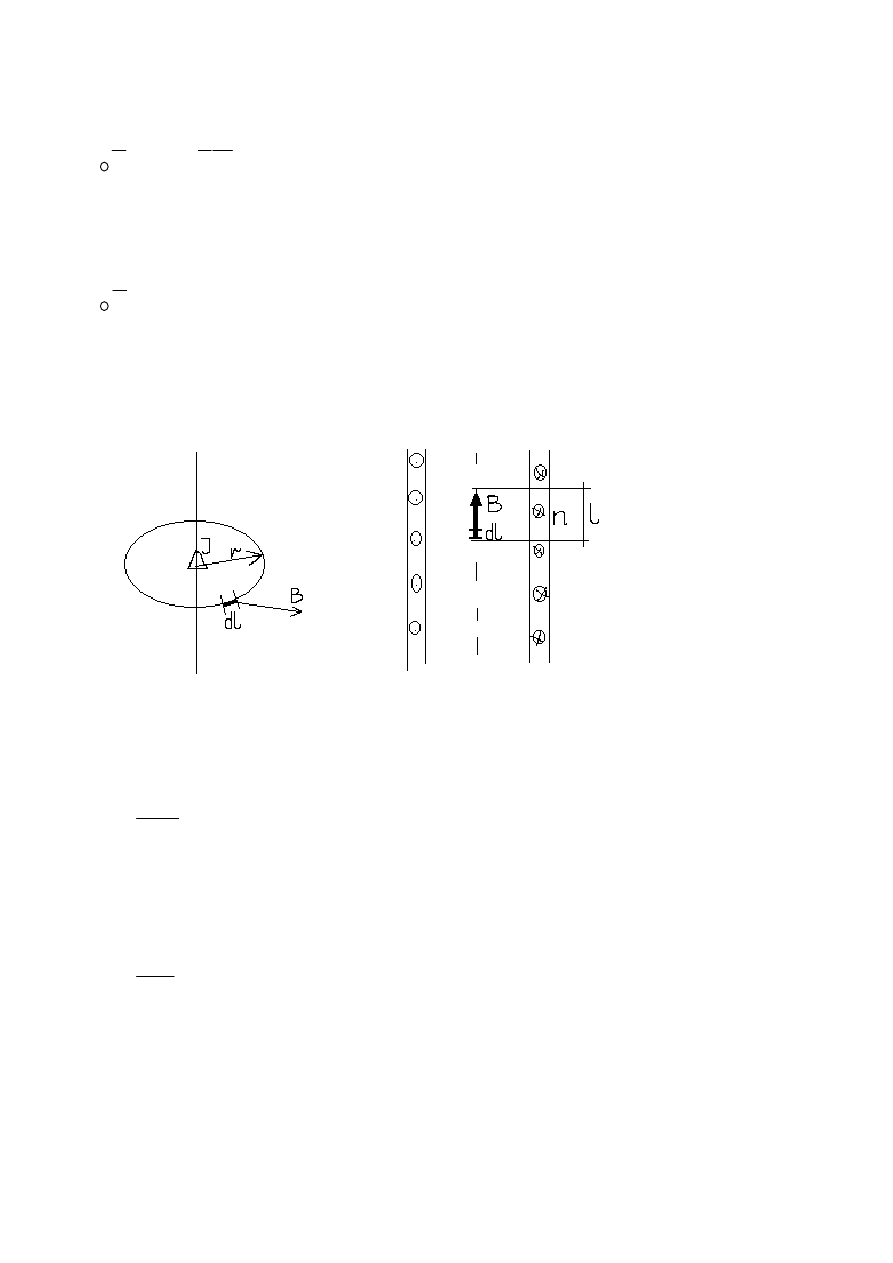
38. Wyznaczanie wektora indukcji magnetycznej.

Wektor indukcji magn. mo

na wyznaczy

na podstawie pierwszego równania Maxwella.

Uwzgl

dniaj

c w nim tw. Stokesa otrzymamy prawo przepływu:

∫

li kontur całkowania

przebiega w ten sposób,

e obejuje on całkowity pr

, to wzór przybiera

posta

∫

na z nich korzysta

w nielicznych przypadkach, bo nie wiadomo, jak

funkcj

współrz

dnych jest

B (tylko wtedy gdy rozkład B na konturze jest okre

lony). Przypadkiem szczególnym jest identyczna

warto

ść

modułu indukcji we wszystkich punktach konturu całkowania.

Dla niesko

czenie długiego przewodu:

Bdl

⋅

∫

Dla niesko

czenie długiego solenoidu wykonuje si

obliczenia na odcinku o dowolnej długo

ci l:

Bdl

∫

, n – liczba zwojów na tym odcinku

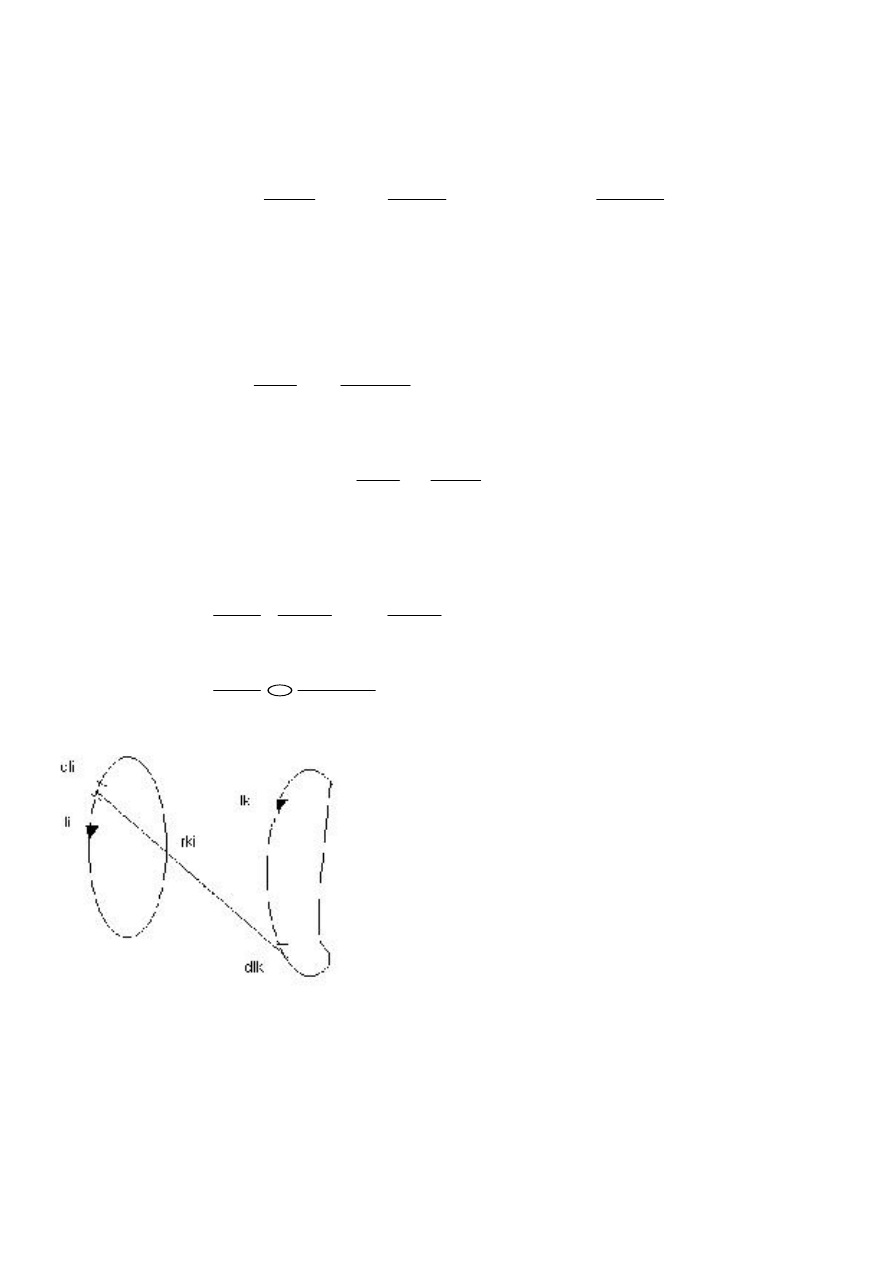
41. Zdefiniowa

poj

cia indukcyjno

ść

własna i wzajemna oraz poda

algorytm ich

wyznaczania.

Indukcyjno

ść

własna – Zmiany nat

ęż

enia pr

du w obwodzie powoduj

zmiany nat

ęż

enia pola

magnetycznego tego pr

du czyli pola, w którym znajduje si

obwód.

Indukcyjno

ść

własna zwi

zana z jednym elementem.

Ω

⋅

∫∫

Ω

– zewn

trzny strumie

sprz

ęż

ony

– wewn

trzny strumie

L= L

+ L

dla przewodu cienkiego

⋅

∫∫

Indukcyjno

ść

wzajemna – mi

dzy obwodami.

- strumie

sprz

ęż

ony z obwodem k, wytworzony przez pr

d I

∫∫

Ω

⋅

Ω

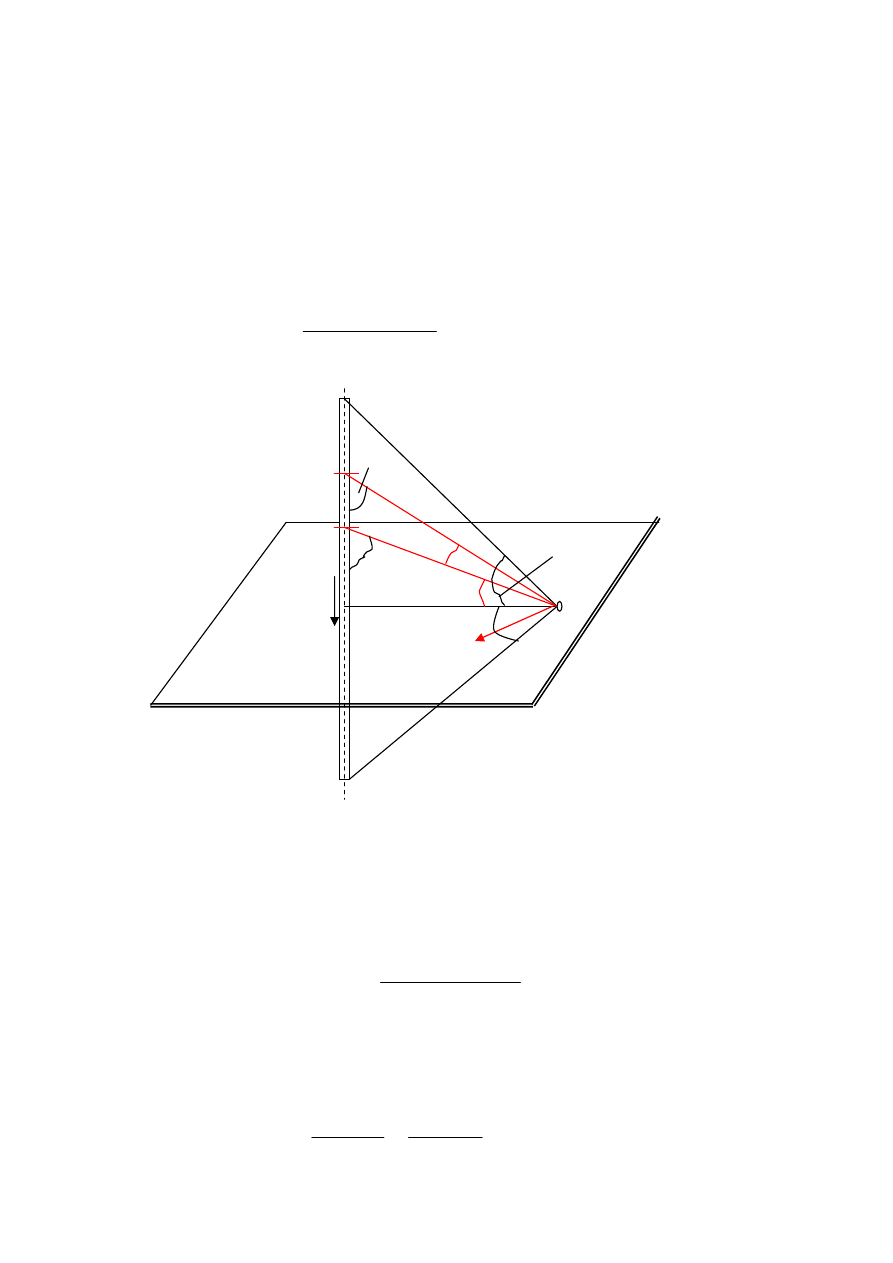
42. Wyznaczy

pole magnetyczne i indukcyjno

ść

przewodów niesko

czenie długich.

Pole magnetyczne układów przewodników z pr

dem mo

na wyznaczy

jedn

z nast

puj

cych

metod:
a) z prawa Amper’a
b) z prawa Biota-Sawarta,
c) z równania Poissona dla wektorowego potencjału magnetycznego.

Pole przewodu prostoliniowego.

Dany jest prostoliniowy przewodnik, przez który płynie pr

d o nat

ęż

eniu I. Indukcj

magnetyczn

punkcie odległym od przewodnika o r znajdujemy z prawa Biota-Savarta

rys. Pole przewodnika prostoliniowego znajduje si

z pomoc

prawa Biota-Savarta. Całkowanie po

długo

ci zast

piono całkowaniem po k

tach. Przy niesko

czonej długo

ci k

ty graniczne s

proste.

w którym

oznacza wzgl

przenikalno

ść

magnetyczn

rodka. W powietrzu i pró

=1 i prawo

Biota-Savarta powraca do poprzednio poznanej postaci. Oznaczaj

c przez

t mi

dzy wektorem

cym element pr

du Idl z punktem działania, a przewodnikiem mo

na napisa

sin

πς

Idl

Przeprowadzamy teraz przez punkt działania płaszczyzn

prostopadł

do przewodnika. K

dzy

a kierunkiem wektora

spełnia zwi

zek

/2. St

cos

sin

πς

µµ

Idl

Iloczyn dlcos

jest rzutem elementu dl na kierunek prostopadły do

i mo

na go zast

elementem

łuku

. St

Poza tym

Podstawiaj

c to wszystko do prawa Biota-Savarta i całkuj

c po k

tach

, otrzymamy

odpowiadaj

com przewodnika. Dla przewodnika niesko

czenie długiego (czyli dla

punktów bliskich realnego przewodnika)

/2, co prowadzi do warto

ci indukcji

i nat

ęż

enia pola

Warunkiem stało

ci indukcji (lub nat

ęż

enia pola) jest r = const. Jest to zarazem równanie linii

pola w płaszczy

nie prostopadłej do przewodnika.

sin

cos

( )

[

]

sin

cos

−

∫

−

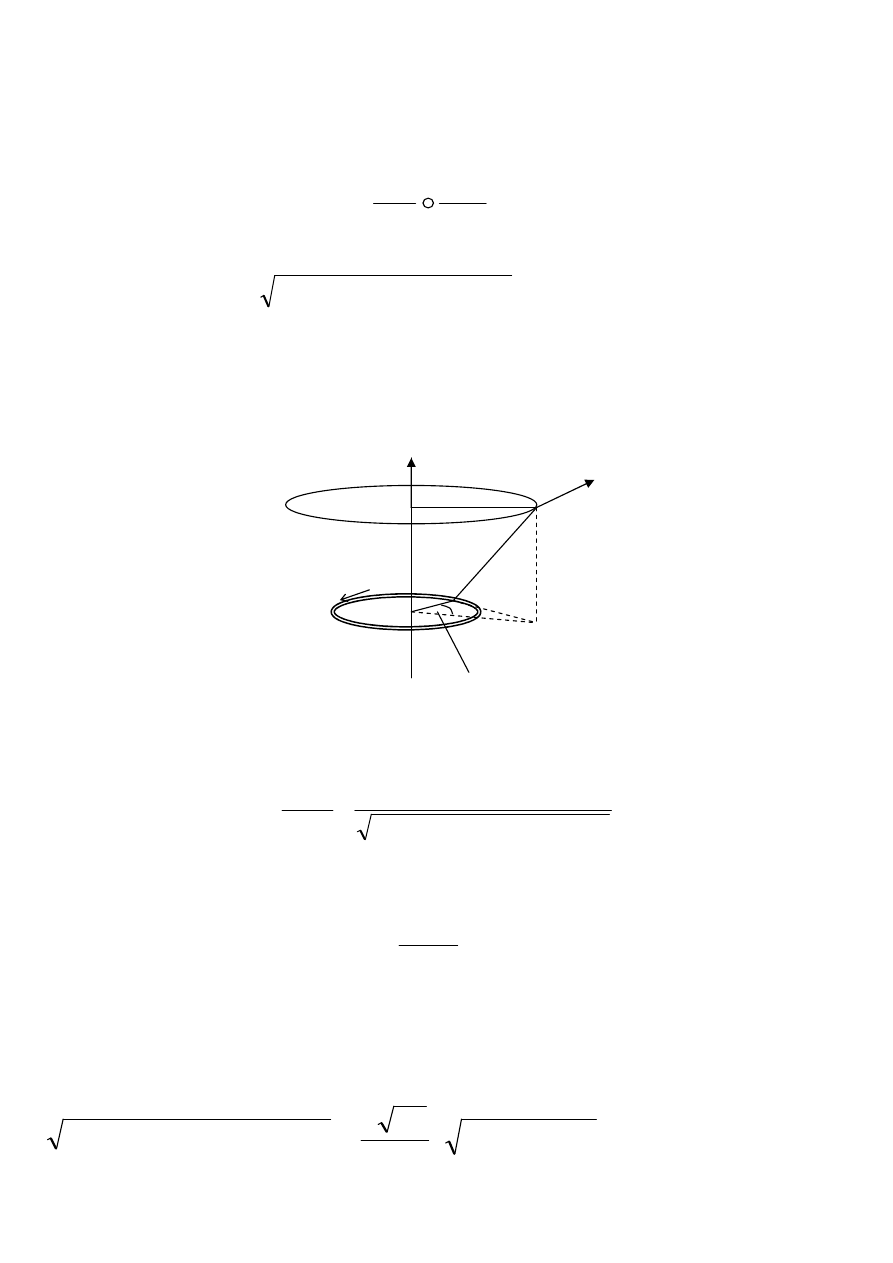
43. Wyznaczy

potencjał i polemagnetyczne w układzie składaj

cym si

z wydr

ąż

onego walca

ferromagnetycznego.

Wydr

ąż

ony walec o promieniu R, przewodz

cy pr

d i. Układ współrz

dnych walcowych.

Ze wzgl

du na symetri

układu, potencjał wektorowy ma tylko skladow

czyli A= l

, przy czym

gdzie:

a drog

całkowania jest o

pier

cienia. Liniami pola wektora A s

okr

gi, których

rodki znajduj

na osi 0z; przykładem jednej lini pola jest okr

g C.

Poniewa

dl=Rd

, a dl tworzy k

z wektorem A, wi

c rzut dl na kierunek tego wektora jest równy

dlcos

, wobec czego:

Wprowadzamy zmienna całkowania

wiec:

po wykonaniu przekształce

otrzymujemy:

∫

cos

∫

−

cos

−

sin

cos

)

cos(

cos

−

sin

cos

−

⋅

−

gdzie:

Wobec powy

szego:

bowiem funkcja podcałkowa jest parzysta wzgl

dem

Przy wykorzystaniu to

samo

otrzymujemy w wyniku

gdzie:

)

(

∫

−

sin

)

sin

(

sin

−









−

)

(

∫

−

sin

∫

−

sin

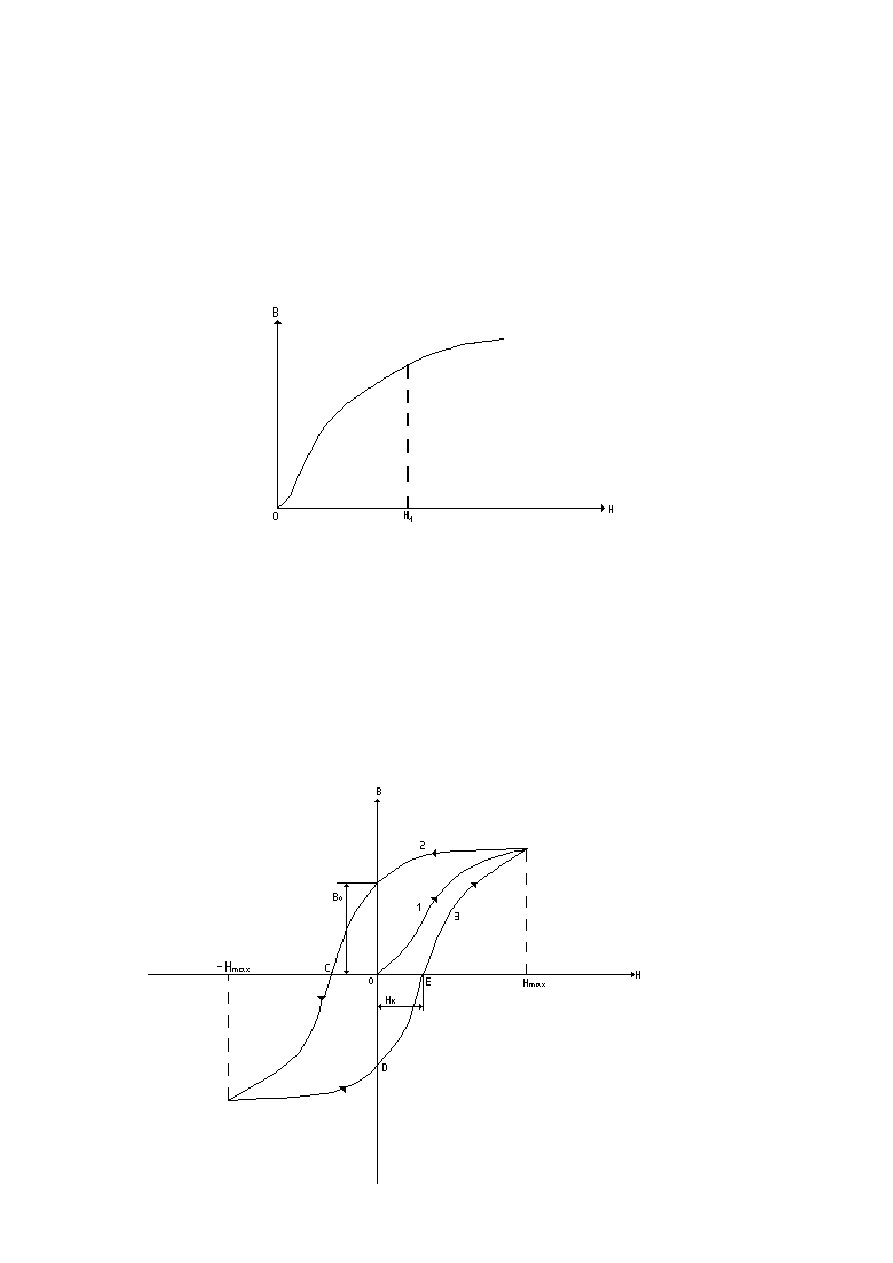
44. Scharakteryzowa

własno

ci magnetyczne ciał i opisa

proces magnesowania

ferromagnetyków.

Poza ciałami diamagnetycznymi i paramagnetycznymi istniej

ciała ferromagnetyczne. Przenikalno

ść

magnetyczna ciał ferromagnetycznych zale

y od nat

ęż

enia H pola magnetycznego, czyli od

magnetycznego ciała. Do ciał ferromagnetycznych nale

elazo, nikiel, kobalt. W przypadku ciał

ferromagnetycznych wykres funkcji B = f(H) nie jest lini

prost

, wobec czego s

rodowiska

nieliniowe. Krzyw

magnesowania lub charakterystyk

magnesowania ciała ferromagnetycznego

nazywamy wykres funkcji B = F(H) otrzymanej przy zwi

kszaniu nat

ęż

enia H od zera w przypadku,

gdy materiał nie był uprzednio magnesowany. Typow

posta

krzywej magnesowania ciał

ferromagnetycznych przedstawia rysunek.

Pocz

tkowy przebieg krzywej magnesowania jest w przybli

eniu prostoliniowy. Nast

pnie wyst

puje

zakrzywienie, zwane kolanem krzywej magnesowania. Po przekroczeniu nat

ęż

enia H

poza

kolanem, krzywa krzywa magnesowania podnosi si

do góry bardzo wolno, wobec czego du

wzrost nat

ęż

enia pola magnetycznego powoduje jedynie nieznaczny wzrost indukcji magnetycznej B;

mówimy wówczas,

e osi

gni

ty został stan nasycenia magnetycznego.

Rozpatrzmy cewk

maj

z zwojów nawini

tych na rdzeniu wykonanym z materiału

ferromagnetycznego o postaci jak na rysunku. Nat

ęż

enie H pola magnetycznego w rdzeniu jest

proporcjonalne do pr

du i w uzwojeniu, wobec czego zmieniaj

c pr

d i powodujemy zmian

nat

ęż

enia H. Przypu

ść

my,

e rdze

nie był uprzednio magnesowany, a wi

c nie ma tzw. Przeszło

magnetycznej.

Przy zmianie pr

du i od 0 do pewnej warto

ci i

max

net

ęż

enie H w rdzeniu zmienia si

od 0 do warto

max

, a indukcja B zmienia si

według odcinka 1 krzywej magnesowania. Przy zmniejszaniu

nat

ęż

enia H od H

max

do –H

max

indukcja magnetyczna B zmienia si

według krzywej 2, której górna

ęść

przebiega nad odcinkiem 1 krzywej magnesowania. Gdy z kolei nat

ęż

enie H wzrasta od –H

max

do +H

max

, wówczas indukcja B zmienia si

według krzywej 3, której cz

ęść

górna przebiega poni

odcinka 1 krzywej magnesowania. Krzywa z rysunku powy

ej zło

ona z gał

zi 2 i 3 nazywa si

histerezy. Lew

gał

ąź

tli histerezy wykorzystuje si

przy zmniejszaniu nat

ęż

enia H od +H

max

-H

max

, a praw

gał

ąź

3 – przy zwi

kszaniu H od –H

max

do +H

max

Zjawisko wyst

puj

ce przy przemagnesowywaniu ciał ferromagnetycznych nazywa si

histerez

magnetyczn

. Histereza magnetyczna jest wynikiem zjawisk zachodz

cych w skupiskach

krystalicznych ciał ferromagnetycznych.

Z powy

szego rysunku widzimy,

e w punkcie A gał

zi 2 w p

tli histerezy w ciele istnieje indukcja B

przy nat

ęż

eniu H=0. Chocia

nat

ęż

enie pola magnetycznego równa si

zeru to jednak indukcja B jest

ró

na od zera, a wi

c w ciele istnieje strumie

magnetyczny. Wielko

ść

nazywamy indukcj

szcz

tkow

. W celu zniszczenia strumienia magnetycznego spowodowanego przez indukcj

szcz

tkow

nale

y zmieni

kierunek linii pola magnetycznego, czyli nale

y zmieni

zwrot pr

du w

cewce. Z rysunku widzimy,

e indukcja B=0, gdy nat

ęż

enie H = -H

=OC , wielko

ść

nazywamy

koercj

Z du

żą

dokładno

na przyj

ąć

e p

tla histerezy jest symetryczna wzgl

dem pocz

tku układu

współrz

dnych. W zwi

zku z tym OA=OD oraz OC=OE.

Ciało magnetyczne twarde maj

szerok

tle histerezy tzn. posiadaj

żą

koercj

. Natomiast

ciała magnetycznie mi

kkie maj

tle histerezy czyli posiadaj

mał

koercj

. Na ogół ciała

kkie magnetyczne s

łatwiej magnesowalne, a indukcja magnetyczna w stanie nasycenia jest

ksza dla tych ciał ni

dla ciał twardych magnetycznie. Gdy p

tla histerezy jest dostatecznie

ska, wówczas w obliczeniach mo

na pomin

ąć

zjawisko histerezy magnetycznej, posługuj

c si

jedynie krzyw

magnesowania.

Materiały magnetycznie mi

kkie to min – stopy

elaza: permaloj, superpermaloj.

Konduktancja tych ciał jest niewielka i dlatego powstaj

dy wirowe czyli s

dodatkowe straty.

Materiały magnetycznie twarde to mi

dzy innymi: stal chromowa, kobaltowa.

Rozmagesowanie magnesów - diamagnetyzacja mo

emy przprowadzi

poprzez:

podgrzewamy materiał magnetyczny do temperatury Curie – wtedy ferromagnetyk staje si

paramagnetykiem.

Z reguły temperatura Cuire jest wy

sza ni

100

działamy zmiennym polem magnetycznym.

45. Algorytm wyznaczania pola magnetycznego we wn

trzu cewki solenoidalnej

Na rdzeniu w kształ

ie walca lub graniastosłupa nawini

to równomiernie uzwojenie zawieraj

ce z

zwojów, w którym płynie pr

d i.Gdy długo

ść

l cewki jest dostatecznie du

a wówczas mo

na przyj

ąć

e w jej wn

trzu pole magnetyczne jest równomierne.Jako drog

całkowania przy stosowaniu prawa

przepływu przyjmiemy lini

ABCA.Powierzchni

o krzywej brzegowej ABCA przenika z zwojów

przewodz

cych pr

d i, wobec czego przepływ przez t

powierzchni

jest równy amperozwojom

,mamy zatem

czyli

W obszarze na zewn

trz cewki pole magnetyczne jest bardzo słabe w porównaniu z polem w jej

trzu.Wskutek tego nie popełnia si

ego bł

du ,gdy w powy

szym wyra

eniu pominie si

całke

Otrzymujemy zatem w przybli

eniu

Ppomijaj

c zniekształcenia pola magnetycznego w obszarze blisko kra

ców cewki,mamy

Wobec czego nat

ęż

enie pola magnetycznego w dowolnym punk

ie obszaru wewn

trznego cewki

wyra

wzorem

46. Opisa

zjawisko indukcji elektromagnetycznej.

Prawo indukcji elektromagnetycznej opisuje prawidłowo

ci, przy której w pewnych warunkach pole

magnetyczne wywołuje napi

cie a zatem i pr

d elektryczny. Zjawisko powstawania (indukowania) w

przewodach elektrycznych napi

cia elektrycznego w przypadku ruchu tych przewodów w polu

magnetycznym odkrył Faraday w 1831. Zjawisko indukcji elektromagnetycznej wyst

puje niezale

nie

od tego, w jakich okoliczno

ciach i z jakich przyczyn nast

puje zmiana strumienia sprz

ęż

onego ze

zwojem. Zmiany te mog

odbywa

np. przez wł

czenie albo wył

czenie pr

du stałego lub przez

periodyczne zmiany pr

du zmiennego. Mo

liwe jest równie

indukowanie napi

cia przez stałe w

czasie pole magnetyczne , ale przewody musz

porusza

w tym polu, aby spowodowa

konieczn

do przebiegu zjawiska zmian

strumienia magnetycznego. Napi

cie indukowane mo

zatem wytwarzane nast

puj

co:

a) w nieruchomych przewodach przez zmienne w czasie pole magnetyczne
b) w ruchomych przewodach przez stałe w czasie pole magnetyczne lub przez nało

enie si

obu

wymienionych form zjawiska

c) w ruchomych przewodach przez zmienne w czasie pole magnetyczne

∫

ABCA

Hdl

∫

BCA

Hdl

∫

BCA

Hdl

∫

Hdl

∫

Hdl

47. Poda

i scharakteryzowa

prawo Ohma oraz prawa Kirchhoffa dla obwodów

magnetycznych
Zgodnie z prawem przepływu całka liniowa wektora nat

ęż

enia pola magnetycznego H po krzywej

zamkni

tej l równa si

dowi przenikaj

cemu przez powierzchni

ograniczon

krzyw

∑

∫

Hdl

∫

lśś

Hdl

W praktyce całka mo

e by

zast

piona sum

iloczynów H

, gdzie k to numer kolejnego odcinka

obwodu magnetycznego, wzdłu

którego nat

ęż

enie pola magnetycznego H

i przenikalno

ść

magnetyczna

pozostaj

niezmienne.

∑

-siła magnetomotoryczna

-przepływ pr

∑

, gdzie U

- napi

cie magnetyczne

Prawo Ohma:

∑

, gdzie

⋅

opór magnetyczny

Prawa Kirhchoffa stosuje si

dla obwodów magnetycznych rozgał

zionych. Dla w

zła obwodu

magnetycznego o b gał

ziach suma algebraiczna strumieni magnetycznych jest równa zeru.

∑

Dla oczka obwodu magnetycznego suma algebraiczna napi

ęć

magnetycznych wszystkich

elementów oczka jest równa sumie algebraicznej sił magnetomotorycznych zawartych w tym
oczku:

∑

oraz

∑

48. Fala płaska – definicja, charakterystyka.
Fala – zmiana stanu fizycznego

rodowiska na skutek miejscowego zaburzenia

Fala bie

żą

ca płaska – własno

ci opisywane s

zale

ciami od jednej współrz

dnej wzi

tej w

kierunku propagacji fali.
Fala elektromagnetyczna – wywołuje zjawiska elektryczne oraz magnetyczne (f. poprzeczna)
Je

eli zaburzenie rozchodzi si

tylko w jednym kierunku, fala jest nazywana fal

płask

. W

danej chwili we wszystkich punktach dowolnie wybranej płaszczyzny prostopadłej do
kierunku rozchodzenia si

fali warunki s

takie same. Powierzchnie falowe s

płaszczyznami,

a promienie fali liniami prostymi równoległymi do siebie.

)

(

)

(

∂

−

, I równanie Maxwella

)

(

)

(

∂

−

∂

, II równanie Maxwella

)

(

)

(

∂

, jednorodne skalarne równanie falowe

Dla fali odbitej: E

(z,t)=E

(z-

t)+E

(z+

Bez odbicia: E

(z,t)=E

sin(

)=E

cos

(t-z/

)

49. Opisa

zjawisko wnikania fali elektromagnetycznej do przewodnika

Gł

boko

ść

wnikania fali elektromagnetycznej.

Fala płaska padaj

ca na powierzchni

rodowiska przewodz

cego cz

ęś

ciowo wnika do wn

trza tego

rodowiska , ulegaj

c silnemu tłumieniu . Intensywno

ść

tłumienia fali przesuwaj

cej si

rodowisku

przewodz

cym charakteryzuje si

gł

boko

wnikania fali elektromagnetycznej , równej odległo

ci ,

wzdłu

której amplituda fali maleje e

≅

2,718 razy.

= E

∆

- gł

boko

ść

wnikania fali

ϖµγ

- stała tłumienia

- przenikalno

ść

, konduktywno

ść

Z okre

lenia gł

boko

ci wnikania wynika

−

∆

ωµγ

∆

Gł

boko

ść

wnikania fali elektromagnetycznej zale

y od cz

stotliwo

ci oraz od przenikalno

magnetycznej i konduktywno

rodowiska magnetycznego.

W odległo

∆

od powierzchni granicznej amplituda fali malej

cej do 36,8

warto

ci pocz

tkowej na

powierzchni granicznej. W odległo

ci 5

∆

od powierzchni granicznej fala praktycznie zanika ,

przybieraj

c warto

ci mniejsze od 1

w stosunku do powierzchni granicznej.

50. Wyprowadzi

zale

ci opisuj

ce wektor Poyntinga.

Wektor

nazywa si

wektorem Poyntinga. Całka powierzchniowa

[

]

∫

⋅

jest strumieniem

wektora Poyntinga przez powierzchni

S i przedstawia moc. Strumie

wektora Poyntinga przez

powierzchni

S nazywany jest cz

sto strumieniem mocy lub moc

wypromieniowan

przez t

powierzchni

, a warto

ść

liczbowa wektora Poyntinga – g

sto

powierzchniow

strumienia mocy.

Całka

[

]

( )

∫

⋅

przedstawia moc wypromieniowan

przez granic

obszaru v. Wyprowadzenie:

rot

∂

⋅

−

⋅

∂

⋅

∂

po odj

ciu stronami

rot

∂

⋅

∂

⋅

−

⋅

przy uwzgl

dnieniu to

samo

ci wektorowej

[

]

[

]

div

rot

div

∂

⋅

∂

⋅

−

⋅

−

⋅

całkujemy w obszarze v

[

]

div

∫













∂

⋅

∂

⋅

−

na mocy twierdzenia Gaussa-Ostrogradskiego

[

]

[

]

( )

∫

⋅

div

gdzie S(v) – powierzchnia ograniczaj

ca obszar v, wektor dS skierowany jest na zewn

trz tej

powierzchni

[

]

( )

∫













∂

⋅

∂

⋅

−

(1)

Przypu

ść

my,

e w cz

ęś

ci obszaru v wytwarzana jest energia elektryczna kosztem innej postaci

energii, na przykład znajduj

w nim

ródła energii elektrycznej. Wówczas:

[

]

gdzie E

– nat

ęż

enie narzuconego pola elektrycznego, wywołanego działaniem czynników obcych w

stosunku do pola elektromagnetycznego. W cz

ęś

ci obszaru, gdzie nie wyst

puje zjawisko

wytwarzania energii elektrycznej mamy E

=0.

(

)













∂

⋅













∂

⋅

∂

⋅

∂

⋅

∂













∂

⋅

−

⋅

−

Po podstawieniu do (1):

[

]

( )

∫

⋅













∂

⋅

(2)

[

]

( )

























∂

−

⋅

∫

gdzie:

∫

⋅

przedstawia moc elektryczn

wytworzon

w obszarze v.

∫

przedstawia moc

przetworzon

na ciepło w obszarze v.

∫













∂

pochodna cxzasowa energii,

przedstawia moc pola elektromagnetycznego zwi

zan

z obszarem v.

Na podstawie wzoru (2) otrzymujemy twierdzenie Poyntinga: moc wytworzona w pewnym obszarze
jest równa sumie mocy przetwarzanej na ciepło, mocy pola magnetycznego w obszarze v oraz mocy
wypromieniowanej przez granic

tego obszaru. Twierdzenie Poyntinga wyra

a zatem prawo

zachowania energii w polu elektromagnetycznym.

51. Równania pola elektromagnetycznego w

rodowisku przewodz

cym.

W tych warunkach dopuszczalne jest pomini

cie pr

dów przesuni

cia. Stosuje si

dlatego równania

Maxwella w postaci zespolonej.

rot

ωµ

−

Przyjmujemy,

stałe.

Potencjał wektorowy harmonicznego pola elektromagnetycznego spełnia niejednorodne równanie
Helmholtza.

−

∇

gdzie

oznacza g

sto

ść

du narzuconego, za













ωµγ

exp

Potencjał skalarny pola wyra

a si

wzorem

div

µγ

−

Nat

ęż

enie pola elektrycznego jest równe

przy czym

grad

−

przedstawiaj

odpowiednio nat

ęż

enie indukowanego i statycznego pola elektrycznego. Zawsze

div

w obszarze

rodowiska przewodz

cego, wobec czego

w tym obszarze. Nat

ęż

enie

pola elektrycznego

równa si

nat

ęż

eniu

indukowanego pola elektrycznego.

Nat

ęż

enie pola magnetycznego wyra

a si

wzorem

rot

52. Zdefiniowa

i opisa

poj

cie impedancji falowej przewodnika.

Impedancj

falow

nazywamy reaktancje indukkcyjn

lub reaktancj

pojemno

ciow

obwodu przy

stotliwo

ci rezonansowej.

53. Poda

ró

nic

dzy impedancj

falow

w dielektryku i przewodniku i oblicczy

jej

obliczy

warto

ść

dla powietrza.

W dielektryku impedancja falowa przedstawia sie wzorem:

[

Ω

]. Jest to iloraz warto

zespolonych E

i H

ϖε

. Impedancj

falow

dielektryka o wzgl

dnych

przenikalno

ciach elektrycznej

i magnetycznej

mozna przedstawi

w postaci wzoru: Z

= 120

Π≈

377[

Ω

]. Impedancja falowa przewodnika wynosi:

ϖε

ϖµ

[

Ω

]. Zale

y ona od pulsacji pola

elektromagnetycznego

, oraz konduktywno

ci o

rodka. Jest ona liczb

zespolon

, co prowadzi do

opó

nienia w fazie wektora H wzgl

dem fali E. W skutek tego fala elektromagnetyczna jest

gwałtownie tłumiona w przewodniku.

58. Scharakteryzowa

pole elektromagnetyczne w strefie dalekiej

Obszar daleki: |x|r>>1, czyli r>>

. Badamy zatem pole elmagn. W du

ych odległo

ciach od

wibratora w porównaniu z długo

fali. Przy du

ych cz

stotliwo

ciach obszar ten zaczyna si

niedu

ej odległo

ci od wibratora; np. przy f=10

Hz długo

ść

fali elmagn. W pró

ni:

⋅

wobec tego obszar daleki zaczyna si

w odległo

ci kilkunastu metrów od wibratora. W obszarze

dalekim wyst

puj

zjawiska falowe. Z tego powodu obszar daleki nazywany jest równie

stref

falow

. Wektory E i H w obsz. dalekim maj

tylko po jednej składowej:













−

⋅













−

⋅

sin

πωε

dko

ść

tych fal obliczamy ró

niczkuj

c wzgl

dem czasu równanie:

const

−

i otrzymujemy

/|k|=1/sqrt(

εµ

)

Iloraz warto

ci chwilowych

=sqrt(

)

jest równy impedancji falowej.

Z zale

ci:

wynika,

e w dowolnej chwili g

sto

ci pola elektrycznego i magnetycznego s

jednakowe w ka

dym

punkcie strefy falowej, czyli w jednostce obj

ci zawarta jest taka sama energia pola elektrycznego

i magnetycznego. Oznacza to,

e połowa energii fali zawarta jest w polu elektrycznym, a druga

połowa w polu magnetycznym.

59. Opisa

zjawisko wnikania fali elektromagnetycznej do przewodnika.

Fala płaska padaj

ca na powierzchni

rodowiska przewodz

cego cz

ęś

ciowo wnika do jego wn

trza,

ulegaj

c silnemu tłumieniu. Intensywno

ść

tłumienia fali przesuwaj

cej si

rod. przewodz

cym

charakteryzuje si

gł

boko

wnikania fali elmagn. Równej odległo

ci, wzdłu

której fala malej

e=2,72 razy.
Gł

boko

ść

wnikania fali elmagn.

∆

zale

y od cz

stotl, przenikalno

ci magnet.

oraz konduktywno

rodowiska elmagn

ωµγ

∆

. Wraz ze zwi

kszaniem si

odległo

ci od pow. granicznej

amplituda fali maleje i praktycznie zanika w odl.

∆

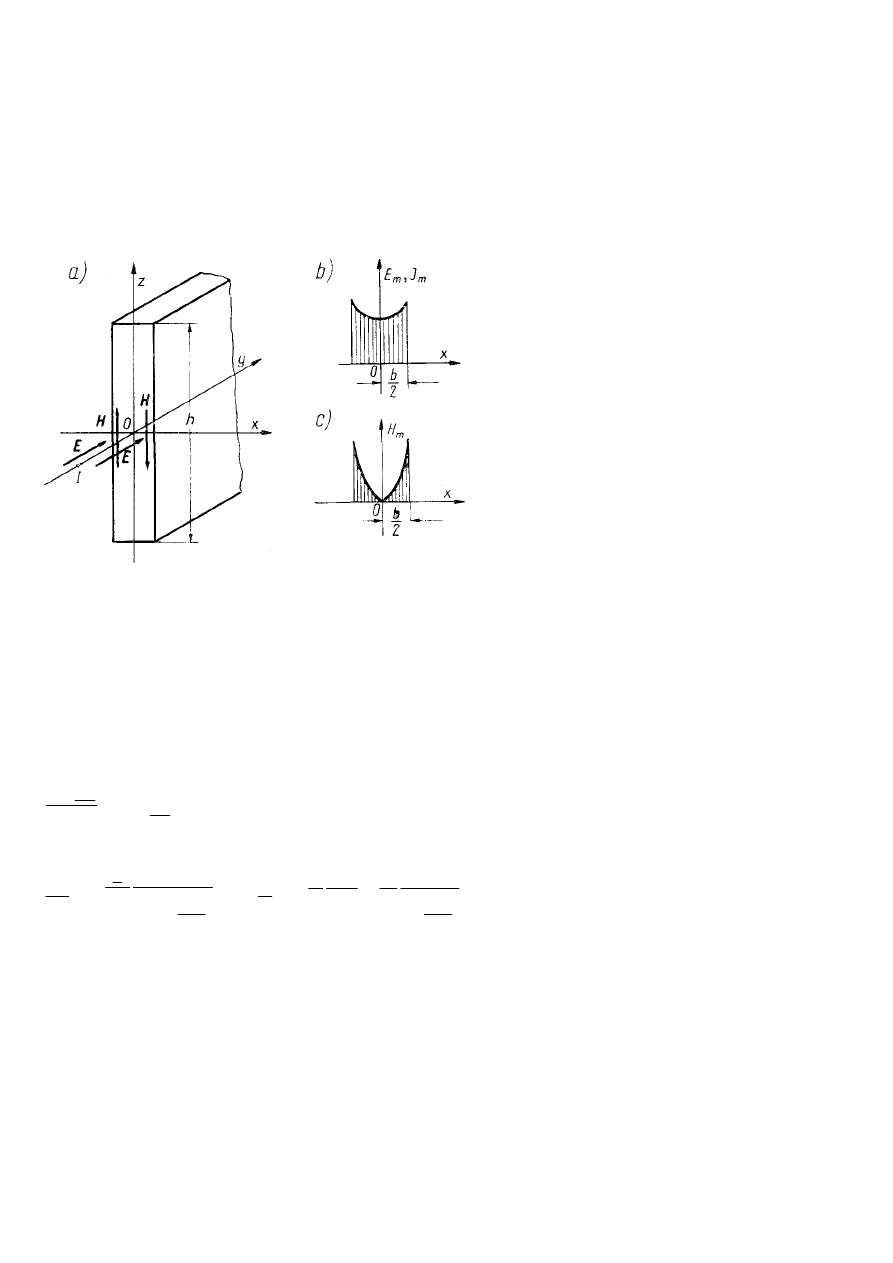
60. Zjawisko naskórkowe

Z tłumieniem fali elektromagnetycznej w przewodniku zwi

zane jest zjawisko naskórkowe.

Zjawisko naskórkowe polega na tym,

e przy przepływie pr

du przemiennego przez przewodnik

sto

ść

du jest w całym przekroju nierównomierna, przy czym ma najwi

ksz

warto

ść

przy

powierzchni zewn

trznej przewodnika.

Przyczyn

zjawiska naskórkowego jest fakt,

e fala elektromagnetyczna, wytworzona w

otaczaj

cym dany przewodnik

rodowisku dielektrycznym na skutek pr

du płyn

cego w

przewodniku, wnika przez powierzchni

zewn

trzn

przewodnika do jego wn

trza i tu jest silnie

tłumiona.

Rys. 28.18. Zjawisko naskórkowe w szynie płaskiej: a) przekrój szyny; b) amplitudy J, E, w funkcji
x; c) amplituda H, w funkcji x

Rozpatrzmy szyn

o przekroju prostok

tnym (rys. 28.18), przez któr

płynie pr

d /. O

y układu

współrz

dnych przyj

to w kierunku długo

ci szyny, o

z w

rodku przekroju szyny równolegle do

wysoko

ci h, os x -w kierunku propagacji fali elektromagnetycznej. Je

eli wysoko

ść

szyny jest

wielokrotnie wi

ksza od jej grubo

ci b (h

b), to mo

na w przybli

eniu traktowa

powierzchnie

boczne szyny jako dwie du

e płaszczyzny.

Zastosujemy równanie

∇

∂

d otrzymamy:

∇

−

∇

−

Orientacyjny rozkład g

sto

ci pr

du podano na rys wy

ej.

Zjawisko naskórkowe wyst

puje równie

przy przepływie pr

du przez przewody o przekroju

kołowym.
Nierównomierna g

sto

ść

du jest powodem silniejszego nagrzewania si

przewodników ni

przy

sto

ci równomiernej. Rezystancja przewodu przy pr

dzie przemiennym jest wi

ksza ni

przy

dzie stałym.

Im wi

ksza jest konduktywno

ść

przy danej przenikalno

ci magnetycznej

i cz

stotliwo

tym

mniejsza jest długo

ść

fali i gł

boko

ść

jej wnikania

Fala elektromagnetyczna nie wnika w nadprzewodnik’ lecz odbija si

od niego.

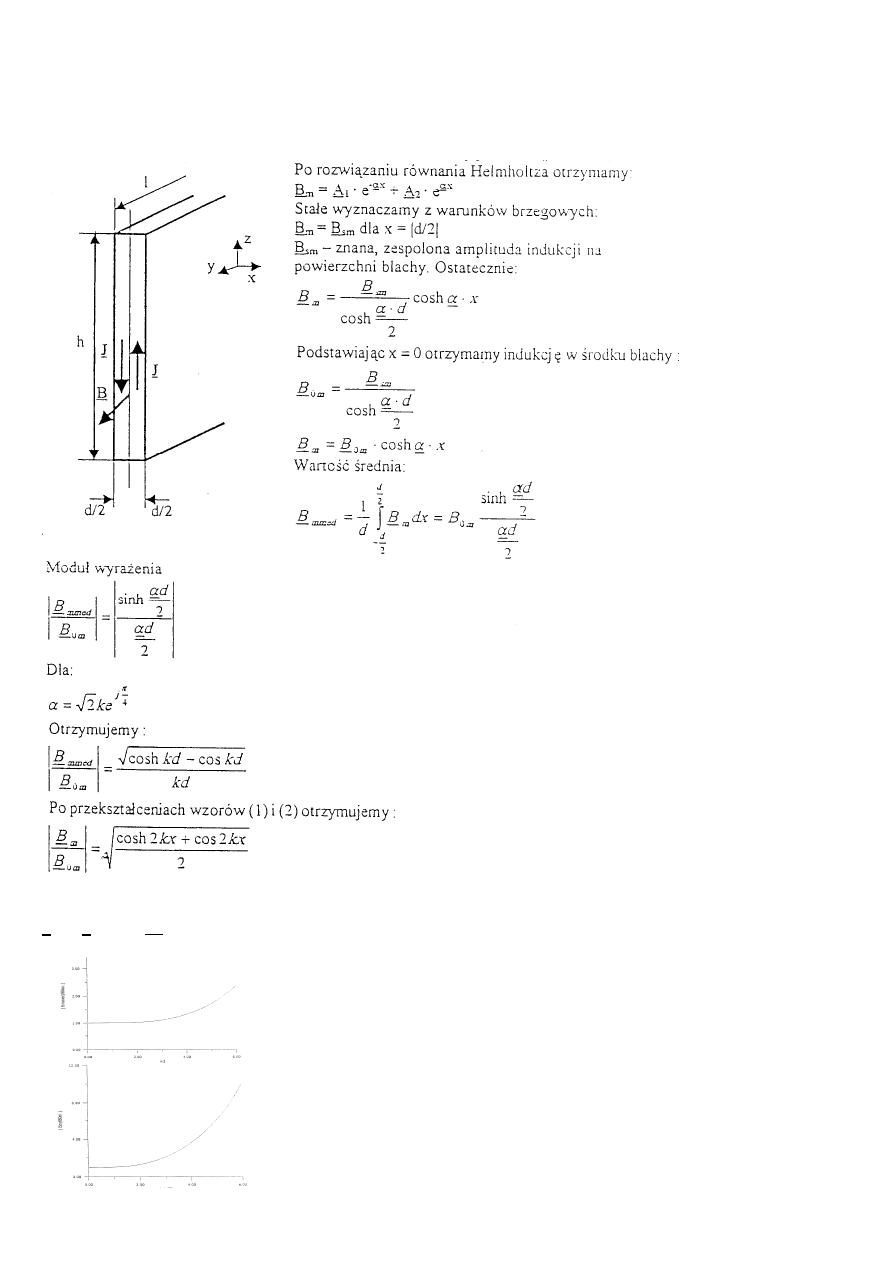
61. Dokona

analizy rozkładu indukcji elektromagnetycznej w blasze transformatorowej.

Magnetowody magnetycznego strumienia przemiennego wykonuje si

z pakietów izolowanych blach

ferromagnetycznych w celu zmniejszenia strat mocy na pr

du wirowe. Magnetowody stosowane dla

pól magnetycznych o cz

stotliwo

ci 50 Hz składaj

z blach o grubo

ci d = 0,1 - 0,5 mm.

Aby upro

rozwa

ania przyjmiemy,

e przenikalno

ść

blachy jest stała (u. = const).Wektor

sto

ci pr

dów wirowych w blasze wyznacza si

korzystaj

c z pierwszego równania Maxwella:

= J

sinh

∝

Bmmed/B0m

Bm/B0m

Wyszukiwarka

Podobne podstrony:
Microsoft Word L22 elementy teorii pola wektorowego
Urbański P Geometryczne podstawy teorii pola
Wprowadzenie do klasycznej teorii pola
E Schmutzer Podstawowe zasady mechaniki klasycznej i klasycznej teorii pola
Elementy teorii pola
rzepka, podstawy teorii pola elektromagnetycznego,test
Baza pytań na test z teorii pola cz2
Microsoft Word W22 Elementy teorii pola wektorowego
Odpowiedzi do teorii
Pytania i odpowiedzi, Zagadnienia - teoria rynku, ZASTOSOWANIE TEORII RYNKU
egzamin z teorii pielęgniarstwa z odpowiedziami (1), Pielęgniarstwo- magisterka cm umk, I rok, Teori
Odpowiedzi do Teorii przedsiebiorstwa
egzamin z teorii pielęgniarstwa z odpowiedziami (2), Pielęgniarstwo- magisterka cm umk, I rok, Teori
egzam odpowiedzi, Politechnika Lubelska, Studia, Studia, sem IV, teoria pola, Teoria Pola
Odpowiedzialność biznesu wstęp do teorii
Podstawy Teorii Okrętów Pytania i Odpowiedzi
Odpowiedzi do pytań z egzaminu ustnego ze Wstępu do Logiki i Teorii Mnogości

więcej podobnych podstron