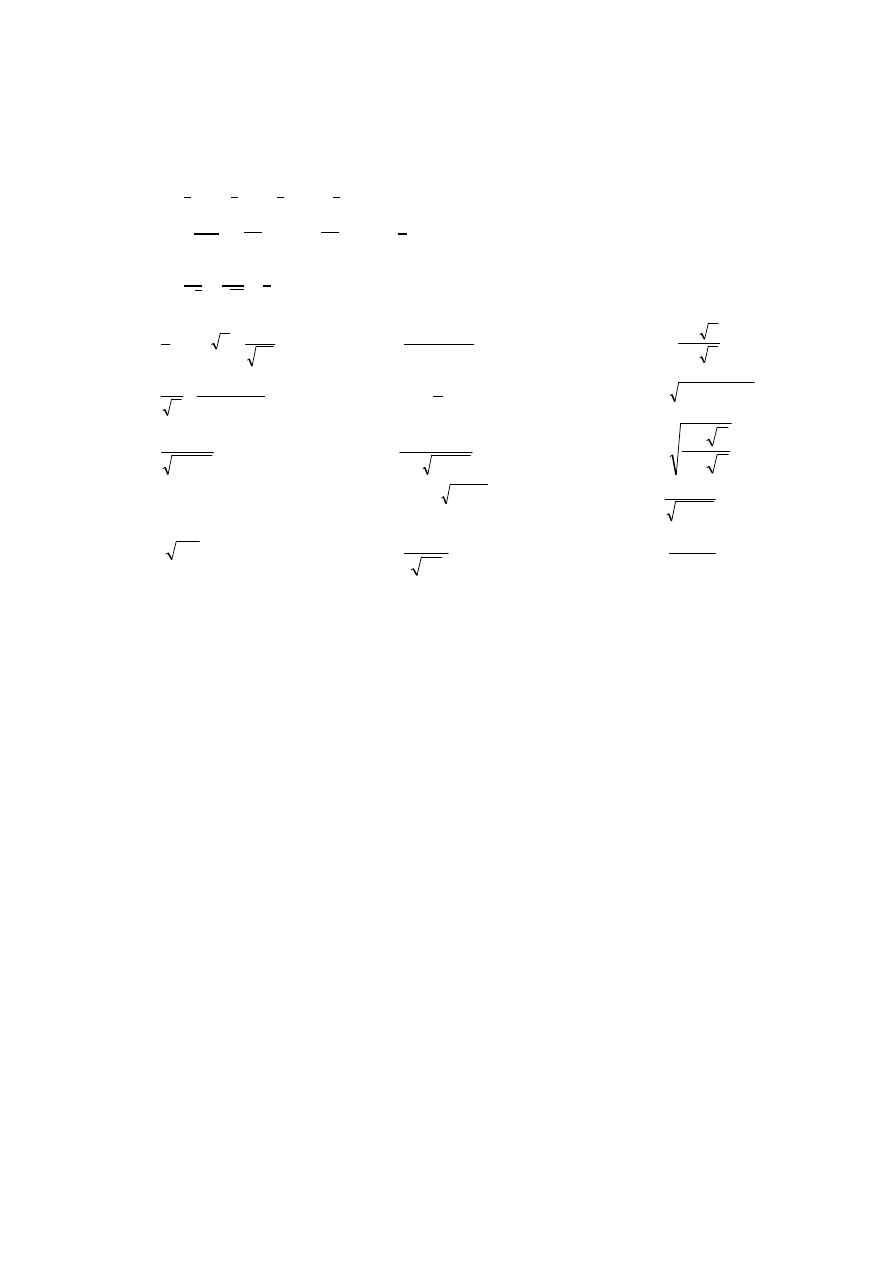
Zadanie 1. Obliczy
ć
pochodne nast
ę
puj
ą
cych funkcji:
a)
3
7
2 1
, gdzie
b)
2
gdzie
0
c)
√ 3√
15 √
2
√
1
, gdzie
0, ∞
d)
√
√
, gdzie
0, ∞
3
3
3
2
3
3
1
x
x
x
y
+
+
=
7
2
5
2
2
+
−
+
=
x
x
x
y
x
x
y
−
+
=
1
1
ln
1
2
1
10
5
2
7
−
+
+
+
=
x
x
x
x
y
6
6
4
7
+
−
=
t
t
y
1
2
2
2
−
+
=
x
x
y
2
2
2
−
−
=
x
x
y
2
9
1
v
v
y
+
−
=
x
x
y
+
−
=
1
1
)
ln(ln x
y
=
+
+
=
2
1
ln
x
x
y
3
3
3
+
=
x
x
y
y-y
)
3
(
sin
2
3
x
x
y
+
=
x
e
x
y
x
2
2
⋅
=
2
3
sin
x
x
x
y
=
Zadanie 2. Znajd
ź
przedziały monotoniczno
ś
ci i ekstrema lokalne funkcji:
1. f (x ) = x
3
+ 3x
2
- 9x + 3
2. f (x ) = x
3
+5x
3. f (x ) = 2x
3
- 9x
2
- 24x - 12
4. f (x ) = xe
x
5. f (x ) = e
x
- x
6. f (x ) = ln x – x
Odpowiedzi:
1. Dla xÎ(-¥, -3) f(x) ro
ś
nie, dla xÎ(-3, 1) f(x) maleje, dla xÎ(1, ¥) f(x) ro
ś
nie;
maksimum lokalne w punkcie x = -3, f(-3) = 30; minimum lokalne dla x = 1, f(1) = -2.
2. Funkcja jest rosn
ą
ca dla xÎR.
3. Dla xÎ(-¥, -1) f(x) ro
ś
nie, dla xÎ(-1, 4) f(x) maleje, dla xÎ(4, ¥) f(x) ro
ś
nie;
maksimum lokalne w punkcie x = -1, f(-1) = 1, minimum lokalne dla x = 4, f(1) = -124.
4. Dla xÎ(-¥, -1) f(x) maleje, dla xÎ(-1, ¥) f(x) ro
ś
nie; minimum lokalne dla x = -1,
f(-1) = -e-1.
5. Dla xÎ(-¥, 0) f(x) maleje, dla xÎ(0, ¥) f(x) ro
ś
nie; minimum lokalne dla x = 0, f(0) = 1.
6. Dla xÎ(0, 1) f(x) ro
ś
nie, dla xÎ(1,¥) f(x) maleje; maksimum lokalne w punkcie x = 1,
f(1) = -1.
Zadanie 3. Znajd
ź
przedziały monotoniczno
ś
ci i ekstrema lokalne funkcji:
2
1
)
(
x
x
x
f
−
=
,
)
1
ln(
)
(
x
x
x
f
+
−
=
,
2
3
2
3
)
(
,.....
1
)
(
x
x
x
f
x
x
x
x
f
−
=
+
+
=
Zadanie 4. Roczna stopa procentowa wynosi 5%, a kapitał pocz
ą
tkowy 1000 zł. Jaka
b
ę
dzie warto
ść
kapitału po czterech latach, je
ś
li odsetki kapitalizowane s
ą
: a) kwartalnie, b)
miesi
ę
cznie, c) rocznie?
Odp:
a) 12199
b) 12209
c) 12155
Zadanie 5. Interesuje nas warto
ść
, jak
ą
po upływie 18 miesi
ę
cy b
ę
dzie mie
ć
kwota 150 zł,
wpłaconych do banku na lokat
ę
3-miesi
ę
czn
ą
, o stałym oprocentowaniu 14% rocznie, z
kapitalizacj
ą
odsetek co 3 miesi
ą
ce.
Odp. 184,39
Zadanie 6. Jak
ą
kwot
ę
wypłacimy z banku po 5 latach , je
ż
eli ulokujemy w nim
10000 zł?
Oprocentowanie roczne w tym banku wynosi 15% i nast
ę
puje roczna kapitalizacja odsetek.
Zadanie 7. Pan Kowalski potrzebuje 35000 zł na zakup samochodu.
Uzbierał ju
ż
25000 zł , a pozostał
ą
sum
ę
zamierza uskłada
ć
przez ulokowanie pieni
ę
dzy
banku z roczn
ą
kapitalizacj
ą
odsetek , w którym oprocentowanie wynosi 16%.
Jak długo Kowalski b
ę
dzie musiał czeka
ć
, aby uzbiera
ć
brakuj
ą
c
ą
sum
ę
?
Zadanie 8. Pa
ń
stwo Kowalscy zamierzaj
ą
przeprowadzi
ć
remont mieszkania , na który
potrzebuj
ą
15000 zł. Wymienion
ą
kwot
ę
Kowalscy zamierzaj
ą
uzyska
ć
przez ulokowanie w
banku na 5 lat oszcz
ę
dno
ś
ci. Oprocentowanie roczne wynosi w tym banku 14% i nast
ę
puje
roczna kapitalizacja odsetek. Jak
ą
sum
ę
musz
ą
ulokowa
ć
w banku Kowalscy?
Zadanie 9. Przedsi
ę
biorca ma 50000 zł i pragnie t
ę
sum
ę
ulokowa
ć
w banku z roczna
kapitalizacj
ą
odsetek. Przedsi
ę
biorca zamierza uzbiera
ć
sum
ę
90000 zł po 5 latach. Jakie
powinno by
ć
oprocentowanie roczne w tym banku?
Zadanie 10..Bank oferuje oprocentowanie roczne 12% oraz kwartaln
ą
kapitalizacj
ę
odsetek.
Ile wyniesie zdeponowany w tym banku kapitał 10000 zł po:
a) jednym roku ,
b) dwóch latach ,
c) trzech i pół roku?
Zadanie 11. Fundusz powierniczy oferuje oprocentowanie 9% i
odsetek , odsetek bank 11% z roczna kapitalizacj
korzystne?
Zadanie 12. Pan Adam ulokował 5000 zł w banku w którym oprocentowanie wynosi 12% i
nast
ę
puje kwartalna kapitalizacja odsetek. Jak
latach?
Zadanie 13. Obliczy
ć
pochodne cz
funkcji:
y
xy
y
x
y
x
f
9
3
1
)
,
(
3
2
2
−
+
−
=
y
x
y
x
y
x
f
12
6
3
2
)
,
(
3
−
−
+
=
10
6
2
)
,
(
2
2
+
−
−
=
y
x
xy
y
x
f
2
2
4
4
12
4
)
,
(
xy
y
x
y
x
y
x
f
−
−
=
5
2
2
)
,
(
3
2
2
−
−
=
xy
y
x
xy
y
x
f
3
4
5
8
12
)
,
(
xy
y
x
xy
y
x
f
−
−
=
2
2
3
3
2
)
,
(
x
y
y
x
y
x
f
+
+
=
y
xy
y
x
y
x
f
9
3
1
)
,
(
3
2
2
−
+
−
=
9
6
)
,
(
3
3
+
+
−
+
=
x
xy
y
x
y
x
f
Fundusz powierniczy oferuje oprocentowanie 9% i półroczn
ą
kapitalizacj
odsetek , odsetek bank 11% z roczna kapitalizacj
ą
odsetek. Które warunki s
ą
Pan Adam ulokował 5000 zł w banku w którym oprocentowanie wynosi 12% i
puje kwartalna kapitalizacja odsetek. Jak
ą
sum
ę
b
ę
dzie mógł wypłaci
ć
pochodne cz
ą
stkowe pierwszego i drugiego rz
ę
du nast
,
y
9
4
2
3
15
y
x
xy
+
120
+
y
9
2
5
+
+
y
ą
kapitalizacj
ę
odsetek. Które warunki s
ą
bardziej
Pan Adam ulokował 5000 zł w banku w którym oprocentowanie wynosi 12% i
dzie mógł wypłaci
ć
po trzech
ę
du nast
ę
puj
ą
cych