1. Obliczanie transmitancji zastępczej
układu
Zadanie 1.1
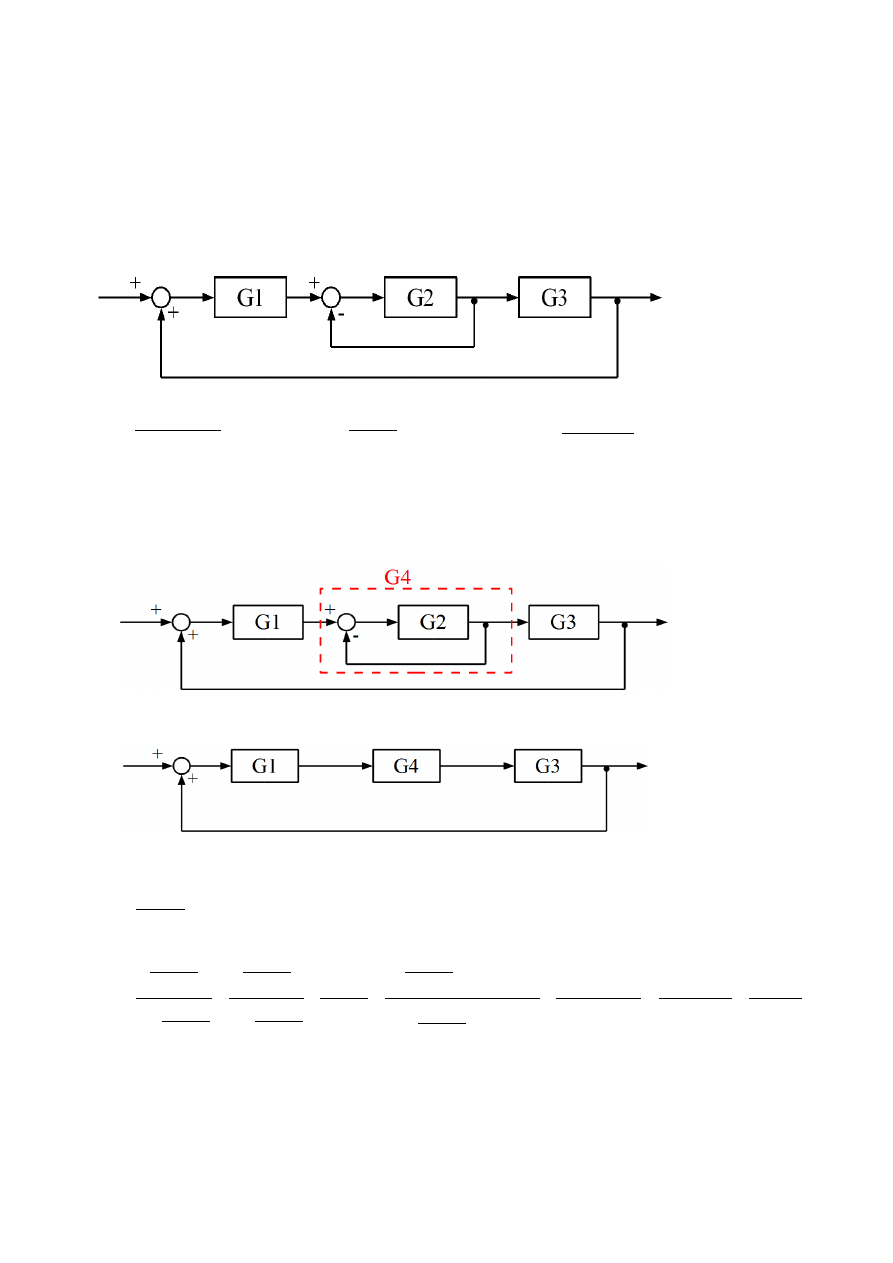
Oblicz transmitancję zastępczą układu z rysunku.
G1=
s2
2 s
2
8 s6
G2=
4
s
2
4s
G3=
s
2
3s2
s3
Obliczanie transmitancji zastępczej polega na kolejnym upraszczaniu schematu stosując
odpowiednie wzory. W tym przykładzie jedyną możliwością jest policzenie transmitancji zastępczej
sprzężenia zwrotnego obejmującego transmitancję G2. Nowy obiekt (zaznaczony na rysunku)
nazwany zostanie G4.
Wówczas schemat można przerysować w postaci:
a transmitancja G4 jest dana wzorem:
G4=
G2
G21
podstawiając wartości otrzymuje się:
G4=
4
s
2
4s
1
4
s
2
4s
=
4
s
2
4s
1
4
s
2
4s
⋅
s
2
4s
s
2
4s
=
4
s
2
4s
⋅
s
2
4s
1
4
s
2
4s
⋅
s
2
4s
=
4
s
2
4s4
=
4
s
2
4s4
=
4
s2
2
Po obliczeniu transmitancji G4 można jedynie obliczyć połączenie szeregowe transmitancji G1, G4
i G3. Co oznaczono na rysunku.
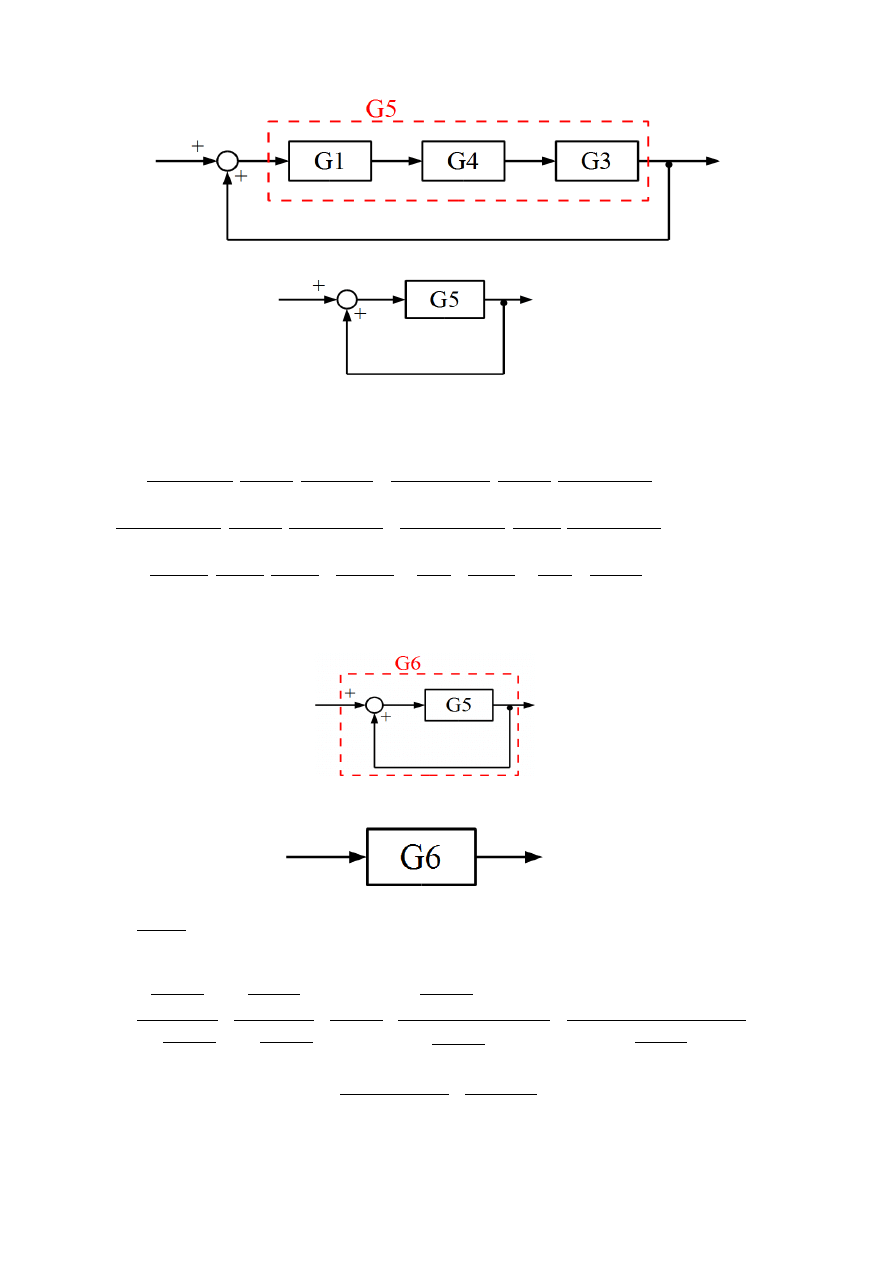
Wówczas schemat można przerysować w postaci:
Transmitancję G5 oblicza się ze wzoru:
G5=G1⋅G4⋅G3
i po podstawieniu wartości otrzymuje się:
G5=
s2
2 s
2
8 s6
⋅
4
s2
2
⋅
s
2
3s2
s3
=
s2
2 s
2
4 s3
⋅
4
s2
2
⋅
s1s2
s3
=
=
s2
2 s1 s3
⋅
4
s2
2
⋅
s1 s2
s3
=
1
2 s1s3
⋅
4
s2
⋅
s1 s2
s3
=
=
1
2 s3
⋅
4
s2
⋅
s2
s3
=
1
2 s3
⋅
4⋅
1
s3
=
1
s3
⋅
2⋅
1
s3
=
2
s3
2
Pozostało policzyć transmitancję zastępczą dodatniego sprzężenia zwrotnego co zobrazowano na
rysunku.
Wówczas schemat można narysować jako pojedynczą transmitancję, co pokazano na poniższym
rysunku.
Transmitancję G6 oblicza się ze wzoru:
G6=
G5
1−G5
Po podstawieniu wartości otrzymuje się:
G6=
2
s3
2
1−
2
s3
2
=
2
s3
2
1−
2
s3
2
⋅
s3
2
s3
2
=
2
s3
2
⋅
s3
2
1−
2
s3
2
⋅
s3
2
=
2
s3
2
−
2
s3
2
⋅
s3
2
=
=
2
s
2
6s9−2
=
2
s
2
6s7
i otrzymano transmitancję zastępczą całego układu.
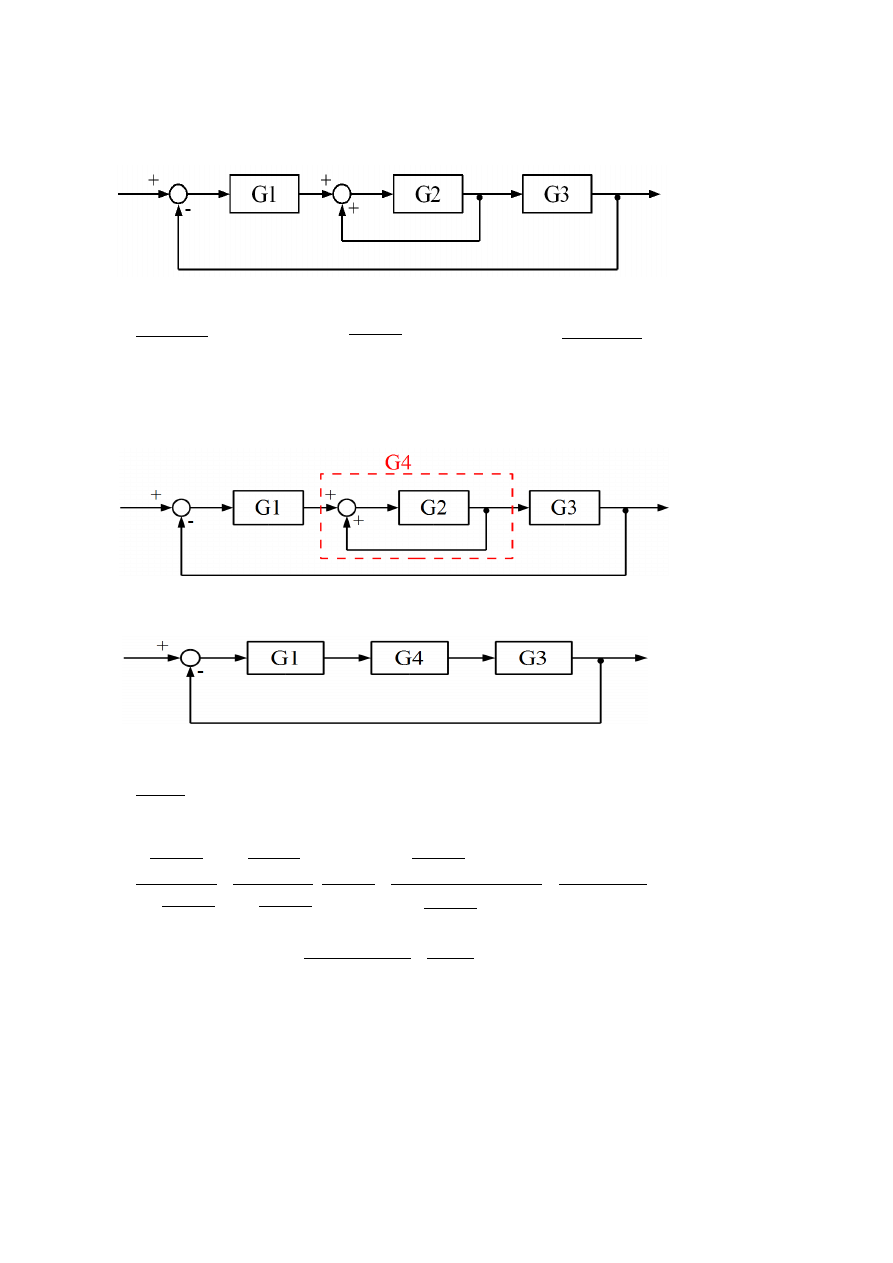
Zadanie 1.2
Oblicz transmitancję zastępczą układu z rysunku.
G1=
s
2
s
s
2
5s6
G2=
9
s3
2
G3=
s
2
8s12
3s3
W tym przykładzie (podobnie jak w zadaniu 1) jedyną możliwością jest policzenie transmitancji
zastępczej dodatniego sprzężenia zwrotnego obejmującego transmitancję G2. Nowy obiekt
(zaznaczony na rysunku) nazwany zostanie G4.
Wówczas schemat można przerysować w postaci:
a transmitancja G4 jest dana wzorem:
G4=
G2
1−G2
podstawiając wartości otrzymuje się:
G4=
9
s3
2
1−
9
s3
2
=
9
s3
2
1−
9
s3
2
⋅
s3
2
s3
2
=
9
s3
2
⋅
s3
2
1−
9
s3
2
⋅
s3
2
=
9
s3
2
−
9
=
=
9
s
2
6s9−9
=
9
s
2
6s
Po obliczeniu transmitancji G4 można jedynie obliczyć połączenie szeregowe transmitancji G1, G4
i G3. Co oznaczono na rysunku.
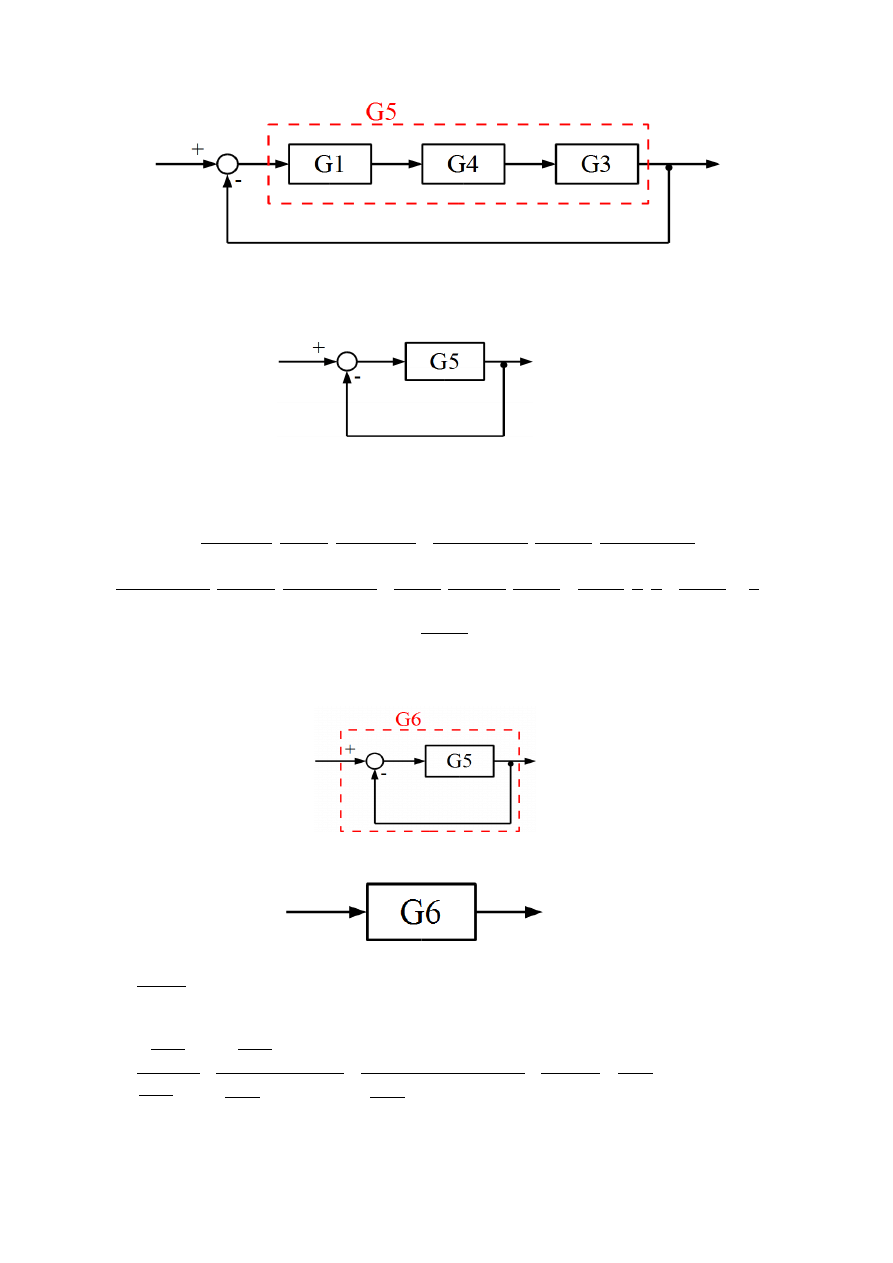
Wówczas schemat można przerysować w postaci:
Transmitancję G5 oblicza się ze wzoru:
G5=G1⋅G4⋅G3
i po podstawieniu wartości otrzymuje się:
G5=
s
2
s
s
2
5s6
⋅
9
s
2
6s
⋅
s
2
8s12
3s3
=
s s1
s2 s3
⋅
9
s s6
⋅
s2s6
3 s1
=
=
s
s2 s3
⋅
9
s s6
⋅
s2s6
3
=
s
s3
⋅
9
s s6
⋅
s6
3
=
s
s3
⋅
9
s
⋅
1
3
=
1
s3
⋅
9⋅
1
3
=
=
3
s3
Pozostało policzyć transmitancję zastępczą ujemnego sprzężenia zwrotnego co zobrazowano na
rysunku.
Wówczas schemat można narysować jako pojedynczą transmitancję, co pokazano na poniższym
rysunku.
Transmitancję G6 oblicza się ze wzoru:
G6=
G5
G51
Po podstawieniu wartości otrzymuje się:
G6=
3
s3
3
s3
1
=
3
s3
⋅
s3
3
s3
1
⋅
s3
=
3
3
s3
⋅
s3 s3
=
3
3s3
=
3
s6
i otrzymano transmitancję zastępczą całego układu.
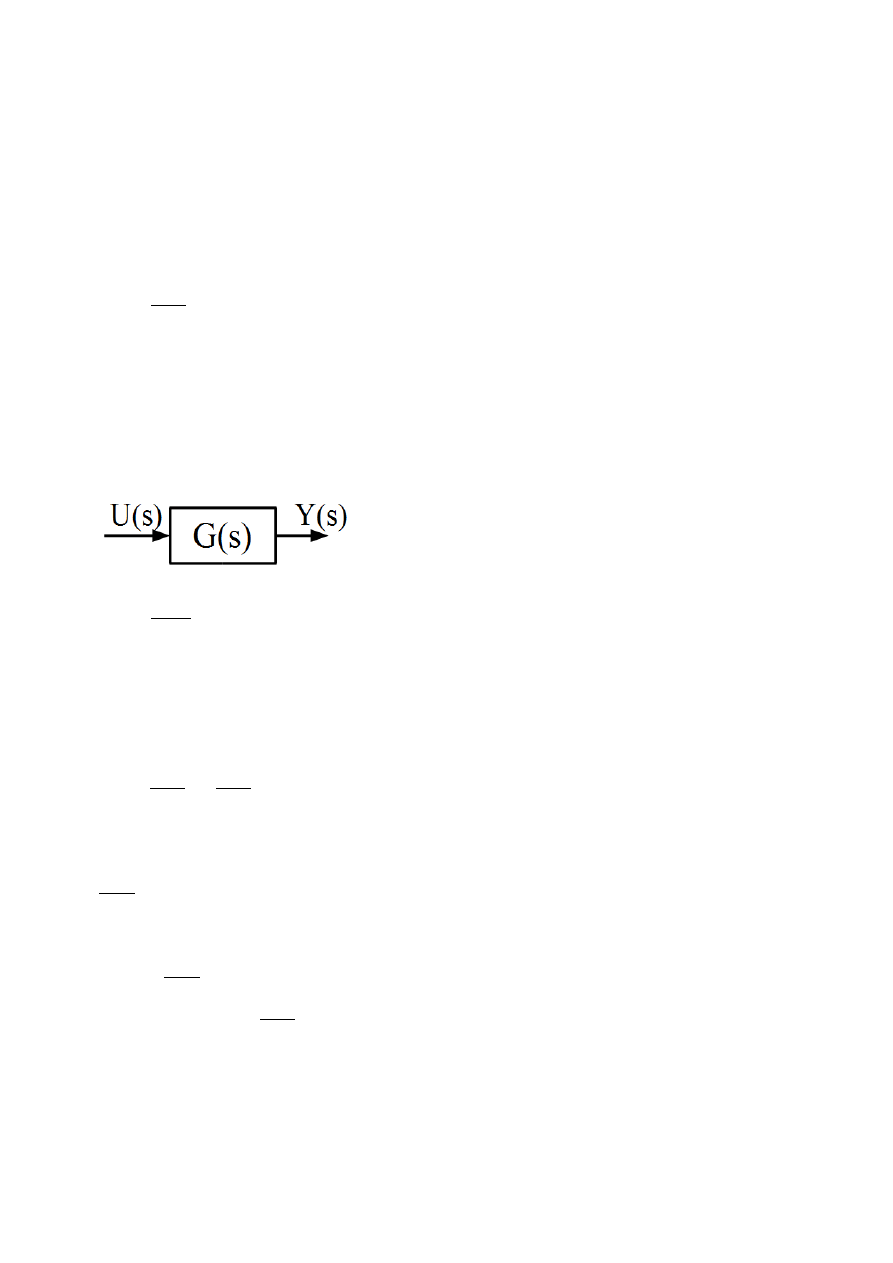
2. Obliczanie odpowiedzi impulsowych i
skokowych transmitancji
Zadanie 2.1
Oblicz i narysuj odpowiedź impulsową obiektu o transmitancji
G s =
2
s2
Zadanie polega na obliczeniu wzoru w postaci rzeczywistej (gdzie dziedziną jest czas) sygnału
wyjściowego y(t) gdy na wejście podano sygnał wejściowy w postaci delty Dirac'a (impuls). Czyli
u t= t . Obliczenia są wykonywane w dziedzinie liczb zespolonych (po transformacji
Laplace'a). Sygnał wejściowy u(t) należy przetransformować do postaci zespolonej, czyli:
u t= t → U s=1
Badany układ można przedstawić graficznie:
Z definicji transmitancji wiemy, że:
G s =
Y s
U s
Przekształcając powyższy wzór otrzymuje się wzór na sygnał wyjściowy Y(s) w postaci zespolonej.
Y s=G s⋅U s
By obliczyć sygnał Y(s) potrzeba:
–
wartości transmitancji (dane w zadaniu)
–
wartości sygnału sterującego U(s) w postaci zespolonej (obliczone wcześniej)
Podstawiając do wzoru te wartości otrzymuje się:
Y s=
2
s2
⋅
1=
2
s2
Wyrażenie powyższe to wzór SYGNAŁU WYJŚCIOWEGO (który jest taki sam jak dana
transmitancja) w postaci zespolonej. Sygnał ten należy przetransformować do postaci rzeczywistej,
korzystając z tabeli z wykładu. Najbardziej podobnym wzorem jakiego należy użyć jest wzór:
1
sa
e
−
a t
Przekształcając wzór na Y(s) otrzymano (liczbę stałą można wyłączyć przed transformatę –
analogicznie jak przy liczeniu np. pochodnej):
Y s=2⋅
1
s2
Korzystając ze wzoru
1
sa
e
−
a t
otrzymuje się ostatecznie:
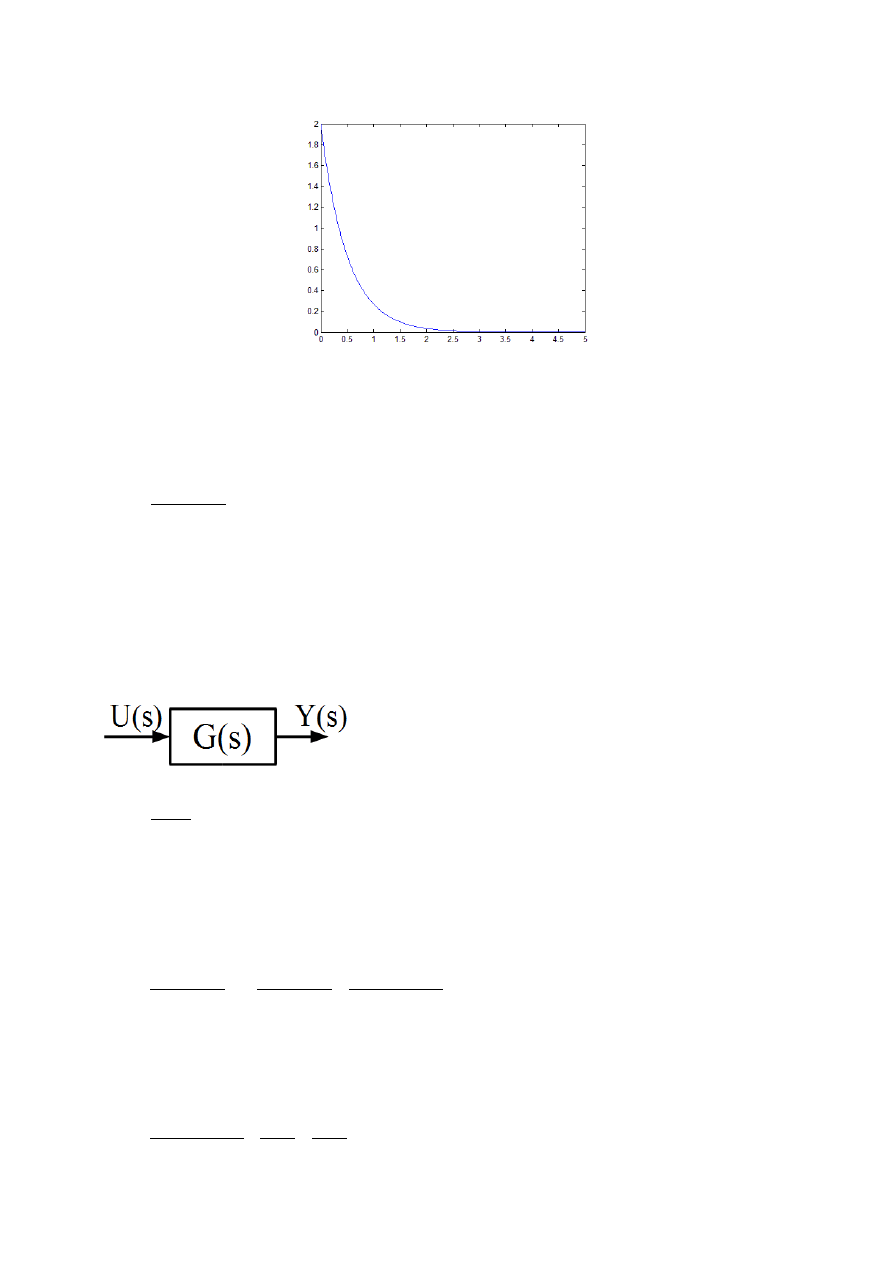
y t=2 e
−
2 t
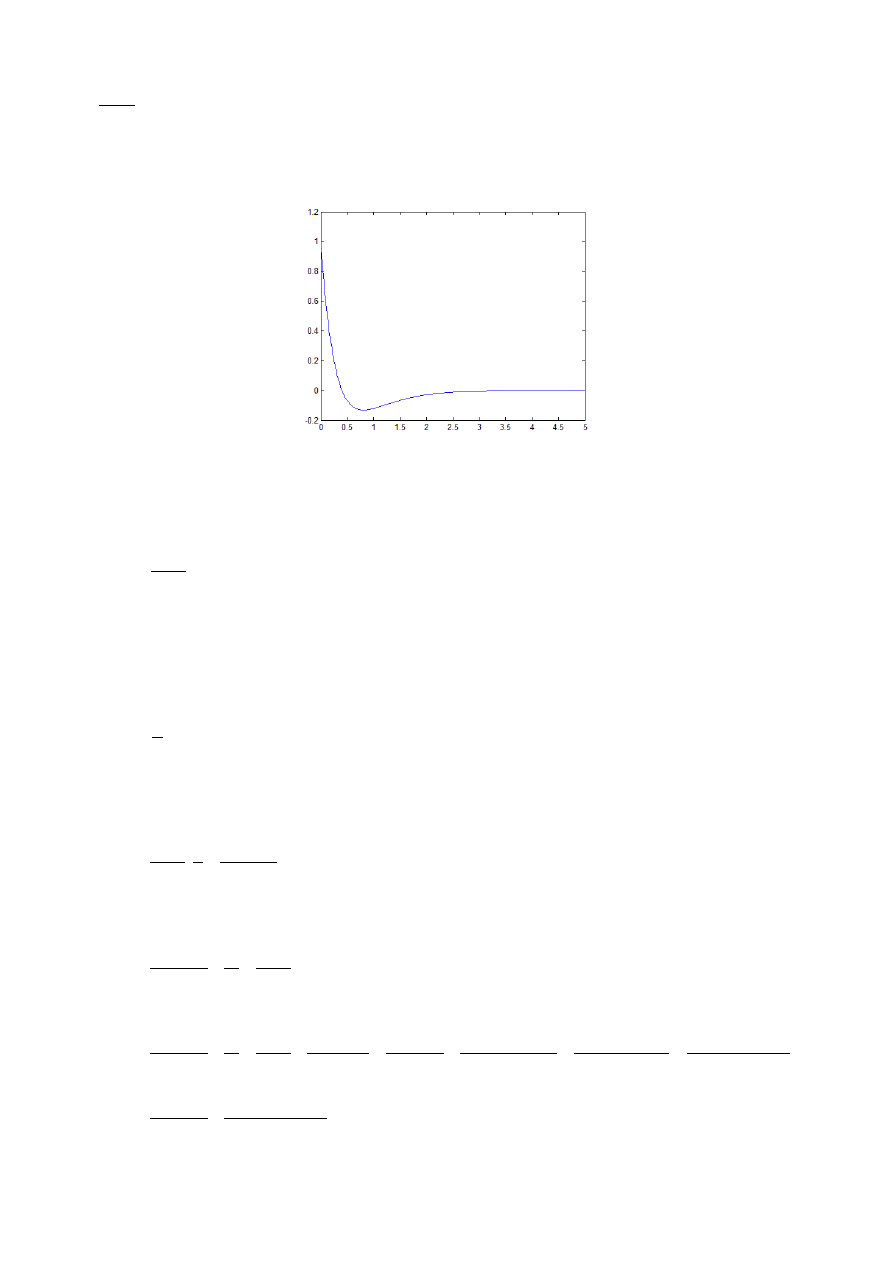
By naszkicować wykres funkcji y(t) zastosowano pakiet Matlab/Simulink. Przebieg sygnału
wyjściowego przedstawiono na poniższym rysunku.
Zadanie 2.2
Oblicz i narysuj odpowiedź impulsową obiektu o transmitancji
G s =
−
2s
s
2
3 s2
Zadanie polega na obliczeniu wzoru w postaci rzeczywistej (gdzie dziedziną jest czas) sygnału
wyjściowego y(t) gdy na wejście podano sygnał wejściowy w postaci delty Dirac'a (impuls). Czyli
u t= t . Obliczenia są wykonywane w dziedzinie liczb zespolonych (po transformacji
Laplace'a). Sygnał wejściowy u(t) należy przetransformować do postaci zespolonej, czyli:
u t= t → U s=1
Badany układ można przedstawić graficznie:
Z definicji transmitancji wiemy, że:
G s =
Y s
U s
Przekształcając powyższy wzór otrzymuje się wzór na sygnał wyjściowy Y(s) w postaci zespolonej.
Y s=G s⋅U s
By obliczyć sygnał Y(s) potrzeba:
–
wartości transmitancji (dane w zadaniu)
–
wartości sygnału sterującego U(s) w postaci zespolonej (obliczone wcześniej)
Podstawiając do wzoru te wartości otrzymuje się:
Y s=
−
2s
s
2
3 s2
⋅
1=
−
2s
s
2
3 s2
=
−
2s
s1s2
Wyrażenie powyższe to wzór SYGNAŁU WYJŚCIOWEGO (który jest taki sam jak dana
transmitancja) w postaci zespolonej. Sygnał ten należy przetransformować do postaci rzeczywistej,
korzystając z tabeli z wykładu. W tym przykładzie okazuje się, że w tabeli nie podano wzoru, z
którego można skorzystać w łatwy sposób jak w poprzednim zadaniu. W tym przypadku należy
rozłożyć ułamek na ułamki zwykłe, tzn. przedstawić ułamek w postaci poniższego schematu:
Y s =
−
2s
s1s2
=
A
s1
B
s2
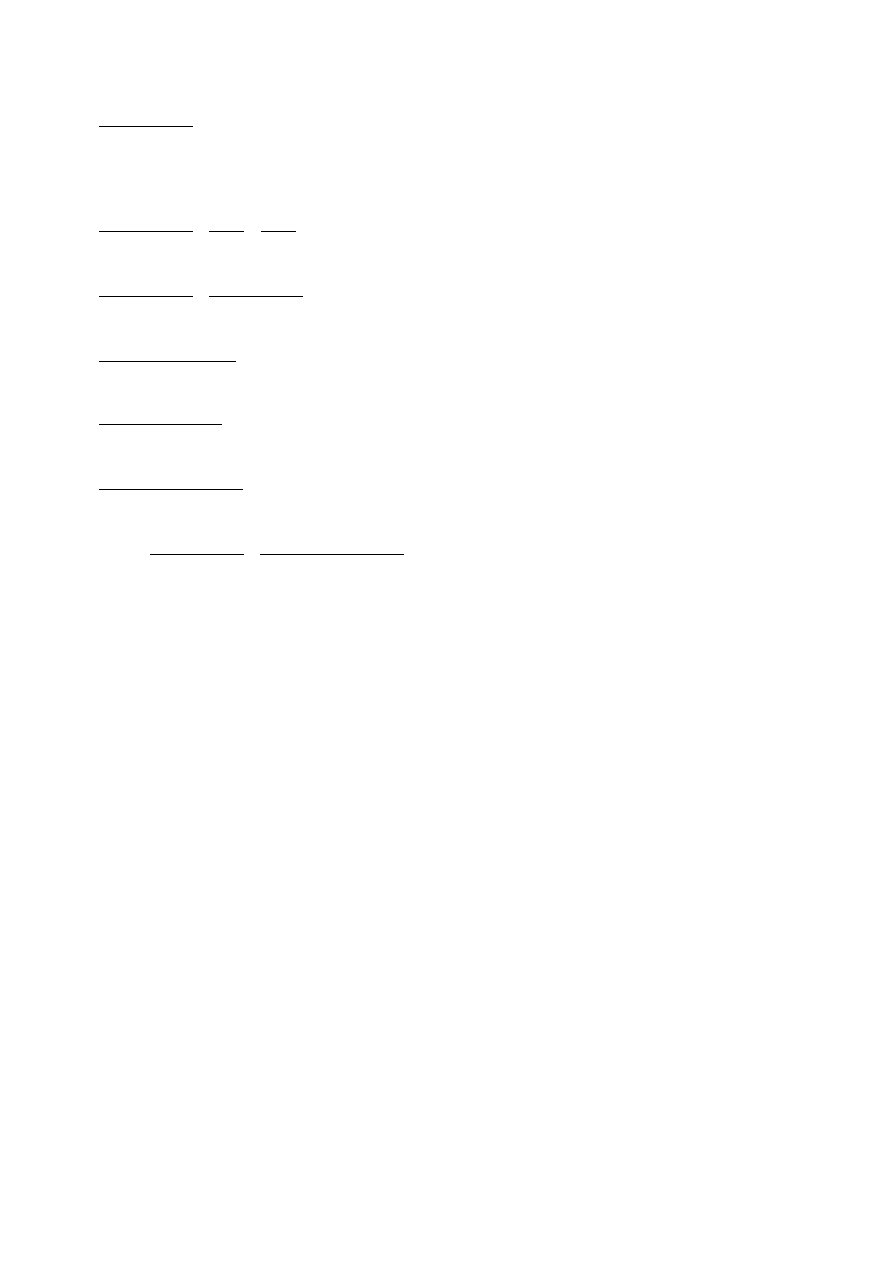
W tym przypadku, należy obliczyć wartości liczb A i B. Jeżeli zostanie to wykonane, ułamek
−
2s
s1s2
zostanie rozłożony na ułamki proste (czyli takie, których nie da się bardziej
rozłożyć).
Obliczanie współczynników A i B.
−
2s
s1s2
=
A
s1
B
s2
=
dodaje się do siebie wszystkie ułamki proste (sprowadzając je
wcześniej do wspólnego mianownika) i otrzymuje się:
A s2
s1s2
B s1
s1 s2
=
pisząc je na jednej kresce ułamkowej otrzymuje się:
A s2B s1
s1 s2
=
wykonuje się działania w nawiasach w liczniku:
As2ABsB
s1 s2
= grupuje się wyrażenia w liczniku ze względu na zmienną 's'
s AB2AB
s1s2
=
i porównuje się wynik z wyjściowym wzorem na Y(s)
Y s=
−
2s
s1s2
=
s A B 2AB
s1 s2
Należy teraz porównać ułamki. Mianowniki tych
ułamków są takie same (ponieważ wcześniej rozłożono ułamek złożony na ułamki proste
korzystając z danych w mianowniku) czyli należy porównać ze sobą liczniki. W licznikach znajdują
się po obu stronach znaku równości wielomiany ze względu na zmienną 's'. Porównując te
wielomiany otrzymuje się ('trzy' kreseczki zamiast znaku równości oznaczają tożsamość):
−
2s≡s AB2AB
By porównać wielomiany ze sobą porównuje się ich współczynniki stojące przy odpowiednich
potęgach zmiennej zespolonej 's', otrzymuje się układ równań ('-2' stoi w lewym wielomianie przy
zmiennej 's' w potędze 1, '(A+B)' stoi w prawym wielomianie przy zmiennej 's'; '0' jest wyrazem
wolnym lewego wielomianu, '(2A+B)' jest wyrazem wolnym prawego wielomianu):
{
A B=−2
2AB=0
Należy rozwiązać ten układ równań. Po rozwiązaniu otrzyma się wartości zmiennych A i B.
Rozwiązywanie układu równań dwu niewiadomych metodą wyznaczników
{
A B=−2
2AB=0
Wyznacznik główny jest równy:
W =
∣
1 1
2 1
∣
=
1⋅1−2⋅1=−1
Wyznaczniki pomocnicze (zmiennych)
W
A
=
∣
−
2 1
0
1
∣
=−
2⋅1−0⋅1=−2
W
B
=
∣
1 −2
2
0
∣
=
1⋅0−−2⋅2=4
Zmienne są równe
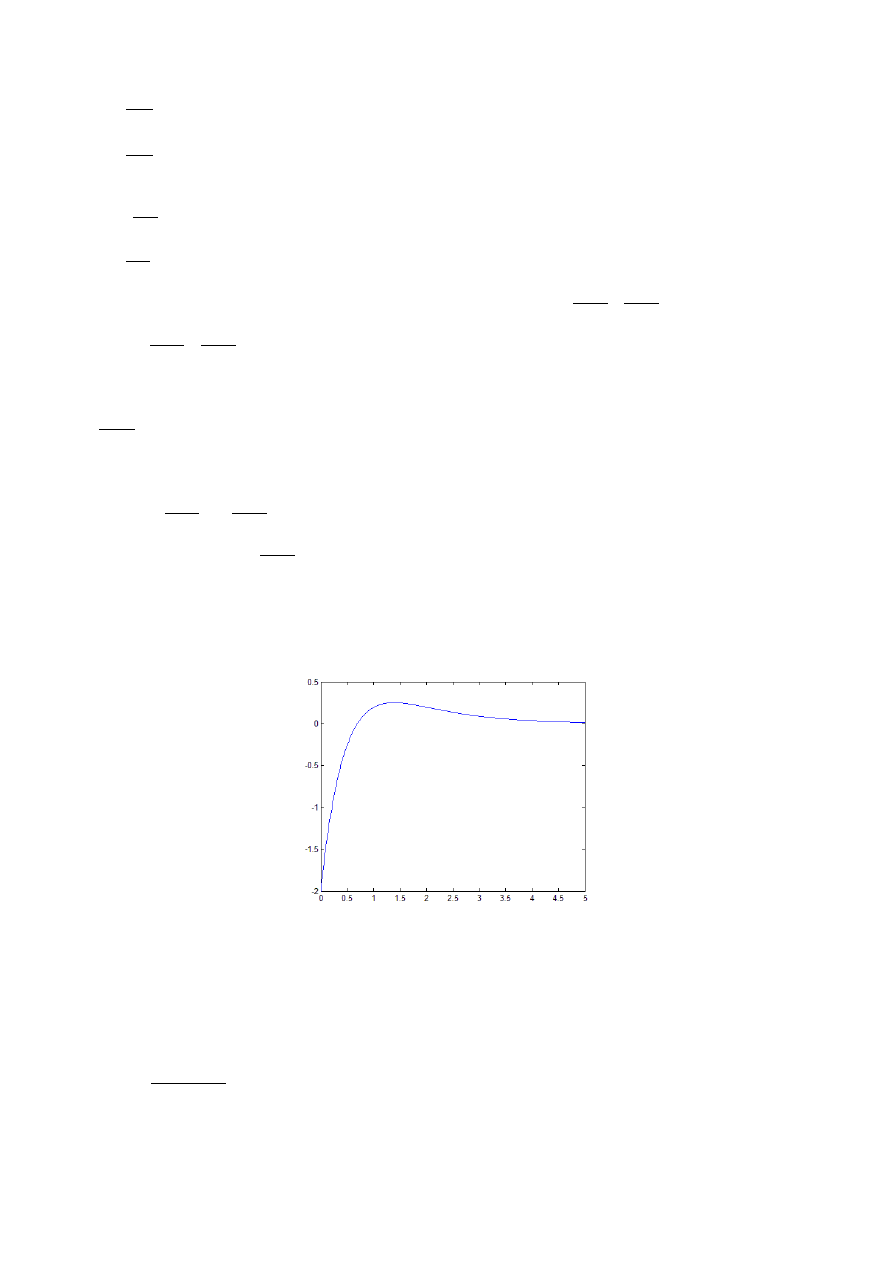
A=
W
A
W
B=
W
B
W
czyli po podstawieniu
A=
−
2
−
1
=
2
B=
4
−
1
=−
4
Podstawiając obliczone zmienne A i B do wzoru na sygnał Y s =
A
s1
B
s2
otrzymuje się:
Y s=
2
s1
−
4
s2
Teraz można zastosować tabelę by policzyć sygnał w postaci rzeczywistej (czyli y(t)). Najbardziej
podobnym wzorem jakiego należy użyć jest wzór:
1
sa
e
−
a t
Przekształcając wzór na Y(s) otrzymano (liczbę stałą można wyłączyć przed transformatę –
analogicznie jak przy liczeniu np. pochodnej):
Y s=2⋅
1
s1
−
4⋅
1
s2
Korzystając ze wzoru
1
sa
e
−
a t
otrzymuje się ostatecznie:
y t=2 e
−
t
−
4 e
−
2 t
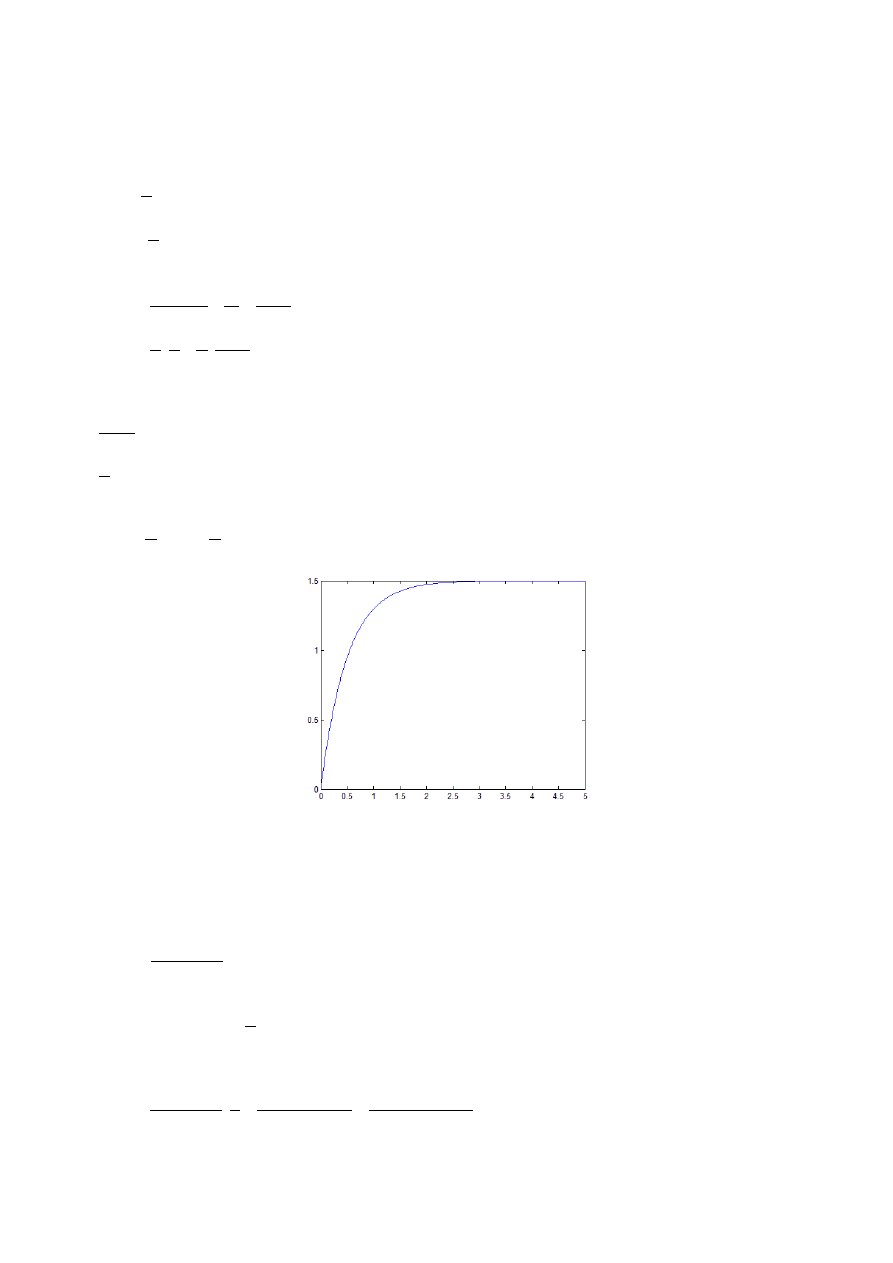
By naszkicować wykres funkcji y(t) zastosowano pakiet Matlab/Simulink. Przebieg sygnału
wyjściowego przedstawiono na poniższym rysunku.
Zadanie 2.3
Oblicz i narysuj odpowiedź impulsową obiektu o transmitancji
G s =
s
s
2
5 s6
W tym zadaniu pominięto w większości opisy słowne, które znajdują się w zadaniach 2.1 oraz 2.2.
Zawarto obliczenia z wynikami.

Z treści zadania wynika, że należy obliczyć odpowiedź impulsową. Oznacza to, że sterowanie jest
równe:
u t= t , przekształcając to równanie stosując transformatę Laplace'a otrzymuje się:
U s=1
W celu obliczenia sygnału wyjściowego y(t) należy najpierw obliczyć ten sygnał w postaci
zespolonej Y(s) stosując wzór:
Y s=G s⋅U s
Po podstawieniu otrzymuje się wyrażenie na sygnał wyjściowy w postaci zespolonej:
Y s=
s
s
2
5 s6
⋅
1=
s
s
2
5 s6
Otrzymane wyrażenie należy przekształcić, by móc skorzystać z tabeli transformat (z wykładu).
Y s=
s
s
2
5 s6
=
s
s2 s3
Otrzymano ułamek złożony. Należy rozłożyć ten ułamek na ułamki proste o mianownikach (s+2)
oraz (s+3). Stosując to rozumowania jak w zadaniu 2.2
Y s=
s
s2 s3
=
A
s2
B
s3
Stosując to rozumowania jak w zadaniu 2.2 oblicz się współczynniki A i B.
Y s=
s
s2 s3
=
A
s2
B
s3
=
A s3
s2 s3
B s2
s2s3
=
A s3B s2
s2 s3
=
=
As3ABs2B
s2 s3
=
s AB3A2B
s2s3
Porównując ułamki
Y s=
s
s2 s3
=
s AB 3A2B
s2s3
porównuje się wielomiany z liczników
s≡s AB3A2B
Wielomiany są sobie równe wtedy i tylko wtedy gdy ich współczynniki przy odpowiednich
potęgach są równe. Po porównaniu współczynników wielomianów otrzymuje się układ równań:
{
AB=1
3A2B=0
Rozwiązując układ równań dowolną metodą (tu metodą wyznaczników):
W =
∣
1 1
3 2
∣
=
1⋅2−1⋅3=−1
W
A
=
∣
1 1
0 2
∣
=
1⋅2−1⋅0=2
W
B
=
∣
1 1
3 0
∣
=
1⋅0−1⋅3=−3
{
A=
W
A
W
=−
2
B=
W
B
W
=
3
Podstawiając te wartości do wyrażenia na sygnał w postaci zespolonej otrzymuje się:
Y s=
A
s2
B
s3
=
−
2
s2
3
s3
=−
2⋅
1
s2
3⋅
1
s3
Przekształcając wyrażenie Y(s) w postaci zespolonej na postać y(t) rzeczywistą korzystając ze
wzoru:
1
sa
e
−
a t
otrzymuje się:
y t=−2 e
−
2 t
3 e
−
3 t
Zadanie 2.4
Oblicz i narysuj odpowiedź skokową obiektu o danej transmitancji:
G s =
3
s2
Schemat zadania jest podobny jak w zadaniach w których oblicza się odpowiedz impulsowe. Z
tematu zadania wiadomo, że należy obliczyć odpowiedź skokową. Oznacza to, że sygnał sterujący
u(t) jest równy skokowi jednostkowemu czyli:
u t=1 t
Wyrażenie to należy przekształcić do postaci zespolonej korzystając z tabeli transformat (ponieważ
wszystkie obliczenia wykonuje się w przestrzeni zespolonej), otrzymuje się:
U s=
1
s
Dalsze postępowanie jest identyczne jak w zadaniach, w których należało obliczyć odpowiedź
impulsową. Korzystając ze wzoru na sygnał w postaci zespolonej, otrzymuje się:
Y s=G s⋅U s
Podstawiając wartości, otrzymuje się:
Y s=
3
s2
⋅
1
s
=
3
s s2
W zadaniach, gdzie należy obliczyć odpowiedź skokową prawie zawsze należy rozłożyć ułamek
złożony na ułamki proste, co należy uczynić i w tym przypadku (mianowniki ułamków prostych
mają postać (s) oraz (s+2) ):
Y s=
3
s s2
=
A
s
B
s2
obliczając zmienne A i B:
Y s =
3
s s2
=
A
s
B
s2
=
A s2
s s2
Bs
s s2
=
A s2Bs
s s2
=
As2A Bs
s s2
=
s AB2A
ss2
porównując ułamki ze sobą, otrzymuje się:
Y s=
3
s s2
=
s AB2A
s s2
Z uwagi na fakt, że mianowniki są sobie równe porównuje się liczniki i otrzymuje się:
3≡s AB2A
Zapisując powyższą tożsamość jako układ równań, otrzymuje się:
{
A B=0
2A=3
i po rozwiązaniu tego układu równań dowolną metodą otrzymuje się:
{
A=
3
2
B=−
3
2
Podstawiając obliczone wartości zmiennych A i B do równania:
Y s=
3
s s2
=
A
s
B
s2
otrzymuje się:
Y s=
3
2
⋅
1
s
−
3
2
⋅
1
s2
W tej postaci sygnał wyjściowy da się przekształcić do postaci rzeczywistej korzystając z
zależności:
1
sa
e
−
a t
oraz
1
s
1t
otrzymuje się:
y t=
3
2
⋅
1 t−
3
2
⋅
e
−
2 t
Zadanie 2.5
Oblicz i narysuj odpowiedź skokową obiektu o danej transmitancji:
G s =
3s6
s
2
4s3
Z tematu zadania otrzymujemy:
u t=1 tU s =
1
s
Stosując wzór na sygnał wyjściowy:
Y s=G s⋅U s podstawiając wartości otrzymuje się:
Y s=
3s6
s
2
4s3
⋅
1
s
=
3s6
s s
2
4s3
=
3s6
s s1 s3
Należy rozbić ułamek złożony na ułamki proste (w tym przypadku na trzy ułamki proste o
mianownikach – (s); (s+1); (s+3)

Y s=
3s6
s s1 s3
=
A
s
B
s1
C
s3
Obliczając wartości zmiennych A, B i C , otrzymuje się:
Y s=
3s6
s s1 s3
=
A
s
B
s1
C
s3
=
As1 s3
s s1 s3
Bs s3
s s1 s3
Cs s1
s s1 s3
=
=
A s1 s3 Bs s3Cs s1
s s1 s3
=
A s
2
4s3Bs
2
3BsCs
2
Cs
ss1 s3
=
=
As
2
4As3ABs
2
3BsCs
2
Cs
s s1s3
=
s
2
A BC s4A3BC 3A
ss1 s3
Porównując ułamki między sobą:
Y s=
3s6
s s1 s3
=
s
2
ABC s 4A3BC 3A
s s1 s3
porównuje się wielomiany między
sobą:
3s6=s
2
ABC s 4A3BC 3A otrzymuje się układ 3ch równań z trzema
niewiadomymi:
{
ABC=0
4A3BC=3
3A=6
rozwiązując układ równań dowolną metodą (tu metodą wyznaczników)
W =
∣
1 1 1
4 3 1
3 0 0
∣
=−
6
W
A
=
∣
0 1 1
3 3 1
6 0 0
∣
=−
12
W
B
=
∣
1 0 1
4 3 1
3 6 0
∣
=
9
W
C
=
∣
1 1 0
4 3 3
3 0 6
∣
=
3
i ostatecznie
{
A=
W
A
W
=
2
B=
W
B
W
=−
3
2
C=
W
C
W
=−
1
2
Podstawiając do wyrażenia wyjściowego:
Y s=
3s6
s s1 s3
=
A
s
B
s1
C
s3
=
2⋅
1
s
−
3
2
⋅
1
s1
−
1
2
⋅
1
s3
Wykorzystując wzory na transformaty z tabeli
1
sa
e
−
a t
oraz
1
s
1t
otrzymuje się:
y t=2⋅1t −
3
2
e
−
t
−
1
2
e
−
3 t
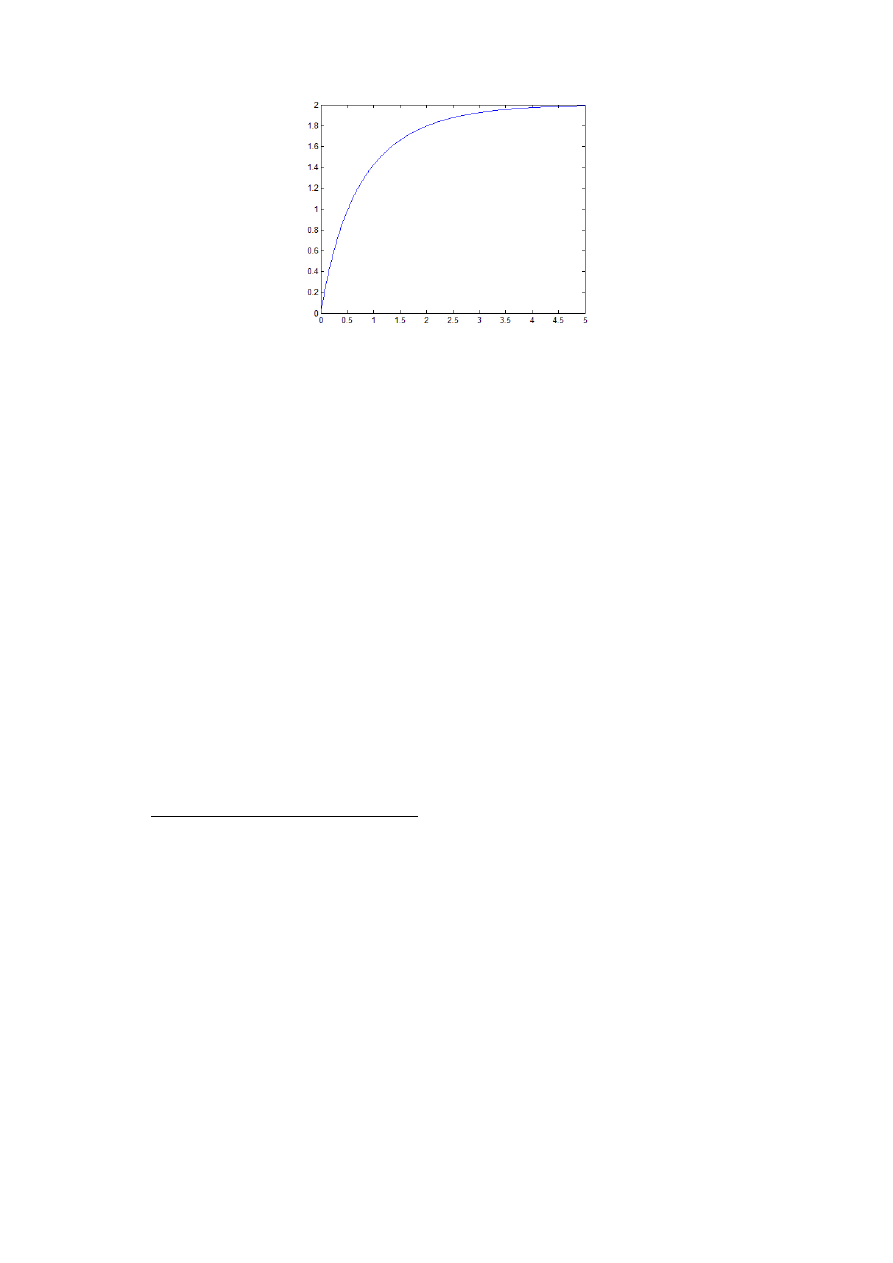
Uwaga!
Jeżeli w zadaniu należy obliczyć odpowiedź impulsową lub skokową a
dotyczy to układu automatyki (złożonego z więcej niż jednej
transmitancji) należy najpierw obliczyć transmitancję zastępczą układu
(jak zadania serii 1) a dopiero później liczyć zadaną odpowiedź (jak
zadania serii 2).
3. Sprawdzanie stabilności metodą
Routh'a
Zadanie 3.1.
Sprawdź dowolną metodą ile pierwiastków równania charakterystycznego obiektu leży w prawej
półpłaszczyźnie Gauss'a.
G s =
1
s
7
2 s
6
3 s
5
4 s
4
2 s
3
2 s
2
s1
W pierwszym kroku sprawdza się warunek konieczny (WK) stabilności, który oznacza, żeby układ
był stabilny stopień wielomianu licznika musi być mniejszy niż stopień wielomianu mianownika.
Ten warunek jest spełniony (stopień wielomianu licznika jest równy 0; stopień wielomiany
mianownika jest równy 7). Ponadto sprawdza się czy wszystkie współczynniki wielomianu z
mianownika istnieją i czy są takich samych znaków. Ten warunek również jest spełniony.
W tej metodzie wypełnia się tabelę Routh'a. Znaki 'x' w tabeli oznaczają liczby, które należy
obliczyć w późniejszych krokach algorytmu. Tabelę zaczyna wypełniać się od pierwszego miejsca
w wierszu 1szym (lewy górny róg), następnie pierwsze miejsce w wierszu 2gim, następnie 2gie
miejsce wiersza 1szego, potem 2gie miejsce wiersza drugiego (na zmianę) i tak do wyczerpania się

wszystkich współczynników wielomianu. Dalsze miejsca w dowolnej ilości można wypełnić 0.
s
7
1 3 2 1 0
s
6
2 4 2 1 0
s
5
x x x x x
s
4
x x x x x
s
3
x x x x x
s
2
x x x x x
s
1
x x x x x
s
0
x x x x x
Stopień wielomianu z mianownika określa ilość wierszy w tabeli (wiersze od s
5
do s
0
należy
obliczyć.
Obliczanie wiersza s
5
. Oznaczono elementy tego wiersza jako b1 … b5
s
7
1
3
2
1
0
s
6
2
4
2
1
0
s
5
b1 b2 b3 b4 b5
s
4
x
x
x
x
x
s
3
x
x
x
x
x
s
2
x
x
x
x
x
s
1
x
x
x
x
x
s
0
x
x
x
x
x
b1=
−
∣
1 3
2 4
∣
2
=−
1
2
⋅
4−6=1
b2=
−
∣
1 2
2 2
∣
2
=
1
b3=
−
∣
1 1
2 1
∣
2
=
1/2
b4=
−
∣
1 0
2 0
∣
2
=
0
Współczynniki od b5 … mają taką samą wartość jak współczynnik b4.
Obliczanie wiersza s
4
. Oznaczono elementy tego wiersza jako c1 … c5. Wstawiono do tabeli
wartości b1 … b5.
s
7
1
3
2
1
0
s
6
2
4
2
1
0
s
5
1
1
1/ 2
0
0
s
4
c1 c2
c3
c4 c5
s
3
x
x
x
x
x
s
2
x
x
x
x
x
s
1
x
x
x
x
x
s
0
x
x
x
x
x
c1=
−
∣
2 4
1 1
∣
1
=
2
c2=
−
∣
2
2
1 1/2
∣
1
=
1
c3=
−
∣
2 1
1 0
∣
1
=
1
c4=
−
∣
2 0
1 0
∣
1
=
0
Współczynniki od c5 … mają taką samą wartość jak współczynnik c4.
Obliczanie wiersza s
3
. Oznaczono elementy tego wiersza jako d1 … d5. Wstawiono do tabeli
wartości c1 … c5.
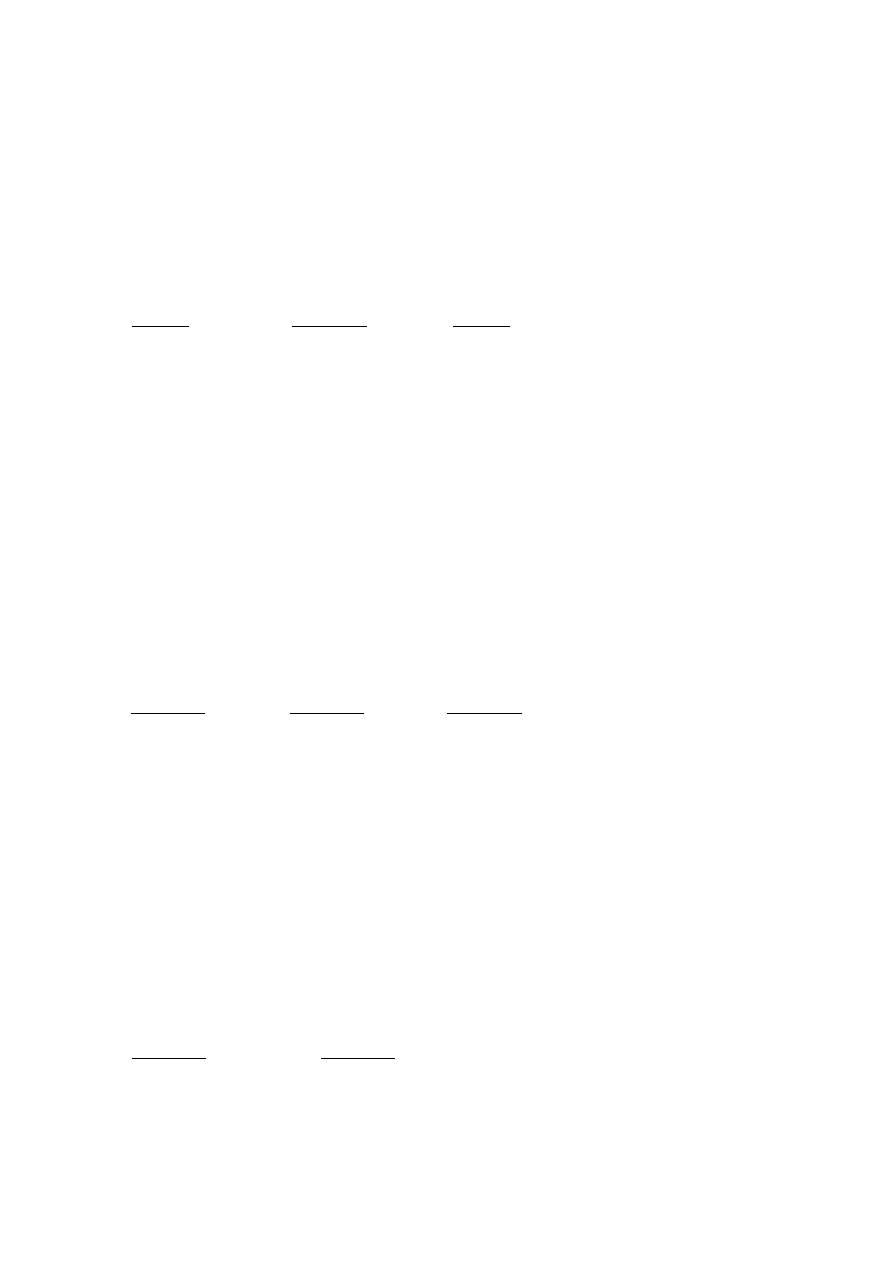
s
7
1
3
2
1
0
s
6
2
4
2
1
0
s
5
1
1
1/ 2
0
0
s
4
2
1
1
0
0
s
3
d1 d2
d3
d4 d5
s
2
x
x
x
x
x
s
1
x
x
x
x
x
s
0
x
x
x
x
x
d1=
−
∣
1 1
2 1
∣
2
=
1 /2
d2=
−
∣
1 1/2
2
1
∣
2
=
0
d3=
−
∣
1 0
2 0
∣
2
=
0
Współczynniki od d4 … mają taką samą wartość jak współczynnik d3.
Obliczanie wiersza s
2
. Oznaczono elementy tego wiersza jako e1 … e5. Wstawiono do tabeli
wartości d1 … d5.
s
7
1
3
2
1
0
s
6
2
4
2
1
0
s
5
1
1
1/ 2
0
0
s
4
2
1
1
0
0
s
3
1/2
0
0
0
0
s
2
e1
e2
e3
e4 e5
s
1
x
x
x
x
x
s
0
x
x
x
x
x
e1=
−
∣
2
1
1/2 0
∣
1/2
=
1
e2=
−
∣
2
1
1 /2 0
∣
1/2
=
1
e3=
−
∣
2
0
1/ 2 0
∣
1/2
=
0
Współczynniki od e4 … mają taką samą wartość jak współczynnik e3.
Obliczanie wiersza s
1
. Oznaczono elementy tego wiersza jako f1 … f5. Wstawiono do tabeli
wartości e1 … e5.
s
7
1
3
2
1
0
s
6
2
4
2
1
0
s
5
1
1
1/2
0
0
s
4
2
1
1
0
0
s
3
1/2
0
0
0
0
s
2
1
1
0
0
0
s
1
f1
f2
f3
f4
f5
s
0
x
x
x
x
x
f1=
−
∣
1/2 0
1
1
∣
1
=−
1/2
f2=
−
∣
1/2 0
1
0
∣
1
=
0
Współczynniki od f3 … mają taką samą wartość jak współczynnik f2.
Obliczanie ostatniego wiersza s
0
. Oznaczono elementy tego wiersza jako g1 … g5. Wstawiono do

tabeli wartości f1 … f5.
s
7
1
3
2
1
0
s
6
2
4
2
1
0
s
5
1
1
1/2
0
0
s
4
2
1
1
0
0
s
3
1/2
0
0
0
0
s
2
1
1
0
0
0
s
1
−
1/2
0
0
0
0
s
0
g1
g2
g3
g4 g5
g1=
−
∣
1
1
−
1/2 0
∣
−
1/2
=
1
g2=
−
∣
1
0
−
1/2 0
∣
−
1 /2
=
0
Współczynniki od g3 … mają taką samą wartość jak współczynnik g2. Wstawiono do tabeli
wartości g1 … g5. Pełna tabela ma poniższą postać.
s
7
1
3
2
1 0
s
6
2
4
2
1 0
s
5
1
1 1/2 0 0
s
4
2
1
1
0 0
s
3
1/2
0
0
0 0
s
2
1
1
0
0 0
s
1
−
1/2 0
0
0 0
s
0
1
0
0
0 0
Określanie stabilności.
W pierwszej kolumnie są dwie zmiany znaków, więc oznacza to, że w prawej półpłaszczyźnie
Gauss'a leżą dwa pierwiastki równania charakterystycznego obiektu (A wszystkich pierwiastków
jest 7). Układ jest niestabilny.
Zadanie 3.2
Sprawdź dowolną metodą ile pierwiastków równania charakterystycznego obiektu leży w prawej
półpłaszczyźnie Gauss'a.
G s =
1
s
7
s
6
4 s
5
2 s
4
4 s
3
s
2
2 s1
Odpowiedź
s
7
1
4
4 2 0
s
6
1
2
1 1 0
s
5
2
3
1 0 0
s
4
1/2
1/2 1 0 0
s
3
1
−
3 0 0 0
s
2
2
1
0 0 0
s
1
−
7/2
0
0 0 0
s
0
1
0
0 0 0
W pierwszej kolumnie są dwie zmiany znaków, więc oznacza to, że w prawej półpłaszczyźnie
Gauss'a leżą dwa pierwiastki równania charakterystycznego obiektu (A wszystkich pierwiastków
jest 7).

Zadanie 3.3
Sprawdź dowolną metodą ile pierwiastków równania charakterystycznego obiektu leży w prawej
półpłaszczyźnie Gauss'a.
G s =
s
2
s1
s
8
2 s
7
2 s
6
2 s
5
3 s
4
3 s
3
2 s
2
s1
Odpowiedź
s
8
1
2
3
2 1
s
7
2
2
3
1 0
s
6
1
3 /2
3/2 1 0
s
5
−
1
0
−
1 0 0
s
4
3/2
1 /2
1
0 0
s
3
1/3
−
1 /3
0
0 0
s
2
2
1
0
0 0
s
1
−
1/2
0
0
0 0
s
0
1
0
0
0 0
W pierwszej kolumnie są cztery zmiany znaków, więc oznacza to, że w prawej półpłaszczyźnie
Gauss'a leżą cztery pierwiastki równania charakterystycznego obiektu (A wszystkich pierwiastków
jest 8).
Zadanie 3.4
Sprawdź dowolną metodą ile pierwiastków równania charakterystycznego obiektu leży w prawej
półpłaszczyźnie Gauss'a.
G s =
−
2 s
2
−
s−1
s
8
2 s
7
3 s
6
4 s
5
3 s
4
3 s
3
2 s
2
3 s1
Odpowiedź
s
8
1
3
3
2 1
s
7
2
4
3
3 0
s
6
1
3/2
1/ 2 1 0
s
5
1
2
1
0 0
s
4
−
1/2 −1 /2
1
0 0
s
3
1
3
0
0 0
s
2
1
1
0
0 0
s
1
2
0
0
0 0
s
0
1
0
0
0 0
W pierwszej kolumnie są dwa zmiany znaków, więc oznacza to, że w prawej półpłaszczyźnie
Gauss'a leżą dwa pierwiastki równania charakterystycznego obiektu (A wszystkich pierwiastków
jest 8).
Wyszukiwarka
Podobne podstrony:
Rezystory obliczanie rezystancji zastępczej
Obliczanie rezystancji zastępczej w obwodach
TRANSMITANCJE ZASTĘPCZE I CHARAKTERYSTYKI UKŁADÓW AUTOMATYCZNEJ REGULACJI
Rezystory obliczanie rezystancji zastępczej
Obliczenia układu torowego
Obliczenia układu torowego
Obliczanie wartości obciążenia granicznego układu belkowo słupowego
Diagnoza rodzin zastępczych w obliczu dylematów współczesności
Podstawowe obliczenia pneumatycznego układu wykonawczego (Wojskowa Akademmia Techniczna)
BADANIE UKŁADU TRANSMISJI RÓWNOLEGŁOEJ 8255, Elektronika
Sprawozdanie 2, log i faz, Wykres logarytmiczny i fazowy transmitancji układu wraz z regulatorem ID
Obliczanie odpowiedzi skokowej obiektu o danej transmitancji
Napęd elektryczny badanie układu napędowego z przetwornicą częstotliwości zeszyt obliczeń
Rozwoj serca i ukladu krazenie
Choroby układu nerwowego ppt
Transmisja WAP
T7 Transformacja układu odniesienia
więcej podobnych podstron