Politechnika Gdańska Teoria

Sprężystości i Plastyczności M-SE4

Wydział Inżynierii Lądowej i Środowiska

sem. VI KBI r. 2005/2006

Katedra Mechaniki Budowli

prowadzący: Wojciech Witkowski, Marek Skowronek

ZADANIA DOMOWE – zestaw nr 2

- algebra tensorów, zastosowanie operatorów różniczkowych –

1. Dane

są wektory

oraz

i

i

a

=

a

e

i

i

b

=

b

e . Zapisać w rozwiniętej formie, stosując zapis

wskaźnikowy, następujące wielkości:

a)

b)

×

a b

⊗

a

b

c) (iloczyn skalarny) d)

⋅

a b

2

a

Przedstawić je, tam, gdzie można, w postaci formalnej, z użyciem wektor bazowych e

i

,

i = 1, 2, 3.

.......................................................................................................................................................

a)

(

)

2 3

3 2

3 1

1 3

1 2

2 1

,

,

T

ijk

i

j

e a b

a b

a b a b

a b a b

a b

× ⇒

=

−

−

−

k

a b

e

b)

1 1

1 2

1 3

2 1

2 2

2 3

3 1

3 2

3 3

i

j

a b

a b

a b

a b

a b

a b

a b

a b

a b

a b

⎡

⎤

⎢

⎥

⊗ ⇒

⊗ =

⊗

⎢

⎥

⎢

⎥

⎣

⎦

i

j

i

j

a

b

e

e

e

e

c)

1 1

2 2

3 3

i

i

a b

a b

a b

a b

⋅ =

=

+

+

a b

d)

2

2

2

2

2

1

2

3

T

i

i

a a

a a

a

a

a

=

=

=

+

+

=

a

a

2.

Dany jest wektor

oraz tensor II walencji

i

i

u

=

u

e

kl

k

l

R

=

⊗

R

e

e . Wykonać działanie

nasunięcia prostego

przedstawiając jego rezultat w postaci wskaźnikowej

(z użyciem wektorów bazowych e

R u

i

, i = 1, 2, 3) wskazać odpowiednik tego zadania

w zestawie ćwiczeń nr 1.

.......................................................................................................................................................

ij

k

ij

k

jk

ij

j

R

u

R u

R u

δ

=

⊗

=

=

i

j

k

i

R u

e

e

e

e

e

i

Odpowiednik z ćwiczeń nr 1 – przykład:

ij

j

A u

3.

Dane jest pole wektorowe:

( )

2

1 2

1 2 3

2

3 2

4x x

x x x

x x

⎛

⎞

⎜

⎟

≡

= ⎜

⎟

⎜

⎟

⎝

⎠

u

u x

Obliczyć: a)

b)

div u

grad

= ∇

u

u

c)

(

)

grad div u

d)

rot

u

e)

f)

(

)

0.5

T

=

∇ + ∇

S

u

u

u

(

)

0.5

T

=

∇ − ∇

A

u

u

u

g)

+

S

A

u

u

Wyrazić każdą z tych wielkości stosując zapis wskaźnikowy.

.......................................................................................................................................................

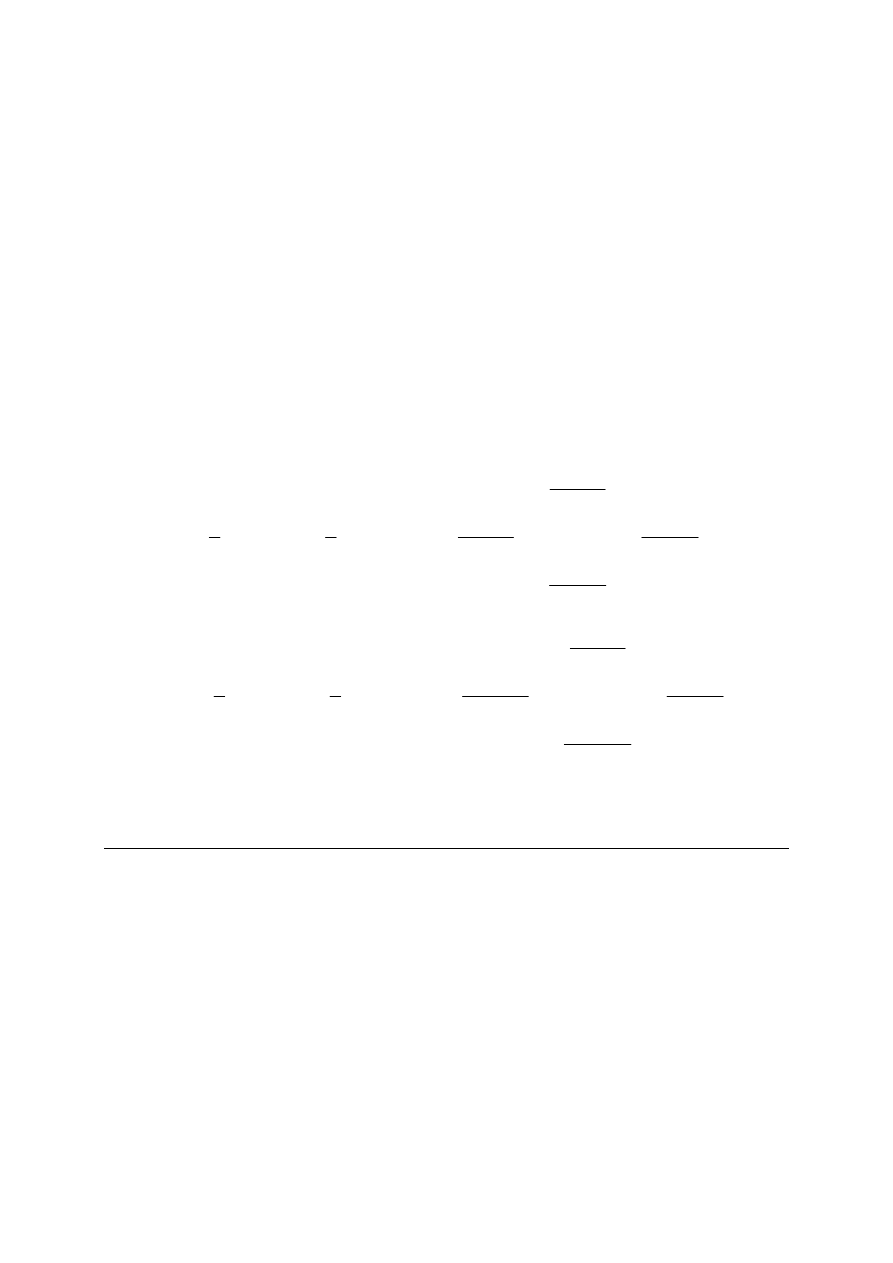
a)

2

2

2

,

1,1

2,2

3,3

2

1 3

2

2

1

4

5

i i

div

u

u

u

u

x

x x

x

x

x x

=

=

+

+

=

+

+

=

+

u

3

2

b)

2

1,1

1,2

1,3

2

1 2

,

2,1

2,2

2,3

2 3

1 3

1

2

3,1

3,2

3,3

2 3

2

4

8

0

0

2

i j

u

u

u

x

x x

grad

u

u

u

u

x x

x x

x x

u

u

u

x x

x

⎡

⎤

⎡

⎤

⎢

⎥

⎢

⎥

=

=

= ⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦ ⎣

⎦

u

c)

(

)

, 1

1,11

2,21

3,31

3

,

, 2

1,12

2,22

3,32

, 3

1,13

2,23

3,33

1

10

j j

j ji

j j

j j

u

u

u

u

x

grad div

u

u

u

u

u

x

u

u

u

u

x

⎡

⎤ ⎡

⎤

+

+

2

⎡

⎤

⎢

⎥ ⎢

⎥ ⎢

⎥

=

=

=

+

+

=

⎢

⎥ ⎢

⎥ ⎢

⎥

⎢

⎥ ⎢

⎥ ⎢

⎥

+

+

⎣

⎦

⎣

⎦

⎣

⎦

u

d)

3,2

2,3

3 2

1 2

1,3

3,1

2,1

1,2

2 3

1 2

2

0

8

u

u

x x

x x

rot

u

u

u

u

x x

x x

⎛

⎞

−

−

⎛

⎞

⎜

⎟ ⎜

⎟

=

−

=

⎜

⎟ ⎜

⎟

⎜

⎟

⎜

⎟

−

−

⎝

⎠

⎝

⎠

u

e)

(

) (

)

2

1

3

2

2

1

3

1

3

,

,

2

1 3

2

2

1

3

2

2

8

4

0

2

8

2

1

1

2

2

2

2

0

2

S

T

i j

j i

x

x

x

x

2

x

x

x

u

u

x

x x

x

x

x

x

x

+

x

⎡

⎤

⎢

⎥

⎢

⎥

+

+

⎢

⎥

=

∇ + ∇

=

+

= ⎢

⎥

⎢

⎥

+

⎢

⎥

⎢

⎥

⎣

⎦

u

u

u

f)

(

) (

)

1

3

2

1

3

1

3

,

,

2

2

1

3

2

8

0

0

2

8

2

1

1

0

2

2

2

2

0

0

2

A

T

i j

j i

x

x

x

2

x

x

x

u

u

x

x

x

x

x

−

x

⎡

⎤

⎢

⎥

⎢

⎥

−

+

−

⎢

⎥

=

∇ − ∇

=

−

= ⎢

⎥

⎢

⎥

− +

⎢

⎥

⎢

⎥

⎣

⎦

u

u

u

g)

S

A

+

= ∇

u

u

u

4.

Dana jest funkcja skalarna (pole skalarne) w R

2

:

( )

4

2 2

1

1

2

2

4

x

x x

x

ϕ ϕ

≡

=

+

+

x

Definiujemy operator różniczkowy:

( )

( )

( )

(

)

4

L

⋅ = ∇ ⋅ = ∆ ∆ ⋅

. Obliczyć

( )

L

ϕ

.

.......................................................................................................................................................

( )

2

2

,11

,22

1

2

14

14

x

x

g

ϕ ϕ

ϕ

∆ =

+

=

+

=

x

( )

( )

,11

,22

56

L

g

g

ϕ

ϕ

= ∆ ∆

= ∆ =

+

=

g