1.
Macierze. Określenie. Własności. Przykłady. Zastosowanie.
•
Tablica
× liczb rzeczywistych zapisanych w postaci
×
=
…
…
⋮
⋮
⋱
⋮
…
×
np.
=
1 5 7
2 3 1
8 7 2
×
Gdzie: n – liczba wierszy
k – liczba kolumn
Dla oznaczenia macierzy
można stosować
= [
]
×
gdzie
- elementy macierzy (wskaźnik
oznacza że element znajduje się w i-tym wierszu i j-tej kolumnie)
•
Macierz której wszystkie elementy są równe zeru nazywamy macierzą zerową
•
Macierz dla której
= nazywa się macierzą kwadratową (k – stopień macierzy)
•
W macierzy kwadratowej
elementy o równych wskaźnikach tworzą główną przekątną w
macierzy
=
1 0 0
2 1 0
0 1 1
×
Główna przekątna
•
Macierz kwadratowa która ma wszystkie elementy poza główną przekątna równe zeru nazywa się
macierzą diagonalną
=
1 0 0
0 51 0
0 0 8
×
•
Jeśli w macierzy diagonalnej wszystkie elementy na głównej przekątnej są jedynkami, macierz
nazywa się macierzą jednostkową i oznacza się
"
×
"
×
=
1 0 0
0 1 0
0 0 1
×
•
Jeśli elementy powyżej (poniżej) przekątnej macierzy kwadratowej są równe zeru macierz nazywa się
macierzą trójkątną górną (dolną)
=
1 7 5
0 2 1
0 0 8
×
=
1 0 0
20 2 0
15 7 8
×
Macierz trójkątna górna Macierz trójkątna dolna
•
Jeśli elementy leżące symetrycznie względem głównej przekątnej macierzy kwadratowej są równe
macierz tą nazywamy macierzą symetryczną
=
1 0 15
0 2 7
15 7 8
×

•
Macierzą transponowaną
(
×
)
%
do macierzy
= [
]
×
nazywamy macierz w której wiersze
zamieniono na kolumny
•
Macierz
nazywamy nieosobliwą gdy &'( ≠ 0
•
Macierz nazywamy schodkową gdy pierwsze niezerowe elementy w kolejnych niezerowych
wierszach znajdują się w kolumnach o rosnących numerach. Rząd macierzy jest równy liczbie jej
„schodków”.
•
Własności:
o
2 macierze są równe jeśli są identyczne
×
= *
×
⇔
= ,
o
Sumą macierzy jest macierz
×
+ *
×
= .
/ + .,
/ = [
+ ,
]
×
o
By pomnożyć macierz przez l. rzeczywistą α należy jej elementy przemnożyć przez α
0
×
= 0 1.
/
×
2 = .0
/
×
o
Iloczynem macierzy
×3
= [
]
×3
, *
3×5
= [,
]
3×5
nazywamy macierz
6
×5
= [7
]
×5
gdzie
7
= ∑
3
9
,
o
+ * = * +
(dodawanie macierzy jest przemienne)
o
( + *) + 6 = + (* + 6) (dodawanie macierzy jest łączne)
o
0 = 0
(mnożenie macierzy przez liczbę jest przemienne)
o
(*6) = (*)6
(mnożenie macierzy łączne)
o
(* + 6) = * + 6
(lewostr. mnożenie macierzy rozdzielne wzgl. dodawania)
o
(* + 6) = * + 6
(prawostr. mnożenie macierzy rozdzielne wzgl. dodawania)
o
(*)
%
= *
%
%
o
%
=
(macierz symetryczna)
•
Zastosowanie:
o
Rozwiązywanie układów równań
o
Druga pochodna funkcji wielu zmiennych
2.
Macierz odwrotna. Definicja. Własności. Metody wyznaczania. Zastosowanie.
•
Macierzą odwrotną do nieosobliwej macierzy
×
nazywamy macierz
×
:
taką że
:
= " =
:
Gdzie
" jest macierzą jednostkową stopnia n
•
Własności:
o
Macierz odwrotna do macierzy odwracalnej jest odwracalna
(
:
)
:
=
o
Iloczyn macierzy odwracalnych jest macierzą odwracalną
(*)
:
= *
:
:
o
Macierz transponowana do macierzy odwracalnej jest odwracalna
(
%
)
:
= (
:
)
%
o
Macierz jednostkowa jest odwracalna oraz
"
:
= "
o
Macierz zerowa jest nieodwracalna a kwadratowa jest również osobliwa
o
Suma macierzy odwracalnych nie musi być macierzą odwracalną
o
Dla nieosobliwej macierzy
zachodzi równość &'(
:
=
;<=>
•
Wyznaczanie:
o
Metoda dopełnień algebraicznych
Jeśli
|| ≠ 0 to
:
= (
1
&'()(7@A)
%
gdzie
7@A = .
/,
= (−1)
C
det
o
Metoda operacji elementarnych
Jeśli
|| ≠ 0 to dokonanie na wierszach macierzy [|"] operacji elementarnych dla rzędu
macierzy tak że otrzymujemy
["|
∗
] daje nam wynik
∗
=
:
3.
Wyznaczniki. Określenie. Własności. Przykłady. Zastosowanie
•
Wyznacznikiem macierzy kwadratowej stopnia n
= [
]
×
nazywamy liczbę oznaczoną
&'(
którą określamy rekurencyjnie w zależności od stopnia n
o
Jeśli
= 1 to &'( =
o
Jeśli
≥ 2 to &'( = ∑ (−1)
ICJ
K
9
a
IJ
detA
IJ
o
gdzie
jest macierzą dopełniającą elementu
np.
= N
O &'( = (−1)
C
&'(
+ (−1)
C
&'(
=
−
Schematy wyznaczania wyznacznika macierzy:
a)
2-ego stopnia
N∙ ∙
∙ ∙O
−
+
b)
3-ego stopnia
I sposób (dopisywanie wierszy)
Q
Q
Q
Q
Q
−
+
II sposób (dopisywanie kolumn)
−
+
•
Zastosowanie
o
Rozwiązywanie układów równań z tw. Cramera
o
Wyznaczanie macierzy odwrotnych
o
Wyznaczanie rzędu macierzy
o
Wyznaczanie minorów macierzy
4.
Wyznaczniki własności
•
Rozwinięcie Laplace’a
&'( = ∑ (−1)
ICR
K
9
a
IR
detA
IR
(rozwinięcie względem i-tego wiersza)
&'( = ∑ (−1)
ICR
K
9
a
RI
detA
RI
(rozwinięcie względem i-tej kolumny)
•
|*| = (||)(|*|)
(wyznacznik iloczynu macierzy jest równy iloczynowi wyznaczników)
•
Wyznacznik macierzy trójkątnej, diagonalnej i jednostkowej jest równy iloczynowi elementów
leżących na głównej przekątnej
•
Wyznacznik macierzy w której przynajmniej 1 kolumna (wiersz) jest zerowa(y) równa się 0

•
Wyznacznik o co najmniej 2-u wierszach (kolumnach) proporcjonalnych jest równy 0
•
Pomnożenie dowolnej kolumny lub dowolnego wiersza przez stałą mnoży przez tę samą
stałą wartość wyznacznika.
•
Zmiana kolejności wierszy (kolumny) zmienia znak wyznacznika na przeciwny
•
det() =
&'(
, gdzie k jest dowolną liczbą, n stopniem macierzy A
•
det(
:
) = (&'()
:
(wyznacznik macierzy odwrotnej równy odwrotności wyznacznika)
•
Transpozycja macierzy nie powoduje zmiany znaku wyznacznika
•
Dodawanie (odejmowanie) jednego wiersza (kolumny) do innego wiersza (kolumny) nie zmienia
znaku wyznacznika
5.
Operacje elementarne nie zmieniające rzędu macierzy. Operacje elementarne prowadzące do
równań liniowych równoważnych. Operacje elementarne nie zmieniające wartości wyznacznika.
•
Dla rzędu macierzy
o
Pomnożenie wszystkich elementów danego wiersza (kolumny) przez liczbę różną od 0
o
Dodanie do elementów wiersza (kolumny) odpowiednich elementów innego wiersza
(kolumny)
o
Skreślenie wiersza (kolumny) którego wszystkie elementy są równe 0
o
Skreślenie jednego z wierszy (kolumn) jednakowych
o
Zmiana kolejności wierszy (kolumn)
•
Dla równań liniowych równoważnych
o
Operacje elementarne nie zmieniające rzędu macierzy wykonywane tylko na wierszach
•
Dla wyznacznika
o
Dodawanie (odejmowanie) jednego wiersza (kolumny) do innego wiersza (kolumny) nie
zmienia znaku wyznacznika
6.
Rząd macierzy. Definicja. Własności. Przykłady. Zastosowanie.
•
Rzędem macierzy A nazywamy liczbę
ST równą największemu ze stopni nieosobliwych podmacierzy
macierzy
•
Własności
o
Operacje elementarne dla rzędu macierzy
a)
Pomnożenie wszystkich elementów danego wiersza (kolumny) przez liczbę różną od 0
b)
Dodanie do elementów wiersza (kolumny) odpowiednich elementów innego wiersza
(kolumny)
c)
Skreślenie wiersza (kolumny) którego wszystkie elementy są równe 0
d)
Skreślenie jednego z wierszy (kolumn) jednakowych
e)
Zmiana kolejności wierszy (kolumn)
o
Operacje elementarne dla rzędu macierzy nie zmieniają rzędu macierzy
o
Rząd macierzy jest równy maksymalnej ilości wersorów w macierzy
•
Zastosowanie
o
Rozwiązywanie układów równań.
7.
Układy równań liniowych. Twierdzenie Kroneckera-Capellego.( Układy nieoznaczone równań
liniowych)* Twierdzenie Cramera
•
Układy równań liniowych
o
Układem równań liniowych nazywamy zależność między macierzą układu (macierz
współczynników przy niewiadomych
3×
), wektorem niewiadomych
UV
×W
oraz
wektorem wyrażeń wolnych
*
×W
3×
UV
×W
= *
×W
o
Ze względu na ilość rozwiązań układy równań liniowych nazywamy:
Oznaczonymi - istnieje 1 rozwiązanie
Nieoznaczonymi - istnieje nieskończenie wiele rozwiązań (zbiór rozwiązań tworzy
rozwiązanie ogólne)
Sprzeczne- nie istnieje ani jedno rozwiązanie (zbiór rozwiązań jest pusty)
•
Układy liniowe nieoznaczone*
o
Zbiór rozwiązań układów nieoznaczonych nazywamy rozwiązanie ogólne układu
UV
XY
.
o
Rozwiązanie szczegółowe układu nieoznaczonego nazywamy ustalony konkretny element
rozwiązania ogólnego
UV
Z
o
Wyznaczanie polega na przekształceniu macierzy rozszerzonej przy pomocy operacji
elementarnych nie zmieniających rzędu macierzy, dokonywanych na wierszach macierzy
rozszerzonej do postaci w której jest tyle kolumn jednostkowych
'
, '
, … ile wynosi rząd
macierzy
S = ST. Wówczas
"UV
[
+ \UV
]
= *
∗
gdzie
" - macierz jednostkowa stopnia r
U
[
– tworzą niewiadome „bazowe”
U
]
– wektor utworzony z pozostałych niewiadomych traktowanych jako
parametry
*
∗
- wektor wyrazów wolnych otrzymany w wyniku operacji elementarnych
•
Tw. Kroneckera-Capellego:
Jeśli rząd macierzy układu jest równy rzędowi macierzy rozszerzonej
ST = ST[|*] to układ nie
jest sprzeczny.
Jeśli
ST = ST[|*] = gdzie n jest ilością niewiadomych to układ jest oznaczony.
Jeśli
ST = ST[|*] = gdzie < to układ jest nieoznaczony i rozwiązanie ogólne zależy od n-k
parametrów
•
Tw. Cramera:
Jeśli macierz układu A jest nieosobliwa to rozwiązanie układu stanowią niewiadome
U
_
=
;<=>
`
;<=>
8.
Metody rozwiązywania układów równań liniowych oznaczonych
•
Metoda szkolna
•
Metoda Cramera
Gdy
&'( ≠ 0 do obliczenia układu równań można zastosować wzory Cramera
U
=
&'(
&'(
gdzie
oznacza macierz otrzymaną przez zamianę w macierzy i-tej kolumny kolumną
wyrazów wolnych układu
•
Metoda operacji elementarnych
Polega na przekształceniu macierzy rozszerzonej przy pomocy operacji elementarnych nie
zmieniających rzędu macierzy, dokonywanych na wierszach, do postaci jednostkowej
[|* → ["|w
gdzie A-macierz główna, B- macierz wyrazów wolnych, X- macierz niewiadomych
•
Metoda eliminacji Gaussa
Polega na przekształceniu macierzy rozszerzonej przy pomocy operacji elementarnych nie
zmieniających rzędu macierzy, dokonywanych na wierszach, do postaci w której jest tyle kolumn
jednostkowych ile wynosi rząd macierzy
S = ST
9.
Granica ciągu liczbowego. Definicja. Własności. Twierdzenia o ciągach zbieżnych. Liczba Eulera.
•
Dla każdej dowolnie małej liczby
x istnieje taki indeks
y
(x) że dla wszystkich >
y
spełniona jest
nierówność:
{ | { |
− }| < x
~
∈
~y
Liczbę
} nazywamy granicą ciągu
lim
→
= }
•
Twierdzenia o ciągach zbieżnych
o
Jeśli ciąg spełnia powyższy warunek jest ciągiem zbieżnym
o
Ciągi które nie są zbieżne określamy jako rozbieżne
o
Jeśli istnieją 2 podciągi ciągu o różnych granicach to ciąg nie ma granicy i jest rozbieżny
•
Własności
o
Ciąg
gdzie ∈ ma co najwyżej jedną granicę
o
Każdy ciąg monotoniczny i ograniczony ma granicę skończoną
o
Jeśli ciąg ma granicę właściwą, to jest ograniczony. Jeśli ciąg liczb rzeczywistych ma
granicę niewłaściwą, to jest nieograniczony
o
Każdy podciąg ciągu zbieżnego jest zbieżny do tej samej granicy
o
Jeśli ciągi
, ,
są zbieżne to
lim
→
(
+ ,
) = lim
→
+ lim
→
,
lim
→
(
,
) = (lim
→
)(lim
→
,
)
lim
→
,
= lim
→
lim
→
,
gdzie
lim
→
,
≠ 0
Jeśli
lim
→
= lim
→
,
= i począwszy od pewnego indeksu
zachodzi
nierówność
≤ 7
≤ ,
to również
lim
→
7
=
o
Przypadki oznaczone
→
0
N
O
→
0
√
→
1 & > 0
√
→
1
√
→
∞
→
0 <=> || < 1
∞∞
→
∞
∞ + ∞
→
∞
o
Przypadki nieoznaczone
[0
[1
[∞
y
N
∞
∞O [0
y
0
0 [∞ − ∞
•
Granicę
= (1 +
)
oznaczamy e i nazywamy liczbą Eulera
' = lim
→
1 +
1
Jeśli
lim
→
,
= ∞ to lim
→
11 +
[
2
[
= '
9*. Szeregi liczbowe
•
Szeregi liczbowe
o
Ciąg sum częściowych nazywamy (
) utworzony z ciągu (
) gdzie
=
=
+
=
+
+ ⋯ +
o
Szeregiem liczbowym zbieżnym nazywamy granicę ciąg sum częściowych
lim
→
=
9
Jeżeli ciąg
jest rozbieżny, szereg jest rozbieżny.
a
K
- ogólny wyraz szeregu
S
K
– ogólny wyraz sum częściowych
lim
K→
S
K
- suma szeregu
•
Tw. Cauchy’ego dla szeregów
o
Szereg
∑
9
jest zbieżny
⇔ gdy
{ | { {|
C
+
C
+ ⋯ +
C
|
∈
~
~y
< x
lim
→
|
|
= } ⋀ } < 1
o
Szereg
∑
9
jest rozbieżny
⇔ gdy lim
→
|
|
= } ∧ } > 1
•
Kryterium d’Lamberta
o
Szereg
∑
9
jest zbieżny
⇔ gdy lim
→
¡¢
= } ∧ } < 1
o
Szereg
∑
9
jest rozbieżny
⇔ gdy lim
→
¡¢
= } ∧ } > 1
•
Kryterium porównawcze
o
Szereg
∑
9
jest zbieżny
⇔ gdy ∑
≤
9
∑
,
9
⋀ ∑
,
9
jest zbieżny
o
Szereg
∑
9
jest rozbieżny
⇔ gdy ∑
≥
9
∑
,
9
⋀ ∑
,
9
jest rozbieżny
•
Warunek zbieżności szeregu
o
Jeśli szereg
∑
9
jest zbieżny to
lim
→
= 0
9
< +∞ ⇒ lim
→
= 0
10.
Funkcja rzeczywista. Określenie. Własności. Przykłady. Zastosowanie
•
Sposób przyporządkowania każdemu elementowi danego zbioru X dokładnie jednego elementu
pewnego zbioru Y nazywamy funkcją. Jeśli dziedzina i przeciwdziedzina funkcji zawierają się w
zbiorze liczb rzeczywistych to funkcję
¤ = A(U) nazywamy funkcją rzeczywistą zmiennej
rzeczywistej.

•
Własności:
o
Jeśli funkcja dla dowolnych argumentów z dziedziny
U
U
gdzie
U
> U
spełnia
warunek
A(U
) ≥ A(U
) ( A(U
) ≤ A(U
) ) to nazywamy ją funkcją monotonicznie
rosnącą (malejącą)
o
Funkcję nazywamy ograniczoną od góry (od dołu) jeśli jej wartości nie przewyższają (nie
są mniejsze od) pewnej ustalonej liczby tzw. kresu górnego (dolnego). Funkcje
ograniczone od góry i od dołu nazywamy funkcjami ograniczonymi.
o
Funkcja
A(U) z dziedziną \ ma w punkcie a maksimum absolutne lub globalne jeżeli dla
wszystkich
U ∈ \
A() ≥ A(U)
o
Funkcja
A(U) ma w punkcie a maksimum względne lub lokalne jeśli nierówność
A() ≥ A(U) jest prawdziwa w pewnym otoczeniu punktu a, tzn. dla wszystkich U takich
że
− x < U < + x
o
Funkcje parzyste spełniają warunek
A(−U) = A(U) sama dziedzina \ funkcji A musi być
symetryczna
(U ∈ \) => (−U ∈ \)
o
Funkcje nieparzyste spełniają warunek
A(−U) = −A(U) sama dziedzina \ funkcji A musi
być symetryczna
o
Funkcje okresowe spełniają warunek
A(U + ¥)= A(U), ¥ = 7@¦( , ¥ ≠ 0
o
Funkcję
A: w → ¨ nazywamy odwracalną gdy istnieje taka funkcja }: ¨ → w taka że
}©A(U)ª = U dla każdego U ∈ w
A©}(¤)ª = ¤ dla każdego ¤ ∈ ¨
Funkcję
} nazywamy funkcją odwrotną do A i oznaczamy symbolem A
:
o
Funkcja
A: w → ¨ jest różnowartościowa (iniekcja) gdy dla dowolnych elementów
, , ∈ w spełniony jest warunek ≠ , ⇒ A() ≠ A(,)
o
Suriekcja: Niech
w oraz ¨ będą dowolnymi zbiorami. Funkcja A: w → ¨ odwzorowuje
zbiór
w na zbiór ¨ gdy każdy element zbioru ¨ jest wartością funkcji w pewnym punkcie
o
Bijekcja: Funkcja będąca jednocześnie funkcją różnowartościową i „na”.
11.
Granica i ciągłość funkcji w punkcie. Własności funkcji ciągłych w przedziałach domkniętych.
•
Niech funkcja będzie funkcją określoną w przedziale (a,b) z wyjątkiem punktu
U
y
gdzie
U
y
∈ (, ,),
liczbę g:
} = lim
→
A(U)
Nazywamy granicą funkcji w punkcie
U
y
wtedy i tylko wtedy gdy dla każdego ciągu argumentów
U
∈
takiego że
U
≠ U
y
oraz
lim U
= U
y
ciąg liczbowy
A(U
)
∈
jest zbieżny do liczby g.
•
Funkcja
A( ) jest ciągła w punkcie U
y
wtedy i tylko wtedy gdy
lim
→
A(U) = A(U
y
)
•
Własności
o
Złożenie funkcji ciągłych jest funkcją ciągłą (superpozycja) funkcji ciągłych jest funkcją
ciągłą
o
Funkcje wielomianowe, funkcja potęgowa, wykładnicza, logarytmiczna, funkcje
trygonometryczne oraz funkcje cyklometryczne są ciągłe w swoich dziedzinach.
o
Suma, różnica, iloczyn, iloraz funkcji ciągłych jest funkcją ciągłą
12.
Funkcje odwrotne. Twierdzenie o istnieniu funkcji odwrotnej. Funkcje
«
¬
, ®¬, ¯°±²³®¬, ¯°±±´²¬,
¯°±µ¶¬, ¯°±±µ¶¬. Określenie. Własności.
•
Funkcję
A: w → ¨ nazywamy odwracalną gdy istnieje taka funkcja }: ¨ → w taka że
}©A(U)ª = U dla każdego U ∈ w
A©}(¤)ª = ¤ dla każdego ¤ ∈ ¨
Funkcję
} nazywamy funkcją odwrotną do A i oznaczamy symbolem A
:
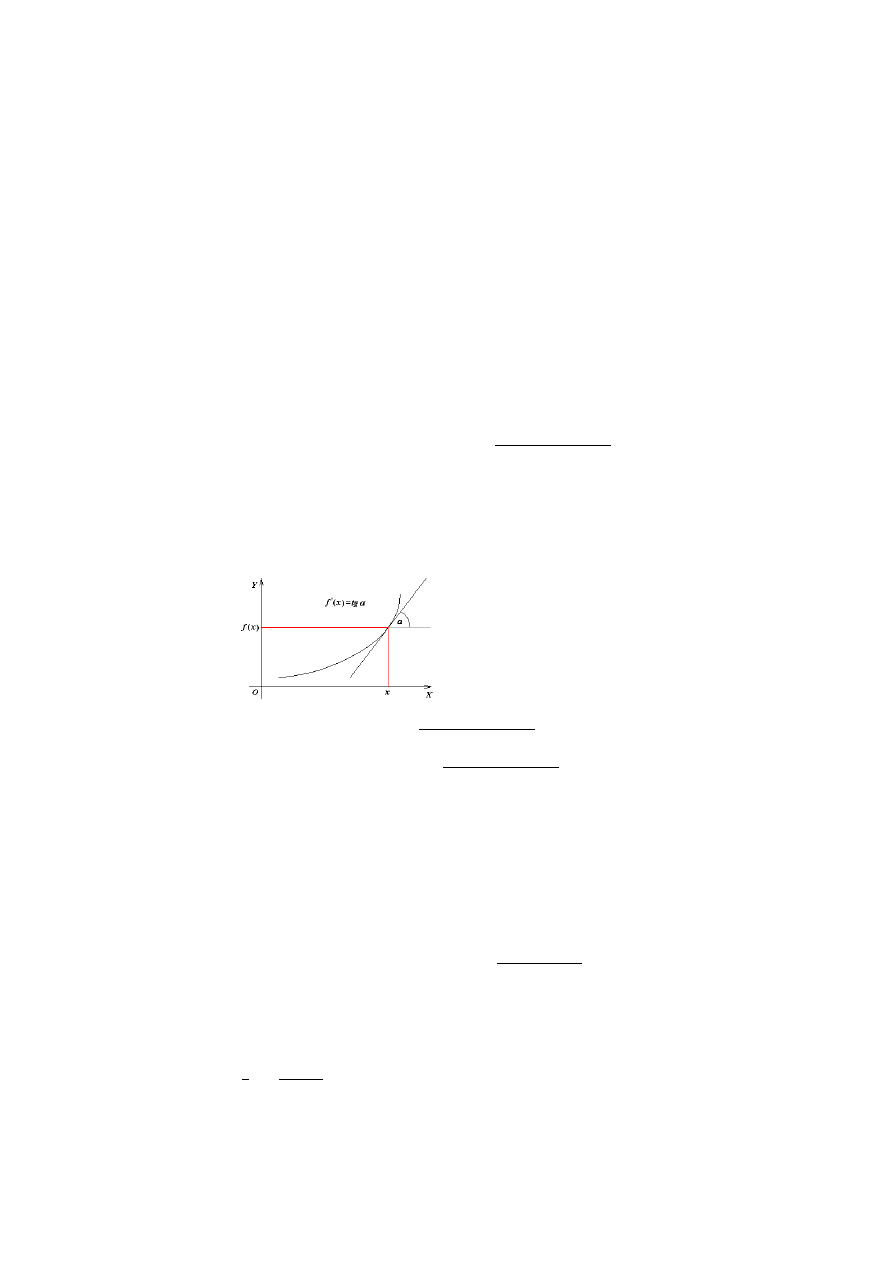
•
Własności:
o
Funkcja odwrotna do funkcji rosnącej jest rosnąca
o
Funkcja odwrotna do funkcji malejącej jest malejąca
o
Funkcja odwrotna do funkcji ciągłej jest ciągła
o
Funkcja odwrotna do funkcji różniczkowalnej
A(U) jest różniczkowalna wszędzie z
wyjątkiem obrazów punktów dla których
A
¸
(U) = 0
o
Wykres funkcji odwrotnej do
A jest symetryczny do wykresu A względem prostej ¤ = U
o
Funkcja odwrotna złożenia funkcji dana jest wzorem
(A ∙ })
:
= }
:
∙ A
:
13.
Pochodna funkcji. Definicja pochodnej w punkcie. Interpretacja geometryczna. Funkcje pochodne.
Własności. Przykłady. Zastosowanie
•
Pochodna funkcji
o
Pochodną
A: \
¹
− º
¹
w punkcie
U
y
nazywamy funkcję
A
¸
(U
y
) która jest granicą iloczynu
różnicowego
A
¸
(U
y
) = lim
»→y
A(U
y
+ ℎ) − A(U
y
)
ℎ
Jeśli ta granica istnieje jest skończona to funkcje nazywamy funkcją różniczkowalną w
punkcie
U
y
.
o
Geometryczna interpretacja pochodnej
A
¸
(U
y
)
A(U
y
+ ℎ) − A(U
y
)
ℎ
= (}0
lim
»→y
A(U
y
+ ℎ) − A(U
y
)
ℎ
= (}0
o
Równanie stycznej do funkcji różniczkowalnej w punkcie
U
y
: A
¸
( U
y
)(U − U
y
) + A(U
y
)
•
Własności:
o
Tw. Rolle’a: Jeśli
A: \
¹
− º
¹
jest ciągła w przedziale domkniętym
A: < , , >∋ \
¹
różniczkowalna wewnątrz tego przedziału oraz
A() = A(,) to istnieje
ξ ∈< , , > taka
że
A
¸
(
¿
)
= 0
o
Tw. Lagrange’a:
Jeśli
A: \
¹
− º
¹
jest ciągła w przedziale domkniętym
A: < , , >∋ \
¹
różniczkowalna wewnątrz tego przedziału to istnieje
ξ ∈< , , > taka że
A
¸
(ξ) =
A(,) − A()
, −
o
[A(U) ± }(U)
¸
= A
¸
(U) ± }
¸
(U)
o
(7A(U))
¸
= 7A
¸
(U)
o
(U
)
¸
= 0U
:
o
(A})
¸
= A
¸
} + }
¸
A
o
(
¹
Y
)
¸
=
¹
Á
Y:Y
Á
¹
Y
Â
o
.A©}(U)ª/
¸
= A
¸
©}(U)ª}
¸
(U)
o
(7)
¸
= 0

o
(7@¦U)
¸
= ¦U
o
(¦U)
¸
= 7@¦U
o
('
)
¸
= '
o
(U)
¸
=
o
(S7¦U)
¸
=
:
Â
o
(S77@¦U)
¸
=
:
:
Â
o
(S7(}U)
¸
=
C
Â
o
(S77(}U)
¸
= −
C
Â
o
(√U)
¸
=
√
•
Zastosowanie
o
Obliczanie granic nieoznaczonych (Tw. L’Hospitala)
o
Wyznaczanie stycznych (równanie stycznej)
o
Badanie przebiegu zmienności funkcji
o
Rozwinięcie funkcji w szereg Maclaurina, Taylora
13*. Szeregi potęgowe
•
Szeregiem potęgowym nazywamy funkcję
(U) =
U
9y
czyli
(U) =
y
+
U +
U
+ ⋯ +
U
+ ⋯
jest uogólnieniem pojęcia wielomianu stopnia n- wielomianu nieskończonego stopnia
•
Jeżeli szereg
∑
U
9y
jest zbieżny w punkcie
U
y
to szereg
∑
U
9y
jest zbieżny w każdym
punkcie przedziału
(−¿x
; ¿U
) gdzie 0 < ¿ < 1
•
Promieniem zbieżności szeregu potęgowego nazywamy taką liczbę dodatnią że szereg jest zbieżny
dla
U spełniającego nierówność |U| < S i rozbieżny dla S < |U|.
Przedział (-r,r) nazywamy przedziałem zbieżności szeregu
14.
Zastosowanie pochodnej do obliczania granicy nieoznaczonej.
•
Tw. L’Hospitala: Jeśli
lim
→
A(U) = 0 (Å, ∞) oraz lim
→
}(U) = 0 (Å, ∞) czyli mamy
doczynienia z przypadkiem
y
y
Å,
to:
lim
→
A(U)
}(U) = lim
→
A
¸
(U)
}
¸
(U)
15.
Badanie przebiegu zmienności funkcji rzeczywistej
•
Monotoniczność funkcji
Funkcja jet monotonicznie rosnąca
⇔ dla dowolnych dwóch argumentów U
, U
jeśli
U
< U
to
A(U
) < A(U
). Analogicznie z malejącą.
Funkcja różniczkowalna jest monotonicznie rosnąca w przedziale
< , , > ⇔ A
¸
(U) > 0.
Analogicznie z malejąca.
•
Różnowartościowość
Funkcja różniczkowalna jest różnowartościowa w przedziale
< , , > ⇔ gdy jest monotoniczna w
przedziale <a,b>.

•
Ekstrema funkcji
Funkcja ma w punkcie
U
y
maksimum (minimum) lokalne
⇔ w otoczeniu punktu U
y
wszystkie
wartości funkcji sa mniejsze (wieksze) niż wartość
A(U
y
)
o
Warunek konieczny istnienia ekstremum
Jeśli funkcja ma w punkcie
U
y
ekstremum to nie istnieje pochodna w punkcie
U
y
lub
A
¸
(U
y
) = 0.
o
Warunek wystarczający na istnienie ekstremum I
Jeśli w otoczeniu punktu spełniającego warunek konieczny pochodna
A
¸
(U
y
) zmienia znak
to funkcja ma w punkcie
U
y
ekstremum (maksimum dla +/-, minimum dla -/+.
o
Warunek wystarczający na istnienie ekstremum II
Jeśli
A
¸
(U
y
) = 0 oraz A
¸¸
(U
y
) ≠ 0 to funkcja ma w punkcie U
y
ekstremum (
A
¸¸
(U
y
) < 0
maksimum,
A
¸¸
(U
y
) > 0 minimum)
•
Punkty przegięcia
o
Warunek konieczny istnienia punktu przegięcia
Jeśli funkcja ma w punkcie
U
y
punkt przegięcia to
A
¸¸
(U
y
) = 0
o
Warunek wystarczający istnienia punktu przegięcia
Jeśli w otoczeniu punktu spełniającego warunek
A
¸¸
(U
y
) = 0 druga pochodna A
¸¸
(U)
zmienia znak to funkcja ma punkt przegięcia w
U
y
•
Wklęsłość/Wypukłość funkcji
o
Jeśli druga pochodna jest dodatnia
A
¸¸
(U
y
) > 0 dla x należących do przedziału <a,b> to
funkcja jest w tym przedziale wklęsła
o
Jeśli druga pochodna jest ujemna
A
¸¸
(U
y
) < 0 dla x należących do przedziału <a,b> to
funkcja jest w tym przedziale wypukła
•
Asymptoty
o
Asymptota ukośna
Asymptotą ukośną funkcji f nazywamy prostą
¤ = U + , taką że
lim[A(U) − (U + ,) = 0
Dla aymptoty ukośnej mamy
= lim
→±
¹()
, = lim
→±
[A(U) − U
o
Asymptota pionowa
Asymptotą pionową f nazywamy prostą
U = U
y
⇔ ÆÇÈ
¬→±
= ±∞
16.
Funkcja pierwotna. Całka nieoznaczona. Określenie. Własności, Przykłady. Zastosowanie.
•
Funkcja pierwotna
o
Funkcja pierwotną do funkcji
A określonej w pewnym obszarze domkniętym nazywamy
taką funkcję
É określoną w tym obszarze, której pochodna jest równa A.
É
¸
(U) = A(U)
o
Jeśli
É jest funkcją pierwotną dla funkcji A( ) to dla dowolnej stałej 6 = 7@¦( funkcja
É(U) + 6
też jest funkcją pierwotną.
•
Całka nieoznaczona
o
Całką nieoznaczoną funkcji podcałkowej
A(U) nazywamy rodzinę funkcji pierwotnych dla
A(U) i oznaczamy
Ê A(U)&U = É(U) + 6

o
Własności
Ë(A(U) ± }(U))&U = Ë A(U)&U ± Ë }(U)&U
Ë 7A(U)&U = 7 Ë A(U)&U
Ë '
&U = '
Ë 7@¦U &U = ¦U + 6
Ë ¦U &U = −7@¦U + 6
Ë
&U = U + 6
Ë U
=
C
U
C
dla
0 ≠ −1
Ë A
¸
(U)}(U)&U = A(U)}(U) − Ë A(U)}
¸
(U)
Ë A(U)&U = Ë A©ℎ(()ªℎ
¸
(()&( (Całkowanie przez podstawienie)
Ë
¹
Á
()
¹()
&U = |A(U)| + 6
o
Zastosowanie
Obliczanie całek oznaczonych
17.
Całka oznaczona Newtona. Własności. Całka jako pole. Twierdzenie watrości średniej dla całki.
Dowód. Interpretacja geometryczna.
•
Całka oznaczona Newtona
o
Całką oznaczoną funkcji ciągłej w przedziale
< , , > nazywamy różnicę wartości funkcji
pierwotnej
É( ) w górnej i dolnej granicy całkowania
Ê A(U)&U = É(,) − É()
[
o
Własności
Granice całkowanie nie ulegają zmianie we własnościach i metodach wyznaczania
całkinieoznaczonej z wyjątkiem metody podstawienia
Jeśli funkcja jest parzysta w przedziale
< −, > to
Ê A(U)&U = 2
:
Ê A(U)&U
Jeśli funkcja jest nieparzysta w przedziale
< −, > to
Ê A(U)&U = 0
:
Ë A(U)&U =
[
Ë A(U)&U +
Ë A(U)&U
[
gdzie
7 ∈< , , >
•
Twierdzenie o wartości średniej dla całki
o
Jeśli funkcja jest ciągła w
< , , > to istnieje ¿ ∈ (, ,) takie że
A(¿) =
1
, − Ê A(U)&U
[
o
Dowód
Z założenia o ciągłości funkcji funkcji wynika że istnieją liczby
Ì i Í takie że
Í(, − ) ≤ Ê A(U)&U ≤ Ì(, − )
[
czyli
Í ≤
1
(, − ) Ê A(U)&U
[
≤ Ì

o
Z twierdzenia Dardoux wynika że istnieje taka
¿ ∈< , , > że A(¿) przyjmuje wszystkie
wartości pośrednie między liczbami
Í a Ì zatem istnieje ¿ takie że
A(¿) =
1
, − Ê A(U)&U
[
17*. Konstrukcja całki Riemanna
•
Niech będzie dana funkcja w przedziale
" =< , , >⊆ Ï. Całką oznaczoną Riemanna funkcji w
przedziale
< , , > nazywamy granicę ciągu sum całkowych
= A(U
X
)|U
C
− U
|
9
gdzie
U
są punktami podziału przedziału
" na rozłącznych przedziałów takich że ciąg najdłuższych
podprzedziałów ma granicę równą .
U
X
jest punktem pośrednim przedziału < U
C
, U
> czyli
U
X
∈ (U
C
, U
). Jeśli
jest zbieżny do skończonej granicy g
lim
= } to mówimy że istnieje
całka funkcji. Liczbę g nazywamy całką oznaczoną w przedziale
< , , >
} = Ê A(U)&U = lim
→
[
Jeśli f(x) jest ujemna dla
U ∈< , , > to pole obszaru między wykresem funkcji, osią Ox a prostymi
U = , U = , wyraża się
− Ê A(U)&U
[
18.
Całki niewłaściwe.
•
Całką niewłaściwą pierwszego rodzaju nazywamy całkę oznaczoną w granicach nieskończonych
o
Ë A(U)&U
= lim
[→
Ë A(U)&U
[
o
Ë A(U)&U
[
:
= lim
→:
Ë A(U)&U
[
o
Ë A(U)&U
–
= Ë A(U)&U +
:
Ë A(U)&U
gdzie
7 ∈ (−∞, ∞)
•
Całką niewłaściwą drugiego rodzaju nazywamy całkę z funkcji nieograniczonej na przedziale
całkowania
o
Jeśli funkcja jest nieograniczona w lewym końcu przedziału całkowania (a,b) to
Ê A(U)&U =
[
lim
→
¡
Ê A(U)&U
[
o
Jeśli funkcja jest nieograniczona w prawym końcu przedziału całkowania (a,b) to
Ê A(U)&U =
[
lim
→[
Ñ
Ê A(U)&U
o
Jeśli funkcja jest nieograniczona dla
U = 7 gdzie 7 ∈ (, ,) to
Ê A(U)&U =
[
Ê A(U)&U +
Ê A(U)&U
[
•
Całka Gauss’a (Poissona)
Ê '
:
Â
&U = √2Ò
:
19.
20.
*Rozwinięcie funkcji okresowej w szereg Fouriera
•
Harmonika
o
Harmoniką nazywamy funkcję rzeczywistą zmiennej t (interpretowana jako czas) o
wartości
Ó(() = sin((Õ + 0)
Wielkości
, Õ, 0 są parametrami tej funkcji
o
Harmonika jest funkją okresową i opisuje ona ruch drgania harmonicznego gdzie
Õ - częstość drgań
|| - amplituda drgań
0 – faza
o
Okresem harmoniki
Ó(() jest ¥ =
Ö
×
o
Jeśli weźmiemy pod uwagę sumę harmonik otrzymamy funkcję również okresową bardziej
złożoną niż funkcja pierwsza np.
ℎ(() = ¦( +
1
2 ¦2( +
1
4 ¦3(
o okresie
2Ò ale różna od ¦U
o
Można pokazać ze funkcję okresową można przedstawić jako sumę sinusoid (harmonik)
ℎ(()
y
+
sin(Õ( + 0
)
9
o
Jeśli zastosować wzór na sin sumy
∢ sin(0 + Ú), 0 = U, Ú = 0
i
y
=
y
,
sin 0
=
,
cos 0
= ,
A(U) =
y
+ (a
K
cos U + b
K
sin U)
9
•
Rozwinięcie w szereg Fouriera
o
Funkcja okresowa o okresie
2Ò całkowalna w przedziale < −Ò, Ò > ma rozwinięcie w
szereg Fouriera
A(U) =
y
+ (a
Ü
cos ÍU + b
Ü
sin ÍU)
39
gdzie
y
= 1
Ö
2 Ë A(U)&U
Ö
:Ö
3
= 1
Ö
2 Ë A(U) cos ÍU &U
Ö
:Ö
Í = 1,2, …
,
3
= 1
Ö
2 Ë A(U) sin ÍU &U
Ö
:Ö
Í = 1,2, …
o
Dowód
Ê A(U)&U
Ö
:Ö
= Ê
y
Ö
:Ö
&U + + Ý
Ê cos U
Ö
:Ö
&U + ,
Ê sin U &U
Ö
:Ö
Þ
9
Ale
Ê cos U &U
Ö
:Ö
= ß
sin U
à
:Ö
Ö
@ST Ê sin U &U = ß
−(cos U)
à
:Ö
Ö
Ö
:Ö
= 0
Zatem
Ê A(U)&U
Ö
:Ö
= 2Ò
y
7T¤
y
=
1
2Ò Ê A(U)&U
Ö
:Ö
Ê A(U) cos U &U =
y
Ê cos U &U +
Ö
:Ö
Ý
Ê cos U cos ÍU &U + ,
Ê sin U cos U
Ö
:Ö
Ö
:Ö
Þ
9
Ö
:Ö

Dla
= Í
Ê 7@¦
ÍU&U =
1
2 Ê(1 + 7@¦2ÍU)&U = Ò
Ö
:Ö
Ö
:Ö
Dla
≠ Í obie całki pod znakiem sumy w przedziale < −Ò, Ò > są równe zeru. Wszystkie
całki poza całką
3
pod znakiem sumy są równe zeru.
21.
Równania różniczkowe zwyczajne. Równania o zmiennych rozdzielnych. Równania Pearsona.
•
Równania różniczkowe zwyczajne
o
Równaniem różniczkowym zwyczajnym pierwszego rzędu nazywamy zależność między
niewiadomą funkcją
¤(U) zmiennej rzeczywistej U i pochodną ¤
¸
(U) (związek między
U, ¤(U), ¤
¸
(U)). Zapis
É(U, ¤(U), ¤
¸
) = 0
o
Całką szczególną (rozwiązaniem szczególnym) równania różniczkowego nazywamy każdą
funkcję
¤(U) spełniającą równanie É(U, ¤(U), ¤
¸
) = 0
o
Całką ogólną (rozwiązaniem ogólnym) równania różniczkowego nazywamy zbiór
wszystkich całek szczególnych
•
Równania różniczkowe o zmiennych rozdzielonych
o
Równanie różniczkowe nazywa się równaniem różniczkowym o zmiennych rozdzielonych
⇔ można je przedstawić w postaci
}(¤)¤
¸
= A(U)
gdzie
}, A są ciągłe na odpowiednim przedziale określoności.
•
Równanie Pearsona
o
Równaniem różniczkowym Pearsona nazywa się równanie różniczkowe (o zmiennych
rozdzielonych) postaci
(U
+ ,U + 7)¤
¸
+ (U + &)¤ = 0
22.
Pochodna kierunkowa. Funkcja dwóch zmiennych. Definicja. Własności. Przykłady. Interpretacja
geometryczna. Twierdzenie o pochodnych kierunkowych.
•
Funkcje dwóch zmiennych
o
Funkcją wielu zmiennych nazywamy odwzorowanie
A: w → Ï gdzie w ∋ Ï
.
Funkcją dwóch zmiennnych jest
A: w → Ï gdzie w ∋ Ï
.
o
Wykresem funkcji dwóch zmiennych jest zbiór {
(U, ¤, T) ∈ Ï
, T = A(U, ¤) tj. płat
powierzchni w przestrzeni
Ï
.
o
Warstwicą funkcji dwóch zmiennych
A(U, ¤) odpowiadającą wartości T
y
nazywamy zbiór
á
â
= (U, ¤): A(U, ¤) = T
y
o
Granicą funkcji dwóch zmiennych w punkcie
(U
y
, ¤
y
) nazywamy liczbę g (o ile istnieje)
} = lim
ã→
,ã
A(U
y
, ¤
y
)
taką że dla każdego ciągu argumentów
(U
y
, ¤
y
) należącego do otoczenia punktu (U
y
, ¤
y
)
takiego że
(U
, ¤
) → (U
y
, ¤
y
) ciąg wartości A(U
, ¤
) przy → ∞ dąży do liczby g.
o
Funkcja
A: w → Ï gdzie w ∋ Ï
jest ciągła w punkcie
(U
y
, ¤
y
) ⇔
lim
ã→
,ã
A(U, ¤) = A(U
y
, ¤
y
)
Funkcja
A: w → Ï gdzie w ∋ Ï
jest ciągła w obszarze S
⇔ jest ciągła w każdym punkcie
obszaru S. Suma, iloczyn, iloraz, różnica funkcji ciągłych jest funkcją ciągłą.
Z łożenie funkcji ciągłych jest funkcją ciągłą.
•
Pochodna kierunkowa
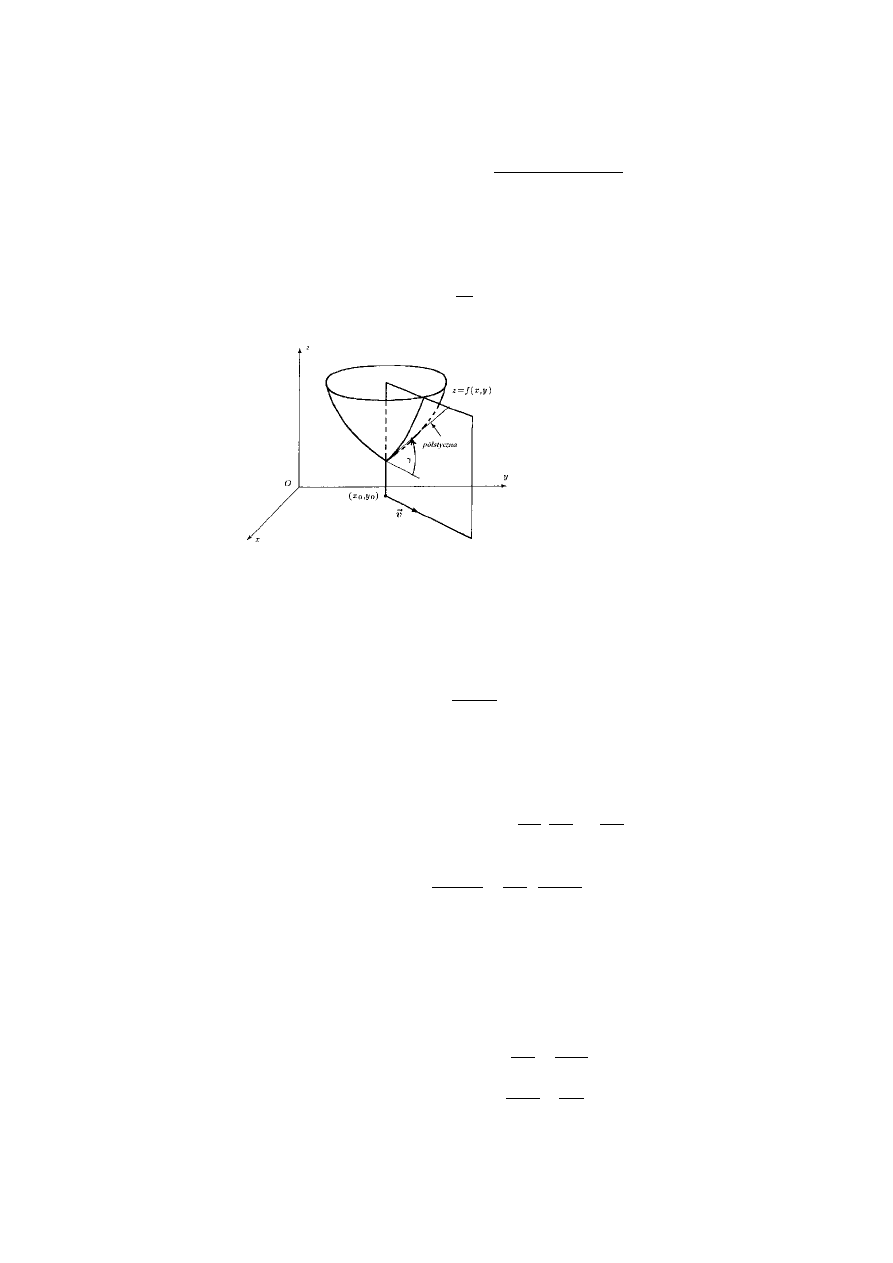
o
Pochodną kierunkową funkcji określonej w obszarze
\ ∋ Ï
w punkcie
U
y
w kierunku
wektora
V nazywamy liczbę
∇
åV
A(U
y
) = lim
»→y
[A(U
y
+ ℎ¦V )– A(U
y
)
ℎ
o
Niech funkcja f będzie określona na otoczeniu punktu (x
0
,y
0
). Ponadto niech
γ
oznacza kąt
nachylenia do płaszczyzny xOy półstycznej do krzywej otrzymanej w wyniku przekroju
wykresu funkcji f półpłaszczyzną przechodzącą przez prostą x = x
0
, y = y
0
oraz równoległą
do wersora
v
r
. Wtedy
æA
æçV (U
y
, ¤
y
) = (}è
Pochodna kierunkowa określa szybkość zmiany wartości funkcji f w kierunku wersora
v
r
.
23.
Pochodna cząstkowa. Gradient funkcji dwóch zmiennych.
•
Pochodna cząstkowa funkcji
o
Pochodną cząstkową funkcji
A: Ï → Ï względem k-tej zmiennej nazywamy pochodną
kierunkową funkcji
A w kierunku k-tego wersora '
æA(¬
é
)
æU
= ∇
ê
ë
f(í
é
)
Pochodna cząstkowa po zmiennej x jest wyznaczona jako pochodna funkcji
A(U, ¤) jednej
zmiennej x. Drugą zmienną y traktujemy jako stałą.
o
Pierwszą pochodną funkcji wielu zmiennych nazywamy wektor którego współrzędne
stanowią kolejne pochodne cząstkowe funkcji f
A
¸
(U
, U
, … , U
) = î
æA
æU
,
æA
æU
, … ,
æA
æU
ï
o
Pochodna cząstkowa drugiego rzędu
æ
A(U
y
)
æU
æU
[
=
æ
æU
[
ð
æA(U
y
)
æU
ñ
Jeśli w otoczeniu punktu
¬
é
pochodne cząstkowe mieszane drugiego rzędu funkcji istnieją
i są ciągłe w punkcie
¬
é
to są sobie równe.
o
Drugą pochodną funkcji
Ï
→ Ï (hesjanem) nazywamy macierz w której w k-tym wierszu
występują kolejne pochodne cząstkowe drugiego rzędu pochodnej cząstkowej pierwszego
rzędu względem zmiennej k-tej. Druga pochodna funkcji dwóch zmiennych jest macierzą
postaci
A
¸¸
(U, ¤) =
ò
ó
ó
ó
ô æ
A
æU
æ
A
æUæ¤
æ
A
æ¤æU
æ
A
æ¤
õ
ö
ö
ö
÷
•
Gradient funkcji

o
Gradientem funkcji w punkcie
¬
é
nazywamy wektor
A
¸
(¬
é
) określony wzorem
}S&A(U
y
, ¤
y
) ≝
æA
æU (U
y
, ¤
y
),
æA
æ¤ (U
y
, ¤
y
)
o
Gradient funkcji w punkcie
¬
é
jest wektorem prostopadłym w punkcie
¬
é
do warstwicy
funkcji przechodzącej przez
¬
é
i jest kierunkiem najszybszego wzrostu wartości funkcji w
¬
é
.
24.
Ekstrema funkcji dwóch zmiennych.
•
Minorem rzędu k macierzy kwadratowej
= [
×
nazywamy wyznacznik podmacierzy
kwadratowej stopnia k
&
= det [
×
•
Macierz kwadratowa jest:
o
dodatnio określona
⇔ wszystkie jej minory są dodatnie &
> 0
o
ujemnie określona
⇔ (−1)
&
> 0
o
półokreślona
⇔ (−1)
&
≥ 0 Å, &
≥ 0
o
W pozostałych przypadkach macierz jest nieokreślona.
•
Warunek konieczny istnienia ekstremum funkcji różniczkowej
Jeśli funkcja f(x) ma ekstremum w punkcie
U
y
i jest różniczkowalna w punkcie
¬
é
i jego otoczeniu to
pochodna
A
¸
(U) = 0.
•
Warunek dostateczny istnienia ekstremum funkcji różniczkowalnej.
Jeśli f(x) jest różniczkowalna w punkcie
¬
é
i jego otoczeniu to pierwsza pochodna
A
¸
(U
y
) = 0 oraz:
o
Macierz wartości drugich pochodnych w punkcie
¬
é
dodatnio określona to funkcja ma w
¬
é
minimum.
o
Macierz wartości drugich pochodnych w
¬
é
jest ujemnie określona to funkcja ma w
¬
é
maksimum.
o
Macierz wartości drugich pochodnych w
¬
é
ma ujemny wyznacznik to funkcja ma w
¬
é
punkt siodłowy.
o
Macierz wartości drugich pochodnych w
¬
é
jest nieokreślona to funkcja w
¬
é
nie ma
ekstremum.
o
Macierz wartości drugich pochodnych w
¬
é
jest półokreślona to istnienie ekstremum jest
przez drugą pochodną funkcji nierozstrzygnięte.
25.
Całka podwójna. Całka iterowana.
•
Niech będzie dana funkcja dwóch zmiennych f(x,y) w obszarze domkniętym
\ ∋ Ï
. Całką funkcji
A( ) na obszarze \ nazywamy granicę ciągu sum całkowych czyli
ù A(U, ¤)&U&¤ = lim
ú
•
Iteracja
o
Jeśli
\ = (U, ¤): < U < ,, 7 < ¤ < & to
ù A(U, ¤
ú
)&U&¤ = Ê ÝÊ A(U, ¤)&U
[
Þ &¤ = Ê ÝÊ A(U, ¤)&¤
;
Þ
[
;
&U
o
Jeśli
\ = (U, ¤): < U < ,, û
(U) < ¤ < û
(U) to
ù A(U, ¤
[ü
Â
ü
¢
)&U&¤ = Ê Ý Ê A(U, ¤)&¤
ü
Â
ü
¢
Þ &U
[
o
Jeśli
\ = (U, ¤): ý
(¤) < U < ý
(¤), 7 < ¤ < & to
ù A(U, ¤
þ
Â
;
þ
¢
)&U&¤ = Ê Ý Ê A(U, ¤)&U
þ
Â
þ
¢
Þ &¤
;
•
Własności
o
Jeśli
A(U, ¤) = }(U)ℎ(¤) to Ë Ë A(U, ¤)&U&¤ = Ë }(U)&U Ë ℎ(¤)&¤
;
[
;
[
o
∬
&U&¤
ú
= |\|
o
∬
A(U, ¤)&U&¤ =
ú
gdzie
jest objętością prostopadłościanu o podstawie
\
27*. Twierdzenie Maclaurina
•
Twierdzenie Maclaurina
o
Jeśli funkcja rzeczywista ma w przedziale <-h,h> pochodne do rzędu
( + 1)-go włącznie
oraz
lim
→
Ï
C
= 0 gdzie Ï
C
= A
(C)
(U¿)
¡¢
(C)!
to istnieje
¿ ∈ (0,1) takie że
A(U) = A(0) + A
¸
(0)
U
1! + A
¸¸
(0)
U
2! + ⋯
o
Przy założeniu twierdzenia Maclaurina mamy wzór
A(U) = A(0) + A
¸
(0)
U
1! + A
¸¸
(0)
U
2! + ⋯ + A
()
(0)
U
! + Ï
C
Ï
C
- reszta szeregu Maclaurina może określać błąd przybliżenia wartości
A(U) w otoczeniu
U
y
= 0 wielomianu stopnia n
•
Twierdzenie Taylora
o
Jeśli w otoczeniu punktu
U = U
y
funkcja ma pochodne dowolnego rzędu oraz są one
wspólnie ograniczone tzn istnieje liczba
Ì taka że A
()
(U) < Ì dla każdego n i każego x
z otoczenia
U
y
A(U) = A(U
y
) + (U − U
y
)
9
A
()
U
y
!
28*. Proces renowacji kapitałowej
•
Tablicą śmiertelności jednostek kapitałowych nazywamy skończony ciąg liczbowy
,
, … ,
taki
że
o
=
> 0 dla ( = 1, …
o
∑
=
= 1
=9
gdzie
=
- procent wszystkich jednostek kapitałowych wymagających wymiany na nowe w
chwili
(.
•
Przeciętnym czasem życia jednostki kapitałowej nazywamy liczbę
Í =
+ 2
+ ⋯ +
•
Zagadnienie renowacji populacji kapitałowej jest następujące: znaleźć takie liczby jednostek
kapitałowych
Å
, Å
… które należy zastąpić w chwilach ( = 1,2, … nowymi aby utrzymać stan
kapitału (wielkość populacji) na stałym poziomie równym
Å
y
.
•
Rozwiązaniem jest ciąg rat renowacyjnych
Å
=
Å
y
Å
=
Å
+
Å
y
⋯
Å
=
Å
:
+
Å
:
+ ⋯ +
Å
:
•
Twierdzenie:
lim
→
Å
=
3
Wyszukiwarka
Podobne podstrony:
Opracowane tezy ustny
OPRACOWANE TEZY
Teologia dogmatyczna - opracowane tezy, KAMI, dokumenty
opracowane tezy z historii Kościoła, 7
opracowane tezy z historii Kościoła, 18
Opracowane tezy na egzamin, Socjologia
opracowane tezy z historii Kościoła, 3
opracowane tezy z historii Kościoła, 3
opracowane tezy z historii Kościoła, 11
opracowane tezy do egzaminu z psychologii klinicznej sem 3, Pedagogika
Opracowane tezy z psychologii klinicznej1
Opracowane tezy 2
Opracowane tezy na egzamin2, Socjologia
opracowane tezy, AWF, Fizjologia
Opracowane tezy
Skrypt - opracowane tezy, KAMI, dokumenty
Opracowane tezy do egzaminu
więcej podobnych podstron