
Egzamin dla Aktuariuszy z 13 grudnia 2010 r.
Matematyka Finansowa
Zadanie 1
n
X martyngałem gdy
(
)
0
1
=
−
+
n
n
n
X
X
E
τ
(
)
(
)
(
)
→
−
+
=
−
−
=
=
=
−
+
+
+
B
p
B
A
p
B
Ap
EX
X
X
X
E
S
S
E
i
n
n
n
n
n
n
)
(
)
1
(
,...,
)
(
1
1
1
1
σ
τ
NIE bo
zależy od parametrów
NIE
ii)
(
- to wynika z (i)
(
)
NIE
B
A
B
B
A
S
S
E
iii
n
n
n
→
−
=
−
+
=
−
+
2
1
2
1
2
1
)
(
)
(
1
τ
(
)
(
)
(
)
NIE
p
B
p
B
A
X
X
X
E
Z
Z
E
iv
n
n
n
n
n
→
−
=
−
+
=
=
−
+
+
1
2
)
(
,...,
)
(
1
1
1
σ
τ
(
)
TAK
B
B
A
B
B
A
Z
Z
E
v
n
n
n
→
=
−
+
+
=
−
+
0
)
(
)
(
1
τ
Czyli 1 stwierdzenie jest prawdziwe
Zadanie 2
[
]
∑
∞
=
=
+
+
+
+
−
+
+
+
+
−
=
+
−
=
1
4
3
2
...
)
4
(
)
3
(
)
2
(
)
1
(
)
1
(
)
(
k
k
k
v
a
v
a
v
a
v
a
v
a
k
a
f
(
) (
) (
)
4
4 3
4
4 2
1
4
4
4
3
4
4
4
2
1
B
A
v
v
v
v
v
v
v
a
...
4
2
...
5
3
...
4
2
5
3
2
+
+
+
+
+
+
−
+
+
=
(
)
(
)
2
2
3
2
3
2
3
3
2
3
5
3
2
7
5
3
2
5
3
1
1
1
2
1
2
...
2
2
1
...
5
3
...
5
3
v
v
v
A
v
v
v
v
v
v
v
v
v
v
v
v
v
v
A
v
v
v
Av
v
v
v
A
−
+
=
→
−
+
=
−
+
−
=
−
+
=
+
+
+
=
−
+
+
+
=
+
+
+
=
(
)
(
)
2
2
2
2
2
4
2
2
6
4
2
4
2
1
2
1
2
...
2
2
1
...
4
2
...
4
2
v
v
B
v
v
v
v
v
B
v
v
Bv
v
v
B
−
=
→
−
=
+
+
=
−
+
+
=
+
+
=
(
) (
)
→
=
−
+
−
+
−
−
=
→
0
1
2
1
1
)
(
2
2
2
2
2
2
v
v
v
v
v
v
av
a
f
(
)
01
,
0
04
,
1
1
gdzie
1
1
2
2
2
2
3
≈
→
=
−
−
−
+
=
→
a
v
v
v
v
v
v
v
a
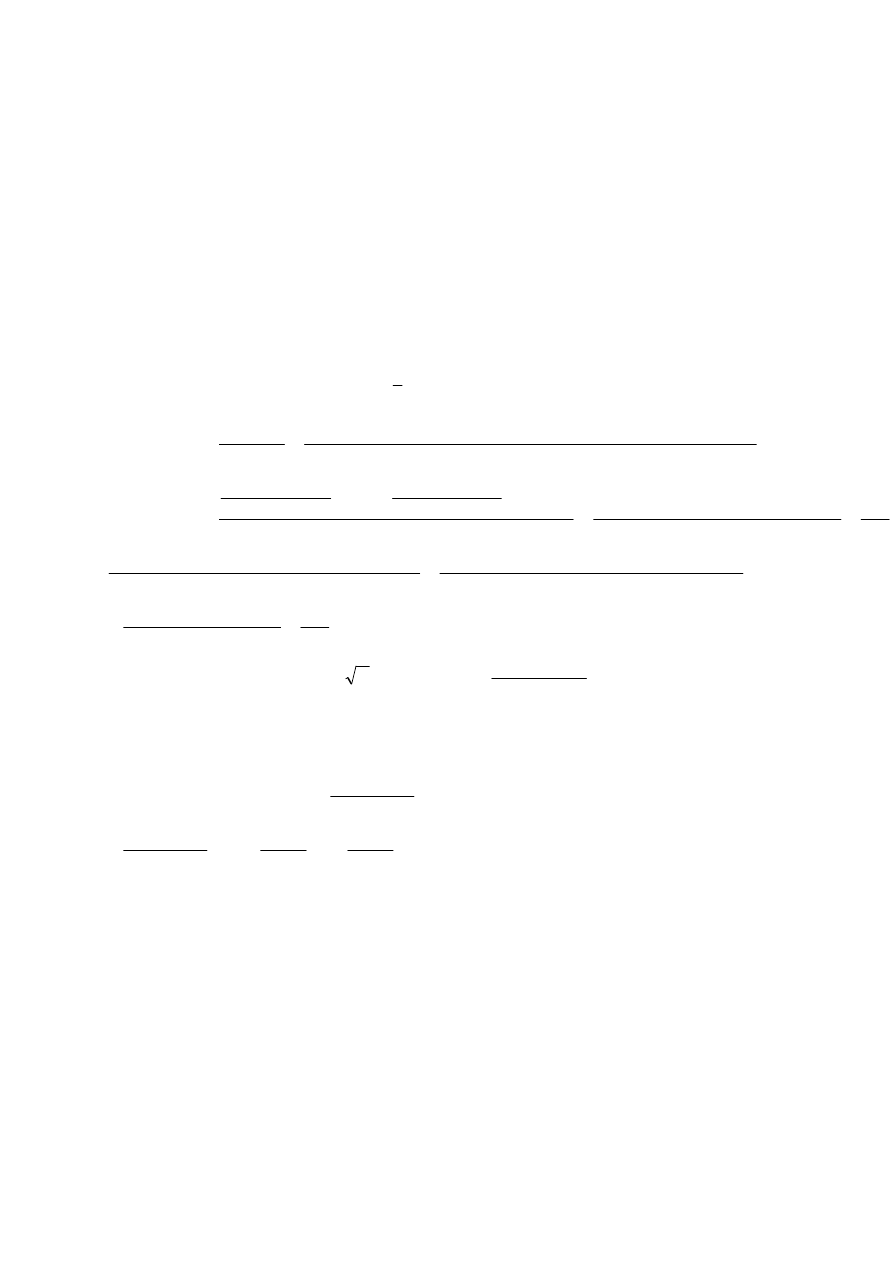
Zadanie 3
UWAGA: renta A stanowi spłatę kredytu zaciągniętego rok przed pierwszą ratą renty A a nie
zaciągniętego w chwili obecnej i spłacanego w sposób odroczony (inaczej wychodzi inny
wynik)
B
A
k
k ,
- momenty pierwszej raty dla odpowiednich rent
B
A
n
n ,
- ilość rat
B
A
n
n
k
k
A
B
B
A
=
+
=
=
+
2
,
1
2
3
(
)
platnosci
pierwszej
moment
jest
to
lim
13
10
)
(
lim
d
k
k
B
A
d
i
B
A
i
∞
→
∞
→
=
→
=
=
+
(
)
(
)
(
)
2
1
13
...
14
13
1
10
...
11
10
)
(
)
(
)
(
lim
0
+
+
+
+
+
+
+
+
−
+
+
+
+
=
=
+
∑
∑
→
A
A
A
A
i
n
B
An
B
n
B
B
A
n
A
A
k
P
k
kP
B
A
d
(
)
(
)
(
)(
)
(
)
31
568
2
2
2
27
19
2
2
2
1
13
13
2
1
10
10
)
(
lim
0
=
+
+
+
+
+
+
=
+
+
+
+
+
+
+
⋅
−
+
+
=
+
→
B
Bn
An
B
n
n
An
n
B
Bn
An
B
n
n
A
n
n
B
A
d
A
A
A
A
A
A
A
A
A
A
A
A
i
(
)
=
+
+
+
+
+
+
+
=
⋅
+
⋅
+
+
+
+
+
+
8
,
4
4
,
2
2
4
,
2
2
,
1
8
,
64
4
,
32
19
2
,
1
4
2
,
1
2
2
2
,
1
2
54
27
19
2
2
2
2
A
A
A
A
A
A
A
A
A
A
A
A
A
A
n
n
n
n
n
n
n
A
An
An
A
n
n
n
An
An
4
,
2726
2
,
2499
8
,
2008
8
,
1667
2
,
68
31
568
8
,
4
4
,
4
8
,
64
8
,
53
2
,
2
2
2
+
=
+
+
→
=
+
+
+
=
A
A
A
A
A
A
n
n
n
n
n
n
13
2
,
68
2
8
,
941
4
,
831
8
,
941
0
6
,
717
4
,
831
2
,
68
2
=
⋅
+
=
→
=
∆
→
=
−
−
A
A
A
n
n
n
15
,
13
,
13
,
10
=
=
=
=
B
A
B
A
n
n
k
k
∑
∑
∑
=
=
=
=
−
=
→
+
−
=
→
=
−
27
13
22
10
13
13
1
2
,
1
1
13
64
,
360
64
,
360
13
k
k
k
k
k
k
v
A
v
A
ODP
v
i
i
A
v
A
A
−
−
−
−
−
+
−
=
v
v
v
v
v
v
v
i
i
1
1
1
1
2
,
1
1
13
64
,
360
13
10
15
13
13
Zadanie 4
20
9
12
11
10
2
5
,
1
3
...
5
,
1
3
3
2
...
18
20
v
v
v
v
v
v
K
⋅
+
+
⋅
+
+
+
+
+
=
18
9
10
9
8
2
5
,
1
3
...
5
,
1
3
3
2
...
14
16
)
2
(
v
v
v
v
v
v
R
⋅
+
+
⋅
+
+
+
+
+
=
17
9
9
8
7
2
5
,
1
3
...
5
,
1
3
3
2
...
12
14
)
3
(
v
v
v
v
v
v
R
⋅
+
+
⋅
+
+
+
+
+
=
14
9
6
5
4
3
2
5
,
1
3
...
5
,
1
3
3
2
4
6
8
)
6
(
v
v
v
v
v
v
v
R
⋅
+
+
⋅
+
+
+
+
+
=
13
9
5
4
3
2
5
,
1
3
...
5
,
1
3
3
2
4
6
)
7
(
v
v
v
v
v
v
R
⋅
+
+
⋅
+
+
+
+
=
7
9
2
4
3
5
,
1
3
...
5
,
1
3
5
,
1
3
)
13
(
v
v
v
R
⋅
+
+
⋅
+
⋅
=
6
9
2
5
4
5
,
1
3
...
5
,
1
3
5
,
1
3
)
14
(
v
v
v
R
⋅
+
+
⋅
+
⋅
=
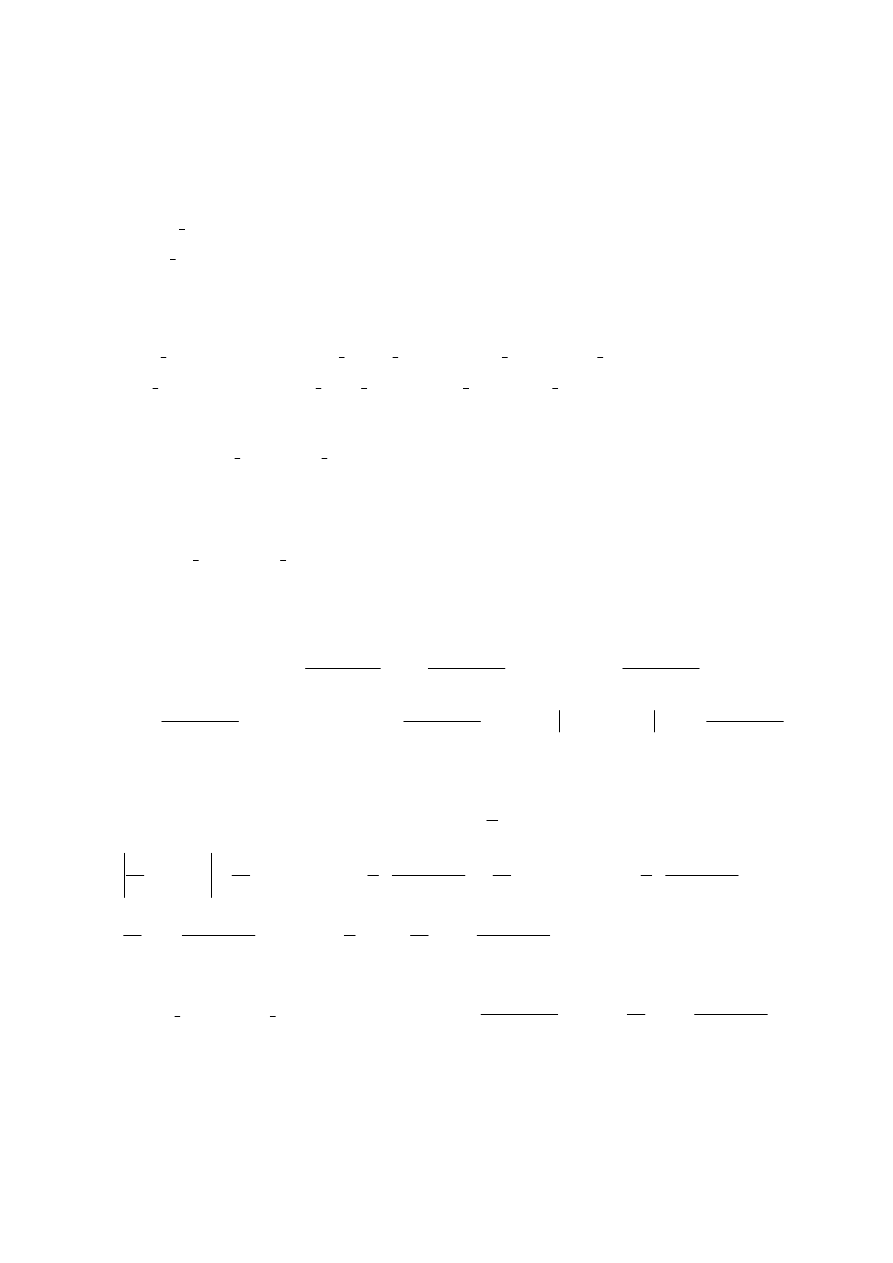
[
]
[
] [
]
)
14
(
)
13
(
)
7
(
)
6
(
8
)
3
(
)
2
(
16
R
R
R
R
R
R
ODP
−
+
−
−
+
−
−
=
[
]
+
⋅
+
−
−
−
−
−
+
+
+
−
=
18
9
17
9
10
2
9
8
7
2
5
,
1
3
5
,
1
...
5
,
1
5
,
1
2
...
2
2
16
v
v
v
v
v
v
v
v
ODP
[
]
−
⋅
+
−
−
−
−
+
+
−
+
14
9
13
9
5
4
3
2
5
,
1
3
5
,
1
...
5
,
1
2
2
2
8
v
v
v
v
v
v
v
[
]
=
⋅
−
+
+
−
7
9
6
9
4
5
,
1
3
5
,
1
...
5
,
1
v
v
v
[
]
+
⋅
+
−
−
−
−
−
−
=
18
9
17
9
10
2
9
8
8
5
,
1
3
5
,
1
...
5
,
1
5
,
1
3
2
16
v
v
v
v
v
a
[
]
+
⋅
+
−
−
−
−
−
+
14
9
13
9
5
4
4
5
,
1
3
5
,
1
...
5
,
1
3
2
8
v
v
v
v
a
[
]
6
9
4
7
9
5
,
1
...
5
,
1
5
,
1
3
v
v
v
−
−
−
⋅
+
DYGRESJA:
(
)
(
)
(
)
4
4
4
4
4
4
4
4
4
8
8
8
8
8
8
8
8
8
8
)
2
8
(
2
8
8
2
8
1
8
2
8
16
2
16
2
16
16
2
16
1
16
2
16
v
a
i
a
v
i
a
a
v
v
a
v
a
i
a
v
i
a
a
v
v
a
+
−
=
−
+
⋅
=
−
+
−
=
−
+
−
=
−
+
⋅
=
−
+
−
=
−
(
)
+
+
+
−
+
−
=
4
4
4
8
2
1
8
)
2
8
(
)
2
16
(
v
v
a
i
a
i
ODP
[
] [
]
+
⋅
−
+
+
+
+
⋅
−
+
+
+
+
14
9
13
9
5
4
14
9
13
9
5
4
4
5
,
1
3
5
,
1
...
5
,
1
3
5
,
1
3
5
,
1
...
5
,
1
3
v
v
v
v
v
v
v
v
v
[
]
=
−
−
−
⋅
+
4
4
4
4
4
3
4
4
4
4
4
2
1
B
v
v
v
6
9
4
7
9
5
,
1
...
5
,
1
5
,
1
3
(
)
+
+
+
−
+
−
=
4
4
4
8
2
1
8
)
2
8
(
)
2
16
(
v
v
a
i
a
i
(
)
[
]
B
v
v
v
v
v
A
+
⋅
−
+
+
+
+
+
4
4
4
4
4
4
4
3
4
4
4
4
4
4
4
2
1
14
10
14
10
5
4
4
5
,
1
3
5
,
1
...
5
,
1
3
1
(
)
( )
(
)
=
−
−
+
−
−
−
=
−
−
+
−
=
v
v
v
v
v
v
v
v
v
v
v
v
A
5
,
1
1
)
5
,
1
(
1
5
,
1
5
,
1
1
5
,
1
1
)
5
,
1
(
1
3
5
,
1
1
5
,
1
1
5
,
1
5
,
1
1
3
10
5
10
4
10
5
10
10
4
[
]
v
v
i
v
iv
d
v
v
v
v
v
v
v
v
v
v
5
,
1
1
)
5
,
1
(
1
3
1
)
2
2
(
5
,
1
1
)
5
,
1
(
1
5
,
1
)
5
,
1
1
(
2
5
,
1
1
)
5
,
1
(
1
5
,
1
10
5
10
4
10
4
−
−
=
=
=
−
=
−
−
−
=
+
−
−
−
=
[
]
[
]
=
+
−
−
−
−
−
⋅
=
−
−
−
−
=
7
6
7
6
6
5
2
7
6
4
6
5
2
5
7
4
5
,
1
5
,
1
5
,
1
...
5
,
1
5
,
1
2
5
,
1
5
,
1
...
5
,
1
5
,
1
3
5
,
1
v
v
v
v
v
v
v
v
v
v
B
(
)
[
]
(
)
=
+
+
+
−
⋅
=
+
+
−
⋅
=
6
6
7
7
4
6
6
7
6
4
5
,
1
...
5
,
1
1
2
1
5
,
1
5
,
1
2
5
,
1
...
1
5
,
1
3
5
,
1
v
v
v
v
v
v
v
=
−
−
+
−
−
=
−
−
−
+
−
=
⋅
=
=
v
v
v
v
v
v
v
v
5
,
1
1
)
5
,
1
(
1
2
1
)
5
,
1
(
1
1
8
81
5
,
1
1
)
5
,
1
(
1
2
1
5
,
1
1
1
8
81
2
5
,
1
8
81
7
7
7
7
7
4
(
)
−
−
−
=
+
−
−
−
−
=
v
v
vi
v
v
v
v
5
,
1
1
)
5
,
1
(
1
1
8
81
2
1
5
,
1
1
5
,
1
1
)
5
,
1
(
1
1
8
81
7
7
(
)
(
)
−
−
−
+
+
−
−
+
+
+
−
+
−
=
v
v
vi
v
v
v
iv
v
v
i
a
i
a
ODP
5
,
1
1
)
5
,
1
(
1
1
8
81
1
5
,
1
1
)
5
,
1
(
1
3
2
1
8
)
2
8
(
)
2
16
(
7
4
10
5
4
4
4
8

Zadanie 5
A – pierwsza rata
503
,
15444
1
06
,
0
06
,
1
73
,
6914
100000
100000
73
,
6914
8
9
9
8
≈
→
−
−
=
→
=
+
A
v
A
v
Aa
100000
)
17
(
...
)
(
)
(
100000
)
6
(
...
)
(
)
(
18
2
7
2
=
−
+
+
−
+
=
+
+
+
+
+
v
R
A
v
R
A
Av
b
v
R
A
v
R
A
Av
a
DYGRESJA:
2
9
8
8
2
8
6
2
8
7
3
2
8
4
3
7
3
2
)
1
(
6
6
1
6
1
1
6
...
)
1
(
6
...
2
6
...
2
v
v
v
v
v
v
v
v
v
v
X
v
v
v
v
v
X
v
v
v
Xv
v
v
v
X
−
+
−
−
=
−
−
−
−
=
→
−
+
+
+
=
−
+
+
+
=
+
+
+
=
2
20
19
19
2
19
17
2
19
18
3
2
19
4
3
18
3
2
)
1
(
17
17
1
17
1
1
17
...
)
1
(
17
...
2
17
...
2
v
v
v
v
v
v
v
v
v
v
Y
v
v
v
v
v
Y
v
v
v
Yv
v
v
v
Y
−
+
−
−
=
−
−
−
−
=
→
−
+
+
+
=
−
+
+
+
=
+
+
+
=
100000
)
(
100000
)
(
18
7
=
−
=
+
RY
Aa
b
RX
Aa
a
11
,
892
1
100000
)
(
7
≈
→
−
−
=
→
R
X
i
v
A
R
a
Y
i
v
A
R
b
100000
1
)
(
18
−
−
=
→
i wstawiamy R z (a) i sprawdzamy czy L=P
Równa się więc R=892,1 około
Zadanie 6
1
C
- cena obligacji zerokuponowej

10
2
10
2
2
10
2
2
1
07
,
1
60000
07
,
1
1
1
07
,
1
1
1
07
,
1
1
4000
07
,
1
1
1
07
,
1
1
1
07
,
1
1
3000
C
letniej
-
10
obligacji
cena
-
46250
)
075
,
0
1
(
50000
+
−
−
⋅
+
−
−
⋅
=
=
−
=
C
C
A – środki własne
(
)
2
1
3
,
0
C
C
A
+
=
(
)
2
1
7
,
0
C
C
kredyt
K
+
=
−
C(5) – cena obligacji 10-letniej po 5 latach
5
4
2
5
3
06
,
1
60000
06
,
1
1
06
,
1
1
3000
06
,
1
1
06
,
1
1
06
,
1
1
4000
)
5
(
+
+
+
+
+
=
C
K(7) – kredyt po 7 latach
(
)
7
2
1
06
,
1
7
,
0
)
7
(
C
C
K
+
=
F(7) – wartość funduszu po 7 latach
(
)
(
)
2
2
3
5
2
4
6
07
,
1
50000
07
,
1
)
5
(
07
,
1
07
,
1
4000
07
,
1
07
,
1
07
,
1
3000
)
7
(
⋅
+
⋅
+
+
+
+
+
=
C
F
%
7
,
4
100
1
)
7
(
)
7
(
7
1
≈
⋅
−
−
=
A
K
F
ODP
Zadanie 7
Bread spread oznacza, że kupujemy opcję z ceną wykonania X i wystawiamy opcję z ceną
wykonania Y i Y<X
Profil wypłaty:
[
)
(
)
(
) (
)
Y
S
X
S
Y
P
X
P
X
S
dla
Y
S
Y
P
X
P
X
Y
S
dla
Y
P
X
P
Y
S
gdy
C
C
C
C
C
C
−
−
−
+
−
≥
−
−
−
∈
−
<
8
8
8
8
8
8
)
(
)
(
)
(
)
(
,
)
(
)
(
Z powyższego i z obrazka widać, że:
Y=70, X=30
)
70
(
)
100
(
C
C
P
P
ODP
−
=
Parytet:
4
,
0
8
05
,
0
100
95
022
,
0
100
95
)
100
(
)
100
(
−
⋅
−
−
+
=
−
+
=
e
e
P
P
P
C
1
,
20
70
95
0124
,
0
100
95
022
,
0
70
95
)
70
(
)
70
(
4
,
0
4
,
0
8
05
,
0
−
≈
+
−
−
−
+
=
→
−
+
=
−
−
⋅
−
e
e
ODP
e
P
P
P
C
Zadanie 8
Pożyczamy 100 z krótkiej sprzedaży akcji, będziemy musieli zwrócić cenę akcji po 6
miesiącach – ile zarobimy?
Zysk arbitrażowy będzie jeżeli zawsze zarobimy więcej niż cena akcji po 6 miesiącach

Inwestujemy 100:
X – cena akcji po 6 miesiącach
a – tyle inwestujemy w aktywa wolne od ryzyka
b – tyle inwestujemy w opcje kupna
c- tyle inwestujemy w opcje sprzedaży
a+b+c=100 gdzie a nieujemne; b i c mogą być ujemne
(
)
(
)
X
X
c
X
b
ae
ZYSK
−
−
+
−
+
=
⋅
0
;
95
max
75
,
0
0
;
95
max
34
,
7
5
,
0
05
,
0
(a)X<95
X
X
c
ae
ZYSK
−
−
+
=
)
95
(
75
,
0
025
,
0
chcemy by ZYSK>0 i nzl od X
Czyli
75
,
0
0
1
75
,
0
−
=
→
=
−
−
c
c
(b)tak samo dla X>95
34
,
7
0
1
34
,
7
)
95
(
34
,
7
025
,
0
=
→
=
−
→
−
−
+
=
b
b
X
X
b
ae
ZYSK
Wtedy ZYSK(a)=ZYSK(b)=
95
025
,
0
−
ae
41
,
93
75
,
0
34
,
7
100
100
=
+
−
=
−
−
=
c
b
a
(
)
756
,
0
95
41
,
93
95
41
,
93
025
,
0
025
,
0
025
,
0
≈
−
=
−
=
−
−
e
e
e
ODP
Zadanie 9
Gdy
(
)
+
=
→
≅
2
2
2
1
exp
,
δ
δ
w
Ee
w
N
X
X
Przy braku arbitrażu:
( )
(
)
→
≅
=
=
=
=
−
−
−
16
,
0
;
0
4
,
0
bo
)
1
(
)
1
(
)
1
(
)
1
(
)
0
(
04
,
0
08
,
0
04
,
0
4
,
0
04
,
0
04
,
0
N
Z
e
A
e
e
A
e
E
A
e
ES
e
S
Z
Z
e
e
S
S
e
S
A
4
,
0
04
,
0
04
,
0
)
0
(
)
1
(
)
0
(
)
1
(
−
−
=
→
=
→
56
,
0
2
04
,
0
5
,
0
44
,
1
12
,
0
2
04
,
0
2
,
1
12
,
0
3
04
,
0
3
)
0
(
)
0
(
)
0
(
)
0
(
)
0
(
)
1
(
e
S
e
e
e
S
e
S
e
e
S
E
e
S
S
E
ODP
Z
=
=
=
=
−
⋅
−
−
−
−
Bo 1,2Z ma rozkład normalny ze średnia 0 i wariancją 1,44
Zadanie 10
05
,
0
1
=
r
(
)
05
,
1
1050
05
,
1
50
16
,
1009
1
1
16
,
1009
1
05
,
1
1050
05
,
1
50
2
2
−
=
=
+
→
=
+
+
y
r
r
x – narzut
16
,
973
)
)(
05
,
1
(
1070
05
,
1
70
=
+
+
+
+
x
y
x
x

)
)(
05
,
1
(
16
,
973
1070
)
(
70
x
y
x
x
y
+
+
=
+
+
1070
70
70
)
05
,
1
(
16
,
973
05
,
1
16
,
973
16
,
973
2
+
+
=
+
+
⋅
+
x
y
x
y
y
x
[
]
0
1070
70
05
,
1
16
,
973
70
)
05
,
1
(
16
,
937
16
,
973
1
,
80
6
,
1888
2
=
−
−
⋅
+
−
+
+
−
≈
≈
4
4
4
4
3
4
4
4
4
2
1
4
4
4
3
4
4
4
2
1
y
y
x
y
x
2
,
3878890
≈
∆
a
b
x
2
∆
+
−
=
→
bo drugi pierwiastek ujemny
%
4
%
15
,
4
≈
≈
→
x
Wyszukiwarka
Podobne podstrony:
2010.12.13 matematyka finansowa
2010 12 13 prawdopodobie stwo i statystykaid 27016
2003.12.06 matematyka finansowa
2010.05.31 matematyka finansowa
2000.12.09 matematyka finansowa
2010 03 15 matematyka finansowaid 26987
1 2010 05 31 matematyka finansowaid 8925
dodawanie (12-13), matematyka
2008.12.15 matematyka finansowa
2008 12 15 matematyka finansowaid 26464
2010.10.04 matematyka finansowa
2010.12.13 prawdopodobie stwo i statystyka
2005 12 05 matematyka finansowaid 25347
2010 10 04 matematyka finansowaid 27009
2007 12 03 matematyka finansowaid 25661
2010 12 13 prawdopodobie stwo i statystykaid 27016
więcej podobnych podstron