
Projekt ”Społeczeństwo wykształcone- największy kapitał współczesnego kraju” jest wspó
ł
finansowany ze środków
Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
KURS VI: Standard 2.1.
Po ukończeniu tego kursu będziesz znał:
I.
Treść standardu 2.1
Prawa i metody statyki stosowane do analizowania p
ł
askich i przestrzennych uk
ł
adów si
ł
I.
Treści kształcenia objęte standardem.
Po realizacji tego kursu powtórzysz wiadomo
ś
ci wymagane na egzaminie potwierdzaj
ą
cym kwalifikacje zawodowe z
zakresu:
-
Poj
ę
cie siły
-
Rodzaje sił
-
Rodzaje układów sił
-
Warunki równowagi dla płaskiego zbie
ż
nego układu sił
-
Moment siły wzgl
ę
dem punktu
-
Warunki równowagi dla płaskiego dowolnego układu sił
Siła jako wektor
Siła
to mechaniczne
oddziaływanie
jednego ciała na
drugie
....
Kierunek
(linia
działania)
zwrot
Punkt
przyło
ż
enia
Warto
ść
(moduł)
Cechy siły:
Nacisk stołu na r
ę
k
ę
.
Nacisk r
ę
ki na stół.
F
SIŁA I JEJ
WŁA
Ś
CIWO
Ś
CI
SIŁA I JEJ
WŁA
Ś
CIWO
Ś
CI

Jednostka warto
ś
ci siły
W układzie SI warto
ść
siły wyra
ż
ana jest w
niutonach
(symbol
N
).
2
1
1
1
s
m
kg
N
⋅
=
Jeden niuton to warto
ść
siły, która masie jednego kilograma
nadaje przy
ś
pieszenie jednego metra na sekund
ę
do kwadratu.
Pochodne jednostki:
kiloniuton
meganiuton
N
kN
3
10
1
1
⋅
=
N
MN
6
10
1
1
⋅
=
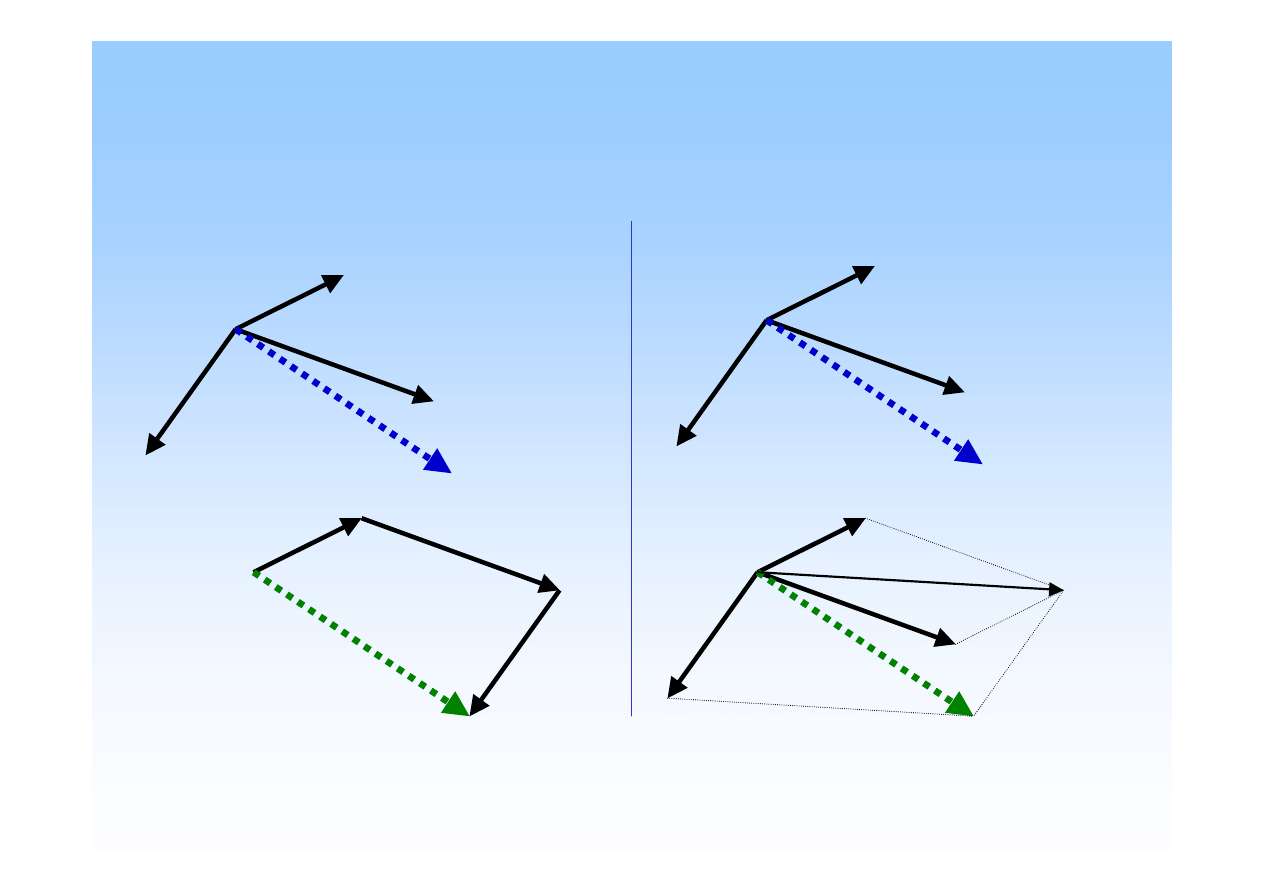
Składanie sił.
Wielobok sił:
Równoległobok sił:
O
F
1
F
2
F
3
F
1
F
2
F
3
S
R
R
- wypadkowa układu sił, która zast
ę
puje działanie tego układu.
S
- suma układu sił
O
F
1
F
2
F
3
R
F
1
F
2
F
3
S
F
12
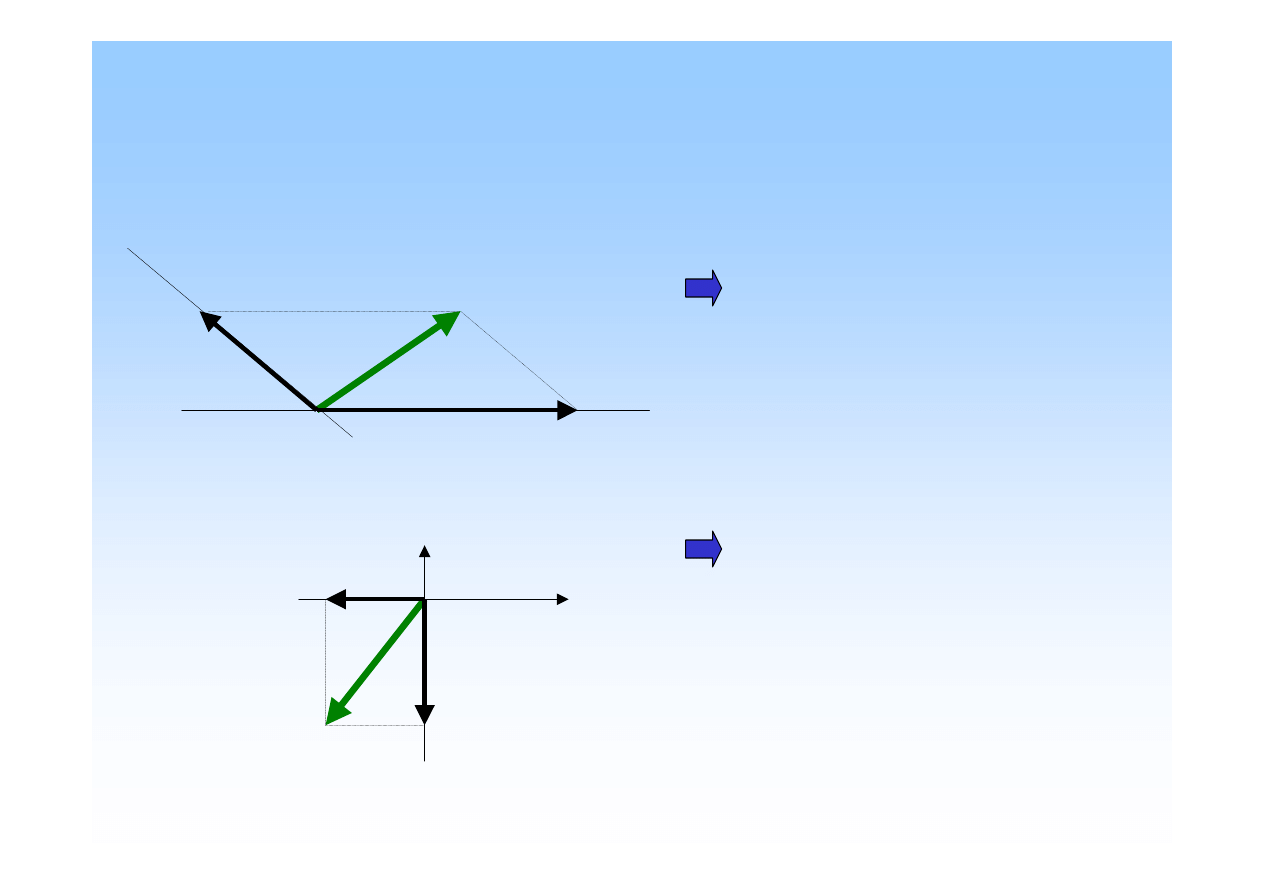
Rozkład siły na składowe
...o kierunkach prostych l, m
m
l
F
F
m
F
l
F
l
, F
m
-
składowe siły
F
na
zadanych kierunkach l, m.
...o kierunkach osi x, y
y
x
F
F
x
F
y
F
x
, F
y
-
składowe siły
F
na
osiach x, y.
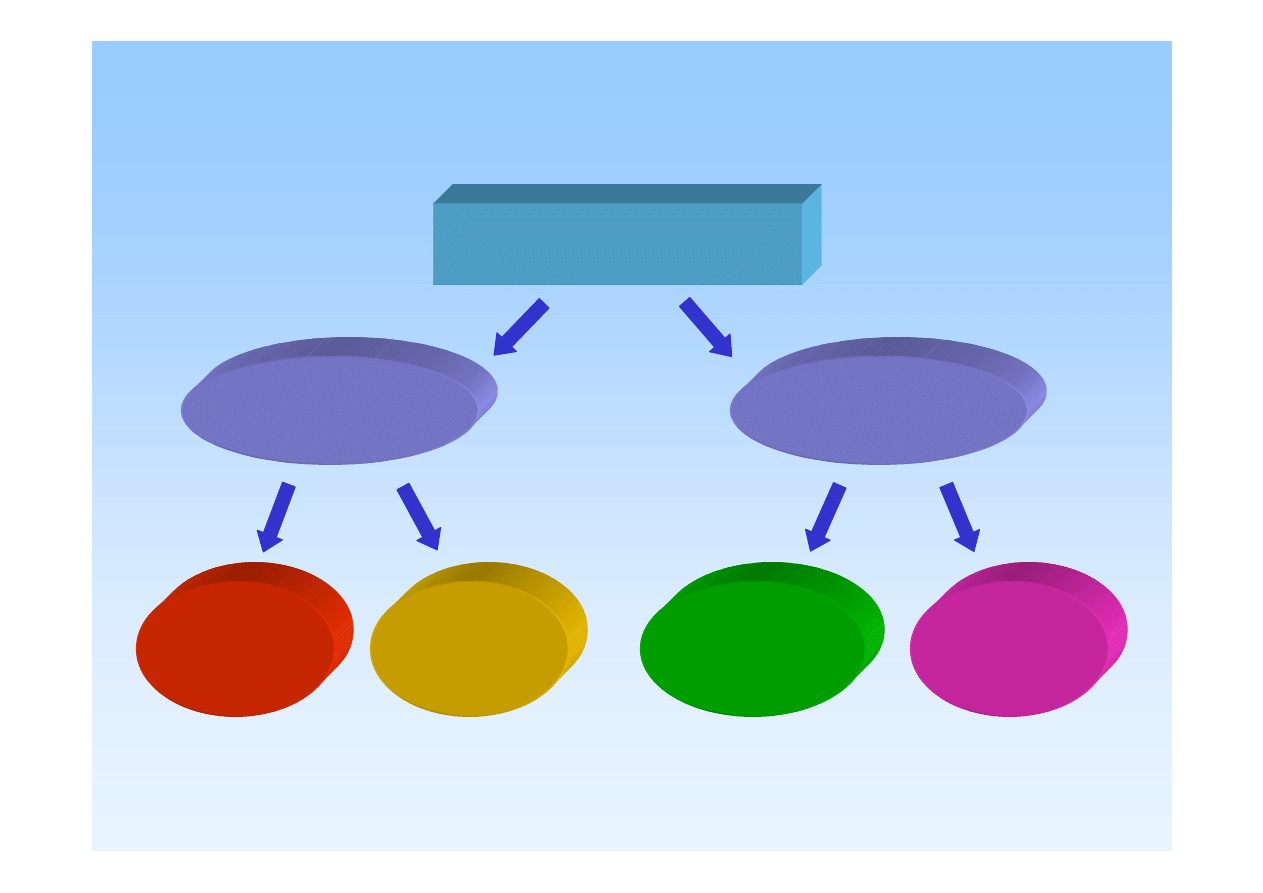
Podział sił
SIŁY MECHANICZNE
WEWN
Ę
TRZNE
ZEWN
Ę
TRZNE
CZYNNE
REAKCJE
MI
Ę
DZY
CZ
Ą
STE
CZKOWE
NAPI
Ę
CIA
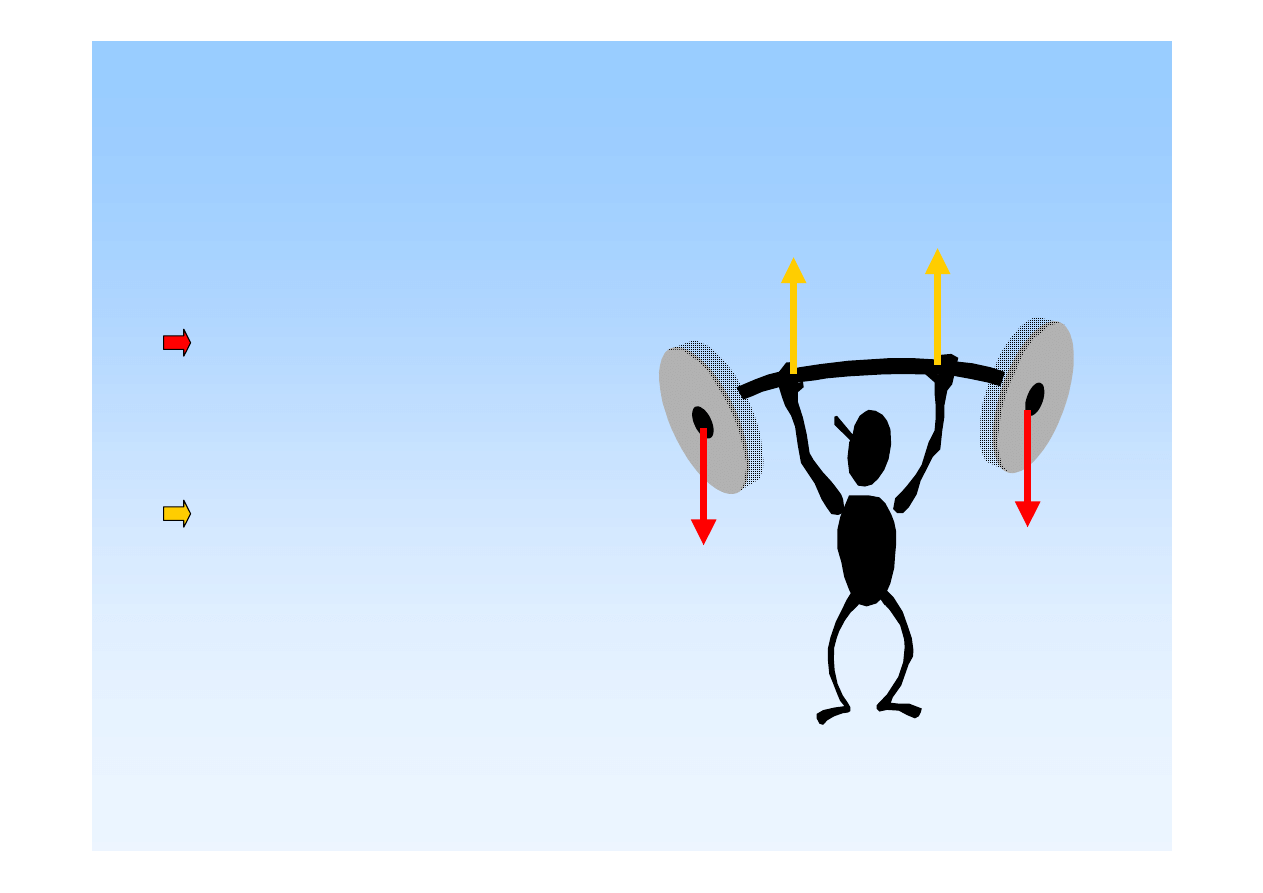
Siły zewn
ę
trzne
Siły te
s
ą
wynikiem działania ciał znajduj
ą
cych si
ę
na zewn
ą
trz
danej bryły (ciała).
Siły czynne d
ążą
do
wywołania ruchu lub jego
zmiany.
Siły reakcji (bierne)
przeciwdziałaj
ą
ruchowi i
wyst
ę
puj
ą
w miejscu podparcia
ciała w chwili przyło
ż
enia sił
czynnych oraz znikaj
ą
po
odci
ąż
eniu ciała.
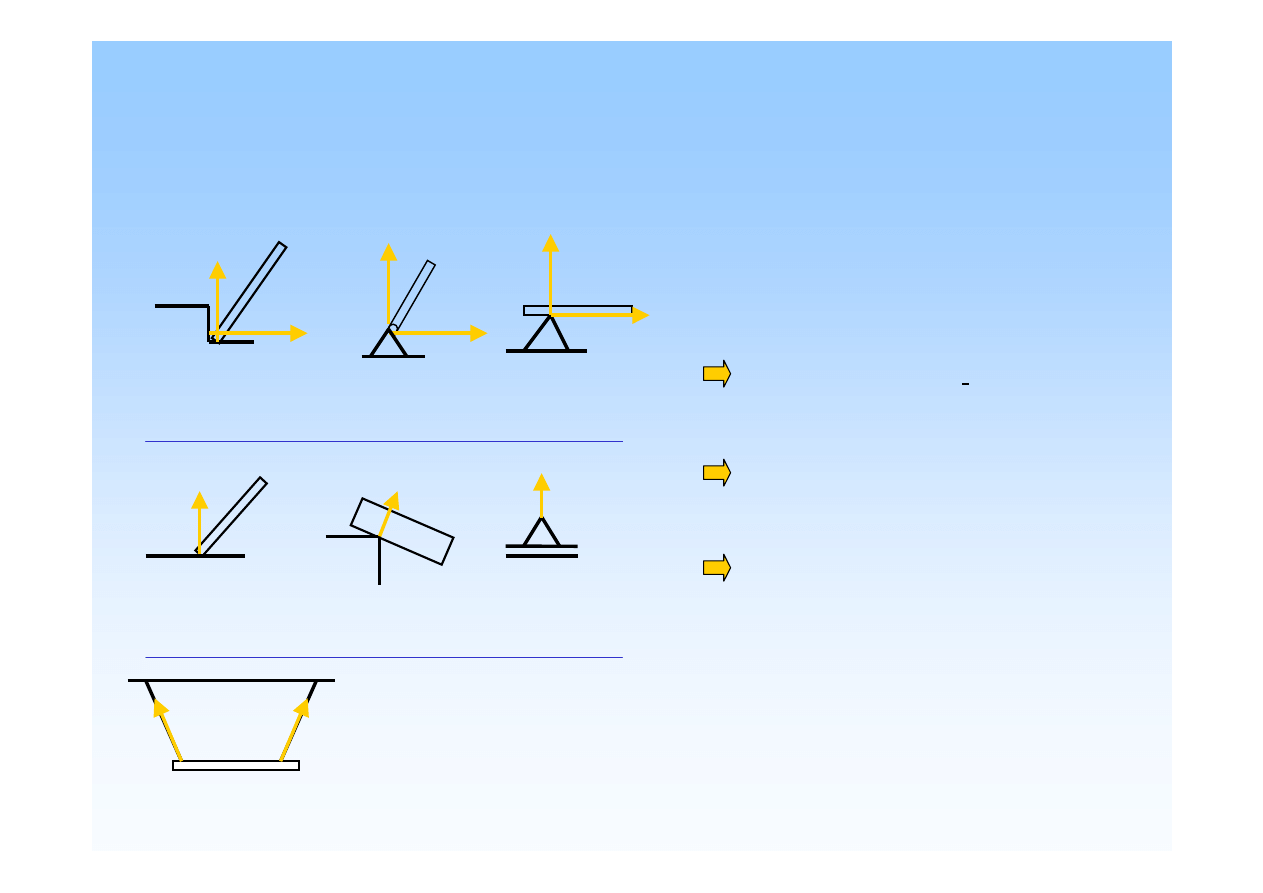
Reakcje
Siły zewn
ę
trzne bierne - ich cechy zale
żą
od rodzaju podpory.
Cechy reakcji
:
punkt przyło
ż
enia
- w punkcie
podparcia
kierunek:
w stałych podporach nieznany,
wprowadza si
ę
reakcje składowe
R
x
i R
y
w ruchomych podporach
prostopadły do powierzchni
podpieraj
ą
cej
w wiotkich podporach wzdłu
ż
osi
podpory
warto
ść
- otrzymana z oblicze
ń
zwrot
- na schemacie przyj
ę
ty
dowolnie, ostatecznie potwierdzony
obliczeniami warto
ś
ci.
uskok
przegub
ło
ż
ysko
stałe
Podpory:
stałe
ruchome
powierzchnia
gładka
ostrze,
pryzma
ło
ż
ysko
ruchome
wiotkie
sznury, liny, ła
ń
cuchy, pr
ę
ty.
R
y
R
x
R
y
R
y
R
x
R
x
R
R
R
R
1
R
2
Sił wewn
ę
trzne
Siły te
wyst
ę
puj
ą
wewn
ą
trz ciała.
Siły mi
ę
dzycz
ą
steczkowe
s
ą
siłami wzajemnego
oddziaływania cz
ą
steczek
powoduj
ą
cymi odpowiednie
fizyko-mechaniczne
wła
ś
ciwo
ś
ci materiału ciała.
Siły napi
ę
cia powstaj
ą
wewn
ą
trz ciała na skutek
działania sił zewn
ę
trznych,
wyst
ę
puj
ą
parami i wzajemnie
równowa
żą
si
ę
.
zewn
ę
trzna
czynna
zewn
ę
trzna
bierna
(reakcja)
Układ sił
Układ sił to zbiór sił czynnych i biernych (reakcji) działaj
ą
cych
jednocze
ś
nie na ciało oswobodzone
.
Oswobodzi
ć
ciało
tzn.
usun
ąć
podpory (wi
ę
zy), a w ich miejsce
wprowadzi
ć
reakcje.
Q
A
B
Ciało nieswobodne.
Q
A
B
R
A
R
B
Ciało oswobodzone.
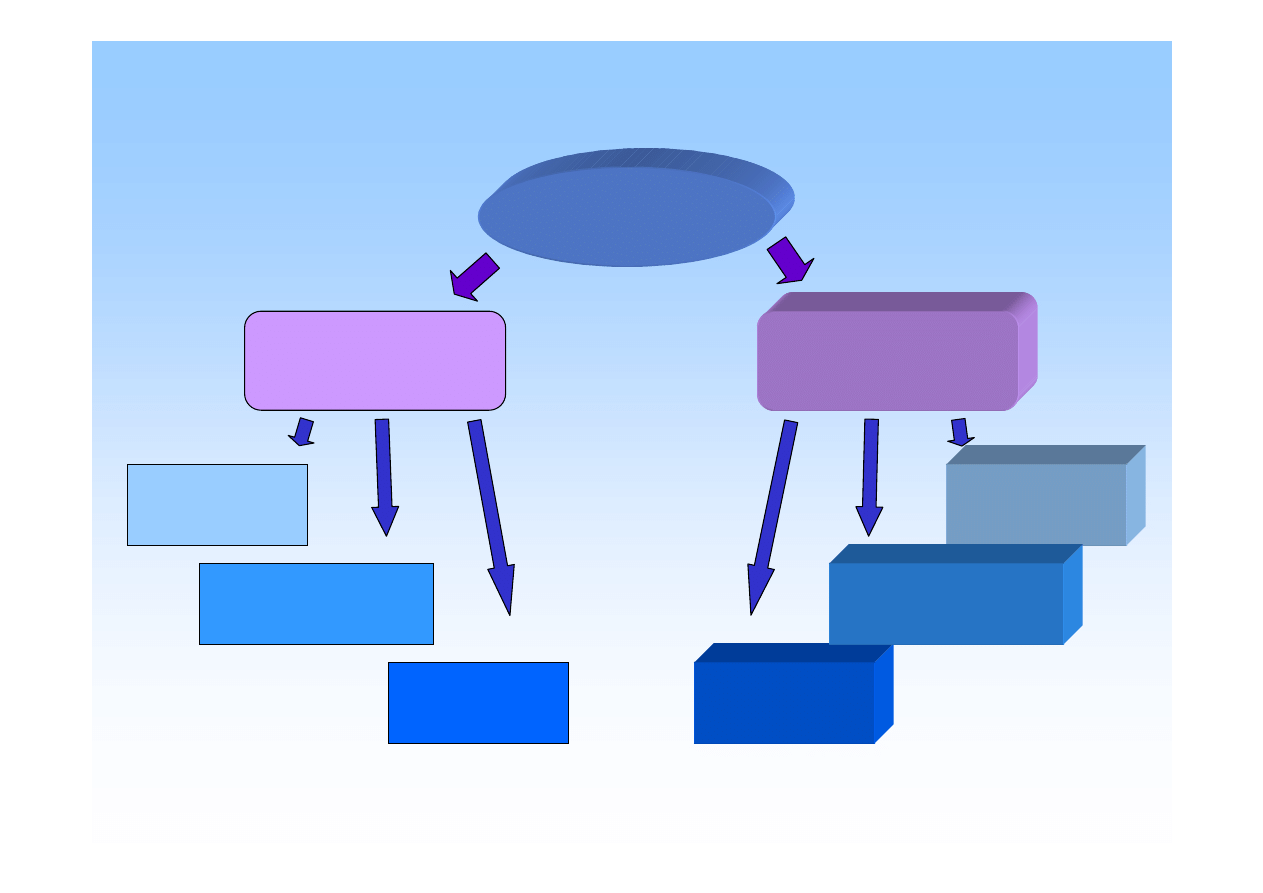
Podział układów sił.
UKŁADY SIŁ
PŁASKIE
PRZESTRZENNE
ZBIE
ś
NE
RÓWNOLEGŁE
DOWOLNE
DOWOLNE
ZBIE
ś
NE
RÓWNOLEGŁE
Płaskie układy sił.
A
C
B
Q
R
C
R
A
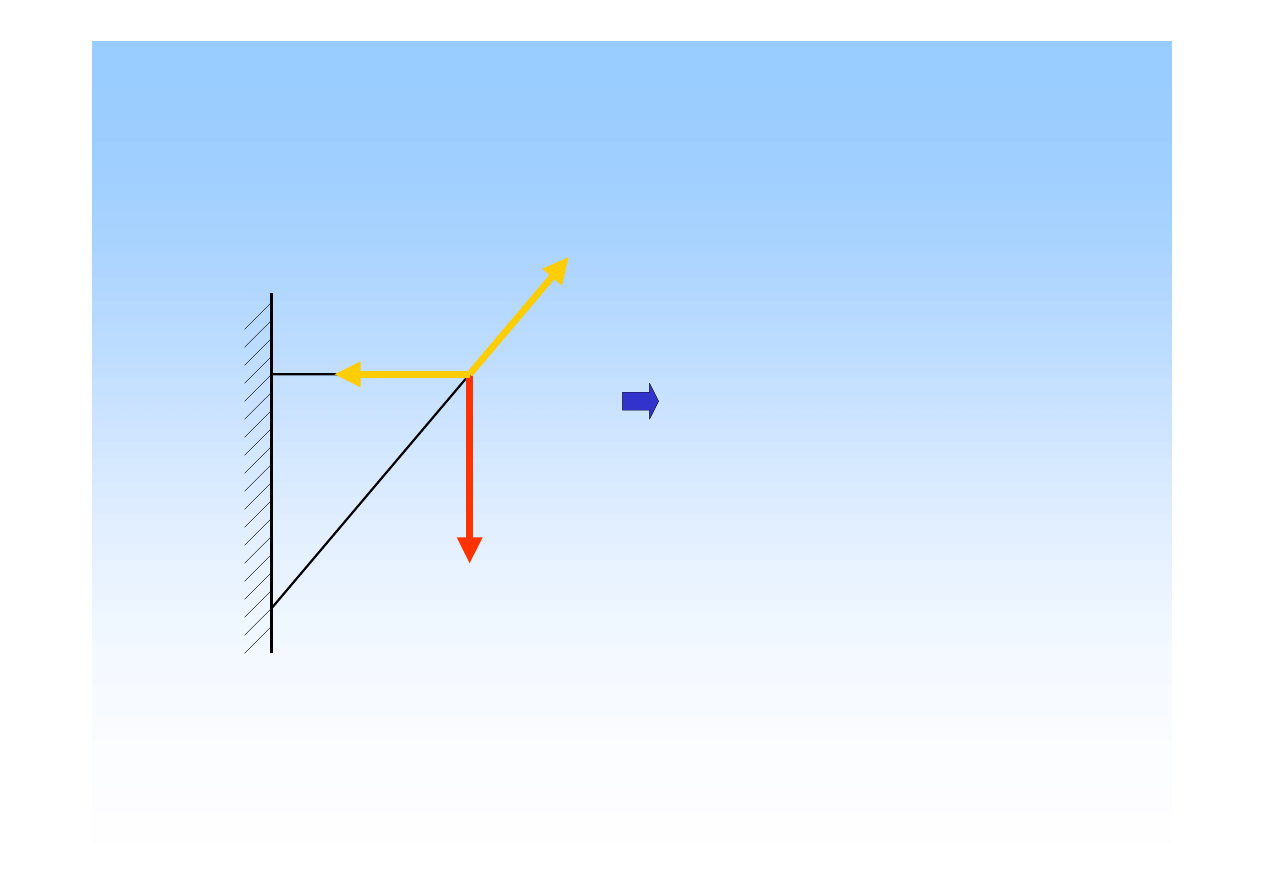
Zbie
ż
ny układ sił
-
zbiór
sił (w jednej płaszczy
ź
nie),
których kierunki przecinaj
ą
si
ę
w jednym punkcie (punkcie
zbie
ż
no
ś
ci).
A
B
F
1
F
2
F
3
R
A
R
B
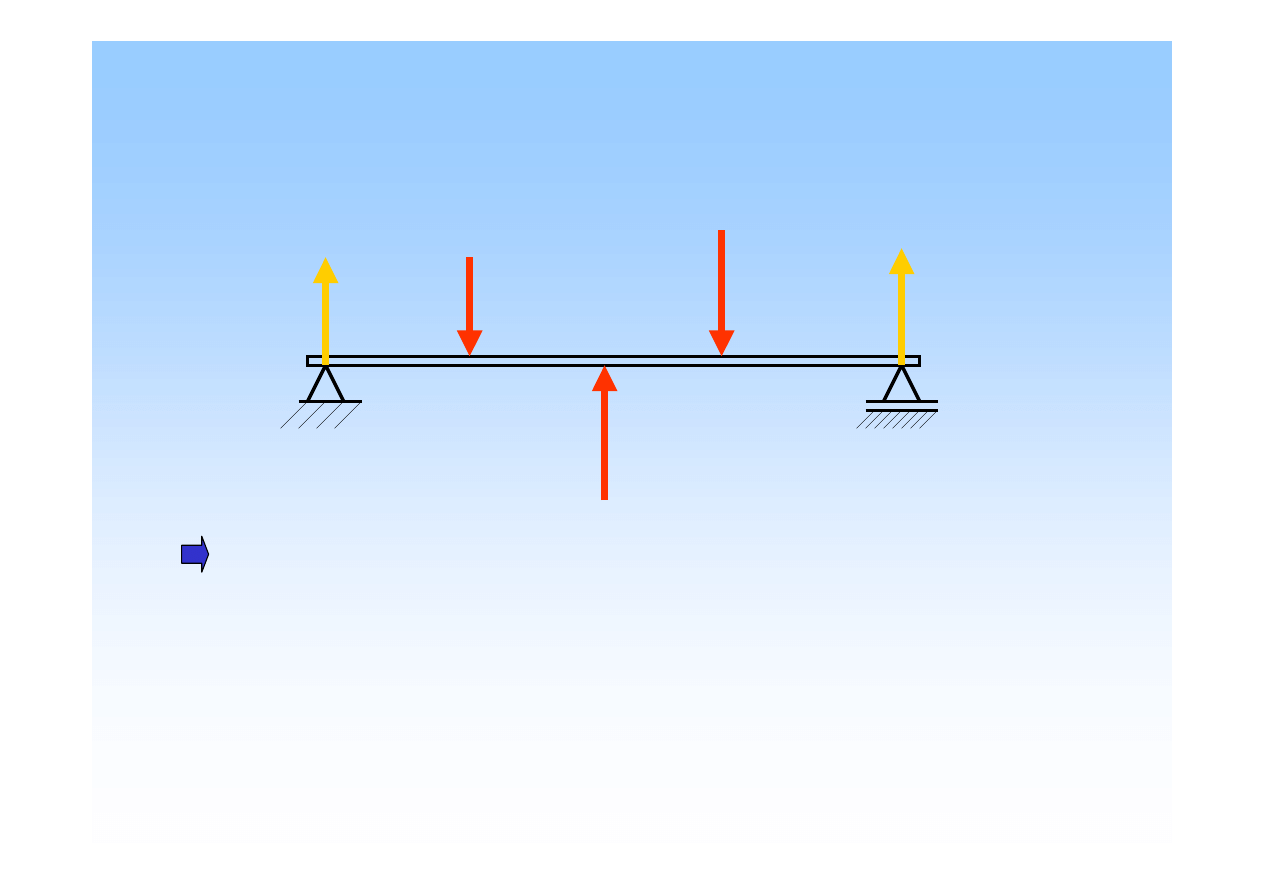
Równoległy układ sił
- zbiór sił (w jednej płaszczy
ź
nie),
których linie działania s
ą
do siebie równoległe, b
ą
d
ź
tworz
ą
jedn
ą
prost
ą
.
Płaskie układy sił.
Płaskie układy sił.
A
B
F
1
F
2
F
3
R
A
R
B
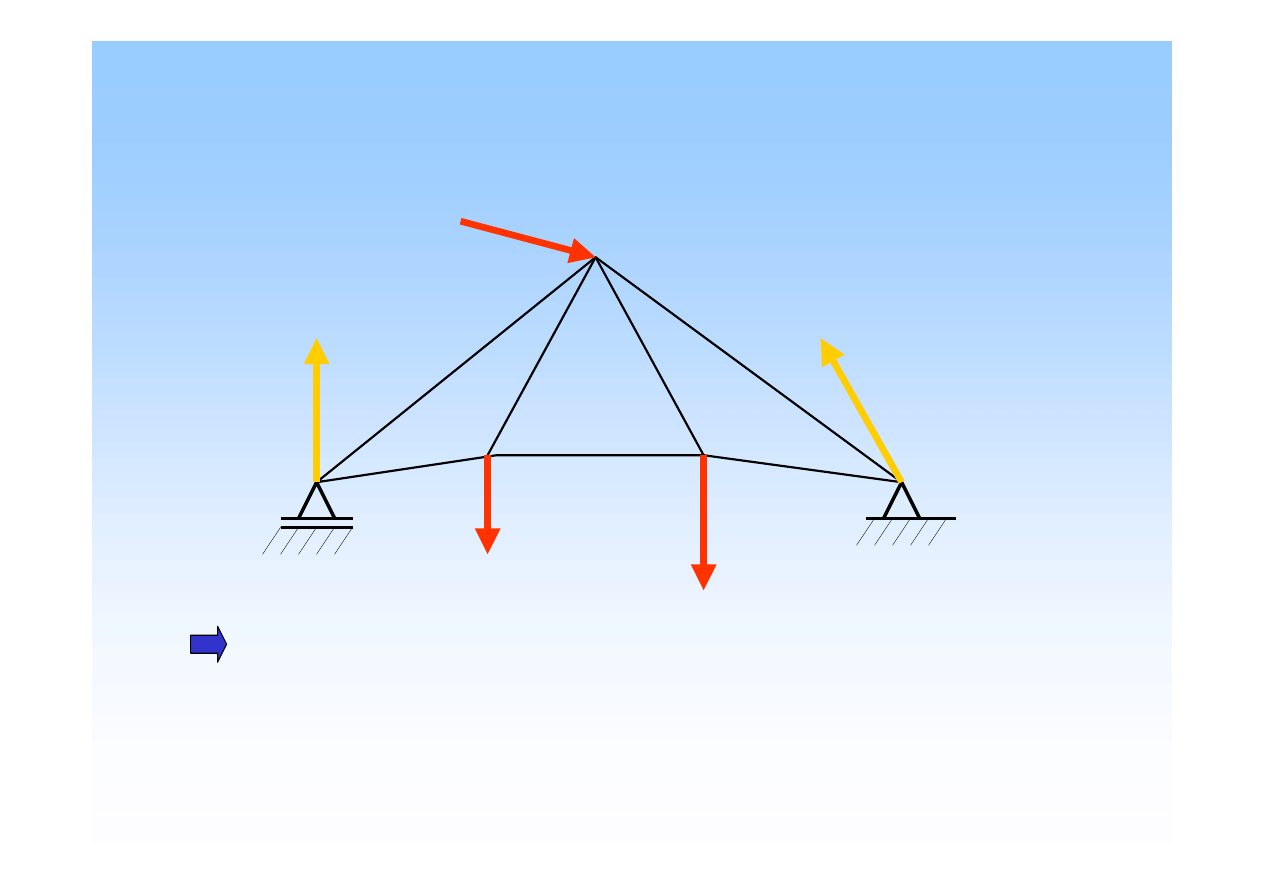
Dowolny układ sił
- zbiór sił (w jednej płaszczy
ź
nie) o
ró
ż
nych kierunkach działania.
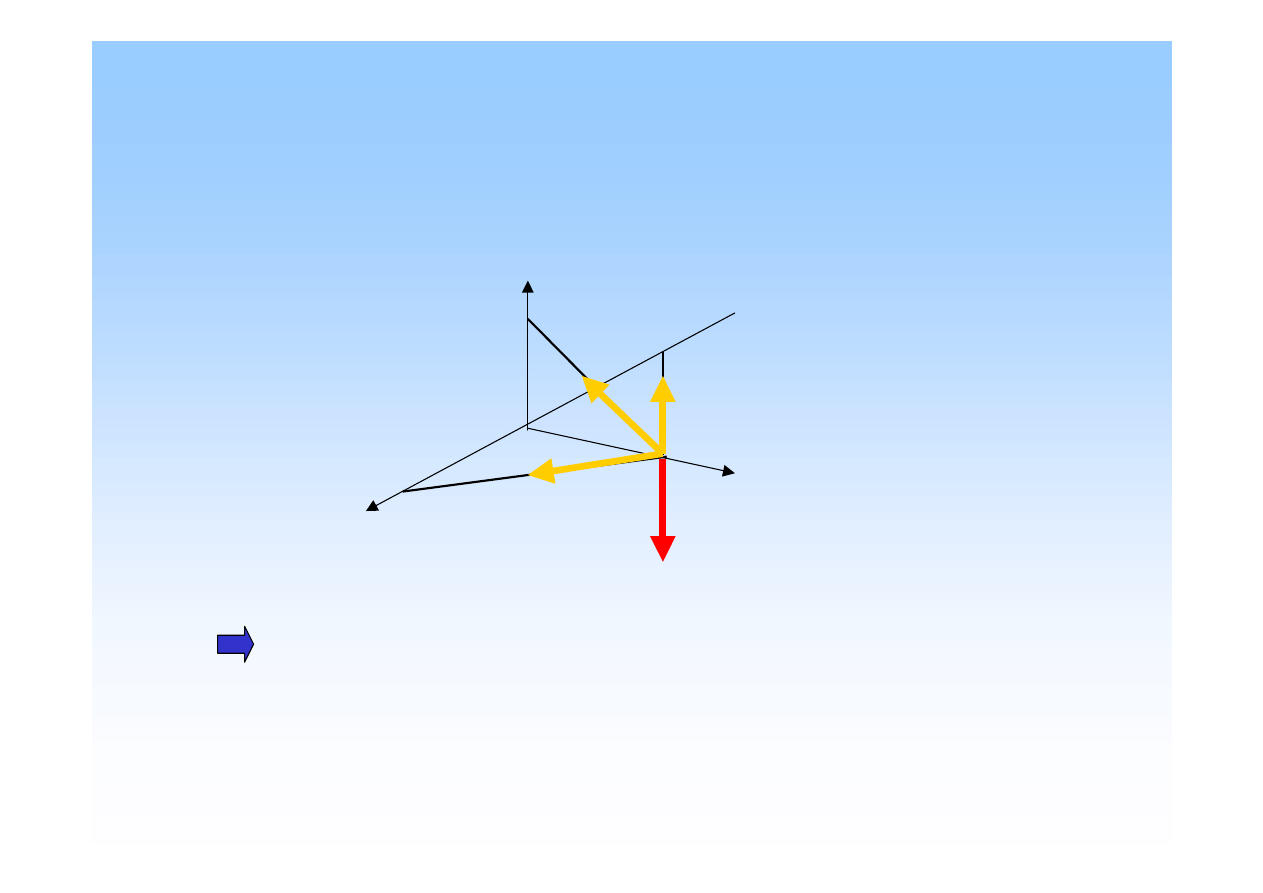
Przestrzenne układy sił.
Układ sił, których linie działania nie le
żą
w jednej płaszczy
ź
nie, lecz
s
ą
rozmieszczone w przestrzeni, nazywamy przestrzennym.
z
y
x
Q
R
1
R
2
R
3
Zbie
ż
ny układ sił
-
kierunki działania sił przecinaj
ą
si
ę
w
jednym punkcie (punkcie zbie
ż
no
ś
ci).
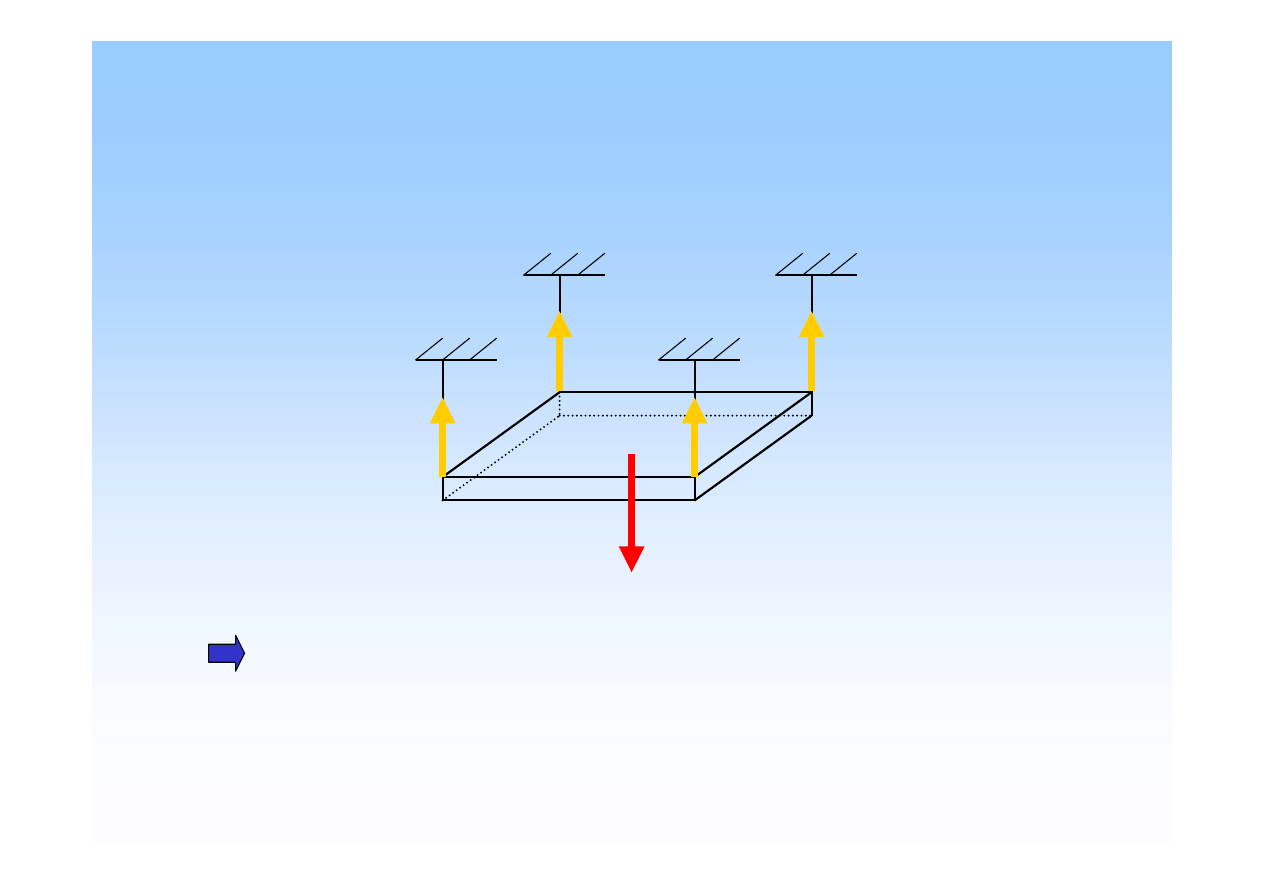
Przestrzenne układy sił.
Układ sił, których linie działania nie le
żą
w jednej płaszczy
ź
nie, lecz
s
ą
rozmieszczone w przestrzeni, nazywamy przestrzennym.
R
1
R
2
R
3
R
4
Q
Równoległy układ sił
-
kierunki działania sił s
ą
do siebie
równoległe.
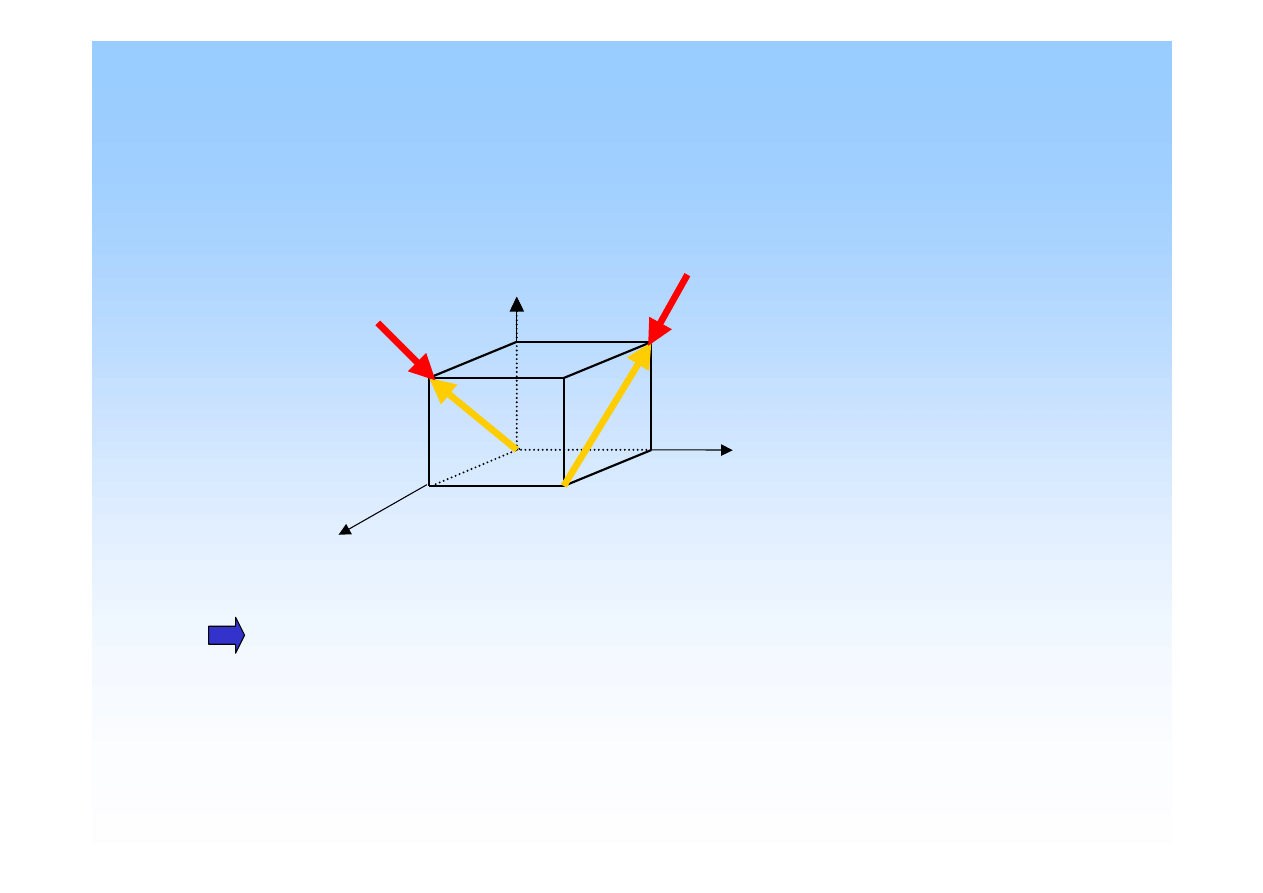
Przestrzenne układy sił.
Układ sił, których linie działania nie le
żą
w jednej płaszczy
ź
nie, lecz
s
ą
rozmieszczone w przestrzeni, nazywamy przestrzennym.
z
y
x
Q
1
Q
2
R
1
R
2
Dowolny układ sił
-
kierunki działania sił s
ą
dowolnie
rozmieszczone w przestrzeni.
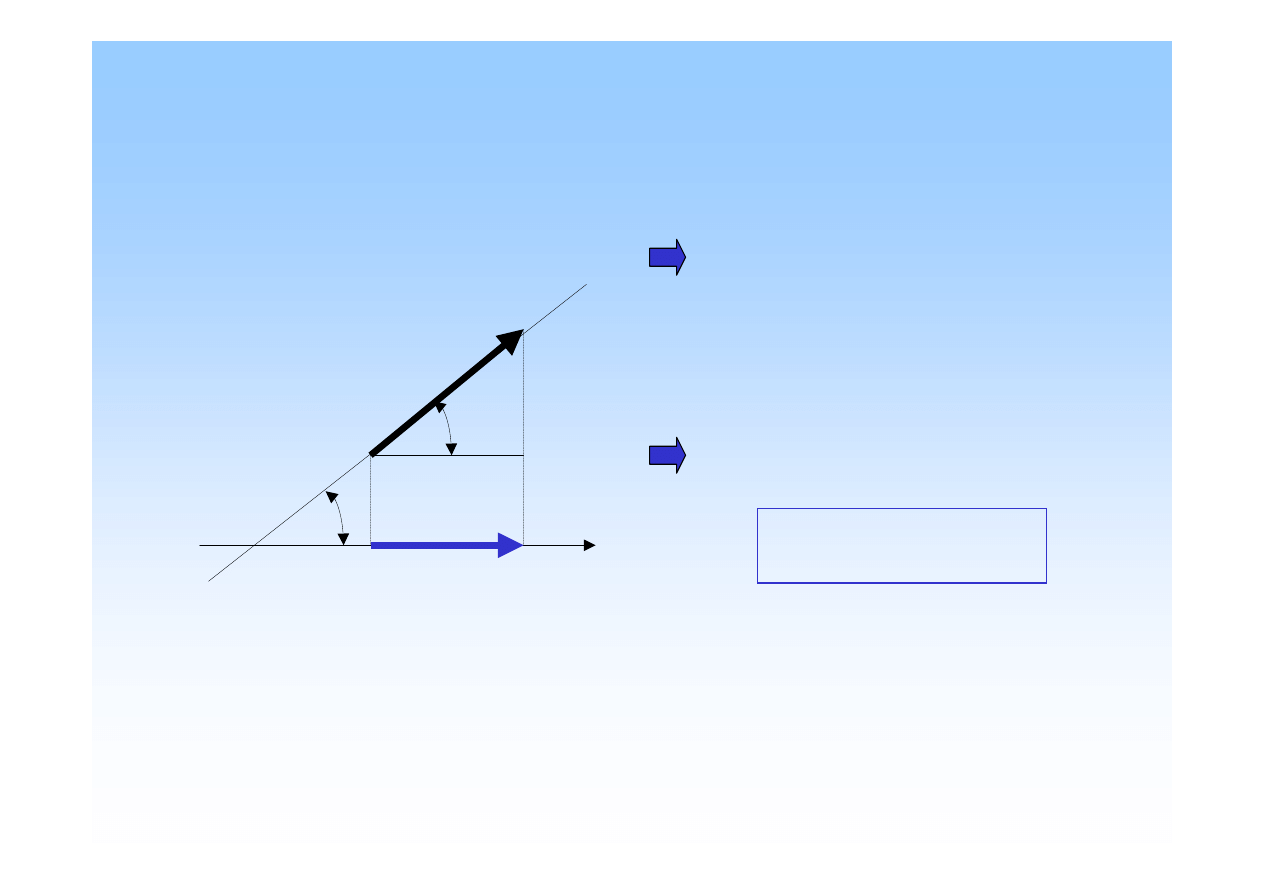
Rzut siły na o
ś
.
m
F
F
m
α
α
Rzutem siły na o
ś
m
(F
m
)
nazywamy wektor
ł
ą
cz
ą
cy rzut pocz
ą
tku z rzutem
ko
ń
ca wektora danej siły na t
ę
o
ś
.
α
cos
⋅
=
F
F
m
Warto
ść
F
m
:
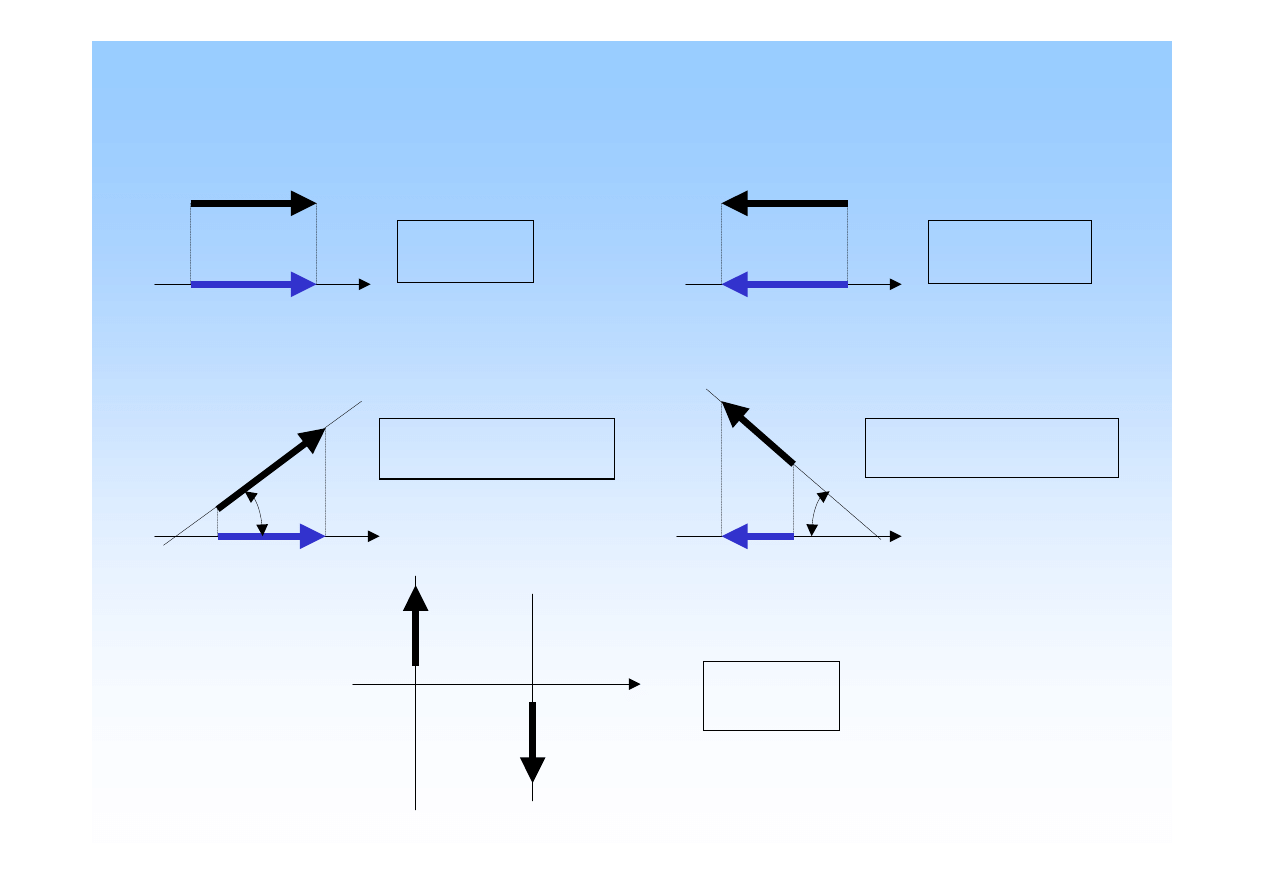
Szczególne przypadki rzutów siły na o
ś
.
m
F
F
m
F
F
m
=
m
F
F
m
F
F
m
−
=
α
cos
⋅
=
F
F
m
m
F
F
m
α
F
m
m
α
F
F
m
α
cos
⋅
−
=
F
F
m
m
F
F
0
=
m
F
uwzgl
ę
dniaj
ą
c znaki (+,-)
rzutów
F
x
i
F
y
okre
ś
la si
ę
,
w stron
ę
której
ć
wiartki
układu x,y zwrócona jest
siła
F
.
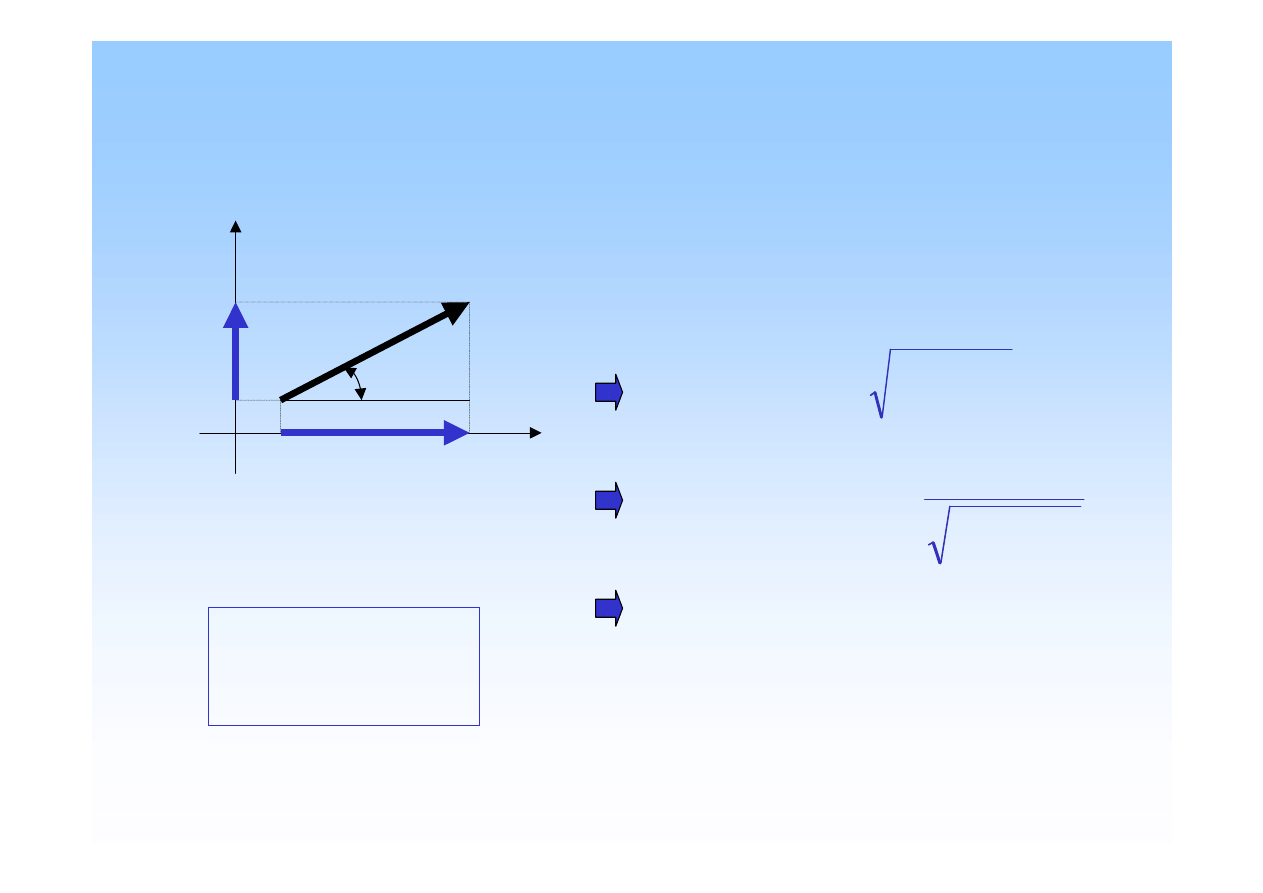
Rzut siły na osie x, y.
O
F
F
x
X
Y
F
y
α
Warto
ść
rzutów siły
F
na osie x i y:
α
α
sin
cos
⋅
=
⋅
=
F
F
F
F
y
x
Rzuty siły F na osie x i y okre
ś
laj
ą
jednoznacznie jej:
warto
ść
:
kierunek:
zwrot:
2
2
y
x
F
F
F
+
=
2
2
cos
y
x
x
F
F
F
+
=
α
Twierdzenie o sumie rzutów sił.
X
Układ sił
F
1
F
2
F
3
F
4
S
Suma rzutów dowolnej liczby sił na o
ś
jest równa rzutowi
sumy tych sił na t
ę
sam
ą
o
ś
.
ny
y
y
y
y
nx
x
x
x
x
F
F
F
F
S
F
F
F
F
S
+
+
+
+
=
+
+
+
+
=
K
K
3
2
1
3
2
1
X
O
F
1
F
2
F
3
Y
F
4
S
F
1x
F
2x
F
3x
F
4x
S
x
F
1y
F
2y
F
3y
F
4y
S
y

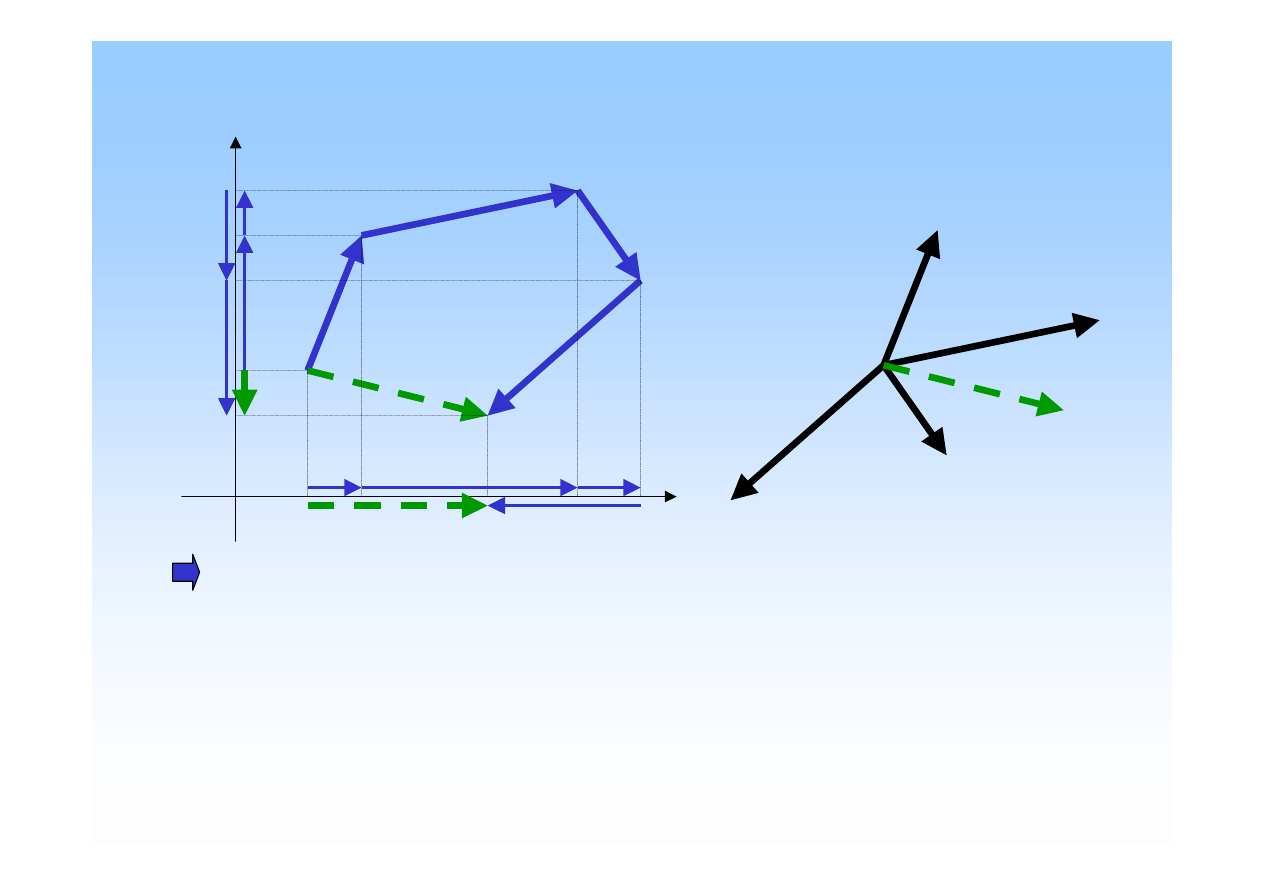
Wypadkowa płaskiego zbie
ż
nego
układu sił.
Istniej
ą
dwie metody wyznaczania wypadkowej płaskiego
zbie
ż
nego układu sił:
metoda analityczna
metoda wykre
ś
lna
W metodzie wykre
ś
lnej mo
ż
na posłu
ż
y
ć
si
ę
wielobokiem
lub
równoległobokiem sił.
Oba sposoby zostały przedstawione na
slajdzie „Składanie sił” w dziale „Siła i jej własno
ś
ci”.
Składanie sił.
Wielobok sił:
Równoległobok sił:
O
F
1
F
2
F
3
F
1
F
2
F
3
S
R
S
- suma układu sił
R
- wypadkowa układu sił, która zast
ę
puje działanie tego układu.
O
F
1
F
2
F
3
R
F
1
F
2
F
3
S
F
12
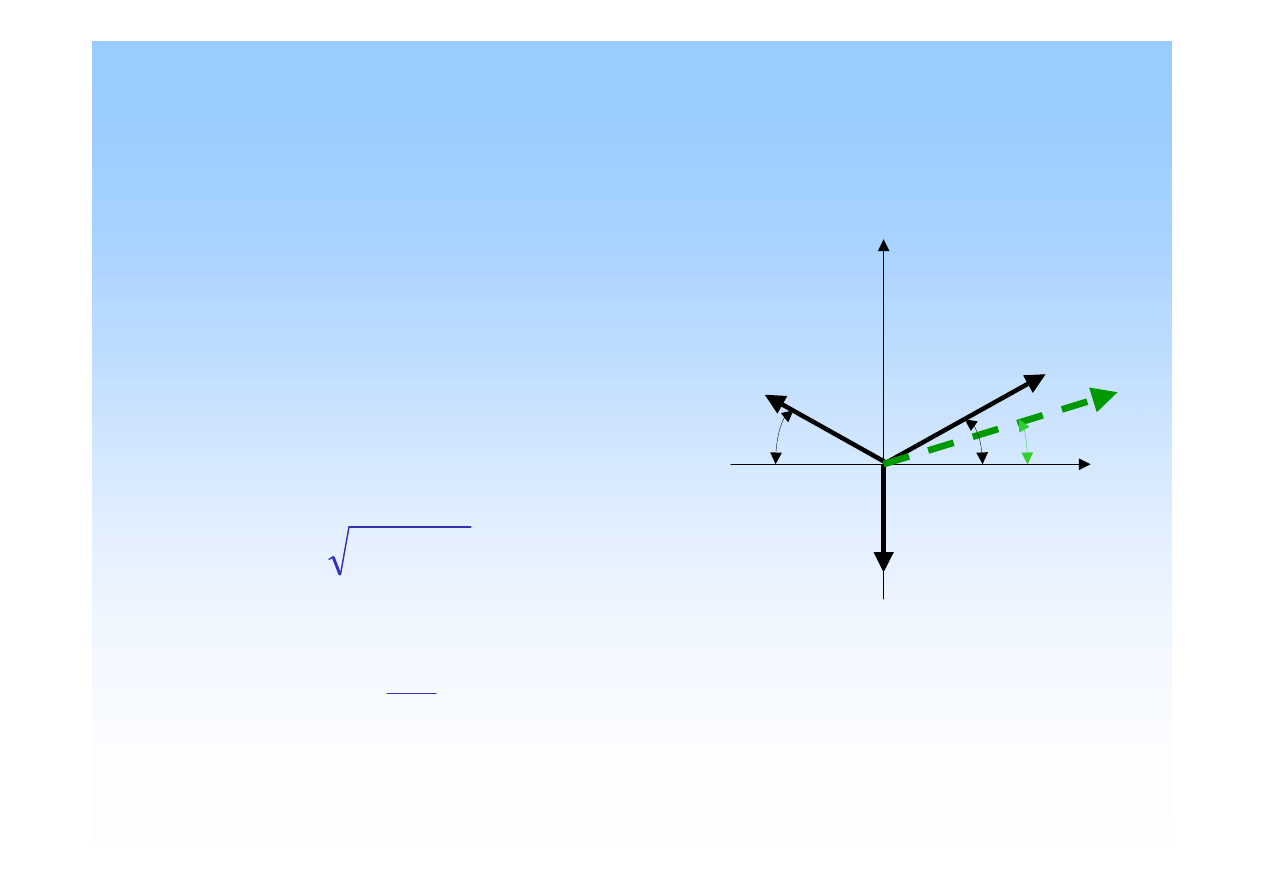
Analityczna metoda
wyznaczania wypadkowej płaskiego zbie
ż
nego
układu sił.
X
F
1
F
2
O
Y
F
3
Kolejno
ść
działa
ń
:
przez punkt zbie
ż
no
ś
ci O poprowadzi
ć
osie x,y
obliczy
ć
warto
ść
rzutów wypadkowej
na osie x,y
obliczy
ć
warto
ść
wypadkowej
R
okre
ś
li
ć
kierunek wypadkowej
R, odczytuj
ą
c z
tablic warto
ść
k
ą
ta
okre
ś
li
ć
zwrot wypadkowej
R według znaków jej
rzutów R
x
i R
y.
3
2
2
1
1
2
2
1
1
sin
sin
cos
cos
F
F
F
R
F
F
R
Y
X
−
⋅
+
⋅
=
⋅
−
⋅
=
α
α
α
α
2
2
Y
X
R
R
R
+
=
α
R
R
X
=
α
cos
R
α
1
α
2
α
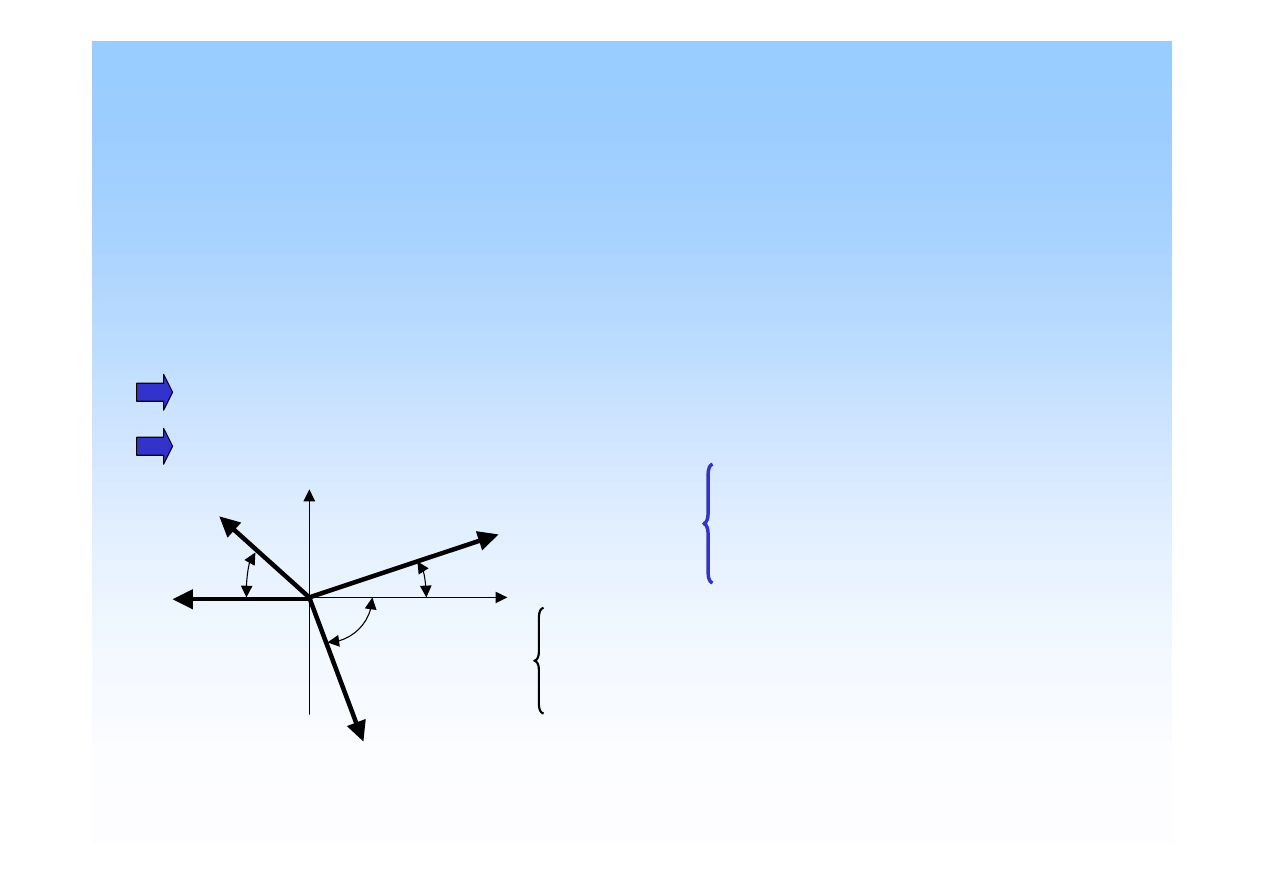
Analityczne warunki równowagi
płaskiego zbie
ż
nego układu sił.
Płaski zbie
ż
ny układ sił jest w równowadze, je
ż
eli punkt materialny
b
ę
d
ą
cy pod jego działaniem pozostaje w spoczynku tzn.
wypadkowa R tego układu ma warto
ść
0.
R
X
= 0
R
Y
= 0
Suma algebraiczna rzutów wszystkich sił na o
ś
x jest równa zeru.
Suma algebraiczna rzutów wszystkich sił na o
ś
y jest równa zeru.
0
sin
sin
sin
0
cos
cos
cos
3
3
2
2
1
1
4
3
3
2
2
1
1
=
⋅
−
⋅
+
⋅
=
−
⋅
+
⋅
+
⋅
−
α
α
α
α
α
α
F
F
F
F
F
F
F
Y
X
O
F
1
F
2
F
3
F
4
1
α
2
α
3
α
Zrównowa
ż
ony
układ sił.
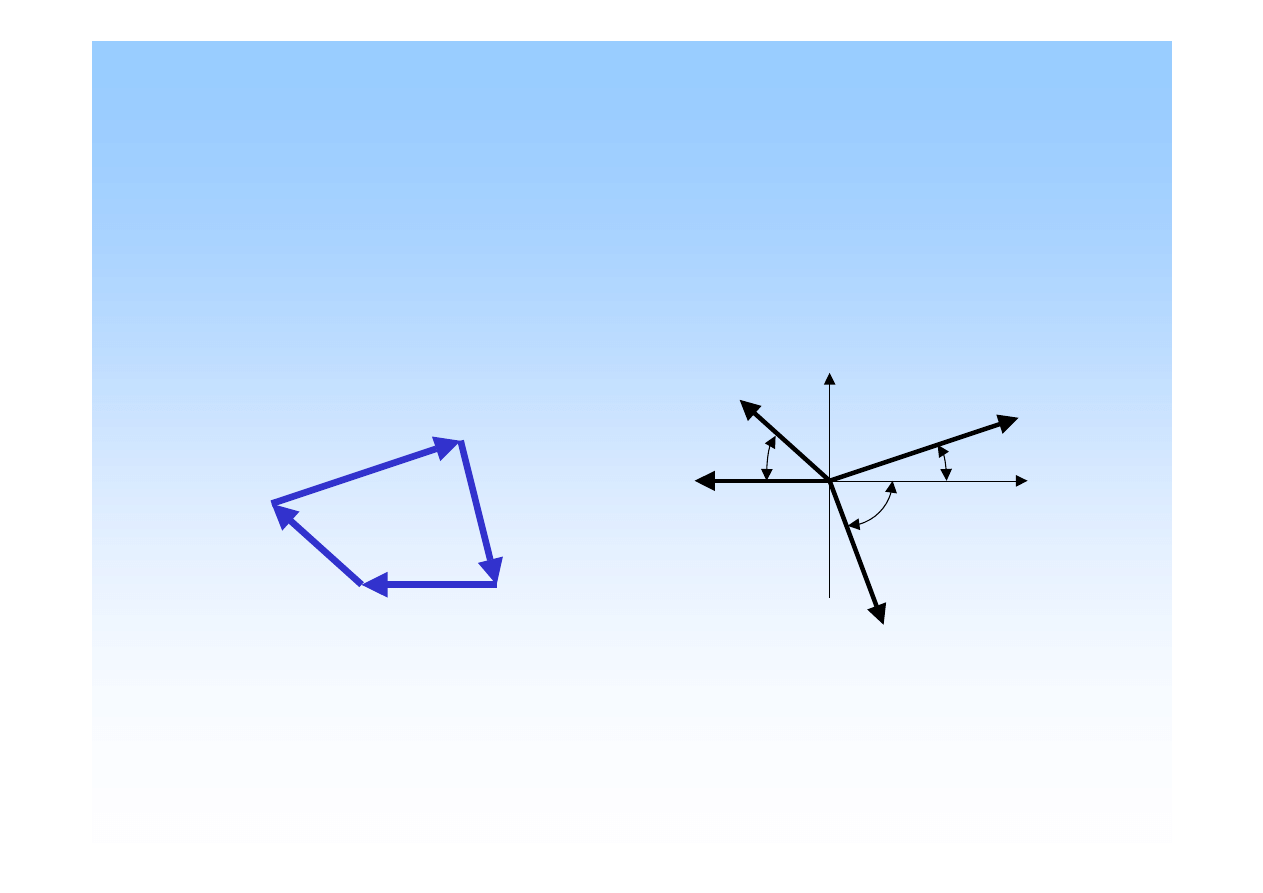
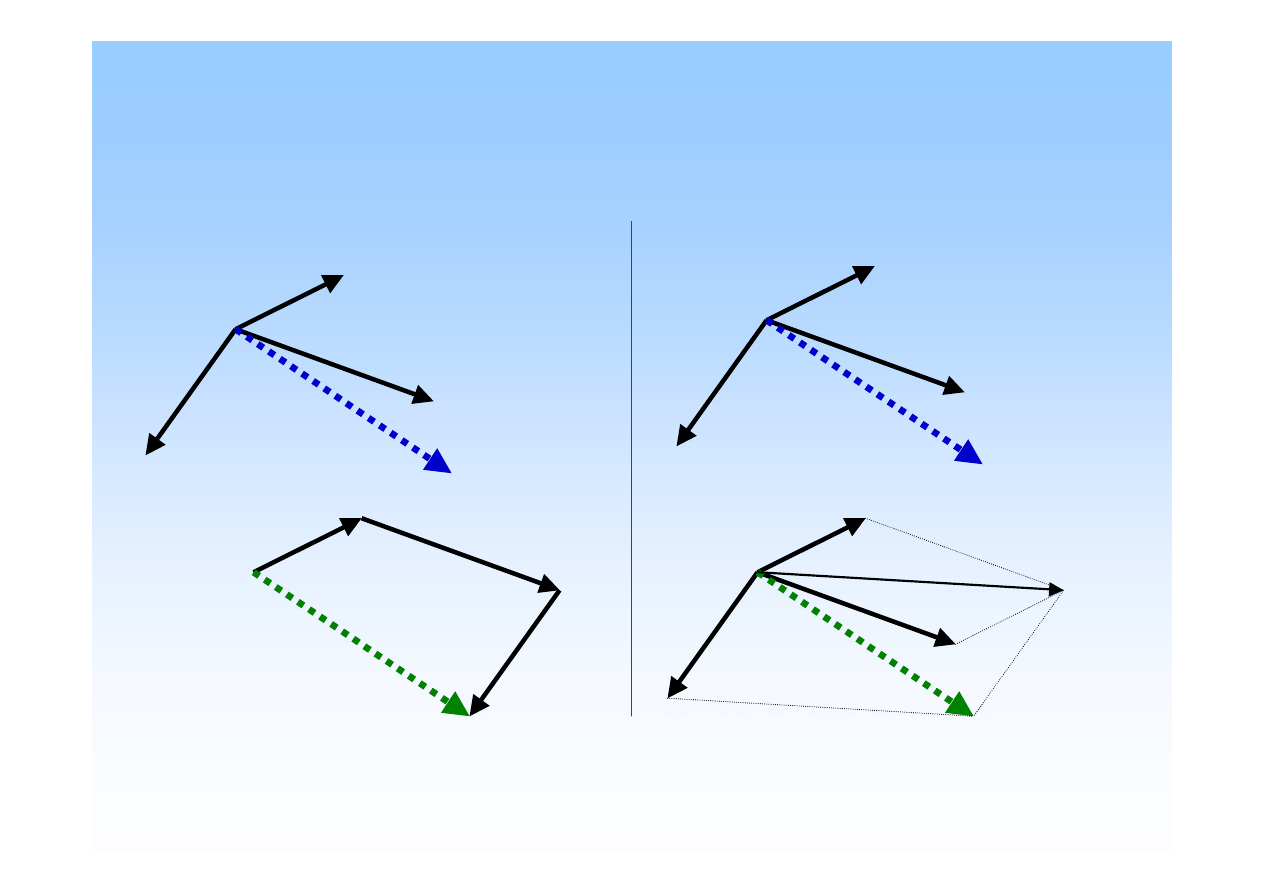
Wykre
ś
lny warunek równowagi
płaskiego zbie
ż
nego układu sił.
Płaski zbie
ż
ny układ sił jest w równowadze, je
ż
eli
wielobok sił tego układu jest zamkni
ę
ty
.
Zamkni
ę
ty
wielobok sił.
F
1
F
2
F
3
F
4
Y
X
O
F
1
F
2
F
3
F
4
1
α
2
α
3
α
Zrównowa
ż
ony
układ sił.

Moment siły
wzgl
ę
dem
punktu
Moment siły
wzgl
ę
dem
punktu
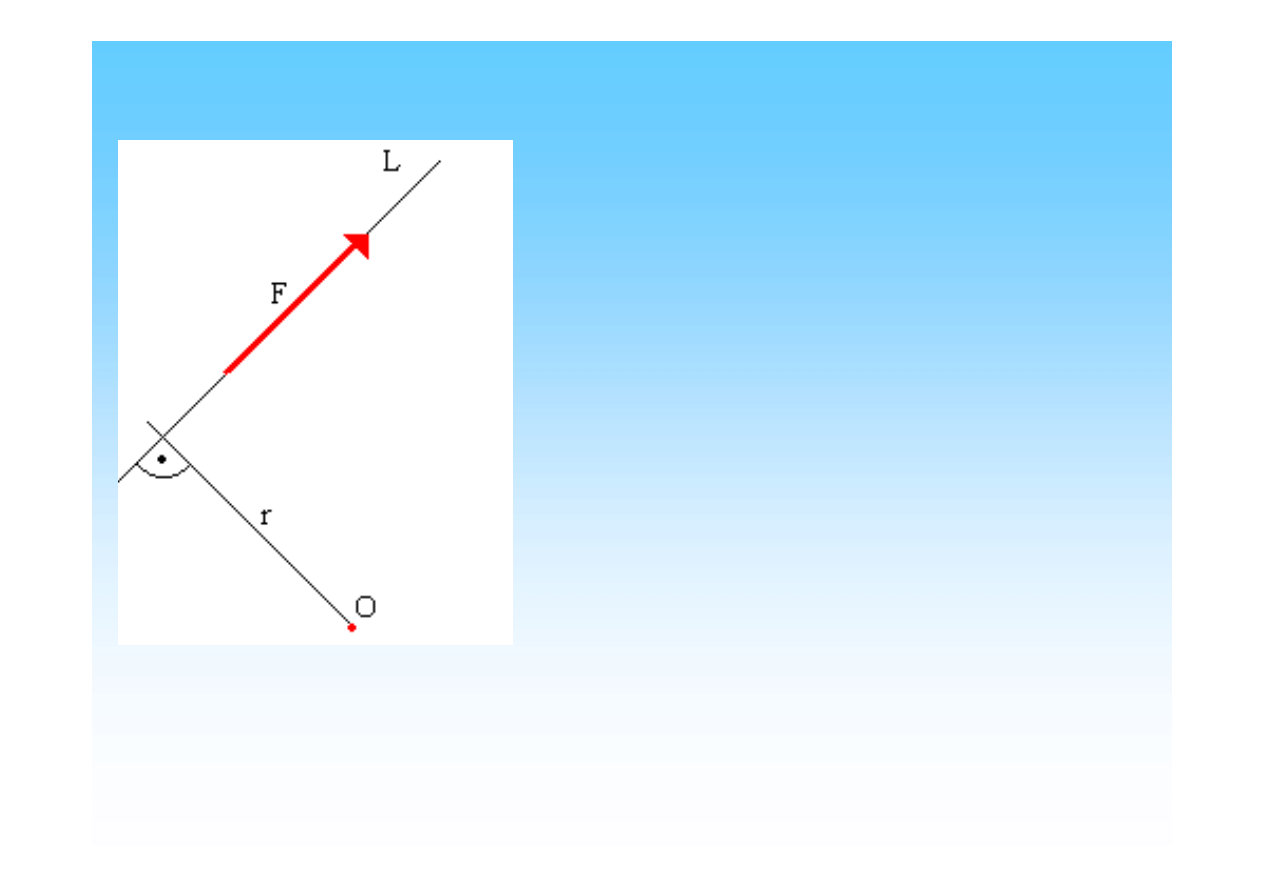
Dana jest Siła F działająca wzdłuż prostej L oraz dowolny punkt O.
Momentem siły F wzgl
ę
dem punktu
(bieguna) O nazywamy iloczyn warto
ś
ci
tej siły przez jej rami
ę
, czyli odległo
ść
obranego punktu od linii działania danej
siły
Mo=F*r
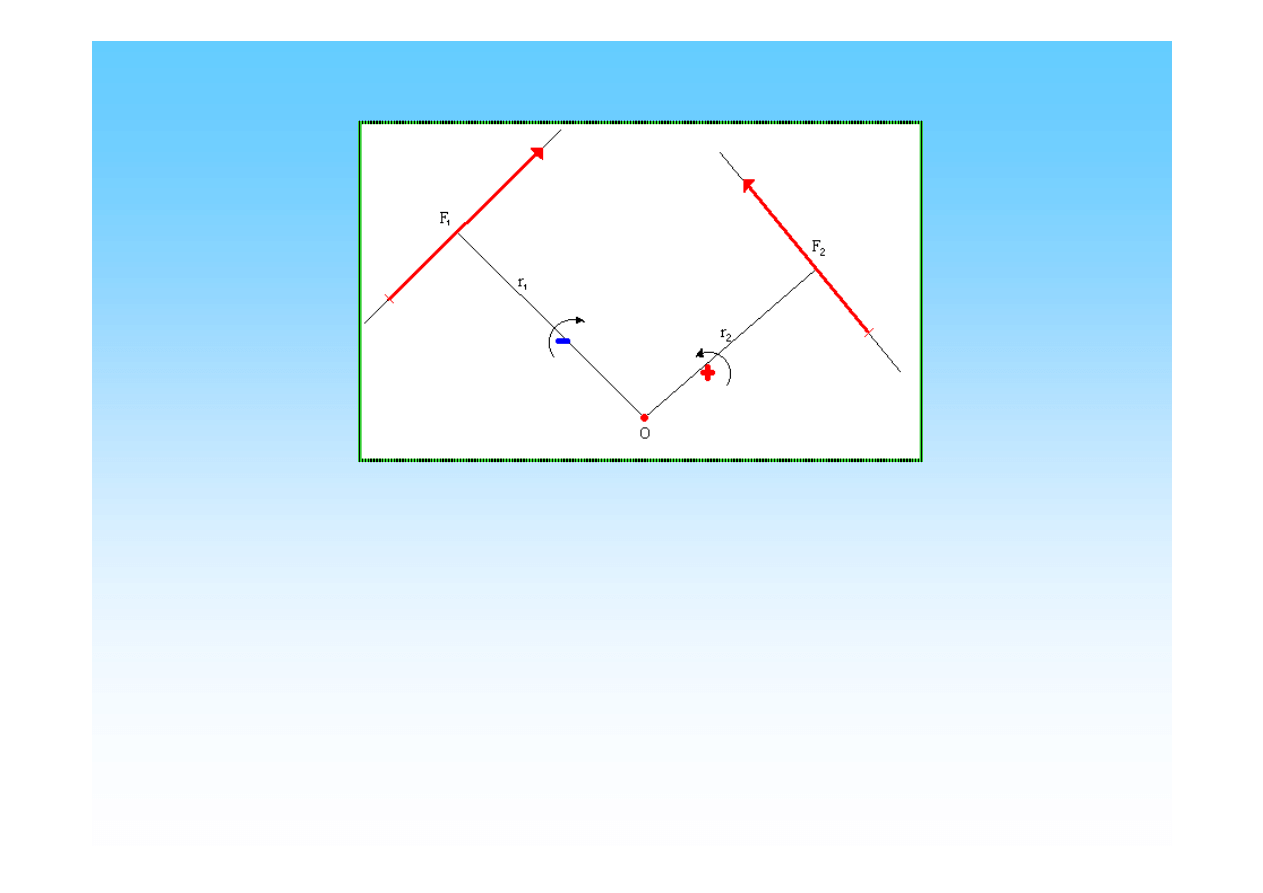
Moment uważamy za dodatni, jeżeli siła dąży do obrócenia swego ramienia
r
dookoła
bieguna
O
w kierunku niezgodnym z ruchem wskazówek zegara
( lewo).
Jeżeli siła dąży do obrócenia swego ramienia
r
w kierunku zgodnym z ruchem
wskazówek zegara,
(w prawo)
moment uważany jest za ujemny.
Moment siły względem punktu jest wektorem i
Moment siły względem punktu jest wektorem i
posiada wszystkie jego cechy.
posiada wszystkie jego cechy.
Wartość- Równą iloczynowi (F*r) wartości siły przez jej ramie.
Kierunek-Prostopadły do płaszczyzny wyznaczonej
przez linię działania siły i biegun.
Zwrot- Przyjmujemy zgodnie z regułą śruby prawej.
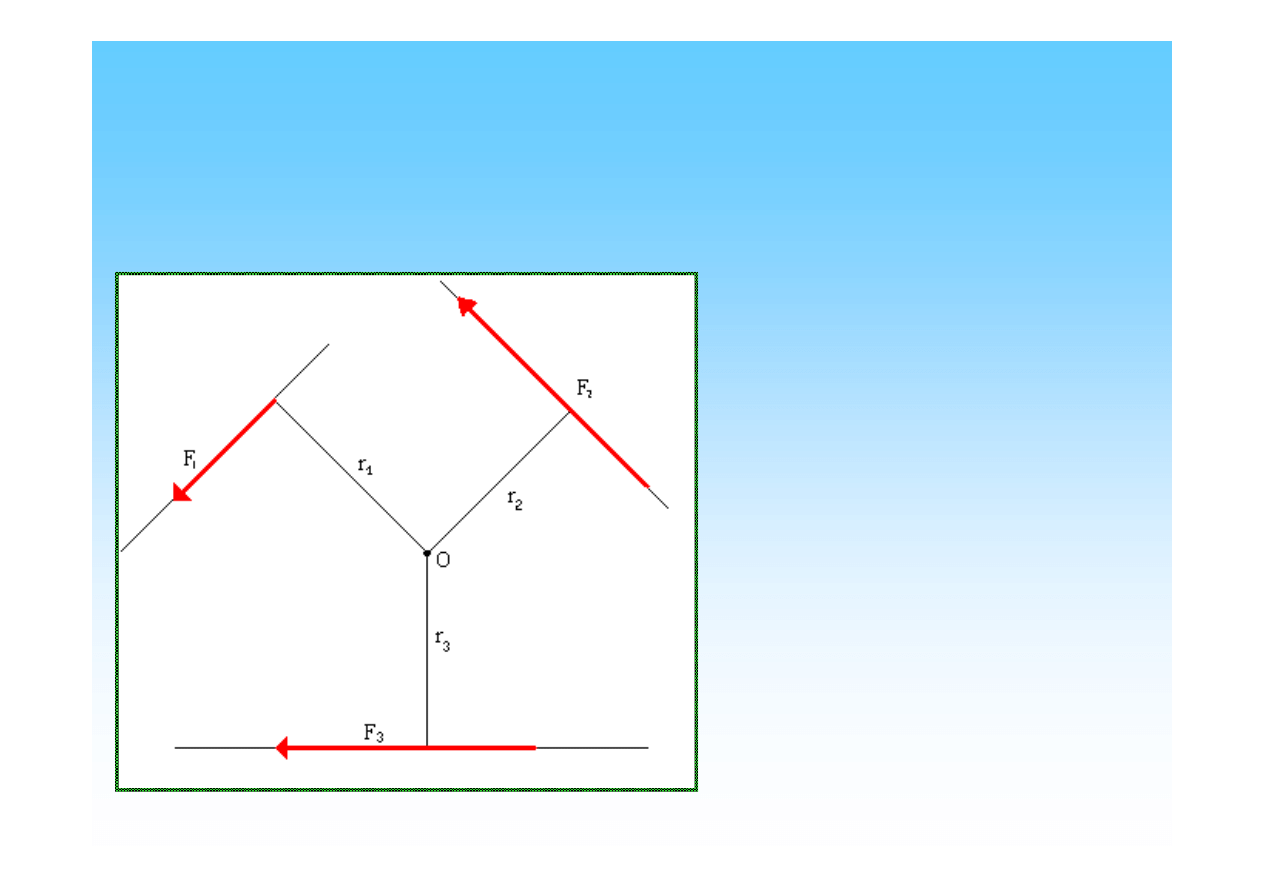
Przyjmujemy w płaszczyźnie trzy siły, których wartości wynoszą:
F1=100 N F2=200 N F3=150 N . Następnie obieramy w płaszczyźnie punkt O, który
uważamy za biegun momentu.
Długości ramion wynoszą r1=0,015 m; r2=0,015 m; r3=0,02 m;
Obliczamy momenty tych sił (Mo=F*r)
które wynoszą
Mo1=100N*0,015m=1,5 N*m
Mo2=200N*0,015m=3 N*m
Mo3= -150N*0,02m=-3 N*m
Tworzymy sumę tych momentów
M
0
=M
01
+M
02
+M
03
Mo=1,5N*m+3N*m-3N*m=1,5N*m
Znaleziony moment nazywamy
Znaleziony moment nazywamy
MOMENTEM GŁÓWNYM
MOMENTEM GŁÓWNYM

Momentem głównym dowolnego układu sił na płaszczyźnie względem przyjętego
bieguna O nazywamy sumę momentów poszczególnych sił tego układu względem
tego samego bieguna O.
M
M
o
o
=M
=M
o1
o1
+M
+M
o2
o2
+M
+M
o3
o3
...
...
Moment wypadkowej R dowolnej liczby sił zbieżnych względem jakie
Moment wypadkowej R dowolnej liczby sił zbieżnych względem jakie
goś bieguna
goś bieguna
O jest równy sumie momentów poszczególnych sił składowych względ
O jest równy sumie momentów poszczególnych sił składowych względ
em tego
em tego
samego bieguna.
samego bieguna.
MoR
MoR
=Mo1+Mo2+Mo3...+
=Mo1+Mo2+Mo3...+
Mon
Mon
Suma momentu wszystkich sił układu zbieżnego znajdującego się w
Suma momentu wszystkich sił układu zbieżnego znajdującego się w
równowadze jest równa zeru dla każdego dowolnie obranego bieguna
równowadze jest równa zeru dla każdego dowolnie obranego bieguna
.
.

Analityczne warunki równowagi
płaskiego dowolnego układu sił.
Płaski dowolny układ sił jest w równowadze, je
ż
eli punkt materialny
b
ę
d
ą
cy pod jego działaniem pozostaje w spoczynku tzn. wypadkowa R tego
układu ma warto
ść
0 i moment główny wszystkich sił wzgl
ę
dem obranego
bieguna jest równy 0.
Suma algebraiczna rzutów wszystkich sił na o
ś
x jest równa zeru.
Suma algebraiczna rzutów wszystkich sił na o
ś
y jest równa zeru.
Suma momentów wszystkich sił wzgl
ę
dem obranego bieguna jest równa zeru.
∑
=
+
+
=
0
...
2
1
F
F
F
x
x
ix
∑
=
+
+
=
0
...
2
1
F
F
F
y
y
iy
∑
=
+
+
=
0
...
2
1
M
M
M
o
o
io

Zadania
Zadania
Przykłady zada
ń
z egzaminu
Przykłady zada
ń
z egzaminu
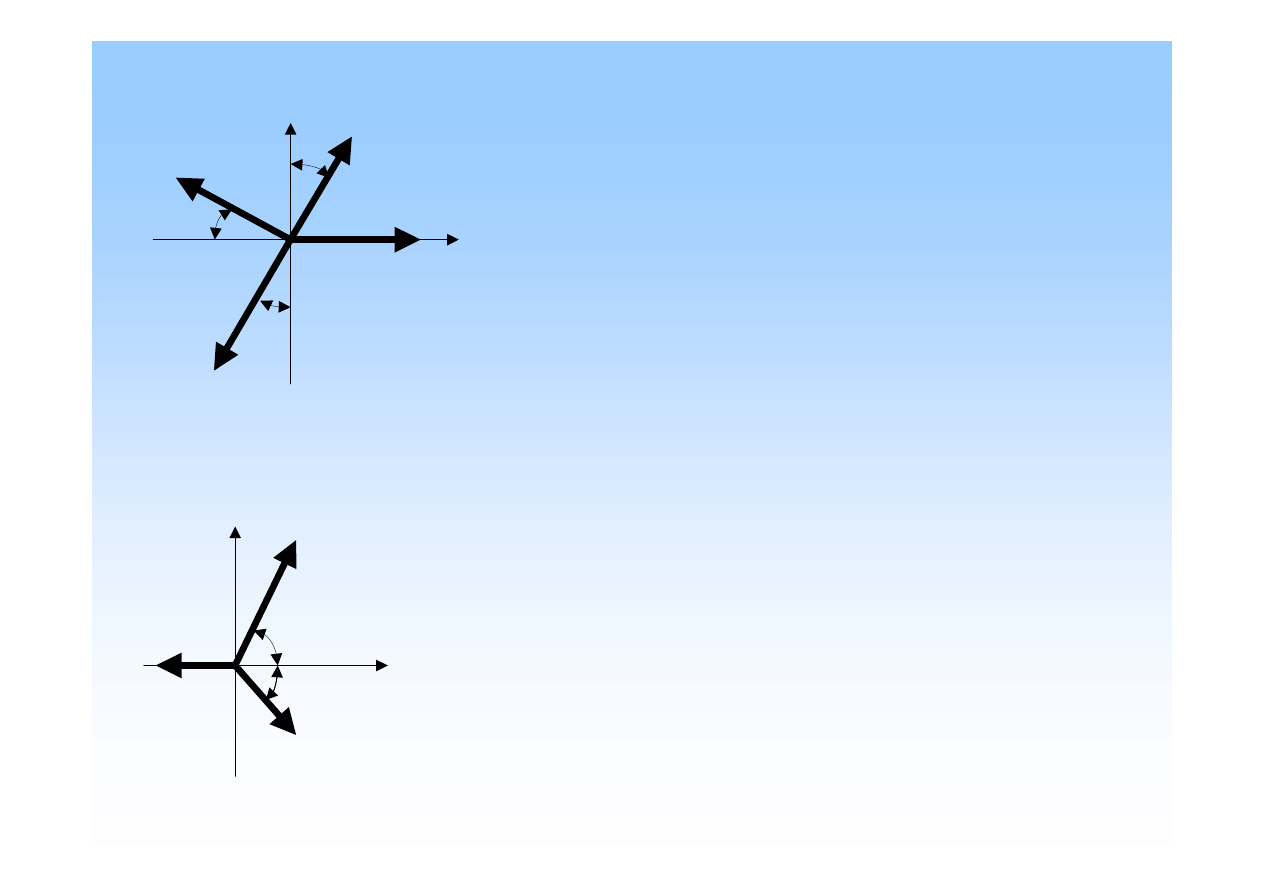
Zadanie 1
Y
X
O
F
4
F
3
F
2
F
1
2
β
3
α
4
β
Równania, które s
ą
zapisanymi warunkami
równowagi danego układu sił.
Rzuty na o
ś
x:
0
sin
cos
sin
4
4
3
3
2
2
1
=
⋅
−
⋅
−
⋅
+
β
α
β
F
F
F
F
Rzuty na o
ś
y:
0
cos
sin
cos
4
4
3
3
2
2
=
⋅
−
⋅
+
⋅
⋅
β
α
β
F
F
F
Y
X
O
F
1
F
2
F
3
2
α
3
α
Zadanie 2
Rzuty wypadkowej R układu sił na osie :
3
3
2
2
1
cos
cos
α
α
⋅
+
⋅
+
−
=
F
F
F
R
X
3
3
2
2
sin
sin
α
α
⋅
−
⋅
=
F
F
R
Y
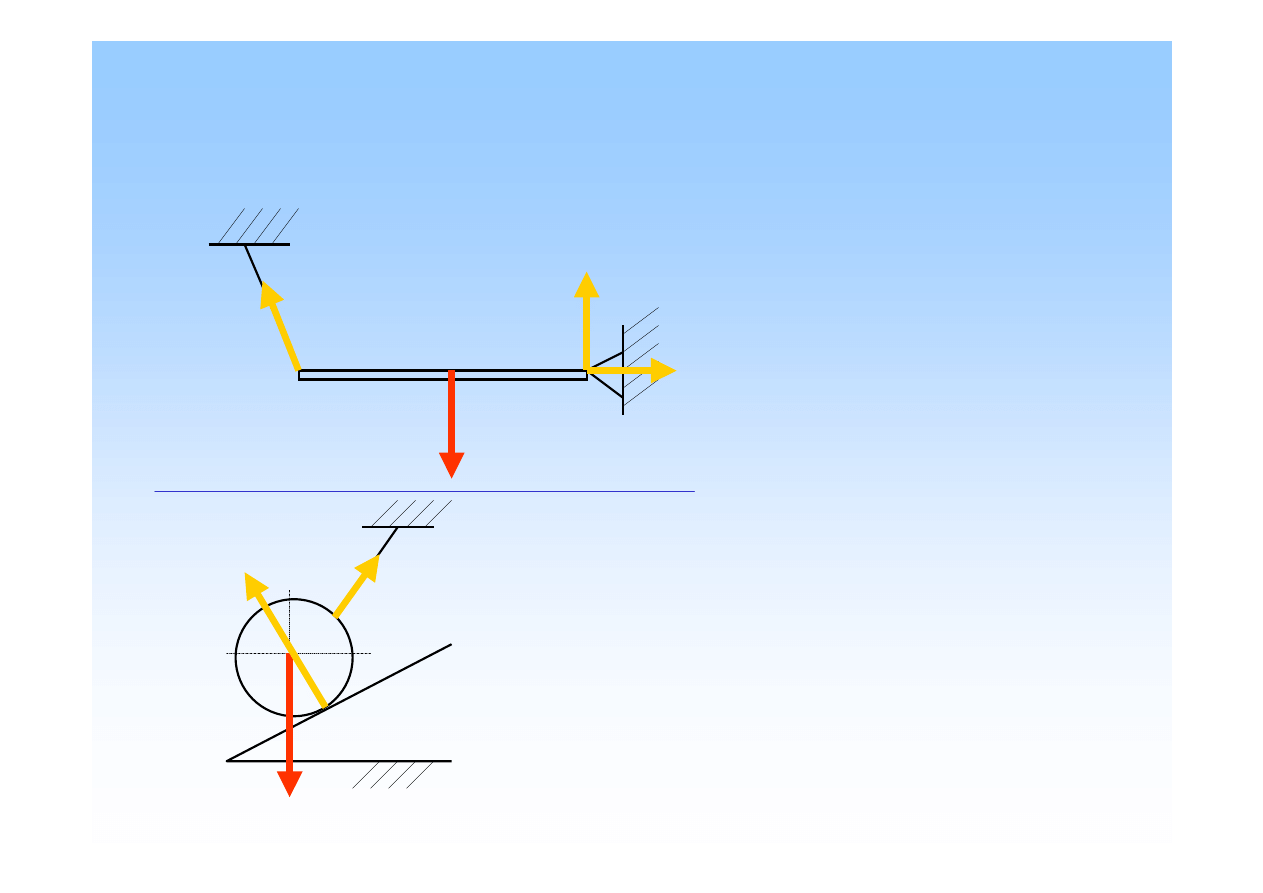
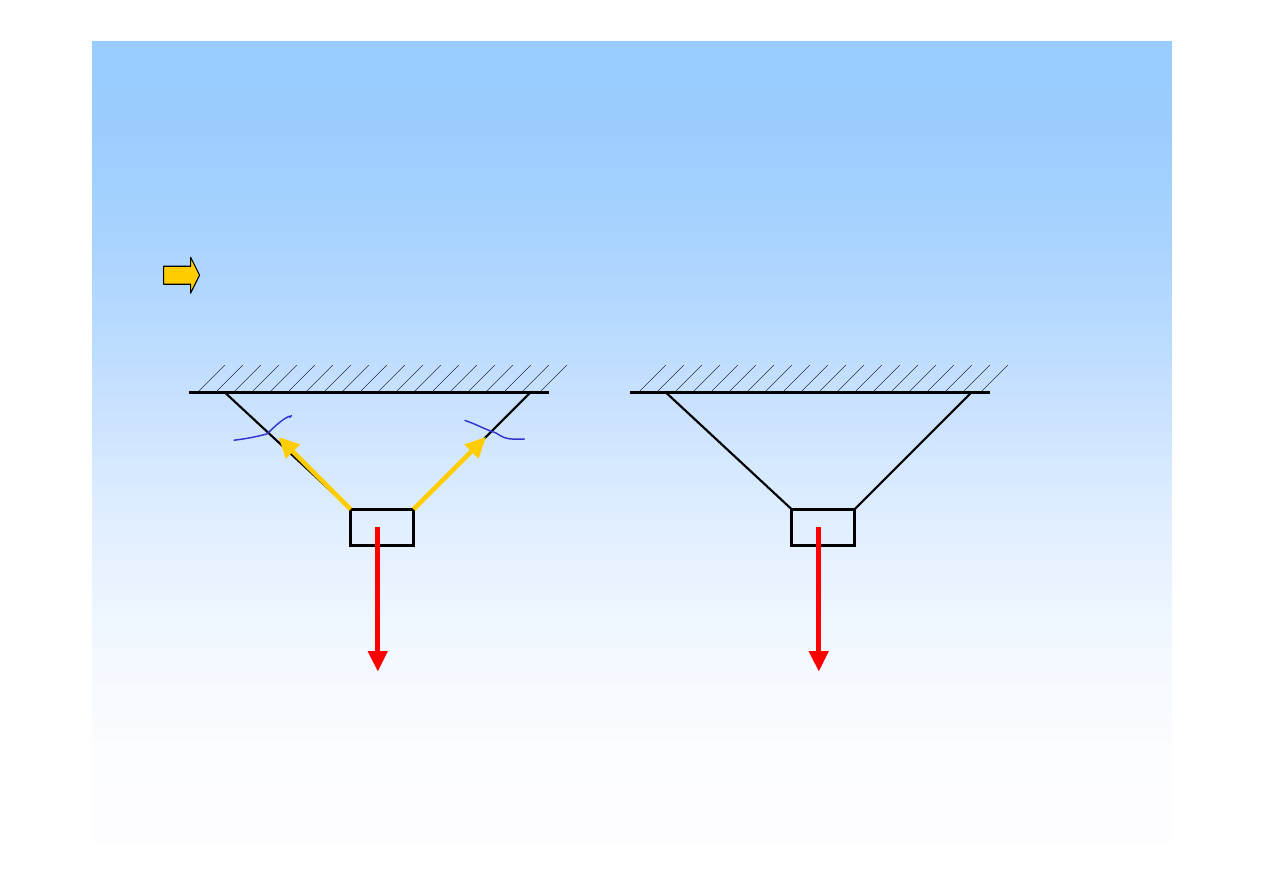
Zadanie 3
poprawnie przedstawione reakcje w podporach
A
B
G
R
A
R
BY
R
BX
A
B
G
R
A
R
B
1.
2.
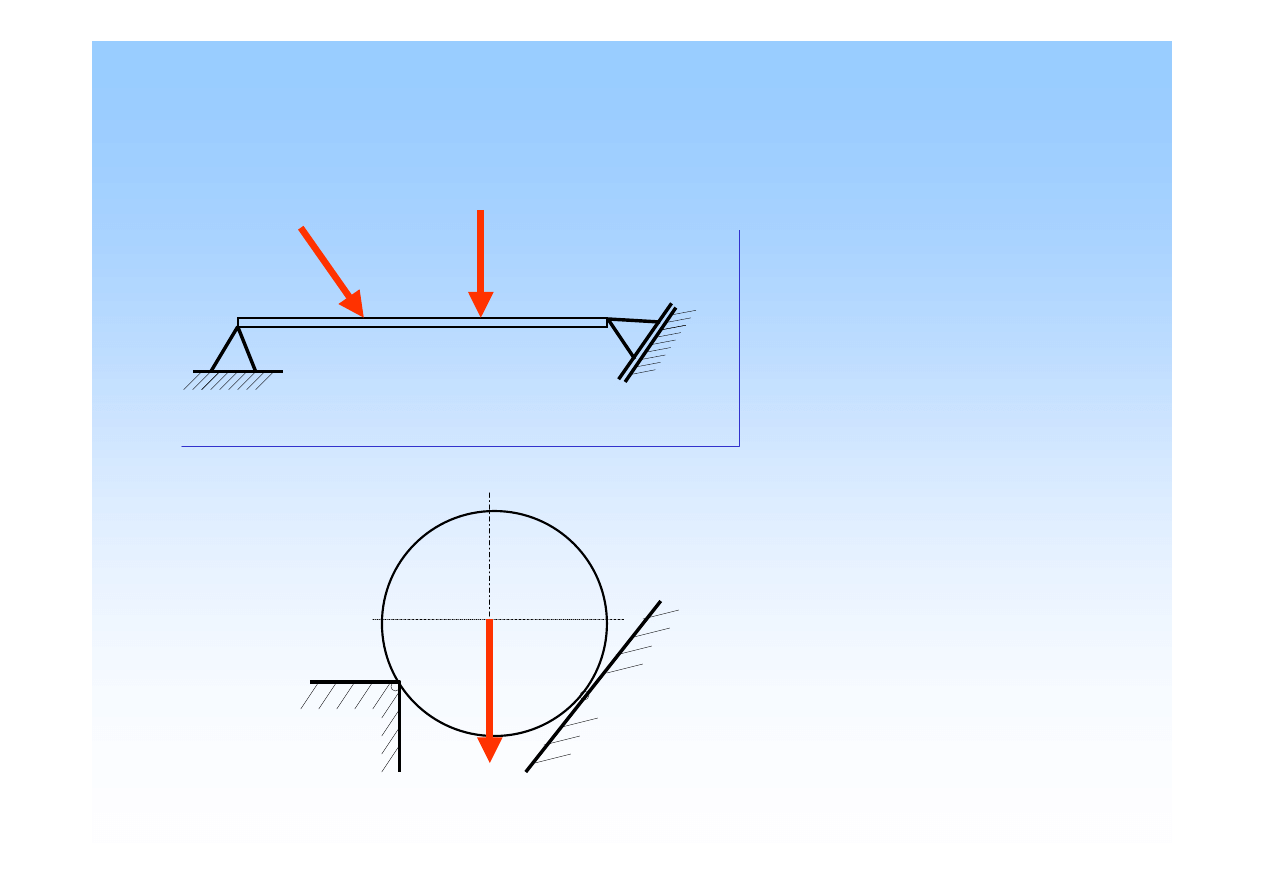
Zadanie 4
Dorysuj reakcje w podporach.
F
1
F
2
A
B
A
B
G
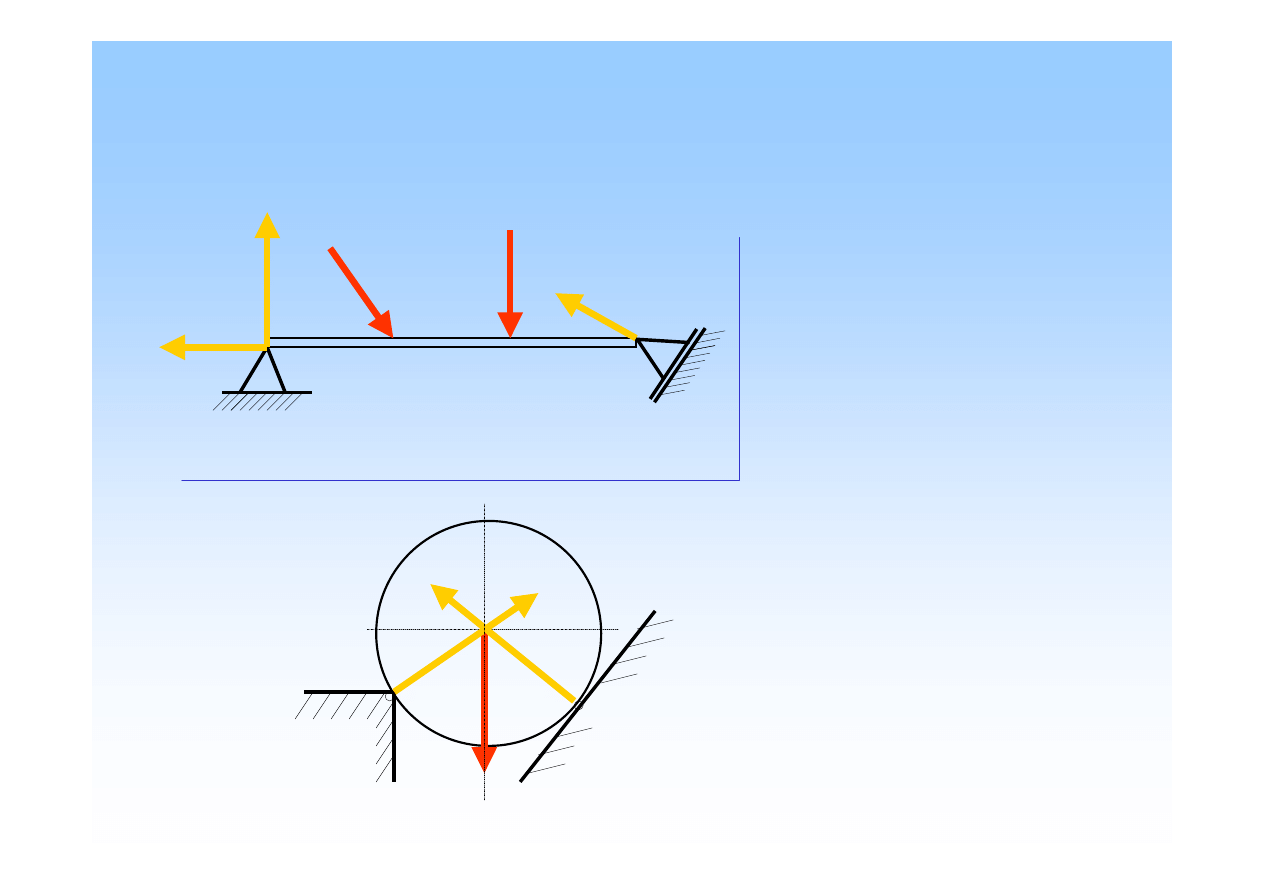
Odpowied
ź
do zad. 4
Czy tak przedstawiłe
ś
reakcje w podporach?
A
B
G
R
A
R
B
F
1
F
2
A
B
R
AX
R
AY
R
B
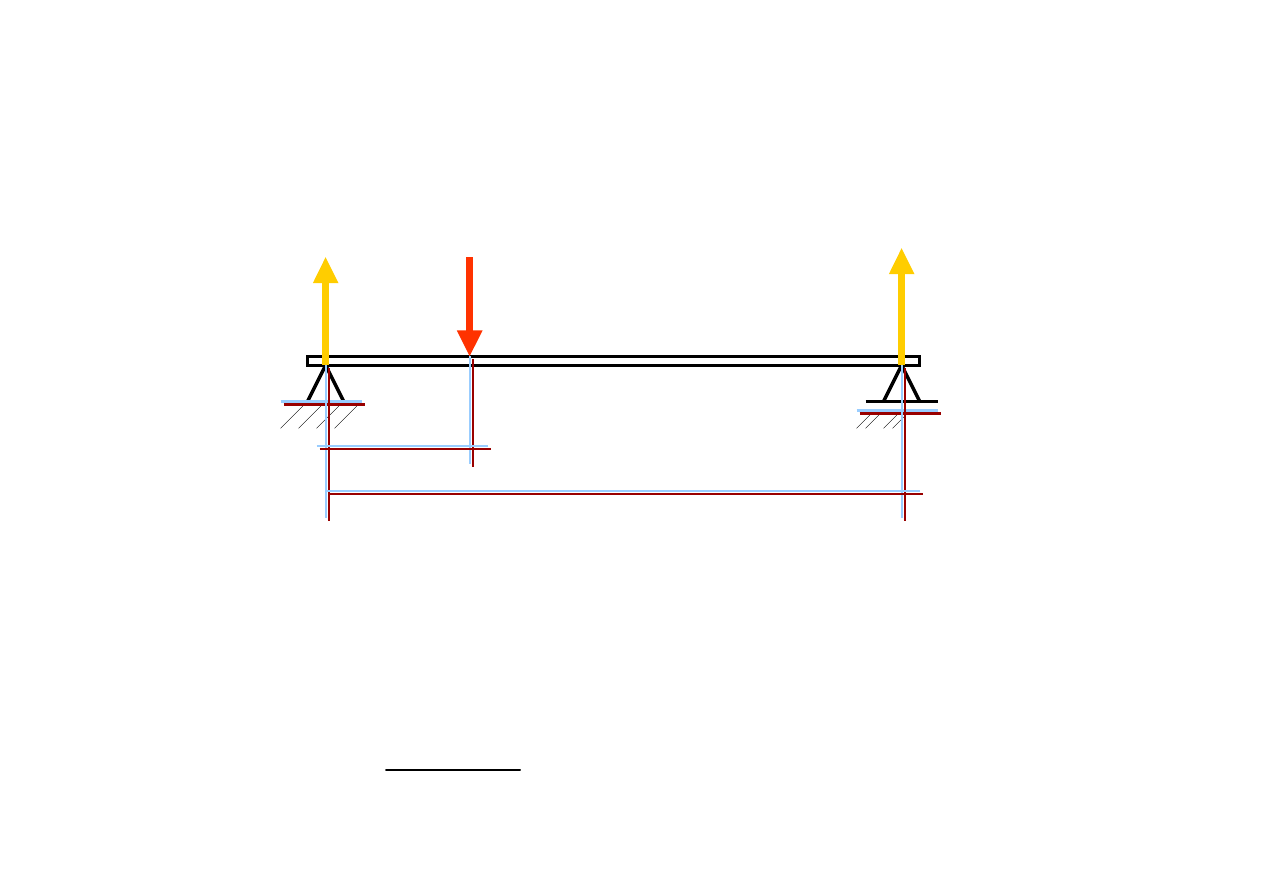
R
A
R
B=25N
F=100N
b
l=8m
Układ b
ę
dzie w równowadze gdy długo
ść
b wyniesie?
A-1m, B-2m, C-3m, D-4m
Odp: Długo
ść
wyznaczysz z warunków równowagi, w tym przypadku nale
ż
y
skorzysta
ć
z równania momentów:
∑
∑
=
⋅
+
⋅
−
=
=
0
8
:
0
m
b
F
R
M
M
B
iA
iA
m
N
m
N
b
m
N
b
N
2
100
200
0
8
25
100
=
⋅
=
=
⋅
+
⋅
−

Powtórzyłeś już niezbędne wiadomości do opanowania standardu 2.1.
Teraz sprawdź swoje wiadomości rozwiązując test wielokrotnego wyboru
z jakim spotkasz się również na egzaminie zawodowym.
Projekt ”Społeczeństwo wykształcone- największy kapitał współczesnego kraju” jest wspó
ł
finansowany ze środków
Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Wyszukiwarka
Podobne podstrony:
kurs VI id 255234 Nieznany
Rozdział 16. Edytory tekstu- vi i emacs, Kurs Linuxa, Linux
kurs html rozdział VI
[Kurs OpenGL, C++] VI Elem
KURS ETYKI
Lekcja kliniczna 2 VI rok WL
Choroba hemolityczna p odu na kurs
zapotrzebowanie ustroju na skladniki odzywcze 12 01 2009 kurs dla pielegniarek (2)
Prezentacja VI Bezrobocie
PS VI
kurs
wady postawy kurs
ostre białaczki 24 11 2008 (kurs)
materialy na diagnoze, Wyklad VI diagnoza
w 13 III rok VI sem
więcej podobnych podstron