Własności prawdopodobieostwa:

Teoria:

1. Przestrzeo probabilistyczna – trójkę , gdzie to

przestrzeo zda. element., P – prawd., Z – rodzina
podzbiorów.

2. Prawdopodobieostwo (def.) –zdarzenia A to iloraz zdarzeo

sprzyjających zdarz. A do liczby wszystkich możliwych
przypadków, zakładając, ze wszystkie przypadki wzajemnie
się wykluczają i są jednakowo możliwe.

3. Prawd. warunkowe: zdarzenia A pod warunkiem B (gdzie

nazywamy liczbę określoną wzorem

4. Prawd. całkowite (zupełne): Jeśli B jest dowolnym

zdarzeniem zaś zdarzenia

spełniają warunki:

a) wykluczają się parami i

b) ich

alternatywa jest zdarzeniem pewnym czyli

oraz c) mają dodatnie prawd. tzn.

to prawd. zdarz. B wyraża się wzorem:

5. Twierdzenie Bayesa: Jeśli B jest dowolnym zdarzeniem o

dodatnim prawd. zaś zdarzenia

spełniają warunki takie jak w prawd. całkowitym, to prawd.
warunkowe

zdarzeo

przy warunku B k=1,2,…,n

wyraża się wzorem:

6. Zdarzenia Niezależne: gdy spełniony jest warunek

7. Zdarzenia Niezależne (war. koniecz.): gdy i

wówczas zachodzi równośd:

8. Zdarzenia Niezależne (dwuwymiarowa): gdy spełniony jest

warunek

Czyli

czy w tabelce: iloczyn tego co jest na kraocach toto co stoi
w miejscu przecięcia tej kolumny z wierszem. (Zobacz na
tabelkę z dystrybuanty dwuwymiarowej)

Dystrybuanta (skokowa) + wykres:

1. Mamy zapisane

(gdzie x to nasze możliwości, a p

to prawdopodobieostwo). Dla ułatwienia można sobie
narysowad oś z zaznaczonymi naszymi

a pod nimi napisad

odpowiednie

.

2. Wypisujemy przedziały prawostronnie domknięte (z

wyjątkiem tu będzie otwarty, taka zasada). I
patrzymy jakie prawdopodobieostwo mamy w tych
przedziałach. np.

to pierwszy przedział

wygląda Nic nie wiemy o tym co się dzieje
kiedy x<3. Tak więc zapisujemy .
Drugi przedział dla

. Bez stresu zapisujemy

przedział i zastanawiamy się jakie będzie
prawdopodobieostwo, że . Od 4 na lewo na osi
spotykamy tylko praw. tak też to zapisujemy:

3. W kolejnych przykładach postępujemy analogicznie.

Bierzemy sobie

kładziemy go to

i patrzymy

jakie

(które ma określone

) spotkaliśmy wcześniej.

to suma tych

której już minęliśmy. W

ostatnim przedziale . Zawsze! Jak Ci nie wychodzi
1 to znaczy, że coś zwaliłeś.

4. Teraz wszystko zapisujemy nasze wyniki w jednej wspólnej

klamerce, tak że np. i
tak dalej. Ta klamerka to nasza dystrybuanta.

5. WYKRES: to nic innego jak narysowanie tych przedziałów z

klamerki. W praktyce to będą takie poziome kreseczki z
prawej strony zamalowane kółeczka, a z lewej otwarte.

Wartośd oczekiwana (skokowa):

1. To nic innego jak dodawanie:

(w zależności ile mamy tych iksów).

Dominanta (skokowa):

1. Wskazujemy liczbę. Może byd ich kilka. Wybieramy te, które

mają największe prawdopodobieostwo.

Wariancja - poziom zróżnicowania - (skokowa):

1. To nic innego jak mnożenie:

- kwadrat wartości oczekiwanej

Odchylenie standardowe (skokowa):

1. To Pierwiastek z wariancji:

Rozkład prawdopodobieostwa (skokowa):

1. Rozkład to np. tabelka, albo takie wypisywanie że

; itd. Generalnie jest to
zadanie odwrotne do dystrybuanty. Masz znaleźd wszystkie

i zapisad. Ja w PD zapisałam w formie tabelki.

2. Tworzysz sobie układ równao. Łatwo jest odgadnąd, że

to pierwsza wartośd dla której x jest pierwszy raz w
konkretnych granicach [ inf czyli nie
konkretnie, - konkretnie bo są liczby].

3. Dalsze przykłady robisz na zasadzie „gdybym liczył

dystrybuantę to bym dodał

i by mi wyszło to co

podają.

znam, więc wyliczam

. Wszystko jest logiczne, i

rób to na spokojnie.

4. Potem wpisujesz do tabelki gdzie w wierszu są

a niżej

czyli odpowiednie prawdopodobieostwa.

Dystrybuanta (ciągła) :

1. Będziemy liczyd całkę . Wyjaśnię to na

przykładzie. Mamy przedziały (PD zad4):
Z treści zadania podają nam z czego będziemy liczyd
całkę i w jakich granicach. Naszym zadaniem jest to
poprawnie zapisad.

2. Masz przedział i dzielisz go takimi liczbami jak 0 i

1 (wniosek z treści zadania). Dla x te przedziały będą
podzielone na 3 części. A dla całki będziesz je sobie
dodawał tak jakby. W pierwszym kroku będziemy liczyd
całkę z 0 (podane w zad.) w granicach dla
Oczywiście wychodzi 0.

3. Następny krok to suma całek: poprzednia całka w granicach

+ całka z funkcji gęstości w granicach
wszystko dla . Myślę, że przedział dla x jest prosty
(taka sama zasada jak przy skokowej). Jeśli nie rozumiesz
przedziału dla całek: nie możesz mied dwóch iksów w
przedziale, dlatego jeden z pierwszej całki zastępujesz
liczbą. Piszesz 0, bo tak wynika z kolei rzeczy. Krok
wcześniej byłeś w przedziale a teraz jesteś
.

4. OK., inaczej. Uznaj, że dla całek to masz sobie dodawad te

granice co pisałeś dla x z tą różnicą, że zawsze na koocu
masz mied „x”. .

5. Liczysz tak kolejny krok.
6. Nie wiesz czy dobrze zrobiłeś? Z reguły dystrybuanta

powinna byd 0 dla x bla bla, jakaś funkcja dla x bla bla, 1 dla
x bla bla. UWAGA: ta jakaś funkcja musi byd zawsze
dodatnia w tym swoim przedziale bla bla. Jeśli nie jest to
jest coś zrypane.

7. Zapisujesz to wszystko w klamerce. Gotowe.

Dominanta (ciągła):

1. Policzymy pochodną tej funkcji co ją dali w zadaniu.
2. Przyrównamy do zera. Rozwiązania tego równania są

podejrzane o ekstremum. Miejmy na nie oko.

3. Liczymy drugą pochodną i wstawiamy do niej pierwsze

rozwiązanie z pkt. 2. Interesuje nas czy ta wartośd będzie
ujemna. Jeśli tak to, w tym punkcie mamy maksimum i tym
samym punkt jest dominantą. Koniec.

Wartośd oczekiwana (ciągła):

1. Policzymy całkę. w granicach, które podali

w zadaniu. Są to stałe granice (np. (0,1) dla zad4 PD).

2. Wyliczona liczba to wartośd oczekiwana.

Funkcja gęstości, a stała C (ciągła):

10.

Policzymy całkę, w podanych stałych granicach, a

później przyrównamy ją do 1.

11.

Wyliczamy c.

Różne prawdopodobieostwa (ciągła):

1. I dlatego powinieneś zaprzyjaźnid się z dystrybuantą. Dzięki

niej szybko policzysz np. (zad4 PD). Jeśli to
mało łapiesz narysuj sobie dystrybuantę. Dla jakiegoś
przedziału będzie P=0, ale innego przedziału praw. będzie
opisane wzorem funkcji, a dla jakiegoś innego przedziału
P=1.

2. Patrzysz sobie w jakim przedziale wypadło twoje 0,75.

Oczywiście w tym środkowym.

3. Zaznaczasz warunek „gdzie x jest większy od 0,75 (bądź

równy). Uwaga: to nie jest przedział . Przecież

ustaliliśmy w pkt2 że 0,75 jest w konkretnych granicach a
nie .

4. Wstawienie 0,75 do równania z dystrybuanty powie ci ile

wynosi . Na to zbój. Wstaw 0,75 to tego
porypanego równania z dystrybuanty.

5. Oblicz.
6. Uwaga: Gdy masz jakieś zlepki, typu

narysuj sobie ten przedział na osi x.

7. Spróbuj ten przedział przedstawid za pomocą takich liczb

(prawdopodobieostwo to liczba xD), że
. Czemu? Bo wyrażenia z takich
schematem jesteś w stanie obliczyd. Wystarczy, że wstawid
coś, inne_coś do funkcji w dystrybuancie i masz
prawdopodobieostwo. W punkcie 4 już o tym mówiłam.

Rozkład (dwupunktowy):

1. Stosujemy, gdzie mamy jedną szansę, gdzie wsytąpi albo

sukces albo porażka.

2.

Rozkład (geometryczny):

1. Stosujemy gdzie powtarzamy doświadczenie, aż osiągniemy

sukces.

2.

3.

Rozkład dwumianowy Bernoullego:

1. Sytuacja gdzie z góry mamy określone ile razy będziemy

powtarzad doświadczenie. Mamy sukces albo porażkę.
Rozkład prawd.

gdzie p jest stałym

prawdopodobieostwem realizacji wyróżnionego zdarzenia

losowego A, przy czym a

dla

2.
3.

4. Dystrybuanta:

Rozkład Poissona:

1. Korzystamy wtedy gdy, gdy prawd. sukcesu jest małe, a

liczba realizacji n na tyle duża, że iloczyn jest
wielkością stałą, dodatnią i niezbyt dużą. Rozkład prawd.

2. Wart. oczekiwana:
3. Wariancja:

Rozkład NORMALNY:

1. standaryzacja:

Dystrybuanta (dwuwymiarowa):

1. Warto zrobid sobie tabelkę.

to

i

wyliczamy. Jest to suma

każdego wiersza/kolumny. np.
dla xi= 0 pi będzie wynosiło
1/3+1/6=1/2. Myślę, że można
to uznad za zrozumiałe jak
tabelka działa. Wyznaczanie
dystrybuanty? Mamy tu takie

wartości jak 0 i 1. Generalnie to sposób wyznaczanie będzie
podobny do tego co już mieliśmy w skokowej. Chcę żebyś
sobie „przesunął” w myślach 0 i 1, tak na te pogrubione
linie. (z wierszami to samo). Na kraocach tabelki będą
odpowiednio . Chcę żebyś sobie to wyobraził.
Wtedy łatwo wyznaczysz przedziały. Tak. Będzie tych
przedziałów od groma bo musisz wyznaczyd wszystkie
możliwości. Nie mniej jednak, trochę sobie ułatwimy, ale o
tym za chwilę.

2. Pierwsza czynnośd: przedział .

Te przedziały to nasz kwadracik gdzie jest napisane xi\yj.
Nic tam nie ma więc wpiszemy 0. Idziemy sobie dalej.
Weźmy sobie taki przedział . Czy
teraz rozumiesz po co chciałam te grube kreski? Teraz łatwo
widzisz gdzie zaczyna się przedział od 0 do 1, i masz czarno
na białym jego wartośd. Patrz: to jest w
prawdzie drugi wiersz. to druga kolumna.
Odczytujemy że w tych przedziałach dystrybuanta wynosi
1/3. Czy to nie wspaniałe? ;D

3. Weźmy coś trudniejszego, np.

Krzyżuje nam się w wartości 1/6. Jakby ci to
wytłumaczyd. Słuchaj, cały czas bazujesz na zasadzie
kwadratu, a ta liczba gdzie ci wychodzi przecięcie
przedziałów to twój prawy dolny róg. Pewnie się
zastanawiasz jakiego kur**** kwadratu?! Kwadratu w
którym masz wartości i je musisz wszystkie dodad. Wynik to
będzie twoja dystrybuanta w danym przedziale. Tak więc
masz sobie wyimaginowany kwadrat z wartościami 1/3,
1/6,1/3,1/6. Wszystko dodajesz i zapisujesz.

4. Jeszcze raz ten mój tajemniczy kwadrat objaśnię. Masz

narysowaną tabelkę. Chcesz się dowiedzied jakie wartości
ma dystrybuanta w danych przedziałach. Wybierasz
przedział dla x i y. Patrzysz gdzie się krzyżują. (Wyobraź
sobie, że pracujesz teraz w PS xD) Klikasz nową warstwę i
rysujesz kwadrat od tego miejsca do początku tabelki z
wartościami (lewy górny róg). Czasami wyjdzie ci kwadrat,
a czasami prostokąt. Grunt by wszystko dodad co się
znalazło w tym zaznaczonym polu.

5. Wzór poprawnego zapisu przypadków: (taki przykład)

Dystrybuantę

zapisujesz normalnie jak w np. w skokowej. Klamerka,
wartości, przedziały.

Wartośd oczekiwana (dwuwymiarowa):

1. Będziesz liczyd dla X i dla Y.
2. Dla X to jest

Czyli mnożysz sobie

pierwszy wyraz z pierwszego wiersza z ostatnim wyrazem
pierwszego wiersza, dodajesz do tego iloczyn (pierwszy
wyraz drugiego wiersza razy ostatni wyraz pierwszego
wiersza) +…. i tak dalej.

3. Dla Y jest analogicznie.

yj 0

1

0

1/3 1/6 1/2

1

1/3 1/6 1/2

2/3 1/3 1

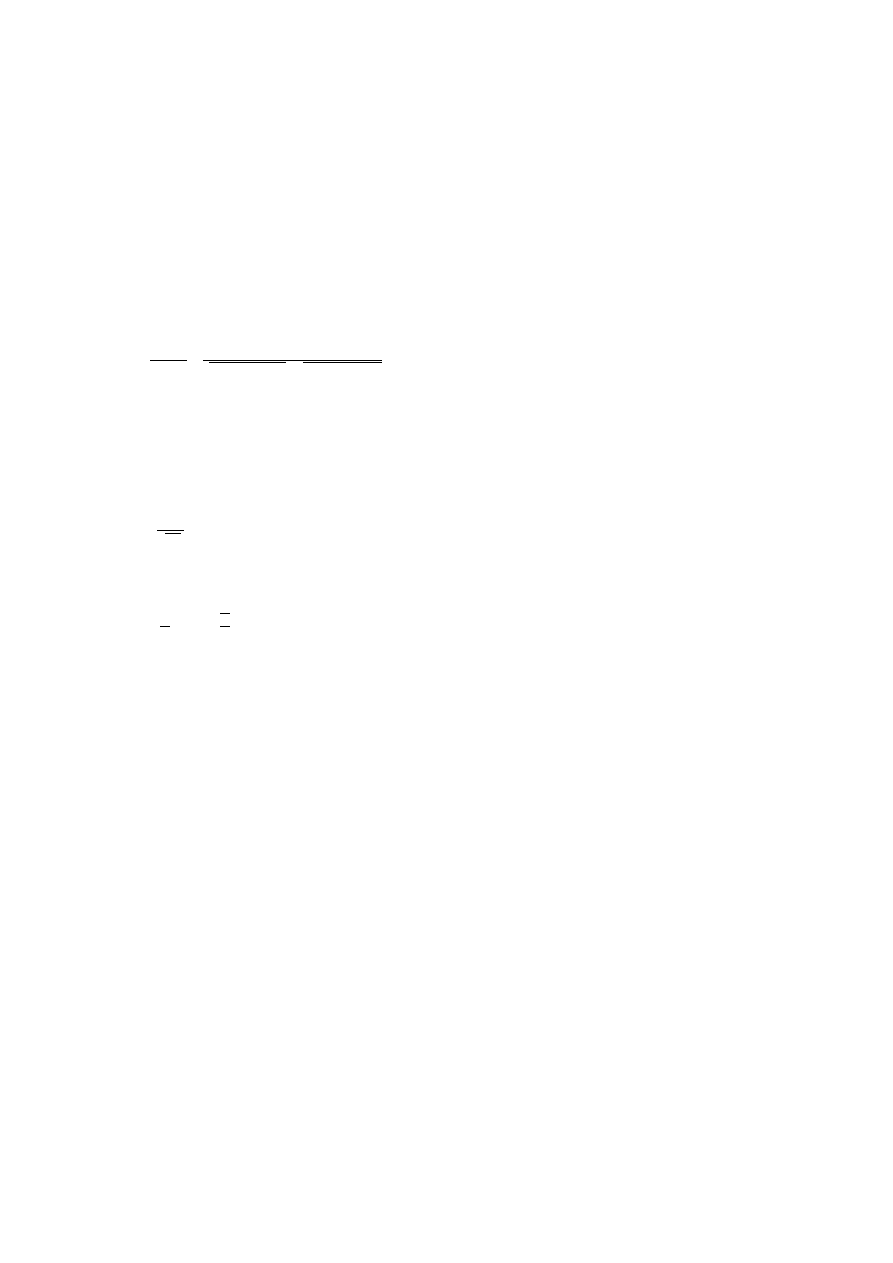
Wariancja (dwuwymiarowa):

1. Będziesz liczyd dla X i dla Y.

2. Dla X. Boże ile liczenia 

Jeśli

zastanawiasz się czy będziesz musiał dodawad cały rządek
jakiś cyferek po przecinku to odpowiedź brzmi: OH SIIIIIII !
xD Wzór jest prosty. Nie ma żadnego nowego oznaczenia.
liczyłeś punkt wcześniej. Jak czegoś nie wiesz to
zobacz sobie na tabelkę, tam jest napisane co jest czym.

3. Dla Y analogicznie.

4. Są na to też inne wzory (do zapoznania w Współczynnik

korelacji).

Współczynnik korelacji (dwuwymiarowa):

1. Będziesz liczyd fajny wzorek:

2.

3. im bliższy tym liczbom tym zmienne są silniej

skorelowane. Jak jest dodatni to korelacja dodatnia, a jak
ujemny to k. ujemna. Natomiast cov to kowariancja.

4.

to takie dziwne to jest wartośd, jakbyś chciał powiedzied

Twierdzenia graniczne:

1. Gdy znany sukces i ilośd doświadczeo:

2.

Twierdzenia graniczne (udziały procentowe):

1. Gdy znana ilośd doświadczeo, a sukces podany w

procentach:

2.