„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

MINISTERSTWO EDUKACJI

NARODOWEJ

Jarosława Bucior

Wykorzystanie badań statystycznych w procesach
decyzyjnych 342[02].Z3.05

Poradnik dla ucznia

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy
Radom 2006

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

1

Recenzenci:
dr hab. inż. Tomasz Nowakowski, prof. nadzw.
dr inż. Marek Młyńczak




Opracowanie redakcyjne:
mgr inż. Halina Bielecka




Konsultacja:
mgr inż. Halina Bielicka




Korekta:




Poradnik stanowi obudowę dydaktyczną programu jednostki modułowej 342[02].Z3.05
Wykorzystanie badań statystycznych w procesach decyzyjnych zawartego w modułowym
programie nauczania dla zawodu technik – spedytor.





















Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom 2006

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

2

SPIS TREŚCI

1. Wprowadzenie

3

2. Wymagania wstępne

5

3. Cele kształcenia

6

4. Materiał nauczania

7

4.1. Zadania i organizacja statystyki

7

4.1.1. Materiał nauczania

7

4.1.2. Pytania sprawdzające

10

4.1.3. Ćwiczenia

11

4.1.4. Sprawdzian postępów

13

4.2. Badania statystyczne. Metody i organizacja badania

14

4.2.1. Materiał nauczania

14

4.2.2. Pytania sprawdzające

16

4.2.3. Ćwiczenia

17

4.2.4. Sprawdzian postępów

19

4.3. Opracowanie materiału statystycznego

20

4.3.1. Materiał nauczania

20

4.3.2. Pytania sprawdzające

23

4.3.3. Ćwiczenia

24

4.3.4. Sprawdzian postępów

26

4.4. Podstawowe wiadomości z analizy statystycznej

27

4.4.1 Materiał nauczania

27

4.4.2. Pytania sprawdzające

38

4.4.3. Ćwiczenia

39

4.4.4. Sprawdzian postępów

42

5. Sprawdzian osiągnięć

44

6. Literatura

49

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

3

1. WPROWADZENIE

Poradnik będzie Ci pomocny w kształtowaniu umiejętności wykorzystania badań

statystycznych w procesach decyzyjnych.

Poradnik ten zawiera:

1. Wymagania wstępne, czyli wykaz niezbędnych umiejętności, które powinieneś mieć

opanowane, aby przystąpić do pracy z poradnikiem.

2. Cele kształcenia programu jednostki modułowej.
3. Materiał nauczania (rozdział 4), który umożliwia samodzielne przygotowanie się do

wykonania ćwiczeń i zaliczenia sprawdzianów. Obejmuje on również ćwiczenia, które
zawierają:

−

wskazówki potrzebne do realizacji ćwiczenia. Jeżeli masz trudności ze
zrozumieniem tematu lub ćwiczenia, to poproś nauczyciela o wyjaśnienie i
ewentualne sprawdzenie, czy dobrze wykonujesz daną czynność,

−

pytania sprawdzające wiedzę potrzebną do wykonania ćwiczenia. Wykorzystaj do
poszerzenia wiedzy wskazaną literaturę oraz inne źródła informacji.

4. Przykłady zadań i ćwiczeń oraz zestaw pytań sprawdzających opanowanie wiedzy

i umiejętności z zakresu całej jednostki. Zaliczenie ćwiczenia jest dowodem osiągnięcia
umiejętności praktycznych określonych w jednostce modułowej.

Jednostka modułowa: Wykorzystanie badań statystycznych w procesach decyzyjnych,
zawiera treści niezbędne do zapoznania się z działalnością przedsiębiorstwa spedycyjnego.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4

Schemat układu jednostek modułowych

342[02].Z3.02

Wspomaganie

komputerowe

procesów transportowo

-

spedycyjnych

342[02].Z3

Narzędzia spedycji i transportu

342[02].Z3.01

Wykorzystanie logistyki

w działalności spedycyjnej

342[02].Z3.03

Ustalenie cen i kosztów

usług transportowo -

spedycyjnych

342[02].Z3.04

Sporządzanie

i prowadzenie

dokumentacji spedycyjnej

342[02].Z3.05

Wykorzystanie badań

statystycznych w

procesach decyzyjnych

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5

2. WYMAGANIA WSTĘPNE

Przystępując do realizacji programu jednostki modułowej Wykorzystanie badań

statystycznych w procesach decyzyjnych powinieneś umieć:

−

posługiwać się obliczeniami w sytuacjach typowych,

−

odczytywać i selekcjonować informacje przedstawione w różnej formie,

−

projektować arkusz kalkulacyjny na podstawie podanych założeń,

−

układać komórki, tak aby ułatwić prezentację danego arkusza,

−

samodzielnie tworzyć formuły dla danego pola w arkuszu kalkulacyjnym,

−

posługiwać się standardowymi opcjami i formułami arkusza kalkulacyjnego,

−

sporządzać wykresy statystyczne i wykresy funkcji, dostosowując ich kształt i opisy do

cech przedstawionych danych,

−

sortować i znajdować dane w tabelach,

−

projektować arkusz dla właściwego stosowania sum pośrednich,

−

analizować i tworzyć modele do podanych zagadnień,

−

opracowywać i interpretować wyniki zgodnie z podanymi wzorami,

−

posługiwać się edytorem tekstowym w zakresie pisania i formatowania tekstów,

−

korzystać z dostępnych za pomocą komputera źródeł informacji,

−

odnajdować strony WWW zawierające potrzebne Ci informacje.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

6

3. CELE KSZTAŁCENIA

W wyniku realizacji programu jednostki modułowej powinieneś umieć:

−

określić rolę statystyki w procesie podejmowania decyzji,

−

posłużyć się wynikami badań statystycznych do analizy procesów decyzyjnych,

−

wykorzystać narzędzia statystyki opisowej do oceny zjawisk, zdarzeń i sytuacji,

−

wykorzystać narzędzia statystyczne do podejmowania decyzji,

−

zgromadzić, uporządkować i opracować informacje statystyczne,

−

dokonać analizy i interpretacji wyników badań statystycznych,

−

posłużyć się materiałami statystycznymi,

−

wykorzystać wyniki badań statystycznych w realizacji zadań operacyjnych.

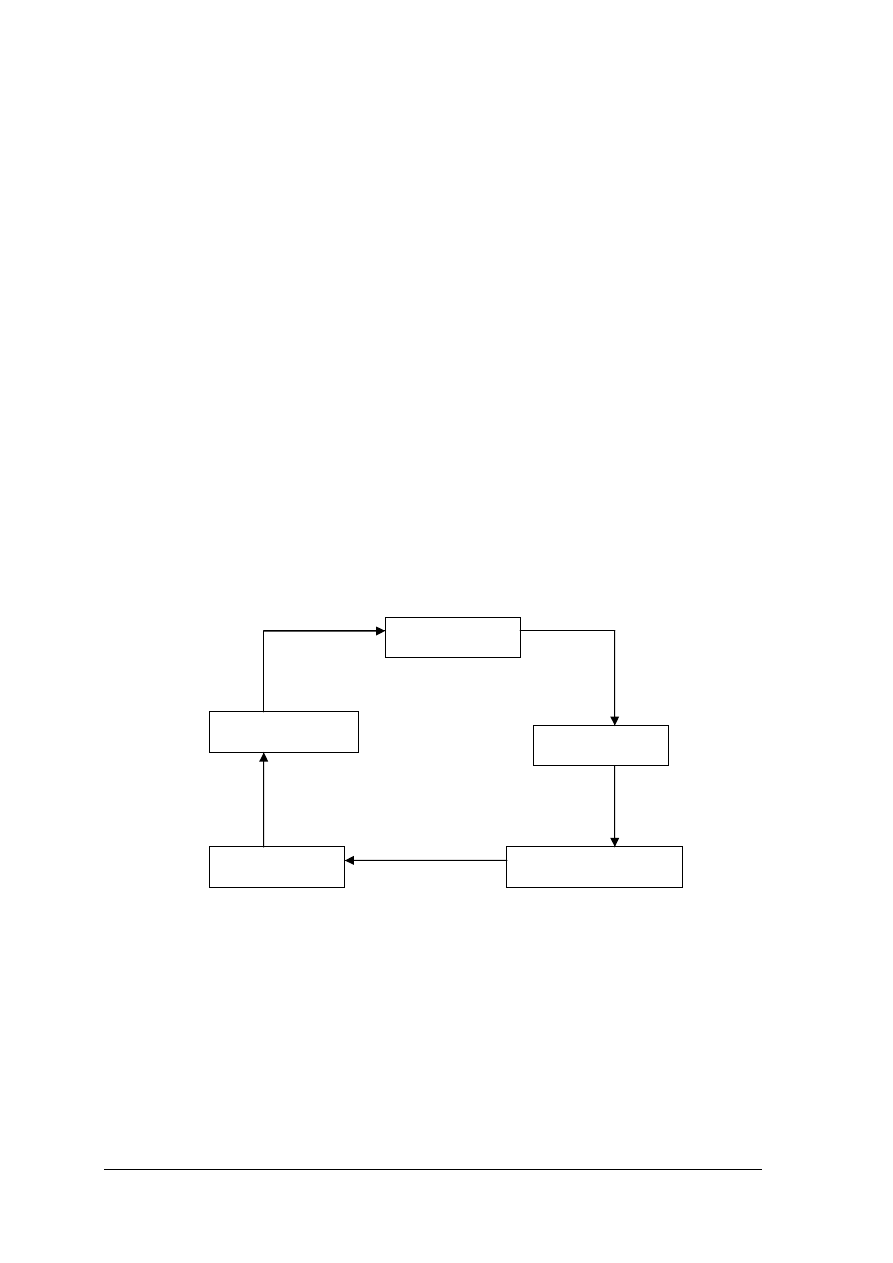
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

7

4. MATERIAŁ NAUCZANIA

4.1. Zadania i organizacja statystyki

4.1.1. Materiał nauczania

Pojęcie statystyki

Termin „statystyka” wywodzi się od łacińskiego słowa „status” – co oznacza stan

rzeczy. Został wprowadzony w połowie XVII w przez uczonego niemieckiego, który
identyfikował ją jako państwoznawstwo czyli naukę o państwie. Za prekursora obecnej
statystyki uznaje się Carla Friedricha Gaussa, który stworzył teorię za pomocą, której na
podstawie szeregu pomiarów jakiegoś obiektu można oszacować jego rzeczywisty wymiar
(im większa liczba pomiarów, tym mniejszy błąd).

Jest to nauka traktująca o metodach ilościowych badania prawidłowości zjawisk

(procesów) masowych. Stosując wypracowane przez siebie metody opracowywania danych
(analiza statystyczna), umożliwia prezentację tych danych i formułowanie wniosków
dotyczących badanych przedmiotów i zjawisk (statystyka opisowa).

Proces podejmowania decyzji, czyli proces dokonywania wyboru jednej z kilku

możliwości, to jedno z najważniejszych zadań zarządzania. Jednym z warunków podjęcia
prawidłowego wyboru jest posiadanie rzetelnych i dokładnych informacji.

Rys.1.Elementy procesu decyzyjnego. [Opracowanie własne]

Badania operacyjne - to naukowa metoda rozwiązywania problemów z zakresu

podejmowania decyzji kierowniczych.

W przypadku statystycznego sterowania procesem decyzje nie są podejmowane na

podstawie intuicji, ale w oparciu o:
− dane statystyczne – zbieranie i analizowanie danych liczbowych,
− proces czyli o ciągłą operację lub serię operacji (przekształcenie materiałów w wyroby

gotowe),

− sterowanie czyli regulacji opartej na sprawdzaniu i podejmowaniu odpowiednich działań.

DECYZJA

POLECENIE

DZIAŁANIE

KONTROLA

INFORMACJE

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

8

Do właściwego sterowania niezbędne jest posiadanie odpowiednich norm odniesienia,
a sterowany proces musi być przewidywalny:- zmienność procesu czyli sprawdzenie, że
w każdym procesie istnieje pewien stały poziom zmienności, którego nie można uniknąć,
który jest nieodłącznie związany z procesem, jest właściwy dla danego procesu. Zmienność
procesu dzielimy na dwie kategorie:
a) zakłócenia losowe są przyczyna zmienności, które jesteśmy w stanie przewidzieć. Powstają
one z przyczyn naturalnych, mają charakter przypadkowy i zawsze towarzyszą procesowi.
Jeśli dokonalibyśmy pomiarów wyrobów z procesu, na który oddziaływałyby tylko przyczyny
losowe i następnie wykreślilibyśmy wyniki tych pomiarów, to powinniśmy oczekiwać, że:
− wszystkie punkty będą leżały w pewnych granicach naturalnej zmienności,
− będą losowo rozłożone wokół linii średniej,
− nie zauważymy występowania żadnych charakterystycznych ciągów kolejnych punktów.
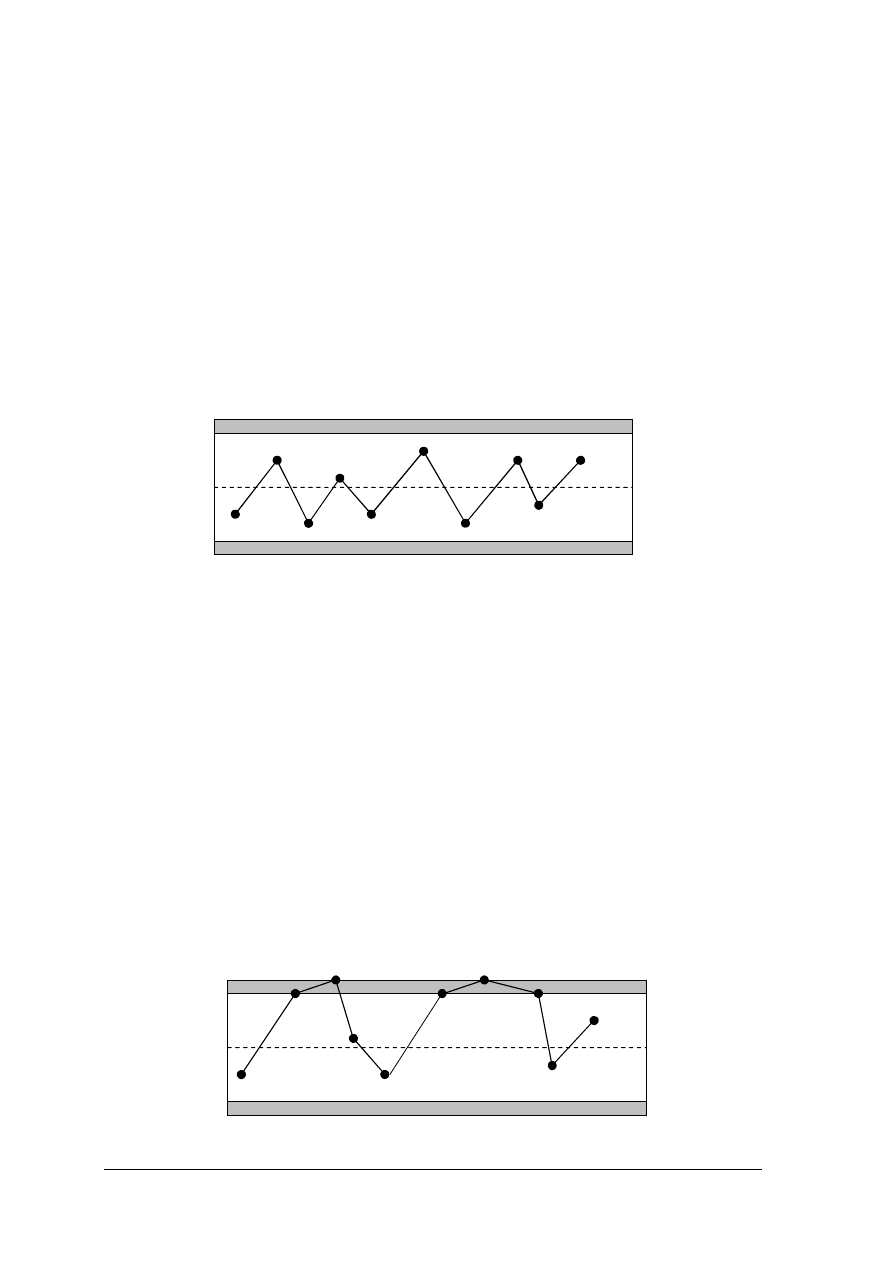
Na rysunku poniżej przedstawiono przykład takiego rozmieszczenie wyników pomiarów.

Rys.2. Wyniki pomiarów przy zakłóceniach losowych. [

Opracowanie własne]

Jeśli stwierdzimy, że wykreślone punkty spełniają powyższe wymagania, to można

powiedzieć, że proces znajduje się w stanie statystycznie uregulowanym, tzn. zmienności
między obserwowanymi wynikami badania próbki mogą być przypisane zespołowi przyczyn
losowych i ten zespół przyczyn nie ulega zmianom w czasie.
b) zakłócenia specjalne są przyczyną powstawania zmienności, których nie jesteśmy
w stanie przewidzieć, a ich przyczyny są wbudowane w proces. Taką przyczyną może być np.
złe samopoczucie operatora, albo nieregularnie działający proces. Do wykrycia zmienności
specjalnych w procesie, a następnie ustalenia ich przyczyn, stosuje się metody statystyczne.
Jeśli dokonalibyśmy pomiarów wyrobów z procesu, w którym występują zakłócenia specjalne
i wykreślilibyśmy te wyniki na wykresie to powinniśmy oczekiwać, że:
− punkty będą wychodziły poza naturalne granice zmienności,
− będą występowały pewne nielosowe układy kolejnych punktów.
Na rysunku poniżej przedstawiono przykład takiego rozmieszczenie wyników pomiarów.

Rys.3. Wyniki pomiarów przy zakłóceniach specjalnych. [

Opracowanie własne]

Linia środkowa

Granica naturalna

Granica naturalna

Linia środkowa

Granica naturalna

Granica naturalna

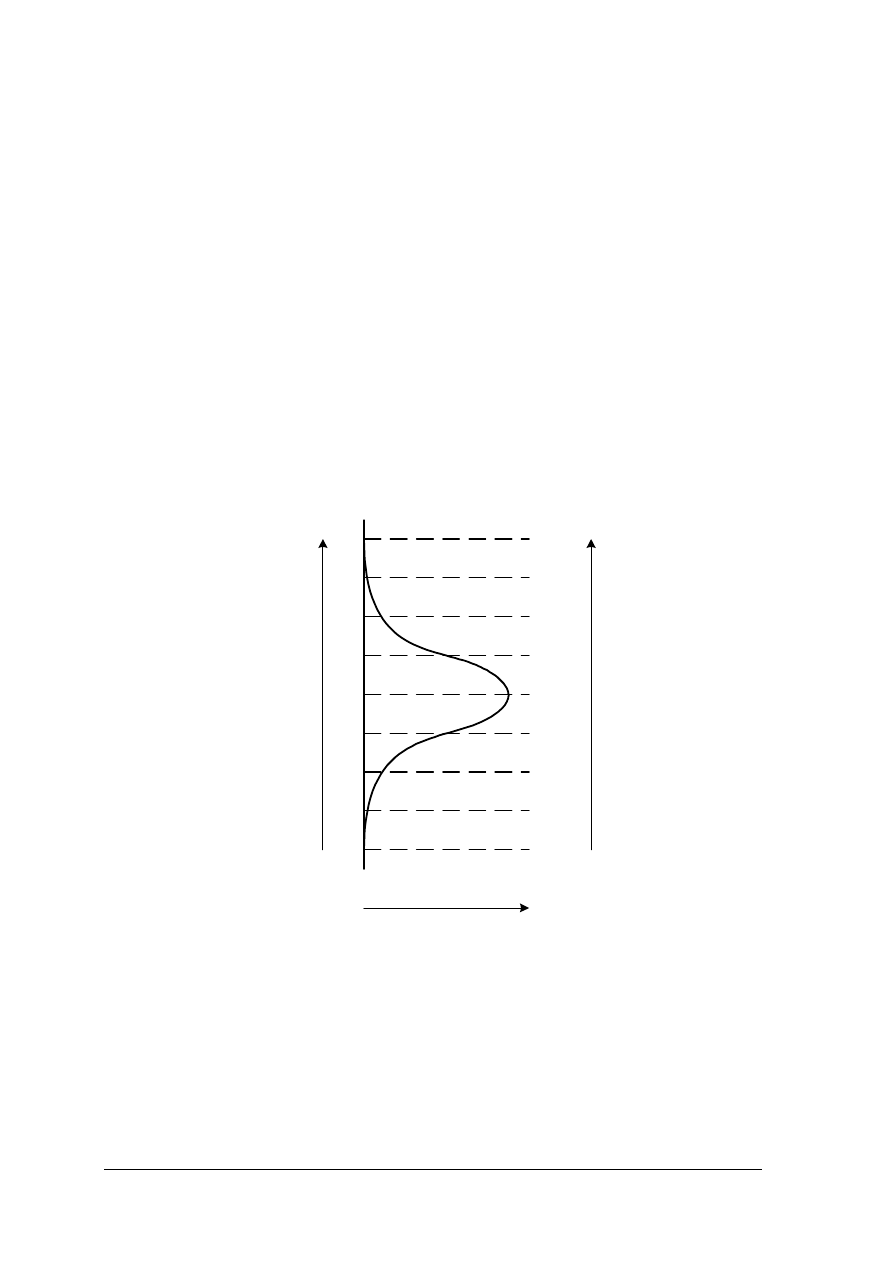
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

9

O procesie, na który mają wpływ przyczyny specjalne mówimy, że jest w stanie
statystyczne nieuregulowanym, jest procesem niestabilnym lub, że jest „poza kontrolą”. Taki
proces jest procesem nieprzewidywalnym, tzn. nie można przewidzieć jak proces będzie się
zachowywał w przyszłości.

Na początku stosowania statystycznego sterowania procesem należy zidentyfikować

i wyeliminować zakłócenia specjalne, tak, aby warunki, w jakich przebiega proces były
przewidywalne, wówczas jesteśmy w stanie sterować procesem statystycznie. Dopiero na tym
etapie jesteśmy w stanie identyfikować i zmniejszać zakłócenia losowe. W przypadku, kiedy
ponownie pojawiają się zakłócenia specjalne, należy je natychmiast wyeliminować, tak, aby
proces znów był pod kontrolą i sterowalny.

Rozkład normalny jest najbardziej powszechny w procesach przemysłowych. Krzywa

rozkładu jest symetryczna i swoim kształtem przypomina dzwon. Rozkład ten posiada dwa
zasadnicze parametry, średnią i odchylenie standardowe. Parametry te pozwalają na
porównanie działania procesu do tego jak działał poprzednio, możliwe jest także porównanie
procesu z innymi procesami.

Jednak najbardziej oczekiwany rozkład wyników pomiarów powinien przypominać

rozkład jak na rysunku poniższym.

+4

+3

+2

+1

0

-1

-2

-3

-4

od

c

h

y

len

ie

s

tanda

rdo

w

e

(

od

śr

edn

ie

j)

w

a

rto

ść

cz

ęstotliwość

wart.

średnia

34%

34%

14%

1,9%

0,1%

14%

1,9%

0,1%

Rys.4. Wyniki pomiarów w postaci rozkładu normalnego. [Opracowanie własne]

Podstawowe pojęcia statystyczne

Zbiorowością statystyczną (masą statystyczną lub populacją generalną) jest zbiór

jednostek objętych badaniem statystycznym.

Liczebność zbiorowości jest to ogół jednostek wchodzących w skład zbiorowości

statystycznej. Często stosuje się podział zbiorowości statystycznej na mniejsze części stosując

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

10

różne kryteria podziału i tworząc w ten sposób zbiorowości cząstkowe (populacje
cząstkowe), podzbiorowości (podpopulacje) lub grupy.

Jednostka statystyczna (jednostka badania lub jednostka obserwacji) to obiekt obserwacji

statystycznej podczas przeprowadzanego badania statystycznego. Jest to najmniejszy obiekt
dostarczający informacji statystycznych. Jednostki statystyczne nie są identyczne, ale mają
wiele cech wspólnych, które pozwalają zakwalifikować je do zbiorowości statystycznej.
O wyborze jednostki decyduje cel badania oraz konieczność zapewnienia dużej dokładności
wyników badania. Cechy statystyczne są to właściwości charakterystyczne dla danej
jednostki zbiorowości statystycznej. Dzielą się na cechy mierzalne zwane wymiernymi lub
ilościowymi oraz na cechy niemierzalne zwane niewymiernymi (jakościowe).

Cechy mierzalne to te właściwości jednostek statystycznych, które da się wyrazić za

pomocą liczb;, mierzymy je i podajemy w odpowiednich jednostkach np.: wzrost w m, waga
w kg, wydatki w zł. wymiary w m, pobór mocy w kWh itp.

Cechy niemierzalne to te właściwości, których nie można zmierzyć, a jedynie stwierdzić,

czy konkretny wariant tej cechy występuje u danej jednostki statystycznej.
Przykładami takich cech są: narodowość, płeć, wykształcenie, zawód, kolor samochodu,
rodzaj muzyki itp.

Warianty cech statystycznych to formy, w jakich mogą występować zarówno cechy

mierzalne jak i niemierzalne. Cechy niemierzalne mają skończoną ilość wariantów np. cecha
niemierzalna „płeć” może mieć dwa warianty: „mężczyzna” albo „kobieta”. Cechy mierzalne
posiadają dwa rodzaje zmienności wartości liczbowych: zmienność ciągłą lub zmienność
skokową.

Zmienność ciągła informuje, że badana cecha może przyjmować dowolne wartości

liczbowe z pewnego przedziału liczbowego np. wielkość zużycia wody przez dane miasto
wyrażona w m

3

.

Zmienność skokowa polega na tym, że badana cecha przyjmuje skończoną liczbę

wartości, które to zmieniają się skokowo; np. liczba wypadków samochodowych w ciągu
roku, liczba zarejestrowanych pojazdów mechanicznych czy spółek.

4.1.2. Pytania sprawdzające

Odpowiadając na pytania sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Jaką rolę pełni statystyka w procesie podejmowania decyzji?
2. Jak opisujemy model procesu decyzyjnego?
3. Na jakie klasy dzielimy proces podejmowania decyzji?
4. Jak rozumiesz pojęcie zbiorowość statystyczna?
5. Jakie warunki musi spełniać zbiór, aby można go uznać za zbiorowość statystyczną?
6. Podziel zbiorowość statystyczną na mniejsze zbiory, omawiając kryteria podziału.
7. Kogo lub co można nazwać jednostką statystyczną?
8. Co rozumiesz przez pojęcie liczebności zbiorowości statystycznej?
9. Co to jest cecha statystyczna? Jak dzielimy cechy statystyczne?
10. Podaj przykłady cech mierzalnych i niemierzalnych, jakie możesz zastosować przy

badaniu cech statystycznych w branży transportowej.

11. Podaj przykłady cech statystycznych o zmienności ciągłej.
12. Podaj przykłady cech statystycznych o zmienności skokowej.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

11

4.1.3. Ćwiczenia

Ćwiczenie 1

Na podstawie zamieszczonego poniżej szeregu statystycznego:
− określ rodzaj cechy statystycznej,
− wskaż warianty cechy,
− wskaż liczebność zbiorowości i liczebności cząstkowe.

Tabela do ćw. 1

.

Pracownicy pewnej firmy transportowej według wieku. [ dane umowne]

Wiek pracowników

Liczba pracowników

Poniżej 20 lat

7

21-30

38

31-40

23

41-50

18

51-60

7

Powyżej 60 lat

2

Razem

95

Sposób wykonania ćwiczenia:

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania dotyczącym zadań i organizacji statystyki,
2) odczytać dane z tabeli i wykonać obliczenia liczebności w stworzonej tabeli,
3) wskazać warianty cechy według podanych podpunktów,
4) zapisać wyniki w zeszycie przedmiotowym,
5) zaprezentować wyniki na forum klasy.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny.

Ćwiczenie 2

Korzystając z zasobów stron internetowych wybierz jedno z przedsiębiorstw lub firmę

spedycyjną i dokonaj krótkiej charakterystyki (analizy opisowej) ze szczególnym
uwzględnieniem profilu działalności. Wybierz te cechy, które będą potrzebne do opisu
i analizy firmy z punktu widzenia analizy statystycznej. Dokonaj klasyfikacji wybranych cech
statystycznych, omów i zaprezentuj różne warianty wybranych cech charakterystycznych dla
tej firmy.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania dotyczącym podstawowych pojęć statystycznych,
2) wejść na stronę internetową i wyszukać informacje o firmach spedycyjnych,
3) wybrać jedną z firm i dokonać krótkiej charakterystyki opisując:

− zakres działania,
− zasady działania,
− politykę jakości,
− koszty logistyki,
− sposób zatrudniania,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

12

− wielkość obrotów,
− inne dostępne statystyki ekonomiczne firmy,

4) rozpatrzyć wybrane cechy pod względem wariantów i cech zmienności,
5) wykonać zestawienie tabelaryczne dokonanego podziału z podpunktu 5.

Wyposażenie stanowiska pracy:
− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny.

Ćwiczenie 3

Na podstawie danych zamieszczonych w tabeli:

− określ rodzaje cech statystycznych,
− wskaż warianty cech,
− wskaż liczebność zbiorowości i liczebności cząstkowe.

Tabela do ćw. 2. Pojazdy i wypadki w latach 1995-2003 [dane umowne]

Okres

Pojazdy samochodowe

Liczba wypadków

1995

7089

36100

1996

7121

38227

1997

7643

43011

1998

8056

41467

1999

8596

46338

2000

9041

50532

2001

9860

54038

2002

11990

54005

2003

15476

54001

Razem

84872

417719

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:
1) zapoznać się z materiałem nauczania dotyczącym podstawowych pojęć statystycznych,
2) scharakteryzować cechy i warianty cech,
3) dokonać obliczeń liczebności zbiorowości i liczebności cząstkowych,
4) zanotować otrzymane wyniki w zeszycie,
5) zaprezentować wyniki na forum klasy.

Wyposażenie stanowiska pracy:
− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

13

4.1.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

zdefiniować pojęcie „statystyka”?





2)

określić rolę statystyki w procesie podejmowania decyzji?





3)

podać klasy podziału procesu decyzyjnego?





4)

określić zbiorowość statystyczną?





5)

podzielić zbiorowość statystyczną na mniejsze podzbiory?





6)

określić liczebność zbiorowości statystycznej?





7)

określić jednostkę statystyczną?





8)

wymienić i opisać cechy statystyczne?





9)

dokonać podziału cech statystycznych?





10) charakteryzować warianty cech statystycznych?





„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

14

4.2. Badanie statystyczne. Metody i organizacja badania

4.2.1. Materiał nauczania

Badanie statystyczne to zebranie, odpowiednie przetworzenie i analiza informacji

dotyczących określonej na początku badania zbiorowości (populacji) statystycznej i jej cech,
które podlegają badaniu.

Przed przystąpieniem do badania określamy przedmiot i zakres badania, czyli definiujemy

zbiorowość, jednostkę i cechy statystyczne, które będziemy badali. Później ustalamy rodzaj
(metodę) badania, który decyduje o jakości badania. Główne kryterium podziału metod badań
statystycznych zależy od liczebności zbiorowości statystycznej objętej badaniem.
Metody badań statystycznych
Metoda badania pełnego (generalnego, kompletnego, całkowitego, wyczerpującego) polega
na tym, że obserwacji poddana zostaje każda jednostka zbiorowości statystycznej, której
badanie dotyczy. Do badań pełnych zaliczamy:
− spis statystyczny – który dostarcza informacji do ustalenia stanu i struktury zjawiska

w ściśle określonym momencie. To badanie jednorazowe, w którym zbierana jest
informacja na odpowiednio przygotowanych formularzach wypełnianych przez
rachmistrzów spisowych. Przykładem takich badań jest spis ludności przeprowadzany
w państwach zwykle, co 10 lat, spis rolny, spis zakładów przemysłowych, spisy placówek
handlowych. Są to badania powszechne, bezpośrednie i podejmowane wyłącznie
w celach statystycznych.

− rejestrację statystyczną – polega na tym, że w terminie wyznaczonym na jej

przeprowadzenie zobowiązane osoby zgłaszają się w punktach rejestracji i udzielają
informacji objętych tematyką rejestracji. Przykładem takiego badania jest rejestracja
kierowców zawodowych, ewidencja urodzeń, ewidencja przychodów w magazynie itp.

− sprawozdawczość statystyczną – polega na tym, że jednostki sprawozdawcze sporządzają

sprawozdania statystyczne na jednolitych formularzach sprawozdawczych, zarówno
w sposób liczbowy jak i opisowy. Przykładem może być sprawozdawczość szkolna
prowadzona na poziomie klas, szkół, poprzez kuratoria oświaty itp.
Metoda badania częściowego (niekompletnego, niepełnego, niecałkowitego) polega na

obserwacji tylko pewnej części (wybranych jednostkach statystycznych) badanej zbiorowości
statystycznej. Jedną z metod badań częściowych jest metoda reprezentacyjna, która polega
na tym, że w celu zbadania całej zbiorowości statystycznej (populacji) wybiera się do badania
tylko pewną liczbę jednostek statystycznych reprezentującą badaną zbiorowość. Ta wybrana
grupa, to próba, a wnioski wysnute z badania próby uogólnia się na całą zbiorowość. Próbę
tworzy się z jednostek wybranych w sposób celowy lub losowy.

Wybór celowy jednostek do próby polega na tym, że prowadzący badanie dobiera

jednostki świadomie, na podstawie ogólnej znajomości badanego zjawiska.

Wybór losowy polega na tym, że dobór jednostek do próby jest przypadkowy, zgodny

z wybraną przez prowadzącego badanie metodą losowania.

Metody losowania próby :

− losowanie z wykorzystaniem tablic liczb losowych (przypadkowych) sprowadza się do

określenia numerami jednostek zbiorowości, które wejdą do próby,

− losowanie warstwowe polega na tym, że przed losowaniem dzielimy badaną zbiorowość

na jakościowo różniące się części (warstwy) i losujemy z każdej warstwy jednostki
zbiorowości próby. Każda jednostka należy tylko do jednej warstwy,

− metoda monograficzna polega na wszechstronnym opisie i szczegółowej analizie

pojedynczej jednostki lub niewielkiej liczby charakterystycznych jednostek badanej

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

15

zbiorowości statystycznej. Wybór jednostki jest świadomy, co oznacza, że wybieramy
jednostkę typową, powszechnie występującą, prowadząc dobór przez eliminacje,

− metoda ankietowa jest badaniem prowadzonym w sytuacjach, w których chcemy ustalić

nie same fakty, lecz opinie o nich. Informacje gromadzone są za pomocą ankiety
rozsyłanej do wytypowanego grona respondentów lub losowo wybranych osób. Nie
prowadzimy wówczas obserwacji bezpośrednio, lecz zwracamy się do ankietowanych
z prośbą o informacje. Ważnym elementem takiego badania jest odpowiednia konstrukcja
ankiety i formularza ankietowego (zwięzłe i jednoznaczne formułowanie pytań).
Szacunek statystyczny (ocena statystyczna) to takie postępowanie, w którym:

− na podstawie pewnych, znanych, cech zbiorowości ustalamy liczbowo inne, nieznane,

cechy tej samej zbiorowości,

− na podstawie cech znanej zbiorowości ustalamy te same lub pokrewne cechy zbiorowości

nieznanej.

Organizacja badania statystycznego

Każde badanie statystyczne składa się z czterech, niezależnych od badanej cechy

zbiorowości statystycznej, etapów badania:
− przygotowanie badania; (ustalenie celu badania, określenie zbiorowości statystycznej,

jednostki badania, jednostki sprawozdawczej),

− zebranie materiału statystycznego i przygotowanie do opracowania,
− opracowanie materiału statystycznego,
− prezentacja danych statystycznych,

Prawidłowa realizacja poszczególnych etapów badania umożliwia osiągnięcie celu badania.

Po ustaleniu celu badania, określeniu zbiorowości statystycznej i jednostki badania oraz po
wybraniu metody badania przystępujemy do gromadzenia danych statystycznych (informacje
indywidualne o każdej jednostce badanej zbiorowości – materiał statystyczny).

Materiał statystyczny pierwotny otrzymujemy wówczas, gdy przeprowadzamy odrębne

badania w celu uzyskania informacji o jednostce np. podczas spisów powszechnych.

Materiał statystyczny wtórny uzyskujemy wówczas, gdy informacje o badanych cechach

jednostki pochodzą z pozastatystycznych źródeł, ale są wykorzystywane w badaniach, np.
dane dotyczące ewidencji i statystyki ruchu naturalnego ludności.

Do zbierania danych statystycznych podczas przeprowadzania badań służą druki

statystyczne. Najczęściej wykorzystywanymi drukami statystycznymi są formularze
statystyczne oraz instrukcje statystyczne. Służą one do sprawozdawczości statystycznej, a tym
samym gromadzeniu materiału statystycznego w formie zapisów.

Formularz statystyczny to zbiór spisanych na papierze pytań dotyczących badanych cech

rozważanej zbiorowości statystycznej. Składa się z trzech głównych części:
− nagłówka (część tytułowa),
− kwestionariusza właściwego,
− części końcowej.

Nagłówek jest tą częścią, w której znajdują się dane identyfikacyjne dotyczące instytucji

prowadzącej badania (nazwa i adres instytucji) oraz dane identyfikacyjne jednostki
sprawozdawczej( nazwa, adres, numer statystyczny), a także tytuł formularza.

Kwestionariusz właściwy to zasadnicza część formularza, gdzie znajdują się pytania

dotyczące przedmiotu badania. Pytania mogą być przedstawione w formie tabelarycznej,
tekstowej lub w postaci mieszanej, tabelaryczno-tekstowej. Klasyczną formą kwestionariusza
jest forma tabelaryczna. Wypełniając formularz należy pamiętać, aby wypełnić wszystkie
pozycje formularza. Pozostawienie pozycji niewypełnionej uniemożliwia jednoznaczną
interpretację faktu.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

16

Jeśli nie możemy wypełnić części pozycji w formularzu, to stawiamy w tych miejscach

znaki umowne. W Polsce stosujemy w drukach statystycznych następujące znaki umowne:

Tabela 1. Znaki stosowane w drukach statystycznych. [3]

Rodzaj znaku Symbol

Znaczenie

kreska

-

zjawisko nie występuje

kropka

.

brak informacji lub brak wiarygodnych informacji o danym zjawisku

zero

0

zjawisko występuje w zbyt małych ilościach, by można je było
wyrazić w przyjętych jednostkach miary

krzyżyk

×

wypełnienie pozycji ze względu na układ formularza jest niemożliwe
lub niecelowe.

Część końcowa formularza statystycznego zawiera podpisy osób odpowiedzialnych za

prawidłowość danych zawartych w formularzu oraz datę. Czasami, gdy wypełnienie
formularza statystycznego wymaga skomplikowanych wyjaśnień dołącza się instrukcję
statystyczną. Jest to zwięzła i czytelna broszura zawierająca następujące dane;
− podstawę prawną, na mocy której jest prowadzone badanie,
− określenie przedmiotu badania,
− ustalenie definicji i wyjaśnienie pojęć, które mogą nasuwać wątpliwości jednostkom

sprawozdawczym,

− omówienie okresów sprawozdawczych,
− terminy przesyłania sprawozdań przez jednostki sprawozdawcze poszczególnych

szczebli,

− rozdzielnik, czyli wykaz jednostek, do których przesyłane są sprawozdania przez

jednostki sprawozdawcze poszczególnych szczebli.

Kontrola materiału statystycznego i jej rodzaje

W zebranym materiale statystycznym (materiał surowy) często występują różnego rodzaju

braki i błędy i dlatego przed wykorzystaniem zebranych informacji poddajemy je kontroli,
najpierw kontroli formalnej materiału statystycznego, która obejmuje kontrolę kompletności
materiału statystycznego, kontrolę zupełności zapisów oraz kontrolę zgodności rachunkowej.

Kontrola materiału surowego powoduje, że część błędów popełnionych przy zbieraniu

informacji eliminujemy. Niemniej jednak materiał przekazywany do opracowania bywa
jeszcze obarczony pewną liczbą błędów, które mogą być błędami przypadkowymi lub
systematycznymi popełnianymi rozmyślnie przez wypełniającego formularz bądź
nieumyślnie.

Badanie statystyczne, które jest celem naszych działań powinno być przeprowadzone

z zagwarantowaniem najwyższej dokładności wyników, jakie można uzyskać w danych
warunkach. Stopień koniecznej dokładności danych wyników jest uzależniony od tematu
i celu badania. Prezentowane dane z badania muszą być danymi pewnymi.

4.2.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Jakie jest główne kryterium podziału badań statystycznych?
2. Jakie badania nazywamy pełnymi, a jakie częściowymi? Podaj przykłady.
3. Wymień etapy badania statystycznego.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

17

4. Jakie znasz przykłady spisów statystycznych przeprowadzonych w dziedzinach życia

gospodarczego?

5. Co to jest szacunek statystyczny, a co to jest rejestracja statystyczna?
6. Jakie znasz metody losowania próby?
7. Jakie znasz zasady doboru jednostek do próby statystycznej?
8. Jakie badanie statystyczną można przeprowadzić metodą reprezentacyjną?
9. Co jest konieczne do precyzyjnego określenia zbiorowości statystycznej i jednostki

statystycznej?

10. Jak dzielimy materiał statystyczny?
11. Jakie znasz rodzaje druków statystycznych?
12. Jak zbudowany jest formularz statystyczny?
13. Co to są tablice statystyczne i z czego się składają?
14. Jakie znasz umowne znaki stosowane w tablicach statystycznych?
15. Co to jest instrukcja statystyczna i gdzie jej używamy?
16. Jakie znasz rodzaje rejestracji podmiotów gospodarczych lub osób fizycznych?
17. Kiedy odbywa się kontrola materiału statystycznego?
18. Jakie znasz rodzaje kontroli materiału statystycznego?
19. Jakie typy i rodzaje błędów statystycznych można spotkać w badaniu statystycznym?
20. Które z błędów statystycznych poważniej odbijają się na jakości opracowywanego

materiału?

4.2.3. Ćwiczenia

Ćwiczenie 1

Zaprojektuj ankietę dla firmy transportowej (istniejącej bądź wymyślonej), która

zostałaby skierowana do potencjalnych klientów tej firmy. W ankiecie należy uzyskać opinię
ewentualnych klientów na temat: Firma spedycyjna w oczach jej klientów:
− skłonności klienta do zainteresowania konkretnie tą firmą,
− potrzeb klienta zgodnych z możliwościami tej firmy,
− innych dodatkowych potrzeb, których oczekiwaliby od firmy,
− ceny, jaką mogliby uiścić za usługi świadczące przez firmę,
− formy świadczonych usług,
− dodatkowych informacji, nie związanych z profilem działalności firmy.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania dotyczącym organizacji badania statystycznego,
2) krótko scharakteryzować wybraną firmę,
3) wybrać istotne elementy świadczonych przez firmę usług,
4) wymienić potrzeby klientów w zakresie świadczonych usług,
5) skonstruować ankietę, pytania mogą mieć różny charakter zgodny z zasadą

konstruowania ankiety.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym edytor tekstu.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

18

Ćwiczenie 2

Wykorzystując podane informacje dotyczące pewnego zjawiska statystycznego oraz

informacje zamieszczone w materiale nauczania dotyczącym organizacji badania
statystycznego wykonaj poniższe ćwiczenie:

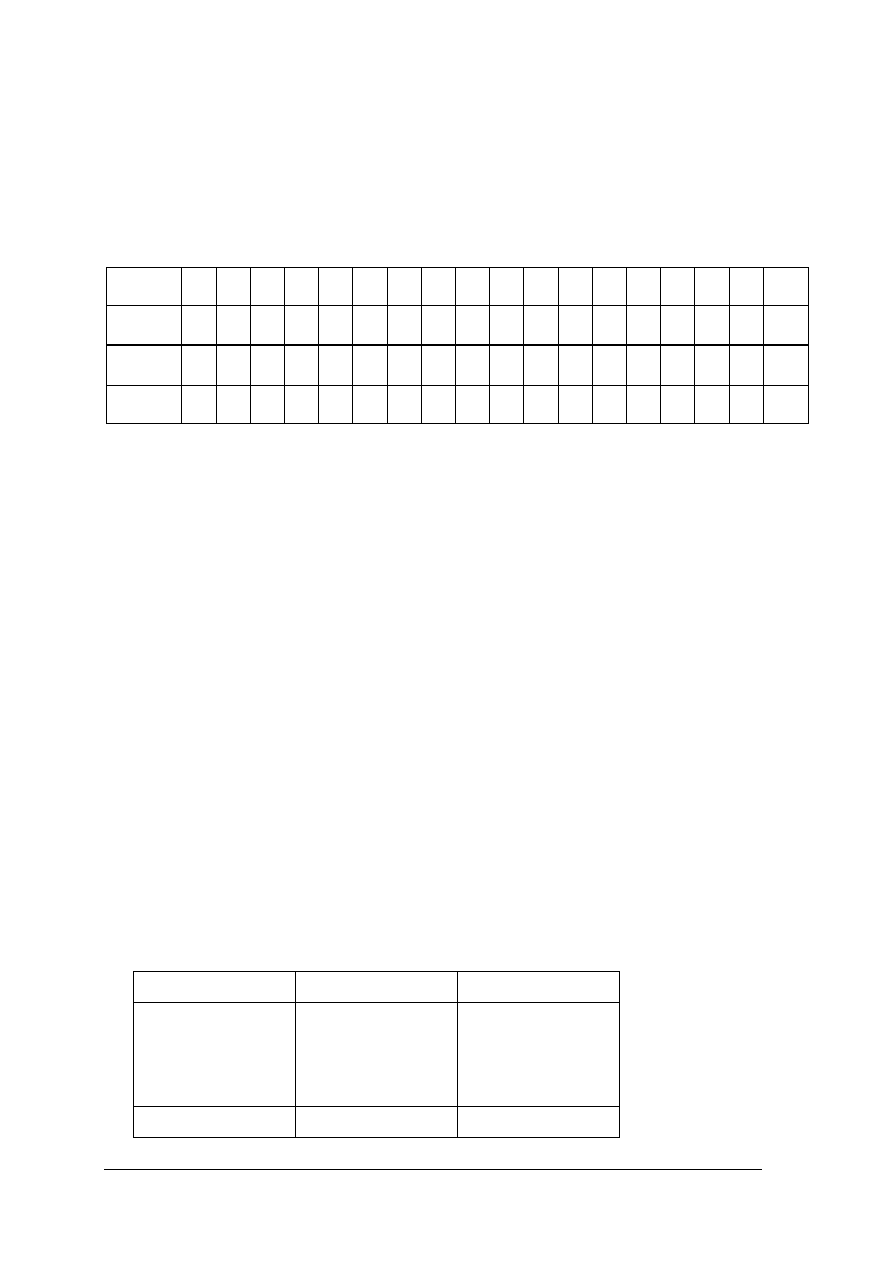
Przewóz towarów w firmie transportowej (w tonach) w okresie rozliczeniowym (36 dni)

kształtował się następująco, według zebranych danych zamieszczonych w tabeli:

Tabela do ćw. 2. [dane umowne]

Kolejny
dzień

1

2

3

4

5

6

7

8

9

10 11 12 13 14 15 16 17 18

Przewóz
[ ton ]

60 67 71 76 78 81 88 96 98 82 56 79 99 77 61 42 51 96

Kolejny
dzień

19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

Przewóz
[ ton ]

89 93 96 58 45 82 77 76 84 58 59 91 87 83 75 71 86 79

Na podstawie powyższych danych wybierz losowo trzy próbki statystyczne składające się:

a) 10 jednostek,
b) 15 jednostek,
b) 20 jednostek.

Oblicz średni przewóz dla każdej próby, a następnie porównaj otrzymane wyniki.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania,
2) utworzyć nowy arkusz w programie Excel,
3) wypełnić arkusz podanymi danymi, kolumny tabeli opatrzyć nagłówkami, a całą tabelę
sformatować,
4) zastosować formuły tablicowe w obliczeniach,
5) wyznaczyć wskazane w ćwiczeniu próbki statystyczne,
6) zastosować funkcje obliczające średni przewóz dla poszczególnych próbek,
7) dokonać interpretacji i analizy otrzymanych rozwiązań.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny.

Ćwiczenie 3

W wyniku badań pełnych, które były przeprowadzone w marcu 2006 r w pewnej firmie

transportowej uzyskano informacje na temat wynagrodzenia pracowników zatrudnionych
w tejże firmie. Uzyskane wyniki zamieszczono w tabeli:

Tabela do ćw. 3. Pracownicy firmy transportowej w marcu 2006r. [ dane umowne]

Płace w zł (x

io

- x

it

> Liczba kobiet

Liczba mężczyzn

2500-2700
2700-2900
2900-3100
3100-3300
3300-3500

70

230
420
370
210

120
320
510
620
330

Razem

1300

1900

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

19

Jaka byłaby optymalna struktura próby statystycznej ( z punktu widzenia płac i płci),

gdyby badanie przeprowadzone było metodą badania częściowego, jeżeli wiadomo, że do
próby należy włączyć 200 pracowników?

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania,
2) utworzyć nowy arkusz w programie Excel,
3) wypełnić arkusz danymi, kolumny tabeli opatrzyć nagłówkami, a tabelę odpowiednio
sformatować,
4) zastosować formuły tablicowe w podanych obliczeniach,
5) dokonać obliczeń dotyczących wynagrodzenia pracowników,
6) dokonać obliczeń dotyczących struktury pracowników w badanej próbie,
7) dokonać interpretacji i analizy otrzymanych rozwiązań.

Wyposażenie stanowiska pracy:

− komputer posiadający arkusz kalkulacyjny.

4.2.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

podać główne kryteria podziału badań statystycznych?





2)

scharakteryzować badania pełne i częściowe oraz podać przykłady?





3)

wymienić etapy badania statystycznego?





4)

wymienić przykłady spisów statystycznych przeprowadzanych w różnych
dziedzinach życia gospodarczego?





5)

wyjaśnić różnice pomiędzy szacunkiem statystycznym a rejestracją
statystyczną?





6)

wymienić metody losowania próby i doboru jednostek do próby?





7)

omówić metodę reprezentacyjną przeprowadzania badania statystycznego?





8)

omówić kryteria podziału materiału statystycznego?





9)

wymienić rodzaje druków statystycznych?





10) omówić budowę i znaczenie formularza statystycznego?





11) omówić budowę i zastosowanie tablic statystycznych?





12) wymienić znaki umowne stosowane w tablicach statystycznych?





13) omówić zasadę zastosowania instrukcji statystycznej?





14) wymienić rodzaje rejestracji podmiotów gospodarczych lub osób

fizycznych?





15) wymienić rodzaje kontroli materiału statystycznego?





16) wymienić rodzaje błędów spotykanych w badaniu statystycznym?





17) omówić znaczenie kontroli i błędów wpływających na badanie

statystyczne?





„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

20

4.3. Opracowanie materiału statystycznego

4.3.1. Materiał nauczania

Grupowanie statystyczne

Pierwszym krokiem w opracowaniu statystycznym jest grupowanie statystyczne, które

jest elementem przejściowym od materiałów informujących o podanych jednostkach
statystycznych do materiałów dających obraz całej zbiorowości lub jej poszczególnych części.

Grupowanie statystyczne polega na podziale badanej zbiorowości statystycznej na

jednorodne części (grupy, klasy) według cech. W zależności od liczby cech, które badamy
podstawą podziału badanej zbiorowości statystycznej są:
− grupowanie proste – badaną zbiorowość dzielimy na mniejsze jednostki ze względu na

jedną cechę charakterystyczną, np.: grupujemy przedsiębiorstwa według wielkości
produkcji lub według ilości zatrudnionych. Przedstawiamy i obserwujemy tylko jeden
aspekt badanego zjawiska.

− grupowanie złożone - w podziale zbiorowości statystycznej uwzględniamy kilka cech

i dzielimy badaną zbiorowość na podgrupy wyodrębnione na podstawie jednej cechy
charakterystycznej np. grupowanie jednostek gospodarczych według działów gospodarki,
a w ramach poszczególnych działów według wielkości produkcji czy zatrudnienia.
Ustalenie liczby grup (stopień podziału zbiorowości statystycznej) zależy od rodzaju

zjawiska i celu badania. Czasami konieczny jest podział zbiorowości statystycznej na bardzo
wiele mniejszych zbiorowości np. podział produkcji przemysłowej na wyroby.

Po podzieleniu zbiorowości na grupy ustalamy kolejność oraz nazwy tych grup

i tworzymy szereg klasyfikacyjny, uporządkowany logicznie i przejrzyście. Dla cech
niemierzalnych podstawową zasadą uporządkowania jest zachowanie kolejności grup np.
grupując pracowników według wykształcenia otrzymujemy następujące grupy wykazu
klasyfikacyjnego:
− wykształcenie wyższe,
− wykształcenie średnie zawodowe,
− wykształcenie średnie ogólnokształcące,
− wykształcenie zasadnicze zawodowe,
− wykształcenie gimnazjalne,
− wykształcenie podstawowe.

Dla cech mierzalnych grupy wykazu porządkujemy zgodnie ze wzrostem cechy, tzn. od

wartości najmniejszej do największej wartości cechy. Wyodrębnione podczas grupowania
części zbiorowości statystycznej są przedziałami klasowymi.

Główną czynnością w opracowaniu materiału statystycznego są prace podliczeniowe

(zliczanie jednostek charakteryzujących się określonymi cechami statystycznymi lub
kombinacjami tych cech). Wybór odpowiedniej metody (techniki) zliczania zależy od
liczebności badanej zbiorowości i rodzaju formularzy wykorzystywanych do zbierania
materiałów statystycznych.

Zliczanie bezpośrednie polega na tym, że zliczamy przypadki lub sumujemy badane

wielkości bezpośrednio z zapisów zamieszczonych w sprawozdaniach, ankietach. Jest to
ręczna metoda opracowania materiału statystycznego, w której wszystkie wyniki
umieszczamy w zbiorczych zestawach tabelarycznych.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

21

Zliczanie sposobem kreskowym polega na tym, że przygotowujemy roboczy arkusz,

w którym obok wyszczególnienia wszystkich cech oraz odmian cech pozostawia się miejsce
na wpisanie kresek. Każda kreska reprezentuje jednostkę statystyczną. Otrzymane wyniki
przenosi się do tabeli zbiorczej.

Opracowanie sposobem maszynowym stosuje się wówczas, gdy występuje duża liczba

badanych jednostek zbiorowości i wiele odmian badanych cech statystycznych. To obecnie
najczęściej stosowana metoda zliczania materiału statystycznego. Poszczególne informacje
w formularzach statystycznych zastępuje się umownymi znakami cyfrowymi, które przenosi
się na karty określonego formatu poprzez wytłaczanie otworów w odpowiednich miejscach
karty.

Elektroniczna technika obliczeniowa polega na tym, że za pomocą odpowiedniego

programu komputerowego oraz magnetycznych nośników informacji (taśma, dyski
magnetyczne, pen drive) zlicza się otrzymane dane o badanej zbiorowości statystycznej
i tworzy banki danych.

Zgromadzony materiał statystyczny, otrzymany w wyniku badania statystycznego

opracowuje się i prezentuje, aby poznać całą badaną zbiorowość. Opracowanie materiału
statystycznego to uporządkowanie i pogrupowanie materiału oraz zaprezentowanie go
w odpowiednio przejrzystej formie.
Rozróżniamy trzy podstawowe formy prezentacji danych statystycznych:
− forma tabelaryczna - przedstawienie danych w tablicach statystycznych,
− forma graficzna -przedstawienie graficzne danych w postaci wykresów statystycznych,
− forma opisowa - włączenie danych do tekstu.

Tabela przedstawia szereg statystyczny pogrupowany według wariantów jednej cechy.

Tabela 2. Sieć miejska kraju w 1997r (stan w dniu 31 XII) [opracowanie własne]

Grupy miast według liczby ludności

Liczba miast

Ogółem

poniżej 5000

5000-9999

10000-19999
20000-49999
50000-99999

100000-199999
200000 i więcej

870
278
181
182
137

50
22
20

Szeregi rozdzielcze (strukturalne) przedstawiają podział zbiorowości statystycznej na

części z określonego, rzeczowego punktu widzenia. Podziału dokonuje się biorąc pod uwagę
czy badana cecha jest niemierzalna czy mierzalna. Szereg rozdzielczy dzieli zbiorowość na
jednorodne części zróżnicowane pod względem badanej cechy. Wśród szeregów
rozdzielczych wyróżnia się szeregi proste i skumulowane. W szeregu prostym podane są
liczebności poszczególnych klas. Szereg skumulowany przedstawia strukturę całej
zbiorowości informując o tym, jaka jest łączna liczebność danej klasy i wszystkich
poprzednich klas.

Innego rodzaju tabelaryczna prezentacja danych to szeregi wyliczające, w których

prezentowane są informacje dotyczące wymienionych kolejno różnych wielkości
statystycznych.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

22

Tabela 3. Ważniejsze dane o sytuacji społeczno-gospodarczej kraju (produkcja niektórych wyrobów)

[opracowanie własne]

L.p.

Wyszczególnienie

Jednostka miary

1999

1
2
3
4
5
6
7
8
9

10

Węgiel kamienny
Energia elektryczna
Stal surowa
Miedź elektrolityczna
Obrabiarki do metalu
Samochody osobowe
Odbiorniki telewizyjne
Tworzywa sztuczne
Cement
Papier

mln t
TWh
mln t

tys. t

tys. szt.
tys. szt.
tys. szt.

tys. t

mln t

tys. t

138
143
11,6
441
17,2
520
3020
860
15,6
1473

Szeregi geograficzne prezentują terytorialne rozmieszczenie lub natężenie badanych

wielkości

statystycznych

(cech,

zjawisk).

To odmiana

szeregów

rozdzielczych

(strukturalnych), gdyż przedstawiają strukturę przestrzenną badanej zbiorowości.

Szeregi dynamiczne przedstawiają rozwój zjawiska w czasie. To odmiana szeregów

rozdzielczych, gdyż pokazują strukturę czasową badanego zjawiska. Szeregi dynamiczne
dzielimy na dwie grupy:
− szeregi okresów, w których zmiany zjawisk przedstawione są w przeciągu pewnego

okresu (roku, kwartału),

− szeregi chwil charakteryzują zmiany badanego zjawiska w ściśle określonych chwilach.
Tablice statystyczne, w których przedstawione są zgrupowane i opracowane materiały
statystyczne służą do prezentacji uporządkowanych informacji o badanym zjawisku
i zbiorowości statystycznej.
Tablica statystyczna składa się z czterech części:
− tytułu,
− właściwej tablicy,
− uwag wyjaśniających,
− informacji o źródle danych.

Tytuł tablicy to krótka informacja o badanej zbiorowości statystycznej, cesze badania,

czasie i miejscu badania.

Tablica właściwa składa się z wierszy, z czego pierwszy to „główka” z tytułami kolumn

oraz pionowych kolumn z wydzieloną pierwszą „boczkiem” tablicy.

Uwagi wyjaśniające to dodatkowe wyjaśnienia wierszy i kolumn lub całej tablicy.

Informacje o źródle danych mówią skąd pochodzą liczby zamieszczone w tablicy.

Graficzna prezentacja danych statystycznych

Za pomocą wykresów możemy przedstawić dane statystyczne (materiały liczbowe)

uzyskane w badaniu. W tablicach statystycznych opisujemy je za pomocą liczb, natomiast
stosując wykresy opis ograniczamy się jedynie do obrazu graficznego. Jest to skondensowana
forma prezentacji danych. Wykresy prezentują badane zjawisko bezpośrednio, przejrzyście
i bardziej obrazowo niż liczby. Szybciej również przemawiają do wyobraźni odbiorcy
i pozwalają zorientować się w całości rozpatrywanych zagadnień, a także są doskonałym
narzędziem popularyzowania i propagowania treści w nich zawartych.

Wykres składa się z kilku elementów; najważniejsze z nich to tytuł, pole wykresu,

legenda oraz informacje o źródle danych.

Metoda liniowa to najpopularniejszy sposób prezentacji danych, w której prezentowane

wielkości przedstawione są w postaci pionowych lub poziomych odcinków. Poszczególne

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

23

odcinki są obrazem, w odpowiedniej skali, rozważanych wielkości statystycznych. Przy
liniach podaje się liczby określające dokładny poziom ilustrowanej wielkości statystycznej.
Rysunek musi zawierać skalę, za pomocą której przedstawiamy zobrazowane wielkości. Jeśli
wykres rysujemy poziomo, to skala jest pod wykresem, jeśli pionowo, to z lewej strony linii
pionowych.

Metoda powierzchniowa polega na stosowaniu wykresów powierzchniowych,

charakteryzujących zbiorowość lub zjawiska za pomocą powierzchni figur płaskich.
W metodzie tej obowiązuje zasada zachowania proporcjonalności powierzchni figur do
prezentowanych wielkości. Najczęściej spotykanymi wykresami są; wykres słupkowy i koła,
czyli wykresy kołowe. W wykresach słupkowych rysujemy prostokąty luźno stojące lub
przylegające do siebie. W wykresach słupkowych prostokąty można rysować pionowo lub
poziomo. W

ilustrowaniu

liczebności

można rysować koła o powierzchniach

proporcjonalnych do liczebności. Należy wówczas pamiętać o zachowaniu proporcji
powierzchni kół w stosunku do liczebności zjawiska.

Metoda ilościowa polega na tym, że wielkość zjawiska zostaje zaprezentowana

wielokrotnością dowolnego znaku graficznego. Pojedynczy znak graficzny wyraża określoną
liczbę jednostek. Jest to dość wyrazista i poprawna metoda, ale nie jest całkowicie dokładana.

Metoda ilościowo-symbolowa (metoda wiedeńska) polega na tym, że zamiast znaków

stosuje się małe rysunki-symbole, które przedstawiają prezentowane zjawisko.

Kartogram to wykres mapowy, który przedstawia terytorialne rozmieszczenie wielkości

statystycznych i jest ilustracją szeregu geograficznego. Najczęściej stosuje się go do
prezentacji zjawisk w obrębie jednostek terytorialnych. Jest sporządzony na mapie lub planie
za pomocą:
− symboli na mapie rozmieszcza się symbole obrazujące zjawisko,
− powierzchni na mapie kreskujemy lub barwimy zgodnie z wartością zjawiska,
− punktów na mapie umieszczamy punkty, ich liczba jest proporcjonalna do wielkości

zjawiska,

− figur geometrycznych na obszarze jednostek terytorialnych przedstawia się jednocześnie

strukturę prezentowanej zbiorowości.
Wykresy w układzie współrzędnych to wykresy słupkowe, czyli histogramy oraz wykresy

liniowe, czyli diagramy. Stosujemy je wówczas, gdy przedstawiamy szeregi rozdzielcze lub,
gdy przedstawiamy rozwój zjawiska w czasie, czyli prezentujemy szeregi dynamiczne.
Wykresy w prostokątnym układzie współrzędnych przedstawiamy zawsze w pierwszej
ćwiartce.

Opisowy charakter prezentacji danych statystycznych umożliwia podkreślenie wybranych

walorów badanego zjawiska, lecz jest mało czytelny i obrazowy.

Metody mieszane polegają na tym, że do prezentacji danych statystycznych używamy

zarówno umiejętnie zbudowanego szeregu lub tablicy statystycznej jako skondensowaną
formę prezentacji, jak i metody opisowej, która od razu objaśnia wszelkie zastosowane dane.
Jest to doskonałe połączenie kilku metod do jednej prezentacji.

4.3.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Jakie znasz podstawowe metody prezentacji materiału statystycznego?
2. Co to jest szereg statystyczny i jakie znasz rodzaje szeregów statystycznych?
3. Jaka jest różnica między szeregiem statystycznym a tablicą statystyczną?
4. Jaki znasz metody graficznej prezentacji danych statystycznych?
5. Jakie znasz odmiany metody powierzchniowej prezentacji danych statystycznych?

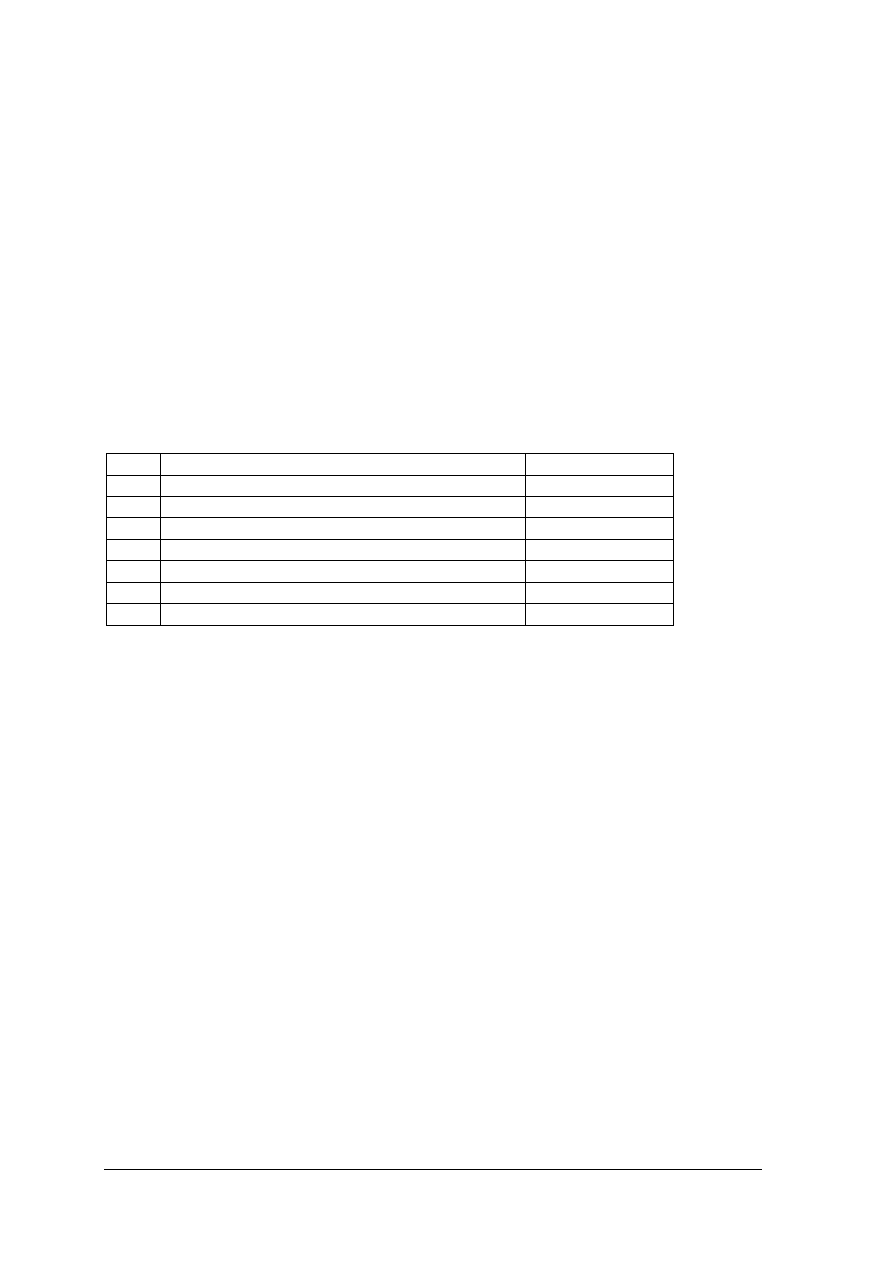
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

24

6. Jakie wykresy zastosujesz do prezentacji szeregów rozdzielczych, a jakie do szeregów

dynamicznych?

7. Kiedy można zastosować metody mieszane prezentacji danych statystycznych? Jakie są

ich zalety?

8. Kiedy można przedstawić materiał statystyczny w układzie współrzędnych?
9. Co to jest histogram i diagram?
10. Co to jest kartogram? Kiedy go stosujemy?

4.3.3. Ćwiczenia

Ćwiczenie 1

Na podstawie danych z tabeli, w której zestawiono koszty logistyki w sprzedaży

przedstaw poniższe dane za pomocą poznanych metod prezentacji materiału statystycznego
wykorzystując dostęp do komputera i arkusza kalkulacyjnego lub innych programów.

Tabela do ćw. 1. Koszty logistyki w wybranym przedsiębiorstwie w roku 2005 [opracowanie własne]

L.p.

Rodzaj kosztów

Wartość w zł.

1.

Koszty transportu

50382303

2.

Kaszty magazynowania

563255

3.

Koszty logistyki wydziałów produkcyjnych

2590022

4.

Koszty sieci dystrybucji

48547723

5.

Koszty administracyjne

1107491

6.

Koszty kapitału zamrożonego w zapasach

5666745

7.

Razem

108857639

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania,
2) przygotować tabelę z danymi dotyczącymi kosztów logistyki w sprzedaży,
3) zaznaczyć odpowiedni zakres danych i uruchomić kreatora wykresów,
4) za pomocą kreatora wykresów wybrać odpowiedni wykres do przedstawionego szeregu

statystycznego i go sformatować,

5) po otrzymaniu wykresu odpowiednio go opisać,
6) przedstawić koszty logistyki za pomocą innych kreatorów,
7) każdy otrzymany wykres sformatować i opisać,
8) dokonać analizy otrzymanych rozwiązań,
9) wykonać prezentację graficzną kosztów logistyki i zaprezentować w klasie.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny.

Ćwiczenie 2

Dokonaj grupowania przedsiębiorstw według liczby zatrudnionych w nich pracowników

wiedząc, że liczba pracowników w poszczególnych przedsiębiorstwach wynosi:

100;125;170; 144; 235; 301; 100; 100;170; 144; 235; 100; 301; 170; 301; 125; 125; 125;

235; 125; 235; 125;125; 100; 144; 301; 144; 144; 170; 144; 144; 144.

Sposób wykonania ćwiczenia

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

25

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania dotyczącym opracowania materiału statystycznego,
2) w arkuszu kalkulacyjnym zbudować tablicę statystyczną,
3) ustalić wariant badanej cechy i rodzaj szeregu statystycznego,
4) dokonać grupowania przedsiębiorstw wg liczby zatrudnionych uwzględniając rozstęp

równomierny w poszczególnych przedziałach klasowych,

5) dokonać obliczeń ile przedsiębiorstw mieści się w wybranym przedziale klasowym

i przedstawić wyznaczony szereg statystyczny na forum klasy.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny.

Ćwiczenie 3

Dokonaj zliczania metodą kreskową materiału statystycznego dotyczącego 35 robotników

firmy transportowej, których badano z punktu widzenia stażu pracy w macierzystym
zakładzie pracy i w transporcie ogółem.

Ogólny staż pracy robotników wynosił: 4; 2; 5; 2; 3; 5; 5; 4; 3; 2; 1; 3; 2; 3; 5; 2; 3; 5; 2;

1; 1; 1; 5; 4; 4; 3; 2; 3; 2; 1; 1; 2; 2; 2; 1,

a staż pracy w firmie transportowej: 3; 2; 4; 2; 3; 1; 1; 1; 1; 1; 4; 4; 4; 3; 2; 1; 2; 1; 1; 2; 1;

2; 2; 5; 5; 2; 3; 2; 1; 2; 2; 2; 5; 1; 1.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:

1) odpowiedzieć, na czym polega metoda zliczania sposobem kreskowym,
2) sporządzić arkusze robocze do zliczania materiału,
3) przygotować tablice wynikowe, aby zaprezentować wyniki zliczania,
4) przedstawić uzyskane wyniki w sposób staranny i czytelny na forum grupy.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny

Ćwiczenie 4

Wyszukaj w małym roczniku statystycznym po jednym przykładzie każdego rodzaju

szeregu statystycznego. W uzyskanych w ten sposób szeregach znajdź i omów umowne znaki
statystyczne stosowane w tablicach statystycznych. Wyjaśnij ich znaczenie. Tak
przygotowane szeregi statystyczne poddaj graficznej prezentacji danych statystycznych,
wykorzystując możliwie najwięcej sposobów i metod graficznej prezentacji danych
statystycznych.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania dotyczącym graficznej prezentacji danych,
2) statystycznych oraz opracowania materiału statystycznego,
3) przynieść mały rocznik statystyczny, uaktywnić dostęp do internetu,
4) wykorzystać dane statystyczne zamieszczone w roczniku i wybrać szeregi statystyczne,
5) wypisać umowne znaki statystyczne i omówić ich znaczenie,
6) skonstruować robocze szeregi statystyczne w arkuszu kalkulacyjnym,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

26

7) wykonać wszystkimi poznanymi metodami graficznymi prezentacje wybranych
8) szeregów statystycznych ( w razie kłopotów poproś o pomoc nauczyciela),
9) dokonać prezentacji wykonanego ćwiczenia innym uczestnikom zajęć.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny,
− drukarka,
− mały rocznik statystyczny.

4.3.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

wymienić metody prezentacji materiału statystycznego?





2)

zdefiniować

szereg

statystyczny

i

wymienić

rodzaje

szeregów

statystycznych?





3)

omówić różnice między szeregiem statystycznym a tablicą statystyczną?





4)

wymienić metody graficznej prezentacji danych statystycznych?





5)

wymienić rodzaje metody powierzchniowej prezentacji materiału
statystycznego?





6)

dostosować rodzaj metody graficznej prezentacji danych do rodzaju szeregu
statystycznego ?





7)

zastosować mieszaną metodę prezentacji danych statystycznych?





8)

przedstawić materiał statystyczny w układzie współrzędnych?





9)

podać różnicę miedzy histogramem a diagramem?





10) zastosować kartogram do prezentacji materiału statystycznego?





„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

27

4.4. Podstawowe wiadomości z analizy statystycznej

4.4.1. Materiał nauczania

Opracowany i odpowiednio przedstawiony materiał statystyczny w dalszej procedurze

podlegać będzie analizie statystycznej, która jest ostatecznym celem każdego badania
statystycznego. Na podstawie dokonanej analizy badania statystycznego wyciągamy
odpowiednie wnioski i uogólniamy zbadany materiał na całość zjawisk i procesów. Analiza
jest więc po to, aby wykryć prawidłowości i związki zachodzące w badanej zbiorowości,
oraz zbadanie przyczyn określonego kształtowania się badanego zjawiska.

Analiza natężenia

Do badania analizy natężenia będziemy posługiwali się pewnymi miarami statystycznymi,

które pomogą nam później w wyciąganiu wniosków i uogólnień stawianych na całą
zbiorowość statystyczną.

Liczby bezwzględne (absolutne) otrzymujemy przez zliczenie poszczególnych jednostek

lub zsumowanie wartości cech mierzalnych; są zawsze wyrażone jako liczby mianowane np.
stan ludności w dniu spisu, waga badanych itp. Nie zawsze są odpowiednim miernikiem do
dalszej analizy, gdyż nie ilustrują w pełni badanych zjawisk i procesów.

Liczby względne (stosunkowe) - są ilorazami liczb bezwzględnych opisujących badane

zjawiska związane ze sobą. Liczby te charakteryzują natężenie (intensywność) zjawisk, czyli
wskaźnik natężenia lub charakteryzują strukturę zjawiska.

Wskaźnik natężenia W

n

(współczynnik natężenia)- obliczamy wtedy, gdy chcemy

przedstawić badaną zbiorowość na tle innej zbiorowości logicznie związanych ze sobą.

Obliczamy go ze wzoru:

2

1

Z

Z

W

n

=

gdzie:

Z

1

- wielkość pierwszej badanej zbiorowości,

Z

2

- wielkość drugiej zbiorowości.

Ze wzoru wynika, że współczynnik natężenia W

n

określa liczbę jednostek pierwszej

zbiorowości przypadającą na określoną jednostkę drugiej zbiorowości. Najczęściej za pomocą
współczynnika natężenia wyraża się: gęstość zaludnienia, urodzenia żywe na 1000 ludności,
mieszkania na 1000 ludności, itp.

Analiza struktury

Dotyczy tych zjawisk i badań, gdy badaną zbiorowość chcemy podzielić na podgrupy

jednostek różniących się od siebie wartościami badanej cechy mierzalnej lub wariantami
cechy niemierzalnej.

Analizy struktury dokonujemy za pomocą wskaźnika struktury (frakcja), który

przedstawia udział poszczególnych części zbiorowości w całej zbiorowości. Wskaźniki
struktury przedstawiają globalne rozmiary zbiorowości, liczebność każdej wybranej części
zbiorowości.

Można je obliczać jako wskaźniki ułamkowe, wskaźniki procentowe lub wskaźniki

promilowe.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

28

Ułamkowe wskaźniki struktury obliczmy ze wzoru:

N

n

p

i

i

=

gdzie:

n

i

– liczebność poszczególnej części całej zbiorowości

N – liczebność całej zbiorowości

Obliczając sumę tych wskaźników otrzymujemy: p

1

+ p

2+

p

3+…..+

p

n

= 1

Procentowe wskaźniki struktury mają postać:

100

⋅

=

N

n

p

i

i

Suma wskaźników wyrażonych w procentach wynosi 100.

Promilowe wskaźniki struktury mają postać:

1000

⋅

=

N

n

p

i

i

Suma wskaźników wyrażonych w promilach wynosi 1000.

Najczęściej stosujemy wskaźniki strukturalne wyrażone w procentach. Prezentują one

udział poszczególnych części zbiorowości w całej badanej zbiorowości. Wskaźnikami tymi
możemy porównywać różne zbiorowości niezależnie od wielkości bezwzględnych.

Analiza tendencji centralnej

Badając cechy mierzalne zbiorowości statystycznej chcemy ustalić w tej zbiorowości

przeciętny poziom wartości badanych cech. Dążymy do znalezienia tendencji centralnej, jaka
występuje w zbiorowości tzn. ustalenia, że pewne wartości cechy (wartości centralne)
występują z większą częstością (częściej) niż inne. Do ustalenia tego przeciętnego poziomu
stosuje się miary statystyczne: średnie, medianę i dominantę.

Średnia jest miarą odzwierciedlającą przeciętny poziom cechy mierzalnej jednostek

zbiorowości statystycznej, charakteryzuje centralnie położona wartość, wokół której skupiają
się jednostki zbiorowości. Do średnich klasycznych zaliczamy średnią arytmetyczną, która
jest najczęściej stosowaną w analizach statystycznych. Otrzymujemy ją w wyniku podzielenia
sumy wartości cechy wszystkich jednostek zbiorowości przez liczebność całej zbiorowości.
Średnia arytmetyczna jest taką wartością cechy, jaką miałyby wszystkie jednostki
zbiorowości przy ustalonej sumie cechy, gdyby nie występowała zmienność. Otrzymujemy ją
ze wzoru:

N

x

x

x

x

n

+

+

+

=

....

2

1

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

29

gdzie:

x - średnia arytmetyczna,

x

i

- wartość cechy dla i-tej jednostki zbiorowości

N - liczebność całej zbiorowości

Dla szeregu rozdzielczego, w którym przedziały klasowe są równe, średnią arytmetyczną
obliczamy ze wzoru:

n

k

i

i

o

t

x

x

∑

=

−

+

=

1

gdzie:

x

o

– wartość wyjściowa, ta wartość cechy, z którą porównujemy wartości pozostałych

wyrazów tego szeregu,

t

i

- różnice między poszczególnymi wartościami zmiennej,

n - ogólna liczba obserwacji.

Dominanta i mediana
Są to wielkości, których wartości wyznaczamy wykorzystując wartości tylko niektórych

wyrazów szeregu. Zanim wyznaczymy te wielkości musimy uporządkować szereg, czyli
ustawić wyrazy szeregu według kolejności rosnącej lub malejącej wartości cechy.

Dominanta (D

x

) jest to wartość cechy, która najczęściej występuje w badanej zbiorowości

statystycznej. Jest to wartość typowa dla danej zbiorowości. Inaczej nazywa się też modalną
lub modą. Ustalenie dominanty w przypadku szeregów indywidualnych jest proste, bo
dominanta to ta wartość cechy, która jest przyjmowana przez największą liczbę jednostek.

Jeżeli materiał statystyczny podany jest w przedziałach klasowych (szereg rozdzielczy), to

dominantę wyznaczamy sposób przybliżony, wewnątrz tego przedziału, którym mieści się
wartość dominanty. Przedział ten nazywamy przedziałem dominanty. Wzór ten stosujemy
wówczas, gdy rozpiętość przedziałów klasowych jest jednakowa.

)

(

)

(

1

1

1

n

n

n

n

n

n

x

D

d

d

d

d

d

d

od

x

L

+

−

−

−

+

−

−

+

=

gdzie:

x

od

- dolna granica przedziału dominanty,

n

d

– liczebność przedziału dominanty,

n

d 1

−

– liczebność przedziału poprzedzającego przedział dominanty,

n

d 1

+

– liczebność przedziału następującego po przedziale dominanty,

L - rozpiętość przedziału dominanty.

Przykład: Na podstawie danych zamieszczonych w tabeli 3 obliczymy wartość najczęściej
występującego poziomu wynagrodzenia w pewnej firmie transportowej w miesiącu marcu
2006 roku.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

30

Tabela 3. Pracownicy firmy transportowej w marcu 2006 roku według poziomu wynagrodzenia.

Wynagrodzenie w zł

(x

io

- x

it

)

Liczba pracowników

n

i

2700-2900

190

2900-3100

710

3100-3300

900

3300-3500

600

3500-3700

300

Razem

2700

Aby wyznaczyć dominantę należy:

1) ustalić, w którym przedziale klasowym jest ona zawarta - 900 pracowników ma pensje
w przedziale 3100-3300 i tam też znajduje się dominanta,
2) wyznaczyć następne wielkości niezbędne do wyznaczenia dominanty:
x

od

– dolna granica przedziału z dominantą - wynosi 3100,

L – rozpiętość przedziału liczbowego z dominantą - wynosi 200,
n

o

– liczebność przedziału z dominantą- wynosi 900,

n

d

-

1

– liczebność przedziału poprzedzającego przedział dominanty – wynosi 710,

n

d+1

– liczebność przedziału następującego po przedziale z dominantą - wynosi 600.

Po ustaleniu wszystkich wartości potrzebnych do wyznaczenia dominanty wstawiamy do

wzoru i wyznaczamy dominantę.

55

,

3177

)

600

900

(

)

710

900

(

710

900

200

3100

=

−

+

−

−

⋅

+

=

D

x

zł.

Najczęściej spotykanym wynagrodzeniem w tej firmie transportowej w miesiącu marcu

2006 roku było wynagrodzenie w wysokości 3177,55zł.

Po obliczeniu dominanty należy sprawdzić, czy uzyskany wynik zawiera się w przedziale,

który przed wykonaniem obliczeń wskazaliśmy jako przedział dominanty. W ten sposób
dokonujemy szacunku wykonanych obliczeń, jeżeli wynik wykracza poza granice przedziału,
należy sprawdzić poprawność obliczeń.

Inną ważną średnią pozycyjną jest mediana (wartość środkowa). Jest to wartość

środkowa, która dzieli zbiorowość, uporządkowany szereg rosnąco lub malejąco na dwie
równe części. W jednej z tych części znajdują się jednostki o wartościach wyższych od
mediany, w drugiej o wartościach niższych. Mediana jest więc tą wartością, która dzieli
szereg na równą liczbę jednostek.

Jeżeli informacje o wartości cechy są przedstawione w postaci indywidualnego szeregu

wartości cechy o nieparzystej liczbie jednostek, to pozycja mediany jest wartością środkową
(numer środkowy wyrazu). Jej odczytana wartość to wartość mediany.

Jeżeli informacje o wartości cechy są przedstawione w postaci indywidualnego szeregu

wartości cechy o parzystej liczbie jednostek, to występują dwa wyrazy środkowe. Średnia
arytmetyczna ich wartości, to wartość szukanej mediany.

Nieco inaczej przebiega wyznaczenie mediany w przypadku, gdy informacje o wartości

cechy są podane w postaci szeregu statystycznego z cechą mierzalną z wartością skokową.
W takim przypadku konieczne jest zbudowanie szeregu skumulowanego i na podstawie
wzoru wykorzystywanego przy indywidualnym szeregu wartości ustala się numer jednostki
mediany, a dalej w oparciu o dane z szeregu skumulowanego ustala się wartość mediany.

W przypadku szeregów statystycznych z cechą mierzalną ze zmiennością ciągłą medianę

można wyznaczyć graficznie albo obliczyć jej przybliżoną wartość na podstawie wzoru:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

31

)

2

(

1

S

n

x

M

sMx

Mx

oMx

x

N

L

−

−

+

=

gdzie:

M

x

- mediana,

x

oMx

- dolna granica przedziału liczbowego mediany,

L – rozpiętość przedziału mediany,
N – liczebność zbiorowości,

n

Mx

- liczebność przedziału mediany,

S

sMx 1

−

- liczebność szeregu skumulowanego w wierszu poprzedzającym wiersz

mediany.

Przykład: Obliczyć i zinterpretować medianę na podstawie informacji zawartych w tabeli 4
wykorzystanej do obliczeń dominanty.
Rozwiązanie: W pierwszej kolejności tworzymy tablicę z szeregiem skumulowanym.

Tabela 4. Pracownicy firmy transportowej w marcu 2006 roku według poziomu wynagrodzenia. [dane umowne]

Wynagrodzenie w zł

(x

io

- x

it

)

Liczba pracowników

n

i

Szereg skumulowany

S

si

2700-2900

190

190

2900-3100

710

900

3100-3300

900

1800

3300-3500

600

2400

3500-3700

300

2700

Razem

2700

×

Kolejnym krokiem przy obliczeniu mediany jest określenie przedziału klasowego,

którym znajduje się mediana poprzez sprawdzenie, w którym wierszu szeregu
skumulowanego jest wyraz środkowy. W naszym przypadku pozycja mediany to 1350
i znajduje się w trzecim wierszu. Oznacza to, że mediana znajduje się w przedziale 3100-
3300. Podstawiamy odczytane wielkości do wzoru i wyznaczamy:

3200

)

900

2

2700

(

900

200

3100

=

−

+

=

M

x

zł

Wartość mediany wynosi 3200zł. Tak więc połowa pracowników tej firmy w marcu 2006

roku zarabiała 3200 zł lub więcej, a połowa zarabiała 3200 zł i mniej.

Pomiędzy miarami tendencji centralnej mogą zachodzić następujące relacje:

− wszystkie miary tendencji centralnej mają taką sama wartość, czyli

=

x

M

x

= D

x

i jest to wówczas rozkład symetryczny, co oznacza, że liczba jednostek statystycznych
posiadająca wartości cechy wyższe niż wartości cechy niższe jest taka sama,
− wartość średniej jest większa niż wartość mediany i wartość mediany jest większa od

wartości dominanty, czyli x > M

x

> D

x

i jest to rozkład o asymetrii prawostronnej, co

oznacza, że wartość cechy większości jednostek statystycznych jest niższa od średniej
arytmetycznej,

− wartość średniej jest mniejsza niż wartość mediany i wartość mediany jest mniejsza od

wartości dominanty, czyli x < M

x

< D

x

i jest to rozkład o asymetrii lewostronnej, co

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

32

oznacza, że wartość cechy większości jednostek statystycznych jest wyższa od średniej
arytmetycznej.

Analiza rozproszenia

Do pomiaru rozproszenia wariantów cechy służą miary rozproszenia inaczej zwane

miarami dyspersji, miarami odchyleń lub miarami zmienności. Do najczęściej stosowanych
miar rozproszenia zaliczamy:

− obszar zmienności (rozstęp),
− odchylenie przeciętne,
− odchylenie standardowe,
− współczynnik zmienności.
Najprostszą miarą rozproszenia jest rozstęp zwany również obszarem zmienności, który

wyznaczamy ze wzoru:

x

x

R

min

max

−

=

Znając obszar zmienności wiemy tylko, jaka jest różnica między krańcowymi wartościami

cechy, jest to miara o małej wartości poznawczej.

Odchylenie przeciętne (d

x

) jest to średnia arytmetyczna bezwzględnych wartości

(modułów) odchyleń wartości faktycznych szeregu od średniej arytmetycznej, które dla
szeregu indywidualnego obliczamy ze wzoru:

N

x

x

d

N

i

i

x

−

=

−

=

∑

1

gdzie:

x

i

- wartość cechy,

x

−

- średnia arytmetyczna wartości zmiennej,

N – liczba obserwacji.

Natomiast, jeżeli zbiorowość przedstawiona jest w postaci szeregu rozdzielczego

z zadanymi klasami, stosujemy wzór:

N

i

N

i

o

i

x

x

x

n

d

∑

=

−

−

=

1

gdzie:

n

i

- liczebność i-tego przedziału klasowego,

o

i

x

- środek i-tego przedziału klasowego,

x - średnia arytmetyczna,
N – liczba obserwacji.

Odchylenie przeciętne jest rzadko stosowane do pomiaru rozproszenia, gdyż jest mało

precyzyjne. Jest wypierane przez odchylenie standardowe.

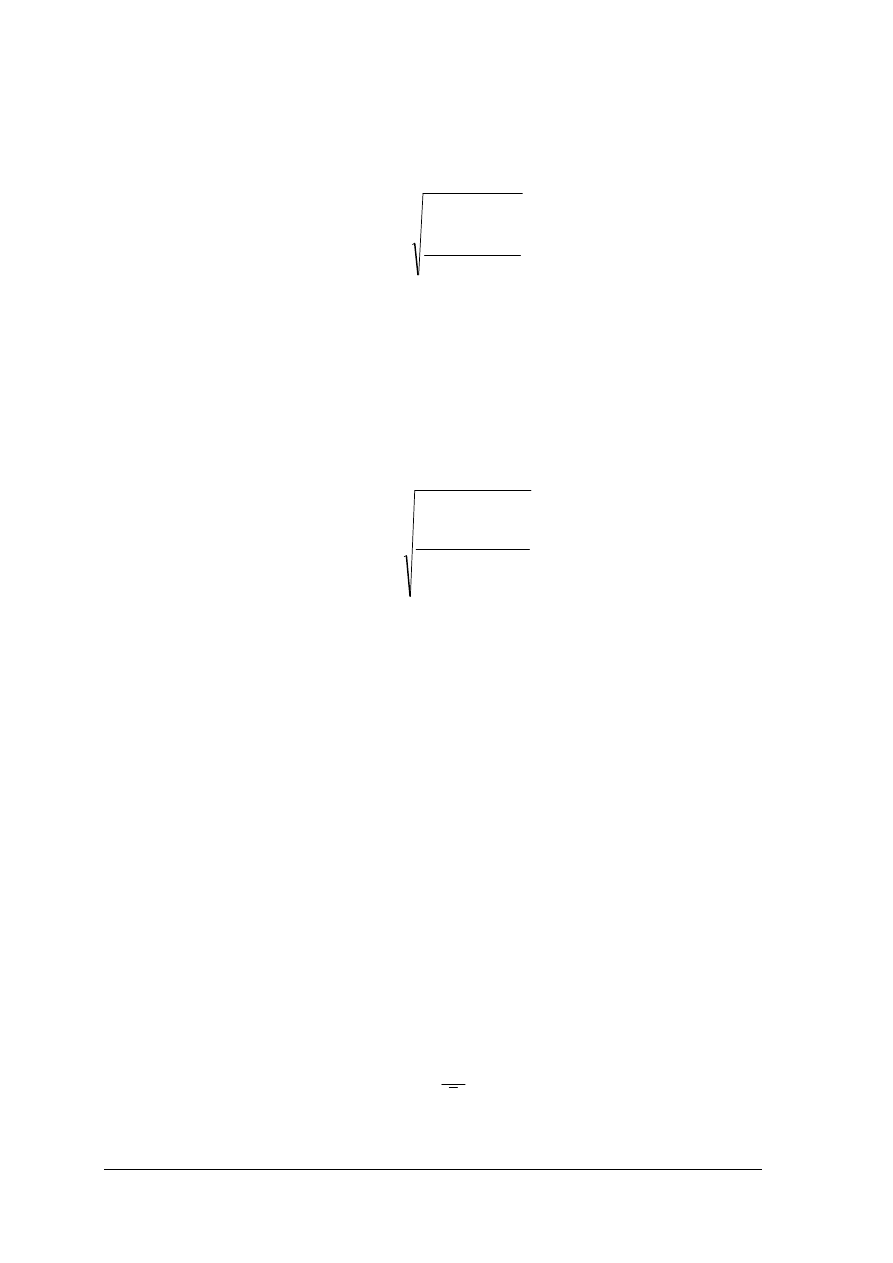
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

33

Odchylenie standardowe (σ

x

) jest to pierwiastek kwadratowy z sumy kwadratów odchyleń

poszczególnych wartości zmiennej x od średniej arytmetycznej, podzielonej przez liczebność
szeregu. Wyznaczamy je ze wzoru:

N

N

i

i

x

x

x

∑

=

−














−

=

1

2

σ

Znaczenie symboli w tym wzorze jest identyczne jak we wzorze na odchylenie przeciętne.

Czasami odchylenie standardowe jest nazywane jako średnie odchylenie kwadratowe lub
dyspersja. Obrazuje ono przeciętne wahania wartości cechy wokół średniej arytmetycznej dla
rozważanego szeregu. Jest to miara bardziej dokładana niż odchylenie przeciętne.

Jeżeli dane prezentowane są w postaci szeregów rozdzielczych, w których wyróżniono

przedziały klasowe, wartość odchylenia standardowego obliczamy zgodnie ze wzorem:

∑

∑

=

−

=











−

=

N

i

i

i

n

i

i

x

n

x

x

n

1

2

1

σ

Znaczenie symboli w tym wzorze jest identyczne, jak we wzorze na odchylenie przeciętne

dla szeregu rozdzielczego.

Wyznaczenie odchylenia standardowego umożliwia ocenę przeciętnego wahania wartości

cechy wokół średniej arytmetycznej, a dzięki temu pozwala wyznaczyć obszar wartości
typowych. Jeżeli rozkład wartości cechy w zbiorowościach jest rozkładem normalnym to:
− około 66% jednostek badanej zbiorowości charakteryzuje się tym, że wartość cechy dla

tych jednostek nie różni się (w gorę lub w dół) od średniej więcej niż o jedno odchylenie
standardowe,

− dla około 90%jednostek wartość cechy nie odbiega od średniej (w dół i w górę) więcej niż

o 2 odchylenia standardowe,

− około 99% jednostek nie różni się od średniej (w górę i w dół) więcej niż o 3 odchylenia

standardowe.
Przedstawione powyżej przedziały, których krańce określamy wykorzystując wyznaczone

wartości średniej arytmetycznej i odchylenia standardowego zwane są obszarami
charakterystycznymi, a przedział, który określamy stosując potrojoną wartość odchylenia
standardowego nazywamy obszarem wartości typowych.

Współczynnik zmienności jest to stosunek bezwzględnej miary odchylenia tj. odchylenia

przeciętnego (d

x

) lub odchylenia standardowego (σ

x

) do średniej arytmetycznej, wyrażony

w procentach:

100

x

d

V

x

x

=

lub

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

34

100

'

x

x

x

V

σ

=

Dzięki współczynnikowi zmienności rozważane zbiorowości można ocenić pod

względem zróżnicowania. Tego typu badania są szczególnie przydatne w porównywaniu
zróżnicowania takich wielkości, jak: dochody, wydajność pracy, absencja w pracy w różnych
przedsiębiorstwach lub działach jednego przedsiębiorstwa.

Analiza dynamiki

W statystyce rozpatrujemy nie tylko zjawiska gospodarcze i społeczne, które są statyczne,

ale także te, które podlegają ciągłym zmianom. Uwzględniamy wówczas rozwój tych zjawisk
w czasie poprzez analizę ich dynamiki. Dynamikę zjawisk prezentuje się w postaci szeregów
dynamicznych. Analiza dynamiki polega na tym, że określamy rozmiar i kierunek rozwoju
(zmian w czasie) badanych zjawisk. Ustalamy w ten sposób stopień poziomu wzrostu lub
spadku badanego zjawiska. Miarami dynamiki są:
− przyrost absolutny,
− przyrost względny,
− indeksy dynamiki.

Przyrost absolutny jest to różnica między wielkością zjawiska w okresie badanym,

a wielkością tego zjawiska w okresie podstawowym i obliczamy ze wzoru:

x

x

x

o

−

=

∆

1

gdzie:

x

∆

- przyrost absolutny,

x

1

- wielkość badanej cechy w okresie badanym,

x

o

- wielkość badanej cechy w okresie podstawowym.

Wielkość ta obrazuje, o ile zmienił się poziom badanego zjawiska w okresie badanym

w porównaniu do okresu podstawowego. Przyrost absolutny jest dodatni, gdy poziom
zjawiska w okresie badanym jest wyższy od poziomu w okresie podstawowym; jest ujemny,
gdy poziom zjawiska w okresie badanym jest niższy od poziomu w okresie podstawowym
oraz nie uległ zmianie, gdy przyjmuje wartość zero.

Przyrost względny jest to przyrost absolutny podzielony przez wielkość zjawiska z okresu

podstawowego i obliczamy go ze wzoru:

x

x

x

x

x

x

o

o

o

w

∆

∆

=

−

=

1

Jest to wielkość niemianowana i umożliwia przeprowadzenie analizy dynamiki zjawisk

o różnych miarach. Miernikiem wywodzącym się z przyrostu względnego jest tempo wzrostu
(t

w

), które określamy jako procentowy przyrost względny, czyli jest to przyrost względny

pomnożony przez 100:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

35

100

100

1

⋅

−

=

⋅

=

∆

x

x

x

x

t

o

o

w

w

Tempo wzrost określa wyrażoną w procentach wielkość przyrostu (spadku) badanego

zjawiska w okresie badanym w stosunku do wielkości tego zjawiska z okresu podstawowego.

Indeksy

W badaniach statystycznych najczęściej do przedstawienia miar dynamiki używamy

indeksów, zwanych również wskaźnikami dynamiki. Indeks jest to wielkość stosunkowa
powstała w wyniku podzielenia wielkości danego zjawiska w okresie badanym przez
wielkość tego zjawiska w okresie podstawowym. Indeks może być przedstawiony w postaci
ułamkowej, w procentach lub w promilach:

− indeks ułamkowy

x

x

I

o

i

u

=

− indeks procentowy

100

⋅

=

x

x

I

o

i

p

− indeks promilowy

1000

⋅

=

x

x

I

o

i

m

Średnie tempo dynamiki, to miara pozwalająca na ustalenie średniego tempa wzrostu

zjawiska. Nie można go wyznaczyć za pomocą indeksów łańcuchowych, ani też innych
indeksów. Ze względu na dość skomplikowany wzór, za pomocą którego obliczamy średnie
tempo wzrostu dynamiki (rachunek logarytmiczny) stosuje się tablice średniego tempa
wzrostu. Jest to publikacja Głównego Urzędu Statystycznego, za pomocą której odczytujemy
wartości średniego tempa wzrostu dla okresów od 2 do 41 lat przy danych dotyczących
stosunku wartości zjawiska w okresie badanym do wartości zjawiska w okresie
podstawowym.

Indeksy agregatowe

Indeksy agregatowe (złożone) charakteryzują zmiany występujące w zbiorowości lub

zjawiskach złożonych. Umożliwiają badanie zmian przez łączne ujęcie zjawisk różnorodnych,
bezpośrednio niewspółmiernych. Konstrukcja tych indeksów jest złożona i często
skomplikowana, dlatego poznamy bliżej zasady obliczania trzech typów indeksów złożonych:
− złożony indeks wartości produkcji,
− złożony indeks wielkości fizycznej (wolumenu) produkcji,
− złożonego indeksu cen.

Złożony indeks wartości produkcji

I

w

obliczamy ze wzoru:

∑

∑

=

=

⋅

⋅

=

k

i

io

io

k

i

i

i

w

p

q

p

q

I

1

1

1

1

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

36

Jeśli chcemy go wyrazić w procentach to otrzymaną wartość mnożymy przez 100.

Złożony indeks wielkości (wolumenu) produkcji

I

q

, który określa o ile zmieniła się

wartość na skutek zmiany ilości wytworzonych wyrobów stosujemy, gdy chcemy ustalić
dynamikę fizycznych rozmiarów produkcji np. dynamikę sprzedaży w przedsiębiorstwie
handlowym.

Obliczmy go ze wzoru:

Jeśli chcemy otrzymać złożony indeks wielkości produkcji wyrażony w procentach, to

otrzymaną wielkość mnożymy przez 100.

Złożony (agregatowy) indeks cen

I

c

budujemy tak, aby wyeliminować wpływ zmian

wielkości produkcji poszczególnych wyrobów i obliczamy go ze wzoru:

∑

∑

=

=

⋅

⋅

=

k

i

io

io

k

i

in

io

c

p

q

p

q

I

1

1

Jeśli chcemy, aby wyrażony był w procentach to obliczona wartość mnożymy przez 100.

We wszystkich powyższych wzorach stosowano ujednolicone oznaczenia, których znaczenie
jest następujące:

q

io

- ilość produkcji i-tego wyrobu w okresie podstawowym,

q

i1

- ilość produkcji i-tego wyrobu w okresie badanym,

p

io

- cena jednostkowa i-tego wyrobu w okresie podstawowym,

p

i1

- cena jednostkowa i-tego wyrobu w okresie badanym.

Analiza współzależności

Bardzo ważnym zadaniem analizy statystycznej jest wykrycie współzależności, czyli

wzajemnego powiązania i uwarunkowania badanych zjawisk oraz zbadanie charakteru tej
współzależności i określenie jej siły. Jeśli istnieje formuła opisująca zależności funkcyjne
i ma ona charakter statyczny, tzn. konkretnej wartości jednej cechy odpowiada pewna
przeciętna wartość drugiej cechy to związek ten określamy związkiem korelacyjnym
(korelacją). Jeśli znajdziemy korelację oraz określimy siłę tego związku, obliczymy
współczynnik korelacji to możemy wykonać analizę przyczynowo-skutkową badanych
procesów gospodarczych.

Podstawowymi metodami wykrywania związków korelacyjnych są:

∑

∑

=

=

⋅

⋅

=

k

i

io

io

k

i

io

in

q

p

q

p

q

I

1

1

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

37

− metoda porównywania przebiegu szeregów statystycznych charakteryzujących badane

zjawisko,

− metoda graficzna,
− metoda specjalnych tablic korelacyjnych.

Metoda porównywania przebiegu szeregów statystycznych polega na tym, że

porównujemy uporządkowane szeregi statystyczne zawierające dane dotyczące badanych
jednostek, zestawiamy je obok siebie i sprawdzamy zgodność tych szeregów, a później
wyznaczamy kierunek związków korelacyjnych. Jeżeli wartości są zgodne to znaczy mają
tendencję wzrostową to występuje korelacja dodatnia (r

xy

> 0), a jeżeli szeregi nie są zgodne,

to znaczy wartości jednego szeregu rosną, a drugiego maleją, to występuje korelacja ujemna
(r

xy

< 0).
Gdy wraz ze wzrostem lub spadkiem wartości w jednym szeregu, w drugim szeregu nie

można zaobserwować wyraźnej tendencji, to miedzy badanymi zjawiskami związek
korelacyjny nie występuje.

Metoda graficzna - w prostokątnym układzie współrzędnych prezentujemy graficznie

indywidualne wykazy wartości cech w postaci rozsianych punktów i otrzymujemy punktowe
wykresy rozsiewu zależności. Na podstawie otrzymanych wykresów w przybliżeniu
określamy siłę związku korelacyjnego w taki sposób, że tworzymy elipsę i spłaszczenie elipsy
informuje o sile związku korelacyjnego (im większe spłaszczenie tym silniejszy związek).

Tablica korelacyjna - w przypadku szeregów statystycznych o dużej liczbie obserwacji

rozpoznanie kierunku, kształtu i siły związku dwóch cech można rozpoznać za pomocą
specjalnie skonstruowanych tablic korelacyjnych.

W badaniach statystycznych stosujemy wiele miar współzależności dwóch cech

mierzalnych. Jedną z nich jest współczynnik korelacji (r

xy

), który jest miarą współzależności

i odzwierciedla znak i rozmiary odchyleń obu cech od ich średnich arytmetycznych.

Współczynnik korelacji, określamy wzorem:

(

∑

∑

∑

=

−

=

−

=

−

−





−

⋅














−



















−

⋅







−

=

⋅

=

n

i

n

i

i

i

n

i

i

i

y

x

xy

xy

y

y

x

x

y

y

x

x

C

r

1

2

1

2

1

σ

σ

gdzie:

x

i

- wartość pierwszej cechy,

x

−

- przeciętny poziom (średnia arytmetyczna) pierwszej cechy,

y

i

- wartość drugiej cechy,

y

−

- przeciętny poziom (średnia arytmetyczna) drugiej cechy.

Znak współczynnika korelacji jest taki sam jak znak kowariancji. W statystyce przejęto

następujący sposób komentowania bezwzględnej wielkości współczynnika korelacji, jeśli
mówimy o ścisłości związku miedzy badanymi cechami:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

38

Tabela 4. Interpretacja współczynników korelacji. [3]

Poziom współczynnika

Siła współzależności

r

xy

= 0

współzależność nie występuje

0 < ׀ r

xy

׀ < 0,3

słaby stopień współzależności

0,3 ≤ ׀ r

xy

׀ < 0,5

umiarkowany(średni)stopień współzależności

0,5 ≤ ׀ r

xy

׀ < 0,7

znaczny stopień współzależności

0,7 ≤ ׀ r

xy

׀ < 0,9

wysoki stopień współzależności

r

xy

≥ 0,9

bardzo wysoki stopień współzależności

r

xy

= 1

współzależność całkowita (ścisłość), tzn. zależność
funkcyjna między rozważanymi cechami.

Współczynnik korelacji rang to również miernik korelacyjnego związku cech. Stosujemy

go wówczas, gdy badamy współzależności cech niemierzalnych. Konstrukcja współczynnika
korelacji rang opiera się na zgodności rang, czyli zgodności pozycji, którą zajmuje każda
z odpowiadających sobie wielkości we wzrastającym lub malejącym szeregu wartości swej
cechy.

Współczynnik korelacji rang (Q) wyznaczamy na podstawie wyznaczonych różnic rang

(d) oraz znanej liczby par obserwacji (N), zgodnie ze wzorem:

N

N

d

n

i

i

Q

−

−

=

∑

=

3

1

2

6

1

gdzie:

r

r

d

y

x

i

−

=

r

x

– rangi, czyli numery porządkowe nadawane wartościom cechy „x” w szeregu

uporządkowanym,

r

y

– rangi, czyli numery porządkowe nadawane wartościom cechy „y” ułożonymi

w kolejności od najmniejszej do największej lub odwrotnie.

Jeśli Q=1 wówczas mamy do czynienia ze zgodnością rang, a zachodzi to tylko wtedy,

gdy różnica rang wynosi zero i wówczas interpretujemy uzyskany wynik jako ścisły dodatni
związek między cechami X i Y.

4.4.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Jakie są główne cele analizy statystycznej?
2. Czym charakteryzują się współczynniki natężenia i gdzie są wykorzystywane?
3. Jakie znasz najczęściej stosowane wskaźniki struktury?
4. Jakie znasz własności średniej arytmetycznej?
5. Na czym polega metoda odchyleń?
6. Podaj definicję i interpretację dominanty.
7. Podaj definicję i interpretację mediany.
8. Jak wyznaczamy medianę dla szeregu rozdzielczego, a jak dla indywidualnego szeregu

wartości?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

39

9. Jak wyznaczamy dominantę dla danych w postaci indywidualnego szeregu, a jak dla

szeregu rozdzielczego?

10. Wymień najczęściej stosowane miary dyspersji (rozproszenia).
11. Podaj definicję obszaru zmienności.
12. Co to jest odchylenie przeciętne?
13. Co to jest odchylenie standardowe?
14. Jakie znasz metody wyznaczania odchylenia standardowego dla danych w postaci

szeregów indywidualnych oraz szeregów rozdzielczych?

15. Jakie praktyczne zastosowanie ma współczynnik zmienności?
16. Na czym polega analiza dynamiki i jakie miary są w niej wykorzystywane?
17. Jakie znasz rodzaje indeksów stosowanych w badaniach statystycznych?
18. Jak wyznaczamy średnie tempo zmian przy różnych postaciach danych liczbowych?
19. Jakie są podstawowe formuły indeksów agregatowych?
20. Jakie są różnice pomiędzy indeksami wartości produkcji, fizycznej wielkości (wolumenu)

produkcji oraz cen?

21. Na czym polega i jak się przejawia współzależność zjawisk?
22. Co rozumiesz przez związek korelacyjny? Jakie są metody wykrywania tego związku?
23. Jakie znasz miary współzależności zjawisk?

4.4.3. Ćwiczenia

Ćwiczenie 1

Dokonaj grupowania przedsiębiorstw według kosztów, jakie poniosły one w roku 2005.

Utwórz szereg statystyczny strukturalny z przedziałami liczbowymi o rozpiętości 20 tys. zł.
Koszty (w tys. zł) badanych przedsiębiorstw były następujące:

58; 103; 73; 96; 97; 82; 91; 87; 89; 60; 47; 71; 83; 96; 100; 27; 45; 64; 51; 92; 105; 49;

105; 49; 62; 94; 87; 104; 82; 105; 51; 99; 87; 27; 66; 42; 95; 92; 26; 50; 34; 41.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania dotyczącym opracowania materiału statystycznego,
2) określić rozstęp między wartością maksymalną i minimalną,
3) ustalić ilość przedziałów liczbowych,
4) dokonać zliczania przedsiębiorstw do określonych przedziałów,
5) w arkuszu kalkulacyjnym utworzyć odpowiedni szereg statystyczny,
6) dokonać obliczeń i przedstawić wyznaczony szereg statystyczny na forum klasy.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny.

Ćwiczenie 2

Na podstawie zamieszczonej poniżej tabeli przedstawiającej wynagrodzenie pracowników

dokonaj analizy tendencji centralnej wyznaczając średnią arytmetyczną, medianę i dominantę
podanego szeregu statystycznego. Wyznaczone wielkości odpowiednio zinterpretuj (ustal
jakie zachodzą relacje między miarami tendencji centralnej).

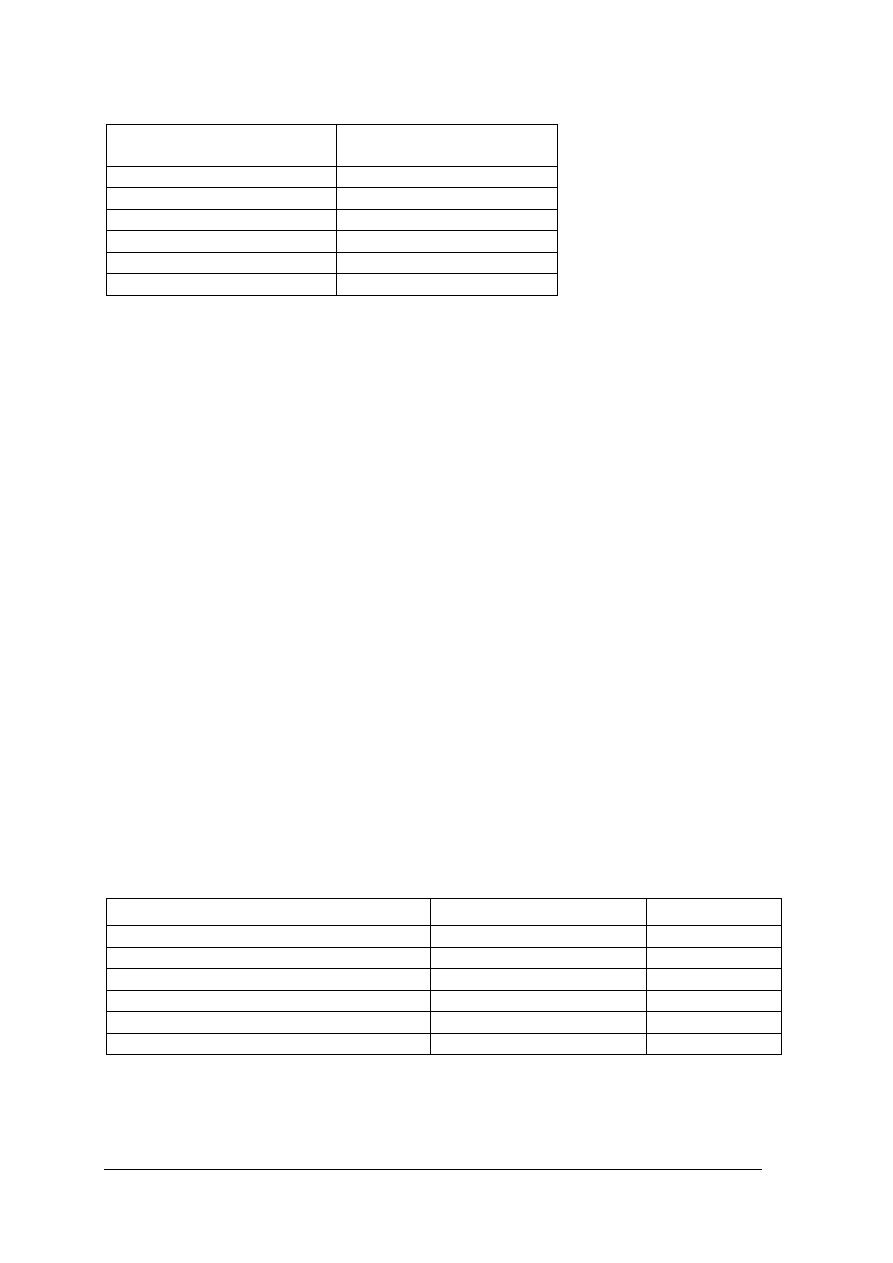
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

40

Tabela do ćw. 2. Pracownicy firmy transportowej w marcu 2006 roku według poziomu wynagrodzenia.

Wynagrodzenie w zł

( x

io

- x

it

>

Liczba pracowników

n

i

2700-2900

190

2900-3100

710

3100-3300

900

3300-3500

600

3500-3700

300

Razem

2700

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:

1) podaną tabelę przenieść do arkusza kalkulacyjnego,
2) skorzystać z odpowiednich formuł i funkcji do obliczeń,
3) utworzyć w przygotowanej tablicy szereg skumulowany,
4) określić przedział klasowy, w którym jest mediana,
5) wyznaczyć medianę z podanego w części teoretycznej wzoru,
6) określić środek każdego przedziału,
7) zsumować iloczyny środka przedziału (wynagrodzenie) i przypadającej mu liczbie

pracowników,

8) wyznaczyć średnią arytmetyczną,
9) wyznaczyć przedział z dominantą i wyznaczyć jej wartość,
10) porównać otrzymane wyniki,
11) podać relacje zachodzące między miarami tendencji centralnej,
12) zinterpretować uzyskane rozwiązanie i ocenić wynagrodzenie pracowników w firmie.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny.

Ćwiczenie 3

Za pomocą wskaźników struktury

i

p przedstaw zależności miedzy poszczególnymi

grupami pracowników zatrudnionych w firmie spedycyjnej we Wrocławiu.

Tabela do ćw. 3. Pracownicy przedsiębiorstwa spedycyjnego we Wrocławiu według stanu na 31 grudnia 2005 r.
[dane umowne]

Grupa pracowników

Stan zatrudnienia

i

p

robotnicy

1250

pracownicy inżynieryjno-techniczni

320

pracownicy administracyjno-biurowi

350

pracownicy obsługi

90

uczniowie

40

Razem

2050

Sposób wykonania ćwiczenia

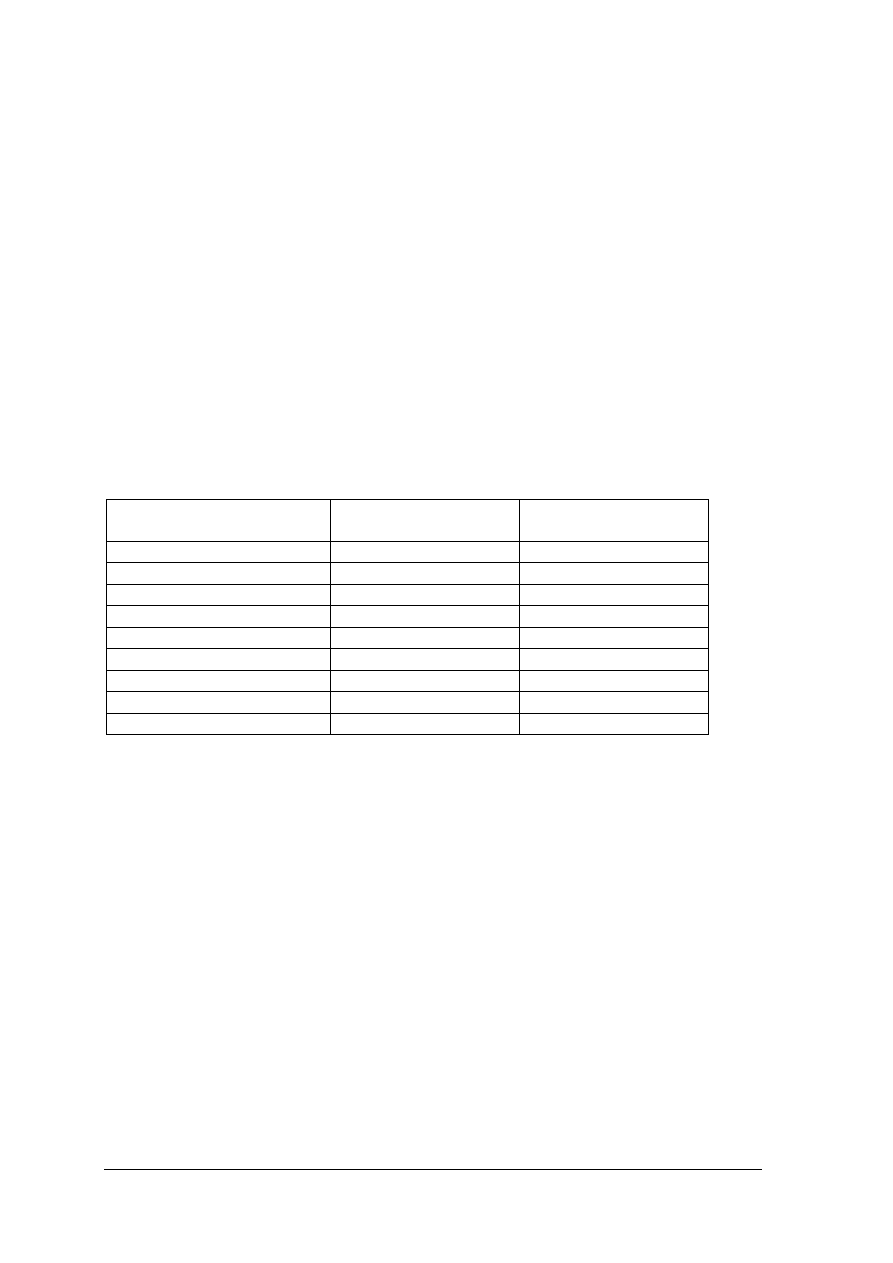
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

41

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania,
2) podaną tabelę przenieść do arkusza kalkulacyjnego,
3) obliczyć w przygotowanej kolumnie tablicy wskaźniki struktury,
4) porównać otrzymane wyniki,
5) podać relacje zachodzące między poszczególnymi wskaźnikami,
6) na podstawie uzyskanych wskaźników ocenić sytuację pracowników w firmie.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny.

Ćwiczenie 4

Na podstawie danych z tabeli zamieszczonej poniżej oblicz średnią arytmetyczną dla obu

zakładów, a następnie dokonaj analizy odchyleń obliczając współczynniki zmienności. Które
z poznanych dotychczas miar byłyby użyteczne przy kompleksowej analizie wypłaconych
premii?

Tabela do ćw. 4. Pracownicy dwóch zakładów przedsiębiorstwa transportowo-spedycyjnego we Wrocławiu
według wysokości wypłaconej premii za II kwartał 2005 r. [dane umowne]

Premia w tys. zł

( x

io

- x

it

>

Liczba pracowników

Zakład I

Liczba pracowników

Zakład II

1,2-1,4

-

2

1,4-1,6

-

7

1,6-1,8

10

15

1,8-2,0

43

32

2,0-2,2

37

25

2,2-2,4

-

21

2,4-2,6

-

12

2,6-2,8

-

6

Razem

90

120

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania dotyczącym analizy rozproszenia,
2) podaną tabelę przenieść do arkusza kalkulacyjnego,
3) obliczyć średnią arytmetyczną dla Zakładu I i dla Zakładu II,
4) dla każdego zakładu wyliczyć odchylenie standardowe i przeciętne,
5) dla każdego zakładu wyliczyć współczynniki zmienności,
6) porównać otrzymane wyniki i dokonać analizy rozproszenia,
7) odpowiedzieć na zadane pytania w oparciu o wyniki analizy.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny.

Ćwiczenie 5

Porównując przebieg szeregów statystycznych z tabeli zamieszczonej poniżej

rozstrzygnij, czy istnieje zależność między wielkością przewiezionego ładunku, a liczbą
zatrudnionych pracowników w przedsiębiorstwie.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

42

Tabela do ćw. 5. Przedsiębiorstwo transportowe według przewiezionego ładunku i liczby zatrudnionych
pracowników w lutym 2006 r. [dane umowne]

L.p.

Przewieziony ładunek w tys. ton

Liczba zatrudnionych

1.

120000

30

2.

140000

31

3.

210000

33

4.

230000

34

5.

150000

32

6.

170000

33

Razem

1020000

193

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie powinieneś:

1) zapoznać się z materiałem nauczania dotyczącym analizy współzależności,
2) podaną tabelę przenieść do arkusza kalkulacyjnego,
3) obliczyć średnią arytmetyczną dla przewiezionego ładunku i dla liczby zatrudnionych,
4) wykonać pomocnicze wyliczenia zgodnie ze wzorem na współczynnik korelacji,
5) zinterpretować uzyskane wartości zgodnie z materiałem źródłowym,
6) ustalić, czy istniej zależność między wielkością przewiezionego ładunku, a liczbą
zatrudnionych pracowników w przedsiębiorstwie.

Wyposażenie stanowiska pracy:

− komputer z zainstalowanym oprogramowaniem zawierającym arkusz kalkulacyjny.

4.4.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) wymienić główne cele analizy statystycznej?





2) określić, czym charakteryzują się współczynniki natężenia i gdzie są

wykorzystywane?





3) wymienić najczęściej stosowane wskaźniki struktury oraz zalety ich

stosowania?





4) wymienić podstawowe własności średniej arytmetycznej?





5) scharakteryzować metodę odchyleń oraz podać procedurę obliczania

metody odchyleń dla danych w postaci różnych rodzajów szeregów
statystycznych?





6) podać definicję i interpretację dominanty?





7) podać definicję i interpretację mediany?





8) wyznaczyć medianę dla szeregu rozdzielczego oraz dla indywidualnego

szeregu wartości?





9) określić, jak wyznaczamy dominantę dla danych w postaci indywidualnego

szeregu, a jak dla szeregu rozdzielczego?





10) wymienić najczęściej stosowane miary dyspersji (rozproszenia) i omówić

do jakich celów one służą?





11) podać definicję obszaru zmienności i omówić zastosowanie tej miary?.





12) określić odchylenie przeciętne?





„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

43

13) omówić własności odchylenia standardowego i metody wyznaczania tej

miary dla danych w postaci szeregów indywidualnych oraz szeregów
rozdzielczych?





14) omówić praktyczne zastosowanie współczynnika zmienności?





15) wyjaśnić, na czym polega analiza dynamiki i jakie miary są w niej

wykorzystywane?





16) wymienić podstawowe rodzaje indeksów stosowanych w badaniach

statystycznych?





17) omówić sposób wyznaczania średniego tempa zmian przy różnych danych

liczbowych?





18) wymienić podstawowe formuły indeksów agregatowych ?





19) omówić różnice pomiędzy indeksami wartości produkcji, fizycznej

wielkości (wolumenu) produkcji oraz cen?





20) wyjaśnić, na czym polega i jak się przejawia współzależność zjawisk





21) wyjaśnić pojęcie związek korelacyjny i podać metody wykrywania tego

związku?





22) omówić własności współczynnika korelacji i zalety jego stosowanie jako

miary współzależności zjawisk.





„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

44

5. SPRAWDZIAN OSIĄGNIĘĆ

Instrukcja dla ucznia

1. Przeczytaj uważnie instrukcję.
2. Podpisz imieniem i nazwiskiem kartę odpowiedzi.
3. Zapoznaj się z zestawem pytań testowych.
4. Test zawiera 20 zadań o różnym stopniu trudności. Są to zadania jednokrotnego wyboru.
5. Udzielaj odpowiedzi tylko na załączonej karcie odpowiedzi:

− w pytaniach jednokrotnego wyboru zaznacz X prawidłową odpowiedź (w przypadku

pomyłki należy błędną odpowiedź zaznaczyć kółkiem, a następnie ponownie zakreślić
odpowiedź prawidłową),

− w zadaniach do uzupełnienia wpisz jeden brakujący wyraz.

6. Pracuj samodzielnie, bo tylko wtedy będziesz miał satysfakcję z wykonanego zadania.
7. Kiedy udzielenie odpowiedzi będzie Ci sprawiało trudność, wtedy odłóż jego

rozwiązanie
na później i wróć do niego, gdy zostanie Ci wolny czas. Trudności mogą przysporzyć Ci
pytania: 16 – 20, gdyż są one na poziomie ponadpodstawowym, a pozostałe na poziomie
podstawowym

Na rozwiązanie testu masz 90 min.

Powodzenia

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

45

ZADANIA TESTOWE

1. Jednym

z

warunków

dokonywania

lub

podejmowania

właściwej

decyzji

w zarządzaniu jest posiadanie rzetelnych i dokładnych:

a) informacji,
b) księgowych,
c) informatorów,
d) danych statystycznych.

2. Jednym z etapów zbierania informacji jest badanie statystyczne, za pomocą którego

badamy pewne cechy:

a) całej zbiorowości,
b) grupy statystycznej,
c) jednostki statystycznej,
d) reprezentatywnej grupy.

3. Jednym z kryteriów podziału badań statystycznych jest częstotliwość ich prowadzenia.

Ze względu na to kryterium dzielą się na:

a) ciągłe, okresowe, sporadyczne,
b) pełne, częściowe, szacunkowe,
c) pełne, częściowe, okresowe,
d) sporadyczne, ciągłe, częściowe.

4.

Formularz statystyczny to zbiór pytań dotyczących jednostek statystycznych objętych
badaniem statystycznym. Składa się z następujących części:

a) nagłówka, kwestionariusza właściwego, części końcowej,
b) części tytułowej, kwestionariusza, legendy,
c) nagłówka, tabeli, podpisu,
d) części tytułowej, tabeli, części końcowej.

5. Pobrany materiał statystyczny poddajemy zawsze kontroli:

a) zupełności zapisów i zgodności rachunkowej,
b) formalnej i merytorycznej,
c) ilościowej i jakościowej,
d) kompletności i formalnej.

6. Badanie statystyczne to czynności, których celem jest określenie prawidłowości

dotyczących badanych cech statystycznych. Prowadzi się je w kilku etapach, których
kolejność jest następująca:

a) przygotowanie badania, zebranie materiału statystycznego i przygotowanie do

opracowania, prezentacja danych i analiza statystyczna, opracowanie materiału
statystycznego,

b) zebranie materiału statystycznego i przygotowanie do opracowania,

przygotowanie badania, prezentacja danych i analiza statystyczna, opracowanie
materiału statystycznego,

c) zebranie materiału statystycznego i przygotowanie do opracowania,

opracowanie materiału statystycznego, przygotowanie badania, prezentacja
danych i analiza statystyczna,

d) przygotowanie badania, zebranie materiału statystycznego i przygotowanie do

opracowania, opracowanie materiału statystycznego, prezentacja danych
i analiza statystyczna.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

46

7. Kropka to znak umowny stosowany w tablicach statystycznych. Oznacza ona:

a) brak informacji,
b) brak wiarygodnych informacji,
c) logiczną sprzeczność wiersza z kolumną,
d) występowanie zjawiska w ilościach mniejszych niż ½ jednostki w tablicy.

8. Tabelaryczna

prezentacja

opracowanego

materiału

to

forma

stosowana

w publikacjach w postaci:

a) szeregu dynamicznego, rozdzielczego, strukturalnego, skumulowanego,
b) szeregu terytorialnego, strukturalnego, czasowego, wyliczającego,
c) szeregu rozdzielczego, geograficznego, wyliczającego, strukturalny,
d) szeregu dynamicznego, czasowego, wyliczającego, strukturalnego.

9. Celem analizy statystycznej badanego materiału jest:

a) wszechstronne pokazanie i zbadanie zjawiska,
b) zbadanie zjawiska i wykrycie prawidłowości,
c) pokazanie, zbadanie i wykrycie prawidłowości,
d) pokazanie zjawiska i wykrycie prawidłowości.

10. Analiza natężenia wyrażona przez……………………………………., określa liczbę

jednostek jednej zbiorowości przypadającą na jednostkę drugiej zbiorowości.

11. Miarami tendencji centralnej są:

a) dominanta, mediana, średnia geometryczna,
b) średnia arytmetyczna, tempo wzrostu, mediana,
c) mediana, dominanta, średnia arytmetyczna,
d) odchylenie standardowe, mediana, dominanta.

12. Analiza struktury zbiorowości statystycznej wyrażona przez …………………………

………………, określa jaką część zbiorowości stanowią jednostki posiadające określony
wariant cechy.

13. Miary rozproszenia to:

a) odchylenie przeciętne, obszar zmienności, przyrost względny,
b) odchylenie standardowe, obszar zmienności, przyrost względny,
c) odchylenie standardowe, odchylenie przeciętne, obszar zmienności,
d) odchylenie standardowe, współczynnik zmienności, średnia arytmetyczna.

14. Analiza dynamiki określa rozmiar i kierunek rozwoju za pomocą miar dynamiki, którymi

są:

a) przyrost absolutny, przyrost względny, tempo dynamiki,
b) indeksy dynamiki, tempo wzrostu, przyrost absolutny,
c) przyrost względny, przyrost bezwzględny, indeksy dynamiki,
d) przyrost absolutny, indeksy dynamiki, przyrost bezwzględny.

15. Indeksy agregatowe, charakteryzujące zmiany w zbiorowościach niejednorodnych to

agregatowe indeksy:

a) wartości, wielkości fizycznej i wzrostu cen,
b) wzrostu wartości, wzrostu cen, wielkości fizycznych,
c) wartości produkcji, wielkości fizycznej produkcji, cen,
d) wartości, wielkości fizycznej, cen.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

47

16. W obszarze wartości typowych dla określonej zbiorowości mieści się :

a) 68% całej zbiorowości,
b) 75% całej zbiorowości,
c) 95% całej zbiorowości,
d) 99,7% całej zbiorowości.

17. Indeksy dynamiki charakteryzują zmiany poziomu zjawiska:

a) w czasie,
b) w przestrzeni,
c) w strukturze,
d) w zbiorowości.

18. Wzajemne powiązanie i uwarunkowanie badanych zjawisk określa analiza

współzależności, którą określają:

a) współczynnik korelacji,
b) współczynnik zmienności,
c) współczynnik współzależności,
d) współczynnik proporcjonalności.

19. Jeśli współczynnik korelacji wynosi 0,5 to siła współzależności jest:

a) słaba,
b) średnia,
c) znaczna,
d) wysoka,

20. W analizie statystycznej wykorzystuje się jako użytkowy program komputerowy:

a) Płatnik,
b) HTML,
c) eMapa,
d) Excel.

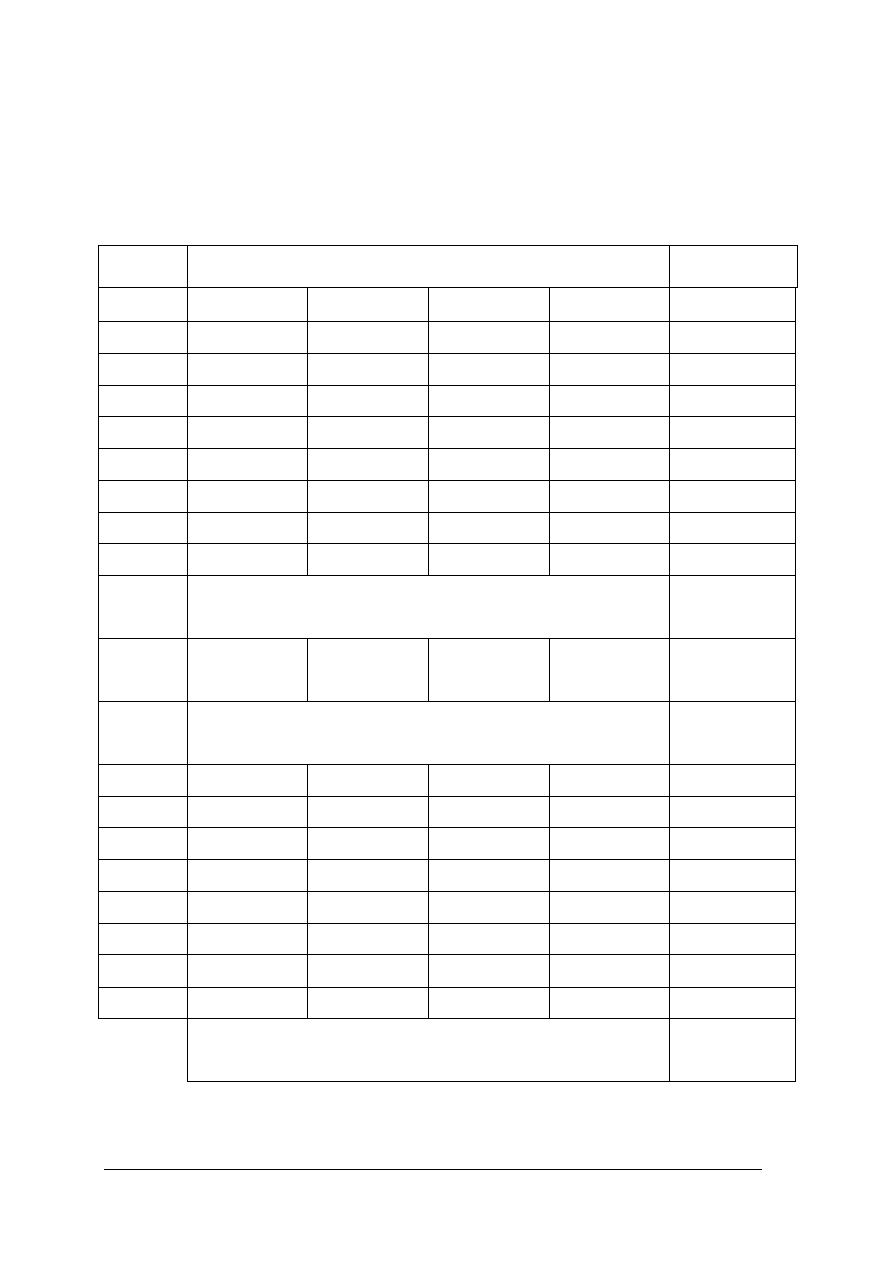
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

48

KARTA ODPOWIEDZI

Imię i nazwisko ……………………………………………………..

Wpisz numer poprawnej odpowiedzi lub brakujące słowo.

Numer

pytania

Odpowiedź

Punktacja

1.

a

b

c

d

2.

a

b

c

d

3.

a

b

c

d

4.

a

b

c

d

5.

a

b

c

d

6.

a

b

c

d

7.

a

b

c

d

8.

a

b

c

d

9.

a

b

c

d

10.

11.

a

b

c

d

12.

13.

a

b

c

d

14.

a

b

c

d

15.

a

b

c

d

16.

a

b

c

d

17.

a

b

c

d

18.

a

b

c

d

19.

a

b

c

d

20.

a

b

c

d

Razem

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

49

6. LITERATURA

1. Kassyk-Rokicka H.: Mierniki statystyczne. Państwowe Wydawnictwo Ekonomiczne,
Warszawa 1986
2. Komosa A.: Szkolny słownik ekonomiczny. Ekonomik, Warszawa 2002
3. Komosa A.: Statystyka. Ekonomik, Warszawa 2003
4. Michalski T.:Statystyka. Wydawnictwa Szkolne i Pedagogiczne, Warszawa 1999
5. Ostasiewicz St. (red.):Statystyka elementy teorii i zadania. Wydawnictwo Akademii

Ekonomicznej we Wrocławiu, Wrocław 1997

6. Sadowski W.:Statystyka na co dzień,. Państwowe Wydawnictwo Naukowe PWN,

Warszawa 1995