Całkowanie numeryczne

- 1 -

Ogólnie numeryczne metody obliczania całki oznaczonej:

polegają na zastąpieniu funkcji podcałkowej wielomianem interpolacyjnym W

n

(x) np. w postaci:

tak aby:

Całkowanie numeryczne

- 2 -

Kwadratury interpolacyjne

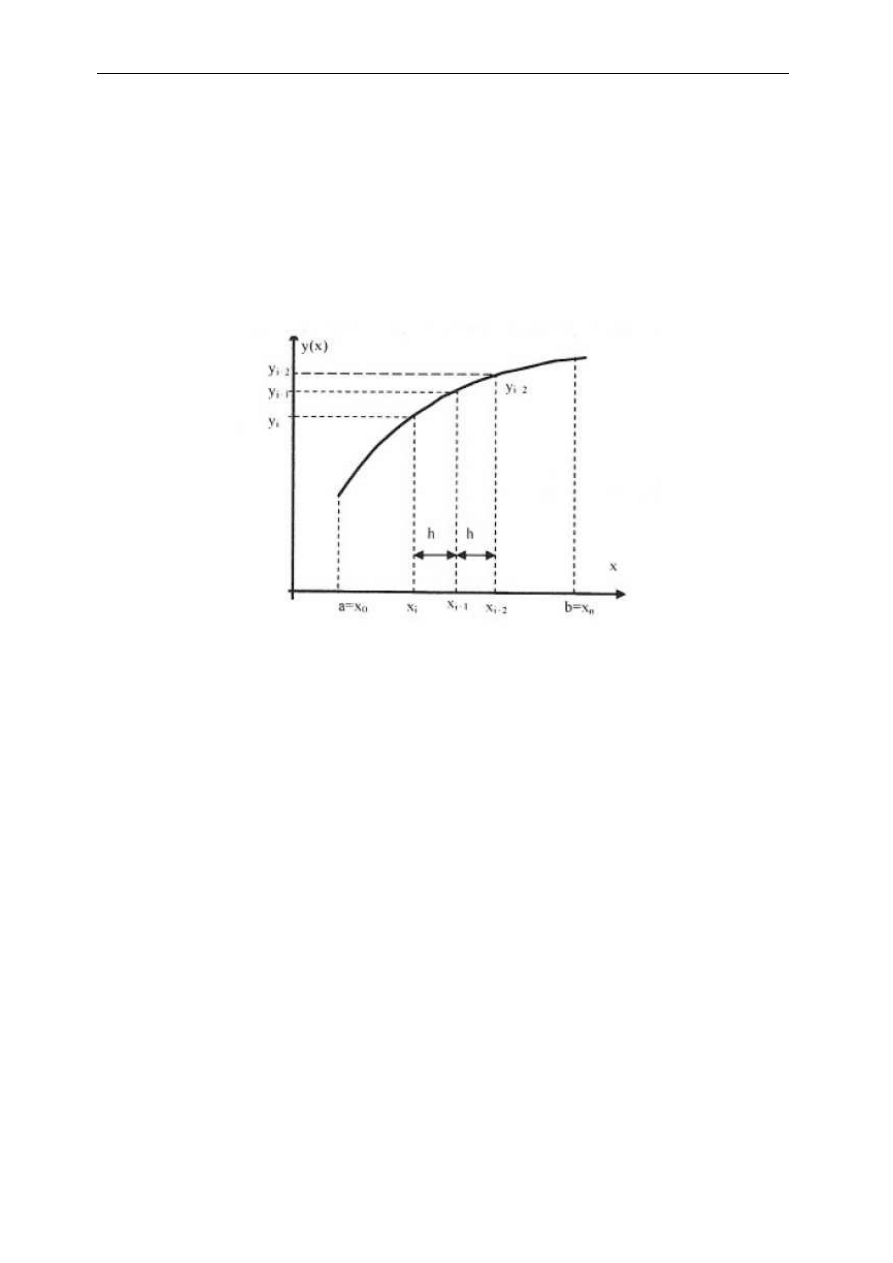
Niech funkcja podcałkowa f(x) jest ciągła w przedziale domkniętym [a,b]. Przedział ten dzieli się

na skończoną liczbę n równych podprzedziałów o długości h:

przy czym

, 0,1,2 … , # 1

Z twierdzeń dotyczących całki oznaczonej wynika, że:

$

%

&'(

%

&

)

*

%

+

*

%

,

*

Przyjmując:

-

%

&'(

%

&

można napisać, że:

$ -

)

*

%

+

*

%

,

*

Metody interpolacyjne polegają na przybliżeniu funkcji f(x) w przedziale

.

,

/ lub w

przedziale odpowiednio poszerzonym wzorem interpolacyjnym W(x), więc:

-

%

&'(

%

&

Można zatem napisać, że:

$

%

&'(

%

&

)

*

Całkowanie numeryczne

- 3 -

Do wyprowadzenia poszczególnych wzorów obliczania przybliżonej wartości całki oznaczonej

wykorzystany zostanie interpolacyjny wzór Newtona w postaci:

0∆

00 1

2!

∆

, 0

gdzie

∆

Całkowanie numeryczne

- 4 -

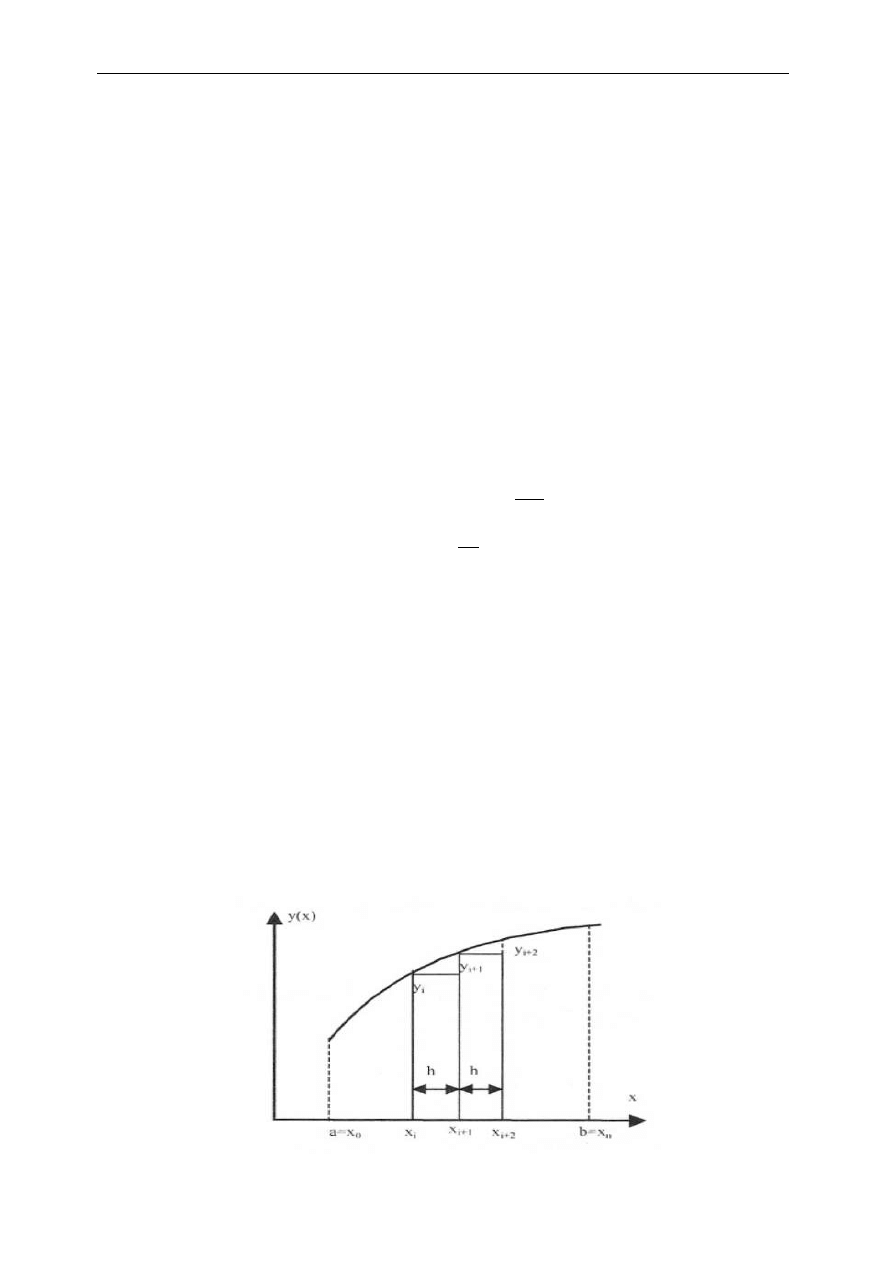
Metoda prostokątów

Uwzględniając tylko pierwszy składnik wielomianu Newtona zachodzi:

gdzie

3

przy czym

4 .

,

/. Oznacza to, że funkcję f(x) w przedziale .

,

/ przybliża się

wartością f

i

czyli:

-

%

&'(

%

&

%

&'(

%

&

Ostatecznie:

$

%

&'(

%

&

)

*

W celu obliczenia całki wprowadzono nową zmienną

0

%)%

&

5

. Stąd otrzymuje się:

0

Dolną granicę całkowania wyznacza się przyjmując

, zatem q = 0. Natomiast górną

przyjmując

, otrzymując q = 1.

Uwzględniając powyższe zależności otrzymujemy:

-

%

&'(

%

&

0

%

&'(

%

&

Ostatecznie:

$

)

*

Ponieważ iloczyn

odpowiada polu prostokąta o bokach

oraz

prezentowana metoda nosi

nazwę metody prostokątów.

Całkowanie numeryczne

- 5 -

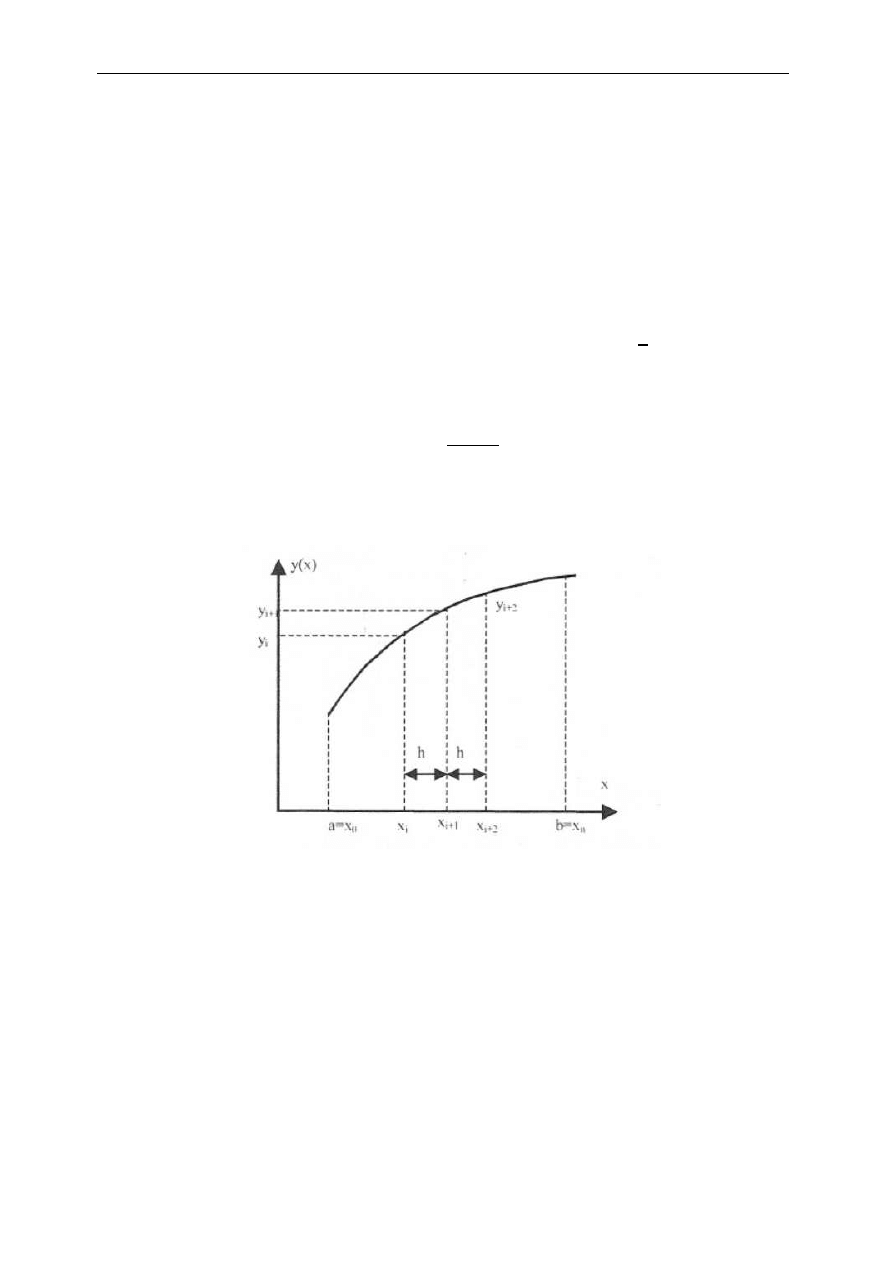
Metoda trapezów

Uwzględniając dwa składniki wielomianu Newtona mamy:

0∆

co daje:

%

&'(

%

&

0∆

%

&'(

%

&

Po wprowadzeniu tak jak uprzednio zmiennej q jest:

-

%

&'(

%

&

0∆

0∆

0

1

2

%

&'(

%

&

Sumując kolejne pola

-

, otrzymuje się:

6

2 $

)

*

7

Wzór ten nazywany jest wzorem trapezów ze względu na fakt, że elementami sumowania są pola

trapezów.

Całkowanie numeryczne

- 6 -

Metoda Simpsona

Jeżeli do wyznaczania całki uwzględni się trzy wyrazy wielomianu Newtona to całkowanie

odbywa się z uwzględnieniem trzech punktów:

-

%

&'8

%

&

9

0∆

00 1

2!

∆

:

3

4

%

&'8

%

&

Należy zaznaczyć, że następuje tu interpolacja funkcji parabolą. Do wyznaczenia jej potrzebne są

trzy punkty:

3

4

2

4

=

2

)

4

)

Wzór ten nazywa się wzorem Simpsona.

Całkowanie numeryczne

- 7 -

Zadania.

1.

Oblicz całkę z funkcji

f(x) = x

2

+ 3 w przedziale [2,5] metodą prostokątów dzieląc przedział

na:

a.

3 części

b.

5 części

c.

10 części.

2.

Oblicz całkę z funkcji

f(x) = x

2

+ 3 w przedziale [2,5] metodą prostokątów dzieląc przedział

na 10 części i licząc wartość funkcji w:

a.

początku przedziału

b.

środku przedziału

c.

końcu przedziału.

3.

Oblicz całkę z funkcji

f(x) = x

2

+ 3 w przedziale [2,5] metodą trapezów dzieląc przedział na:

a.

3 części

b.

5 części

c.

10 części.

4.

Oblicz całkę z funkcji

f(x) = x

2

+ 3 w przedziale [2,5] metodą Simpsona dzieląc przedział na

a.

6 części

b.

10 części.