1

Przedmiot kinematyka i dynamika ukła-
dów.

1.1

KINEMATYKA

dział mechaniki zajmujący się matematycznym opisem ruchu punktu ma-
terialnego; badaniem trajektorii punktu, abstrahując od działających sił
i bezwładności ciał.

1.2

DYNAMIKA

dział mechaniki zajmujący się opisem ruchu ciał materialnych pod wpły-
wem sił. W zależności od modelu mechanicznego, którym się zajmujemy
wyróżniamy dynamikę punktu materialnego, bryły sztywnej, płynów itp.

2

Trajektoria punktu materialnego, trój-
ścian Freneta.

Trajektoria określa położenie w R

3

w zależności od czasu.

C : R → R

3

C(t) = [c

1

(t), c

2

(t), c

3

(t)]

T

trajektoria musi być: ciągła, gładka(różniczkowalna w sposób ciągły)

RYS. Trójścian Freneta tworzą 3 prostopadłe do siebie wektory

¯

t, ¯

n, ¯

b.

¯

t =

˙c(t)

|| ˙c(t)||

- wektor jednostkowy ||¯

t|| = 1, o kierunku i zwrocie zgodnym z

˙c(t).

¯

n - wektor normalny ||¯

n|| = 1¯

n ∈ π

1

, π

2

,

π

1

⊥ ¯

t,

¯

t ∈ ¯

π

2

¯

b - wektor binormalny ¯

b = ¯

t × ¯

n

¯

K(s) = K(s)¯

n,

K(s) = |

d¯

t(s)

ds

| - krzywizna toru ruchu mówi jak

bardzo tor ruchu różni cię od linii prostej
T (s) = |

d¯

b(s)

ds

|- skręcenie, torsja mówi jak bardzo niepłaska jest trajekto-

ria.
T (s) = 0 jeśli ciało trajektoria leży w 1 płaszczyźnie

3

Zasada determinizmu i niezmienniczości
w mechanice newtonowskiej

3.1

Zasada determinizmu

Ruch układu jest wyznaczony przez położenie i prędkości początkowe.
¨

c(t) = F (t, c(t), ˙c(t)),

c(0),

˙c(0)

3.2

Zasada względności (niezmienniczości)

Prawo ruchu F, powinno być niezmiennicze ze względu na:

• przesunięcie w czasie

∀s[F

i

(c, ˙c, t) = F

i

(c, ˙c, t + s)]

można zatem stwierdzić, że (F

i

(c, ˙c, t) = F

i

(c, ˙c, 0)) prawo ruchu F

nie zależy wiec jawnie od czasu t.

¨

c = F

i

(c, ˙c)

1

• przesunięcie w przestrzeni

∀u[F

i

(c

1

, c

2

, . . . , c

n

, ˙c) = F

i

(c

1

+ u, c

2

+ u, . . . , c

n

+ u, ˙c)]

jesli u = −c

j

, to F

i

(c

1

− c

j

, . . . , c

j−1

− c

j

, c

j+1

− c

j

, . . . , c

n

− c

j

, ˙c)

F

i

- zależy od względnych położeń

• ruch jednostajny c

i

+ vt,

˙c

i

+ v

∀v[F

i

(c, ˙c

1

+ v, . . . , ˙c

n

+ v) = F

i

(c, ˙c

1

, . . . , ˙c

n

)]

jeśli v = − ˙c

j

, to F

i

= (c, ˙c

1

− ˙c

j

, . . . , ˙c

j−1

− ˙c

j

, ˙c

j+1

− ˙c

j

, . . . , ˙c

n

− ˙c

j

)

F

i

- zależy id względnych prędkości

• obrót w przestrzeni

∀RF

i

(Rc

1

, . . . , Rc

n

, R ˙c

1

, . . . , Rc ˙c

n

) = RF

i

(c, ˙c) = R ˙c

4

Zasady dynamiki Newtona

• Jeśli na ciało nie działa żadna siła, lub działające siły się równoważą

to ciało pozostaje w spoczynku lub porusza się ruchem jednostaj-
nym. ¨

c = 0

• Jeżeli na ciało działa niezrównoważona siła zewnętrzna to ciało

porusza się ruchem przyśpieszonym, z przyśpieszeniem proporcjo-
nalnym do działającej siły

¨

c

i

= F

i

(c, ˙c) =

1

m

i

f

i

• Jeżeli ciało A działa na ciało B siłą F

A

B, to ciało B działa na

ciało A siłą reakcji F

B

A równą co do wartości i kierunku, lecz o

przeciwnym zwrocie.

¯

F

A

B = − ¯

F

B

A

5

Pęd, moment pędu i energia układu
punktów materialnych

• pęd p =

P

n
i=1

p

i

=

P

n
i=1

m

i

˙c

i

zauważmy też, ze:

dp

dt

=

n

X

i=1

˙

m

i

˙c

i

+

n

X

i=1

m

i

¨

c

i

−−−→

˙

m = 0

n

X

i=1

m

i

˙c

i

=

n

X

i=1

F

i

jeśli działające siły F

i

równoważą się

dp

dt

= 0 ⇒ p =const.

• moment pędu

M =

n

X

i=1

M

i

=

n

X

i=1

c

i

× p

i

dM

dt

=

n

X

i=1

˙c

i

× ˙p

i

+

n

X

i=1

c

i

˙

p

i

=

n

X

i=1

˙c

i

× (m

i

˙c

i

) +

n

X

i=1

c

i

× F

i

Jeżeli działające momenty sił równoważą się tzn.

n

X

i=1

c

i

× F

i

= 0, to

dM

dt

= 0 ⇒ M = const.

2

• energia całkowita E = K + V

– energia kinetyczna

K =

P

n
i=1

1
2

m

i

( ˙c, ˙c) =

P

n
i=1

1
2

m

i

˙c

T

˙c

– energia potencjalna

V (c) = V (c

1

, c

2

, . . . , c

n

) siła F

i

jest potencjalna jeśli F

i

= −

∂V
∂c

i

W =

R

b

a

F

T

dc - praca nie zależy od drogi lecz od położenia

początkowego - a, i końcowego - b.

dE

dt

=

P

n
i=1

(F

i

+

∂V
∂c

i

)

T

˙c

i

jeśli działające siły są potencjalne tzn.

F

i

= −

∂V
∂c

i

dE

dt

= 0 ⇒ E = const.

6

Zasada najmniejszego Działania Hamil-
tona

Układ porusza się, tak żeby minimalizować działanie

I =

Z

t

1

t

0

L(q(t), ˙

q(t), t)dt → min

względem trajektorii - q(. ) = {(t, q(t))|t

0

¬ t ¬ t

1

}

7

Równanie Eulera - Lagrange’a

Jeżeli znana jest funkcja Lagrange’a opisująca układ, korzystając z zasa-
dy Najmniejszego Działania Hamiltona otrzymujemy równania postaci:

−

∂L

∂q

+

d

dt

∂L

∂ ˙

q

!

= 0

F - siły nie potencjalne

gdzie

∂L

∂q

i

= F

i

siła uogólniona

∂L

∂ ˙

q

i

= p

i

pęd uogólniony

Wyprowadzenie:

F (γ + h) ∼

= F (γ) + DF (γ)h ⇒ DF (γ)h = F (γ + h) − F (γ)

niech F (γ) =

R

t

1

t

0

L(q, ˙

q, t)dt

DF (γ)h =

Z

t

1

t

0

∂L(q, ˙

q, t)

∂q

· h +

∂L(q, ˙

q, t)

∂ ˙

q

· ˙h

!

dt

∂L(q, ˙

q, t)

∂ ˙

q

˙h =

∂L

∂ ˙

q

h(t)

t

1

t

0

+

Z

t

1

t

0

∂L

∂q

−

d

dt

∂L

∂ ˙

q

!

dt

wybieramy taką funkcję zakłócenia h(t), aby h(t

0

) = h(t

1

) = 0

∂L

∂ ˙

q

h(t)

t

1

t

0

= 0

oraz

Z

t

1

t

0

∂L

∂q

hdt = 0

DF (γ)h =

Z

t

1

t

0

∂L

∂q

−

d

dt

∂L

∂ ˙

q

!!

dt = 0 ⇔

∂L

∂q

−

d

dt

∂L

∂ ˙

q

= 0

3

8

Równanie Poincare’go

Jest

to

pewnego

rodzaju

rozszerzenie

równań

Eulera-Lagrange’a

(F (γ) = L(q, ˙

q, t)). Teraz zakładamy: F (γ) =

R

t

1

t

0

L(q, ˙

q, . . . , q

(k)

(t), t)dt

oraz wybieramy zakłócenie h(t) takie, że: h(t

0

) = h(t

1

) = 0 , ˙h(t

0

) =

˙h(t

1

) = 0, . . . , h

(k−1)

(t

0

) = h

(k−1)

(t

1

) = 0

DF (γ)h =

Z

t

1

t

0

∂L

∂q

−

d

dt

∂L

∂ ˙

q

+

d

2

dt

2

∂L

∂ ¨

q

+ . . . + (−1)

k

d

k

dt

k

∂L

∂q

(k)

!

Ponownie korzystając z zasady najmniejszego działania

DF (γ)h = 0 ⇔

∂L

∂q

−

d

dt

∂L

∂ ˙

q

+

d

2

dt

2

∂L

∂ ¨

q

+ . . . + (−1)

k

d

k

dt

k

∂L

∂q

(k)

= 0

9

Mechanika lagranżowska

Dział mechaniki opisujący ruch układu w oparciu o funkcję Lagrange’a

L(q, ˙

q, t) = K(q, ˙

q, t) − V (q),

zasadę najmniejszego działania

Z

t

1

t

0

L(q, ˙

q, t)dt → min

względem trajektorii q(·) = {t, q(t) | t

0

¬ t ¬ t

1

} oraz równania Eulera–

Lagrange’a

d

dt

∂L

∂ ˙

q

−

∂L

∂q

= 0 (F – siły niepotencjalne),

gdzie

∂L

∂q

i

= F

i

– siła uogólniona

∂L

∂ ˙

q

i

= p

i

– pęd uogólniony

K(q, ˙

q, t) =

1

2

˙

q

T

Q(q) ˙

q =

1

2

n

X

i,j=1

Q

ij

(q) ˙

q

i

˙

q

j

Macierz Q(q) jest symetryczna Q = Q

T

i dodatnio określona, więc istnieje

macierz do niej odwrotna Q

−1

. Niech V (q) = 0.

Wtedy L = K(q, ˙

q, t) =

1
2

P

n
i,j=1

Q

ij

(q) ˙

q

i

˙

q

j

∂L

∂ ˙

q

k

=

1

2

n

X

j=1

Q

kj

˙

q

j

+

1

2

n

X

i=1

Q

ki

˙

q

i

Q – symetryczna

P

n
j=1

Q

ik

=

P

n
i=1

Q

kj

∂L

∂ ˙

q

k

=

n

X

j=1

Q

kj

˙

q

j

∂L

∂q

k

=

1

2

n

X

i,j=1

∂Q

ij

∂q

k

˙

q

i

˙

q

j

oraz równanie Eulera – Lagrange’a ma postać

d

dt

∂L

∂ ˙

q

k

!

−

∂L

∂q

k

=

n

X

j=1

Q

kj

¨

q

j

+

1

2

n

X

i,j=1

∂Q

ik

∂q

j

˙

q

i

˙

q

j

+

+

1

2

n

X

i,j=1

∂Q

kj

∂q

i

˙

q

i

˙

q

j

−

1

2

n

X

i,j=1

∂Q

ij

∂q

k

˙

q

i

˙

q

j

= 0

4

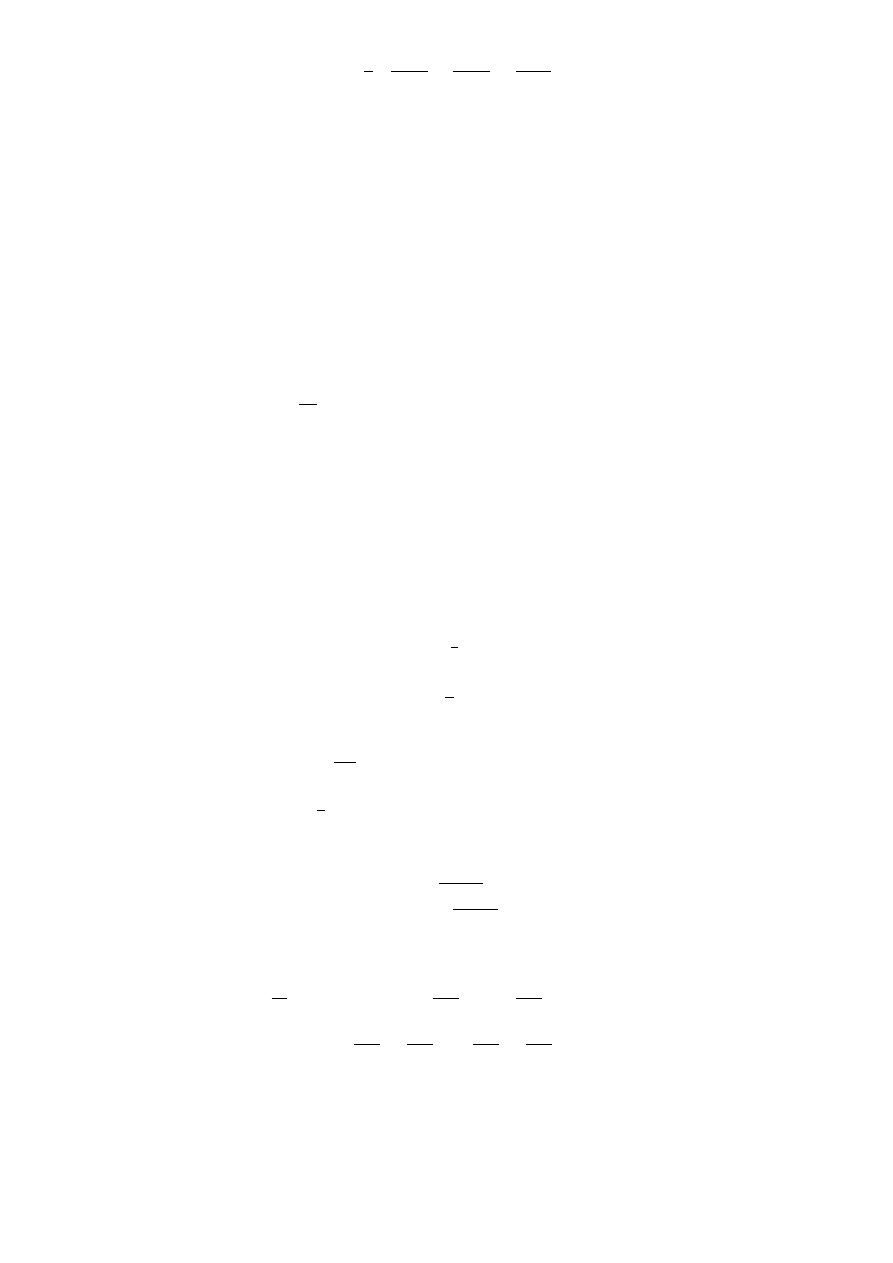
Wprowadźmy teraz symbol Christoffela I rodzaju

c

k
ij

=

1

2

∂Q

ik

∂q

j

+

∂Q

kj

∂q

i

−

∂Q

ij

∂q

k

!

.

Można zapisać k-te równanie

n

X

j=1

Q

kj

¨

q

j

+

n

X

i,j=1

c

k
ij

˙

q

i

˙

q

j

= 0

oraz postać wektorową:

Q(q) + C(q, ˙

q) ˙

q = 0,

gdzie C(q, ˙

q)

kj

=

P

n
i=1

c

k
ij

˙

q

i

oraz postać bardziej ogólną, gdy V (q) 6= 0:

Q(q)¨

q + C(q, ˙

q) ˙

q + D(q) = F,

gdzie Q(q) - macierz bezwładności, C(q, ˙

q) - macierz sił Coriolisa i odśrod-

kowych, D(q) =

∂V

∂q

- macierz sił potencjalnych, F - siły niepotencjalne.

10

Mechanika hamiltonowska

Część mechaniki zajmująca się opisem ruchu układu w oparciu o Hamil-
tonian oraz kanoniczne równania ruchu Hamiltona.

Jeśli znamy funkcję Lagrange’a opisującą układ L(q, ˙

q, t) można wy-

prowadzić Hamiltonian dzięki przekształceniu Legendre’a:

H(q, p) = max

v

(p

T

v − L(q, v))

Lagranżian jest z reguły równy L =

1
2

v

T

Q(q)v + V (q).

H(q, p) = p

T

v −

1

2

v

T

Q(q)v + V (q)

oraz

p =

∂L

∂v

= Q(q)v ⇒ V (q, p) = Q

−1

(q)p

H(q, p) =

1

2

p

T

Q

−1

p + V (q) – całkowita energia układu

Równania kanoniczne Hamiltona:







˙

q =

∂H(q,p)

∂p

˙

p = −

∂H(q,p)

∂q

Zauważmy ponadto:

d

dt

(H(q(t), p(t))) = (

∂H

∂q

)

T

˙

q + (

∂H

∂p

)

T

˙

p =

= (

∂H

∂q

)

T

(

∂H

∂p

) − (

∂H

∂p

)

T

(

∂H

∂q

) = 0

Hamiltonian jest całką pierwszą (stałą ruchu) układu równań kano-

nicznych.

5

11

Stałe ruchu układu hamiltonowskiego,
nawias Poissona

Stała ruchu - wielkość fizyczna, która jest stała (nie zmienia się) pod-

czas ruchu. Z istnienia stałych ruchu można wyprowadzić zasady
zachowania. Przykłady stałych ruchu:

– energia całkowita: E = H(q

1

, . . . , q

n

, p

1

, . . . , p

n

)

– pęd - jego zachowanie jest związane z niezmienniczością przestrzeni

względem przesunięcia / brak zewnętrznych sił → układ izolowany

– moment pędu - jego zachowanie jest związane z niezmienniczością

przestrzeni względem obrotu / brak momentów sił zewnętrznych

Nawias Poissona - jest to funkcja będąca pewnego rodzaju mnożeniem

funkcji, f : R

2n

→ R.

Funkcje F z nawiazem Poissona tworzą algebrę Liego.
Własności:

* liniowość {αF

1

+ βF

2

, F

3

} = α{F

1

, F

3

} + β{F

2

, F

3

}

* antysymetria {F

1

, F

2

} = −{F

2

, F

1

}

* tożsamość

Jacobiego

{F

1

, {F

2

, F

3

}}

+

{F

2

, {F

1

, F

3

}}

+

{F

3

{F

1

, F

2

}} = 0

{F

1

, F

2

} =

∂F

1

∂q

!

T

∂F

2

∂p

!

−

∂F

1

∂p

!

T

∂F

2

∂q

!

Jeśli F

1

, F

2

- stałe ruchu, to {F

1

, F

2

}, także stała ruchu.

12

Twierdzenie Liouvielle’a o kwadratu-
rach

Załóżmy, F

1

, F

2

, . . . , F

n

są stałymi ruchu układu równań kanonicznych

Hamiltona oraz F

1

= H.

Jeśli stałe są niezależne oraz w inwolucji:

* niezależność

rank






∂F

1

∂q

1

,

∂F

1

∂q

2

, . . . ,

∂F

1

∂q

n

∂F

1

∂p

1

, . . . ,

∂F

1

∂p

n

. . .

∂F

n

∂q

1

,

∂F

n

∂q

2

, . . . ,

∂F

n

∂q

n

∂F

n

∂p

1

, . . . ,

∂F

n

∂p

n






= η

* inwolucja

∀i, j{F

i

, F

j

} = 0 mając ’n’ stałych, nie można utworzyć już więcej

F

1

, F

2

, . . . , F

n

- są wypasione

to:

– trajektorie układu leżą w n-wymiarowej rozmaitości

M

a

= {(q, p) ∈ R

2n

|F

1

(q, p) = a

1

, . . . , F

n

(q, p) = a

n

}

– równania kanoniczne można rozwiązać przez kwadratury

M

a

- wszystkie trajektorie leżą w M

a

, nie mogą z niej wyjść.

6

13

Twierdzenie Liouviella o dywergencji

Niech dany będzie układ dynamiczny ˙x = f (x), posiadający strumień
φ

t

(x) oraz V (t) = vol(φ

t

(D)), V (0) = vol(D) - objętość

Jeżeli div(f (x)) = tr

∂f
∂x

(x) = 0, to V (t) = const.

div(f (x)) = tr





∂

2

H

∂q∂p

∂

2

H

∂p

2

−

∂

2

H

∂q

2

−

∂

2

H

∂p∂q





=

n

X

i=1

∂

2

H

∂q

i

∂p

i

−

n

X

i=1

∂

2

H

∂p

i

∂q

i

= 0

Strumień układu hamiltonowskiego zachowuje objętość. (namalować

portret fazowy wahadła i przekształcające się trójkąciki, których kształty
się zmieniają, a których pole powierzchni jest stałe).

14

Twierdzenie Poincare’go o powrocie

Niech dany będzie układ dynamiczny ˙x = f (x), φ

t

(x) = x(t) oraz

div(f (x)) = 0.

Niech D będzie ograniczonym (vol(D) < ∞) oraz niezmienniczym

(φ

t

(D) = D) zbiorem. Wówczas dla każdego x ∈ D i dla każdego oto-

czenia U (x ∈ U ) istnieje punkt y (y ∈ U ) taki, że w pewnej chwili
φ

t

(y) = U .

Niech dany będzie układ hamiltonowski

q, p ∈ R

n

,

H(p, y),

˙

q =

∂H

∂p

˙

p =

∂H

∂q

Oznaczmy

x =

q
p

!

oraz

f (x) =

∂H

∂p

∂H

∂q

!

Z twierdzenia Liouvielle’a o dywergencji div(f (x)) = 0 oraz strumień

układu hamiltonowskiego zachowuje objętość.

Wniosek: dla układu hamiltonowskiego spełnione są warunki twier-

dzenia Poincare’ o powrocie.

(namalować przykład trajektorii zamkniętej i otwartej spełniającej

powyższy warunek)

15

Ograniczenia konfuguracyjne i fazowe

Ograniczenia (więzy) to każdy rodzaj ograniczenia ruchu nałożonego na
poruszające się ciało. Ograniczenia można podzielić na:
- holonomiczne (całkowalne) – takie, które można opisać prostymi rów-
naniami różniczkowymi
- nieholonomiczne (niecałkowalne) – nie można ich opisać RR.

Ograniczenia fazowe można zapisać w formie Pfaffa jako macierz A(q),

spełniającą warunek A(q) ˙

q = 0.

A(q) ˙

q = A(q)

dq

dt

= 0 ⇒ A(q)dq = 0

Spróbujmy znaleźć macierz M (q)

l×l

taką, że:

M (q)A(q)dq = dF = 0,

wtedy F (q) = const.

Ograniczenia A(q) ˙

q = 0 są holonomiczne, jeżeli istnieje macierz M (q)

o rozmiarze l × l taka, że detM (q) 6= 0, a także funkcja F : R

n

→ R

l

:

F (q) = (F

1

(q), F

2

(q), . . . , F

l

(q)) taka, że

7

M (q)A(q) =

dF

dq

W przypadku ograniczeń holonomicznych można wyeliminować l

współrzędnych, istotne jest tylko (n − l) współrzędnych.

16

Równania dynamiki układu z ograni-
czeniami

Równanie układu

Q(q)¨

q + C(q, ˙

q) ˙

q + D(q) = F,

gdzie Q(q) - macierz bezwładności, C(q, ˙

q) - macierz sił Coriolisa i od-

środkowych, D(q) =

∂V

∂q

- macierz sił potencjalnych, F - siły powodujące

spełnienie ograniczeń (np. siły tarcia).

Używamy zasady d’Alemberta.

Siły F nie wykonują pracy na dopuszczalnych przemieszczeniach

A(q) ˙

q = 0 ⇒ F

T

˙

q = 0

F

T

= λ

T

A(q) ⇒ F = A

T

(q)λ,

gdzie λ - wektor mnożników Lagrange’a.

Równania układu mają postać:

Q(q)¨

q + C(q, ˙

q) ˙

q + D(q) = A

T

λ

A(q) ˙

q = 0. Niech ˙

q = G(q)η oraz A(q)G(q) = 0

G

T

Q¨

q + G

T

C ˙

q + G

T

D = (GA)

T

λ = 0

G

T

Q( ˙

Gη + G ˙

η) + G

T

CGη + D = 0

Równania układu nieholonomicznego:

(

˙

q = G(q)η

˙

η = (G

T

QG)

−1

(−G

T

Q ˙

Gη − G

T

CGη − G

T

D)

8