PMEW1 – pytania z egzaminu

Termin 1

1.Sformułować i uzasadnić warunki równowagi dla układów przestrzennych

2.Pojęcie momentu bezwładności. Obliczyć wartość momentów dla:

3.Opisać wykres rozciągania, zachowanie się w poszczególnych strefach wykresu, podać strefę, w której zawarte są

naprężenia niezbędne do obliczeń wytrzymałościowych.

4.Udowodnić wzór, jakiego przypadku dotyczy, jakie są założenia, przykład.

? max =

M

2F?min

5.Dla belki określić przekrój, równanie linii ugięcia, obliczyć równanie i ugięcie. Dane: P, a, kg

Termin 2

1.Obliczyć siłę wypadkową

2a

P

a

a

c

3c

P

L=3a

c

r

A

B

C

D

2.Twierdzenie Steinera. Obliczyć moment bezwładności figury.

3.Skręcanie rurki cienkościennej.

4.Definicja naprężenia i odkształcenia

5.Dla belki określić przekrój, równanie linii ugięcia, obliczyć równanie i ugięcie.

a)

b)

1.Reg. Pappusa-Guldina
Powierzchnia zakreślona przez obrót odcinka linii płaskiej dookoła osi leżącej na płaszczy żnie tej linii i nie przecinającej jej równa się iloczynowi długości jej i drogi jaką opisuje przy obrocie środek masy tej
linii. P=2pixcL
Objętość bryły zatoczonej przez obrót figury płaskiej dookoła osi leżącej na płaszczyźnie figury i nie przecinającej jej równa się iloczynowi powierzchni figury i długości drogi jaką opisuje środek masy figury
V=2pixcP(powierz)

2 Skrętnik oś centralna
Układ złożony z wektora głównego i składowej momentu głównego leżącej na linii działania wektora głównego -skrętnik.
Prosta względem której punktów momenty główne są do niej równoległe nazywa się osią skrętnika. Linia działania wektora głównego i składowej momentu głównego

23Centroidy
Miejscem geometrycznym kolejnych położeń chwilowych środków obrotu ciała poruszającego się ruchem płaskim na płaszczyźnie nieruchomej jest krzywa płaska- centroida stała.
M.g.k.p.ś.o. na płaszczyźnie ruchomej poruszającej się wraz z bryłą jest krzywa płaska- centroida ruchoma (r lin ch ś ob)
Podczas r. płaskiego c. ruch. toczy się bez poślizgu po c. stał.

6Prawo zmienności energii p m
Różniczka energii kinetycznej punktu materialnego jest równa elementarnej pracy siły działającej na ten punkt dEk=d’L
Przyrost energii kinetycznej poruszającego się punktu równy jest pracy siły działającej na ten punkt na drodze jaką ten punkt przebył EkB-EkA=LAB

9Redukcja dowoli przes ukł sił
Dowolny przestrzenny układ sił działających na ciało sztywne możemy zastąpić siłą R przyłożoną do dowolnie wybranego środka redukcji O równą sumie geometrycznej wszystkich sił układu (wektor główny)
oraz parą sił o momencie Mo równym sumie geometrycznej momentów tych sił względem środka redukcji (moment główny).

13Prawo zmienności krętu
Pochodna krętu punktu materialnego względem danego bieguna równa jest momentowi sił działających na dany punkt względem tego bieguna K=Mo(F)=r?F
Kręt punktu materialnego względem bieguna jest stały jeżeli moment sił działający na punkt względem tego bieguna jest równy zeru Mo(F)=0 Ko=C

17Elipsoida bezwładności
Elipsoidę będącym miejscem geometrycznym końców odcinków odwrotnie proporcjonalnych do ramion bezwładności ciała względem prostych przechodzących przez dany punkt O nazywamy elipsoidą
bezwładności ciała dla punktu O

20Red ukł sił do wypadkowej
W przypadku gdy suma geometryczna układu sił P1,P2,..,Pn działających w jednej płaszczy-żnie na ciało sztywne różna jest od zera układ zastąpić możemy jedną siłą wypadkową równą wektorowi głównemu
R. Jeżeli suma geometryczna jest równa zeru to układ sił może (ale nie musi) redukować się do pary której wektor jest prostopadły do płaszczyzny działania sił.

P

2P

3P

c

c

3c

3c

P

L=3a

d

d

d

c

Równanie linii działania wypadkowej wyznacza się z warunku że moment wypadkowej względem początku układu równa się momentowi głównemu Mo równemu sumie momentów danych sił względem
początku układu współrzędnych rw # W = Mo

10Prę i przys pkt we wsp bieg
Położenie punktu M we współrzędnych biegunowych określa-my za pomocą promienia wodzącego r i kąta jaki tworzy on ze stałym kierunkiem.
Prędkość punktu M jest pochodną względem czasu promienia- wektora r v=dr/dt=
Przyspieszenie p jest pochodną względem czasu prędkości v

24Aksoidy bryły w r. pł. rys
Chwilowym środkom obrotów płaszczyzny ruchomej odpowiadają osie obrotów chwilowych brył które są prostopadłe w punktach krzywej- centroidy ruchomej do ruchomej płaszczyzny . Osie te tworzą w
układzie ruchomym powierzchnię walcową- aksoidę ruchomą.
Proste prostopadłe w punktach krzywej-centroidy stałej do płaszczyzny stałej utworzą w przestrzeni nieruchomej powierzchnię walcową- aksoidę stałą.
W każdej chwili jedna z tworzących aksoidy ruchomej układu sztywnego poruszającego się ruchem płaskim pokrywa się z odpowiednia tworząca aksoidy stałej. Tworząca ta jest w tej chwili osią obrotu
chwilowego układu. W r. płaskim układu sztywnego aks. ruchoma toczy się bez poślizgu po aks. stałej.

38Aksjomaty mech klasycznej
1Jeżeli na ciało nie działa żadna siła to ten punkt porusza się ruchem jednostajnym prostoliniowym (może być bezruch).
2Przyspieszenie punktu materialnego jest wprost proporcjonalne do siły działającej na punkt. Współczynnikiem proporcjonalności jest masa p=F/m
3Dwa punkty materialne oddziaływają na siebie siłami które są równe co do wartości, przeciwnie skierowane i leża na linii łączącej te punkty.
Przestrzeń jest jednorodna gdy odcinek umieszczony w każdym miejscu tej przestrzeni ma tą samą długość.
Przestrzeń jest izotropowa gdy właściwości przestrzeni nie zależą od kierunku.
Przestrzeń jest anizotropowa gdy właściwości zmieniają się w zależności od kierunku (ruch w jedną stronę jest trudniejszy niż w drugą).
4Czas jest jednorodny.

27Środki geom,masy,ciężkości
Środek masy-punkt mający tę właściwość że wektor wodzący tego punktu pomnożony przez masę układu równa się sumie iloczynów wektorów wodzących wszystkich punktów układów pomnożonych przez
ich masy.
Na układ lub ciało znajdujące się w polu przyciągania Ziemi działają siły ciążenia punktów układu lub ciała. Siły te zastępu-jemy wypadkową siłą ciężkości. Przy założeniu że wymiary układu są małe w
stosunku do wymiarów Ziemi można siły ciężkości punktów układu uważać za równoległe. W takim razie możemy wyznaczyć środek równoległych sił ciężkości. Punkt ten to środek ciężkości ciała lub
układu. W punkcie tym można przyłożyć wypadkową siłę ciężkości układu. Na położenie tego punk-tu nie wpływa obrót układu lub ciała.
Gdy układ o małych rozmiarach- siły ciężkości punktów zależą tylko od ich mas a pomijalne są różnice przyspieszenia ziemski-ego wynikające z różnych odległości punktów układu od środka Ziemi.
W warunkach ziemskich występuje więc pokrywanie się położeń środka masy i środka ciężkości. Istnieje jednak zasadnicza różnica między tymi pojęciami. Pojęcie środka masy ma sens niezależnie od
działających sił oraz rozmiarów układu. Pojęcie położenia środka ciężkości przestaje być ścisłe przy dużych rozmiarach układu a w przestrzeni pozbawionej ciążenia traci sens.

32Stożek tarcia rys
Biorąc pod uwagę wszystkie możliwe położenia reakcji ciał chropowatych odpowiadające różnym kierunkom działania siły stycznej P otrzymamy jako miejsce geometryczne wektorów R stożek którego osią
jest prosta działania reakcji normalnej N a którego tworząca zawiera z osią kąt tarcia .Stożek ten to stożek tarcia. W przypadku ciał izotropowych tarcie nie zależy od kierunku działania siły T stożek ten jest
stożkiem kołowym, dla ciał anizotropowych stożek ma podstawę eliptyczną.

33Ciało kuliste
Ciało kuliste-ciało którego elipsoidą bezwładności jest kula. Wszystkie proste przechodzące przez środek masy są osiami głównymi (kula, jednorodny sześcian). Dla tego ciała wszystkie momenty
bezwładności są jednakowe.

42Kąty Eulera rys
Kąty Eulera określają położenie układu osi związanego z ciałem sztywnym względem układu x,y,z. Kątami Eulera są:
kąt obrotu właściwego -utworzony przez linię węzłów (prosta powstała z przecięcia płaszczyzny AXY z A ) A i oś
kąt precesji -utworzony przez oś X i linię węzłów A
kąt nutacji -utworzony przez osie Z i
39Prawo zmienności pędu p m
Pochodna pędu punktu materialnego równa jest sile działającej na ten punkt 1B’=F 2B=mv
Rzutując równanie 1 na osie układu współrzędnych otrzymujemy trzy równania skalarne:
Bx’=d/dt(mx’)=Fx y i z
Przyrost pędu p.m. równy jest elementarnemu impulsowi siły działającej na ten punkt dB=dI=Fdt
Pęd p.m. na który nie działają żadne siły jest stały F=0 ,B=C
Prawo pędu w postaci różniczkowej 1 może służyć do układania równań różniczkowych ruchu na równi z II prawem Newtona. W przypadku siły stałej prawo pędu pozwala na szybkie rozwiązanie pewnych
zadań dynamiki bez konieczności pełnego rozwiązywania równań ruchu. Prawo pędu jest wtedy określone równaniami wiążącymi ze sobą prędkości początkowe i końcową wartość siły oraz przedział czasu.

47Ruch post płas obrót śrub
Ruch postępowy- szczególny przypadek ruchu bryły taki, że wartości wszystkich kątów są stałe (osie zachowują swoje kierunki w czasie ruchu).Każdy odcinek łączący dwa punkty bryły zachowuje stale
położenie równoległe do pierwotnego.(tłok)
Ruch kulisty- ruch bryły przy którym jeden z punktów układu ruchomego związanego z bryłą jest nieruchomy.(koła stożk,bąk)
Ruch obrotowy- ruch przy którym dwa punkty bryły pozostają stale nieruchome. Wszystkie punkty prostej przeprowadzone przez te dwa punkty także pozo-staną nieruchome. Pozostałe punkty powinny
zostać w stałej odległości od nieruchomej prostej a więc mogą one poruszać się po okręgach których płaszczyzny są prostopadłe do danej prostej a ich środki leżą na tej prostej.
Ruch płaski-ruch w którym odległości wszystkich jego punktów od pewnej nieruchomej płaszczyzny są stałe. Wszystkie punkty ciała poruszają się w płaszczyznach równoległych do danej płaszczyzny
nieruchomej. Kąty precesji i nutacji są stałe zmieniać się może jedynie kąt
Ruch śrubowy-ruch bryły przy którym obraca się ona wokół nieruchomej prostej i jednocześnie przemieszcza postępowo wzdłuż tej prostej. Każdy punkt bryły porusza się po powierzchni walcowej której
osią jest oś obrotu. Torem punktu jest linia śrubowa.

15Zakleszczenie
Zakleszczenie jest to zjawisko utrzymania stanu równowagi przy dowolnie dużych siłach zewnętrznych.(musi być tarcie).
Musi być odpowiednia relacja pomiędzy alfa, ni, promień
Samohamowność jest to zjawisko w którym ruchome ciało po usunięciu siły powodującej ruch utrzymane jest w równowadze tylko przez siły tarcia
Pmin=0- układ samohamowny
Pmax—nieskończoność - układ zakleszczający się

8Red pł uk sił wielobok sznur
Dowolny płaski układ sił można zastąpić przez dwie siły działające wzdłuż skrajnych boków wieloboku sznurowego. Wartości tych sił są wyrażone przez dług-ości odpowiednich promieni wieloboku sił a
zwroty są takie że wektorowa suma tych sił jest równa wektorowi głównemu R. Linia działania wypadkowej W=R przechodzi przez punkt przecięcia skrajnych boków wieloboku sznurowego.
Przy redukcji płaskiego układu sił mogą występować przypadki:
1Wielobok sił nie zamyka się - układ sił redukuje się do jednej siły wypadkowej
2Wielobok sił zamyka się a wielobok sznurowy nie zamyka się- układ sił redukuje się do pary sił
3Wielobok sił i wielobok sznurowy zamykają się- układ sił znajduje się w równowadze

49Precesja regularna rys
Precesja regularna jest to szczególny przypadek ruchu kulistego ciała, w którym ciało obraca się wokół osi własnej z prędkością kątową a oś ta obraca się wokół osi stałej z z prędkością kątową .Kąt
między osiami jest stały. W ruchu tym prędkości kątowe obrotu własnego i precesji są stałe = =const, = =const a prędkość kątowa nutacji jest równa zeru więc kąt nutacji jest stały =0, = =const
Przykładem precesji regularnej jest ruch bąka symetrycznego. Bąk wiruje z prędkością wokół osi własnej która obraca się wokół stałej osi pionowej z prędkością kątową .Osie tworzą kąt . Moment sił
zewnętrznych utrzymujący ruch precesyjny jest momentem siły ciężkości bąka.

12Tarcie opasania
Tarciem opasania nazywamy siły tarcia występujące między powierzchniami cylindrycznymi i cięgnami taśmami sznurami pasami lub linami na nie nawiniętymi. Siły te w hamulcach taśmowych hamują
wzajemny poślizg koła i taśmy natomiast w przypadku kół pasowych nie dopuszczają do wzajemnego poślizgu koła i pasa

22Ruch pod działaniem siły za
F=F(t) x’’=1/mFx(t) y z}
x’=S1/mFx(t)dt+C1
x=S[S1/mFx(t)dt+C1]dt+C2
x(0)=x0, vx(0)=v0x
x=S[S1/mFx(t)dt]dt+v0xt+x0
mx’’=F(x’) mdv/dt=F(v) t=Sm/F(v)dv+C1 t=t(v) v=v(t)
dx=v(t)dt x=x(t) mdx/dtdv=F(v)dx|mvdv/F(v)=dx x=Smvdv/F(v)+C2 x=x(v)

18Moment bezwładnoś Steiner
Iloczyn masy punktu materialne-go i kwadratu odległości od danego punktu, prostej lub płaszczyzny nazywamy momentem bez-władności tego p.m. odpowiednio względem punktu, prostej lub płaszczyzny
I=mro2
xyz-nieruchomy o osiach XYZ II do poprzednich związany z ciałem i przyłożony do jego środka masy C roi wektor określający położenie dowolnego punktu ciała względem środka masy ri- względem
punktu O(xyz) ri=rc+roi Moment bezwładności ciała względem punktu O Io= Druga z całek jest =0 pierwsza =masie ciała trzecia=momentowi bezwładności ciała względem środka masy Io=Ic+mrc2
Moment bezwładności ciała względem dowolnego punktu równy jest sumie momentu względem środka masy i iloczynu masy ciała i kwadratu odległości danego punktu od środka masy

21Potencjał energ pot pola sił
Obszar przestrzeni w której na znajdujący się w nim punkt materialny działa siła nazywamy polem sił. Istnieje dla danego po-la funkcja V=V(r,t) taka że siła działająca na punkt może być określona jako
gradient tej funkcji ze znakiem ujemnym F=-gradV(r,t) Funkcję V nazywamy potencjałem a pole sił polem potencjalnym. Jeżeli potencjał zależy od czasu to pole jest niestacjonarne jeśli zaś od czasu nie zależy
polem stacjonarnym. Potencjał jest nazywany w tym przypadku także energią potencjalną a pole jest polem zachowawczym V=Ep=V(r)

16Prawo zmien ene w po poten
Praca sił pola przy przemieszczaniu punktu z jednego położenia w drugie równa jest różnicy potencjałów w punkcie początkowym i końcowym i nie zależy od toru po którym przemieszcza się punkt
przyłożenia siły i równa jest pracy siły działającej na punkt materialny przy tym przejściu. Sumę energii kinetycznej i potencjalnej punktu materialnego nazywamy energią mechaniczną p.m. E. Energia
mechaniczna p.m. poruszającego się w polu potencjalnym ma wartość stałą.

34Promień bezwładności ciała
Promień bezwładności ciała k względem punktu, prostej lub płaszczyzny jest to odległość punktu materialnego odpowiednio od danego punktu, prostej lub płaszczyzny. Gdyby masę całego ciała zgrupować w
jednym punkcie położonym w odległości k od danego punktu, prostej lub płaszczyzny to moment bezwładności takiego p.m. byłby taki sam jak moment bezwładności danego ciała
mk2=I k=pierw I/m k2=I/m=niSpoVro2dV/niV=I’/V
Wartość promienia bezwładności jest jednakowa zarówno dla ciała jednorodnego jak i dla figury geometrycznej określającej jej kształt.

19Moment dewiacji Steiner

Momentem dewiacji ciała względem dwóch prostopadłych płaszczyzn nazywamy granicę sumy iloczynów mas elementów ciała i odległości tych elementów od danych płaszczyzn
Ixy=S po m xydm
Układ wsp XYZ o środku w środku masy ciała. Odległości płaszczyzn xyz od XYZ są równe xc, yc, zc. Całka 2 i 3 to momenty statyczne ciała względem płaszczyzn przechodzących przez środek masy są
więc =0
Ixy=IXY+mxcyc Moment dew. względem dwóch płaszczyzn prostopadłych =jest sumie momentu dew wzgl płasz II do danych i przechodzących przez środek masy ciała oraz iloczynu masy skupionej w
środku masy ciała i odległości odpowiednich płaszczyzn.

45Int geo skład przys w r kul
Przyspieszenie można przedstawić jako sumę 3 składowych:
pA-przysp dowolnego punktu A bryły przyjętej za początek ruchomego układu odniesienia, jednakowe dla wszystkich punktów ciała
po-przysp obrotowe skierowane prostopadle do promienia ro
pd-przysp dośrodkowe gdzie d jest wektorem prostopadłym do osi obrotu przedstawiającym odległość punktu bryły od osi obrotu.
W ruchu kulistym o środku w A składowa pA=0 i pozostają tylko składowe wynikające z ruchu kulistego

1.Reg. Pappusa-Guldina
Powierzchnia zakreślona przez obrót odcinka linii płaskiej dookoła osi leżącej na płaszczy żnie tej linii i nie przecinającej jej równa się iloczynowi długości jej i drogi jaką opisuje przy obrocie środek masy tej
linii. P=2pixcL
Objętość bryły zatoczonej przez obrót figury płaskiej dookoła osi leżącej na płaszczyźnie figury i nie przecinającej jej równa się iloczynowi powierzchni figury i długości drogi jaką opisuje środek masy figury
V=2pixcP(powierz)

2 Skrętnik oś centralna
Układ złożony z wektora głównego i składowej momentu głównego leżącej na linii działania wektora głównego -skrętnik.
Prosta względem której punktów momenty główne są do niej równoległe nazywa się osią skrętnika. Linia działania wektora głównego i składowej momentu głównego

23Centroidy
Miejscem geometrycznym kolejnych położeń chwilowych środków obrotu ciała poruszającego się ruchem płaskim na płaszczyźnie nieruchomej jest krzywa płaska- centroida stała.
M.g.k.p.ś.o. na płaszczyźnie ruchomej poruszającej się wraz z bryłą jest krzywa płaska- centroida ruchoma (r lin ch ś ob)
Podczas r. płaskiego c. ruch. toczy się bez poślizgu po c. stał.

6Prawo zmienności energii p m
Różniczka energii kinetycznej punktu materialnego jest równa elementarnej pracy siły działającej na ten punkt dEk=d’L
Przyrost energii kinetycznej poruszającego się punktu równy jest pracy siły działającej na ten punkt na drodze jaką ten punkt przebył EkB-EkA=LAB

9Redukcja dowoli przes ukł sił
Dowolny przestrzenny układ sił działających na ciało sztywne możemy zastąpić siłą R przyłożoną do dowolnie wybranego środka redukcji O równą sumie geometrycznej wszystkich sił układu (wektor główny)
oraz parą sił o momencie Mo równym sumie geometrycznej momentów tych sił względem środka redukcji (moment główny).

13Prawo zmienności krętu
Pochodna krętu punktu materialnego względem danego bieguna równa jest momentowi sił działających na dany punkt względem tego bieguna K=Mo(F)=r?F
Kręt punktu materialnego względem bieguna jest stały jeżeli moment sił działający na punkt względem tego bieguna jest równy zeru Mo(F)=0 Ko=C

17Elipsoida bezwładności
Elipsoidę będącym miejscem geometrycznym końców odcinków odwrotnie proporcjonalnych do ramion bezwładności ciała względem prostych przechodzących przez dany punkt O nazywamy elipsoidą
bezwładności ciała dla punktu O

20Red ukł sił do wypadkowej
W przypadku gdy suma geometryczna układu sił P1,P2,..,Pn działających w jednej płaszczy-żnie na ciało sztywne różna jest od zera układ zastąpić możemy jedną siłą wypadkową równą wektorowi głównemu
R. Jeżeli suma geometryczna jest równa zeru to układ sił może (ale nie musi) redukować się do pary której wektor jest prostopadły do płaszczyzny działania sił.
Równanie linii działania wypadkowej wyznacza się z warunku że moment wypadkowej względem początku układu równa się momentowi głównemu Mo równemu sumie momentów danych sił względem
początku układu współrzędnych rw # W = Mo

10Prę i przys pkt we wsp bieg
Położenie punktu M we współrzędnych biegunowych określa-my za pomocą promienia wodzącego r i kąta jaki tworzy on ze stałym kierunkiem.
Prędkość punktu M jest pochodną względem czasu promienia- wektora r v=dr/dt=
Przyspieszenie p jest pochodną względem czasu prędkości v

24Aksoidy bryły w r. pł. rys
Chwilowym środkom obrotów płaszczyzny ruchomej odpowiadają osie obrotów chwilowych brył które są prostopadłe w punktach krzywej- centroidy ruchomej do ruchomej płaszczyzny . Osie te tworzą w
układzie ruchomym powierzchnię walcową- aksoidę ruchomą.
Proste prostopadłe w punktach krzywej-centroidy stałej do płaszczyzny stałej utworzą w przestrzeni nieruchomej powierzchnię walcową- aksoidę stałą.
W każdej chwili jedna z tworzących aksoidy ruchomej układu sztywnego poruszającego się ruchem płaskim pokrywa się z odpowiednia tworząca aksoidy stałej. Tworząca ta jest w tej chwili osią obrotu
chwilowego układu. W r. płaskim układu sztywnego aks. ruchoma toczy się bez poślizgu po aks. stałej.

38Aksjomaty mech klasycznej
1Jeżeli na ciało nie działa żadna siła to ten punkt porusza się ruchem jednostajnym prostoliniowym (może być bezruch).
2Przyspieszenie punktu materialnego jest wprost proporcjonalne do siły działającej na punkt. Współczynnikiem proporcjonalności jest masa p=F/m
3Dwa punkty materialne oddziaływają na siebie siłami które są równe co do wartości, przeciwnie skierowane i leża na linii łączącej te punkty.
Przestrzeń jest jednorodna gdy odcinek umieszczony w każdym miejscu tej przestrzeni ma tą samą długość.
Przestrzeń jest izotropowa gdy właściwości przestrzeni nie zależą od kierunku.
Przestrzeń jest anizotropowa gdy właściwości zmieniają się w zależności od kierunku (ruch w jedną stronę jest trudniejszy niż w drugą).
4Czas jest jednorodny.




27Środki geom,masy,ciężkości
Środek masy-punkt mający tę właściwość że wektor wodzący tego punktu pomnożony przez masę układu równa się sumie iloczynów wektorów wodzących wszystkich punktów układów pomnożonych przez
ich masy.
Na układ lub ciało znajdujące się w polu przyciągania Ziemi działają siły ciążenia punktów układu lub ciała. Siły te zastępu-jemy wypadkową siłą ciężkości. Przy założeniu że wymiary układu są małe w
stosunku do wymiarów Ziemi można siły ciężkości punktów układu uważać za równoległe. W takim razie możemy wyznaczyć środek równoległych sił ciężkości. Punkt ten to środek ciężkości ciała lub
układu. W punkcie tym można przyłożyć wypadkową siłę ciężkości układu. Na położenie tego punk-tu nie wpływa obrót układu lub ciała.
Gdy układ o małych rozmiarach- siły ciężkości punktów zależą tylko od ich mas a pomijalne są różnice przyspieszenia ziemski-ego wynikające z różnych odległości punktów układu od środka Ziemi.
W warunkach ziemskich występuje więc pokrywanie się położeń środka masy i środka ciężkości. Istnieje jednak zasadnicza różnica między tymi pojęciami. Pojęcie środka masy ma sens niezależnie od
działających sił oraz rozmiarów układu. Pojęcie położenia środka ciężkości przestaje być ścisłe przy dużych rozmiarach układu a w przestrzeni pozbawionej ciążenia traci sens.

32Stożek tarcia rys
Biorąc pod uwagę wszystkie możliwe położenia reakcji ciał chropowatych odpowiadające różnym kierunkom działania siły stycznej P otrzymamy jako miejsce geometryczne wektorów R stożek którego osią
jest prosta działania reakcji normalnej N a którego tworząca zawiera z osią kąt tarcia .Stożek ten to stożek tarcia. W przypadku ciał izotropowych tarcie nie zależy od kierunku działania siły T stożek ten jest
stożkiem kołowym, dla ciał anizotropowych stożek ma podstawę eliptyczną.

33Ciało kuliste
Ciało kuliste-ciało którego elipsoidą bezwładności jest kula. Wszystkie proste przechodzące przez środek masy są osiami głównymi (kula, jednorodny sześcian). Dla tego ciała wszystkie momenty
bezwładności są jednakowe.

42Kąty Eulera rys
Kąty Eulera określają położenie układu osi związanego z ciałem sztywnym względem układu x,y,z. Kątami Eulera są:
kąt obrotu właściwego -utworzony przez linię węzłów (prosta powstała z przecięcia płaszczyzny AXY z A ) A i oś
kąt precesji -utworzony przez oś X i linię węzłów A
kąt nutacji -utworzony przez osie Z i
39Prawo zmienności pędu p m
Pochodna pędu punktu materialnego równa jest sile działającej na ten punkt 1B’=F 2B=mv
Rzutując równanie 1 na osie układu współrzędnych otrzymujemy trzy równania skalarne:
Bx’=d/dt(mx’)=Fx y i z
Przyrost pędu p.m. równy jest elementarnemu impulsowi siły działającej na ten punkt dB=dI=Fdt
Pęd p.m. na który nie działają żadne siły jest stały F=0 ,B=C
Prawo pędu w postaci różniczkowej 1 może służyć do układania równań różniczkowych ruchu na równi z II prawem Newtona. W przypadku siły stałej prawo pędu pozwala na szybkie rozwiązanie pewnych
zadań dynamiki bez konieczności pełnego rozwiązywania równań ruchu. Prawo pędu jest wtedy określone równaniami wiążącymi ze sobą prędkości początkowe i końcową wartość siły oraz przedział czasu.

47Ruch post płas obrót śrub
Ruch postępowy- szczególny przypadek ruchu bryły taki, że wartości wszystkich kątów są stałe (osie zachowują swoje kierunki w czasie ruchu).Każdy odcinek łączący dwa punkty bryły zachowuje stale
położenie równoległe do pierwotnego.(tłok)
Ruch kulisty- ruch bryły przy którym jeden z punktów układu ruchomego związanego z bryłą jest nieruchomy.(koła stożk,bąk)
Ruch obrotowy- ruch przy którym dwa punkty bryły pozostają stale nieruchome. Wszystkie punkty prostej przeprowadzone przez te dwa punkty także pozo-staną nieruchome. Pozostałe punkty powinny
zostać w stałej odległości od nieruchomej prostej a więc mogą one poruszać się po okręgach których płaszczyzny są prostopadłe do danej prostej a ich środki leżą na tej prostej.
Ruch płaski-ruch w którym odległości wszystkich jego punktów od pewnej nieruchomej płaszczyzny są stałe. Wszystkie punkty ciała poruszają się w płaszczyznach równoległych do danej płaszczyzny
nieruchomej. Kąty precesji i nutacji są stałe zmieniać się może jedynie kąt
Ruch śrubowy-ruch bryły przy którym obraca się ona wokół nieruchomej prostej i jednocześnie przemieszcza postępowo wzdłuż tej prostej. Każdy punkt bryły porusza się po powierzchni walcowej której
osią jest oś obrotu. Torem punktu jest linia śrubowa.

15Zakleszczenie
Zakleszczenie jest to zjawisko utrzymania stanu równowagi przy dowolnie dużych siłach zewnętrznych.(musi być tarcie).
Musi być odpowiednia relacja pomiędzy alfa, ni, promień
Samohamowność jest to zjawisko w którym ruchome ciało po usunięciu siły powodującej ruch utrzymane jest w równowadze tylko przez siły tarcia
Pmin=0- układ samohamowny
Pmax—nieskończoność - układ zakleszczający się

8Red pł uk sił wielobok sznur
Dowolny płaski układ sił można zastąpić przez dwie siły działające wzdłuż skrajnych boków wieloboku sznurowego. Wartości tych sił są wyrażone przez dług-ości odpowiednich promieni wieloboku sił a
zwroty są takie że wektorowa suma tych sił jest równa wektorowi głównemu R. Linia działania wypadkowej W=R przechodzi przez punkt przecięcia skrajnych boków wieloboku sznurowego.
Przy redukcji płaskiego układu sił mogą występować przypadki:
1Wielobok sił nie zamyka się - układ sił redukuje się do jednej siły wypadkowej
2Wielobok sił zamyka się a wielobok sznurowy nie zamyka się- układ sił redukuje się do pary sił
3Wielobok sił i wielobok sznurowy zamykają się- układ sił znajduje się w równowadze

49Precesja regularna rys
Precesja regularna jest to szczególny przypadek ruchu kulistego ciała, w którym ciało obraca się wokół osi własnej z prędkością kątową a oś ta obraca się wokół osi stałej z z prędkością kątową .Kąt
między osiami jest stały. W ruchu tym prędkości kątowe obrotu własnego i precesji są stałe = =const, = =const a prędkość kątowa nutacji jest równa zeru więc kąt nutacji jest stały =0, = =const
Przykładem precesji regularnej jest ruch bąka symetrycznego. Bąk wiruje z prędkością wokół osi własnej która obraca się wokół stałej osi pionowej z prędkością kątową .Osie tworzą kąt . Moment sił
zewnętrznych utrzymujący ruch precesyjny jest momentem siły ciężkości bąka.

12Tarcie opasania
Tarciem opasania nazywamy siły tarcia występujące między powierzchniami cylindrycznymi i cięgnami taśmami sznurami pasami lub linami na nie nawiniętymi. Siły te w hamulcach taśmowych hamują
wzajemny poślizg koła i taśmy natomiast w przypadku kół pasowych nie dopuszczają do wzajemnego poślizgu koła i pasa

22Ruch pod działaniem siły za
F=F(t) x’’=1/mFx(t) y z}
x’=S1/mFx(t)dt+C1
x=S[S1/mFx(t)dt+C1]dt+C2
x(0)=x0, vx(0)=v0x
x=S[S1/mFx(t)dt]dt+v0xt+x0
mx’’=F(x’) mdv/dt=F(v) t=Sm/F(v)dv+C1 t=t(v) v=v(t)
dx=v(t)dt x=x(t) mdx/dtdv=F(v)dx|mvdv/F(v)=dx x=Smvdv/F(v)+C2 x=x(v)













18Moment bezwładnoś Steiner
Iloczyn masy punktu materialne-go i kwadratu odległości od danego punktu, prostej lub płaszczyzny nazywamy momentem bez-władności tego p.m. odpowiednio względem punktu, prostej lub płaszczyzny
I=mro2
xyz-nieruchomy o osiach XYZ II do poprzednich związany z ciałem i przyłożony do jego środka masy C roi wektor określający położenie dowolnego punktu ciała względem środka masy ri- względem
punktu O(xyz) ri=rc+roi Moment bezwładności ciała względem punktu O Io= Druga z całek jest =0 pierwsza =masie ciała trzecia=momentowi bezwładności ciała względem środka masy Io=Ic+mrc2
Moment bezwładności ciała względem dowolnego punktu równy jest sumie momentu względem środka masy i iloczynu masy ciała i kwadratu odległości danego punktu od środka masy

21Potencjał energ pot pola sił
Obszar przestrzeni w której na znajdujący się w nim punkt materialny działa siła nazywamy polem sił. Istnieje dla danego po-la funkcja V=V(r,t) taka że siła działająca na punkt może być określona jako
gradient tej funkcji ze znakiem ujemnym F=-gradV(r,t) Funkcję V nazywamy potencjałem a pole sił polem potencjalnym. Jeżeli potencjał zależy od czasu to pole jest niestacjonarne jeśli zaś od czasu nie zależy
polem stacjonarnym. Potencjał jest nazywany w tym przypadku także energią potencjalną a pole jest polem zachowawczym V=Ep=V(r)

16Prawo zmien ene w po poten
Praca sił pola przy przemieszczaniu punktu z jednego położenia w drugie równa jest różnicy potencjałów w punkcie początkowym i końcowym i nie zależy od toru po którym przemieszcza się punkt
przyłożenia siły i równa jest pracy siły działającej na punkt materialny przy tym przejściu. Sumę energii kinetycznej i potencjalnej punktu materialnego nazywamy energią mechaniczną p.m. E. Energia
mechaniczna p.m. poruszającego się w polu potencjalnym ma wartość stałą.




















34Promień bezwładności ciała
Promień bezwładności ciała k względem punktu, prostej lub płaszczyzny jest to odległość punktu materialnego odpowiednio od danego punktu, prostej lub płaszczyzny. Gdyby masę całego ciała zgrupować w
jednym punkcie położonym w odległości k od danego punktu, prostej lub płaszczyzny to moment bezwładności takiego p.m. byłby taki sam jak moment bezwładności danego ciała
mk2=I k=pierw I/m k2=I/m=niSpoVro2dV/niV=I’/V
Wartość promienia bezwładności jest jednakowa zarówno dla ciała jednorodnego jak i dla figury geometrycznej określającej jej kształt.

19Moment dewiacji Steiner
Momentem dewiacji ciała względem dwóch prostopadłych płaszczyzn nazywamy granicę sumy iloczynów mas elementów ciała i odległości tych elementów od danych płaszczyzn
Ixy=S po m xydm
Układ wsp XYZ o środku w środku masy ciała. Odległości płaszczyzn xyz od XYZ są równe xc, yc, zc. Całka 2 i 3 to momenty statyczne ciała względem płaszczyzn przechodzących przez środek masy są
więc =0
Ixy=IXY+mxcyc Moment dew. względem dwóch płaszczyzn prostopadłych =jest sumie momentu dew wzgl płasz II do danych i przechodzących przez środek masy ciała oraz iloczynu masy skupionej w
środku masy ciała i odległości odpowiednich płaszczyzn.

45Int geo skład przys w r kul
Przyspieszenie można przedstawić jako sumę 3 składowych:
pA-przysp dowolnego punktu A bryły przyjętej za początek ruchomego układu odniesienia, jednakowe dla wszystkich punktów ciała
po-przysp obrotowe skierowane prostopadle do promienia ro
pd-przysp dośrodkowe gdzie d jest wektorem prostopadłym do osi obrotu przedstawiającym odległość punktu bryły od osi obrotu.
W ruchu kulistym o środku w A składowa pA=0 i pozostają tylko składowe wynikające z ruchu kulistego

2. Ruch płaski

Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie punkty ciała poruszają się w płaszczyznach równoległych do pewnej płaszczyzny, zwanej płaszczyzną ruchu płaskiego (płaszczyzna kierująca).

1- Wyznaczenie prędkości.

a) metoda chwilowego śr. obrotu

C

Ω

V

A

A

B

V

B

(dane : V

A

)

V

A

=

Ω⋅AC => Ω=V

A

/ AC

V

B

=

Ω⋅BC => V

A

=BC / AC

b) metoda superpozycji

V

A

V

A

A

B

V

B

V

BA

V

B

= V

A

+ V

BA

(V

A

– dane)

V

BA

=

Ω ⋅ AB

Prędkość dowolnego punktu B pręta AB (ciała sztywnego) poruszającego się ruchem płaskim = sumie geometrycznej prędkości unoszenia dowolnie obranego punku A tego pręta oraz prędkości względnej punktu B
względem punktu A, czyli prędkości punktu B w ruchu obrotowym pręta wokół punktu A. Prędkość kątowa tego ruchu obrotowego nie zależ przy tym od wyboru p. A.

c)z twierdzenia u rzutach na prostą sztywną (łączącą p. A i B).
V

A

α

V

B

’

V

A

’

A

β B

V

B

V

A

⋅ cosα = V

B

⋅ cosβ

V

A

’ = V

B

’

d) rzut analityczną (metodą)

dt

t

dX

V

B

B

)

(

=

+ równania więzów

(

)

2

2

)

(

dt

t

X

d

a

B

B

=

2- Wyznaczenie przyspieszenia

a) metoda superpozycji

a

BA

τ

Ω ε

a

BA

n

A

B

a

A

a

A

τ

η

η

BA

BA

A

B

a

a

a

a

r

r

r

r

+

+

=

r. post. bieguna r. obrot. wokół bieg.

t

B

n

B

B

a

a

a

r

r

r

+

=

b) metoda chwilowego środka (bieguna) przyspieszeń.

Chwilowy środek (biegun) przyspieszeń – taki punkt P , którego przyspieszenie w ruchu płaskim pręta AB (ciała
sztywnego) jest równe zeru

Ω ε a

B

A

B

α

a

A

a

PA

n

a

PA

α

a

PA

t

P

a

A

a

P

=a

A

+ a

PA

a

PA

= a

PA

n

+ a

PA

t

a

PA

n

=

ω

2

⋅ AP

a

PA

t

=

ε ⋅ AP

a

P

= 0 to a

PA

= - a

A

;

2

4

ε

ω +

= BP

a

B

kierunek określa kąt

α wyznaczony ze wzoru: tgα = ε / ω

2

c) metoda analityczna

[

] [

]

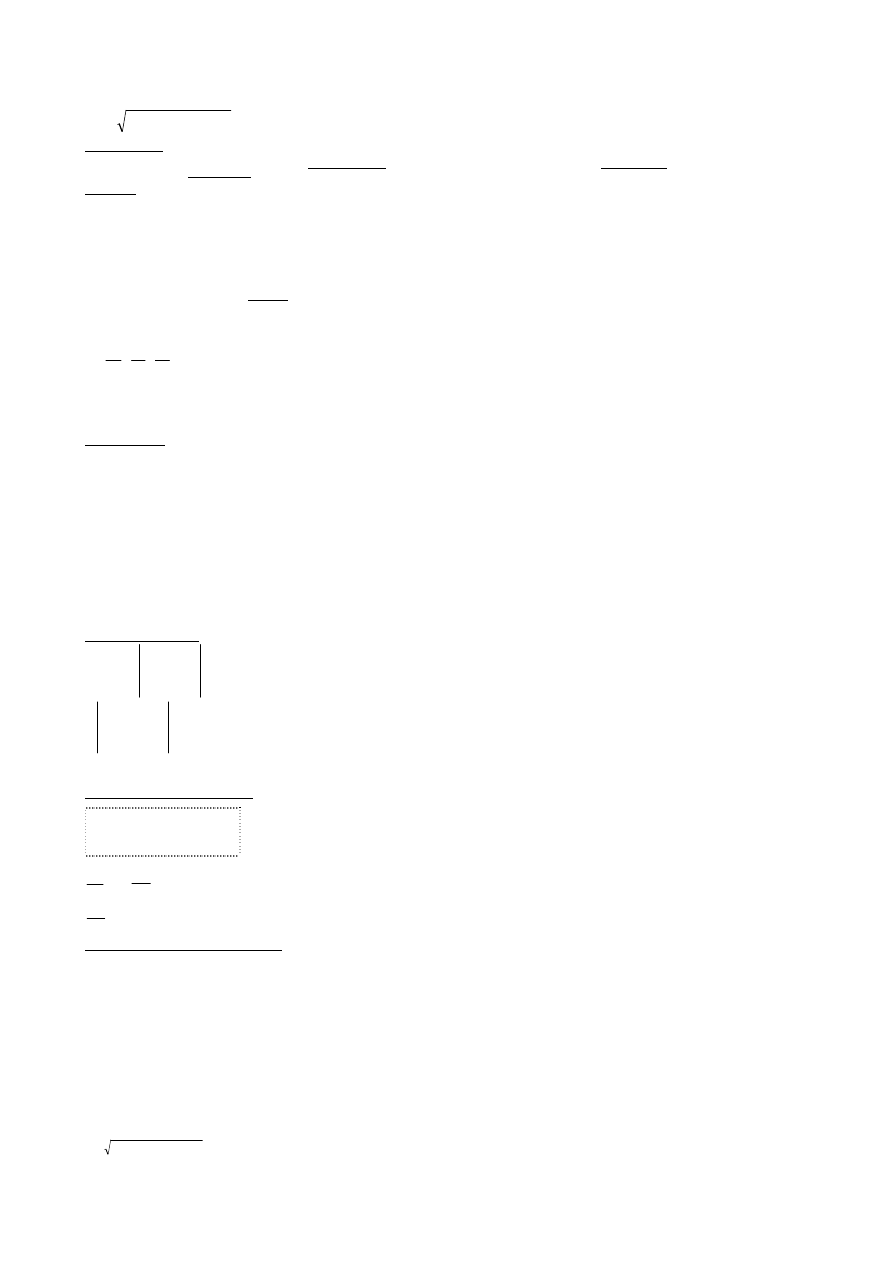
2

2

)

(

)

(

t

Y

t

X

a

B

B

B

+

=

Metoda analityczna obliczania przyspieszenia polega na zróżniczkowaniu prędkości rozpatrywanego punktu ciała sztywnego.
3. Ruch złożony punktu.

Ruch punktu M względem układu nieruchomego 0

XYZ

nazywamy ruchem bezwzględnym. Ruch punktu M względem układu ruchomego 0

xyz

nazywamy ruchem względnym. Ruch układu ruchomego 0

xyz

względem układu

nieruchomego 0

XYZ

nazywamy ruchem unoszenia.

4. Ruch kulisty.
Ruch ciała sztywnego, podczas którego jeden jego punkt pozostaje nieruchomy.
(ruch obr. wokół chwilowej osi obr. przechodzącej przez środek r. kulistego)

W celu opisu ruchu kulistego ciała szt. przyjmujemy dwa układy odniesienia o wspólnym początku, znajdującym się w środku ruchu kulistego.

x,y,z – osie układu nieruchomego

ξ,η,ζ - osie układu ruchomego (związanego na stałe z elem. poruszającym się ruchem kulistym)
0 – środek ruchu kulistego

Wsp. kątowe Eulera:

υ - kąt nutacji – zawarty między osią 0

ζ

ukł. ruchomego związanego z ciałem, a osią 0

Z

nier. ukł. wsp.

ψ- kąt precesji – określa położenie osi 0

n

zwanej linią węzłów (będącej śladem płaszczyzny 0

ξη

na nieruch. pł 0

xy

) i zawarty jest między osią 0

x

a prostą 0

n

.

ϕ - kąt obrotu własnego – tworzy go oś 0

ξ

z linią węzłów 0

n

.

Ciało sztywne w ruchu kulistym ma trzy stopnie swobody.

∆θ = ∆ψ + ∆ϕ + ∆υ | : ∆t

dt

d

dt

d

dt

d

ϑ

ϕ

ψ

ω

r

r

r

r

+

+

=

3

2

1

ω

ω

ω

ω

r

r

r

r

+

+

=

(

ω - chw. pr. kątowa wokół chw. osi obr. - znajduje się na chw. osi obrotu)

1 – pr. kątowa precesji – (w) skierowany wzdłuż osi 0

z

układu nieruchomego

2 – pr. kątowa obr. własnego – (w) skierowany wzdłuż osi 0

ζ

3- pr. kątowa nutacji – (w) skierowany wzdłuż linii węzłów 0

n

Aksoida stała i ruchoma.

Aksoida ruchoma jest to miejsce geometryczne chwilowych osi obrotu w układzie
ruchomym.

Aksoida stała jest to miejsce geometryczne chwilowych osi obrotu w układzie nieruchomym.

W nieruchomym ukł. wsp.:

ω = ω

x

+

ω

y

+

ω

z

ω

x

=

ω

2

sin

υ sinϕ + ω

3

cos

ψ

ω

y

= -

ω

2

sin

υ + ω

3

sin

ψ

ω

z

=

ω

1

+

ω

2

cos

υ

(rzutowanie na osie układu wsp.)

Prędkość liniowa w ruchu kulistym.

=

=

×

=

z

y

x

k

j

i

r

v

z

y

x

ω

ω

ω

ω

1

1

1

r

r

r

r

r

r

ζ

η

ξ

ω

ω

ω

ζ

η

ξ

2

2

2

k

j

i

r

r

r

=

wartość: v =

ω r sin α = ω h

Przyspieszenie kątowe ciała szt. w ruchu kulistym.

(

)

3

1

2

3

1

3

3

2

2

1

1

ω

ω

ω

ω

ω

ω

ω

ω

ε

r

r

r

r

r

r

&

r

&

r

&

r

×

+

×

+

+

+

+

+

=

k

k

k

0

1

=

dt

k

d

v

;

(

)

2

3

1

2

k

dt

k

d

r

r

r

v

×

+

=

ω

ω

;

3

1

3

k

dt

k

d

r

v

×

=

ω

Przyspieszenie dowolnego p. M ciała szt. w ruchu kulistym.

v

r

a

r

r

r

r

r

×

+

×

=

ω

ε

a

1

a

2

a = a

1

+ a

2

a

1

=

ε × r (przysp. obrotowe)

a

2

=

ω × v (przysp. doosiowe)

Precesja regularna

Szczególny przypadek ruchu kulistego ciała sztywnego, w którym kąt nutacji jest stały, a prędkości kątowe precesji i obrotu własnego mają stałe wartości:

υ = const ; ω

1

= const ;

ω

2

= cons

Prędkość kątowa nutacji:

ω

3

= d

υ / dt = 0

zatem chwilowa prędkość kątowa ciała

ω jest równa sumie geometr. pr. kątowej precesji i prędkości kątowej obrotu własnego:

ω = ω

1

+

ω

2

to:

ϑ

ω

ω

ω

ω

ω

cos

2

2

1

2

2

2

1

+

+

=

Przyspieszenie kątowe precesyjne:

ω

ω

ε

r

r

r

×

=

1

to (z pow.)

(

)

2

1

2

1

1

ω

ω

ω

ω

ω

ε

r

r

r

r

r

r

×

=

+

×

=

gdyż

0

1

1

=

×

ω

ω

r

r

Wektor przysp. kątowego o przyjętym początku w środku ruchu kulistego 0 jest prostopadły do wektorów

ω

1

i

ω

2

, a więc jest skierowany wzdłuż linii węzłów 0

n

.

Przyspieszenie liniowe (W):
a = a

1

+ a

2

a

1

=

ε × r = (ω

1

× ω

2

)

× r (przysp. preces.)

a

2

=

ω × v = (ω

1

+

ω

2

)

× v

5. Przyspieszenie Coriolisa

ω

ω

v

a

C

r

r

r

×

= 2

gdzie

ω jest wektorem prędkości kątowej obrotowego (np. ruchu kuli ziemskiej).

Otrzymujemy z obrotu wektora V

w

o 90

0

w kierunku prędkości obrotowej

ω.

MECHANIKA Ogólna

I – Statyka

1. Zbieżny układ sił – układ sił, których linie działania przecinają się w jednym punkcie; może być płaski lub przestrzenny.

Jeżeli na ciało sztywne działa zbieżny płaski/przestrzenny układ sił (wektory) P

1

,P

2

...P

n

– linie działania przecinają się w punkcie 0, to wypadkowa (wP) działania sił jest równa ich sumie geometr. i jej linia działania przechodzi przez punkt 0.

Wypadkowa sił zbieżnych:
(płaszczyzna)

∑

∑

=

=

=

=

=

n

i

i

n

i

x

x

Pi

Pi

P

1

1

0

cos

α

∑

∑

=

=

=

=

=

n

i

i

n

i

y

y

Pi

Pi

P

1

1

0

cos

β

(+ przestrzeń)

∑

∑

=

=

=

=

=

n

i

i

n

i

z

z

Pi

Pi

P

1

1

0

cos

γ

2. Twierdzenie o trzech siłach – Trzy nierównoległe siły na płaszczyźnie są w równowadze statycznej, tylko wtedy, gdy linie działania tych sił przecinają się w jednym punkcie, a wektory tych sił tworzą trójkąt zamknięty.

Siły zbieżne leżące w jednej płaszczyźnie są w równowadze, jeżeli sumy tych sił na dwie równoległe osie układu współrzędnych będą równe zeru.
Równania równowagi s.z. (płascz.):

0

1

=

∑

=

n

i

x

Pi

0

1

=

∑

=

n

i

y

Pi

kratownica – układ prętów połączonych przegubami
rama – układ prętów połączonych na stałe

3. Dowolny układ sił

Momentem siły (w)P względem punktu 0 nazywamy odłożony z punktu 0 wektor (w)M

0

, równy iloczynowi wektorowemu promienia wektora (w)r i wektora siły (w)P .

P

r

M

r

r

r

×

=

0

z

k

y

j

x

i

r

r

r

r

r

+

+

=

Pz

k

Py

j

Px

i

P

r

r

r

r

+

+

=

Mz

k

My

j

Mx

i

M

r

r

r

r

+

+

=

0

- wektor M

0

jest prostopadły do płaszczyzny określonej wektorami r i P o zwrocie określonym regułą śruby prawoskrętnej,

- indeks wskazuje punkt (oś) względem którego moment jest obliczany

)

,

sin(

0

P

r

P

r

M

r

r

r

⋅

⋅

=

Moment siły względem osi jest rzutem na tę oś momentu siły względem dowolnego punktu na tej osi i pochodzi tylko od składowej tej siły leżącej na płaszczyźnie prostopadłej do osi.
Wartość (moduł) momentu siły (w)P względem osi l równa się iloczynowi modułu tej siły (w)P i jej odległości h od osi l , pomnożonemu przez sinus kąta zawartego między siłą (w)P a prostą l.
Moment siły względem osi jest równy zeru, gdy: - wartość siły = 0, - linia działania siły przecina się z osią, - siła jest równoległa do osi.

4. MOMENT PARY SIŁ
para sił – układ dwóch sił o równych wartościach, lecz różnych zwrotach.

M
P


P

h

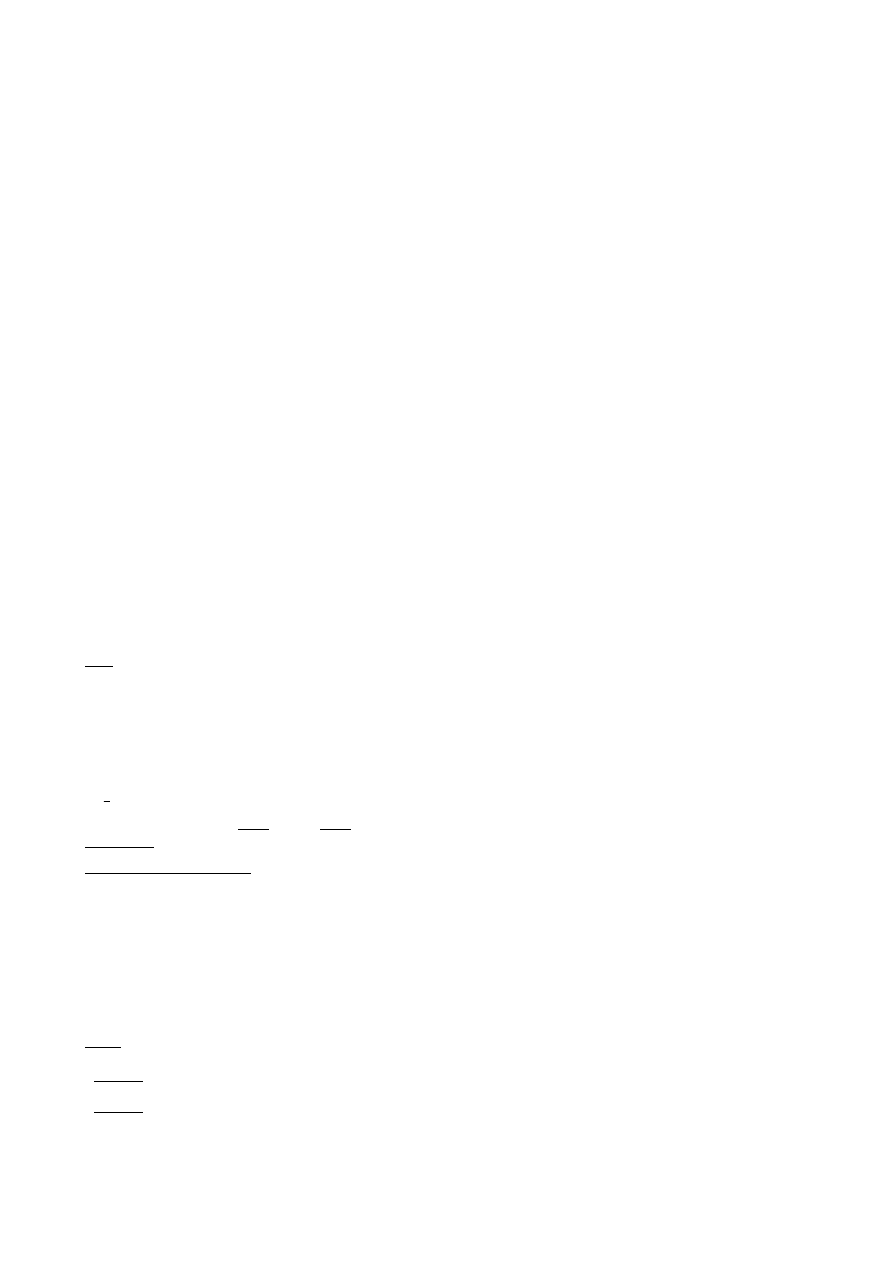
– nie zależy od położenia wektora swobodnego w przestrzeni;

„Równoległe przesunięcie sił”

Wypadkowa dwóch sił równoległych zgodnie skierowanych działa równolegle do tych sił i ma zwrot zgodny ze zwrotami tych sił. Jej wartość jest równa sumie wartości tych sił, a jej linia działania dzieli wewnętrzne odległości
między liniami działania sił w stosunku odwrotnie proporcjonalnym do wartości tych sił.

Twierdzenia o parach sił:

1- Dwie pary sił o tej samej płaszczyźnie działania są sobie statycznie równoważne, gdy
mają równe momenty;

2- Zachowując niezmieniony moment, parę sił można przenieść do dowolnej płaszczyzny
równoległej do jej płaszczyzny działania;

3- Dwie pary sił działające w jednej płaszczyźnie można zastąpić przez jedną parę sił
działającą w tej płaszczyźnie o momencie równym sumie momentów dwóch danych par

4- Dwie pary sił działające w przecinających się płaszczyznach są równoważne jednej parze
sił o momencie równym wektorowej sumie momentów tych par.

Redukcja przestrzennego układu sił

Układ przestrzenny redukuje się do:
- skrętnika
- dwóch sił skośnych
- pary sił

Skrętnik – układ złożony z wektora głównego (w)R i składowej momentu głównego (w)M

0

’ , leżącej na linii działania wektora (w)R.

R

r

M

r

r

r

×

=

''

0

∑

=

=

+

+

+

=

n

i

i

n

P

P

P

P

R

1

2

1

...

r

r

r

r

r

ϕ

cos

0

0

M

R

R

M

r

r

=

Przestrzenny układ sił daje się sprowadzić do dwóch sił wichrowatych (skośnych), z których jedna przechodzi przez środek redukcji 0.

Redukcja do pary sił – gdy wektor główny R=0, moment główny M

0

≠0 – układ redukuje się do pary sił których moment jest równy momentowi głównemu układu (M

0

). Moment gł. w rozpatrywanym przypadku nie zależy od

wyboru punktu 0, gdyż suma geometryczna momentów sił tworzących parę sił jest stała dla wszystkich punktów przestrzeni i równa momentowi pary.

Równowaga dowolnego przestrzennego układu sił
1- Przestrzenny układ n sił jest w równowadze, jeżeli jego suma geometryczna R jest równa zeru oraz moment główny M

0

układu względem dowolnego punktu 0 jest równy zeru.

2- Dowolny przestrzenny układ sił P

i

jest w równowadze, jeżeli suma rzutów wszystkich sił na trzy osie układu równa jest zeru i suma momentów wszystkich sił względem trzech osi układu jest równa zeru.

∑

=

=

n

i

ix

P

1

0

∑

=

=

n

i

iy

P

1

0

∑

=

=

n

i

iz

M

1

0

(dla ukł. płaskiego)

∑

=

=

n

i

iz

P

1

0

∑

=

=

n

i

ix

M

1

0

∑

=

=

n

i

iy

M

1

0

(+ dla ukł. przestrzennego)

5. TARCIE
Zjawisko powstawania sił stycznych do powierzchni styku dwóch ciał. Siły te nazywamy siłami tarcia. Można je zdefiniować jako siły oporu, zapobiegające ruchowi, który by powstał, gdyby tarcia nie było.
Przyczyną powstawania sił tarcia jest chropowatość powierzchni.

a- tarcie ślizgowe

N

T

R

r

v

r

+

=

T=

µN (µ - wsp. tarcia)

b- tarcie toczenia

)

(

)

(

t

t

T

N

R

Q

P

W

r

r

r

r

r

+

=

=

+

=

(przyp. Granica ruchu krążka)
f(mm) – ramię tarcia tocznego
Aby nastąpiło toczenie walca, wartość siły tarcia tocznego (w)T musi być mniejsza od wartości siły tarcia ślizgowego

µ(w)N rozwiniętego, co wyraża się nierównością (f/r)<µ T=f/r G < µN = µG

Stąd f/r <

µ

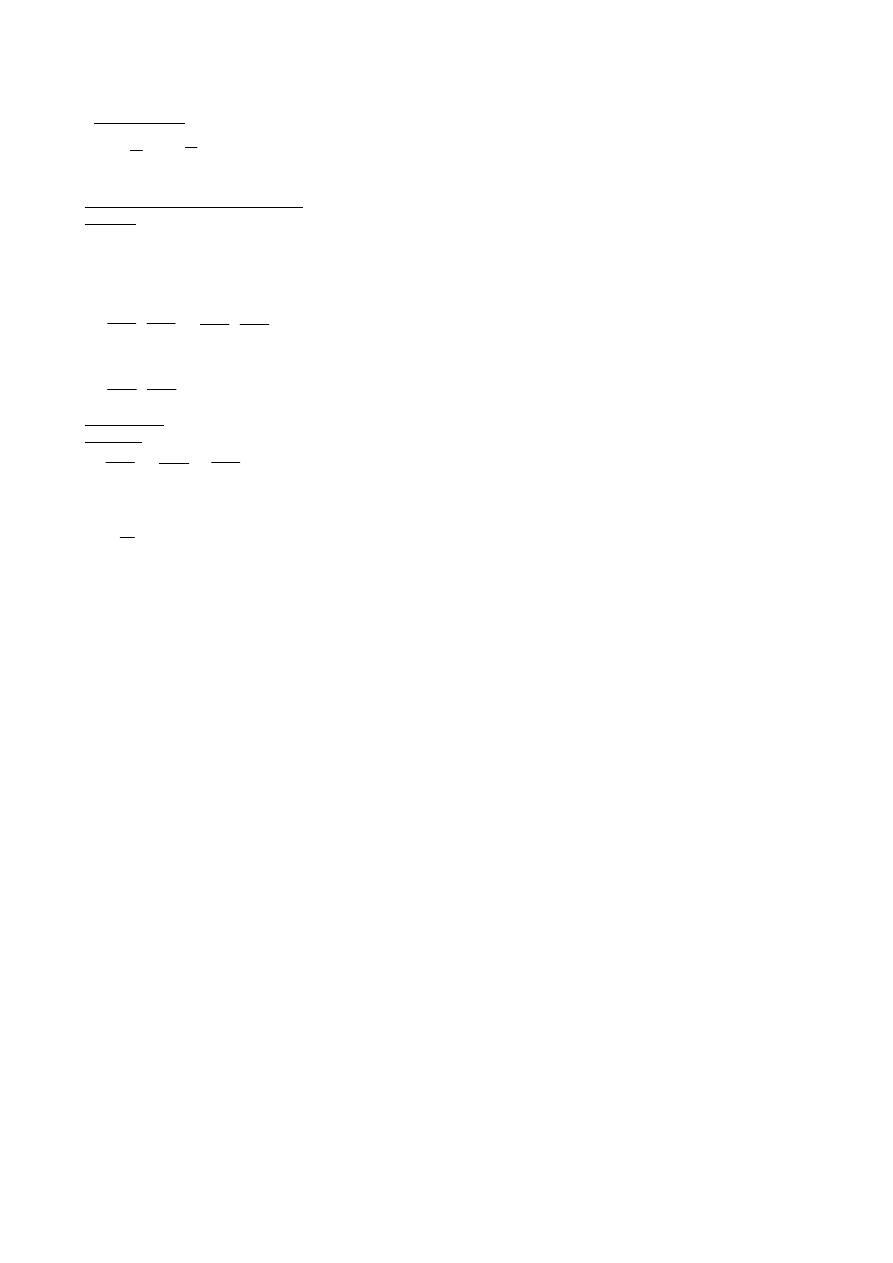
c- tarcie cięgna o stały krążek
Siły tarcia występujące między powierzchniami cylindrycznymi i cięgnami, taśmami lub linami na nie nawiniętymi.

∫

∫

=

2

1

0

S

S

S

dS

d

α

ϕ

µ

=>

α

µ

=

1

2

ln

S

S

stąd:

α

µ

e

S

S

1

2

=

µ α > 0 to S

2

>S

1

6. ŚRODEK SIŁ RÓWNOLEGŁYCH (śr. masy – śr. sił ciężkości).

Tw. Varignona.
Moment siły wypadkowej W względem dowolnego punktu równa się sumie momentów układu sił względem tego samego punktu.

W = R =

Σ P

i

r

i

= i x

i

= j y

i

(

)

∑

=

×

=

×

=

n

i

C

i

i

W

r

P

r

M

1

0

r

r

r

r

r

gdzie wektor r

C

= x

C

i + y

C

j określa linię działania wypadkowej.

Stąd:

∑

∑

∑

=

=

=

=

=

n

i

i

n

i

i

i

n

i

i

i

C

P

x

P

W

x

P

x

1

1

1

∑

∑

∑

=

=

=

=

=

n

i

i

n

i

i

i

n

i

i

i

C

P

y

P

W

y

P

y

1

1

1

obracając o ten sam (dowolny) kąt:

∑

∑

∑

=

=

=

=

=

n

i

i

n

i

i

i

n

i

i

i

C

P

z

P

W

z

P

z

1

1

1

Środek sił równoległych jest to punkt C mający tę własność, że przechodzi przez niego wypadkowa układu sił równoległych niezależnie od kierunku tych sił (przy niezmienionych punktach przyłożenia i wartościach sił).

Środek ciężkości.

∫

∫

=

V

V

C

dV

xdV

x

γ

γ

∫

∫

=

V

V

C

dV

ydV

y

γ

γ

∫

∫

=

V

V

C

dV

zdV

z

γ

γ

gdzie


jest całkowitym ciężarem ciała, natomiast

γ oznacza ciężar właściwy w danym punkcie:

V

G

V

∆

∆

=

→

∆

0

lim

γ

.

∫

=

V

dV

G

γ

II – Kinematyka

1. Kinematyka punktu.

a) ruch punktu opisany promieniem - wektorem

W przypadku ruchu p. M promień r zmienia z upływem czasu swą wartość i swój kierunek -jest opisany funkcją wektorową czasu:
(W.) r = r (t) V = dr / dt
r

x

= x (t) r

y

= y (t) r

z

= z (t)

b) ruch opisany za pomocą wsp. prostokątnych









wsp. x,y,z są funkcjami czasu:
x = f(t) ; y = f(t) ; z = f(t)
- równania skończone ruchu punktu (parametr – czas t)
Poprzez wyrugowanie z tych równań parametru t , otrzymujemy równania opisujące tor punktu (trajektorię) i krzywą, po której M się porusza powstałą z przecięcia dwóch powierzchni:
F

1

(x, y, z) = 0 ; F

2

(x, y, z) = 0

c) ruch opisany za pomocą wsp. naturalnych










Współrzędna s – mierzona wzdłuż toru s=~M

0

M

Prędkość: V = ds / dt przyspieszenie:

τ

η

τ

η

a

a

a

r

r

r

+

=

a = dV / dt ; a

n

= V

2

/

ς ; k = 1/ς krzywizna

2

2

τ

η

a

a

a

−

=

gdzie

2

2

2

z

y

x

a

a

a

a

+

+

=

a=a

n

+a

τ

ruch krzywoliniowy punktu










krzywizna toru

dS

d

S

k

S

ϕ

ϕ

ρ

=

∆

∆

=

=

→

∆

0

lim

1

promień krzywizny

ϕ

ρ

d

dS

=

prędkość

v

V

dt

dS

dt

V

V

t

0

0

lim

τ

r

r

r

r

=

=

∆

=

→

∆

przyspieszenie

η

ϕ

τ

r

r

dt

ds

ds

d

V

dt

dV

a

⋅

+

⋅

=

0

η

τ

a

a

a

r

r

r

+

=

(przysp. w ruchu krzywol.)

η

ρ

τ

r

r

2

0

V

dt

dV

a

+

⋅

=

(dla ruchu po okręgu:
prędkość kątowa:









=

=

s

dt

d

1

ϕ

ϕ

ω

&

r

r

r

przyspieszenie kątowe:









=

=

2

2

2

1

s

dt

d

dt

d

ω

ϕ

ε

r

r

prędkość liniowa: V =

ω r sinα = ω r

K

)

d) ruch opisany współrzędnymi krzywoliniowymi
- współrzędne biegunowe

)

(

1

t

f

r

=

;

r

V

r

r

=

;

2

ϕ

&

&

&

r

r

a

r

−

=

)

(

2

t

f

=

ϕ

;

ϕ

ϕ

&

r

V

=

;

ϕ

ϕ

ϕ

&

&

&

&

r

r

a

+

= 2

2

2

ϕ

V

V

V

r

+

=

;

2

2

ϕ

a

a

a

r

+

=

- wsp. cylindryczne

)

(

1

t

f

r

=

;

r

V

r

&

=

;

)

(

2

t

f

=

ϕ

;

ϕ

ϕ

&

r

V

=

;

2

2

2

z

r

V

V

V

V

+

+

=

ϕ

)

(

3

t

f

z

=

;

z

V

z

&

=

;;;

2

ϕ&

&

&

r

r

a

r

−

=

;

2

2

2

z

r

a

a

a

a

+

+

=

ϕ

ϕ

ϕ

ϕ

&

&

&

r

r

a

−

= 2

;

- wsp. sferyczne

)

(

1

t

f

r

=

;

prędk.:

2

2

2

ϑ

ϕ

V

V

V

V

r

+

+

=

)

(

2

t

f

=

ϕ

; przysp.:

2

2

2

ϑ

ϕ

a

a

a

a

r

+

+

=

)

(

3

t

f

=

ϑ

;

Semestr I

Ruch mechaniczny obiektu materialnego – zmiana położenia punktu materialnego względem innych obiektów materialnych zachodzącą w czasie. Czas uważa się za niezależny od przestrzeni, materii,
obserwatora i za płynący jednakowo we wszystkich układach.
Punkt materialny – twór fizyczny o nieskończenie małych wymiarach obdarzony masą.
Układ materialny – zbiór punktów materialnych wzajemnie na siebie oddziaływujących.
Ciało sztywne – ciągły zbiór punktów materialnych, których odległości są stałe.
Siła – miara wzajemnego oddziaływania ciał na siebie.
Równowaga statyczna – zachodzi gdy punkt materialny pod działaniem układu sił pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Statyka – zajmuje się warunkami równowago ciał.
Kinematyka – zajmuje się opisem matematycznym ruchu ciał bez rozpatrywania przyczyn.
Dynamika – bada przyczyny ruchu obiektów, oraz związki między ich ruchem i wzajemnym oddziaływaniem.
Wektor – skierowany odcinek linii prostej, którego początkowy punkt umieszczony jest w początku układu współrzędnych, zaś końcowy opisany współrzędnymi (a

X

a

Y

a

Z

) rys.1

Iloczyn skalarny dwóch wektorów: jest to skalar powstały przez pomnożenie przez siebie długości obu wektorów oraz cosinusa kąta zawartego między nimi a8

888b5ab cos

α

(iloczyn ten jest przemienny) rys. 2

Iloczyn wektorowy dwóch wektorów : a×

×××b5 ab sin

α

Iloczynem tym jest trzeci wektor prostopadły do płaszczyzny utworzonej przez wektory a i b. Wartość wektora c jest równa polu powierzchni

równoległoboku zbudowanego na wektorach a i b. Do iloczynu wektorowego nie stosuje się prawa przemienności można natomiast stosować prawo rozdzielności rys. 3
Aksjomaty czyli podstawowe prawa fizykalne.
1) Ruch swobodnego ciała sztywnego nie ulegnie zmianie pod działaniem dwóch sił, gdy siły te mają jednakowe wartości (moduły) jeden kierunek działania i przeciwne zwroty czyli stanowią zerowy układ sił

rys 4.

2) Ruch ciała sztywnego nie ulegnie zmianie jeśli do działającego układu sił dodamy lub odejmiemy układ sił równoważny zero. Działanie sił na ciało sztywne nie zmieni się jeżeli punkt A zaczepienia siły F

zostanie przeniesiony od innego punktu B leżącego na linii działania tej siły rys. 5

3) Reguła równoległoboku. Wypadkowa dwóch sił działających w jednym punkcie ciała sztywnego przyłożona jest w tym punkcie i jest siłą o module równym przekątnej równoległoboku opisanego tymi siłami

leży na tej przekątnej i ma zwrot od punktu A do B rys. 6

4) Akcja i reakcja. Siły którymi działają na siebie dwa ciała mają jednakowe wartości są skierowane wzdłuż jednej prostej lecz ich zwroty są przeciwne rys. 7
5) Zasada zesztywnienia. Jeżeli ciało odkształcalne znajdzie się w równowadze pod działaniem pewnego układu sił to również ciało absolutnie sztywne pozostanie w równowadze pod działaniem tego samego

układu sił. Warunki równowagi będące koniecznymi i wystarczającymi dla ciała sztywnego nie muszą być takie same dla ciała odkształcalnego.

6) Zasada oswobodzenia od więzów. Każde ciało nieswobodne można rozpatrywać jako swobodne jeżeli myślowo uwolnimy je od więzów zastępując działanie więzów siłami więzów tzn. reakcjami więzów.
Moment siły względem punktu – Momentem wektora siły względem punktu O nazywamy wektor M umiejscowiony w punkcie O prostopadły do płaszczyzny

∏ utworzonej przez siłę F i punkt O, którego

wartość (moduł) równy jest iloczynowi wartości siły i promienia r razy sin kąta zawartego między wektorami r i F rys. 8
(pod rysunkiem: M = r3F, ?M?5r.F.sin (r,F), h = r.sin (r,F),⇒M = h.

...F

Para sił – nazywamy układ dwóch wektorów sił o równych modułach leżących na dwóch prostych równoległych mających przeciwne zwroty. Płaszczyzna pary sił to płaszczyzna na której leżą oba wektory,
ramie pary sił to odległość pomiędzy liniami ich działania, suma pary sił jest równa zero. Wielkością charakteryzującą parę sił jest jej moment, który nie zależy od punktu względem którego go liczymy jest więc
wektorem swobodnym rys. 9
Środkowy układ sił płaskich - taki układ sił w którym wektory i kierunki sił przecinają się w pewnym punkcie.
Płaski układ sił – taki układ, którego kierunki i wektory leżą w jednej płaszczyźnie. (pod rysunkiem F

2

1 F

1

= W

1,

F

3

1 W

1

= W

2,

F

4

1 W

2

= W

1

) rys. 10.

Warunki równowagi środkowego układu sił – ciało sztywne znajdujące się pod działaniem środkowego układu sił jest w równowadze gdy siły te tworzą wielobok zamknięty a ich wypadkowa jest równa zero
rys. 11
Tw. o trzech siłach – aby swobodne ciało sztywne znajdowało się w równowadze pod działaniem trzech sił nierównoległych leżących w jednej płaszczyźnie to linie ich działania muszą przeciąć się w jednym
punkcie a wypadkowa musi być równa zero.
Tarcie - wywołane jest nierównościami powierzchni stykających się ciał które stawiają opór przeciwko zamierzonemu lub istniejącemu ruchowi. W miarę zwiększania gładkości stykających się powierzchni
opór maleje lecz dochodzi do zmniejszenia się pustych obszarów oddzielających powierzchnie co owocuje wzrostem sił przyciągania międzycząsteczkowego. Rozróżniamy trzy rodzaje tarcia ślizgowego: suche,
półsuche, płynne.
Prawo Culomba – stosowane jest zarówno gdy stykające się powierzchnie ślizgają się po sobie oraz gdy siły tarcia uniemożliwiają poślizg. Prawo to odnosi się do suchych wygładzonych powierzchni bez
widocznych chropowatości. Siła tarcia ślizgowego leży w płaszczyźnie stycznej trących się ciał i jest skierowana przeciwnie do kierunku możliwego przesuwu. Wartość siły tarcia zależy od sił czynnych i jest
zawarta między 0 a swą maksymalną wartością, którą osiąga w chwili utraty równowagi 0

[T[Tmax. Maksymalna siła tarcia ślizgowego nie zależy od pola powierzchni styku trących się siał i jest proporcjonalna

do reakcji normalnej. T =

µN. Współczynnik tarcia ślizgowego µ zależy od charakteru chropowatości, właściwości materiałów trących i warunków otoczenia.

Tarcie płynne – równe jest iloczynowi współczynnika lepkości, pola stykających się powierzchni, prędkości względnej do grubości warstwy smaru. Tp =

ν.A.(V/h)

Moment siły względem prostej – momentem siły F względem prostej l nazywamy rzut wektora Mo na prostą l, gdy punkt O znajduje się na prostej l.

Mo = r E sinω = hF rys. 12 .Rzut na prostą l momentu

siły względem dowolnego punktu O tej prostej jest stały i nie zależy od położenia punktu O na prostej l . Wartość bezwzględna momentu siły względem prostej równa jest iloczynowi modułu siły F i odległości h
od prostej pomnożonej sin

ω kąta zawartego między kierunkami wektora siły F a kierunkiem prostej l. M

L

= F

.h.sinω. Wartość rzutu siły na płaszczyznę ∏ równa jest: F’ = F.sinω. Wnioski: moment siły F

względem prostej l jest równy zero jeżeli: 1) siła ma wartość zero 2) kierunek wektora siły F przecina prostą l wówczas ramie (h) jest zero 3) gdy siła F jest równoległa do prostej l
Redukcja dowolnego przestrzennego układu sił – Dwa układy sił nazywamy równoważnymi jeśli mają równe sumy (wypadkowe) i równe momenty względem dowolnego punktu. Dowolny przestrzenny układ
sił da się sprowadzić do jednego wektora i pary sił rys. 13. Każdy przestrzenny układ sił działający na ciało sztywne jest równoważny układowi składającemu się z dwóch sił, z których jedna zaczepiona jest w
dowolnie obranym punkcie.
Warunki równowagi przestrzennego układu sił:
1) Gdy kierunki sił przecinają się wówczas taki układ zwany jest przestrzennym zbieżnym i sprowadza się do wypadkowej S warunek równowagi S równe zero.
2) Gdy układ sił znajdujący się w równowadze sprowadza się do wypadkowej siły S i pary sił wystarcza aby i wypadkowa była zero i moment pary był też równy zero.{S

X

50, S

Y

50, S

Z

50, M

X

50, M

Y

50, M

Z

50,

Momentem statycznym układu punktów materialnych względem danego punktu O nazywamy sumę iloczynów elementarnych mas punktów i ich wektorów promieni rys.14. S5

555Σ r

i

∆m

i

( i = 1,2 ... n) Można

znaleźć taki punkt C którego wektor promień r

C

pomnożony przez masę skupioną w tym punkcie da wartość momentu statycznego S. S5m.

...r

C

....c

(Pod rysunkiem S

XX

5Σr

X

....∆m

i

, S

YY

5Σr

Y

....∆m

i

, S

ZZ

5Σr

Z

....∆m

i

, S5

555 S

XX

i + S

YY

j1 S

ZZ

k

)

Więzy – są to ograniczenia ruchu ciała nakładane przez inne ciała; siły oddziaływania więzów na podlegające im ciała nazywamy siłami reakcji więzów lub reakcjami więzów. Każde ciało
nieswobodne można rozpatrywać jako swobodne jeżeli myślowo uwolnimy je od więzów zastępując ich działanie reakcjami więzów. Rodzaje więzów:

- Przegub walcowy – w tym przypadku ciało osadzone jest na walcowym sworzniu przechodzącym przez otwór wykonany w tym ciele; reakcja sworznia na ciało ma kierunek normalny do powierzchni

styku. Linia jej działania przechodzi przez oś sworznia.

- Podpora przesuwna – ciało połączone jest z podporą za pomocą przegubu walcowego; ponadto cała podpora umieszczona jest na rolkach umożliwiających przesuw w kierunku równoległym do

płaszczyzny po której toczą się rolki.

- Przegub kulisty – ma zakończenia wykonane w kształcie kuli osadzonej na kulistym łożysku. Po zaniedbaniu sił tarcia przyjmujemy że reakcja w przegubie przechodzi przez środek kuli.

Liczba stopni swobody – liczba więzów jaką należy wprowadzić aby unieruchomić dany punkt materialny, układ punktów materialnych lub bryłę sztywną. Punkt materialny ma w przestrzeni 3
stopnie swobody, układ punktów materialnych ma 3n stopni swobody (n – liczba punktów), bryła sztywna ma 6 stopni swobody.

Semestr II

Różniczkowanie i całkowanie wektorów.
Jeżeli każdej wartości zmiennego skalara t odpowiada określony wektor a to wektor ten jest funkcja zmiennej niezależnej t.

a

a

dt

d

t

&r

r

=

)

(

)

(

. Jeżeli t jest czasem to stosujemy oznaczenie

a

dt

a

t

t

a

t

t

a

t

a

t

&

r

r

r

=

∆

=

∆

−

∆

+

=

∆

∆

→

∆

)

(

)

(

lim

lim

0

Newtona:

2

2

2

z

y

x

a

a

a

a

&

&

&

&

r

+

+

=

,

dt

dax

a

x

=

&

dt

day

y

a

=

&

dt

daz

z

a

=

&

.

Zasady różniczkowania wektorów względem skalarnego argumentu t: 1) pochodna wektora stałego jest równa 0; 2) pochodna wersora:

1

=

e

:

2

sin

2

ϕ

∆

=

∆

e

e

,

=

∆

=

→

e

e

d

d

lim

0

ϕ

2

sin

2

lim

0

ϕ

ϕ

∆

→

∆

e

ϕ

d

=

,

ϕ

&

&

=

e

,

dt

de

dt

d

=

ϕ

,

n

e

ϕ&

&

=

,

n

dt

d

dt

e

d

ϕ

=

;

3) pochodna sumy geometrycznej wektorów jest sumą geometryczną ich pochodnych

=

+

=

+

=

+

b

a

b

a

b

a

dt

d

&

&

r

r

o

)

(

)

(

dt

b

d

dt

a

d

+

; 4) Pochodna wektora, który jest funkcją t poprzez inną funkcję S(t) wyrażamy następująco:

dt

ds

ds

a

d

dt

a

d

⋅

=

; 5) pochodna wektora promienia:

=

⋅

+

⋅

=

⋅

=

=

e

r

e

dt

r

d

e

r

dt

d

dt

r

d

r

&

&r

)

(

n

r

e

r

n

r

e

dt

dr

ϕ

ϕ

+

=

+

&

&

&

do rysunku:

e

r

t

r

r

=

=

)

(

,

1

=

= n

e&

; 6) Pochodna iloczynu skalara f(t) i wektora

)

(t

a

:

dt

a

d

f

a

dt

df

t

a

t

f

dt

d

t

t

t

t

)

(

)

(

)

(

)

(

)]

(

)

(

[

⋅

+

⋅

=

⋅

)

(

)

(

)

(

)

(

t

a

t

f

t

a

t

f

&

&

+

=

; 7) Pochodna iloczynu skalarnego dwóch wektorów:

a

a

b

b

dt

b

d

a

b

dt

a

d

b

a

dt

d

⋅

=

⋅

=

+

=

&

&

o

2

2

)

(

a = b, pochodne tworzą przyrost pod kątem 90 stopni, cos(

a

a

&

,

)=0; 8)

Pochodna iloczyny wektorowego dwóch wektorów:

=

× )

(

b

a

dt

d

=

×

+

×

dt

b

d

a

b

dt

a

d

dt

a

d

b

dt

b

d

a

×

−

×

,

c

a

b

b

a

=

×

−

×

&

&

.

Całkowanie wektorów.
Gdy wektor a jako funkcja jednej zmiennej t jest określony składowymi a

x

, a

y

, a

z

w prostokątnym układzie współrzędnych to jego całkę można określić w granicach od t

0

do t

1

:

∫

=

1

0

t

t

dt

a

b

;

∫

=

1

0

t

t

axdt

bx

;

∫

=

1

0

t

t

aydt

by

;

∫

=

1

0

t

t

azdt

bz

;

2

2

2

z

y

x

b

b

b

b

+

+

=

;

a

dt

b

d

=

.

Kinematyka.
Określenie ruchu. Ruchem punktu względem danego układu współrzędnych nazywamy zmianę jego płożenia w czasie. Poruszający się punkt po torze można określić następująco: 1) przez promień
wektora

)

(t

r

r

=

; 2) przez składowe promienia we współrzędnych prostokątnych: F= F(t) {

)

(

),

(

),

(

t

z

z

t

y

y

t

x

x

=

=

=

; 3) przez składowe wektora promienia we współrzędnych biegunowych: r = r(t),

)

(

),

(

t

t

ϕ

ϕ

θ

θ

=

=

; 4)

przez równanie toru: S = S(t).

Ruch punktu może odbywać się po torach prostoliniowym na płaszczyźnie i przestrzeni, w krzywoliniowym na płaszczyźnie i przestrzeni. Punkt po tych torach może się poruszać ruchem jednostajnym i
jednostajnie zmiennym. RP rys.15 wektory

0

r

,

1

r

,

2

r

określają położenie w czasie punktu na prostej. Jeżeli

.

const

t

r =

∆

∆

tzn. że geometryczny przyrost wektora promienia jest stały w różnych przyrostach czasu

⇒

=

=

=

−

−

=

∆

∆

=

0

,

,

;

0

1

1

0

1

0

1

t

t

t

S

S

t

t

S

S

t

S

V

Vt

S

S

+

=

0

- wzór na drogę w ruchu jednostaj. Jeżeli

.

const

t

r

V

≠

∆

∆

=

jest wartością zmienną a więc zależy od chwili początkowej i końcowej przedziału czasu

t

∆

i n – y prędkość

średnią

t

r

V

śr

∆

∆

=

,

r

dt

r

d

t

r

V

t

&

=

=

∆

∆

=

→

∆

0

lim

t

S

V

śr

∆

∆

=

,

S

t

S

V

t

&

=

∆

∆

=

→

∆

0

lim

; przyspieszenie w RP:

t

V

a

śr

∆

∆

=

,

V

dt

V

d

t

V

a

t

&

=

=

∆

∆

=

→

∆

0

lim

,

∫

∫

=

→

=

dt

a

dV

dt

dV

a

,

C

at

V

+

=

, t = 0,

C

V

V

=

=

0

at

V

V

±

=

⇒

0

;

∫

∫

+

=

→

+

=

=

dt

at

V

dS

at

V

dt

dS

V

)

(

0

0

;

0

2

0

0

2

S

S

at

t

V

S

=

→

+

+

=

,

0

,

0

V

V

t

=

=

,

V

S

at

t

V

S

+

+

+

=

0

2

0

2

(RJZ)

RK rys. 16. Załóżmy że jakieś cząstki poruszające się po krzywoliniowym torze przyjmą w chwili t położenie

)

(t

r

a w chwili (t + dt) położenie

)

(

dt

t

r

+

. Wektor

)

(

dt

t

r

+

można przedstawić jako sumę

wektorową wektorów

)

(t

r

i wektora przemieszczenia liniowego dN; prędkość i przyspieszenie chwilowe:

r

dt

r

d

t

r

V

t

&

=

=

∆

∆

=

→

∆

0

lim

;

2

2

0

lim

dt

V

d

dt

dV

t

V

a

t

=

=

∆

∆

=

→

∆

(pierwsza pochodna – prędkość po czasie, a prędkość jest pierwszą

pochodną wektora położenia po czasie więc przyspieszenie jest drugą pochodną położenia po czasie).

W ruch zmiennym

t

r

∆

∆

jest zmienne w czasie zatem stosunek ten zależy od chwili początkowej i końcowej przedziału czasu

t

∆

:

r

dt

r

d

t

r

V

t

&

=

=

∆

∆

=

→

∆

0

lim

,

S

dt

dS

t

S

V

t

&

=

=

∆

∆

=

→

∆

0

lim

}

S

V

=

⇒

;

t

r

V

śr

∆

∆

=

[krzywa A A1 jest

hotografem wektora promienia. Zatem wektor V musi być styczny do hotografu wektora promienia]:

t

V

a

śr

∆

∆

=

,

V

dt

V

d

t

V

a

t

&

=

=

∆

∆

=

→

∆

0

lim

wektor przyspieszenia jest styczny do hotografu prędkości i można go uważać

za prędkość końca wektora prędkości poruszającego się po krzywej.
Przyspieszenie normalne i styczne w RK:

ds

d

k

d

ds

d

ds

n

ϕ

ρ

ϕ

ρ

ϕ

ρ

τ

=

=

=

=

=

=

1

,

,

,

1

τ

V

V

=

,

dt

d

V

dt

dV

Vd

dt

d

dt

V

d

a

τ

τ

τ

+

=

=

=

)

(

;

n

dt

d

dt

r

d

ϕ

=

0

,

0

0

,

1

r

dt

d

dt

n

d

n

V

ϕ

−

=

=

=

,

n

dt

d

r

r

dt

dr

dt

r

d

V

ϕ

+

=

=

0

,

r

dt

r

d

V

r

&

=

=

,

ϕ

ϕ

ϕ

r

dt

d

r

V

=

=

,

)

(

0

n

dt

d

r

r

dt

dr

dt

d

dt

r

d

a

ϕ

+

=

=

,

+

+

−

=

n

dt

r

d

r

r

dt

d

n

r

dt

r

d

a

2

2

0

2

0

2

2

)

(

ϕ

n

d

r

a

a

r

a

dt

d

dt

dr

r

n

⋅

+

⋅

=

+

=

+

ϕ

ϕ

ϕ

0

2

,

,

2

ϕ

&

&

&

r

r

a

r

−

=

n

r

r

a

ϕ

ϕ

ϕ

&

&

&

&

2

+

=

Kinematyka ruchu ciała sztywnego. Ruch postępowy bryły – to taki ruch przy, którym każda prosta należąca do bryły pozostaje stale równoległa do swego początkowego położenia:

A

r

=

B

r

+

BA

r

rys. 17.

Równość i równoległość odcinków AB , A1B1 pociąga za sobą równość i równoległość odcinków AA1 i BB1 oraz podobnie dalsze łamane są liniami przystającymi. Punkty bryły poruszające się ruchem

postępowym opisują jednakowe tory, na tych torach jednakowe odcinki drogi w tych samych czasach. W ruch postępowym bryły wszystkie jej punkty mają jednakowe prędkości i przyspieszenia:

r&

=

B

r&

+

BA

r&

;

BA

r

= const. ;

BA

r&

= 0 ;

B

r

r

&

&

&

&

=

;

A

r&

=

B

r&

;

A

a

=

B

a

.

Ruch obrotowy bryły wokół stałej osi – to taki ruch przy którym dwa punkty ciała pozostają stale nieruchome. Prosta przechodząca przez te punkty jest nieruchoma i n – a osią obrotu. Prędkość każdego
punktu bryły znajdującej się w ruchu obrotowym jest prostopadła do płaszczyzny przechodzącej przez ten punkt i oś obrotu rys. 18.

ω

ϕ

ϕ

=

= &

)

(

dt

d

;

t

śr

∆

∆

=

ϕ

ω

;

dt

d

t

śr

t

ϕ

ϕ

ω

ω

=

∆

∆

=

=

→

∆

lim

lim

0

(Jedno. ruch Obro.)

.

const

dt

d

=

=

ϕ

ω

;

∫

∫

=

dt

d

ω

ϕ

;

c

t

+

=

ω

ϕ

;

t

ω

ϕ

ϕ

+

=

0

; t = 0,

0

ϕ

ϕ =

, c =

0

ϕ

. Prędkość każdego punktu bryły znajdującego się w ruch obrotowym jest

prostopadła do pt – y przechodzącej przez rozpatrywany punkt osi obrotu:

t

śr

∆

∆

=

ω

ε

;

.

lim

0

const

dt

d

t

t

=

=

∆

∆

=

→

∆

ω

ω

ε

∫

∫

=

dt

d

ε

ω

;

.

const

=

ε

;

D

t

+

=

ε

ω

;

t

ε

ω

ω

+

=

0

;

.

const

≠

ω

;

t

dt

ε

ω

+

=

0

;

∫

∫

+

=

tdt

dt

d

ε

ω

ϕ

0

;

2

2

0

2

D

t

t

+

+

=

ε

ω

ϕ

;

0

2

ϕ

=

D

;

t

t

0

2

0

2

ω

ε

ϕ

ϕ

+

+

=

;

]

/

1

[

];

/

1

[

2

s

s

ε

ω

.

W jednostajnym ruchu obrotowym bryła obraca się o jednakowe kąty w jednakowych przedziałach czasu w technice podaje się ilość obrotów na min. n[obr./min.]. 1 pełny obrót = zmiana kąta o 2

Π

; jeżeli ciało

w ciągu 1 min. wykona n obrotów to zmiana kąta obrotu wyniesie 2

Π

n, a zatem

30

/

60

/

2

Π

=

Π

=

n

ω

]

/

1

[

s

.

Płaski ruch bryły (rys. 19) – to taki ruch w którym odległości punktów bryły oddanej nieruchomej płaszczyzny pozostają jednakowe, lub stałe, Wszystkie punkty bryły poruszają się w płaszczyznach
równoległych do danej płaszczyzny nie ruchomej. W płaszczyźnie

Π

2

porusza się figura płaska s. W czasie ruchu jest zawsze równoległa do

1

Π

. Płaszczyzna

1

Π

jest płaszczyzną kierującą. W ruchu płaskim punkty

A

1

, A

2

B

1

, B

2

, pozostają na prostej prostopadłej do płaszczyzny

Π

1

. Pędy punktów A

1

, A

2

B

1

, B

2

w każdej chwili są jednakowe. Jeżeli bryła porusza się ruchem płaskim to wektory pędów punktów leżących na

prostej prostopadłej do płaszczyzny kierującej są jednakowe i równe prędkościom rzutów tych punktów na tę płaszczyznę. Ruch każdego punktu figury płaskiej s określa ruch każdego punktu leżącego na
prostej prostopadłej do płaszczyzny kierującej

Π

2

. Zatem badanie ruchu płaskiego można sprowadzić do badania figury płaskiej S. Figura płaska poruszająca się ruchem płaskim ma trzy stopnie swobody.

Chwilowy środek obrotu. 1 def. Jeżeli figura płaska porusza się ruchem płaskim a punkty A i B tej figury znajdują się na płaszczyźnie

Π

2

to w pewnej chwili t ich prędkości będą wynosić V

A

i V

B

wektory te

leżą na płaszczyźnie

Π

2

. Proste prostopadłe do wektorów V

A

i V

B

wystawione z punktów A i B przetną się w jednym punkcie C zwanym chwilowym środkiem obrotu. Punkt C leży na płaszczyźnie

Π

2

.

Prędkości wszystkich punktów leżących na prostej prostopadłej do płaszczyzny

Π

2

wystawionej z punktu C w rozpatrywanej chwili t są równe zero. [Ruch układu w chwili t jest obrotowy a osią obrotu jest

prosta prostopadła do płaszczyzny kierującej wystawiona z punktu C]. Po upływie czasu

∆t wektory prędkości V

A

i V

B

zmieniają swoje położenie a proste prostopadłe do wektorów V’

A

i V’

B

przetną się w

punkcie C’ który będzie innym chwilowym środkiem obrotu po upływie czasu

∆t. Gdy proste CA i CB prostopadłe do wektorów prędkości V

A

i V

B

są do siebie równoległe to ruch ciała w chwili t jest

chwilowym ruchem postępowym. W każdej chwili ruch płaski układu lub ciała sztywnego jest chwilowym ruchem obrotowym wokół chwilowego środka obrotu lub chwilowym ruchem postępowym.
Chwilowy środek obrotu 2 def. gdy prędkości V

A

i V

B

są prostopadłe do prostej łączącej punkty A i B to punkt C będzie wyznaczony przez prostą AB i prostą łączącą końce wektorów V

A

i V

B

.

Chwilowy środek przyspieszeń – W ruchu płaskim figury w każdej chwili występuje taki punkt którego przyśpieszenie jest równe zero. Punkt ten jest chwilowym środkiem przyśpieszeń.
Chwilowy środek obrotu nie pokrywa się z chwilowym środkiem przyśpieszeń.

Ruch złożony – (rys. 20) (pod rysunkiem: X,Y,Z – układ nieruchomy; X1,Y1,Z1 – układ ruchomy) Układ związany z poruszającym się ciałem nazywa się układem ruchomym lub względnym. Ruch punktu M
względem układu ruchomego X1,Y1,Z1 nazywamy względnym. Ruch punktu M względem układu nieruchomego X,Y,Z nazywamy bezwzględnym. Równania ruchu względnego punktu dane są w postaci

{X1

= X1(t), Y1 = Y1(t), Z1 = Z1(t)

⇒ r

i

5 r

1

.X.i

1

1 r

1

.Y.j

1

1 r

1

.Z.k

1

Ruch układu ruchomego opisany jest równaniami:

{X0 = X0(t), Y0 = Y0(t), Z0= Z0(t)⇒ r

0

5 r

0

.X.i1 r

0

.Y.j1 r

0

.Z.k

. Prędkość punktu M

względem punktu O1 otrzymamy różniczkując wektor r

1

. Prędkość bezwzględną punktu M którego wektorem promieniem w układzie nieruchomym jest wektor r a w układzie ruchomym r

1

określamy jako

pochodną sumy wektorów: r5r

0

1r

i

stąd

dt

r

d

dt

r

d

r

r

dt

d

dt

r

d

V

1

0

1

0

)

(

+

=

+

=

=

gdzie dr

0

/dt

5V

0

- prędkość układu ruchomego w ruchu unoszenia. Drugą składową prędkości punktu M otrzymujemy różniczkując wektor r

1

który ulega zmianie na skutek zmiany składowych X1,Y1,Z1 oraz na skutek obrotu układu X1,Y1,Z1 względem punktu O1. Ostatecznie prędkość w ruchu złożonym wyraża się wzorem: V5V

0

1 V

W

1ϖ

ϖ

ϖ

ϖ3r

1

-

wyprowadzenie:

=

+

+

=

)

(

1

1

1

1

1

1

1

k

z

r

j

y

r

i

x

r

dt

d

dt

r

d

+

+

+

=

1

1

1

1

1

1

k

dt

z

dr

j

dt

y

dr

i

dt

x

dr

dt

k

d

z

r

dt

j

d

y

r

dt

i

d

x

r

1

1

1

1

1

1

+

+

,

,

,

,

1

1

1

1

1

1

k

k

j

j

i

i

×

=

×

=

×

=

ω

ω

ω

&

&

&

)

(

1

1

1

1

1

1

0

k

z

r

j

y

r

i

x

r

V

V

V

w

+

+

×

+

+

=

ω

Przyspieszenie w ruchu złożonym:

=

×

+

+

=

=

)

(

1

0

r

V

V

dt

d

dt

V

d

a

w

ω

dt

V

d

r

dt

d

dt

V

d

w

+

×

+

)

(

1

0

ω

,

dt

V

d

a

0

0

=

- przysp. ruchu postępow. początku układu

ruchomego;

=

×

+

×

=

×

dt

dr

r

dt

d

r

dt

d

1

1

1

)

(

ω

ω

ω

1

1

r

V

r

dt

d

w

×

×

+

×

+

×

ω

ω

ω

ω

,

1

1

r

V

dt

r

d

w

×

+

=

ω

,

+

×

×

+

×

+

+

=

1

0

r

V

a

a

a

w

u

ω

ω

ω

w

w

V

a

×

+

+

ω

,

w

n

u

t

u

w

V

a

a

a

a

a

×

+

+

+

+

=

ω

2

0

,

1

,

2

r

a

V

a

t

u

w

cor

×

=

×

=

ε

ω

,

cor

u

w

a

a

a

a

+

+

=

Przyspieszenie bezwzględne punktu w ruchu złożonym równe jest sumie wektorowej przyśpieszenia unoszenia a

U

, przyśpieszenia względnego a

W

, i przyśpieszenia Coriolisa a

C

. Odpowiednie przyśpieszenia

wyrażają się poniższymi wzorami: a

U

5a

O

1 a

U

N

1 a

U

T

5 dV

0

/dt 1 ε

εεε3 r

1

1ϖ

ϖ

ϖ

ϖ3ϖ

ϖ

ϖ

ϖ3r

1

; a

C

52ϖ

ϖ

ϖ

ϖ. V

W

. Przyśpieszenie Coriolisa zwane odśrodkowym, dewiacyjnym, wywołane jest obrotem układu względnego i wynosi

zero gdy ruch tego układu jest postępowy. Przyśpieszenie względne jest drugą pochodną wektora promienia r

1

względem czasu.

Ruch kulisty – ruchem kulistym ciała sztywnego (bryły) nazywamy taki ruch podczas którego jeden z jego punktów pozostaje nieruchomy (stały) (rys. 21). Każde ciało w ruchu kulistym mające nieruchomy
punkt można przeprowadzić z jednego położenia w drugie za pomocą jednego obrotu wokół osi przechodzącej przez nieruchomy punkt tego ciała. Dowolny ruch kulisty między dwoma bardzo bliskimi
położeniami można zastąpić z niewielkim przybliżeniem wokół osi przeprowadzonej przez nieruchomy punkt S. Dowolny ruch kulisty może być traktowany jako złożenie następujących po sobie małych
obrotów wokół osi przechodzących przez nieruchomy punkt S. Chwilowa oś jest granicznym położeniem osi obrotu rozumianego jako zmiana położenia ciała w nieskończenie małym odstępie czasu. Prędkość
w ruchu kulistym: V5ϖ

ϖ

ϖ

ϖ3r ;

+

−

+

−

=

j

r

r

i

r

r

V

z

x

x

z

y

z

z

y

)

(

)

(

ω

ω

ω

ω

k

r

r

x

y

y

x

)

(

ω

ω

−

+

,

2

2

2

Vz

Vy

Vx

V

+

+

=

, V5V

X

.i1 V

Y

.j1 V

Z

.k (rys. 22) Vx,Vy,Vz – składowe prędkości liniowej dowolnego punktu w

układzie nieruchomym. Położenie układu ruchomego będzie znane gdy zostaną określone kąty między wersorami układu ruchomego a układu nieruchomego. Zamiast kątów można rozpatrywać cosinusy
kierunkowe oznaczane przez:

α1, α2, α3, β1, β2, β3, γ1, γ2, γ3. Przykładowo α1 – cosinus kierunkowy kąta jaki tworzy oś X1 z osią X (rys. 23). Przyśpieszenie w ruchu kulistym :

2

1

ω

ω

ω

+

=

,

0

0

,

1

L

L

ω

ω

=

=

,

),

(

r

dt

d

dt

V

d

a

×

=

=

ω

dt

r

d

r

dt

d

a

×

+

×

=

ω

ω

,

dt

L

d

L

dt

d

L

dt

d

dt

d

0

0

0

)

(

ω

ω

ω

ω

+

=

=

,

0

1

0

L

dt

L

d

×

=

ω

,

×

+

=

×

+

=

1

0

1

0

1

0

1

)

(

ω

ε

ω

ω

ε

ω

L

L

L

dt

d

)

0

L

ω

×

,

p

dt

d

ε

ε

ω

+

=

1

,

0

1

1

=

=

ε

ω

dt

d

,

V

r

r

r

a

p

p

×

+

×

=

×

×

+

×

=

ω

ε

ω

ω

ε

)

(

r

V

×

=

1

ω

,

.

,

1

1

const

p

≠

×

=

ω

ω

ω

ε

,

r

a

p

×

+

=

)

(

1

1

ε

ε

;a5a

1

1a

2

gdzie a

1

5εεεε3r (przyśpieszenie obrotowe) ; a

2

5ϖ

ϖ

ϖ

ϖ(ϖ

ϖ

ϖ

ϖ.r)2ϖ^2.r (przyśpieszenie doosiowe)

Dynamika.

I zasada dynamiki Newtona: ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym gdy nie działają na niego żadne siły zewnętrzne albo działające siły równoważą się:

0

=

∑

n

i

i

F

;

a

= 0 ;

V

=

.

const

II Z. D. N: całkowita siła działająca na ciało jest równa iloczynowi masy i przyspieszenia, masa ciała m przeciwstawia się zmianie ruchu, a więc jest miarą bezwładności

a

m

F

⋅

=

.

III Z. D. N: (prawo akcji i reakcji) jeżeli dwa ciała oddziaływają na siebie to wektor siły F1 wywierany przez ciało pierwsze na ciało drugie jest równy co do wielkości, ma ten sam kierunek lecz przeciwny

zwrot co wektor siły F2 oddziaływania ciała drugiego na pierwszy: F = d/dt (m

V

) =

dt

p

d

;

V

m

p

=

(słuszne w układzie inercjalnym).

I zagadnienie: gdy dane są równania ruchu należy określić siłę wywołującą ten ruch. II zagadnienie: gdy dana jest siła działająca na punkt należy określić równanie parametryczne ruchu.

)

(t

r

r

=

;

i

r

r

x

=

+

j

r

y

+

k

r

z

;

2

2

2

z

y

x

r

r

r

r

+

+

=

; x = x(t) ,

)

(t

x

x

&

&

=

,

)

(t

x

x

&

&

&

&

=

również dla y, z ;

k

z

j

y

i

x

a

&

&

&

&

&

&

+

+

=

;

2

2

2

z

y

x

a

&

&

&

&

&

&

+

+

=

; { x = m

x

&

&

, y = m

y

&

&

, z = m

z

&

&

; F = x i + y j + z k ;

2

2

2

z

y

x

F

+

+

=

.

Pęd i popęd:

- dla punktu materialnego:

dt

d

(m

V

) =

F

, d (m

V

) =

F

dt: Wektor m

V

nazywany jest pędem lub ilością ruchu materialnego w chwili t natomiast

F

dt elementarnym impulsem siły lub popędem siły:

∫

∫

=

2

1

2

1

)

(

t

t

t

t

dt

F

V

m

d

;

1

2

1

2

V

m

V

m

dt

F

t

t

−

=

∫

gdy na punkt materialny nie działają siły zewnętrzne wówczas przyrost jest równy 0

0

=

∆p

,

p

=

.

const

,

1

2

V

m

V

m

=

,

1

2

mV

mV

=

- zasada zachowania pędu dla punktu

materialnego.

- Dla układu punktów materialnych (rys. 24):

∑

=

n

mi

m

1

0

,

n

V

V

V

+

+

=

...

1

0

,

0

0

0

1

V

m

p

pi

n

=

=

∑

,

i

i

n

n

V

m

i

p

∑

∑

=

1

1

. Pochodna pędu ogólnego układu punktów materialnych równa się wypadkowej sił zewnętrznych

działających na ten układ. Siły wewnętrzne nie mają wpływu na pęd układu i są pomijane.

0

,

,

0

,

0

1

0

0

0

0

=

=

=

=

∑

p

F

F

F

F

p

n

i

&

&

,

0

01

02

0

0

.,

p

p

p

const

p

∆

=

=

−

=

i

V

m

i

V

m

i

n

n

i

1

1

1

2

∑

∑

=

zasada zachowania pędu układu punktów.

Pęd układu punktów materialnych zachowuje stałą wartość i kierunek jeśli na układ ten nie działają siły zewnętrzne lub gdy ich suma równa jest 0.

Kręt i pokręt:
- dla punktu materialnego (rys. 25): wektor krętu jest wektorem momentu pędu.

V

m

r

p

r

K

V

m

p

×

=

×

=

=

,

,

)

(

V

m

r

dt

d

dt

dk

K

×

=

=

&

,

a

dt

V

d

dt

V

d

m

r

V

m

dt

r

d

K

=

×

+

×

=

,

&

)

,

sin(

,

c

b

c

b

a

c

b

a

⋅

⋅

=

×

=

M

F

r

a

m

r

K

=

×

=

×

=

&

M

dt

K

d

K

=

=

&

&

(druga postać IIZ.D.N) Pochodna krętu punktów materialnych

względem dowolnego bieguna punktu jest równa momentowi sił działających na niego względem tegoż bieguna.

Kzk

Kyj

Kxi

K

+

+

=

,

2

2

2

z

y

x

K

K

K

K

+

+

=

,

;

)

2

(

)

1

(

2

1

∫

∫

=

t

K

t

K

t

t

dt

M

K

d

∫

=

−

2

1

1

2

t

t

Mdt

K

K

, M = 0,

0

=

∆K

, K =

.

const

,

0

1

2

=

− K

K

zasada zachowania krętu punktu materialnego.

- Dla układu punktów materialnych (rys. 26) . Układ punktów materialnych o masach równych m1, m2, mn oraz dowolnie dobrany biegun O (w początku kartezjańskiego układu współrzędnych). Kręt

pojedynczego punktu materialnego o masie m względem bieguna O równy jest iloczynowi wektorowemu wektora promienia

i

r

poprowadzonego z bieguna O

i

pędu

i

i

V

m

. Suma geometryczna momentów

pędu wszystkich punktów materialnych należących do rozpatrywanego układu zwana jest krętem układu punktów materialnych względem bieguna O i oznaczana przez

∑

=

×

=

n

i

i

i

V

mi

r

K

1

0

;

∑

=

n

mi

m

1

0

,

k

rz

j

ry

i

rx

r

+

+

=

0

,

n

V

V

V

+

+

=

...

1

0

,

0

0

0

0

V

m

r

K

×

=

; Pochodna krętu układu punktów materialnych względem punktu (bieguna) jest równa momentowi sił działających na ten układ punktów materialnych

względem tego bieguna. Pochodna krętu ogólnego jest równa momentowi ogólnemu sił zewnętrznych względem bieguna.

0

0

0

0

0

0

0

)

(

F

r

dt

d

V

m

r

dt

K

d

K

×

=

×

=

=

&

0

0

M

K

=

,

0

0

M

dt

K

d

=

∫

∫

=

2

1

2

1

0

0

t

t

t

t

dt

M

K

d

,

∫

=

−

2

1

0

01

02

t

t

dt

M

K

K

M

0

= 0, K

0

=

.

const

,

0

0

=

∆K

,

0

01

02

=

− K

K

- zasada zachowania krętu – w przypadku gdy momenty wszystkich sił zewnętrznych układu punktów materialnych względem pewnego nieruchomego bieguna O są równe

zeru, wówczas kręt układu względem tego bieguna nie ulega zmianie tzn.

.

0

const

K

=

Kręt ogólny układu zachowuje stałą wartość i kierunek jeśli moment ogólny sił zewnętrznych równy jest zeru. Siły zewnętrzne nie mają wpływu na kręt układu.

Pracą elementarną (rys. 27) siły F na drodze

r

d

nazywamy wyrażenie: L =

r

d

F

⋅

, dL =

r

d

F

⋅

, L =

∫

AB

F

d

F

. Aby określić pracę musimy znać drogę, a więc jej równanie x = x(t) , y = y(t) , z = z(t) warunki

początkowe i końcowe: (x1, y1, z1) i (x2, y2, z2) , Fx = Fx(t), Fy = Fy(t), Fz = Fz(t);

+

=

i

F

F

x

+

j

y

F

k

z

F

,

k

dz

j

dy

i

dx

r

d

+

+

=

, L =

∫

+

+

AB

dt

dt

Fzdz

Fydy

Fxdx

/

)

(

,

∫

+

+

=

2

1

)

(

t

t

dt

FzVz

FyVy

FxVx

L

, L =

∫

2

1

)

(

t

t

dt

V

F

.

Energia kinetyczna. Energia ciała jest jego zdolnością do wykonywania pracy i odwrotnie praca może powodować przyrost energii. W układzie izolowanym jeśli nie ma zmian energii na inne postacie to praca

sumy sił działających na punkt materialny równa jest przyrostowi jej energii kinetycznej.

2

2

mV

E

k

=

,

dt

V

d

V

=

&

,

V

m

F

&

=

, L =

∫

∫

∫

=

=

AB

AB

AB

dr

dt

V

d

m

r

d

V

m

r

d

F

&

, L =

2

2

1

2

1

2

2

2
1

2

1

mV

mV

mV

V

d

V

m

V
V

V

V

−

=

=

∫

, L =

k

E

∆

.

Energia potencjalna. Do określenia energii potencjalnej konieczna jest znajomość pola sił potencjalnych.
Pole sił – jest to obszar na powierzchni, którego w każdym punkcie działa określona siła na punkt materialny, a wartość zależy od położenia jej w układzie współrzędnym o środku w centrum pola; pole sił jest
określone gdy w każdym jego punkcie mamy określoną siłę F.

)

(r

F

F

=

, Fx = Fx(x, y, z) , Fy = Fy(x, y, z) , Fz = Fz(x, y, z) . Gdy współrzędne sił zależą od czasu to mamy wówczas zmienne pole sił w czasie.

Linie sił określamy jako linie styczne w każdym punkcie linii pola do wektorów sił. Równania różniczkowe sił można przedstawić w postaci równania różniczkowego: dx/ Fx(x, y, z) = dy/ Fy(x, y, z) = dz/ Fz(x,
y, z) po całkowaniu uzyskamy rodzinę linii: G1(x, y, z) = C1, G2(x, y, z) = C2. Spełnienie jednoczesne obu równań oznacza ich przecięcie się a więc otrzymujemy rodzinę linii.
Jeżeli istnieje taka funkcja skalarowa EP, że siła F spełnia następujący warunek:

p

gradE

F

−

=

, a Fx =

x

E

p

∂

∂

−

, Fy =

y

E

p

∂

∂

−

, Fz =

z

E

p

∂

∂

−

to pole sił nazywamy potencjalnym, siłę F siłą potencjalną, energię potencjalną

potencjałem. Pole sił ma wtedy potencjał gdy jest polem bezwirowym a więc rotacja siły F = 0 , rot F = 0,

y

Fx

∂

∂

=

x

Fy

∂

∂

;

z

Fy

∂

∂

=

y

Fz

∂

∂

;

x

Fz

∂

∂

=

z

Fx

∂

∂

. Związek pomiędzy EP a pracą wynika z określenia pracy:

Fzdz

Fydy

Fxdx

r

d

F

dL

+

+

=

=

,

Ep

dz

z

Ep

dy

y

Ep

dx

x

Ep

dL

∆

−

=

∂

∂

+

∂

∂

+

∂

∂

−

=

)

(

dL =

p

E

∆

−

. Praca elementarna sił potencjalnych jest ujemną różniczką zupełną energii potencjalnej: L =

∫

−

2

1

Ep

Ep

p

dE

=

=

−

−

]

[

1

2

Ep

Ep

2

1

p

p

E

E

−

. Praca sił

potencjalnych niezależy od drogi przejścia lecz tylko od wartości energii w punkcie początkowym i końcowym. Gdy droga jest krzywą zamkniętą to praca równa przyrostowi energii potencjalnej jest równa 0.
Zasada zachowania energii.

Suma EK i EP jest energią mechaniczną:

k

p

m

E

E

E

+

=

. Jeśli nie ma przemian masy w energie, jeśli układ w rozważanym okresie czasu nie wykonał pracy, ani praca nie została włożona to energia

mechaniczna układu izolowanego jest wielkością stałą: L’ =

1

2

k

k

E

E

−

, L” =

2

1

p

p

E

E

−

} L’ – L” = 0,

2

2

p

k

E

E

+

=

1

1

p

k

E

E

+

, E

2

= E

1

=

.

const

Gdy przemiany EM odbywają się w polu potencjalnym sił to energia

mechaniczna jest wielkością stałą.
Moc. Jeśli siła wykonuje pracę

L

∆

w czasie

t

∆

to stosunek tej pracy do czasu nazywamy mocą średnią Nśr. =

L

∆

/

t

∆

,

=

⋅

=

=

⋅

=

=

=

→

∆

V

F

dt

V

d

F

V

F

dt

d

dt

dl

dt

dl

N

t

)

(

lim

0

)

,

cos(

V

F

FV

N

⋅

=

=

, 1J/1s = W (wat) [1kM] = 736 [W].

EK układu punktów materialnych i ruchu środka masy (rys. 28):

∑

=

=

n

i

i

i

k

V

m

E

1

2

2

1

. EK układów punktów materialnych zależy od pracy sił zewnętrznych. Masę ogólną układu punktów materialnych określa się jako sumę mas wszystkich punktów:

∑

=

n

i

c

m

m

1

, współrzędne środka masy:

c

n

i

i

n

i

n

i

n

i

i

c

m

r

m

m

r

m

m

S

r

∑

∑

∑

∑

⋅

=

=

=

1

1

1

1

,

k

z

r

j

y

r

i

x

r

r

c

c

c

c

+

+

=

,

2

2

2

z

r

y

r

x

r

r

c

c

c

c

+

+

=

,

,

,

,

1

1

1

∑

∑

∑

∑

∑

∑

=

=

=

=

=

=

i

n

i

i

z

i

cz

i

n

i

i

y

i

cy

i

n

i

i

x

i

cx

m

r

m

r

m

r

m

r

m

r

m

r

∑

=

⋅

n

i

i

c

c

r

m

m

r

1

,

∑

=

⋅

n

i

c

c

mi

dt

r

d

dt

d

m

r

1

,

∑

=

⋅

n

i

c

c

mi

dt

r

d

dt

d

m

r

1

&

&

,

F

p

dt

p

d

m

a

c

c

c

c

=

=

=

⋅

&

- siła działająca na układ punktów

materialnych przyłożona w punkcie C.
Środek masy układu punktów materialnych porusza się tak jakby w nim była skupiona masa ogólna układu jakby na niego działała suma wszystkich sił zewnętrznych działających na układ. Pęd układu
punktów materialnych liczony względem środka masy równy jest 0.
Kręt układu punktów materialnych względem środka masy układu poruszającego się ruchem postępowym w stosunku do układu inercjalnego równa się iloczynowi prędkości kątowej i iloczynowi
bezwładności a pochodna tego krętu równa się momentowi pędu:

z

M

K

=

&

.

Kręt ogólny punktów materialnych równy jest krętowi masy ogólnej układu skupionej w środku masy powiększonej o kręt układu względem środka masy:

c

c

c

K

mV

r

K

+

×

=

0

.

Energia kinetyczna układu punktów materialnych równa jest energii jego masy ogólnej skupionej w środku masy powiększonej o energię kinetyczną względem środka masy:

kc

c

c

k

E

V

m

E

+

=

2

2

0

.

Geometria mas.
Momenty masowe II stopnia (rys. 29):
Masowymi momentami bezwładności układu punktów materialnych względem płaszczyzn xy, yz, zx nazywamy sumy iloczynów masy każdego punktu przez kwadrat jego odległości od danej płaszczyzny:

∑

∑

=

=

n

xi

i

n

xi

i

r

m

r

m

Jxx

1

2

1

2

,

∑

=

n

yi

i

r

m

Jyy

1

2

,

∑

=

n

zi

i

r

m

Jzz

1

2

. Dla ciała sztywnego:

x

r

x

=

,

y

r

y

=

,

z

r

z

=

∫

∫

∑

=

=

=

→

∞

→

m

x

m

n

xi

i

m

n

dm

r

dmrx

r

m

Jxx

i

2

2

1

0

lim

,

∫

=

m

y

dm

r

Jyy

2

,

∫

=

m

z

dm

r

Jzz

2

. Momenty bezwładności względem osi (dla układu punktów

materialnych):

∑

+

=

n

zi

yi

i

r

r

m

Jx

1

2

2

)

(

,

∑

+

=

n

zi

xi

i

r

r

m

Jy

1

2

2

)

(

,

∑

+

=

n

xi

yi

i

r

r

m

Jz

1

2

2

)

(

,

∫

∑

+

=

+

=

→

∞

→

m

z

y

yi

n

yi

i

m

n

dm

r

r

r

r

m

Jx

i

)

(

)

(

2

2

2

1

2

0

lim

,

∫

+

=

m

z

x

dm

r

r

Jy

)

(

2

2

,

∫

+

=

m

x

y

dm

r

r

Jz

)

(

2

2

,

Jzz

Jyy

dm

z

y

Jx

m

+

=

+

=

∫

)

(

2

2

,

Jxx

Jzz

dm

x

z

Jy

m

+

=

+

=

∫

)

(

2

2

Jyy

Jxx

dm

y

x

Jz

m

+

=

+

=

∫

)

(

2

2

.

Biegunowy moment bezwładności dla układu punktów materialnych:

0

2

2

2

2

J

Jzz

Jyy

Jxx

Jz

Jy

Jx

=

+

+

=

+

+

, dla ciała sztywnego:

∑

∆

=

n

i

i

r

m

J

1

2

0

,

∫

∫

∑

+

=

=

∆

=

=

∆

∞

→

m

m

i

n

i

m

n

dm

x

dm

r

r

m

Jx

i

2

2

2

1

0

lim

∫

∫

+

m

m

dm

z

dm

y

2

2

; biegunowy moment bezwładności

równa się sumie momentów względem płaszczyzn prostopadłych w punkcie, który jest początkiem układu współrzędnych.
Masowy moment dewiacji. Momentami dewiacji Jxy, Jyz, Jzx, Jyx, Jzy, Jxz dla układu punktów materialnych nazywamy sumę iloczynów mas elementarnych przez ich odległości od dwóch płaszczyzn:

∑

∑

∑

∆

=

∆

=

∆

=

n

i

i

i

n

i

i

i

n

i

i

i

x

z

m

Jzx

z

y

m

Jyz

y

x

m

Jxy

1

1

1

,

,

∫

∑

=

∆

=

→

∆

∞

→

m

i

i

n

i

m

n

xydm

y

x

m

Jxy

i

1

0

lim

,

∫

=

m

yzdm

Jyz

,

∫

=

m

zxdm

Jzx

,

Jxz

Jzx

Jzy

Jyz

Jyx

Jxy

=

=

=

,

,

.

Tensor bezwładności jest to wielkość utworzona z osiowych momentów bezwładności i momentów dewiacji zapisana w postaci macierzy:

Jz

Jzy

Jzx

Jzy

Jy

Jyx

Jzx

Jyx

Jx

J

−

−

−

−

−

−

=

momenty bezwładności osiowe i dewiacji są

współrzędnymi tensora bezwładności.
Tw. Huygensa – Steinera:

z

z

z

y

y

y

x

x

x

c

A

c

A

c

A

′

+

=

′

+

=

′

+

=

,

,

,

∫

∫

=

′

+

=

=

m

c

m

A

dm

x

x

dm

x

Jxx

2

2

)

(

dm

x

dm

x

x

dm

x

m

m

c

m

c

∫

∫

∫

′

+

′

+

=

2

2

2

2

,

Jzz

mz

Jzz

c

+

=

2

; momenty bezwładności względem osi centralnych są mniejsze spośród

wszystkich momentów bezwładności liczonych względem osi równoległych do nich:

)

(

{

2

2

c

c

z

y

m

Jxc

Jx

+

+

=

,

)

(

2

2

c

c

x

z

m

Jyc

Jy

+

+

=

,

)

(

2

2

c

c

y

x

m

Jzc

Jz

+

+

=

,

c

c

c

c

y

mx

y

Jx

Jxy

+

=

,

)

c

c

c

c

z

my

z

Jy

Jyz

+

=

)

c

c

c

c

x

mz

x

Jz

Jzx

+

=

,

)

(

2

2

2

2

0

c

c

c

z

y

x

m

Jc

mr

Jc

J

+

+

+

=

+

=

; osie względem których moment

bezwładności dewiacji jest równy 0 to osie są osiami głównymi, a jeżeli przechodzą przez środek masy to są to osi główne centralne. Momenty liczone względem tych osi są momentami głównymi lub głównymi
centralnymi, a ich wartości są ekstremalne.
Dynamika ciała sztywnego

bryły; ciało sztywne jeśli układ punktów materialnych zachowuje stałe odległości między sobą.

Dynamika ruchu postępowego:

1

1

w

c

V

V

V

+

=

,

0

=

wi

V

,

i

V

V

V

=

=

=

...

2

1

,

∑

∑

=

=

∆

=

n

n

c

c

i

i

p

V

m

V

m

p

i

1

1

,

∑

∑

×

=

n

n

i

i

p

r

V

i

1

1

)

(

,

∑

=

n

i

w

i

V

m

p

1

1

; kręt układu w ruch postępowym:

2

2

c

mV

Ek

=

. W ruchu postępowym po torze prędkość i przyspieszenie wszystkich punktów

ciała są jednakowe, a więc należy wyznaczyć je dla środka masy, wtedy będzie znany ruch ciała. Aby ruch był postępowy to suma sił zewnętrznych dających moment działający na ciało względem środka masy
musi być równa 0.

Pochodna krętu:

=

×

=

'

'

c

c

c

p

r

K

=

′

′

−

′

′

′

′

′

′

=

×

=

ω

m

x

y

z

y

x

k

j

i

V

m

r

c

c

c

c

c

c

0

'

]

'

)

'

'

(

'

'

'

'

'

'

[

2

2

k

y

x

m

j

z

my

i

x

mz

c

c

c

c

c

c

+

+

−

−

=

ω

=

'

'

'

'

'

'

'

'

k

Jz

j

z

Jy

i

x

Jz

c

c

c

c

c

ω

ω

ω

+

−

−

=

;

z

M

K

=

&

- moment od sił zewnętrznych;

=

c

K

&

−

′

′

′

−

′

′

′

−

′

′

′

−

j

z

y

J

i

x

z

J

i

x

z

J

c

c

c

c

c

c

&

&

&

&

&

ω

ω

ω

k

z

J

k

z

J

j

z

y

J

c

c

c

c

′

′

+

′

′

+

′

′

′

−

&

&

&

&

ω

ω

ω

,

=

c

K

&

+

′

′

′

+

′

′

′

−

′

′

′

−

′

′

′

−

=

i

z

y

J

j

z

y

J

j

x

z

J

i

x

z

J

c

c

c

c

c

c

c

c

2

2

ω

ω

ω

ω

&

&

&

&

k

z

J

c

′

′

+

ω&

,

−

′

′

′

−

′

′

′

−

′

′

′

=

j

x

z

J

i

x

z

J

i

z

y

J

K

c

c

c

c

c

c

c

2

2

ω

ε

ω

&

&

k

Mz

j

My

i

Mx

k

Jc

j

z

y

J

c

c

'

'

'

'

'

+

+

=

′

+

′

′

′

−

ε

ε

Równania w ruch obrotowym wynikające z pochodnej pędu po czasie. Jeśli na ciało sztywne poruszające się ruchem obrotowym działają siły zewnętrzne, których suma wynosi

F

a moment względem

bieguna =

M

to z pochodnej pędu możemy zapisać, że:

=

+

+

=

=

'

'

'

k

z

j

y

i

x

p

F

&

'

)

'

(

'

)

'

'

(

2

2

j

x

y

m

i

y

x

m

c

c

c

c

c

c

ε

ω

ε

ω

+

−

+

+

−

=

'

'

y

x

p

p

&

&

+

; z tw. krętu (o pochodnej krętu) wynika, że:

'

'

'

'

'

'

k

Mz

j

My

i

Mx

K

+

+

=

&

=

k

Jz

j

z

Jy

x

Jz

i

x

Jz

z

Jy

ω

ε

ω

ε

ω

&

'

'

)

'

'

'

'

(

'

)

'

'

'

'

(

2

2

+

+

−

−

=

'

'

'

z

K

y

K

x

K

&

&

&

+

−

.

Ruch płaski bryły (rys. 30) jest ruchem złożonym z ruchu postępowego i ruchu obrotowego przy czym ruch postępowy odbywa się w płaszczyznach prostopadłych do chwilowej osi obrotu a oś obrotu Cx nie
zmienia swego kierunku. Siły F

1

, F

2

, F

2

, leżą w płaszczyźnie YZC. Dla bryły swobodnej ruch postępowy i obrotowy są wzajemnie niezależne. Umieszczając oś obrotu w środku masy C otrzymujemy ruch

postępowy określony ruchem punktu c i ruch obrotowy wokół centralnej osi Cx przechodzącej przez środek masy C. Oś obrotu bryły nie zmieni swego kierunku jeśli jest osią główną lub główną centralną osią
bezwładności, wówczas kręt ogólny jak i jego pochodna leżeć będą na tej osi i nie będą mogły zmieniać jej kierunku. Siły działające na bryłę muszą dawać moment ogólny równy pochodnej krętu po czasie,
którego kierunek i zwrot pokrywa się z kierunkiem osi Cx.
Ruch bryły swobodnej jest płaski jeśli chwilowe osie obrotu nie zmieniają kierunku pozostają stale równoległe do głównej centralnej osi bezwładności (ruch odbywać się będzie w płaszczyźnie):

y

m

y

P

y

F

&

&

&

=

=

,

z

m

z

P

c

F

&

&

&

=

=

,

x

Jx

Jc

c

K

Mc

ω

ω

&

&

&

=

=

=

,

j

F

i

F

F

y

x

+

=

Drgania wywoływane są siłami zmiennymi w czasie zwanymi siłami dynamicznymi. Polegają one na okresowych przemianach energii potencjalnej, kinetycznej oraz stanowią ruch okresowy wokół położenia
równowagi. W technice występują następujące rodzaje drgań: wzdłużne, skrętne, giętne każde z nich mogą być: swobodne, nieswobodne bądź: nie tłumione, tłumione.
Drgania swobodne występują wówczas gdy na układ mechaniczny nie działają siły zmienne w czasie.
Drgania nieswobodne (wymuszone) występują wówczas gdy na układ działają siły zmienne w czasie – najczęściej okresowe.
Gdy układ drgający nie traci energii mechanicznej w czasie wówczas występują drgania nie tłumione. Gdy układ traci energię w czasie występują drgania tłumione w czasie.
Drgania o jednym stopniu swobody to takie, przy których położenie elementu drgającego da się opisać jedną zmienną.
Drgania o skończonej liczbie stopni swobody to takie przy, których położenia układu drgającego można opisać skończoną liczbą zmiennych uogólnionych.
D.S.T układu o jednym stopniu swobody. Najczęściej spotykamy układy rozpraszające energię: 1) z tłumieniem, których siła oporu jest proporcjonalna do prędkości a więc tłumienie może jest liniowe; 2)
tłumienie jest proporcjonalne do nacisku normalnego.