
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
1
Aula 14 – Parte 2
CORRELAÇÃO ............................................................................................................................................... 2
REGRESSÃO LINEAR ................................................................................................................................ 17
Relação das questões comentadas .................................................................................................... 27
Gabaritos ...................................................................................................................................................... 34
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
2
CORRELAÇÃO
Vamos pensar em duas variáveis que possuam alguma relação. Suponha que
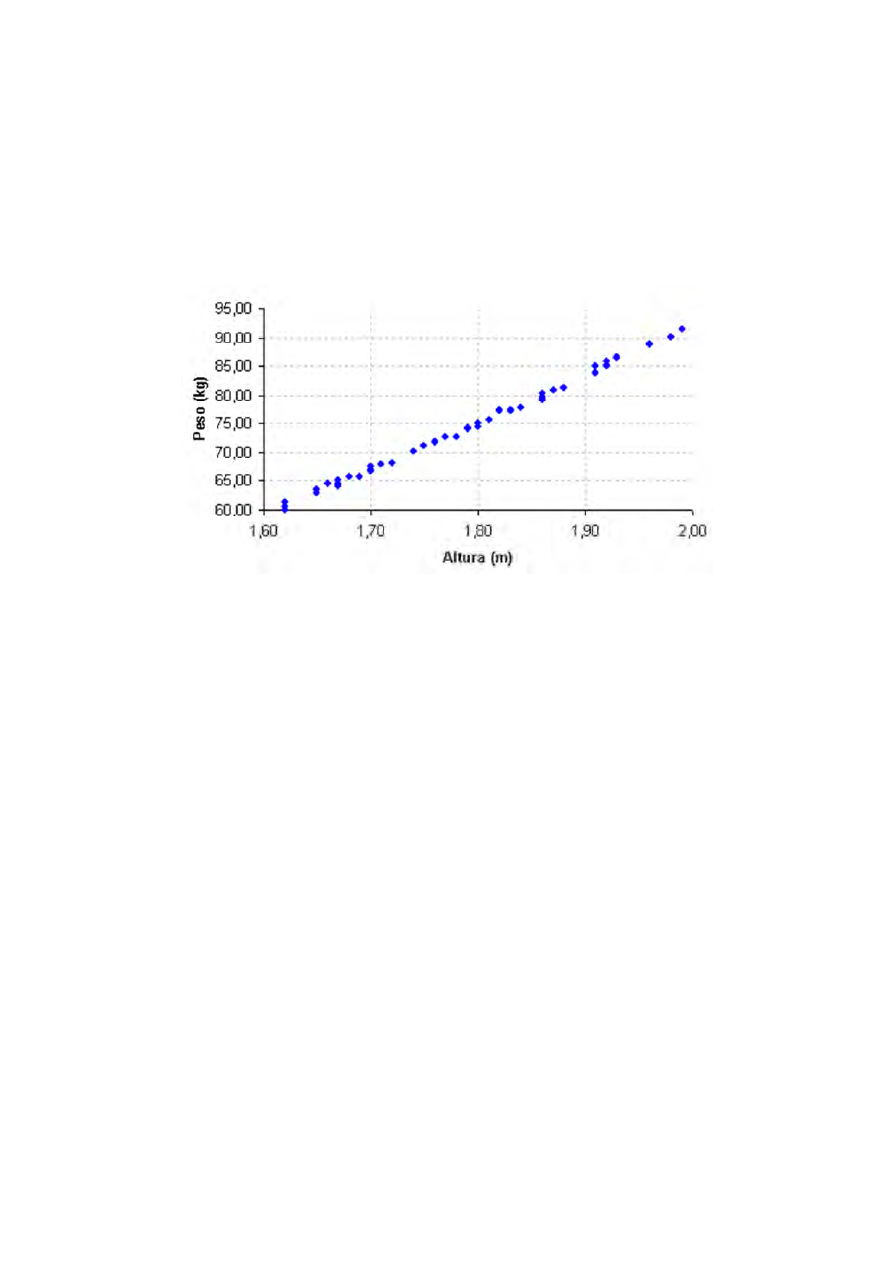
estas variáveis são peso e altura de um grupo de indivíduos adultos. O gráfico
abaixo mostra um conjunto de possíveis valores.
Figura 1 – Diagrama de dispersão peso x altura
Este gráfico acima é chamado de diagrama de dispersão.
Apesar de as variáveis peso e altura, para o grupo pesquisado, não se
comportarem exatamente segundo uma reta, a relação existente é quase uma
reta. Ou seja, é quase linear.
Isto pode ser útil para estimarmos valores. Podemos, sabendo apenas a altura
da pessoa, tentar identificar seu peso (é mais ou menos isso que faremos
quando estudarmos regressão linear).
Neste exemplo ficou extremamente claro que existe uma reta que aproxima
bem a relação entre peso e altura. É que os dados não foram obtidos a partir
de uma pesquisa. Eu construí os dados de forma que ficasse bem evidente a
relação quase linear entre peso e altura.
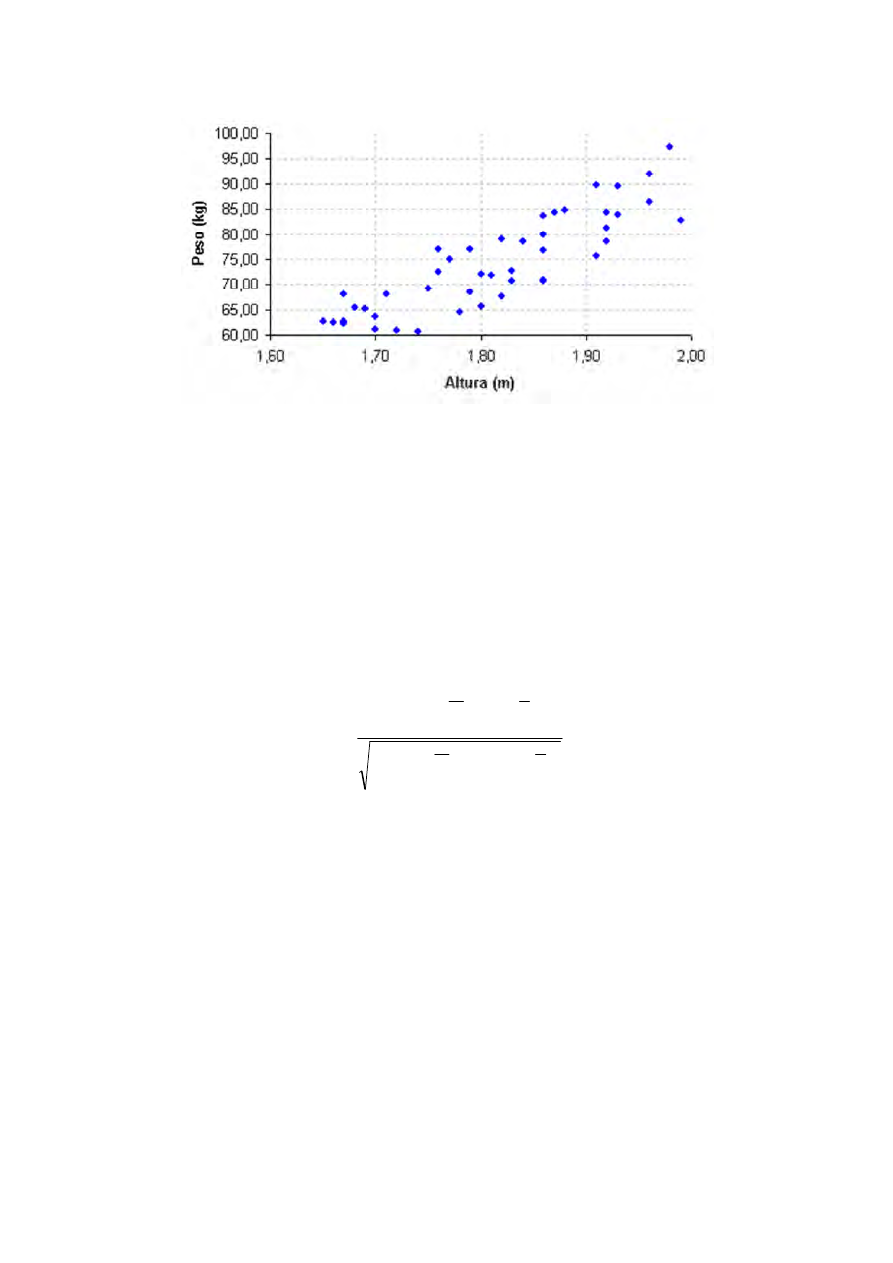
Em situações reais é comum surgirem casos em que a relação linear não é
assim tão evidente. O diagrama de dispersão a seguir ilustra uma situação
assim.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
3
Figura 2 – Diagrama de dispersão peso x altura – relação linear menos
intensa
A Figura 2 representa uma outra população, em que a relação entre os pesos e
as alturas dos indivíduos não segue uma relação linear tão forte quanto na
população representada na Figura 1.
De todo modo, no diagrama acima, ainda fica razoável afirmar que há uma
relação linear entre peso e altura. Mas a relação não é tão próxima assim de
uma reta quanto era no caso da Figura 1.
Pois bem, aí entra o coeficiente de correlação linear. Ele vai nos dar uma
medida do quão forte é a relação linear entre duas variáveis.
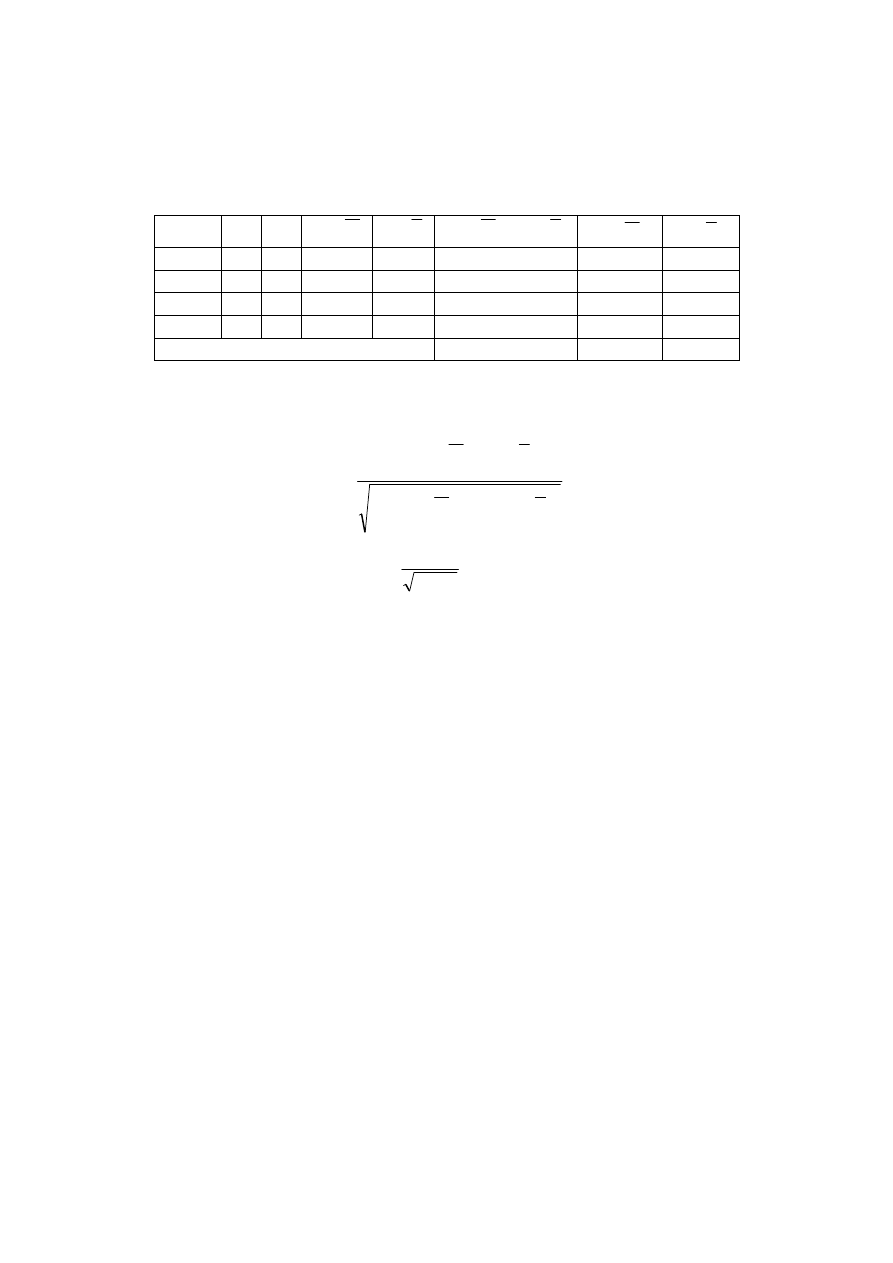
A fórmula do coeficiente de correlação linear é:
(
) (
)
[
]
(
)
(
)
∑
∑
∑
=
=
=
−
×
−
−
×
−
=
n
i
n
i
i
i
n
i
i
i
Y
Y
X
X
Y
Y
X
X
r
1
1
2
2
1
O coeficiente acima é chamado de coeficiente de correlação linear de Pearson.
É possível demonstrar que o coeficiente de correlação assume valores apenas
no intervalo de
1
−
a 1.
1
1
≤
≤
−
r
Quanto mais próximo de zero está o coeficiente de correlação, menor é a
relação linear entre as duas variáveis. Quanto mais afastado de zero está o
coeficiente de correlação, maior é a relação linear entre as duas variáveis.
Alguns comentários importantes.
O fato de o coeficiente de correlação ser próximo de zero não significa que não
exista relação entre duas variáveis. Significa apenas que as duas não têm
relação linear. Pode ser que as variáveis se relacionem de outras maneiras.
Pode ser uma relação quadrática, exponencial, etc.
O fato do coeficiente de correlação ser muito próximo de 1 (ou -1) não
significa que as duas variáveis tenham uma relação de causa e conseqüência.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
4
Não implica que uma delas tenha efeito direto ou indireto sobre a outra. Pode
ser que as duas sofram influência de outras variáveis de maneira que isso dê
origem a uma forte correlação entre ambas.
Outro comentário: o coeficiente de correlação é geralmente calculado a partir
de uma amostra de valores de X e Y. Considere que a amostra tem n pares
ordenados (X, Y). Se a amostra for grande (isto é, se n for grande), então o
coeficiente de correlação deve dar um bom indício do que ocorre na população.
Neste caso, se
0
≅
r
, então é bem possível que não exista relação linear entre
X
e Y.
Se n for grande e
1
≅
r
ou
1
−
≅
r
, novamente temos um forte indício de que há
relação linear perfeita entre X e Y.
Contudo, se a amostra for pequena, ela pode fornecer resultados enganosos.
Basta pensar numa amostra de tamanho 2. Se temos apenas dois pares
ordenados, nosso diagrama de dispersão terá apenas dois pontos. Dois pontos
distintos sempre estão ao longo de uma mesma reta. Neste caso, o coeficiente
de correlação será igual a 1 (ou -1).
Pergunta: neste caso, podemos afirmar, com certeza, que há relação linear
perfeita entre X e Y? Não, não podemos. Nossa amostra é que foi pobre, muito
pequena. É bem possível que nossa amostra esteja fornecendo um resultado
enganoso.
Para os dados da Figura 1, o coeficiente de correlação é 0,998. Como a
quantidade de dados é muito grande, não vou detalhar o cálculo aqui. Apenas
observem que o coeficiente de correlação é muito próximo de 1. Ou seja, a
relação linear é muito forte. Isto já dava pra ver no próprio gráfico. Os pontos
praticamente formavam uma reta.
Vejamos um outro exemplo, com menos números envolvidos.
Um grupo de quatro alunos estudou junto para as provas finais. Feitas as
provas, eles obtiveram se seguintes notas:
Aluno
Nota de
matemática
( )
X
Nota de
física
( )
Y
1
2
6
2
6
7
3
8
7
4
10
8
Média
6,5
7
Calcule o coeficiente de correlação linear entre as notas de física e matemática.
Resolução
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
5
As notas em física e matemática guardam certa relação linear. Vamos calcular
o coeficiente de correlação para vermos a intensidade da relação linear
existente entre elas.
Aluno
X
Y
X
X −
Y
Y −
(
)
×
− X
X
(
)
Y
Y −
(
)
2
X
X −
(
)
2
Y
Y −
1
2
6
-4,5
-1
4,5
20,25
1
2
6
7
-0,5
0
0
0,25
0
3
8
7
1,5
0
0
2,25
0
4
10 8
3,5
1
3,5
12,25
1
TOTAL
8
35
2
Aplicando a fórmula:
(
) (
)
[
]
(
)
(
)
∑
∑
∑
=
=
=
−
×
−
−
×
−
=
n
i
n
i
i
i
n
i
i
i
Y
Y
X
X
Y
Y
X
X
r
1
1
2
2
1
956
,
0
2
35
8
≅
×
=
r
Veja que o coeficiente de correlação é bem próximo de 1. Ou seja, existe
intensa relação linear entre as notas de física e matemática.
Sinal do coeficiente de correlação
Mais alguns comentários sobre o coeficiente de correlação.
O sinal do coeficiente indica se as grandezas possuem uma relação direta ou
inversa. No caso da relação entre peso e altura, vimos que o coeficiente tinha
sinal +. Ou seja, a relação entre peso e altura é direta. Quando a altura
aumenta, o peso tende a aumentar também.
Se o sinal for negativo, as grandezas têm uma relação inversa. Seria o caso da
relação entre o preço de um produto e a sua demanda. Quanto maior o preço,
menor sua demanda. E quanto menor o preço, maior a demanda.
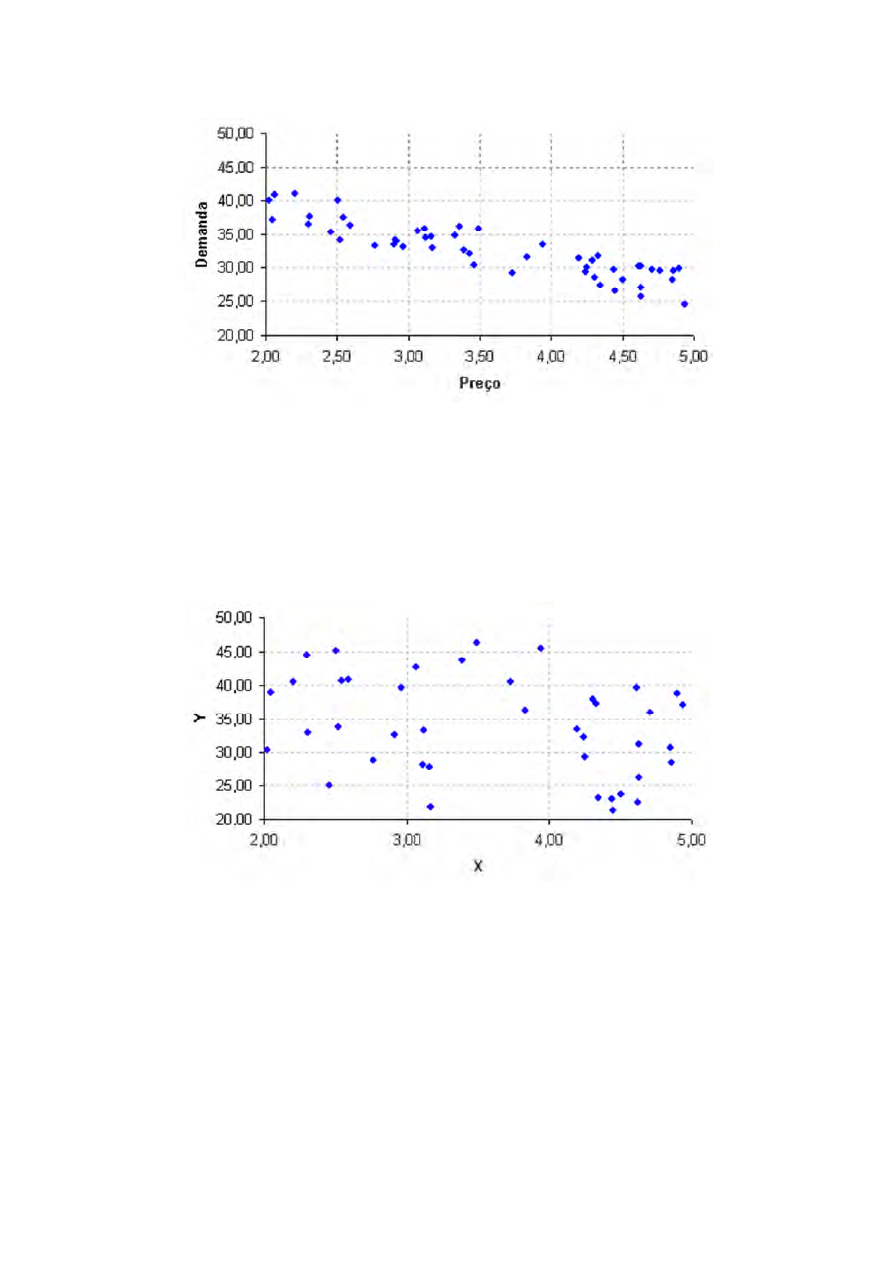
O diagrama abaixo poderia representar duas variáveis com correlação
negativa:
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
6
Figura 3 – Diagrama de dispersão demanda x preço
O preço é dado em R$. A demanda é em milhares de unidades. Quando o
preço está por volta de R$ 2,00, a demanda é em torno de 40.000 unidades.
Quando o preço aumenta, chegando a valores próximos de R$ 5,00, a
demanda cai para cerca de 30.000 unidades.
Quando a correlação é próxima de zero, o diagrama de dispersão não nos
deixa nenhuma dica se a relação é direta ou inversa. Seria o caso do diagrama
abaixo:
Figura 4 – Diagrama de dispersão Y x X – correlação próxima de zero
No diagrama acima ainda é possível notar uma relação inversa (correlação
negativa). Mas bem fraca, quase nula. Novamente, isto não significa que as
variáveis X e Y não tenham relação. Significa apenas que não há relação linear.
Lembrete de Coeficiente de correlação
Mede o quão forte é a relação linear entre duas variáveis.
Quando vale zero: não há relação linear.
Quando vale 1 ou -1: relação linear perfeita.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
7
Fórmula:
(
) (
)
[
]
(
)
(
)
∑
∑
∑
=
=
=
−
×
−
−
×
−
=
n
i
n
i
i
i
n
i
i
i
Y
Y
X
X
Y
Y
X
X
r
1
1
2
2
1
01. (CAPES 2008 CESGRANRIO) Considere as asserções a seguir.
O Coeficiente de Correlação Linear de Pearson é necessariamente um número
no intervalo
)
1
,
1
(
−
.
PORQUE
O Coeficiente de Correlação Linear de Pearson só pode ser calculado para
variáveis quantitativas.
Analisando-se as asserções, conclui-se que
(A) as duas asserções são verdadeiras, e a segunda é uma justificativa correta
da primeira.
(B) as duas asserções são verdadeiras, e a segunda não é uma justificativa
correta da primeira.
(C) a primeira asserção é verdadeira, e a segunda é falsa.
(D) a primeira asserção é falsa, e a segunda é verdadeira.
(E) a primeira e a segunda asserções são falsas.
Resolução
A primeira frase está correta. Como vimos, o coeficiente de correlação sempre
assume valores entre -1 e 1.
A segunda frase também está correta. O coeficiente de correlação depende de
cálculo de somatório, o que só pode ser feito para variáveis quantitativas.
Um frase não justifica a outra. Há diversas grandezas que só podem ser
calculadas para variáveis quantitativas, mas que assumem valores fora do
intervalo entre -1 e 1. Exemplo: a variância só pode ser calculada para
variáveis quantitativas. No entanto, ela pode assumir qualquer valor maior ou
igual a zero.
Letra B
02. (INEP 2008 CESGRANRIO) Considere as afirmações a seguir a respeito do
Coeficiente de Correlação (r) de Pearson entre duas variáveis.
I - Se r = 1, as observações estão todas sobre uma linha reta no diagrama de
dispersão.
II - Se r > 0, a variável independente aumenta quando a variável dependente
aumenta.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
8
III - Se r < 0, a variável independente decresce quando a variável dependente
decresce.
IV - Se r = 0, não existe relação entre as duas variáveis.
São corretas APENAS as afirmações
(A) I e II
(B) I e III
(C) II e III
(D) II e IV
(E) III e IV
Resolução
Item I.
Se
1
=
r
, a relação linear é perfeita e, além disso, as duas variáveis têm relação
direta (quando uma aumenta, a outra aumenta; quando uma diminui, a outra
diminui). Item correto.
Item II.
Se
0
>
r
, a relação entre as variáveis é direta (quando uma aumenta, a outra
aumenta; quando uma diminui, a outra diminui). Item correto.
Item III
Se
0
<
r
, a relação é inversa (quando uma aumenta, a outra diminui). Item
errado.
Item IV.
Se
0
=
r
, temos um forte sinal de que não haja relação linear, o que não
impede que haja outro tipo de relação (exponencial, logarítmica, etc). Item
errado.
Letra A
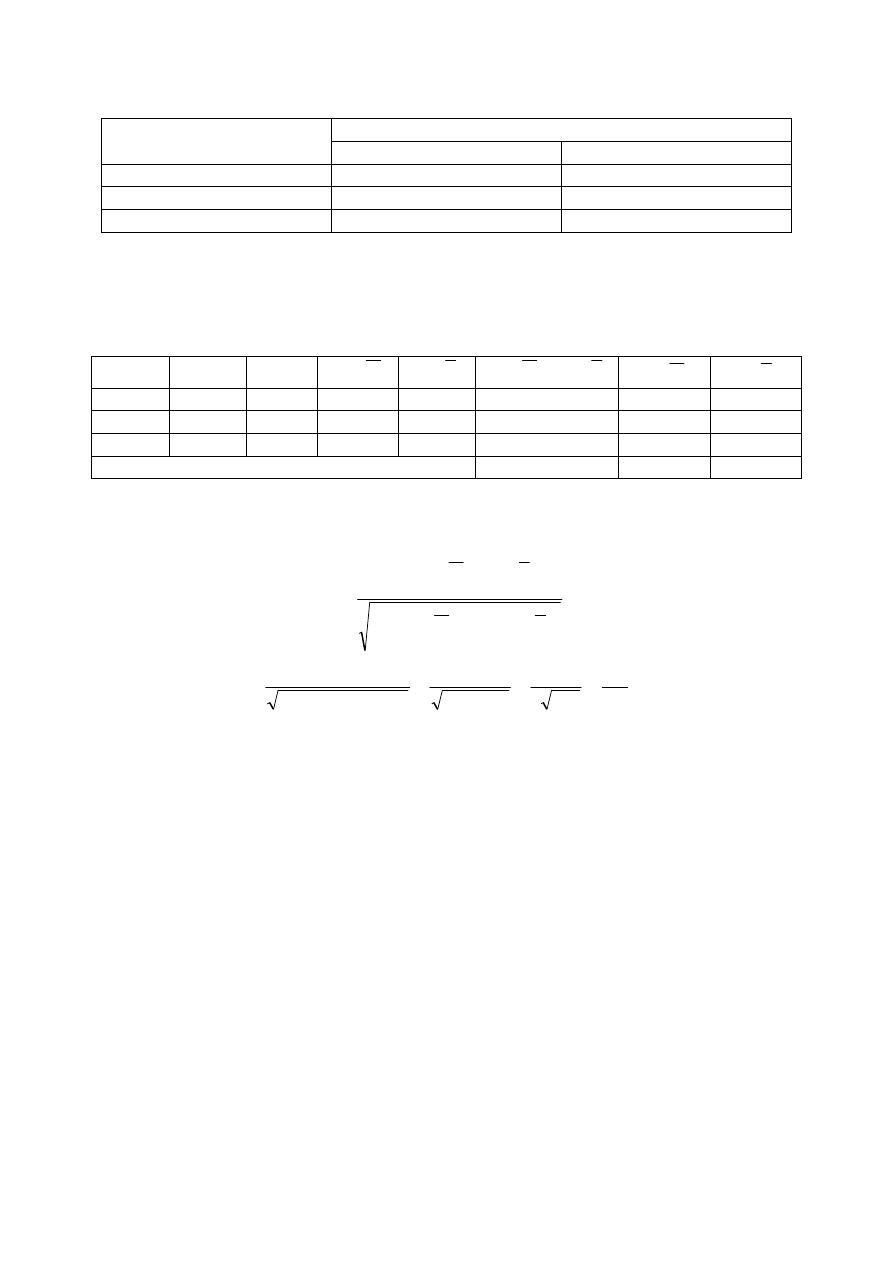
03. (TCU 2008 CESPE-UnB) Uma agência de desenvolvimento urbano divulgou
os dados apresentados na tabela
a seguir, acerca dos números de imóveis ofertados (X) e vendidos (Y) em
determinado município, nos anos de 2005 a 2007.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
9
Ano
Número de imóveis
Ofertados (X)
Vendidos (Y)
2005
1.500
100
2006
1.750
400
2007
2.000
700
Considerando as informações do texto, julgue o item subseqüente.
O coeficiente de correlação linear entre X e Y é inferior a 0,8.
Resolução
Ano
X
Y
X
X −
Y
Y −
(
)
×
− X
X
(
)
Y
Y −
(
)
2
X
X −
(
)
2
Y
Y −
2005
1.500
100
-250
-300
75.000
62.500
90.000
2006
1.750
400
0
0
0
0
0
2007
2.000
700
250
300
75.000
62.500
90.000
TOTAL
150.000
125.000 180.000
A fórmula do coeficiente de correlação é:
(
) (
)
[
]
(
)
(
)
∑
∑
∑
=
=
=
−
×
−
−
×
−
=
n
i
n
i
i
i
n
i
i
i
Y
Y
X
X
Y
Y
X
X
r
1
1
2
2
1
1
150
150
900
5
150
180
125
150
000
.
180
000
.
125
000
.
150
=
=
=
×
=
×
=
r
As contas foram relativamente tranqüilas.
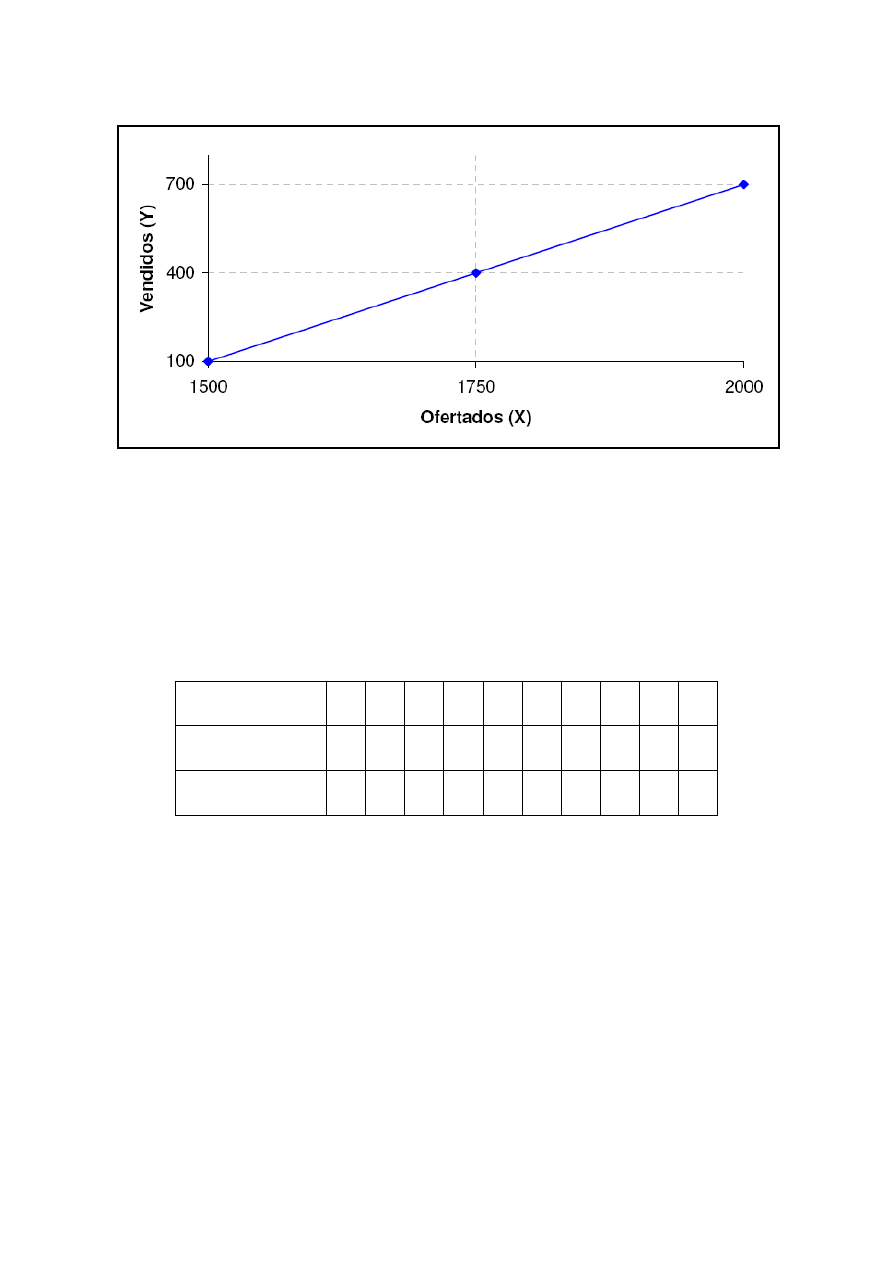
Só um detalhe. Era possível resolver a questão sem fazer contas. Note como
os valores de X e Y estão exatamente ao longo de uma reta. Para cada
variação de 250 em X, temos uma variação de 300 em Y. Ou seja, os três
pares ordenados fornecidos estão ao longo de uma mesma reta. Para deixar
mais claro, segue o gráfico:
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
10
O coeficiente de correlação linear nos dá uma medida de quão forte é a relação
linear entre duas variáveis. Acontece que, para os valores fornecidos, temos
uma relação linear perfeita (é exatamente uma reta). Por isso já dava para
falar que este coeficiente é igual a 1. Portanto, o coeficiente não é inferior a
0,8. Item errado.
04. (AFRF 2005 ESAF) Para uma amostra de dez casais residentes em um
mesmo bairro, registraram-se os seguintes salários mensais (em salários
mínimos):
Identificação
do casal
1
2
3
4
5
6
7
8
9 10
Salário do
marido (Y)
30 25 18 15 20 20 21 20 25 27
Salário da
esposa (X)
20 25 12 10 10 20 18 15 18 23
Sabe-se que:
221
10
1
=
∑
=
i
i
Y
;
5069
10
1
2
=
∑
=
i
i
Y
171
10
1
=
∑
=
i
i
X
;
3171
10
1
2
=
∑
=
i
i
X
3940
10
1
=
∑
=
i
i
i
Y
X
Assinale a opção cujo valor corresponda à correlação entre os salários dos
homens e das mulheres.
a) 0,72
b) 0,75

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
11
c) 0,68
d) 0,81
e) 0,78
Resolução
As médias de X e Y podem ser facilmente calculadas. Basta somar todos os
valores e dividir por 10.
1
,
17
10
171
10
10
1
=
=
=
∑
=
i
i
X
X
(lembre que a soma de todos os valores de X foi fornecida
no enunciado).
Para Y, o cálculo é o mesmo.
1
,
22
10
221
10
10
1
=
=
=
∑
=
i
i
Y
Y
Vamos agora ao cálculo do coeficiente de correlação.
Há duas formas de fazer. A primeira é aplicar a fórmula.
(
) (
)
[
]
(
)
(
)
∑
∑
∑
=
=
=
−
×
−
−
×
−
=
n
i
n
i
i
i
n
i
i
i
Y
Y
X
X
Y
Y
X
X
r
1
1
2
2
1
Detalhamos os cálculos na tabela abaixo:
Casal
X
Y
X
X −
Y
Y −
(
)
×
− X
X
(
)
Y
Y −
(
)
2
X
X −
(
)
2
Y
Y −
1
20 30
2,9
7,9
22,91
8,41
62,41
2
25 25
7,9
2,9
22,91
62,41
8,41
3
12 18
-5,1
-4,1
20,91
26,01
16,81
4
10 15
-7,1
-7,1
50,41
50,41
50,41
5
10 20
-7,1
-2,1
14,91
50,41
4,41
6
20 20
2,9
-2,1
-6,09
8,41
4,41
7
18 21
0,9
-1,1
-0,99
0,81
1,21
8
15 20
-2,1
-2,1
4,41
4,41
4,41
9
18 25
0,9
2,9
2,61
0,81
8,41
10
23 27
5,9
4,9
28,91
34,81
24,01
TOTAL
160,9
246,9 184,9
E o coeficiente de correlação fica:

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
12
(
) (
)
[
]
(
)
(
)
75
,
0
9
,
184
9
,
246
9
,
160
1
1
2
2
1
≅
×
=
−
×
−
−
×
−
=
∑
∑
∑
=
=
=
n
i
n
i
i
i
n
i
i
i
Y
Y
X
X
Y
Y
X
X
r
Além da infinidade de contas, ainda chegamos ao final com uma raiz quadrada.
O problema desta resolução é que demora um tempão. Especialmente sem
calculadora. Tivemos que calcular cada valor de
X
X −
, de
(
)
Y
Y −
, de
(
)
2
X
X −
,
de
(
)
2
Y
Y −
, depois ainda fazer algumas multiplicações e somas.
O ideal é tentar utilizar as informações dadas no exercício. O exercício seria
bastante interessante se, com as informações utilizadas, as contas fossem
diminuídas. Não é exatamente o que ocorre.
Vamos a uma solução alternativa, para utilizar as informações sobre os valores
dos somatórios fornecidos.
Para tanto, é necessário conhecer algumas igualdades envolvendo somatório.
Transformações importantes:
(
) (
)
[
]
(
)
Y
X
n
Y
X
Y
Y
X
X
n
i
i
i
n
i
i
i
−
×
=
−
×
−
∑
∑
=
=
1
1
(
)
( )
2
1
2
1
2
X
n
X
X
X
n
i
i
n
i
i
−
=
−
∑
∑
=
=
(
)
( )
2
1
2
1
2
Y
n
Y
Y
Y
n
i
i
n
i
i
−
=
−
∑
∑
=
=
Repare que todas as igualdades são bem parecidas. Se você gravar a primeira,
pode facilmente chegar nas outras duas. Basta fazer o caso em que Y = X.
A primeira igualdade é:
(
) (
)
[
]
(
)
Y
X
n
Y
X
Y
Y
X
X
n
i
i
i
n
i
i
i
−
×
=
−
×
−
∑
∑
=
=
1
1
Substituindo os valores da média de X e da média de Y:
(
) (
)
[
]
(
)
1
,
22
1
,
17
1
1
×
×
−
×
=
−
×
−
∑
∑
=
=
n
Y
X
Y
Y
X
X
n
i
i
i
n
i
i
i
Substituindo os valores informados no enunciado:
(
) (
)
[
]
9
,
160
171
1
,
22
10
3940
1
=
×
×
−
=
−
×
−
∑
=
n
i
i
i
Y
Y
X
X
A segunda igualdade é:
(
)
( )
2
1
2
1
2
X
n
X
X
X
n
i
i
n
i
i
−
=
−
∑
∑
=
=

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
13
Substituindo os valores do enunciado:
(
)
9
,
246
1
,
17
10
3171
2
1
2
=
×
−
=
−
∑
=
n
i
i
X
X
A terceira igualdade é:
(
)
( )
2
1
2
1
2
Y
n
Y
Y
Y
n
i
i
n
i
i
−
=
−
∑
∑
=
=
Portanto:
(
)
9
,
184
1
,
22
10
5069
2
1
2
=
×
−
=
−
∑
=
n
i
i
Y
Y
Até aqui, até que não deu tanta conta.
O problema é que, mesmo a pessoa conhecendo estas igualdades, ainda chega
ao final com a seguinte conta:
(
) (
)
[
]
(
)
(
)
75
,
0
9
,
184
9
,
246
9
,
160
1
1
2
2
1
≅
×
=
−
×
−
−
×
−
=
∑
∑
∑
=
=
=
n
i
n
i
i
i
n
i
i
i
Y
Y
X
X
Y
Y
X
X
r
Está aí novamente a tal da raiz quadrada. Ou seja, as contas nem ficaram tão
fáceis assim...
Agora uma dica de contas. Extrair a raiz quadra é meio trabalhoso. Eu,
particularmente, procuro evitar.
Então, em vez de calcular o coeficiente de correlação, eu calcularia o quadrado
do coeficiente de correlação:
9
,
184
9
,
246
9
,
160
2
2
×
=
r
Mas esta conta ainda é meio ruim de fazer. Aproximando os valores:
567
,
0
695
.
45
921
.
25
185
247
161
9
,
184
9
,
246
9
,
160
2
2
2
=
=
×
≅
×
=
r
Feito isto, eu testaria as alternativas.
0,72
2
=0,5184 (deu menor que 0,567)
0,75
2
=0,5625 (deu bem próximo de 0,567)
0,68
2
é menor que 0,49
0,78
2
=0,6084
0,81
2
é maior que 0,60.
E marcaria a letra B.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
14
Outra maneira é usar a aproximação da raiz quadrada (acesse o link
http://www.pontodosconcursos.com.br/admin/imagens/upload/4950_D.pdf
) .
Ficaria assim:
·
quadrado perfeito mais próximo: 0,49
·
aproximação da raiz:
755
,
0
4
,
1
057
,
1
49
,
0
2
567
,
0
49
,
0
567
,
0
=
=
×
+
≅
Ao meu ver, o grande problema desta questão é que, mesmo a pessoa tendo
conseguido manipular bem os somatórios (o que já é um sinal de que o
candidato estava muito bem preparado), as contas ainda são muito
trabalhosas. Eu achei a questão um despropósito... Seu eu tivesse feito esse
concurso do AFRF, sinceramente, teria pulado esta questão.
Então resumindo: além da fórmula usual do coeficiente de correlação, há
exercícios que são muito facilitados se você souber as igualdades do quadro 1.
Infelizmente, neste exercício do AFRF 2005, a questão não se limitou a cobrar
tais igualdades. Ainda exigiu um esforço “braçal”, envolvendo muitas contas.
05. (Instituto de Gestão Previdenciária do Estado do Pará – 2005 CESPE-UnB)
Considere que r(x,y) seja o coeficiente de correlação entre duas variáveis
aleatórias x e y. Nesse caso, se ‘a’ e ‘b’ são dois números reais, então o
coeficiente de correlação r(ax, by) é igual a:
a)
)
,
(
y
x
r
ab ×
b)
)
,
(
2
2
y
x
r
b
a
×
c)
)
,
(
y
x
r
, se
0
>
ab
d)
)
,
(
y
x
r
b
a
ab
×
+
e)
ab
y
x
r
)
,
(
Resolução
Vou fazer um resuminho de uma propriedade que ainda não falei.
Seja r o coeficiente de correlação entre X e Y.
Se multiplicarmos cada uma destas variáveis por duas constantes a e b, o
novo coeficiente
'
r
é dado por:
r
r =
'
, se
0
>
ab
r
r
−
=
'
, se
0
<
ab
Se somarmos (ou subtrairmos), a cada uma destas variáveis, uma constante,
o coeficiente de correlação fica inalterado.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
15
Letra C
06. (CAPES 2008 CESGRANRIO)
Se as variáveis
Y
e
1
X forem transformadas, respectivamente, para
5
,
0
2
1
+
−
=
Y
Y
e
5
,
0
'
1
1
+
−
= X
X
, o coeficiente de correlação entre
1
Y e
'
1
X
(A) 0,382
(B) 0,059
(C) - 0,059
(D) - 0,118
(E) - 0,382
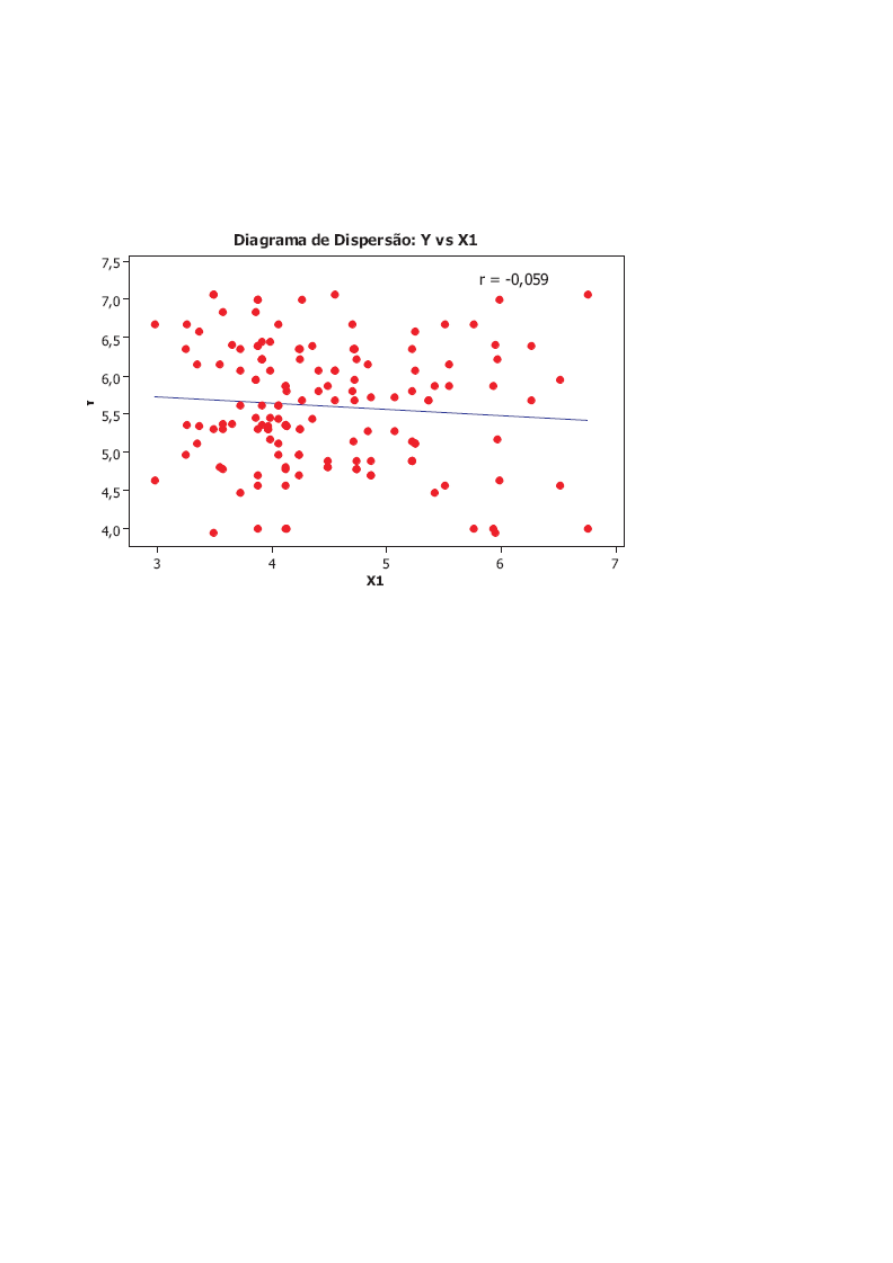
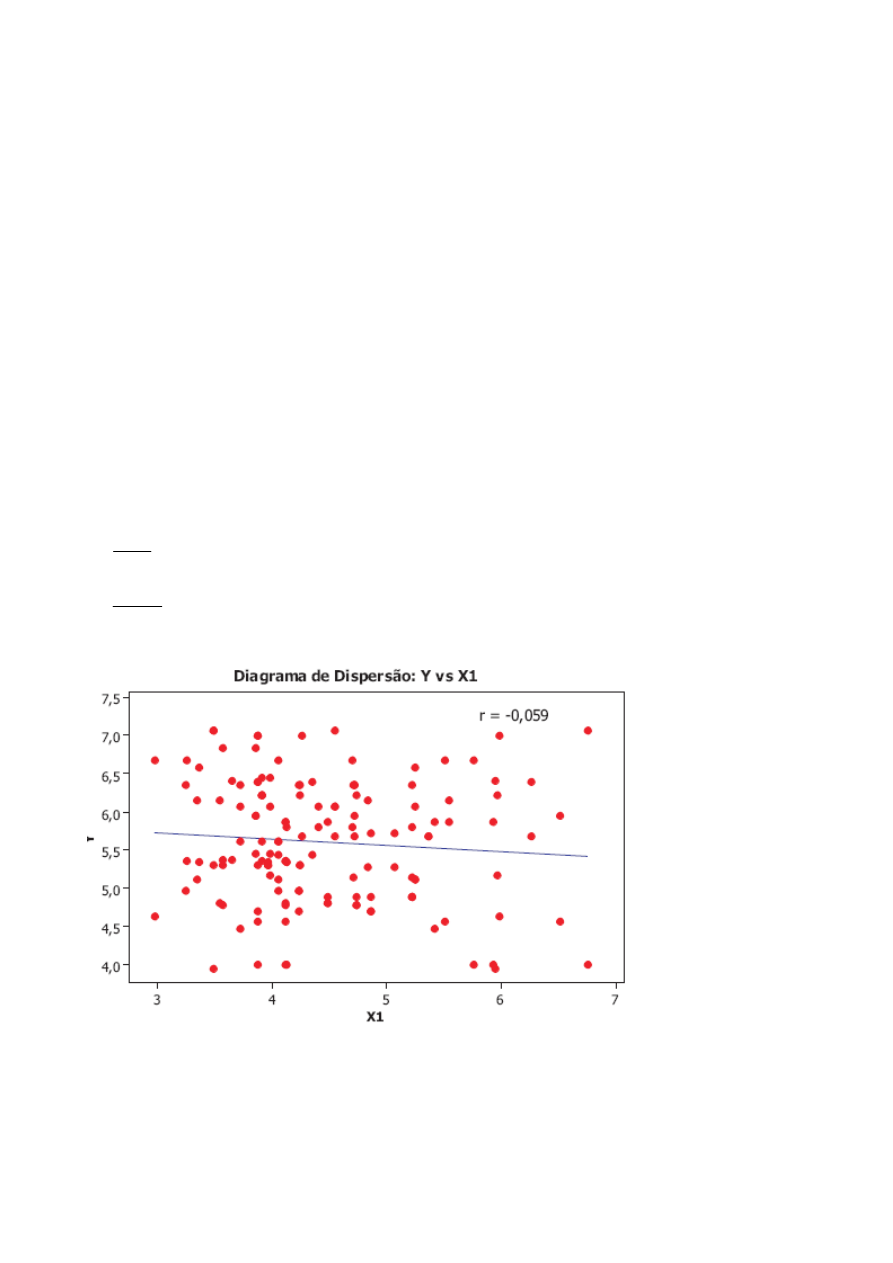
Resolução.
O coeficiente de correlação entre
Y
e
1
X é de
059
,
0
−
(ver figura). A partir
destas variáveis, criamos outras, por meio de uma multiplicação e uma soma.
As somas não interferem no coeficiente de correlação. As multiplicações podem
interferir no sinal do coeficiente de correlação. As multiplicações foram feitas
por
2
−
e
1
−
. As duas constantes têm o mesmo sinal. Com isso, o coeficiente
de correlação permanece igual ao da situação inicial.
059
,
0
'
−
=
= r
r
Letra C

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
16
07. (MP RO 2005 CESGRANRIO) Analise as afirmativas a seguir, a respeito do
coeficiente de correlação linear de Pearson entre duas variáveis positivas X e
Y
:
I - é positivo;
II - não se altera quando adicionamos uma constante positiva aos valores de
X
;
III - não se altera quando multiplicamos por uma constante positiva os valores
de X.
Está(ão) correta(s) a(s) afirmativa(s):
(A) II somente.
(B) I e II somente.
(C) I e III somente.
(D) II e III somente.
(E) I, II e III.
Resolução.
O sinal do coeficiente de correlação depende da relação existente entre as
variáveis (direta ou inversa). Se for uma relação direta, o sinal é positivo. Se
for uma relação inversa, o sinal é negativo.
O primeiro item está errado.
Somas e subtrações não interferem no coeficiente de correlação. O segundo
item está certo.
Se multiplicarmos X por uma constante positiva k, e não alterarmos Y (o que
equivale a multiplicar por 1), então as duas constantes envolvidas (k e 1) têm
o mesmo sinal. O coeficiente de correlação não se altera. O terceiro item está
certo.
Letra D
08. (Petrobrás 2004 CESPE-UnB) Julgue o item que segue:
O coeficiente de correlação de Pearson é usado para medir o grau de
linearidade (associação) entre duas variáveis (eventos), podendo assumir
qualquer valor entre +1 e –1. Os valores de coeficientes iguais a +1 e -1
indicam, respectivamente, relação linear perfeita e ausência total de relação
linear entre as variáveis.
Resolução

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
17
Questão errada. O coeficiente igual a -1 indica também uma relação linear
perfeita. Só que a reta que representa a função entre as duas variáveis é
decrescente.
Quando o coeficiente de correlação assume o valor zero é que temos um
indicativo de ausência total de relação linear.
Gabarito: ERRADO
09. (Prefeitura de Rio Branco CESPE-UnB) A análise de regressão linear
simples e a análise de correlação são técnicas freqüentemente usadas na
interpretação de pares de dados. Com relação a essas técnicas, julgue o item a
seguir.
O coeficiente de correlação mede o grau de associação entre duas variáveis.
Resolução
O coeficiente de correlação mede o grau de relação linear entre duas variáveis.
O exercício está chamando essa relação linear de associação. O item está
certo.
REGRESSÃO LINEAR
Na correlação linear, estávamos interessados em ver se duas variáveis X e Y
tinham uma relação linear forte ou não.
Pois bem, considerem que X e Y tenham uma relação linear forte. Ou seja, a
relação entre ambas é quase uma reta. Neste caso, que reta seria essa? Qual a
reta que melhor descreve a relação linear entre X e Y?
É justamente isso que a regressão linear vai nos dizer.
1.
Cálculo da reta de regressão
Sejam X e Y duas variáveis. Um modelo de regressão linear que as relaciona é
da seguinte forma:
i
i
i
X
Y
ε
β
α
+
+
=
Neste modelo,
α
e β são constantes e
ε
é uma
variável aleatória de média
zero
.
Um método para encontrar a melhor reta de regressão é chamado de métodos
de mínimos quadrados. A função de primeiro grau que pretendemos encontrar
é da forma:
i
i
bX
a
Y
+
=
ˆ
Onde a é uma estimativa de
α
, b é uma estimativa de β e
Yˆ
é uma
estimativa de
Y
.
À diferença entre Y e sua estimativa, chamamos desvio. O desvio é dado por:

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
18
Y
Y
e
ˆ
−
=
Pelo método de mínimos quadrados, tentamos obter uma reta de tal modo que
a soma dos quadrados dos valores de e (desvio) seja mínima.
É possível demonstrar que os valores de a e b (estimadores de
α
e β ),
obtidos a partir da consideração de que a soma dos quadrados dos desvios
seja mínima, são:
(
) (
)
[
]
(
)
2
∑
∑
−
−
×
−
=
X
X
Y
Y
X
X
b
i
i
i
X
b
Y
a
−
=
Ou seja, a partir dos valores de X e Y pertencentes à amostra, obtemos os
valores de a e b descritos acima. A partir deles, construímos a reta
i
i
bX
a
Y
+
=
ˆ
.
O modelo de regressão linear faz algumas considerações. São elas:
·
0
)
(
=
i
E
ε
·
2
)
(
σ
ε
=
i
V
·
0
)
,
cov(
=
j
i
ε
ε
, para
j
i ≠
Na primeira consideração, temos que o erro (variável aleatória
ε
) tem média
zero. Esta condição é um pouco mais fácil de entender.
Basta imaginar a situação em que a variável erro não tem média zero.
Significa que já se espera que, em média, se cometa um erro diferente de
zero. Já se sabe que a regressão tem um viés (que pode ser positivo ou
negativo). Ou seja, o modelo não está muito adequado. É melhor reformular o
modelo.
A segunda consideração nos diz que a variância do erro é constante. Este fato
é denominado homocedasticia.
A terceira condição nos diz que os erros cometidos não são correlacionados.
Não se preocupe muito com estas hipóteses!!
Nosso trabalho é só aplicar as fórmulas para achar a e b . Só as mencionei
porque, se a questão falar qualquer coisa a respeito, aí vocês não precisam
ficar preocupados, achando que é uma “coisa de outro mundo”. É só calcular
normalmente os coeficientes a e b, e pronto.
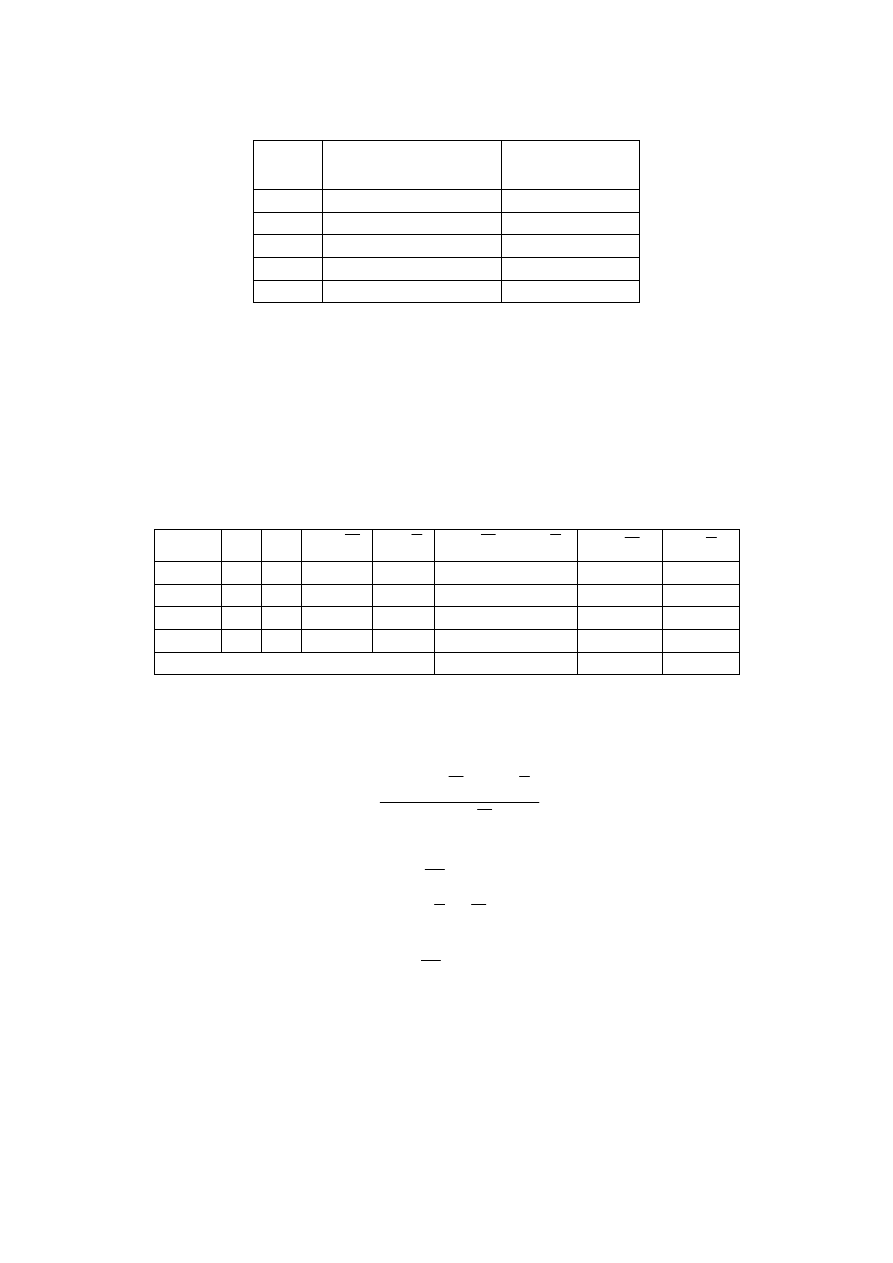
Para praticar, vamos calcular a reta de regressão para o caso dos quatro
alunos que fizeram as provas de física e matemática. Vamos considerar que
estes 4 alunos são uma amostra de um conjunto maior de estudantes que se
submeteram à tal prova.
As notas desses alunos são:
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
19
Aluno
Nota de
matemática
( )
X
Nota de
física
( )
Y
1
2
6
2
6
7
3
8
7
4
10
8
Média
6,5
7
Estamos supondo que a população de notas de física da qual foram tiradas as
notas acima pode ser descrita segundo o seguinte modelo:
i
i
i
X
Y
ε
β
α
+
+
=
Ou seja, estamos supondo que existe uma relação entre as notas de
matemática e física. A parcela
ε
é um erro aleatório. Engloba todas outras
variáveis (distintas da nota em matemática) que influenciam na nota de física.
A partir destes valores de notas, construímos o quadro abaixo:
Aluno
X
Y
X
X −
Y
Y −
(
)
×
− X
X
(
)
Y
Y −
(
)
2
X
X −
(
)
2
Y
Y −
1
2
6
-4,5
-1
4,5
20,25
1
2
6
7
-0,5
0
0
0,25
0
3
8
7
1,5
0
0
2,25
0
4
10 8
3,5
1
3,5
12,25
1
TOTAL
8
35
2
Vamos calcular os coeficientes a e b .
(
) (
)
[
]
(
)
2
∑
∑
−
−
×
−
=
X
X
Y
Y
X
X
b
i
i
i
23
,
0
35
8
≅
=
b
X
b
Y
a
−
=
51
,
5
5
,
6
35
8
7
≅
×
−
=
a
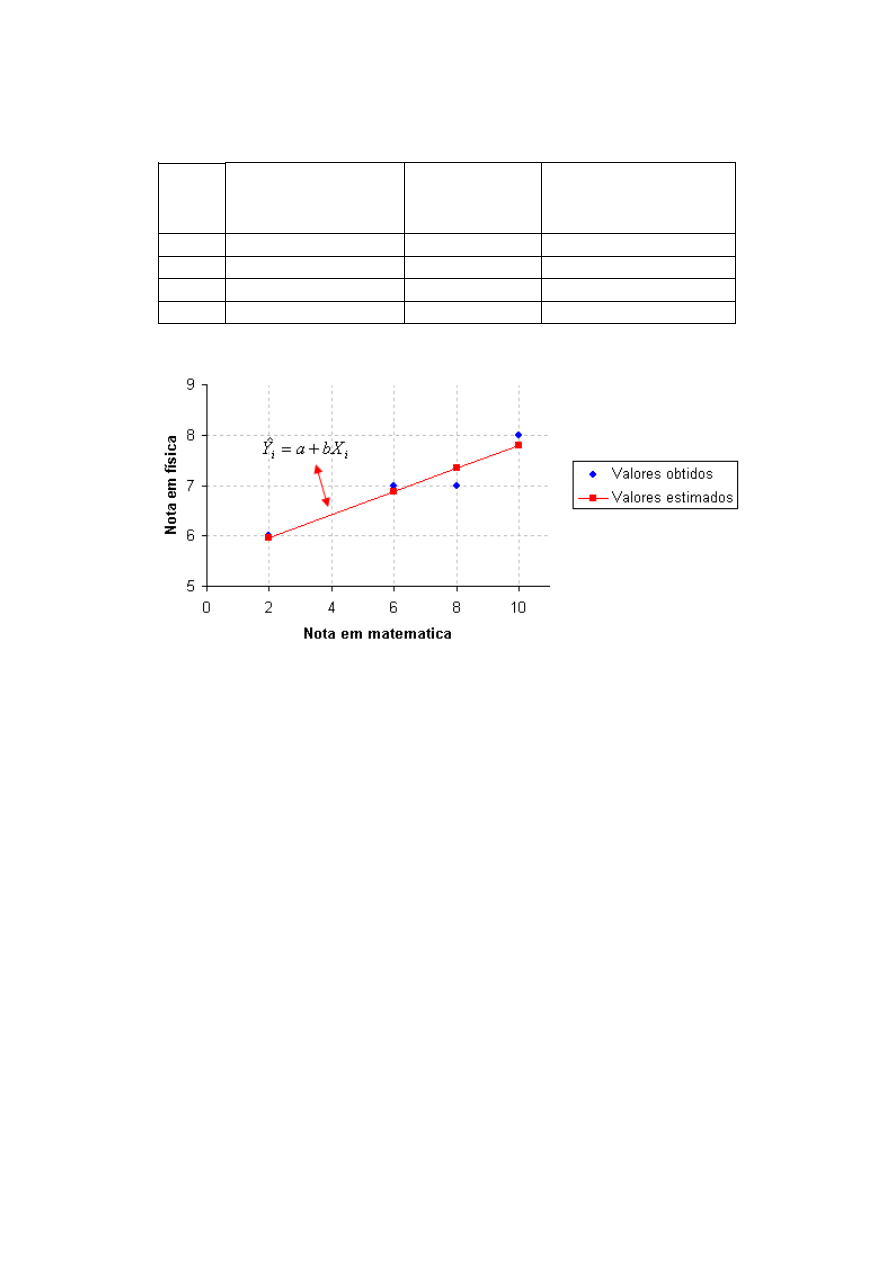
E a reta de regressão estimada (“calculada”) fica:
X
Y
23
,
0
51
,
5
ˆ
+
=
Repare que não sabemos se esta é a real reta de regressão. Mas, a partir dos
valores de nossa amostra, esta é a nossa estimativa para a reta de regressão.
É uma reta tal que a soma dos quadrados dos desvios é mínima. Lembrando
que o desvio corresponde à diferença entre valor observado (
Y
) e sua
estimativa (
Yˆ
).
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
20
A tabela abaixo mostra os valores estimados da nota de física, dados os
valores da nota de matemática.
Aluno
Nota de
matemática
( )
X
Nota de
física
observada
( )
Y
Nota de física
estimada
( )
Yˆ
1
2
6
5,97
2
6
7
6,89
3
8
7
7,34
4
10
8
7,80
Plotando estes valores num gráfico, ficamos com:
Reta de regressão estimada
A reta em vermelho é tal que a soma dos quadrados dos desvios em relação às
notas de física realmente obtidas é mínima. É a nossa reta estimada
(“calculada”).
O modelo de regressão é:
i
i
i
X
Y
ε
β
α
+
+
=
Como não temos acesso à população inteira, não sabemos quais os valores de
α
e β . Temos condições apenas de estimá-los (obtendo a e b )
Com isso, a reta de regressão estimada é:
i
i
bX
a
Y
+
=
ˆ
Ou seja, a e b são estimadores para
α
e β . São estimadores não viciados.
Isto porque, obedecidas algumas condições (aquelas que indicamos
anteriormente:
0
)
(
=
i
E
ε
;
2
)
(
σ
ε
=
i
V
e
0
)
,
cov(
=
j
i
ε
ε
, para
j
i ≠
), é possível
demonstrar que:
β
=
)
(b
E
e
α
=
)
(a
E

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
21
Nos cálculos envolvidos com a regressão linear, utilizaremos algumas
transformações com uma certa freqüência. São elas:
·
(
)(
)
[
]
Y
X
n
Y
X
Y
Y
X
X
i
i
i
i
−
=
−
−
∑
∑
·
(
)
∑
∑
−
=
−
2
2
2
X
n
X
X
X
i
i
São as mesmas transformações que fizemos no início da aula.
10. (PETROBRAS 2008/2 CESGRANRIO) Na estimativa de uma regressão
linear, o problema da heterocedasticidade ocorre quando
(A) os dados são transversais.
(B) há autorrelação dos resíduos.
(C) há correlação positiva entre as variáveis independentes.
(D) a variância dos erros não é constante.
(E) as variáveis independentes são negativas.
Resolução
Vimos que uma das hipóteses do modelo é que a variância dos erros seja
constante (homocedasticia). Se a variância dos erros não é constante, temos a
heterocedasticidade.
Letra D
11. (BACEN – 2006 FCC) Uma empresa, com finalidade de determinar a
relação entre gastos anuais com propaganda (X), em R$ 1.000,00 e o lucro
bruto anual (Y), em R$ 1.000,00, optou por utilizar o modelo linear simples
i
i
i
X
Y
ε
β
α
+
+
=
, em que
i
Y é o valor do lucro bruto auferido no ano i e
i
ε
o
erro aleatório com as respectivas hipóteses consideradas para a regressão
linear simples (
α
e β são parâmetros desconhecidos). Considerou, para o
estudo, as seguintes informações referentes às observações nos últimos 10
anos da empresa:
100
10
1
=
∑
=
i
i
Y
;
60
10
1
=
∑
=
i
i
X
;
650
=
×
∑
i
i
Y
X
;
( )
400
10
1
2
=
∑
=
i
i
X
;
( )
1080
10
1
2
=
∑
=
i
i
Y
Utilizando a equação da reta obtida pelo método dos mínimos quadrados, tem-
se que, caso haja um gasto anual com propaganda de 80 mil reais, a previsão
do lucro bruto anual, em mil reais, será de:
a) 84
b) 102,5

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
22
c) 121
d) 128,4
e) 158
Resolução
As hipóteses que o enunciado disse que foram obedecidas são aquelas que
indicamos anteriormente -
0
)
(
=
i
E
ε
;
2
)
(
σ
ε
=
i
V
e
0
)
,
cov(
=
j
i
ε
ε
, para
j
i ≠
.
Para calcular a previsão, precisamos encontrar os valores de a e b do modelo
de regressão.
(
) (
)
[
]
(
)
2
∑
∑
−
−
×
−
=
X
X
Y
Y
X
X
b
i
i
i
(
)
( )
2
2
X
n
X
Y
X
n
Y
X
b
i
i
i
−
−
=
∑
∑
2
6
10
400
10
6
10
650
×
−
×
×
−
=
b
25
,
1
40
50
360
400
600
650
=
=
−
−
=
b
E o valor de a fica:
X
b
Y
a
−
=
5
,
2
5
,
7
10
10
60
25
,
1
10
100
=
−
=
×
−
=
a
Portanto, o modelo de regressão é:
i
i
bX
a
Y
+
=
ˆ
i
i
X
Y
25
,
1
5
,
2
ˆ
+
=
Quando
80
=
i
X
, a estimativa do lucro bruto fica:
5
,
102
80
25
,
1
5
,
2
ˆ
=
×
+
=
i
Y
Letra B
12. (SEFAZ SP 2006 FCC) Em um determinado país, deseja-se determinar a
relação entre a renda disponível (Y), em bilhões de dólares, e o consumo (C),
também em bilhões de dólares. Foi utilizado o modelo linear simples
i
i
i
Y
C
ε
β
α
+
+
=
, em que C
i
é o consumo no ano i, Y
i
é o valor da renda
disponível no ano i e
i
ε
o erro aleatório com as respectivas hipóteses para a

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
23
regressão linear simples,
α
e β são parâmetros desconhecidos, cujas
estimativas foram obtidas através do método dos mínimos quadrados. Para
obtenção desta relação considerou-se ainda as seguintes informações colhidas
através da observação nos últimos 10 anos:
∑
=
=
10
1
90
i
i
C
,
∑
=
=
10
1
100
i
i
Y
,
∑
=
=
10
1
100
.
1
i
i
i
C
Y
,
∑
=
=
10
1
2
250
.
1
i
i
Y
,
∑
=
=
10
1
2
010
.
1
i
i
C
Para o cálculo do coeficiente de correlação de Pearson (r), usou-se a fórmula:
)
(
)
(
)
,
cov(
C
DP
y
DP
C
Y
r
×
=
em que
)
,
cov(
C
Y
é a covariância entre Y e C,
)
(Y
DP
é o desvio
padrão de Y e
)
(C
DP
é o desvio padrão de C.
Então:
a) obtendo para um determinado ano uma previsão para o consumo de 10
bilhões de dólares, significa que a renda disponível considerada foi de 12,5
bilhões de dólares.
b) o valor da estimativa encontrado para o parâmetro β é igual a 0,4
c) o valor da estimativa encontrado para o parâmetro
α
é igual a 10.
d) o coeficiente de explicação r
2
correspondente é 64%.
e) utilizando a equação da reta obtida pelo método dos mínimos quadrados,
tem-se que, em um ano, caso a renda disponível seja igual a 15 bilhões de
dólares, o consumo será igual a 13 bilhões de dólares.
Resolução
Vamos encontrar os valores de a e b.
(
) (
)
[
]
(
)
2
∑
∑
−
−
×
−
=
X
X
Y
Y
X
X
b
i
i
i
(
)
( )
2
2
X
n
X
Y
X
n
Y
X
b
i
i
i
−
−
=
∑
∑
Só que aqui, no lugar de X temos Y. E no lugar de Y temos C.
(
)
( )
2
2
Y
n
Y
Y
C
n
C
Y
b
i
i
i
−
−
=
∑
∑
8
,
0
250
200
10
10
250
.
1
10
9
10
100
.
1
2
=
=
×
−
×
×
−
=
b
Assim, a estimativa para o parâmetro β é igual a 0,8. A letra B está errada.
X
b
Y
a
−
=
Só que aqui, em vez de X temos Y e em vez de Y temos C.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
24
Y
b
C
a
−
=
1
10
8
,
0
9
=
×
−
=
a
A estimativa do parâmetro
α
é igual a 1. A letra C está errada.
Se para um determinado ano a previsão de consumo for de 10 bilhões, então a
renda considerada foi:
bY
a
C
+
=
Y
8
,
0
1
10
+
=
(
)
25
,
11
8
,
0
1
10
=
−
=
Y
A letra A também está errada.
Caso a renda disponível seja de 15 bilhões, o consumo será:
bY
a
C
+
=
13
15
8
,
0
1
=
×
+
=
C
A letra E está correta.
Letra E
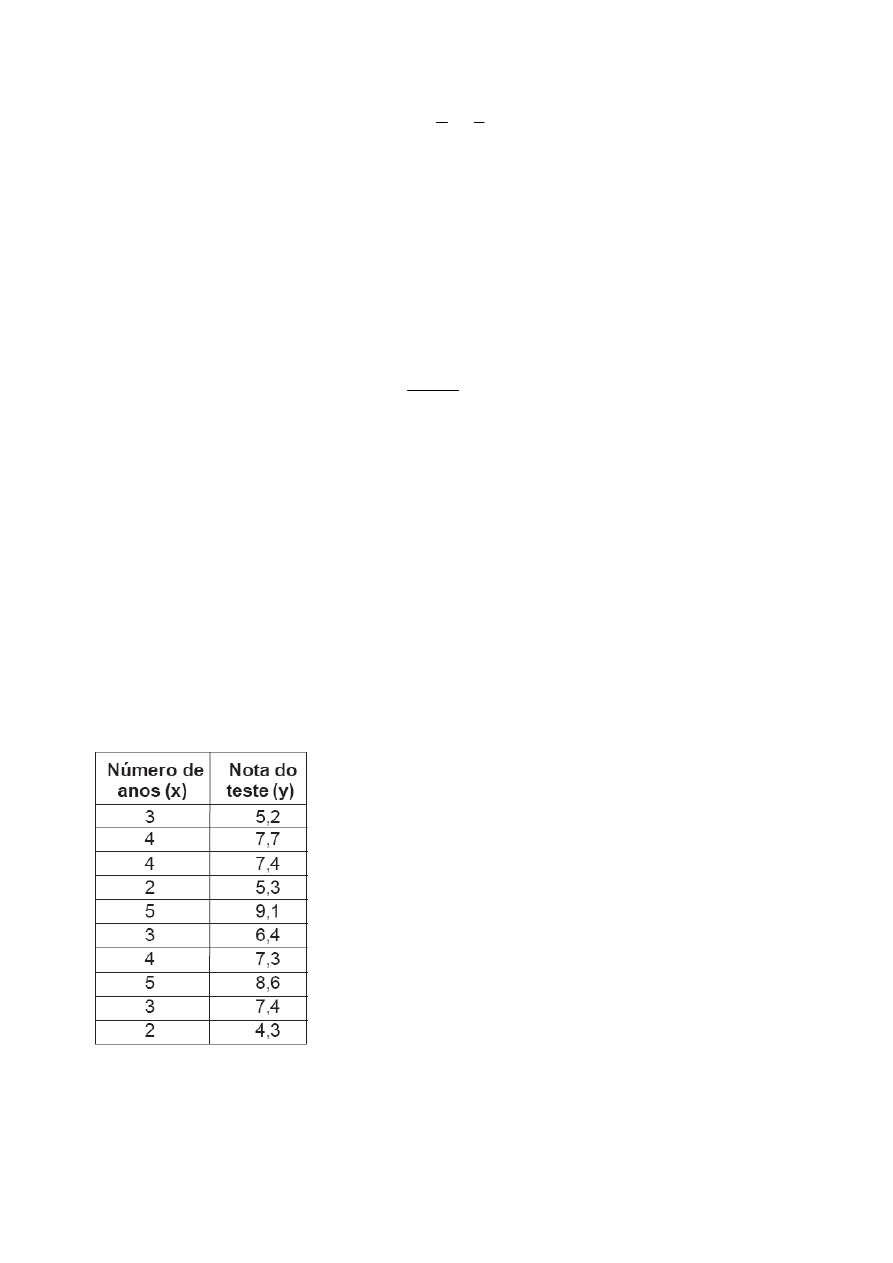
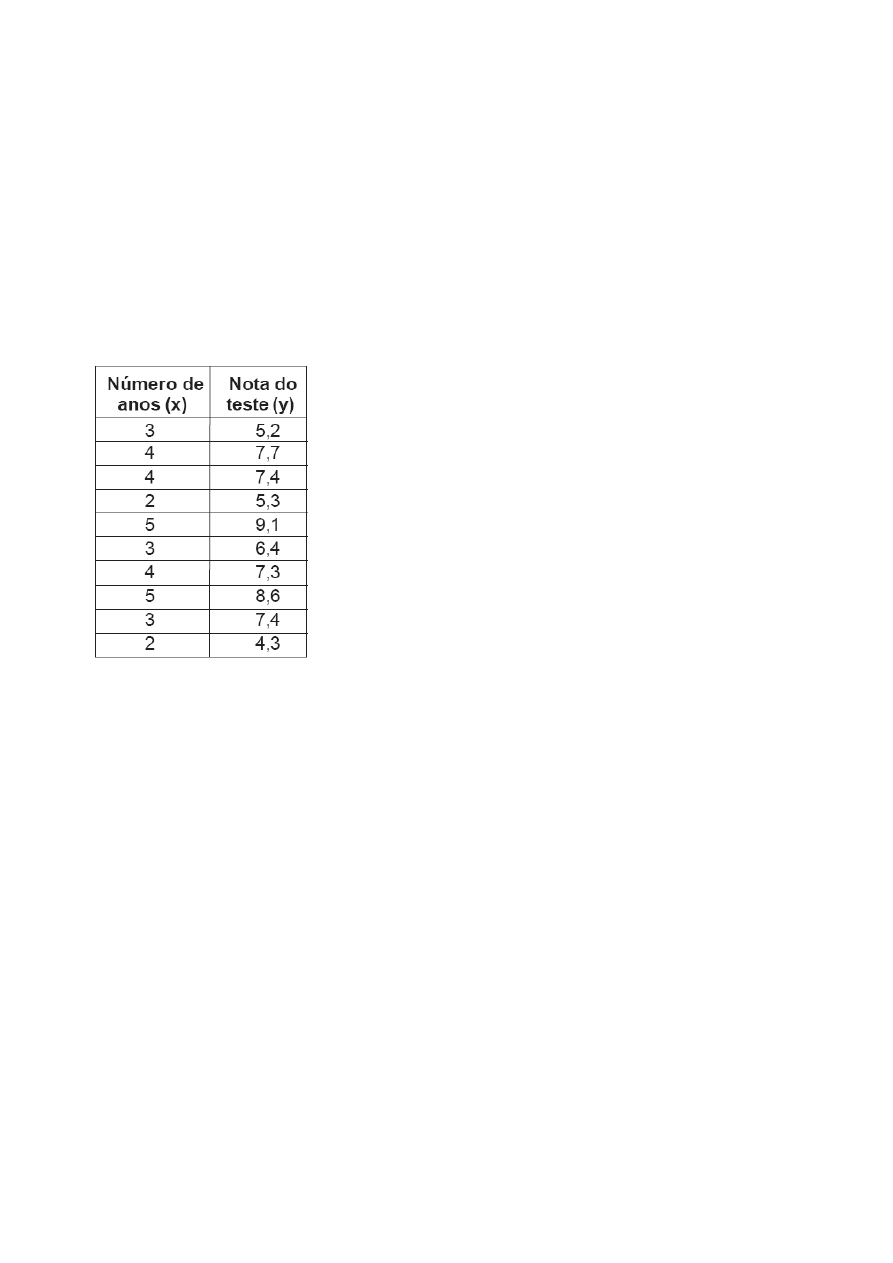
13. (MP RO 2005 CESGRANRIO)
Considere os dados amostrais de um estudo
da relação entre o número de anos que os candidatos a empregos em um
determinado banco comercial estudaram inglês na faculdade e as notas
obtidas em um teste de proficiência nessa língua.
Com base nessas informações, a reta de mínimos quadrados que melhor
explica a relação entre o número de anos de estudo e a nota do teste de inglês
é igual a:
(A) y = 1,33 + 3,56x

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
25
(B) y = 2,25 + 1,32x
(C) y = 6,97 + 3,56x
(D) y = 35,32 + 10,9x
(E) y = 254,56 + 13,3x
Resolução
Nas questões anteriores, o enunciado sempre fornecia diversos somatórios,
para facilitar o trabalho braçal. Isto não aconteceu nesta questão. Ou seja,
para calcular a reta de regressão, precisaríamos fazer todas as contas na mão,
o que toma muito tempo.
Talvez por este motivo a questão apresente alternativas muito diferentes entre
si.
Observem que, para qualquer valor de x entre 2 e 5, y não supera 10. Já
podemos descartar as alternativas C, D, E, que prevêem valores altos para y
(muito superiores a 10), mesmo quando x é baixo.
Para se ter uma idéia, considere a letra E. Se fizermos x igual a 1, y será
aproximadamente igual a 270, algo totalmente incompatível com a tabela
fornecida.
Ficamos entre as alternativas A e B. Para escolher entre ambas, vamos
trabalhar com os valores extremos de x. Quando x é igual a 2, as retas das
letras A e B prevêem os seguintes valores para y:
Letra A: 8,45
Letra B: 4,89
Observem que o valor da Letra B é muito mais próximo dos valores que y
realmente assume, quando x é igual a 2. Já dá para marcar letra B.
Se você ainda ficar em dúvida, pode fazer o mesmo teste para x igual a 5.
Neste caso, as estimativas seriam:
Letra A: 19,13
Letra B: 8,85
Novamente, a estimativa da letra B foi bem melhor.
Letra B
14. (TJ PARÁ 2009 FCC) Em uma determinada empresa é realizado um estudo
sobre a relação entre os gastos com publicidade, em R$ 1.000,00, e o
acréscimo no faturamento anual, em R$ 1.000,00. Foi escolhido para análise o
modelo linear simples Yi = α + βXi + εi, sendo que Yi é o acréscimo no
faturamento do ano i, Xi representa os gastos com publicidade no ano i e εi é o
erro aleatório com as respectivas hipóteses consideradas para a regressão
linear simples (α e β são parâmetros desconhecidos ). Para obtenção das

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
26
estimativas de α e β utilizou-se o método dos mínimos quadrados com base
nas informações dos últimos 10 anos da empresa, ou seja:
180
10
1
=
∑
=
i
i
Y
;
100
10
1
=
∑
=
i
i
X
;
912
.
1
10
1
=
∑
=
i
i
i
Y
X
;
080
.
1
10
1
2
=
∑
=
i
i
X
;
440
.
3
10
1
2
=
∑
=
i
i
Y
Utilizando a equação da reta obtida pelo método dos mínimos quadrados, tem-
se que se a empresa almejar um acréscimo no faturamento, em um
determinado ano, de R$ 25.000,00 deverá apresentar, neste período, um total
em gastos com publicidade de
(A) R$ 20.000,00.
(B) R$ 18.000,00.
(C) R$ 17.000,00.
(D) R$ 16.000,00.
(E) R$ 15.000,00.
Resolução:
4
,
1
1000
1080
1800
1912
=
−
−
=
b
4
10
4
,
1
18
=
×
−
=
a
Modelo:
X
Y
4
,
1
4
ˆ
+
=
15
4
,
1
4
25
=
⇒
+
=
X
X
Letra E
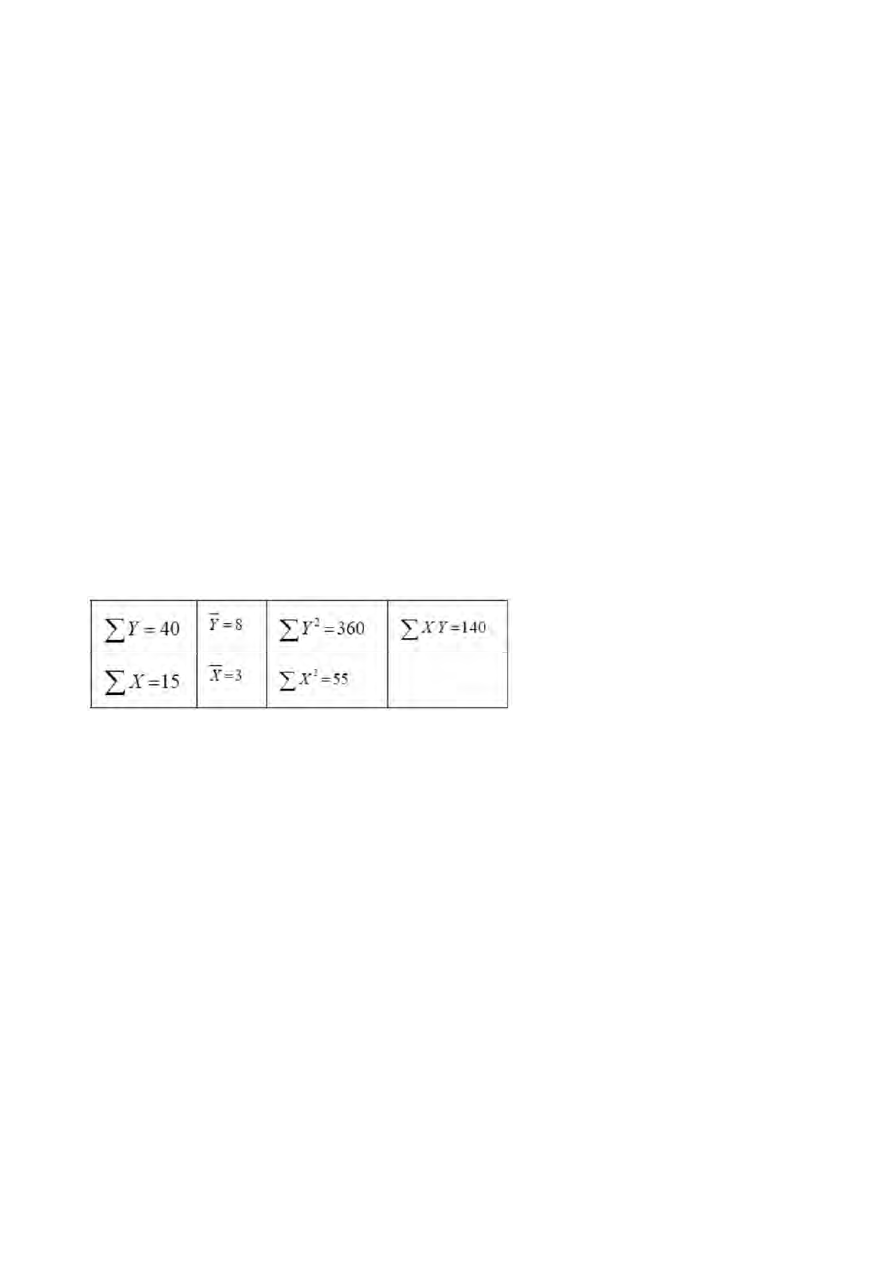
15. (MPOG 2006 ESAF)
Com o objetivo de estimar-se o modelo Y = α + β X, foi
retirada uma amostra com cinco pares de observações (X,Y), obtendo-se os
seguintes resultados:
Desse modo,
a) Y = – 2 – 2X
b) Y = 2 – 2X

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
27
c) Y = 2X
d) Y = 2 + 2X
e) Y = – 2 + 2X
Resolução:
(
)
( )
2
10
20
45
55
120
140
3
5
55
8
3
5
140
2
2
2
=
=
−
−
=
⋅
−
⋅
⋅
−
=
−
−
=
∑
∑
X
n
X
Y
X
n
Y
X
i
i
i
β
2
3
2
8
=
⋅
−
=
−
=
X
b
Y
α
Assim, Y = α + β X=2+2x
Letra D
Relação das questões comentadas
01. (CAPES 2008 CESGRANRIO) Considere as asserções a seguir.
O Coeficiente de Correlação Linear de Pearson é necessariamente um número
no intervalo
)
1
,
1
(
−
.
PORQUE
O Coeficiente de Correlação Linear de Pearson só pode ser calculado para
variáveis quantitativas.
Analisando-se as asserções, conclui-se que
(A) as duas asserções são verdadeiras, e a segunda é uma justificativa correta
da primeira.
(B) as duas asserções são verdadeiras, e a segunda não é uma justificativa
correta da primeira.
(C) a primeira asserção é verdadeira, e a segunda é falsa.
(D) a primeira asserção é falsa, e a segunda é verdadeira.
(E) a primeira e a segunda asserções são falsas.
02. (INEP 2008 CESGRANRIO) Considere as afirmações a seguir a respeito do
Coeficiente de Correlação (r) de Pearson entre duas variáveis.
I - Se r = 1, as observações estão todas sobre uma linha reta no diagrama de
dispersão.
II - Se r > 0, a variável independente aumenta quando a variável dependente
aumenta.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
28
III - Se r < 0, a variável independente decresce quando a variável dependente
decresce.
IV - Se r = 0, não existe relação entre as duas variáveis.
São corretas APENAS as afirmações
(A) I e II
(B) I e III
(C) II e III
(D) II e IV
(E) III e IV
03. (TCU 2008 CESPE-UnB) Uma agência de desenvolvimento urbano divulgou
os dados apresentados na tabela
a seguir, acerca dos números de imóveis ofertados (X) e vendidos (Y) em
determinado município, nos anos de 2005 a 2007.
Ano
Número de imóveis
Ofertados (X)
Vendidos (Y)
2005
1.500
100
2006
1.750
400
2007
2.000
700
Considerando as informações do texto, julgue o item subseqüente.
O coeficiente de correlação linear entre X e Y é inferior a 0,8.
04. (AFRF 2005 ESAF) Para uma amostra de dez casais residentes em um
mesmo bairro, registraram-se os seguintes salários mensais (em salários
mínimos):
Identificação
do casal
1
2
3
4
5
6
7
8
9 10
Salário do
marido (Y)
30 25 18 15 20 20 21 20 25 27
Salário da
esposa (X)
20 25 12 10 10 20 18 15 18 23
Sabe-se que:
221
10
1
=
∑
=
i
i
Y
;
5069
10
1
2
=
∑
=
i
i
Y
171
10
1
=
∑
=
i
i
X
;
3171
10
1
2
=
∑
=
i
i
X
3940
10
1
=
∑
=
i
i
i
Y
X
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
29
Assinale a opção cujo valor corresponda à correlação entre os salários dos
homens e das mulheres.
a) 0,72
b) 0,75
c) 0,68
d) 0,81
e) 0,78
05. (Instituto de Gestão Previdenciária do Estado do Pará – 2005 CESPE-UnB)
Considere que r(x,y) seja o coeficiente de correlação entre duas variáveis
aleatórias x e y. Nesse caso, se ‘a’ e ‘b’ são dois números reais, então o
coeficiente de correlação r(ax, by) é igual a:
a)
)
,
(
y
x
r
ab ×
b)
)
,
(
2
2
y
x
r
b
a
×
c)
)
,
(
y
x
r
, se
0
>
ab
d)
)
,
(
y
x
r
b
a
ab
×
+
e)
ab
y
x
r
)
,
(
06. (CAPES 2008 CESGRANRIO)
Se as variáveis
Y
e
1
X forem transformadas, respectivamente, para
5
,
0
2
1
+
−
=
Y
Y
e
5
,
0
'
1
1
+
−
= X
X
, o coeficiente de correlação entre
1
Y e
'
1
X
(A) 0,382
(B) 0,059

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
30
(C) - 0,059
(D) - 0,118
(E) - 0,382
07. (MP RO 2005 CESGRANRIO) Analise as afirmativas a seguir, a respeito do
coeficiente de correlação linear de Pearson entre duas variáveis positivas X e
Y
:
I - é positivo;
II - não se altera quando adicionamos uma constante positiva aos valores de
X
;
III - não se altera quando multiplicamos por uma constante positiva os valores
de X.
Está(ão) correta(s) a(s) afirmativa(s):
(A) II somente.
(B) I e II somente.
(C) I e III somente.
(D) II e III somente.
(E) I, II e III.
08. (Petrobrás 2004 CESPE-UnB) Julgue o item que segue:
O coeficiente de correlação de Pearson é usado para medir o grau de
linearidade (associação) entre duas variáveis (eventos), podendo assumir
qualquer valor entre +1 e –1. Os valores de coeficientes iguais a +1 e -1
indicam, respectivamente, relação linear perfeita e ausência total de relação
linear entre as variáveis.
09. (Prefeitura de Rio Branco CESPE-UnB) A análise de regressão linear
simples e a análise de correlação são técnicas freqüentemente usadas na
interpretação de pares de dados. Com relação a essas técnicas, julgue o item a
seguir.
O coeficiente de correlação mede o grau de associação entre duas variáveis.
10. (PETROBRAS 2008/2 CESGRANRIO) Na estimativa de uma regressão
linear, o problema da heterocedasticidade ocorre quando
(A) os dados são transversais.
(B) há autorrelação dos resíduos.
(C) há correlação positiva entre as variáveis independentes.
(D) a variância dos erros não é constante.
(E) as variáveis independentes são negativas.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
31
11. (BACEN – 2006 FCC) Uma empresa, com finalidade de determinar a
relação entre gastos anuais com propaganda (X), em R$ 1.000,00 e o lucro
bruto anual (Y), em R$ 1.000,00, optou por utilizar o modelo linear simples
i
i
i
X
Y
ε
β
α
+
+
=
, em que
i
Y é o valor do lucro bruto auferido no ano i e
i
ε
o erro
aleatório com as respectivas hipóteses consideradas para a regressão linear
simples (
α
e β são parâmetros desconhecidos). Considerou, para o estudo, as
seguintes informações referentes às observações nos últimos 10 anos da
empresa:
100
10
1
=
∑
=
i
i
Y
;
60
10
1
=
∑
=
i
i
X
;
650
=
×
∑
i
i
Y
X
;
( )
400
10
1
2
=
∑
=
i
i
X
;
( )
1080
10
1
2
=
∑
=
i
i
Y
Utilizando a equação da reta obtida pelo método dos mínimos quadrados, tem-
se que, caso haja um gasto anual com propaganda de 80 mil reais, a previsão
do lucro bruto anual, em mil reais, será de:
a) 84
b) 102,5
c) 121
d) 128,4
e) 158
12. (SEFAZ SP 2006 FCC) Em um determinado país, deseja-se determinar a
relação entre a renda disponível (Y), em bilhões de dólares, e o consumo (C),
também em bilhões de dólares. Foi utilizado o modelo linear simples
i
i
i
Y
C
ε
β
α
+
+
=
, em que C
i
é o consumo no ano i, Y
i
é o valor da renda
disponível no ano i e
i
ε
o erro aleatório com as respectivas hipóteses para a
regressão linear simples,
α
e β são parâmetros desconhecidos, cujas
estimativas foram obtidas através do método dos mínimos quadrados. Para
obtenção desta relação considerou-se ainda as seguintes informações colhidas
através da observação nos últimos 10 anos:
∑
=
=
10
1
90
i
i
C
,
∑
=
=
10
1
100
i
i
Y
,
∑
=
=
10
1
100
.
1
i
i
i
C
Y
,
∑
=
=
10
1
2
250
.
1
i
i
Y
,
∑
=
=
10
1
2
010
.
1
i
i
C
Para o cálculo do coeficiente de correlação de Pearson (r), usou-se a fórmula:
)
(
)
(
)
,
cov(
C
DP
y
DP
C
Y
r
×
=
em que
)
,
cov(
C
Y
é a covariância entre Y e C,
)
(Y
DP
é o desvio
padrão de Y e
)
(C
DP
é o desvio padrão de C.
Então:
a) obtendo para um determinado ano uma previsão para o consumo de 10
bilhões de dólares, significa que a renda disponível considerada foi de 12,5
bilhões de dólares.
b) o valor da estimativa encontrado para o parâmetro β é igual a 0,4
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
32
c) o valor da estimativa encontrado para o parâmetro
α
é igual a 10.
d) o coeficiente de explicação r
2
correspondente é 64%.
e) utilizando a equação da reta obtida pelo método dos mínimos quadrados,
tem-se que, em um ano, caso a renda disponível seja igual a 15 bilhões de
dólares, o consumo será igual a 13 bilhões de dólares.
13. (MP RO 2005 CESGRANRIO)
Considere os dados amostrais de um estudo
da relação entre o número de anos que os candidatos a empregos em um
determinado banco comercial estudaram inglês na faculdade e as notas obtidas
em um teste de proficiência nessa língua.
Com base nessas informações, a reta de mínimos quadrados que melhor
explica a relação entre o número de anos de estudo e a nota do teste de inglês
é igual a:
(A) y = 1,33 + 3,56x
(B) y = 2,25 + 1,32x
(C) y = 6,97 + 3,56x
(D) y = 35,32 + 10,9x
(E) y = 254,56 + 13,3x
14. (TJ PARÁ 2009 FCC) Em uma determinada empresa é realizado um estudo
sobre a relação entre os gastos com publicidade, em R$ 1.000,00, e o
acréscimo no faturamento anual, em R$ 1.000,00. Foi escolhido para análise o
modelo linear simples Yi = α + βXi + εi, sendo que Yi é o acréscimo no
faturamento do ano i, Xi representa os gastos com publicidade no ano i e εi é o
erro aleatório com as respectivas hipóteses consideradas para a regressão
linear simples (α e β são parâmetros desconhecidos ). Para obtenção das
estimativas de α e β utilizou-se o método dos mínimos quadrados com base
nas informações dos últimos 10 anos da empresa, ou seja:
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
33
180
10
1
=
∑
=
i
i
Y
;
100
10
1
=
∑
=
i
i
X
;
912
.
1
10
1
=
∑
=
i
i
i
Y
X
;
080
.
1
10
1
2
=
∑
=
i
i
X
;
440
.
3
10
1
2
=
∑
=
i
i
Y
Utilizando a equação da reta obtida pelo método dos mínimos quadrados, tem-
se que se a empresa almejar um acréscimo no faturamento, em um
determinado ano, de R$ 25.000,00 deverá apresentar, neste período, um total
em gastos com publicidade de
(A) R$ 20.000,00.
(B) R$ 18.000,00.
(C) R$ 17.000,00.
(D) R$ 16.000,00.
(E) R$ 15.000,00.
15. (MPOG 2006 ESAF)
Com o objetivo de estimar-se o modelo Y = α + β X, foi
retirada uma amostra com cinco pares de observações (X,Y), obtendo-se os
seguintes resultados:
Desse modo,
a) Y = – 2 – 2X
b) Y = 2 – 2X
c) Y = 2X
d) Y = 2 + 2X
e) Y = – 2 + 2X

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
34
Gabaritos
01. B
02. A
03. Errado
04. B
05. C
06. C
07. D
08. Errado
09. Certo
10. D
11. B
12. E
13. B
14. E
15. D
Wyszukiwarka
Podobne podstrony:
Aula 14 Parte 02
Aula 07 Parte 02
Aula 15 Parte 02
Aula 05 Parte 02
Aula 09 Parte 02
Aula 14 Parte 01
Aula 10 Parte 02
Aula 07 Parte 02
Aula 06 Parte 02
Aula 12 Parte 02
Aula 08 Parte 02
Aula 07 Parte 02
Aula 15 Parte 02
Aula 05 Parte 02
Aula 14 Parte 01
Aula 08 Parte 02
Aula 07 Parte 02
Aula 09 Parte 02
więcej podobnych podstron